បង្កើតសមាមាត្រនិងគណនាដែនកំណត់.
តើវាមកពីណា? តារាងនៃនិស្សន្ទវត្ថុ និងច្បាប់ភាពខុសគ្នា? សូមអរគុណដល់ដែនកំណត់តែមួយគត់។ វាហាក់ដូចជាវេទមន្ត ប៉ុន្តែតាមពិតវាជាដៃតូច ហើយមិនមានការក្លែងបន្លំឡើយ។ នៅមេរៀន តើអ្វីជានិស្សន្ទវត្ថុ?ខ្ញុំចាប់ផ្តើមមើលឧទាហរណ៍ជាក់លាក់ដែលដោយប្រើនិយមន័យ ខ្ញុំបានរកឃើញដេរីវេនៃអនុគមន៍លីនេអ៊ែរ និងចតុកោណ។ សម្រាប់គោលបំណងនៃការឡើងកំដៅនៃការយល់ដឹង យើងនឹងបន្តរំខាន តារាងនៃនិស្សន្ទវត្ថុដោយគោរពក្បួនដោះស្រាយ និងដំណោះស្រាយបច្ចេកទេស៖
ឧទាហរណ៍ ១
ជាសំខាន់ អ្នកត្រូវបញ្ជាក់ករណីពិសេសនៃដេរីវេនៃអនុគមន៍ថាមពល ដែលជាធម្មតាលេចឡើងក្នុងតារាង៖ .
ដំណោះស្រាយបច្ចេកទេសជាផ្លូវការតាមពីរវិធី។ ចូរចាប់ផ្តើមជាមួយនឹងវិធីសាស្រ្តដំបូងដែលធ្លាប់ស្គាល់រួចមកហើយ៖ ជណ្ដើរចាប់ផ្តើមដោយបន្ទះក្តារ ហើយមុខងារដេរីវេចាប់ផ្តើមដោយដេរីវេនៅចំនុចមួយ។
ចូរយើងពិចារណា ខ្លះ(ជាក់លាក់) ចំណុចដែលជាកម្មសិទ្ធិ ដែននៃនិយមន័យមុខងារដែលមានដេរីវេ។ ចូរយើងកំណត់ការកើនឡើងនៅចំណុចនេះ។ (ជាការពិតណាស់នៅក្នុងវិសាលភាពo/o
-ខ្ញុំ)និងបង្កើតការបង្កើនមុខងារដែលត្រូវគ្នា៖
តោះគណនាដែនកំណត់៖
ភាពមិនប្រាកដប្រជា 0:0 ត្រូវបានលុបចោលដោយបច្ចេកទេសស្ដង់ដារ ដែលត្រូវបានពិចារណាក្នុងសតវត្សទីមួយមុនគ.ស។ គុណភាគយក និងភាគបែងដោយកន្សោមរួម ![]() :
:
បច្ចេកទេសសម្រាប់ដោះស្រាយដែនកំណត់បែបនេះត្រូវបានពិភាក្សាលម្អិតនៅក្នុងមេរៀនណែនាំ។ អំពីដែនកំណត់នៃមុខងារ.
ដោយសារអ្នកអាចជ្រើសរើសចំណុចណាមួយនៃចន្លោះពេលជាគុណភាព នោះដោយបានធ្វើការជំនួស យើងទទួលបាន៖
ចម្លើយ
ជាថ្មីម្តងទៀត សូមរីករាយជាមួយលោការីត៖
ឧទាហរណ៍ ២
ស្វែងរកដេរីវេនៃអនុគមន៍ដោយប្រើនិយមន័យនៃដេរីវេ
ដំណោះស្រាយ៖ សូមពិចារណាវិធីផ្សេងមួយដើម្បីលើកកម្ពស់កិច្ចការដូចគ្នា។ វាគឺដូចគ្នាបេះបិទ ប៉ុន្តែសមហេតុផលជាងនៅក្នុងលក្ខខណ្ឌនៃការរចនា។ គំនិតគឺដើម្បីកម្ចាត់ subscript នៅដើមនៃដំណោះស្រាយហើយប្រើអក្សរជំនួសឱ្យអក្សរ។
ចូរយើងពិចារណា បំពានចំណុចដែលជាកម្មសិទ្ធិរបស់ ដែននៃនិយមន័យមុខងារ (ចន្លោះពេល) ហើយកំណត់ការបន្ថែមនៅក្នុងវា។ ប៉ុន្តែនៅទីនេះ ដោយវិធីនេះ ដូចក្នុងករណីភាគច្រើន អ្នកអាចធ្វើបានដោយគ្មានការកក់ទុក ចាប់តាំងពីអនុគមន៍លោការីតគឺអាចខុសគ្នាត្រង់ចំណុចណាមួយនៅក្នុងដែននៃនិយមន័យ។
បន្ទាប់មកការបង្កើនមុខងារដែលត្រូវគ្នាគឺ៖
ចូរយើងស្វែងរកដេរីវេ៖
ភាពសាមញ្ញនៃការរចនាគឺមានតុល្យភាពដោយការយល់ច្រលំដែលអាចកើតឡើងសម្រាប់អ្នកចាប់ផ្តើមដំបូង (និងមិនត្រឹមតែប៉ុណ្ណោះ) ។ យ៉ាងណាមិញ យើងធ្លាប់ដឹងពីការពិតដែលថាអក្សរ “X” ផ្លាស់ប្តូរនៅក្នុងដែនកំណត់! ប៉ុន្តែនៅទីនេះអ្វីៗគឺខុសគ្នា៖ - រូបសំណាកបុរាណមួយ និង - អ្នកទស្សនានៅរស់ ដើរយ៉ាងលឿនតាមច្រករបៀងនៃសារមន្ទីរ។ នោះគឺ "x" គឺ "ដូចជាថេរ" ។
ខ្ញុំនឹងធ្វើអត្ថាធិប្បាយលើការលុបបំបាត់ភាពមិនច្បាស់លាស់ជាជំហានៗ៖

(1) យើងប្រើទ្រព្យសម្បត្តិរបស់លោការីត។
(2) ក្នុងវង់ក្រចក ចែកភាគយកដោយភាគបែងដោយពាក្យ។
(3) ក្នុងភាគបែង យើងគុណ និងចែកដោយ "x" សិប្បនិម្មិត ដើម្បីទាញយកប្រយោជន៍ពី ដែនកំណត់គួរឱ្យកត់សម្គាល់ ![]() ខណៈពេលដែលជា គ្មានដែនកំណត់ឈរចេញ។
ខណៈពេលដែលជា គ្មានដែនកំណត់ឈរចេញ។
ចម្លើយ៖ តាមនិយមន័យនៃដេរីវេ៖
ឬនិយាយឱ្យខ្លី៖
ខ្ញុំស្នើឱ្យបង្កើតរូបមន្តតារាងពីរបន្ថែមទៀតដោយខ្លួនឯង៖
ឧទាហរណ៍ ៣
ក្នុងករណីនេះ វាជាការងាយស្រួលក្នុងការកាត់បន្ថយភ្លាមៗនូវការកើនឡើងដែលបានចងក្រងទៅជាភាគបែងរួម។ គំរូប្រហាក់ប្រហែលនៃកិច្ចការនៅចុងបញ្ចប់នៃមេរៀន (វិធីសាស្ត្រទីមួយ)។
ឧទាហរណ៍ 3៖ដំណោះស្រាយ
៖ ពិចារណាចំណុចខ្លះ
ជាកម្មសិទ្ធិរបស់ដែននិយមន័យនៃមុខងារ
. ចូរយើងកំណត់ការកើនឡើងនៅចំណុចនេះ។
និងបង្កើតការបង្កើនមុខងារដែលត្រូវគ្នា៖
ចូរយើងស្វែងរកដេរីវេនៅចំណុច
:
ចាប់តាំងពី ក
អ្នកអាចជ្រើសរើសចំណុចណាមួយ។
ដែនមុខងារ
, នោះ។
និង
ចម្លើយ
:
តាមនិយមន័យនៃដេរីវេ
ឧទាហរណ៍ 4
ស្វែងរកដេរីវេតាមនិយមន័យ
ហើយនៅទីនេះអ្វីគ្រប់យ៉ាងត្រូវកាត់បន្ថយ ដែនកំណត់ដ៏អស្ចារ្យ. ដំណោះស្រាយត្រូវបានធ្វើជាផ្លូវការតាមវិធីទីពីរ។
មួយចំនួនទៀត។ ដេរីវេនៃតារាង. បញ្ជីពេញលេញអាចរកបាននៅក្នុងសៀវភៅសិក្សារបស់សាលា ឬឧទាហរណ៍ ភាគទី 1 នៃ Fichtenholtz ។ ខ្ញុំមិនឃើញចំណុចច្រើនទេក្នុងការចម្លងភស្តុតាងនៃច្បាប់នៃភាពខុសគ្នាពីសៀវភៅ - ពួកគេក៏ត្រូវបានបង្កើតដោយរូបមន្តផងដែរ។
ឧទាហរណ៍ទី ៤៖ដំណោះស្រាយ
, ជាកម្មសិទ្ធិរបស់
ហើយកំណត់ចំនួនបន្ថែមនៅក្នុងវា។
ចូរយើងស្វែងរកដេរីវេ៖
ការប្រើប្រាស់ដែនកំណត់ដ៏អស្ចារ្យ
ចម្លើយ
:
a-priory
ឧទាហរណ៍ 5
ស្វែងរកដេរីវេនៃអនុគមន៍ដោយប្រើនិយមន័យនៃដេរីវេ
ដំណោះស្រាយ៖ យើងប្រើរចនាប័ទ្មរចនាដំបូង។ ចូរយើងពិចារណាចំណុចមួយចំនួនដែលជាកម្មសិទ្ធិរបស់ ហើយបញ្ជាក់ការបន្ថែមនៃអាគុយម៉ង់នៅវា។ បន្ទាប់មកការបង្កើនមុខងារដែលត្រូវគ្នាគឺ៖
ប្រហែលជាអ្នកអានមួយចំនួនមិនទាន់បានយល់ច្បាស់អំពីគោលការណ៍ដែលការបង្កើនចាំបាច់ត្រូវធ្វើនោះទេ។ យកចំណុចមួយ (លេខ) ហើយរកតម្លៃនៃមុខងារនៅក្នុងវា៖ ![]() នោះគឺចូលទៅក្នុងមុខងារ ជំនួសអោយ"X" គួរតែត្រូវបានជំនួស។ ឥឡូវនេះ យើងក៏យកលេខជាក់លាក់មួយ ហើយជំនួសវាទៅក្នុងមុខងារ ជំនួសអោយ"iksa": ។ យើងសរសេរភាពខុសគ្នា ហើយវាចាំបាច់ ដាក់ទាំងស្រុងនៅក្នុងតង្កៀប.
នោះគឺចូលទៅក្នុងមុខងារ ជំនួសអោយ"X" គួរតែត្រូវបានជំនួស។ ឥឡូវនេះ យើងក៏យកលេខជាក់លាក់មួយ ហើយជំនួសវាទៅក្នុងមុខងារ ជំនួសអោយ"iksa": ។ យើងសរសេរភាពខុសគ្នា ហើយវាចាំបាច់ ដាក់ទាំងស្រុងនៅក្នុងតង្កៀប.
ការបង្កើនមុខងារដែលបានចងក្រង វាអាចមានប្រយោជន៍ក្នុងការធ្វើឱ្យសាមញ្ញភ្លាមៗ. ដើម្បីអ្វី? សម្របសម្រួល និងកាត់បន្ថយដំណោះស្រាយឱ្យនៅកម្រិតមួយបន្ថែមទៀត។
យើងប្រើរូបមន្ត បើកតង្កៀប និងកាត់បន្ថយអ្វីគ្រប់យ៉ាងដែលអាចកាត់បន្ថយបាន៖ 
ទួរគីត្រូវខ្ទេចគ្មានបញ្ហាជាមួយនឹងសាច់អាំងទេ៖
ដោយសារយើងអាចជ្រើសរើសចំនួនពិតណាមួយជាតម្លៃ យើងធ្វើការជំនួស និងទទួលបាន ![]() .
.
ចម្លើយ: ![]() a-priory ។
a-priory ។
សម្រាប់គោលបំណងផ្ទៀងផ្ទាត់ ចូរស្វែងរកដេរីវេដោយប្រើ តារាងនិងច្បាប់នៃការបែងចែក:
វាតែងតែមានប្រយោជន៍ និងរីករាយក្នុងការដឹងចម្លើយត្រឹមត្រូវជាមុន ដូច្នេះវាជាការប្រសើរក្នុងការបែងចែកមុខងារដែលបានស្នើឡើងតាមរបៀប "រហ័ស" ទាំងផ្លូវចិត្ត ឬក្នុងសេចក្តីព្រាង នៅដើមដំបូងនៃដំណោះស្រាយ។
ឧទាហរណ៍ ៦
ស្វែងរកដេរីវេនៃអនុគមន៍តាមនិយមន័យនៃដេរីវេ
នេះជាឧទាហរណ៍សម្រាប់អ្នកដោះស្រាយដោយខ្លួនឯង។ លទ្ធផលគឺជាក់ស្តែង៖
ឧទាហរណ៍ ៦៖ដំណោះស្រាយ
៖ ពិចារណាចំណុចខ្លះ
, ជាកម្មសិទ្ធិរបស់
ហើយកំណត់ការបន្ថែមនៃអាគុយម៉ង់នៅក្នុងវា។
. បន្ទាប់មកការបង្កើនមុខងារដែលត្រូវគ្នាគឺ៖

ចូរយើងគណនាដេរីវេ៖

ដូចនេះ៖ ![]()
ដោយសារតែដូច
បន្ទាប់មក អ្នកអាចជ្រើសរើសលេខពិតណាមួយ។
និង
ចម្លើយ
:
a-priory ។
តោះត្រឡប់ទៅរចនាប័ទ្មលេខ 2៖
ឧទាហរណ៍ ៧
![]()
ចូរយើងស្វែងយល់ភ្លាមៗនូវអ្វីដែលគួរកើតឡើង។ ដោយ ច្បាប់នៃភាពខុសគ្នានៃមុខងារស្មុគស្មាញ:
ដំណោះស្រាយ៖ ពិចារណាចំណុចបំពានដែលជាកម្មសិទ្ធិរបស់ កំណត់ការកើនឡើងនៃអាគុយម៉ង់នៅវា ហើយសរសេរការបង្កើនមុខងារ៖
ចូរយើងស្វែងរកដេរីវេ៖ 
(1) ប្រើ រូបមន្តត្រីកោណមាត្រ ![]() .
.
(2) នៅក្រោមស៊ីនុស យើងបើកតង្កៀប នៅក្រោមកូស៊ីនុស យើងបង្ហាញពាក្យស្រដៀងគ្នា។
(3) នៅក្រោមស៊ីនុស យើងកាត់បន្ថយពាក្យ នៅក្រោមកូស៊ីនុស យើងបែងចែកភាគយកដោយភាគបែងដោយពាក្យ។
(4) ដោយសារតែភាពចម្លែកនៃស៊ីនុស យើងដក "ដក" ចេញ។ នៅក្រោមកូស៊ីនុស យើងបង្ហាញថាពាក្យ .
(5) យើងអនុវត្តការគុណសិប្បនិម្មិតនៅក្នុងភាគបែងដើម្បីប្រើប្រាស់ ដែនកំណត់ដ៏អស្ចារ្យដំបូង. ដូច្នេះហើយ ភាពមិនប្រាកដប្រជាត្រូវបានលុបចោល ចូរយើងរៀបចំលទ្ធផល។
ចម្លើយ៖ a-priory
ដូចដែលអ្នកអាចឃើញការលំបាកចម្បងនៃបញ្ហាដែលកំពុងពិចារណាគឺស្ថិតនៅលើភាពស្មុគស្មាញនៃដែនកំណត់ខ្លួនឯង + ភាពប្លែកបន្តិចនៃការវេចខ្ចប់។ នៅក្នុងការអនុវត្ត វិធីសាស្រ្តទាំងពីរនៃការរចនាកើតឡើង ដូច្នេះខ្ញុំរៀបរាប់អំពីវិធីសាស្រ្តទាំងពីរនេះឱ្យបានលម្អិតតាមដែលអាចធ្វើទៅបាន។ ពួកវាគឺសមមូល ប៉ុន្តែនៅតែក្នុងចំណាប់អារម្មណ៏ជាប្រធានបទរបស់ខ្ញុំ វាជាការគួរសមសម្រាប់អ្នកដែលអត់ចេះសោះក្នុងការប្រកាន់ភ្ជាប់ជម្រើសទី 1 ជាមួយ "X-zero"។
ឧទាហរណ៍ ៨
ដោយប្រើនិយមន័យ ស្វែងរកដេរីវេនៃអនុគមន៍
ឧទាហរណ៍ ៨៖ដំណោះស្រាយ
៖ ពិចារណាចំណុចដែលបំពាន
, ជាកម្មសិទ្ធិរបស់
កំណត់ការបង្កើននៅក្នុងវា។
និងបង្កើតការបង្កើនមុខងារ៖
ចូរយើងស្វែងរកដេរីវេ៖

យើងប្រើរូបមន្តត្រីកោណមាត្រ
និងដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង:

ចម្លើយ
:
a-priory
សូមក្រឡេកមើលកំណែដ៏កម្រនៃបញ្ហា៖
ឧទាហរណ៍ ៩
ស្វែងរកដេរីវេនៃអនុគមន៍នៅចំណុចដោយប្រើនិយមន័យនៃដេរីវេ។
ទីមួយ តើអ្វីគួរជាចំណុចសំខាន់? ចំនួន
ចូរយើងគណនាចម្លើយតាមវិធីស្តង់ដារ៖ 
ដំណោះស្រាយ៖ តាមទស្សនៈច្បាស់លាស់ កិច្ចការនេះគឺសាមញ្ញជាង ដោយសាររូបមន្តនេះចាត់ទុកតម្លៃជាក់លាក់មួយជំនួសវិញ។
ចូរកំណត់ការបន្ថែមនៅចំណុច ហើយសរសេរការបង្កើនដែលត្រូវគ្នានៃមុខងារ៖
ចូរយើងគណនាដេរីវេនៅចំណុច៖
យើងប្រើរូបមន្តភាពខុសគ្នាតង់សង់ដ៏កម្រមួយ។ ![]() ហើយម្តងទៀតយើងកាត់បន្ថយដំណោះស្រាយទៅ ដែនកំណត់ដ៏អស្ចារ្យដំបូង:
ហើយម្តងទៀតយើងកាត់បន្ថយដំណោះស្រាយទៅ ដែនកំណត់ដ៏អស្ចារ្យដំបូង:
ចម្លើយ៖ តាមនិយមន័យនៃដេរីវេនៅចំណុចមួយ។
បញ្ហាគឺមិនពិបាកទេក្នុងការដោះស្រាយ "ជាទូទៅ" - វាគ្រប់គ្រាន់ដើម្បីជំនួសឬគ្រាន់តែអាស្រ័យលើវិធីសាស្ត្ររចនា។ ក្នុងករណីនេះ វាច្បាស់ណាស់ថា លទ្ធផលនឹងមិនមែនជាលេខទេ ប៉ុន្តែជាមុខងារដែលទទួលបាន។
ឧទាហរណ៍ 10
ដោយប្រើនិយមន័យ ស្វែងរកដេរីវេនៃអនុគមន៍ ![]() នៅចំណុចមួយ (មួយក្នុងចំណោមនោះអាចនឹងក្លាយទៅជាគ្មានកំណត់) ដែលខ្ញុំបានពិពណ៌នារួចហើយក្នុងពាក្យទូទៅលើ មេរៀនទ្រឹស្តីអំពីដេរីវេ.
នៅចំណុចមួយ (មួយក្នុងចំណោមនោះអាចនឹងក្លាយទៅជាគ្មានកំណត់) ដែលខ្ញុំបានពិពណ៌នារួចហើយក្នុងពាក្យទូទៅលើ មេរៀនទ្រឹស្តីអំពីដេរីវេ.
អនុគមន៍ដែលបានផ្តល់ឱ្យជាដុំៗខ្លះក៏អាចខុសគ្នានៅចំណុច "ប្រសព្វ" នៃក្រាហ្វ ឧទាហរណ៍ catdog មានដេរីវេរួម និងតង់សង់ទូទៅ (អ័ក្ស x) នៅចំណុច។ កោង ប៉ុន្តែអាចខុសគ្នាដោយ ! អ្នកដែលចាប់អារម្មណ៍អាចផ្ទៀងផ្ទាត់វាដោយខ្លួនឯងដោយប្រើឧទាហរណ៍ដែលទើបតែដោះស្រាយ។
© 2015-2019 គេហទំព័រ
សិទ្ធិទាំងអស់ជាកម្មសិទ្ធិរបស់អ្នកនិពន្ធ។ គេហទំព័រនេះមិនទាមទារភាពជាអ្នកនិពន្ធទេ ប៉ុន្តែផ្តល់ការប្រើប្រាស់ដោយឥតគិតថ្លៃ។
កាលបរិច្ឆេទបង្កើតទំព័រ៖ 2017-06-11
ខ្លឹមសារនៃអត្ថបទ
ដេរីវេ- ដេរីវេនៃមុខងារ y = f(x) ដែលបានផ្តល់ឱ្យនៅចន្លោះពេលជាក់លាក់មួយ ( ក, ខ) នៅចំណុច xនៃចន្លោះពេលនេះត្រូវបានគេហៅថាដែនកំណត់ដែលសមាមាត្រនៃការកើនឡើងនៃមុខងារមាននិន្នាការ fនៅចំណុចនេះចំពោះការកើនឡើងដែលត្រូវគ្នានៃអាគុយម៉ង់ នៅពេលដែលការកើនឡើងនៃអាគុយម៉ង់មាននិន្នាការទៅសូន្យ។
និស្សន្ទវត្ថុត្រូវបានបញ្ជាក់ជាធម្មតាដូចខាងក្រោមៈ
ការរចនាផ្សេងទៀតក៏ត្រូវបានគេប្រើយ៉ាងទូលំទូលាយផងដែរ:
ល្បឿនភ្លាមៗ។
សូមឱ្យចំណុច មផ្លាស់ទីក្នុងបន្ទាត់ត្រង់មួយ។ ចម្ងាយ សចំណុចផ្លាស់ទី រាប់ពីទីតាំងដំបូងមួយចំនួន ម 0 , អាស្រ័យលើពេលវេលា t, i.e. សមានមុខងារនៃពេលវេលា t: ស= f(t). អនុញ្ញាតឱ្យនៅចំណុចណាមួយនៅក្នុងពេលវេលា tចំណុចផ្លាស់ទី មគឺនៅចម្ងាយ សពីទីតាំងចាប់ផ្តើម ម 0 ហើយនៅពេលបន្ទាប់ t+ ឃ tបានរកឃើញខ្លួនឯងនៅក្នុងទីតាំងមួយ។ ម 1 - នៅចម្ងាយ ស+ ឃ សពីទីតាំងដំបូង ( មើលរូប.).
ដូច្នេះក្នុងរយៈពេលមួយ D tចម្ងាយ សផ្លាស់ប្តូរដោយចំនួន D ស. ក្នុងករណីនេះពួកគេនិយាយថាក្នុងអំឡុងពេលចន្លោះពេល D tរ៉ិចទ័រ សបានទទួលការបង្កើន D ស.
ល្បឿនជាមធ្យមមិនអាចកំណត់បានត្រឹមត្រូវក្នុងគ្រប់ករណីទាំងអស់នៃល្បឿននៃចលនានៃចំណុចមួយ។ មនៅចំណុចមួយនៅក្នុងពេលវេលា t. ប្រសិនបើឧទាហរណ៍រាងកាយនៅដើមនៃចន្លោះពេល D tបានផ្លាស់ទីយ៉ាងលឿន ហើយនៅចុងបញ្ចប់យឺតបំផុត នោះល្បឿនមធ្យមនឹងមិនអាចឆ្លុះបញ្ចាំងពីលក្ខណៈដែលបានចង្អុលបង្ហាញនៃចលនារបស់ចំណុចនោះទេ ហើយផ្តល់គំនិតអំពីល្បឿនពិតនៃចលនារបស់វានៅពេលនេះ។ t. ដើម្បីបង្ហាញឱ្យកាន់តែច្បាស់នូវល្បឿនពិតដោយប្រើល្បឿនមធ្យម អ្នកត្រូវចំណាយពេលខ្លីជាង D t. ភាគច្រើនកំណត់យ៉ាងពេញលេញនូវល្បឿននៃចលនានៃចំណុចមួយនៅពេលនេះ tដែនកំណត់ដែលល្បឿនជាមធ្យមមានទំនោរនៅ D t® 0. ដែនកំណត់នេះត្រូវបានគេហៅថាល្បឿនបច្ចុប្បន្ន៖
ដូច្នេះល្បឿននៃចលនានៅពេលណាមួយត្រូវបានគេហៅថាដែនកំណត់នៃសមាមាត្របង្កើនផ្លូវ D សដល់ការបង្កើនពេលវេលា D tនៅពេលដែលការកើនឡើងពេលវេលាមានទំនោរទៅសូន្យ។ ដោយសារតែ
អត្ថន័យធរណីមាត្រនៃដេរីវេ។ តង់សង់ទៅក្រាហ្វនៃអនុគមន៍។
ការសាងសង់បន្ទាត់តង់សង់គឺជាបញ្ហាមួយក្នុងចំណោមបញ្ហាទាំងនោះដែលនាំឱ្យមានកំណើតនៃការគណនាឌីផេរ៉ង់ស្យែល។ ការងារដែលបានបោះពុម្ពផ្សាយដំបូងទាក់ទងនឹងការគណនាឌីផេរ៉ង់ស្យែលដែលសរសេរដោយ Leibniz មានចំណងជើង វិធីសាស្រ្តថ្មីនៃ maxima និង minima ក៏ដូចជា tangents ដែលមិនមានប្រភាគ ឬ irrational quantity គឺជាឧបសគ្គ ហើយប្រភេទពិសេសនៃ calculus សម្រាប់ការនេះ.
សូមឱ្យខ្សែកោងជាក្រាហ្វនៃអនុគមន៍ y =f(x) នៅក្នុងប្រព័ន្ធកូអរដោណេចតុកោណ ( សង់ទីម៉ែត. អង្ករ។ )
នៅតម្លៃខ្លះ xមុខងារសំខាន់ y =f(x) តម្លៃទាំងនេះ xនិង yចំណុចនៅលើខ្សែកោងត្រូវគ្នា។ ម 0(x, y) ប្រសិនបើអាគុយម៉ង់ xផ្តល់ឱ្យ បង្កើន D xបន្ទាប់មកតម្លៃថ្មីនៃអាគុយម៉ង់ x+ ឃ xត្រូវនឹងតម្លៃមុខងារថ្មី។ y+ឃ y = f(x + ឃ x) ចំណុចដែលត្រូវគ្នានៃខ្សែកោងនឹងជាចំណុច ម 1(x+ ឃ x,y+ ឃ y) ប្រសិនបើអ្នកគូរឃ្លា ម 0ម 1 និងតំណាងដោយ j មុំដែលបង្កើតឡើងដោយការឆ្លងកាត់ដែលមានទិសដៅវិជ្ជមាននៃអ័ក្ស គោពីរូបភាពវាច្បាស់ភ្លាមៗថា .
បើពេលនេះ D xទំនោរទៅសូន្យ បន្ទាប់មកចំណុច ម 1 ផ្លាស់ទីតាមខ្សែកោងទៅជិតចំណុច ម 0 និងមុំ j ការផ្លាស់ប្តូរជាមួយ D x. នៅ Dx® 0 មុំ j ទំនោរទៅដែនកំណត់ជាក់លាក់ a និងបន្ទាត់ត្រង់ឆ្លងកាត់ចំណុច ម 0 និងសមាសធាតុដែលមានទិសដៅវិជ្ជមាននៃអ័ក្ស x មុំ a នឹងជាតង់សង់ដែលចង់បាន។ ជម្រាលរបស់វាគឺ៖
អាស្រ័យហេតុនេះ f´( x) = tga
ទាំងនោះ។ តម្លៃដេរីវេ f´( x) សម្រាប់តម្លៃអាគុយម៉ង់ដែលបានផ្តល់ឱ្យ xស្មើនឹងតង់ហ្សង់នៃមុំដែលបង្កើតឡើងដោយតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ f(x) នៅចំណុចដែលត្រូវគ្នា។ ម 0(x,y) ជាមួយនឹងទិសដៅអ័ក្សវិជ្ជមាន គោ.
ភាពខុសគ្នានៃមុខងារ។
និយមន័យ។ ប្រសិនបើមុខងារ y = f(x) មានដេរីវេនៅចំណុច x = x 0 បន្ទាប់មកមុខងារគឺខុសគ្នានៅចំណុចនេះ។
ការបន្តនៃអនុគមន៍ដែលមានដេរីវេ។ ទ្រឹស្តីបទ។
ប្រសិនបើមុខងារ y = f(x) អាចខុសគ្នាត្រង់ចំណុចខ្លះ x = x 0 បន្ទាប់មកវាបន្តនៅចំណុចនេះ។
ដូច្នេះ អនុគមន៍មិនអាចមានដេរីវេនៅចំនុចដាច់ទេ។ ការសន្និដ្ឋានផ្ទុយគឺមិនត្រឹមត្រូវ, i.e. ពីការពិតដែលថានៅចំណុចណាមួយ។ x = x 0 មុខងារ y = f(x) គឺបន្តមិនមានន័យថាវាខុសគ្នាត្រង់ចំណុចនេះទេ។ ឧទាហរណ៍មុខងារ y = |x| បន្តសម្រាប់មនុស្សគ្រប់គ្នា x(–Ґ x x = 0 មិនមានដេរីវេទេ។ នៅចំណុចនេះមិនមានតង់សង់ទៅក្រាហ្វទេ។ មានតង់សង់ខាងស្តាំ និងខាងឆ្វេង ប៉ុន្តែវាមិនស្របគ្នា។
ទ្រឹស្តីបទខ្លះអំពីមុខងារដែលអាចបែងចែកបាន។ ទ្រឹស្តីបទលើឫសនៃដេរីវេ (ទ្រឹស្តីបទរ៉ូល)។ប្រសិនបើមុខងារ f(x) គឺបន្តនៅលើផ្នែក [ក,ខ] មានភាពខុសប្លែកគ្នានៅគ្រប់ចំណុចខាងក្នុងនៃផ្នែកនេះ និងនៅចុងបញ្ចប់ x = កនិង x = ខទៅសូន្យ ( f(ក) = f(ខ) = 0) បន្ទាប់មកនៅខាងក្នុងផ្នែក [ ក,ខ] យ៉ាងហោចណាស់មានចំណុចមួយ។ x= ជាមួយ, ក c b ដែលក្នុងនោះដេរីវេ fў( x) ទៅសូន្យ, i.e. fў( គ) = 0.
ទ្រឹស្តីបទបង្កើនកម្រិតកំណត់ (ទ្រឹស្តីបទរបស់ Lagrange) ។ប្រសិនបើមុខងារ f(x) គឺបន្តនៅចន្លោះពេល [ ក, ខ] និងអាចខុសគ្នានៅគ្រប់ចំណុចខាងក្នុងនៃផ្នែកនេះ បន្ទាប់មកនៅខាងក្នុងផ្នែក [ ក, ខ] យ៉ាងហោចណាស់មានចំណុចមួយ។ ជាមួយ, ក c b នោះ។
f(ខ) – f(ក) = fў( គ)(ខ– ក).
ទ្រឹស្តីបទស្តីពីសមាមាត្រនៃការបង្កើនមុខងារពីរ (ទ្រឹស្តីបទរបស់ Cauchy) ។ប្រសិនបើ f(x) និង g(x) - មុខងារពីរបន្តនៅលើផ្នែក [ក, ខ] និងអាចខុសគ្នានៅគ្រប់ចំណុចខាងក្នុងនៃផ្នែកនេះ និង gў( x) មិនបាត់ទៅណាទេនៅក្នុងផ្នែកនេះ បន្ទាប់មកនៅខាងក្នុងផ្នែក [ ក, ខ] មានចំណុចបែបនេះ x = ជាមួយ, ក c b នោះ។
ដេរីវេនៃការបញ្ជាទិញផ្សេងៗ។
អនុញ្ញាតឱ្យមុខងារ y =f(x) មានភាពខុសប្លែកគ្នានៅចន្លោះពេលខ្លះ [ ក, ខ] តម្លៃដេរីវេ f ў( x) និយាយជាទូទៅអាស្រ័យលើ x, i.e. ដេរីវេ f ў( x) គឺជាមុខងារមួយផងដែរ។ x. នៅពេលបែងចែកមុខងារនេះ យើងទទួលបានអ្វីដែលហៅថា ដេរីវេទី 2 នៃអនុគមន៍ f(x) ដែលតំណាងឱ្យ f ўў ( x).
ដេរីវេ n-លំដាប់នៃមុខងារ f(x) ត្រូវបានគេហៅថា (លំដាប់ទីមួយ) ដេរីវេនៃដេរីវេ n- 1- th និងត្រូវបានតំណាងដោយនិមិត្តសញ្ញា y(ន) = (y(ន- ១)) ў។
ភាពខុសគ្នានៃការបញ្ជាទិញផ្សេងៗ។
មុខងារឌីផេរ៉ង់ស្យែល y = f(x) កន្លែងណា x- អថេរឯករាជ្យ បាទ ឌី = f ў( x)dx, មុខងារមួយចំនួនពី x, ប៉ុន្តែពី xមានតែកត្តាដំបូងប៉ុណ្ណោះដែលអាចពឹងផ្អែកបាន។ f ў( x) កត្តាទីពីរ ( dx) គឺជាការកើនឡើងនៃអថេរឯករាជ្យ xនិងមិនអាស្រ័យលើតម្លៃនៃអថេរនេះទេ។ ដោយសារតែ ឌីមានមុខងារពី xបន្ទាប់មកយើងអាចកំណត់ឌីផេរ៉ង់ស្យែលនៃមុខងារនេះ។ ឌីផេរ៉ង់ស្យែលឌីផេរ៉ង់ស្យែលនៃអនុគមន៍ត្រូវបានគេហៅថាឌីផេរ៉ង់ស្យែលទីពីរ ឬឌីផេរ៉ង់ស្យែលលំដាប់ទីពីរនៃអនុគមន៍នេះ ហើយត្រូវបានតាង ឃ 2y:
ឃ(dx) = ឃ 2y = f ўў( x)(dx) 2 .
ឌីផេរ៉ង់ស្យែល n-នៃលំដាប់ទីមួយត្រូវបានគេហៅថាឌីផេរ៉ង់ស្យែលទីមួយនៃឌីផេរ៉ង់ស្យែល n- 1- លំដាប់៖
d n y = ឃ(ឌីន–1y) = f(ន)(x)dx(ន).
ដេរីវេដោយផ្នែក។
ប្រសិនបើមុខងារមួយមិនអាស្រ័យលើមួយ ប៉ុន្តែនៅលើអាគុយម៉ង់ជាច្រើន។ x ខ្ញុំ(ខ្ញុំប្រែប្រួលពី 1 ទៅ ន,ខ្ញុំ= 1, 2,… ន),f(x 1,x 2,… x ន) បន្ទាប់មកនៅក្នុងការគណនាឌីផេរ៉ង់ស្យែល គោលគំនិតនៃដេរីវេដោយផ្នែកត្រូវបានណែនាំ ដែលកំណត់លក្ខណៈនៃអត្រានៃការផ្លាស់ប្តូរមុខងារនៃអថេរជាច្រើននៅពេលដែលមានតែអាគុយម៉ង់មួយផ្លាស់ប្តូរឧទាហរណ៍។ x ខ្ញុំ. ដេរីវេដោយផ្នែកនៃលំដាប់ទី 1 ទាក់ទងនឹង x ខ្ញុំត្រូវបានកំណត់ថាជាដេរីវេធម្មតា ហើយវាត្រូវបានសន្មតថាអាគុយម៉ង់ទាំងអស់លើកលែងតែ x ខ្ញុំរក្សាតម្លៃថេរ។ សម្រាប់និស្សន្ទវត្ថុដោយផ្នែក ការសម្គាល់ត្រូវបានណែនាំ
និស្សន្ទវត្ថុជាផ្នែកនៃលំដាប់ទី 1 ដែលកំណត់តាមវិធីនេះ (ជាមុខងារនៃអាគុយម៉ង់ដូចគ្នា) អាចមាននិស្សន្ទវត្ថុដោយផ្នែកផងដែរ ទាំងនេះគឺជានិស្សន្ទវត្ថុផ្នែកលំដាប់ទីពីរ។ល។ និស្សន្ទវត្ថុបែបនេះបានមកពីអំណះអំណាងផ្សេងៗគ្នាត្រូវបានគេហៅថាចម្រុះ។ និស្សន្ទវត្ថុចម្រុះបន្តគ្នានៃលំដាប់ដូចគ្នាមិនអាស្រ័យលើលំដាប់នៃភាពខុសគ្នា និងស្មើនឹងគ្នាទៅវិញទៅមក។
Anna Chugainova
អនុញ្ញាតឱ្យអនុគមន៍ y = f (x) ត្រូវបានកំណត់ក្នុងចន្លោះពេល X ។ ដេរីវេមុខងារ y = f (x) នៅចំណុច x o ត្រូវបានគេហៅថាដែនកំណត់
=
![]() .
.
ប្រសិនបើដែនកំណត់នេះ។ កំណត់,បន្ទាប់មកមុខងារ f(x) ត្រូវបានហៅ ខុសគ្នានៅចំណុច x o; លើសពីនេះទៅទៀត វាប្រែទៅជាបន្តនៅត្រង់ចំណុចនេះ។
ប្រសិនបើដែនកំណត់ដែលកំពុងពិចារណាគឺស្មើនឹង (ឬ - ) បន្ទាប់មកបានផ្តល់ថាមុខងារនៅចំណុច X oគឺបន្ត យើងនឹងនិយាយថា អនុគមន៍ f(x) មាននៅចំណុច X o ដេរីវេគ្មានកំណត់.
ដេរីវេត្រូវបានតំណាងដោយនិមិត្តសញ្ញា
y , f (x o), , .
ការស្វែងរកដេរីវេត្រូវបានគេហៅថា ភាពខុសគ្នាមុខងារ។ អត្ថន័យធរណីមាត្រនៃដេរីវេគឺថាដេរីវេគឺជាជម្រាលនៃតង់សង់ទៅខ្សែកោង y = f (x) នៅចំណុចដែលបានផ្តល់ឱ្យ X o ; អត្ថន័យរាងកាយ -គឺថាដេរីវេនៃផ្លូវទាក់ទងទៅនឹងពេលវេលាគឺជាល្បឿនភ្លាមៗនៃចំណុចផ្លាស់ទីមួយក្នុងអំឡុងពេលចលនា rectilinear s = s (t) នៅពេលនេះ t o ។
ប្រសិនបើ ជាមួយគឺជាចំនួនថេរ ហើយ u = u(x), v = v(x) គឺជាមុខងារផ្សេងគ្នាមួយចំនួន បន្ទាប់មកច្បាប់នៃភាពខុសគ្នាខាងក្រោមមានសុពលភាព៖
1) (c) " = 0, (cu) " = cu";
2) (u+v)" = u"+v";
3) (uv)" = u"v+v"u;
4) (u/v)" = (u"v-v"u)/v 2;
5) ប្រសិនបើ y = f(u), u = (x), i.e. y = f((x)) - មុខងារស្មុគស្មាញឬ superpositionផ្សំឡើងពីមុខងារផ្សេងគ្នា និង f បន្ទាប់មក , ឬ
6) ប្រសិនបើសម្រាប់អនុគមន៍ y = f(x) មានអនុគមន៍ផ្សេងគ្នាបញ្ច្រាស x = g(y) និង 0 បន្ទាប់មក។
ដោយផ្អែកលើនិយមន័យនៃនិស្សន្ទវត្ថុ និងច្បាប់នៃភាពខុសគ្នា គេអាចចងក្រងបញ្ជីនៃនិស្សន្ទវត្ថុតារាងនៃអនុគមន៍បឋម។
1. (u )" = u 1 u" ( រ).
2. (a u)" = a u lna u" ។
3. (e u)" = e u u" ។
4. (log a u)" = u"/(u ln a) ។
5. (ln u)" = u"/u ។
6. (sin u)" = cos u u" ។
7. (cos u)" = - sin u u" ។
8. (tg u)" = 1/ cos 2 u u " ។
9. (ctg u)" = - u" / sin 2 u ។
10. (arcsin u)" = u" / .
11. (arccos u)" = - u" / .
12. (arctg u)" = u"/(1 + u 2) ។
13. (arcctg u)" = - u"/(1 + u 2) ។
ចូរយើងគណនាដេរីវេនៃកន្សោមអិចស្ប៉ូណង់ស្យែល y=u v , (u>0) ដែល យូនិង vខ្លឹមសារនៃមុខងារពី Xមាននិស្សន្ទវត្ថុនៅចំណុចដែលបានផ្តល់ឱ្យ យូ",v".
យកលោការីតនៃសមភាព y = u v យើងទទួលបាន ln y = v ln u ។
សមីការនិស្សន្ទវត្ថុទាក់ទងនឹង Xពីភាគីទាំងពីរនៃសមភាពលទ្ធផលដោយប្រើវិធាន 3, 5 និងរូបមន្តសម្រាប់ដេរីវេនៃអនុគមន៍លោការីត យើងនឹងមាន៖
y"/y = vu"/u +v" ln u, whence y" = y (vu"/u +v" ln u) ។
(u v)"=u v (vu"/u+v" ln u), u > 0 ។
ឧទាហរណ៍ ប្រសិនបើ y = x sin x បន្ទាប់មក y" = x sin x (sin x/x + cos x ln x) ។
ប្រសិនបើអនុគមន៍ y = f(x) អាចខុសគ្នាត្រង់ចំណុច x, i.e. មាននិស្សន្ទវត្ថុកំណត់នៅចំណុចនេះ។ y"បន្ទាប់មក = y"+ ដែល 0 នៅ х 0; ហេតុនេះ y = y" х + x ។
ផ្នែកសំខាន់នៃការបង្កើនមុខងារ លីនេអ៊ែរទាក់ទងនឹង x ត្រូវបានគេហៅថា ឌីផេរ៉ង់ស្យែល មុខងារហើយត្រូវបានតំណាងដោយ dy: dy = y" х ប្រសិនបើយើងដាក់ y = x ក្នុងរូបមន្តនេះ យើងទទួលបាន dx = x" х = 1х = х ដូច្នេះ dy = y" dx ពោលគឺនិមិត្តសញ្ញា សម្រាប់ការសម្គាល់ដេរីវេអាចត្រូវបានគិតថាជាប្រភាគ។
ការបង្កើនមុខងារ yគឺជាការកើនឡើងនៃការចាត់តាំងនៃខ្សែកោង និងឌីផេរ៉ង់ស្យែល ឃ yគឺជាការបង្កើនតង់សង់។
ចូរយើងស្វែងរកអនុគមន៍ y=f(x) ដេរីវេរបស់វា y = f (x)។ ដេរីវេនៃដេរីវេនេះត្រូវបានគេហៅថា ដេរីវេនៃលំដាប់ទីពីរមុខងារ f(x) ឬ ដេរីវេទី ២និងត្រូវបានកំណត់ ![]() .
.
ខាងក្រោមនេះត្រូវបានកំណត់ និងកំណត់តាមរបៀបដូចគ្នា៖
ដេរីវេនៃលំដាប់ទីបី
-
![]() ,
,
ដេរីវេនៃលំដាប់ទីបួន -
![]()
ហើយជាទូទៅនិយាយ ដេរីវេនៃលំដាប់ទី
-
![]() .
.
ឧទាហរណ៍ ៣.15. គណនាដេរីវេនៃអនុគមន៍ y=(3x 3 −2x+1)sin x ។
ដំណោះស្រាយ។តាមក្បួនទី 3 y"=(3x 3 -2x+1)"sin x + (3x 3 -2x+1)(sin x)" = = (9x 2 -2) sin x + (3x 3 -2x) +1) cos x ។
ឧទាហរណ៍ 3.16 . រក y", y = tan x + ។
ដំណោះស្រាយ។ដោយប្រើច្បាប់សម្រាប់ការបែងចែកផលបូកនិងផលបូក យើងទទួលបាន៖ y"=(tgx +)" = (tgx)" + ()" = + ![]() =
=
![]()
![]() .
.
ឧទាហរណ៍ ៣.17. ស្វែងរកដេរីវេនៃអនុគមន៍ស្មុគ្រស្មាញ y= , u=x 4 +1 ។
ដំណោះស្រាយ។យោងតាមច្បាប់នៃភាពខុសគ្នានៃអនុគមន៍ស្មុគ្រស្មាញ យើងទទួលបាន៖ y" x = y " u " x = ()" u (x 4 +1)" x = (2u + ។ ចាប់តាំងពី u = x 4 +1 អញ្ចឹង។ (2 x 4 + 2+ ![]() .
.
និស្សន្ទវត្ថុគឺជាគោលគំនិតសំខាន់បំផុតក្នុងការវិភាគគណិតវិទ្យា។ វាកំណត់លក្ខណៈនៃការផ្លាស់ប្តូរមុខងារនៃអាគុយម៉ង់ xនៅចំណុចណាមួយ។ លើសពីនេះ ដេរីវេខ្លួនវាគឺជាមុខងារនៃអាគុយម៉ង់ x
ដេរីវេនៃមុខងារមួយ។ នៅចំណុចមួយគឺជាដែនកំណត់ (ប្រសិនបើវាមាន ហើយមានកំណត់) នៃសមាមាត្រនៃការកើនឡើងនៃអនុគមន៍ ទៅនឹងការបង្កើនអាគុយម៉ង់ ផ្តល់ថាចុងក្រោយមានទំនោរទៅសូន្យ។
ដែលប្រើជាទូទៅបំផុតមានដូចខាងក្រោម ការសម្គាល់ដេរីវេ :
ឧទាហរណ៍ ១.ទាញយកប្រយោជន៍ និយមន័យនៃដេរីវេស្វែងរកដេរីវេនៃអនុគមន៍
ដំណោះស្រាយ។ ពីនិយមន័យនៃដេរីវេតាមគ្រោងការណ៍ខាងក្រោមសម្រាប់ការគណនារបស់វា។
ចូរផ្តល់អាគុយម៉ង់ជាការបង្កើន (delta) ហើយស្វែងរកការបន្ថែមនៃអនុគមន៍៖
ចូរយើងស្វែងរកសមាមាត្រនៃការបង្កើនមុខងារទៅនឹងការបង្កើនអាគុយម៉ង់៖

ចូរយើងគណនាដែនកំណត់នៃសមាមាត្រនេះ ដែលផ្តល់ថាការកើនឡើងនៃអាគុយម៉ង់មានទំនោរទៅសូន្យ ពោលគឺដេរីវេដែលទាមទារនៅក្នុងសេចក្តីថ្លែងការណ៍បញ្ហា៖
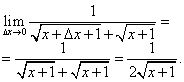
អត្ថន័យរូបវិទ្យានៃដេរីវេ
TO គំនិតនៃដេរីវេ បាននាំទៅដល់ការសិក្សារបស់ Galileo Galilei អំពីច្បាប់នៃការដួលរលំដោយសេរីនៃសាកសព ហើយក្នុងន័យទូលំទូលាយ - បញ្ហានៃល្បឿនភ្លាមៗនៃចលនា rectilinear មិនឯកសណ្ឋាននៃចំណុចមួយ។
សូមលើកដុំគ្រួសចេញរួចចេញពីការសម្រាក។ ផ្លូវ សឆ្លងកាត់តាមពេលវេលា tគឺជាមុខងារនៃពេលវេលា។ s = s(t) ប្រសិនបើច្បាប់នៃចលនានៃចំណុចមួយត្រូវបានផ្តល់ឱ្យ នោះល្បឿនជាមធ្យមសម្រាប់រយៈពេលណាមួយអាចត្រូវបានកំណត់។ សូមឱ្យគ្រួសស្ថិតនៅទីតាំង កហើយនៅពេលនេះ - នៅក្នុងទីតាំង ខ. ក្នុងរយៈពេលមួយ (ពី tទៅ) ចំណុចបានឆ្លងកាត់ផ្លូវ។ ដូច្នេះ ល្បឿនមធ្យមនៃចលនាក្នុងរយៈពេលនេះ ដែលយើងកំណត់ដោយ , គឺ
![]() .
.
ទោះជាយ៉ាងណាក៏ដោយ ចលនារបស់រាងកាយដែលធ្លាក់ចុះដោយសេរីគឺច្បាស់ជាមិនស្មើគ្នា។ ល្បឿន vការដួលរលំកំពុងកើនឡើងឥតឈប់ឈរ។ ហើយល្បឿនជាមធ្យមគឺលែងគ្រប់គ្រាន់ដើម្បីកំណត់លក្ខណៈល្បឿននៃចលនានៅលើផ្នែកផ្សេងៗនៃផ្លូវ។ រយៈពេលកាន់តែខ្លី លក្ខណៈនេះកាន់តែត្រឹមត្រូវ ដូច្នេះ គំនិតខាងក្រោមត្រូវបានណែនាំ៖ ល្បឿនភ្លាមៗនៃចលនា rectilinear (ឬល្បឿននៅពេលកំណត់។ t) ត្រូវបានគេហៅថាដែនកំណត់ល្បឿនមធ្យមនៅ៖
![]()
(ផ្តល់ថាដែនកំណត់នេះមាន ហើយមានកំណត់)។
ដូច្នេះវាប្រែថាល្បឿនភ្លាមៗគឺជាដែនកំណត់នៃសមាមាត្រនៃការកើនឡើងនៃមុខងារ ស(t) ដល់ការកើនឡើងនៃអាគុយម៉ង់ t at This is the derivative, which in general form ត្រូវបានសរសេរដូចខាងក្រោម:.
![]() .
.
ដំណោះស្រាយចំពោះបញ្ហាដែលបានចង្អុលបង្ហាញគឺ អត្ថន័យរូបវន្តនៃដេរីវេ . ដូច្នេះ ដេរីវេនៃមុខងារ y=f(x) នៅចំណុច xត្រូវបានគេហៅថាដែនកំណត់ (ប្រសិនបើវាមាន ហើយមានកំណត់) នៃការកើនឡើងនៃអនុគមន៍មួយទៅនឹងការបង្កើនអាគុយម៉ង់ ដែលផ្តល់ថា ក្រោយមកទៀតមានទំនោរទៅសូន្យ។
ឧទាហរណ៍ ២.ស្វែងរកដេរីវេនៃមុខងារ
![]()
ដំណោះស្រាយ។ ពីនិយមន័យនៃដេរីវេ គ្រោងការណ៍ខាងក្រោមសម្រាប់ការគណនារបស់វាដូចខាងក្រោម។
ជំហាន 1. ចូរយើងបង្កើនអាគុយម៉ង់ ហើយស្វែងរក

ជំហានទី 2. ស្វែងរកការបង្កើនមុខងារ៖

ជំហានទី 3. ស្វែងរកសមាមាត្រនៃការបង្កើនមុខងារទៅនឹងការបង្កើនអាគុយម៉ង់៖

ជំហានទី 4. គណនាដែនកំណត់នៃសមាមាត្រនេះនៅ មានន័យថា ដេរីវេ៖
អត្ថន័យធរណីមាត្រនៃដេរីវេ
អនុញ្ញាតឱ្យអនុគមន៍ត្រូវបានកំណត់នៅលើចន្លោះពេលមួយហើយអនុញ្ញាតឱ្យចំណុច មនៅលើក្រាហ្វនៃអនុគមន៍ត្រូវគ្នានឹងតម្លៃនៃអាគុយម៉ង់ និងចំណុច រ- អត្ថន័យ។ ចូរយើងគូរតាមចំនុច មនិង របន្ទាត់ត្រង់ហើយហៅវា។ សិត. ចូរយើងបញ្ជាក់ដោយមុំរវាងលេខនិងអ័ក្ស។ ជាក់ស្តែងមុំនេះអាស្រ័យលើ។
ប្រសិនបើមាន
![]()
ការឆ្លងកាត់ចំណុចនេះត្រូវបានគេហៅថា ទីតាំងកំណត់នៃ secant លោកនៅ (ឬនៅ) ។
តង់សង់ទៅក្រាហ្វនៃអនុគមន៍នៅចំណុចមួយ។ មហៅថាទីតាំងកំណត់នៃសេកាន លោកនៅ , ឬ , ដែលដូចគ្នានៅ .
តាមនិយមន័យវាដូចខាងក្រោមថាសម្រាប់អត្ថិភាពនៃតង់សង់វាគ្រប់គ្រាន់ហើយដែលមានដែនកំណត់
![]() ,
,
ហើយដែនកំណត់គឺស្មើនឹងមុំទំនោរនៃតង់ហ្សង់ទៅអ័ក្ស។
ឥឡូវនេះ ចូរយើងផ្តល់និយមន័យច្បាស់លាស់នៃតង់សង់។
តង់សង់ទៅក្រាហ្វនៃអនុគមន៍នៅចំណុចមួយ គឺជាបន្ទាត់ត្រង់ឆ្លងកាត់ចំណុច ហើយមានជម្រាល ពោលគឺឧ។ បន្ទាត់ត្រង់ដែលមានសមីការ
ពីនិយមន័យនេះវាធ្វើតាមនោះ។ ដេរីវេនៃមុខងារមួយ។ គឺស្មើនឹងចំណោទនៃតង់ហ្សង់ទៅក្រាហ្វនៃអនុគមន៍នេះនៅចំណុចជាមួយ abscissa x. នេះគឺជាអត្ថន័យធរណីមាត្រនៃដេរីវេ។
