Teoreem. Laske funktsioonil x=φ(t) pidev mingis punktis a ja funktsioon y=f(x) pidev mingis punktis b=φ(a). Siis kompleksfunktsioon y=f[φ(t)]=F(t) pidev mingis punktis a.

Lase x=φ(t) Ja y=f(x)- lihtsaimad elementaarfunktsioonid, millel on palju väärtusi (x) funktsioonid x=φ(t) on funktsiooni ulatus y=f(x). Nagu me teame, on elementaarfunktsioonid pidevad antud domeeni igas punktis. Seetõttu on eelmise teoreemi kohaselt kompleksfunktsioon y=f(φ(t)), st kahe elementaarfunktsiooni superpositsioon on pidev. Näiteks funktsioon on pidev mis tahes punktis x ≠ 0, kahe elementaarfunktsiooni kompleksfunktsioonina x=t -1 Ja y = sin x. Samuti funktsioon y=ln sin x pidev mis tahes ajavahemike punktis (2kπ,(2k+1)π), k ∈ Z (sin x>0).

Definitsioon. Olgu funktsioon y = f(x) defineeritud punktis x0 ja mõnes selle ümbruses. Kutsutakse funktsioon y = f(x). pidev punktis x0, Kui:

1. on olemas
2. see piir on võrdne funktsiooni väärtusega punktis x0:

Piirmäära defineerimisel rõhutati, et f(x) ei tohi olla defineeritud punktis x0 ja kui see on selles punktis defineeritud, siis f(x0) väärtus ei osale piiri määramises kuidagi. Järjepidevuse määramisel on oluline, et f(x0) eksisteeriks ja see väärtus peab olema võrdne lim f(x)-ga.

Definitsioon. Olgu funktsioon y = f(x) defineeritud punktis x0 ja mõnes selle ümbruses. Funktsiooni f(x) nimetatakse pidevaks punktis x0, kui kõigi ε>0 korral on positiivne arv δ, nii et kõigi x punktide δ-naabruses punkti x0 (st |x-x0|
Siin on arvestatud, et piiri väärtus peab olema võrdne f(x0), seetõttu, võrreldes piirmäära määratlusega, eemaldatakse δ-naabruse 0 punktsiooni tingimus.
Andkem veel üks (eelmisega samaväärne) määratlus juurdekasvu osas. Tähistame Δх = x - x0; me nimetame seda väärtust argumendi juurdekasvuks. Kuna x->x0, siis Δx->0, st Δx - b.m. (lõpmatult väike) kogus. Tähistame Δу = f(x)-f(x0), nimetame seda väärtust funktsiooni juurdekasvuks, kuna |Δу| peaks olema (piisavalt väikese |Δх| puhul) väiksem kui suvaline arv ε>0, siis on ka Δу- b.m. väärtus seega

Definitsioon. Olgu funktsioon y = f(x) defineeritud punktis x0 ja mõnes selle ümbruses. Kutsutakse funktsioon f(x). pidev punktis x0, kui argumendi lõpmatu väike juurdekasv vastab funktsiooni lõpmatu väikesele juurdekasvule.

Definitsioon. Funktsioon f(x), mis ei ole pidev punktis x0, nimetatakse katkendlikuks sel hetkel.

Definitsioon. Funktsiooni f(x) nimetatakse pidevaks hulgal X, kui see on pidev selle hulga igas punktis.

Teoreem summa, korrutise, jagatise pidevuse kohta

Teoreem piirile ülemineku kohta pideva funktsiooni märgi all

Teoreem pidevate funktsioonide superpositsiooni pidevuse kohta

Olgu funktsioon f(x) defineeritud intervallil ja olla sellel intervallil monotoonne. Siis saab f(x) sellel lõigul omada ainult esimest tüüpi katkestuspunkte.

Vaheväärtuste teoreem. Kui funktsioon f(x) on lõigul pidev ja kahes punktis a ja b (a on väiksem kui b) on ebavõrdsed väärtused A = f(a) ≠ B = f(b), siis mis tahes arvu C korral A ja B vahel on punkt c ∈, kus funktsiooni väärtus võrdub C-ga: f(c) = C.

Teoreem pideva funktsiooni piirituse kohta intervallil. Kui funktsioon f(x) on intervallil pidev, siis on see selle intervalliga piiratud.

Teoreem miinimum- ja maksimumväärtuste saavutamise kohta. Kui funktsioon f(x) on intervallil pidev, siis saavutab see sellel intervallil oma alumise ja ülemise piiri.

Teoreem pöördfunktsiooni pidevuse kohta. Olgu funktsioon y=f(x) pidev ja rangelt kasvav (kahanev) intervallil [a,b]. Siis on lõigul pöördfunktsioon x = g(y), mis on ka monotoonselt kasvav (kahanev) ja pidev.

Funktsiooni järjepidevus. Murdepunktid.

Sõnn kõnnib, kõigub, ohkab minnes:
- Oh, laud hakkab otsa saama, nüüd ma kukun!

Selles õppetükis käsitleme funktsiooni pidevuse kontseptsiooni, katkestuspunktide klassifikatsiooni ja levinud praktilist probleemi funktsioonide järjepidevusuuringud. Juba teema nime järgi arvavad paljud intuitiivselt, mida arutatakse, ja arvavad, et materjal on üsna lihtne. See on tõsi. Kuid hooletusse jätmise ja pealiskaudse lähenemise eest karistatakse kõige sagedamini just lihtsaid ülesandeid. Seetõttu soovitan teil artiklit väga hoolikalt uurida ja mõista kõiki peensusi ja tehnikaid.

Mida pead teadma ja oskama? Mitte väga. Et õppetund hästi õppida, peate mõistma, mis see on funktsiooni piir. Madala ettevalmistustasemega lugejatele piisab artiklist aru saamisest Funktsioonide piirid. Näited lahendustest ja vaadake juhendis piiri geomeetrilist tähendust Elementaarfunktsioonide graafikud ja omadused. Samuti on soovitatav end kurssi viia graafikute geomeetrilised teisendused, kuna praktika hõlmab enamikul juhtudel joonise koostamist. Väljavaated on kõigi jaoks optimistlikud ja isegi täis veekeetja saab järgmise tunni või paari jooksul ülesandega iseseisvalt hakkama!

Funktsiooni järjepidevus. Katkestuspunktid ja nende klassifikatsioon

Funktsiooni järjepidevuse mõiste

Vaatleme mõnda funktsiooni, mis on pidev kogu arvureal:

Või lühidalt öeldes on meie funktsioon pidev sees (reaalarvude hulk).

Mis on järjepidevuse "filisti" kriteerium? Ilmselgelt saab pideva funktsiooni graafiku joonistada ilma pliiatsit paberilt tõstmata.

Sel juhul tuleks selgelt eristada kahte lihtsat mõistet: funktsiooni domeen Ja funktsiooni järjepidevus. Üldiselt see pole sama asi. Näiteks:

See funktsioon on määratletud tervel arvureal, st jaoks kõik"X" tähendusel on "y" oma tähendus. Eelkõige, kui , siis . Pange tähele, et teine ​​punkt on kirjavahemärgiga, sest funktsiooni definitsiooni järgi peab argumendi väärtus vastama sellele ainuke asi funktsiooni väärtus. Seega domeeni meie funktsioon: .

Kuid see funktsioon ei ole pidevalt sisse lülitatud! On üsna ilmne, et hetkel ta kannatab lõhe. Mõiste on ka üsna arusaadav ja visuaalne, tõepoolest, siin tuleb pliiats nagunii paberilt maha rebida. Veidi hiljem vaatame murdepunktide klassifikatsiooni.

Funktsiooni pidevus punktis ja intervallil

Konkreetse matemaatilise ülesande puhul saame rääkida funktsiooni pidevusest punktis, funktsiooni pidevusest intervallil, poolintervallist või funktsiooni pidevusest segmendil. See on, pole olemas "lihtsat järjepidevust"– funktsioon võib KUSALIKULT olla pidev. Ja kõige muu põhiline "ehituskivi" on funktsiooni järjepidevus punktis .

Matemaatilise analüüsi teooria annab funktsiooni pidevuse definitsiooni punktis, kasutades “delta” ja “epsilon” naabrusi, kuid praktikas on kasutusel erinev definitsioon, millele pöörame suurt tähelepanu.

Kõigepealt meenutagem ühepoolsed piirid kes tungisid meie ellu esimeses õppetunnis funktsioonigraafikute kohta. Mõelge igapäevasele olukorrale:

Kui läheneme teljele punktile vasakule(punane nool), siis lähevad "mängude" vastavad väärtused piki telge punktini (karmiinpunane nool). Matemaatiliselt fikseeritakse see fakt kasutades vasakpoolne piirang:

Pöörake tähelepanu sisestusele (vasakul on "x kipub ka"). "Lisand" "miinus null" sümboliseerib , sisuliselt tähendab see, et läheneme numbrile vasakult poolt.

Samamoodi, kui lähenete punktile "ka" paremal(sinine nool), siis saavad „mängud” sama väärtuse, kuid mööda rohelist noolt ja parema käe piir vormindatakse järgmiselt:

"Lisaaine" sümboliseerib , ja kirje kõlab järgmiselt: "x kipub paremal olema ka."

Kui ühepoolsed piirid on lõplikud ja võrdsed(nagu meie puhul): , siis ütleme, et on olemas ÜLDpiirang. See on lihtne, üldine piir on meie "tavaline" funktsiooni piir, võrdne lõpliku arvuga.

Pange tähele, et kui funktsioon pole defineeritud (torkake graafiku harul must täpp välja), jäävad ülaltoodud arvutused kehtima. Nagu on juba mitu korda märgitud, eriti artiklis lõpmata väikeste funktsioonide kohta, väljendid tähendavad, et "x" lõpmatult lähedal läheneb punktile, samas POLE TÄHTIS, kas funktsioon ise on antud punktis defineeritud või mitte. Hea näide on järgmises lõigus, kui funktsiooni analüüsitakse.

Definitsioon: funktsioon on punktis pidev, kui funktsiooni piir antud punktis on võrdne funktsiooni väärtusega selles punktis: .

Määratlus on üksikasjalikult kirjeldatud järgmistes mõistetes:

1) Funktsioon peab olema punktis defineeritud, st väärtus peab olemas olema.

2) Funktsioonil peab olema üldine piirmäär. Nagu eespool märgitud, tähendab see ühekülgsete piiride olemasolu ja võrdsust: .

3) Funktsiooni piirväärtus antud punktis peab olema võrdne funktsiooni väärtusega selles punktis: .

Kui rikutakse vähemalt üks kolmest tingimusest, siis funktsioon kaotab pidevuse omaduse punktis .

Funktsiooni järjepidevus üle intervalli on sõnastatud leidlikult ja väga lihtsalt: funktsioon on intervalli pidev, kui ta on pidev antud intervalli igas punktis.

Eelkõige on paljud funktsioonid pidevad lõpmatul intervallil, st reaalarvude hulgal. See on lineaarne funktsioon, polünoomid, eksponentsiaal, siinus, koosinus jne. Ja üldiselt mis tahes elementaarne funktsioon pidev selle peal määratluspiirkond, näiteks logaritmiline funktsioon on intervallil pidev. Loodetavasti on teil praeguseks üsna hea ettekujutus sellest, millised põhifunktsioonide graafikud välja näevad. Täpsemat infot nende järjepidevuse kohta saab lahkelt Fichtenholtzilt.

Funktsiooni järjepidevuse segmendil ja poolintervallidel pole ka kõik keeruline, kuid sellest on õigem rääkida tunnis funktsiooni minimaalse ja maksimaalse väärtuse leidmise kohta segmendis, kuid ärgem praegu selle pärast muretsege.

Murdepunktide klassifikatsioon

Funktsioonide põnev elukäik on rikas kõikvõimalike eripunktide poolest ja murdepunktid on vaid üks nende eluloo lehekülg.

Märge : igaks juhuks peatun ühel elementaarsel punktil: murdepunkt on alati üks punkt– pole olemas “mitu vaheajapunkti järjest”, see tähendab, et pole olemas sellist asja nagu “vaheaeg”.

Need punktid jagunevad omakorda kahte suurde rühma: esimest tüüpi rebendid Ja teist tüüpi rebendid. Igal lõhe tüübil on oma iseloomulikud tunnused, mida me praegu vaatame:

Esimest tüüpi katkestuspunkt

Kui järjepidevuse tingimust mingis punktis rikutakse ja ühepoolsed piirid lõplik , siis nimetatakse seda esimest tüüpi katkestuspunkt.

Alustame kõige optimistlikuma juhtumiga. Tunni algse idee kohaselt tahtsin teooriat rääkida "üldiselt", kuid materjali reaalsuse demonstreerimiseks otsustasin konkreetsete tegelastega.

See on kurb, nagu foto noorpaaridest igavese leegi taustal, kuid järgmine võte on üldiselt aktsepteeritud. Kujutame joonisel funktsiooni graafikut:


See funktsioon on pidev kogu arvureal, välja arvatud punkt. Ja tegelikult ei saa nimetaja olla võrdne nulliga. Kuid vastavalt piiri tähendusele saame lõpmatult lähedal läheneda nullile nii vasakult kui ka paremalt, see tähendab, et ühepoolsed piirid on olemas ja ilmselgelt langevad kokku:
(Järjepidevuse tingimus nr 2 on täidetud).

Kuid funktsioon ei ole selles punktis määratletud, seetõttu rikutakse järjepidevuse tingimust nr 1 ja funktsioon kannatab selles punktis katkestuse all.

Seda tüüpi paus (koos olemasolevaga üldine piirmäär) kutsutakse parandatav vahe. Miks eemaldatav? Kuna funktsioon saab uuesti määratleda murdepunktis:

Kas see näeb imelik välja? Võib olla. Aga selline funktsiooni tähistus ei räägi millegi vastu! Nüüd on vahe kinni ja kõik on rahul:


Teeme ametliku kontrolli:

2) – on olemas üldine piirmäär;
3)

Seega on kõik kolm tingimust täidetud ja funktsioon on punktis pidev vastavalt funktsiooni pidevuse punktis määratlusele.

Kuid matani vihkajad võivad funktsiooni näiteks halvasti määratleda :


Huvitav on see, et siin on täidetud kaks esimest järjepidevuse tingimust:
1) – funktsioon on defineeritud antud punktis;
2) – on üldine piirmäär.

Kuid kolmas piir ei ole ületatud: st funktsiooni piir punktis pole võrdne antud funktsiooni väärtus antud punktis.

Seega esineb teatud hetkel funktsiooni katkestus.

Teist, kurvemat juhtumit nimetatakse esimest tüüpi rebend hüppega. Ja kurbust kutsuvad esile ühekülgsed piirid, mis piiratud ja erinev. Näide on toodud õppetunni teisel joonisel. Selline lõhe tekib tavaliselt sisse tükkhaaval määratletud funktsioonid, mida on artiklis juba mainitud graafiteisenduste kohta.

Mõelge tükipõhisele funktsioonile ja me lõpetame selle joonise. Kuidas graafikut koostada? Väga lihtne. Poolintervallil joonistame parabooli fragmendi (roheline), intervallile - sirge lõigu (punane) ja poolintervallile - sirge (sinine).

Veelgi enam, ebavõrdsuse tõttu määratakse ruutfunktsiooni väärtus (roheline punkt) ja ebavõrdsuse tõttu lineaarfunktsiooni väärtus (sinine punkt):

Kõige keerulisemal juhul peaksite kasutama graafiku iga osa punkt-punkti konstrueerimist (vt esimest õppetund funktsioonide graafikute kohta).

Nüüd huvitab meid ainult punkt. Uurime seda järjepidevuse tagamiseks:

2) Arvutame ühepoolsed piirid.

Vasakul on punane joon, nii et vasakpoolne piirang on:

Paremal on sinine sirgjoon ja parempoolne piir:

Selle tulemusena saime lõplikud arvud, ja nemad pole võrdne. Kuna ühepoolsed piirid piiratud ja erinev: , siis meie funktsioon talub esimest tüüpi katkestus hüppega.

On loogiline, et tühimikku ei saa kõrvaldada - funktsiooni ei saa tõesti täpsemalt määratleda ja "kokku liimida", nagu eelmises näites.

Teist tüüpi katkestuspunktid

Tavaliselt liigitatakse kõik muud rebenemise juhtumid nutikalt sellesse kategooriasse. Ma ei loetle kõike, sest praktikas tekib 99% probleemidest lõputu vahe– kui olete vasaku- või paremakäeline, ja sagedamini, on mõlemad piirid lõpmatud.

Ja loomulikult on kõige ilmsem pilt hüperbool punktis null. Siin on mõlemad ühepoolsed piirid lõpmatud: , seetõttu kannatab funktsioon punktis teist tüüpi katkestus.

Püüan oma artikleid täita võimalikult mitmekesise sisuga, nii et vaatame veel kohatu funktsiooni graafikut:

vastavalt standardskeemile:

1) Funktsioon pole praegu määratletud, kuna nimetaja läheb nulli.

Muidugi võime kohe järeldada, et funktsioon kannatab punktis katkestuse, kuid hea oleks liigitada katkestuse olemust, mida tingimus sageli nõuab. Selle jaoks:

Lubage mul teile meelde tuletada, et salvestamise all peame silmas lõpmata väike negatiivne arv ja kirje all - lõpmata väike positiivne arv.

Ühepoolsed piirid on lõpmatud, mis tähendab, et funktsioonil esineb punktis 2. tüüpi katkestus. Y-telg on vertikaalne asümptoot graafiku jaoks.

Pole harvad juhud, kui eksisteerivad mõlemad ühepoolsed piirid, kuid ainult üks neist on lõpmatu, näiteks:

See on funktsiooni graafik.

Uurime järjepidevuse punkti:

1) Funktsioon pole praegu määratletud.

2) Arvutame ühepoolsed piirid:

Selliste ühekülgsete piiride arvutamise meetodist räägime loengu kahes viimases näites, kuigi paljud lugejad on kõike juba näinud ja ära arvanud.

Vasakpoolne piir on lõplik ja võrdne nulliga (me “ei lähe punkti enda juurde”), aga parempoolne piir on lõpmatu ja graafiku oranž haru läheneb lõpmatult lähedale. vertikaalne asümptoot, mis on antud võrrandiga (must punktiirjoon).

Nii et funktsioon kannatab teist tüüpi katkestus punktis .

Mis puutub 1. tüüpi katkestustesse, siis funktsiooni saab määratleda katkestuspunktis endas. Näiteks tükipõhise funktsiooni jaoks Võid julgelt panna koordinaatide alguspunkti musta paksu täpi. Paremal on hüperbooli haru ja parempoolne piir on lõpmatu. Ma arvan, et peaaegu kõigil on aimu, milline see graafik välja näeb.

Mida kõik ootasid:

Kuidas kontrollida funktsiooni järjepidevust?

Funktsiooni järjepidevuse uurimine punktis viiakse läbi juba kehtestatud rutiinskeemi järgi, mis koosneb kolme pidevuse tingimuse kontrollimisest:

Näide 1

Uurige funktsiooni

Lahendus:

1) Ainus punkt ulatuses on see, kus funktsioon pole määratletud.

2) Arvutame ühepoolsed piirid: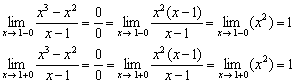

Ühepoolsed piirid on lõplikud ja võrdsed.

Seega esineb funktsioonil eemaldatav katkestus.

Kuidas selle funktsiooni graafik välja näeb?

Ma tahaksin lihtsustada , ja tundub, et saadakse tavaline parabool. AGA algne funktsioon ei ole punktis määratletud, seega on vajalik järgmine klausel:

Teeme joonise:

Vastus: funktsioon on pidev kogu arvureal, välja arvatud punkt, kus tal on eemaldatav katkestus.

Funktsiooni saab edasi defineerida nii hästi kui ka mitte nii hästi, kuid vastavalt tingimusele pole see vajalik.

Ütlete, et see on kaugeleulatuv näide? Üldse mitte. Praktikas on seda juhtunud kümneid kordi. Peaaegu kõik saidi ülesanded pärinevad reaalsest iseseisvast tööst ja testidest.

Vabaneme oma lemmikmoodulitest:

Näide 2

Uurige funktsiooni järjepidevuse nimel. Määrake funktsiooni katkestuste olemus, kui need on olemas. Teostage joonis.

Lahendus: Mingil põhjusel õpilased kardavad ja neile ei meeldi mooduli funktsioonid, kuigi neis pole midagi keerulist. Selliseid asju oleme tunnis juba veidi puudutanud. Graafikute geomeetrilised teisendused. Kuna moodul ei ole negatiivne, laiendatakse seda järgmiselt: , kus "alfa" on mingi väljend. Sel juhul tuleks meie funktsioon kirjutada tükkhaaval: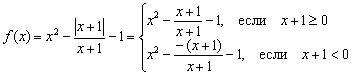

Kuid mõlema tüki murde tuleb vähendada . Vähendamine, nagu eelmises näites, ei toimu ilma tagajärgedeta. Algne funktsioon ei ole punktis määratletud, kuna nimetaja läheb nulli. Seetõttu peaks süsteem täiendavalt täpsustama tingimust ja muutma esimese ebavõrdsuse rangeks:

Nüüd VÄGA KASULIKust otsustustehnikast: enne ülesande viimistlemist mustandil on kasulik teha joonis (olenemata sellest, kas tingimused seda nõuavad või mitte). See aitab esiteks kohe näha järjepidevuse ja katkestuspunkte ning teiseks kaitseb teid 100% vigade eest ühepoolsete piiride leidmisel.

Teeme joonistamise. Vastavalt meie arvutustele on punktist vasakule vaja joonistada parabooli fragment (sinine värv) ja paremale parabooli tükk (punane värv), samas kui funktsioon ei ole punktis määratletud. punkt ise:

Kui kahtlete, võtke paar x väärtust ja ühendage need funktsiooniga (pidage meeles, et moodul hävitab võimaliku miinusmärgi) ja kontrollige graafikut.

Uurime järjepidevuse funktsiooni analüütiliselt:

1) Funktsioon ei ole punktis määratletud, seega võime kohe öelda, et see ei ole selles pidev.

2) Teeme kindlaks katkestuse olemuse, selleks arvutame ühepoolsed piirid:

Ühepoolsed piirid on lõplikud ja erinevad, mis tähendab, et funktsioon kannatab 1. tüüpi katkestuse ja hüppega punktis . Jällegi pange tähele, et piiride leidmisel ei ole vahet, kas murdepunktis olev funktsioon on defineeritud või mitte.

Nüüd jääb üle vaid mustandist joonis üle kanda (see on tehtud justkui uurimistöö abil ;-)) ja ülesanne täita:

Vastus: funktsioon on pidev kogu arvureal, välja arvatud punkt, kus tal esineb hüppega esimest tüüpi katkestus.

Mõnikord nõuavad nad katkestushüppe täiendavat märki. See arvutatakse lihtsalt - parempoolsest piirist peate lahutama vasakpoolse piiri: , see tähendab, et murdepunktis hüppas meie funktsioon 2 ühikut allapoole (nagu miinusmärk ütleb).

Näide 3

Uurige funktsiooni järjepidevuse nimel. Määrake funktsiooni katkestuste olemus, kui need on olemas. Tee joonistus.

See on näide, mida saate ise lahendada, näidislahendus tunni lõpus.

Liigume edasi ülesande kõige populaarsema ja levinuma versiooni juurde, kui funktsioon koosneb kolmest osast:

Näide 4

Uurige funktsiooni pidevust ja joonistage funktsiooni graafik .

Lahendus: on ilmselge, et funktsiooni kõik kolm osa on vastavatel intervallidel pidevad, seega jääb üle kontrollida vaid kahte tükkide vahelist “ristumispunkti”. Esmalt teeme eskiisjoonise, ehitustehnikat kommenteerisin piisavalt üksikasjalikult artikli esimeses osas. Ainus asi on see, et peame hoolikalt järgima oma ainsuse punkte: ebavõrdsuse tõttu kuulub väärtus sirgele (roheline punkt) ja ebavõrdsuse tõttu kuulub väärtus paraboolile (punane punkt):


Noh, põhimõtteliselt on kõik selge =) Jääb vaid otsus vormistada. Iga kahe "liitumispunkti" puhul kontrollime tavaliselt kolme järjepidevuse tingimust:

ma) Uurime järjepidevuse punkti

1)

Ühepoolsed piirid on lõplikud ja erinevad, mis tähendab, et funktsioon kannatab 1. tüüpi katkestuse ja hüppega punktis .

Arvutame katkestushüppe parempoolse ja vasakpoolse piiri erinevusena:
, see tähendab, et graafik tõusis ühe ühiku võrra ülespoole.

II) Uurime järjepidevuse punkti

1) – funktsioon on defineeritud antud punktis.

2) Leidke ühepoolsed piirid:

– ühepoolsed piirid on lõplikud ja võrdsed, mis tähendab, et on olemas üldine piir.

3) – funktsiooni piirväärtus punktis on võrdne selle funktsiooni väärtusega antud punktis.

Viimases etapis kanname joonise üle lõppversiooni, mille järel paneme viimase akordi:

Vastus: funktsioon on pidev kogu arvureal, välja arvatud punkt, kus tal esineb hüppega esimest tüüpi katkestus.

Näide 5

Uurige funktsiooni pidevust ja koostage selle graafik .

See on näide iseseisvaks lahendamiseks, lühilahendus ja ülesande ligikaudne näidis õppetunni lõpus.

Võib jääda mulje, et ühel hetkel peab funktsioon olema pidev, teises aga katkestus. Praktikas see alati nii ei ole. Püüdke mitte jätta tähelepanuta ülejäänud näiteid - seal on mitmeid huvitavaid ja olulisi funktsioone:

Näide 6

Antud funktsioon . Uurige punktide pidevuse funktsiooni. Koostage graafik.

Lahendus: ja uuesti viivitamatult teostada mustandil olev joonis:

Selle graafiku eripära on see, et tükipõhine funktsioon on antud abstsisstelje võrrandiga. Siin on see ala joonistatud rohelisega, kuid märkmikus on see tavaliselt lihtsa pliiatsiga paksus kirjas esile tõstetud. Ja muidugi ärge unustage meie jäärasid: väärtus kuulub puutuja harule (punane punkt) ja väärtus sirgjoonele.

Jooniselt on kõik selge - funktsioon on pidev kogu arvujoonel, jääb üle vaid vormistada lahendus, mis viiakse täieliku automatiseerimiseni sõna otseses mõttes pärast 3-4 sarnast näidet:

ma) Uurime järjepidevuse punkti

1) – funktsioon on defineeritud antud punktis.

2) Arvutame ühepoolsed piirid:

, mis tähendab, et on olemas üldine limiit.

Igaks juhuks tuletan meelde triviaalset tõsiasja: konstandi piir on võrdne konstandi endaga. Sel juhul on nulli piir võrdne nulliga endaga (vasakukäeline piir).

3) – funktsiooni piirväärtus punktis on võrdne selle funktsiooni väärtusega antud punktis.

Seega on funktsioon punktis pidev funktsiooni punktis pidevuse definitsiooni järgi.

II) Uurime järjepidevuse punkti

1) – funktsioon on defineeritud antud punktis.

2) Leidke ühepoolsed piirid:

Ja siin – ühe piir on võrdne ühiku endaga.

– on üldine piirmäär.

3) – funktsiooni piirväärtus punktis on võrdne selle funktsiooni väärtusega antud punktis.

Seega on funktsioon punktis pidev funktsiooni punktis pidevuse definitsiooni järgi.

Nagu tavaliselt, kanname pärast uurimist oma joonise lõppversiooni.

Vastus: funktsioon on punktides pidev.

Pange tähele, et tingimusel, et meilt ei küsitud midagi järjepidevuse kogu funktsiooni uurimise kohta ja seda peetakse heaks matemaatiliseks vormiks sõnastada täpne ja selge vastus esitatud küsimusele. Muide, kui tingimused ei nõua graafiku koostamist, siis on teil täielik õigus seda mitte koostada (kuigi hiljem võib õpetaja teid sundida seda tegema).

Väike matemaatiline “keelekeeraja” selle ise lahendamiseks:

Näide 7

Antud funktsioon . Uurige punktide pidevuse funktsiooni. Klassifitseerige katkestuspunktid, kui neid on. Teostage joonis.

Proovige kõiki "sõnu" õigesti "hääldada" =) Ja joonistage graafik täpsemalt, täpsus, see pole kõikjal üleliigne;-)

Nagu mäletate, soovitasin joonise kohe mustandina valmis teha, kuid aeg-ajalt tuleb ette näiteid, kus ei saa kohe aru, milline graafik välja näeb. Seetõttu on mõnel juhul soodne esmalt leida ühekülgsed piirid ja alles seejärel uuringu põhjal oksad kujutada. Kahes viimases näites õpime ka mõne ühepoolse piirmäära arvutamise tehnikat:

Näide 8

Uurige funktsiooni pidevust ja koostage selle skemaatiline graafik.

Lahendus: halvad punktid on ilmsed: (vähendab astendaja nimetaja nulli) ja (taandab kogu murdosa nimetaja nulliks). Ei ole selge, kuidas selle funktsiooni graafik välja näeb, mis tähendab, et parem on esmalt veidi uurida.

Definitsioon
Funktsioon f (x) helistas pidev punktis x 0 selle punkti naabruses ja kui piir kui x kaldub x-le 0 võrdne funktsiooni väärtusega x 0 :
.

Kasutades funktsiooni piiri Cauchy ja Heine definitsioone, saame anda funktsiooni punktis pidevuse laiendatud määratlused .

Järjepidevuse mõiste saame sõnastada aastal juurdekasvu osas. Selleks võtame kasutusele uue muutuja, mida nimetatakse muutuja x juurdekasvuks punktis. Siis on funktsioon pidev punktis if
.
Tutvustame uut funktsiooni:
.
Nad kutsuvad teda funktsiooni juurdekasv punktis . Siis on funktsioon pidev punktis if
.

Järjepidevuse määratlus paremal (vasakul)
Funktsioon f (x) helistas pidev paremal (vasakul) punktis x 0 , kui see on määratletud selle punkti mõnes parempoolses (vasakpoolses) naabruses ja kui parem (vasak) piir punktis x 0 võrdne funktsiooni väärtusega x 0 :
.

Teoreem pideva funktsiooni piirituse kohta
Olgu funktsioon f (x) on pidev punktis x 0 . Siis on naabruskond U (x0), mille funktsioon on piiratud.

Teoreem pideva funktsiooni märgi säilimise kohta
Olgu funktsioon punktis pidev. Ja olgu sel hetkel positiivne (negatiivne) väärtus:
.
Siis on selle punkti ümbrus, kus funktsioonil on positiivne (negatiivne) väärtus:
aadressil .

Pidevate funktsioonide aritmeetilised omadused
Olgu funktsioonid ja pidevad punktis .
Siis funktsioonid ja on pidevad punktis .
Kui , siis funktsioon on pidev punktis .

Vasak-parem järjepidevuse omadus
Funktsioon on pidev punktis siis ja ainult siis, kui see on pidev paremal ja vasakul.

Omaduste tõestused on toodud lehel “Punktis pidevate funktsioonide omadused”.

Kompleksfunktsiooni järjepidevus

Kompleksfunktsiooni pidevuse teoreem
Olgu funktsioon punktis pidev. Ja olgu funktsioon punktis pidev.
Siis on kompleksfunktsioon punktis pidev.

Keerulise funktsiooni piir

Teoreem funktsiooni pidevfunktsiooni piiri kohta
Olgu funktsiooni limiit , ja see on võrdne:
.
Siin on punkt t 0 võib olla lõplik või lõpmatult kauge: .
Ja olgu funktsioon punktis pidev.
Siis on keerulise funktsiooni piirang ja see on võrdne:
.

Teoreem kompleksfunktsiooni piiri kohta
Laske funktsioonil olla piir ja kaardistada punkti läbimurtud naabruskond punkti punkteeritud ümbrusega. Olgu see funktsioon sellel naabruskonnal määratletud ja sellel on piirang.
Siin on viimased või lõpmatult kauged punktid: . Naabruskonnad ja neile vastavad piirid võivad olla kas kahe- või ühepoolsed.
Siis on keerulise funktsiooni piirang ja see on võrdne:
.

Murdepunktid

Murdepunkti määramine
Olgu funktsioon defineeritud punkti mõnel punkteeritud naabruskonnal. Punkti nimetatakse funktsiooni katkestuspunkt, kui on täidetud üks kahest tingimusest:
1) ei ole määratletud ;
2) on defineeritud kohas , kuid ei ole selles punktis.

1. tüüpi katkestuspunkti määramine
Punkti nimetatakse esimest tüüpi katkestuspunkt, kui on murdepunkt ja vasakul ja paremal on lõplikud ühepoolsed piirangud:
.

Funktsioonihüppe definitsioon
Hüppa Δ funktsioon punktis on parem- ja vasakpoolsete piiride vahe
.

Murdepunkti määramine
Punkti nimetatakse eemaldatav katkestuspunkt, kui on piir
,
kuid funktsioon punktis ei ole kas defineeritud või ei ole võrdne piirväärtusega: .

Seega on eemaldatava katkestuse punkt 1. tüüpi katkestuspunkt, mille juures funktsiooni hüpe on võrdne nulliga.

2. tüüpi katkestuspunkti määramine
Punkti nimetatakse teist tüüpi katkestuspunkt, kui see ei ole 1. tüüpi katkestuspunkt. See tähendab, et kui punktis ei ole vähemalt ühte ühepoolset piiri või vähemalt üks ühepoolne piir on võrdne lõpmatusega.

Intervallil pidevate funktsioonide omadused

Intervalli pideva funktsiooni definitsioon
Funktsiooni nimetatakse pidevaks intervallil (at), kui see on pidev avatud intervalli (at) kõigis punktides ning punktides a ja b.

Weierstrassi esimene teoreem intervallil pideva funktsiooni piirituse kohta
Kui funktsioon on intervallil pidev, siis on see selle intervalliga piiratud.

Maksimumi (miinimum) saavutatavuse määramine
Funktsioon saavutab hulgal oma maksimumi (miinimum), kui selle jaoks on argument
kõigi jaoks .

Ülemise (alumise) näo ligipääsetavuse määramine
Funktsioon saavutab hulga ülemise (alumise) piiri, kui selle jaoks on argument
.

Weierstrassi teine ​​teoreem pideva funktsiooni maksimumi ja miinimumi kohta
Lõigul pidev funktsioon saavutab sellel oma ülemise ja alumise piiri või, mis on sama, saavutab lõigul oma maksimumi ja miinimumi.

Bolzano-Cauchy vaheväärtuste teoreem
Olgu funktsioon lõigul pidev. Ja olgu C suvaline arv, mis asub segmendi otstes oleva funktsiooni väärtuste vahel: ja . Siis on punkt, mille jaoks
.

Järeldus 1
Olgu funktsioon lõigul pidev. Ja laske funktsiooni väärtustel segmendi otstes olla erinevad märgid: või . Siis on punkt, kus funktsiooni väärtus on võrdne nulliga:
.

Järeldus 2
Olgu funktsioon lõigul pidev. Lase sel minna . Seejärel võtab funktsioon intervalli kõik väärtused alates ja ainult need väärtused:
aadressil .

Pöördfunktsioonid

Pöördfunktsiooni definitsioon
Olgu funktsioonil definitsioonipiirkond X ja väärtuste hulk Y. Ja las tal on vara:
kõigi jaoks .
Siis saab hulga Y mis tahes elemendiga seostada ainult ühe hulga X elemendi, mille jaoks . See vastavus määratleb funktsiooni nimega pöördfunktsioon Et . Pöördfunktsioon on tähistatud järgmiselt:
.

Definitsioonist järeldub, et
;
kõigi jaoks ;
kõigi jaoks .

Lemma otse- ja pöördfunktsioonide vastastikuse monotoonsuse kohta
Kui funktsioon on rangelt kasvav (kahanev), siis on olemas pöördfunktsioon, mis on samuti rangelt kasvav (kahanev).

Otseste ja pöördfunktsioonide graafikute sümmeetria omadus
Otse- ja pöördfunktsioonide graafikud on sirge suhtes sümmeetrilised.

Teoreem pöördfunktsiooni olemasolu ja pidevuse kohta intervallil
Olgu funktsioon pidev ja segmendil rangelt kasvav (kahanev). Seejärel määratletakse ja katkeb pöördfunktsioon segmendil, mis rangelt suureneb (väheneb).

Funktsiooni suurendamiseks. Vähendamiseks -.

Teoreem pöördfunktsiooni olemasolu ja pidevuse kohta intervallil
Olgu funktsioon pidev ja rangelt kasvav (kahanev) avatud lõplikul või lõpmatul intervallil. Seejärel määratletakse pöördfunktsioon ja see on intervallil pidev, mis rangelt suureneb (väheneb).

Funktsiooni suurendamiseks.
Vähendamiseks:.

Sarnaselt saame sõnastada teoreemi pöördfunktsiooni olemasolu ja pidevuse kohta poolintervallil.

Elementaarfunktsioonide omadused ja järjepidevus

Elementaarfunktsioonid ja nende pöördväärtused on oma määratlusvaldkonnas pidevad. Allpool esitame vastavate teoreemide sõnastused ja toome lingid nende tõestustele.

Eksponentfunktsioon

Eksponentfunktsioon f (x) = ax, alusega a > 0 on jada piir
,
kus on suvaline ratsionaalarvude jada, mis kaldub x-le:
.

Teoreem. Eksponentfunktsiooni omadused
Eksponentfunktsioonil on järgmised omadused:
(P.0) määratletud jaoks , kõigile ;
(lk 1) jaoks ≠ 1 sellel on palju tähendusi;
(lk 2) rangelt suureneb , rangelt väheneb juures , on konstantne juures ;
(lk 3) ;
(lk 3*) ;
(lk 4) ;
(lk 5) ;
(lk 6) ;
(lk 7) ;
(lk 8) pidev kõigile;
(lk 9) kell ;
aadressil .

Logaritm

Logaritmiline funktsioon ehk logaritm, y = logi x, alusega a on eksponentsiaalfunktsiooni pöördväärtus alusega a.

Teoreem. Logaritmi omadused
Logaritmiline funktsioon alusega a, y = logi x, sellel on järgmised omadused:
(L.1) määratletud ja pidev, jaoks ja , argumendi positiivsete väärtuste jaoks;
(L.2) sellel on palju tähendusi;
(L.3) rangelt suureneb kui , rangelt väheneb kui ;
(L.4) kell ;
kell ;
(L.5) ;
(L.6) kell ;
(L.7) kell ;
(L.8) kell ;
(L.9) aadressil .

Eksponent ja naturaallogaritm

Eksponentfunktsiooni ja logaritmi definitsioonides esineb konstant, mida nimetatakse astme baasiks või logaritmi baasiks. Matemaatilises analüüsis saadakse enamikul juhtudel lihtsamad arvutused, kui aluseks võtta arv e:
.
Eksponentfunktsiooni, mille alus on e, nimetatakse eksponendiks: , ja logaritmi baasiga e nimetatakse naturaallogaritmiks: .

Eksponendi omadused ja naturaallogaritm on toodud lehekülgedel
"Astendent, e x astmega",
"looduslik logaritm, funktsioon ln x"

Toitefunktsioon

Astmefunktsioon koos eksponendiga p on funktsioon f (x) = x p, mille väärtus punktis x on võrdne eksponentsiaalfunktsiooni väärtusega alusega x punktis p.
Lisaks on f (0) = 0 p = 0 p > jaoks 0 .

Siin käsitleme võimsusfunktsiooni y = x p omadusi argumendi mittenegatiivsete väärtuste jaoks. Ratsionaalarvude puhul paaritu m korral on võimsusfunktsioon defineeritud ka negatiivse x jaoks. Sel juhul saab selle omadused saada paaris või paaritu abil.
Neid juhtumeid käsitletakse üksikasjalikult ja illustreeritakse lehel "Toitefunktsioon, selle omadused ja graafikud".

Teoreem. Võimsusfunktsiooni omadused (x ≥ 0)
Astmefunktsioonil y = x p eksponendiga p on järgmised omadused:
(C.1) võtteplatsil määratletud ja pidev
kell ,
aadressil ".

Trigonomeetrilised funktsioonid

Teoreem trigonomeetriliste funktsioonide pidevuse kohta
Trigonomeetrilised funktsioonid: siinus ( sin x), koosinus ( cos x), puutuja ( tg x) ja kotangent ( ctg x

Pöördtrigonomeetriliste funktsioonide pidevuse teoreem
Trigonomeetrilised pöördfunktsioonid: arcsiinus ( arcsin x), kaarekoosinus ( arccos x), arktangent ( arctan x) ja kaartangens ( arcctg x), on oma määratlusvaldkonnas pidevad.

Viited:
O.I. Besov. Loengud matemaatilisest analüüsist. 1. osa. Moskva, 2004.
L.D. Kudrjavtsev. Matemaatilise analüüsi kursus. 1. köide. Moskva, 2003.
CM. Nikolski. Matemaatilise analüüsi kursus. 1. köide. Moskva, 1983.