Suur nafta ja gaasi entsüklopeedia

Vastame suuliselt! Kas vastab tõele, et sfääri saab kirjeldada mis tahes kolmnurkse püramiidi ümber? Kas on võimalik kirjeldada sfääri ümber suvalise nelinurkse püramiidi? Millised omadused peavad olema püramiidil, et kirjeldada seda ümbritsevat sfääri? Püramiid on kirjutatud sfääri, mille külgserv on aluse suhtes risti. Kuidas leida kera keskpunkt? Kera kirjeldatakse korrapärase püramiidi lähedal. Kuidas asub selle keskpunkt püramiidi elementide suhtes?

Slaid 17 esitlusest „Geomeetriaülesanded“ 11. klass. Arhiivi suurus koos esitlusega on 1032 KB.

Geomeetria 11. klass

muude ettekannete kokkuvõte

“Keskse sümmeetria kontseptsioon” – ruumi kaardistamine iseendaga. Keskne sümmeetria. Figuuri nimetatakse sümmeetriliseks. Keskne sümmeetria on liikumine. Ruumi liikumine. Punkte M ja M1 nimetatakse sümmeetrilisteks. Kinnisvara. Liikumised. Saime tuttavaks lennuki liikumistega. Ülesanne. Tsentraalne sümmeetria on pöörlemise erijuhtum.

"Kolmnurga pindala arvutamise probleemid" - Ivan Niven. Ühe probleemi lahendamine. Tunni moto. Isiklikud eesmärgid. Leidke joonise pindala. Matemaatiline diktaat. Kolmnurga pindala leidmise meetodid. Valige avaldus. Kehalise kasvatuse minut. Arvutage joonise pindala. Figuuri pindala. Edenemise kontrollimine. Ruut.

“Stereomeetria ülesanded” – leidke tippude vahelise kauguse ruut. Ülesanded. Pliipalli läbimõõt. Palli ja selle osade maht. Leidke hulktahuka nurk. Leidke püramiidi ruumala. Leidke punkti A ordinaat. Ringsektor. Leidke silindri maht V. Leidke hulktahuka pindala. Leidke trapetsi pindala. Ümbermõõt.

"Arvutage pöörleva keha maht" - kera. Silinder ja koonus. Koonus. Silindrid on kõikjal meie ümber. Koonuse V maht. Kuubik Koonuse määratlus. Pöörlemiskehade tüübid. Pall. Pöörlevate kehade mahud. Joonis. Leidke helitugevus. Silindriline anum. Silindri definitsioon. Raadii. Silinder. Koonuse maht.

“Pöördekehade mahud ja pinnad” – hüpoteeside väljapakkumine ja kontrollimine. Tehke teadmistest kokkuvõte. Pöörlemiskehade mahud ja pinnad. Määrake geomeetriline kuju. Probleemi sõnastamine. Probleem. Näited praktilistest tegevustest. Miks termomeetri paak soojeneb kiiremini? Pallikujulise teekannu pindala on väikseim. Mahud.

"Meie ümber pöörlevad kehad" - meie ümber pöörlevad kehad. Tööstuslikud seadmed. Leia pöörlevad kehad. Metskäbi kuusk. Kaldus torn Itaalias. Kosmoses. Melnikovi maja. Koonus. Ümmargused tornid. Ümmarguse hoone ajalugu. Kosmilised kehad.

Mitmetahuliste ja ümarate kehade kombinatsioonid

Kera ja palli mõisted.

Kera on kujund, mis koosneb kõigist ruumipunktidest, millest igaühe kaugus antud punktini O on võrdne antud positiivse arvuga r. Punkti O nimetatakse Keskus sfäär ja segment, mis ühendab punkti sfääri mis tahes punktiga, on selle segment raadius. Kõik kera raadiused on pikkusega r. Arvu r nimetatakse sfääri raadiuseks.

Sfäär jagab kõigi sinna mittekuuluvate ruumipunktide hulga kaheks alamhulgaks: sisemine Ja välised pindala sfääri suhtes. Sisemine piirkond hõlmab neid ruumipunkte, millest igaühe kaugus keskpunktist on väiksem kui raadius, ja välimine piirkond hõlmab neid punkte, mille kaugus igaühest keskpunktini on suurem kui raadius.

Pall on kujund, mis koosneb kõigist ruumipunktidest, millest igaühe kaugus antud punktini O ei ole suurem kui antud positiivne arv r. Punkti O nimetatakse Keskus pall ja arv r on selle raadius. Nimetatakse sfääri O keskpunktiga raadiusega r pinnale või palli piir. Kõiki palli punkte, mis ei kuulu selle pinnale, nimetatakse palli sisepunktideks või palli sees asuvateks punktideks. Seega on pall kujund, mis koosneb sfääri (kuuli pinna) kõigi punktide ühendusest ja kõigi selle sfääriga seotud sisemiste punktide hulgast.

Kuuli pinna puutujatasandit nimetatakse puutuja tasapind pallile. Tasand on kuuli puutuja siis ja ainult siis, kui see läbib kuuli pinnal olevat punkti, mis on risti selle punkti raadiusega. Pange tähele ka seda, et läbi palli pinna iga punkti läbib üks ja ainult üks palli puutuja tasapind.

Hulktahuka ümber piiratud kera.

Definitsioon. Sfääri nimetatakse kirjeldatud hulktahuka ümber, kui kõik hulktahuka tipud asuvad keral.

1. teoreem.Sfääri saab kirjeldada mis tahes kolmnurkse püramiidi ümber.

Püramiidi aluse tippudest võrdsel kaugusel olevate punktide kogum on risti, mis on tõmmatud aluse lähedal asuva piiritletud ringi keskpunktist (antud hulknurga tippudest võrdsel kaugusel asuvas ruumis on HMT olemas, kui selle ümber saab kirjeldada ringi hulknurk ja selle hulknurga tasapinnaga on tõmmatud risti läbi piiratud ringi keskpunkti ). Ümberringjoone keskpunkt on püramiidi aluse risti poolitajate lõikepunkt.

Piiratud sfääri keskpunkti leidmiseks tõmmake punkti M läbiv tasapind – külgserva AD keskpunkt. See tasapind lõikub risti (varem näidatud) punktis S. Konstruktsioonist SA=SB=SC ja ka sellest, et kolmnurk ASD on võrdhaarne (ka konstruktsioonilt), järeldub, et SA=SD. Seetõttu on kaugused kõigist püramiidi tippudest punktini S võrdsed ja see kaugus on võrdne püramiidi ABCD lähedal asuva piiritletud sfääri raadiusega (SA=SB=SC=SD=R).

Näide 1 . Leidke korrapärase tetraeedri ümber piiratud sfääri raadius.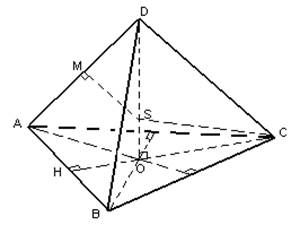

Vaatleme kolmnurka SOC. See on ristkülikukujuline täisnurgaga O (konstruktsiooni järgi on OD püramiidi kõrgus).

, kuna O on mediaanide lõikepunkt.

, kus DO on püramiidi kõrgus.

Siis Pythagorase teoreemi järgi järeldub, et või

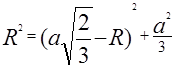
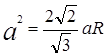
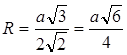
Vastus: Korrapärase tetraeedri ümber piiritletud sfääri raadius on võrdne

2. teoreem. Kui püramiidi aluse ümber saab kirjeldada ringi, siis püramiidi ümber saab kirjeldada kera.

Oleme juba käsitlenud erijuhtumit. Üldjuhul on tõestus sarnane.

3. teoreem . Kaldprisma lähedal olevat kera on võimatu kirjeldada; sirge prisma lähedal saab kirjeldada sfääri, kui prisma aluse lähedal saab kirjeldada ringi.

1) Vaatleme esmalt juhtumit, mil prisma on kaldu (võtame näitena kolmnurkprisma). Punktidest A, B ja C võrdsel kaugusel asuv punkt on sirgel OS 1, mis on risti kolmnurga ABC tasandiga ja ristnurga alus on kolmnurga ABC külgedele tõmmatud pooliste ristnurkade lõikepunktis. .

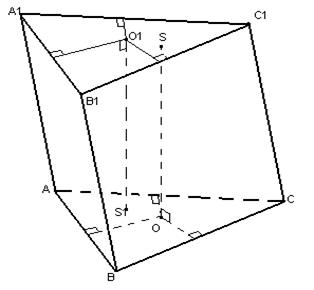
Samamoodi asuvad punktidest A 1, B 1, C 1 võrdsel kaugusel olevad punktid kolmnurga A 1 B 1 C 1 – O 1 S tasandiga risti. Kuna prisma on kaldu, siis sirged OS 1 ja O 1 S on olema paralleelsed, kuid mitte sobima. Ja see tähendab, et neil ei ole ühiseid punkte: pole sellist punkti, mille kaugus prisma kõigi tippude vahel oleks sama, mis on sarnane kaldprisma ümber kirjeldatud sfääri konstrueerimise võimatusega.

2) Vaatleme sirget prismat, mille aluse lähedal saab kirjeldada ringi. Punktid O ja O 1 on piiritletud ringide keskpunktid vastavalt alumise ja ülemise aluse lähedal. Kuna prisma on sirge, on sirge OO 1 risti aluse tasanditega.

Siis on külgribide keskosa läbiv tasapind paralleelne aluse tasapinnaga ja lõikub OO 1 punktis S - OO 1 keskkohaga. Siis on prisma kõigi tippude ja käru S kaugus (konstruktsiooni järgi) sama, seetõttu on S tavalise prisma ümber kirjeldatud sfääri keskpunkt.

Seega oleme veendunud, et kaldprisma lähedal on sfääri kirjeldamine võimatu, kuid sirge prisma lähedal on see võimalik, kui ringjoont saab kirjeldada selle aluse lähedal.

4. teoreem. Kera saab kirjeldada ümber kärbitud püramiidi siis ja ainult siis, kui selle aluste ümber saab kirjeldada ringe ja nende ringide keskpunkte ühendav sirgjoon on risti aluste tasanditega.

Esimene tingimus tähendab, et eksisteerivad hulknurkade tippudest võrdsel kaugusel olevate aluste ristid, mis on HMT, ja teine tingimus, et need langevad kokku, seega on punkt, mis on võrdsel kaugusel kõigist tippudest. kärbitud püramiid.

XV LINNA AVATUD ÕPILASTE KONVERENTS

"XXI SAJANDI INTELLEKTUAALID"

Sektsioon: MATEMAATIKA

Kirjeldatud ala olümpiaadidel ja ühtsel riigieksamil

Kiyaeva Anna Anatolevna

Orenburg – 2008

1.2 Kirjeldatud ulatust

1.2.1 Põhiomadused ja määratlused

1.2.2 Püramiidi kombinatsioon

1.2.3 Kombinatsioon prismaga

1.2.4 Kombinatsioon silindriga

1.2.5 Kombinatsioon koonusega

2 Olümpiaadiülesannete näited

2.1 Näiteid olümpiaadiülesannetest püramiidiga

2.2 Olümpiaadiülesannete näited prismaga

2.3 Olümpiaadiülesannete näited silindriga

2.4 Näiteid olümpiaadiülesannetest koonusega

3.3 Näited ühtse riigieksami ülesannetest silindriga

3.4 Koonusega ühtse riigieksami ülesannete näited

Sissejuhatus

Seda tööd tehakse osana projektist, mille eesmärk on luua internaatlütseumi veebisaidil koolinoortele mõeldud matemaatiline leht ja see postitatakse rubriiki “Matemaatikameetodid”.

Sihtmärk töö - teatmeraamatu loomine, mis on pühendatud kirjeldatud sfääriga geomeetriliste ülesannete lahendamise meetodile olümpiaadidel ja ühtsel riigieksamil.

Selle eesmärgi saavutamiseks pidime lahendama järgmise ülesandeid :

1) tutvuda kirjeldatud sfääri mõistega;

2) uurib kirjeldatud kera püramiidi, prisma, silindri ja koonusega kombinatsioonide tunnuseid;

3) geomeetriliste ülesannete hulgast valida need, mis sisaldavad kirjeldatud sfääri olemasolu tingimust;

4) analüüsib, süstematiseerib ja liigitab kogutud materjali;

5) teeb iseseisvaks lahendamiseks ülesannete valiku;

6) esitleb uurimistulemust referaadi vormis.

Praktiline tähtsus– meie koostatud materjale saab kasutada koolinoorte ettevalmistamisel olümpiaadiks, ühtseks riigieksamiks ja sellele järgnevaks õppeks ülikoolis.

1 Kera ja pall

1.1 Kera ja pall: põhimõisted ja määratlused

Kera on pind, mis koosneb kõigist ruumipunktidest, mis asuvad antud punktist etteantud kaugusel.

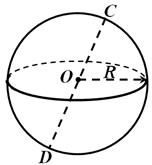
Seda punkti nimetatakse sfääri keskpunkt(punkt KOHTA joonisel fig. 1) ja see kaugus sfääri raadius. Mis tahes segmenti, mis ühendab sfääri keskpunkti ja mis tahes punkti, nimetatakse ka sfääri raadiuseks. Nimetatakse sirglõiku, mis ühendab sfääri kahte punkti ja läbib selle keskpunkti sfääri läbimõõt(joonelõik DC joonisel fig. 1). Pange tähele, et kera saab saada poolringi ümber selle läbimõõdu pööramisega.

Pall nimetatakse sfääriga piiratud kehaks. Nimetatakse ka sfääri keskpunkti, raadiust ja läbimõõtu Keskus , raadius Ja palli läbimõõt. Ilmselgelt raadiusega pall R tsentreeritud aadressil KOHTA sisaldab kõiki ruumipunkte, mis asuvad punktist KOHTA kaugusel, mis ei ületa R(kaasa arvatud punkt KOHTA) ja ei sisalda muid punkte. Pall nimetatakse ka poolringi pöördeks ümber selle läbimõõdu. Palli segment- osa pallist on sellest mingi tasapinnaga ära lõigatud. Iga palli lõik tasapinnal on ring. Selle ringi keskpunkt on kuuli keskpunktist lõiketasandile tõmmatud risti alus. Kuuli keskpunkti läbivat tasapinda nimetatakse diametraalne tasapind. Kuuli läbilõiget diametraaltasandil nimetatakse suur ring, ja sfääri lõik on suur ring. Palli sektor – geomeetriline keha, mis saadakse ringikujulise sektori, mille nurk on väiksem kui 90°, pööramisel ümber sirgjoone, mis sisaldab ühte ringikujulist sektorit piiravatest raadiustest. Sfääriline sektor koosneb sfäärilisest segmendist ja koonusest, millel on ühine alus.

Kera pindala:

S = 4π R 2 ,

Kus R- palli raadius, S- sfääri pindala.

Sfääri maht

Kus V- palli maht

Pallisektori maht

V – sfäärilise segmendi maht.

Segmendi pindala

- segmendi kõrgus, segmendi pindala

Segmendi aluse raadius

, - segmendi aluse raadius, - segmendi kõrgus, 0<H < 2R .

Kuulisegmendi sfääriline pindala

- sfäärilise segmendi sfäärilise pinna pindala.

Kosmoses on palli ja lennuki puhul võimalik kolm juhtumit:

1) Kui kaugus palli keskpunktist tasapinnani on suurem kui kuuli raadius, siis ei ole kuulil ja tasapinnal ühiseid punkte.

2) Kui kaugus kuuli keskpunktist tasapinnani on võrdne kuuli raadiusega, siis on tasapinnal ainult üks ühine punkt kuuli ja seda piirava sfääriga.

3) Kui kaugus palli keskpunktist tasapinnani on väiksem kui kuuli raadius, siis on kuuli ristumiskoht tasapinnaga ringjoon. Selle ringi keskpunkt on kuuli keskpunkti projektsioon antud tasapinnale. Tasapinna ristumiskoht sfääriga on määratud ringi ümbermõõt.

1.2 Kirjeldatud sfäär

1.2.1 Mõisted ja omadused

Sfääri nimetatakse kirjeldatud hulktahuka ümber(ja hulktahukas on kuuluvad sfääri), kui kõik hulktahuka tipud asuvad keral.

Kirjeldatud sfääri määratlusest tuleneb kaks fakti:

1) kõik sfääri kirjutatud hulktahuka tipud on teatud punktist (piiratud sfääri keskpunktist) võrdsel kaugusel;

2) sfääri sisse kirjutatud hulktahuka iga tahk on hulknurk, mis on kantud kindlasse ringi, just selles ringis, mis saadakse sfääri lõikes sfääri tasapinnaga; sel juhul on tahkude tasapinnal piiritletud sfääri keskpunktist langetatud perpendikulaaride aluseks tahkude ümber piiratud ringide keskpunktid.

1. teoreem . Sfääri saab kirjeldada polüeedri ümber siis ja ainult siis, kui on täidetud mõni järgmistest tingimustest:

a) ringjoont saab kirjeldada ümber hulktahuka tahkude ja hulktahuka tahkude ümber kirjeldatud ringide teljed ristuvad ühes punktis;

b) hulktahuka servadega risti olevad ja nende keskpunkte läbivad tasapinnad lõikuvad ühes punktis;

c) hulktahuka kõigist tippudest on üks punkt võrdsel kaugusel.

Tõestus.

Vajadus. Olgu kirjeldatud hulktahuka ümber kera. Tõestame, et tingimus a) on täidetud. Tõepoolest, kuna hulktahuka antud tahu tasapind lõikub sfääriga piki ringi, siis sfäärile kuuluva tahu tipud ja näo tasapind kuuluvad nende lõikejoonele - ringile. Kuna sfääri keskpunkt on antud tahu kõigist tippudest võrdsel kaugusel, asetseb see selle küljega risti, mis on tõmmatud läbi tahu ümberpiiratud ringi keskpunkti.

Adekvaatsus. Olgu tingimus a) täidetud. Tõestame, et sfääri saab kirjeldada ümber hulktahuka. Tegelikult, kuna läbi tahkudega ümbritsetud ringide keskpunktide tõmmatud tahkude ühine punkt on polühedri kõigist tippudest võrdsel kaugusel, kirjeldatakse hulktahuka ümber kera, mille keskpunkt on selles punktis.

Tingimus a) on antud juhul samaväärne tingimustega b ja c).

Kui kera on ümbritsetud hulktahuka ümber, siis: a) sfääri keskpunktist suvalise tahu külge langetatud ristnurga alus on selle tahu ümber ümbritsetud ringi keskpunkt (nagu püramiidi kõrguse alus, mille kõrgus on võrdne külgmised servad - sfääri raadiused, mis on tõmmatud selle keskpunktist antud tahu tippudeni ); b) ümber hulktahuka ümbritsetud sfääri keskpunkt võib asuda hulktahukas sees, selle pinnal (ümber tahu ümbritsetud ringi keskpunktis, eelkõige mõne serva keskel), polüeedrist väljaspool.

1.2.2 Piiratud kera ja püramiid

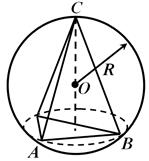
Teoreem 2 . Püramiidi ümber olevat kera saab kirjeldada siis ja ainult siis, kui saab kirjeldada ringi ümber selle aluse.

Tõestus. Olgu kirjeldatud ring ümber püramiidi aluse. Seejärel määratlevad see ring ja selle ringi tasapinnast väljaspool asuv punkt – püramiidi tipp – ühe sfääri, mis on ümbritsetud püramiidiga. Ja tagasi. Kui kera on ümbritsetud püramiidi ümber, siis sfääri läbilõige püramiidi aluse tasandi järgi on ümber aluse ümbritsetud ring.

Järeldus 1. Sfääri saab kirjeldada mis tahes tetraeedri ümber.

Järeldus 2. Iga tavalise püramiidi ümber võib kirjeldada sfääri, mille kese asub püramiidi või selle laiendi kõrgusel.

Püramiidi lähedal kirjeldatud sfääri keskpunkt võib olla:

· püramiidi tipuga ühel pool selle aluse tasapinda - püramiidi sees, külgpinna tasapinnal (selle tahu ümber kirjeldatud ringi keskel), väljaspool püramiidi;

· aluse tasapinnas - aluse lähedal kirjeldatud ringi keskel;

· püramiidi tipuga selle aluse tasapinna vastaskülgedel.

3. teoreem . Kui püramiidi külgmised servad on selle aluse tasapinna suhtes võrdselt kallutatud, saab püramiidi ümber kirjeldada kera.

Tõestus. Kuna külgservad on püramiidi aluse tasapinna suhtes võrdselt kaldu, saab püramiidi aluse lähedal kirjeldada ringi ja seejärel püramiidi lähedal kera.

Seda teoreemi saab sõnastada erinevalt: kui püramiidil on võrdsed külgmised servad, siis saab püramiidi ümber kirjeldada kera.

Pöördeteoreem pole tõsi

4. teoreem. Kui palli kirjeldatakse püramiidi lähedal, siis on selle keskpunkt kõigi nende servadega risti püramiidi servade keskpunktide kaudu tõmmatud tasapindade lõikepunkt.

Tõestus. Tegelikult asub iga punkt, mis on võrdsel kaugusel kahest ühe servaga külgnevast püramiidi tipust, tasapinnal, mis on tõmmatud läbi selle püramiidi servaga risti läbi selle keskosa. Seetõttu peab püramiidi kõigist tippudest võrdsel kaugusel paikneva piiritletud kuuli keskpunkt asuma igal sellisel tasapinnal, s.o. see on kõigi nende tasandite lõikepunkt. Koolilapsed paigutavad joonise tegemisel sageli kirjeldatud palli keskpunkti juhuslikult, etteantud ruumikonfiguratsiooni piisavalt hästi ette kujutamata ja eriti selle keskpunkti asukoha üle arutlemata. Sel juhul asetatakse keskpunkt reeglina püramiidi sisse. Samal ajal võib kirjeldatud palli kese asuda püramiidi sees, väljas või pinnal (olenevalt konkreetsest püramiidi tüübist).

5. teoreem . Kera saab kirjeldada ümber kärbitud püramiidi siis ja ainult siis, kui on täidetud üks järgmistest tingimustest:

a) püramiidi aluste lähedal kirjeldatakse ringe, mille keskpunktide joon on nende tasanditega risti;

b) püramiidi kõik külgmised servad on ühe aluse tasapinna suhtes võrdselt kallutatud;

c) püramiidi kõik külgmised servad on üksteisega võrdsed;

d) püramiidi kõik külgpinnad on võrdkülgsed trapetsid.

Tõestus. Oletame, et ringjooni saab kirjeldada antud kärbitud püramiidi aluste lähedal ja nende ringide tasapinnad on risti nende keskpunktide joonega. Siis, nagu on teada, määratlevad sellised kaks ringi ühe sfääri, mis on selle püramiidi ümber piiratud.

Oletame vastupidi, et antud kärbitud püramiidi ümber on kirjeldatud sfääri. Siis on sfääri lõigud püramiidi aluste tasandite järgi ringid, mida kirjeldatakse aluste ümber. Edasi. Sirge, mis on risti püramiidi aluste tasanditega ja läbib kera keskpunkti, läbib aluste ümber kirjeldatud ringide keskpunkte.

Seisund a) on tingimustega samaväärne b), c), d).

Tagajärg. Sfääri saab kirjeldada mis tahes korrapärase kärbitud püramiidi ümber.

1.2.3 Piiratud kera ja prisma

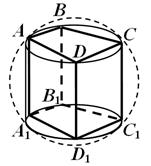
6. teoreem. Kera saab kirjeldada prisma ümber siis ja ainult siis, kui prisma on sirge ja selle aluse ümber saab kirjeldada ringjoont.

Tõestus.

Vajadus. Kui prisma on kantud sfääri, siis on selle iga tahk sisse kirjutatud ringi - sfääri lõigus selle tahu tasapinnaga. See tähendab, et ringjoont saab kirjeldada prisma aluse lähedal ja kõik prisma külgpinnad on nagu ringidesse sisse kirjutatud rööpkülikud – ristkülikud ja seetõttu on prisma sirge.

Adekvaatsus. Olgu prisma sirge ja selle aluse ümber kirjeldatakse ringjoont. Seejärel määravad prisma aluste ümber olevad ringid, mille tasandid on risti nende keskpunktide joonega, ühe sfääri, mis on ümbritsetud prisma ümber.

Tagajärjed:

a) sfääri saab kirjeldada mis tahes korrapärase prisma ümber;

b) sfääri saab kirjeldada mis tahes täisnurkse kolmnurkse prisma ümber;

c) sfääri saab kirjeldada mis tahes ristkülikukujulise rööptahuka ümber;

Prisma ümber ümbritsetud sfääri keskpunkt on prisma aluste tasapindadest võrdsel kaugusel ja võib asuda prisma sees, selle külgpinnal (tahu kohta kirjeldatud ringi keskel), prismast väljaspool.

1.2.4 Piiratud kera ja silinder

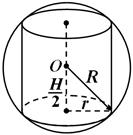
Sfääri nimetatakse silindri kohta kirjeldatud, kui sellel asuvad silindri aluste ringid (joonis 4). Silindri ümber olevat kera saab alati kirjeldada.

1.2.5 Piiratud kera ja koonus

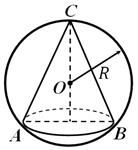
Sfääri nimetatakse kirjeldatud koonuse ümber, kui sellel asetsevad tipp ja koonuse aluse ring (joon. 5). Alati on võimalik kirjeldada kera ümber koonuse; selle raadius on võrdne koonuse telglõike ümber kirjeldatud ringi raadiusega. Kärbitud koonust nimetatakse sisse kirjutatud palliks, kui selle alused on palli pinna lõigud.

2 Olümpiaadiülesannete näited

2.1 Näiteid olümpiaadiülesannetest püramiidiga

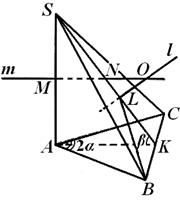
Näide 1. Kolmnurkses püramiidis S ABC serv BC on võrdne a, AB=AC, serv S Ja risti ABC püramiidi põhjaga, kahetahuline nurk servas S A on võrdne 2α , ja serval BC on võrdne β (joonis 6) . Leia piiritletud sfääri raadius.

Lahendus. Mõelge püramiidile S ABC, mida käsitletakse probleemipüstituses. Alates servast S.A. risti aluse tasapinnaga, siis

VA S = CAS= 90° ja seega ka nurk SINA on täpselt kahetahulise nurga lineaarnurk servas S.A.. Seega asub püramiidi põhjas võrdhaarne kolmnurk, mille nurk on 2 α ülaosas ja püramiidi kõrgus langeb kokku servaga S A.

Kuna külgmiste ribide projektsioonid S.B. Ja S KOOS aluse tasapinnal on võrdsed, siis on need servad ise võrdsed. Seetõttu serv IN S KOOS- võrdhaarne kolmnurk, mille kõrgus on tipust langetatud S, langeb keskele TO ribid Päike. Kolme risti teoreemi järgi AK- kolmnurga kõrgus SINA. Sellest on selge, et nurk S CA- kahetahulise nurga lineaarne nurk servas päike, st.

S CA = β .

Piiratud kuuli keskpunkt asub joone ristumiskohas l, tasapinnaga risti IN S KOOS ja läbides kolmnurga ümber piiritletud ringi keskpunkti IN S KOOS, serva keskosa läbiva tasapinnaga A S sellega risti. Otse l asub lennukis A S SAADA: tegelikult lennuk IN S KOOS läbib sirget päike, tasapinnaga risti A S TO, st lennukid IN S KOOS Ja A S TO risti; samal ajal otse l tasapinnaga risti IN S KOOS ja läbib nende tasandite lõikejoont nii, et see asub tasapinnal A S TO .

Niisiis, palli keskpunkt asub tasapinnal A S TO. Viime selle lennuki spetsiaalsele joonisele. Palli keskus KOHTA asub siis joone ristumiskohas l ja sirge m, risti A S ja läbib selle keskosa. Kuid üldiselt võib esineda kolm võimalust: otsene l Ja T lõikuvad kolmnurga sees või väljaspool A S TO või tema poolel ja me peame kaaluma kõiki neid võimalusi (vt joonis 7, 8, 9). Allpool näitame arvutuste käigus, et kahte neist ei ole tegelikult rakendatud. Oleme huvitatud raadiusest R piiritletud pall, st. kaugus punktist KOHTA- perpendikulaaride lõikepunktid T Ja l nurga külgedele TO S A- asja juurde S, selle nurga tipud. Kõigepealt leiame SL- vajaliku kauguse projekteerimine küljele S.K. kolmnurk KAS. Kuna kolmnurgas AK B(joon. 6) tunneme jalga VK=

A ja nurk KAV = α, See AK= A ctg α .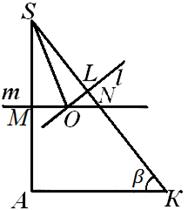

S.K. =

Sest L- kolmnurga kohta kirjeldatud keskpunkt IN S KOOS siis ringid L.S. = L IN, a sest kolmnurgast VC L leiame selle ( S TO- SL ) 2 +HF 2 =B L 2 , st.

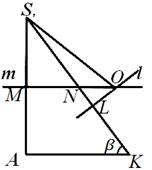
Märkides, et segmendi arvutused SL ei sõltunud kuidagi keskuse asukohast KOHTA kirjeldatud palli, pöördume tagasi joonise fig. 7, 8, 9. Tähistagem N sirge lõikepunkt m küljega S TO. On selge, et otse l Ja T ristuvad väljaspool kolmnurk CA S , Kui SN <SL(joonis 8); kui S N> SL , siis punkt KOHTA asub selle kolmnurga sees (joonis 7); lõpuks, kui SN = SL , siis punkt KOHTA asub küljel S TO see kolmnurk (joon. 9). Uurime välja, milline neist sätetest tegelikult aset leiab.

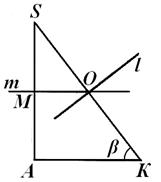
Sest MN CA S , See SN =

S TO. Segmentide pikkuste võrdlemine SN Ja SL, saame seda hõlpsalt tõestada mis tahes puhul a, α Ja

(geomeetrilistest kaalutlustest järeldub, et A> 0,0°<

< 90° ja 0°< β < 90°). Следовательно, каковы бы ни были размеры A , α Ja β püramiidid S ABC, Keskus KOHTA piiritletud pall asub alati väljaspool püramiidi. See omakorda tähendab, et tasapinnaline konfiguratsioon, mille oleme tasapinnas välja võtnud CA S võib olla ainult joonisel 8 näidatud kujul; asukohad, mis on näidatud joonisel fig. 7 ja 9 ei saa tegelikult toimuda. Vaadates joonist fig. 8, saame hõlpsasti näidata, et = β , ning seetõttu L.O. = NL tg β = (SL -S N) tg β. Asendades siin ülaltoodud avaldised SL Ja S N, saame pärast ilmseid arvutusi:

L O =

A tg α patt β .

Lõpuks täisnurksest kolmnurgast KOHTA L.S. leiame

= .

Nagu näeme, osutusid ülesande arvutused lihtsaks - lahenduse peamine raskus seisneb arutluskäigus, mis määrab piiritletud kuuli keskpunkti asukoha.

Vastus: R =

Näide 2. Korrapärane kolmnurkne püramiid, mille tipus on tasane nurk , on kantud kuuli raadiusega R. Leidke püramiidi ruumala ja näidatud püramiidi ümber kirjeldatud koonuse külgpind .

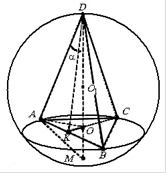
Lahendus. Püramiidi aluse külg olgu a, on selle püramiidi ümber kirjeldatud koonuse aluse raadius võrdne r, Siis

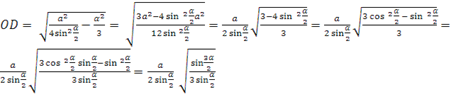(joonis 10). Püramiidi tahud on võrdhaarsed kolmnurgad. Siis DK– kõrgus, mediaan ja poolitaja  ABD. Täisnurksest kolmnurgast ADK meil on . Leia püramiidi kõrgus täisnurksest kolmnurgast AOD : ,

DM- palli läbimõõt. Seejärel läbimõõduga palli lõigus DM ja periood A, saame täisnurkse kolmnurga AMD. Meil on täisnurkse kolmnurga meetrilistest seostest

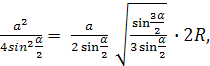kus

Seejärel leiame aluse pindala järgmise valemi abil:

Ja valemist

leida püramiidi ruumala: .

Edge AD definitsiooni järgi on piiritletud koonus selle generatrix. Seejärel leiame valemi abil piiritletud koonuse külgpinna S külg =  r l :

Vastus:

;

Näide 3. Püramiidi põhjas asub ruut küljega a. Püramiidi kõrgus läbib aluse ühe serva keskosa ja on võrdne

. Leidke püramiidi ümber piiratud sfääri raadius.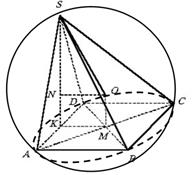

Lahendus. Tüüpiline viga selle ülesande lahendamisel on väide, et kirjeldatud sfääri keskpunkt asub serval SBC(joonis 11). Tegelikkuses punkti asukoht KOHTA pole servaga ühendatud SBC.

Punkti võrdse kauguse tõttu KOHTA tippudest S, A, B, C, D järgib seda OABCD- korrapärane nelinurkne püramiid. Seega äärele ABCD punkt KOHTA projitseeritakse punkti M– diagonaalide lõikepunkt. Kolmnurk A.S.D. võrdhaarne, siis püramiidi kõrgus S.K. on kolmnurga mediaan A.S.D. ,

. Täisnurksest kolmnurgast S.A.K. me leiame S.A. :

Seetõttu kolmnurk S.A.D.– võrdkülgsed ja OASD- korrapärane kolmnurkne püramiid. Siis punkt KOHTA projitseeritud äärele S.A.D. kolmnurga keskmesse S.A.D.. Siit

Kolmnurgast POEG leida vajalik raadius NII,

Vastus:

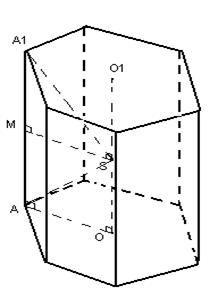
Näide 4. Raadiusega pallini R sisse on kirjutatud korrapärane kuusnurkne kärbitud püramiid, mille alumise aluse tasapind läbib kuuli keskpunkti ja külgserv moodustab aluse tasapinnaga nurga 60°

. Määrake püramiidi ruumala.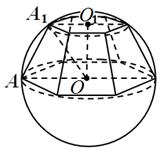

Lahendus. Tingimuste järgi,

OAA 1 = 60 (joonis 12); Tähendab, KOHTA 1 OA 1 = 30 ja A 1 KOHTA 1 = A 1 O = ,O.O. 1 = .

S alumine alus = 6

, Süleval põhilised = madalam põhilised .

Lõpuks saame

Vastus:

2.2 Olümpiaadiülesannete näited prismaga

Näide 1. Palliks, mille maht on võrdne V , täisnurkne kolmnurkne prisma on sisse kirjutatud. Prisma alus on teravnurgaga täisnurkne kolmnurk

ja selle suurim külgkülg on ruut. Leidke prisma ruumala.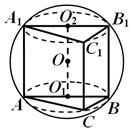

Lahendus. Esiteks määrame palli keskpunkti asukoha prisma suhtes. Kuuli lõigud prisma aluste tasandite järgi on ringid, millesse need alused on kantud (joonis 13) ja kuna prisma põhjad on võrdsed, on sektsioonide ringid võrdsed ja võrdsel kaugusel prisma alustest. palli keskpunkt. Iga keskus KOHTA 1 ja KOHTA 2 langeb kokku vastava hüpotenuusi keskkohaga.

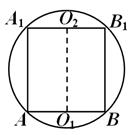
Kuuli lõikude omadustest tasapinna järgi on teada, et kuuli keskpunktist tõmmatud risti KOHTA ristlõike ringi tasapind, läbib selle ringi keskpunkti. Seega KOHTA 1 KOHTA

lennuk ABC. Otse KOHTA 1 KOHTA läbib ka O 2 ja tasapinnaga risti. Seega asub kuuli keskpunkt segmendi keskel asuval küljel O 1 O. Kõik prisma külgmised küljed on ristkülikud ja tahk - suurim neist (alates AB - kolmnurga hüpotenuus A Päike). See nägu on kokkuleppeliselt ruut. Palli osa näo tasapinnast on palli suur ring, seega on ringi raadius näidatud joonisel fig. 14, võrdne kuuli raadiusega R . Pange tähele, et prisma kõrgus AA 1 = a 4 = . Nüüd jääb üle vaid leida aluse pindala:

S A B KOOS =

. Alates (joonis 15)

meil on AC = AB

, Tähendab,

S A B KOOS =

Nüüd saame:

V auhind.

Tingimuste järgi,

R 3 = V ,

kus R 3 =

, järelikult,

V auhind.

Vastus: V auhind.

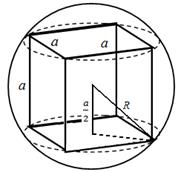
Näide 2. Leia vastavalt kera pinna ja ruumala suhe sissekirjutatud kuubi pinna ja ruumalaga

Lahendus. Olgu palli raadius R , kuubi serv on võrdne A;

Siis R 2 -

, kus a= .

Tähistame vastavalt sfääri ja kuubi ruumalasid ja pindu V 1 , V 2 , Ja S 1 , S 2 .

, V 2 = = , S 1 =4, S 2 = 6A 2 =8R 2 , V 2 = , S 1 S 2 = .

Vastus: V 1

V 2 = , S 1 S 2 = .

2.3 Olümpiaadiülesannete näited silindriga

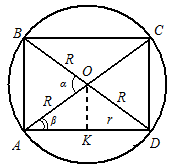
Näide. Leidke kera ruumala ja sellesse sfääri kantud parempoolse ringsilindri ruumala suhe, kui on teada, et silindri teljesuunalise lõigu diagonaalide vaheline väiksem nurk on võrdne

ja aluse läbimõõt on suurem kui silindri kõrgus (joon. 18).

Lahendus. Me teame sfääri mahtu

, ja leiame valemi abil silindri ruumala, kuid seetõttu

Lase ABCD- silindri teljesuunaline osa (vt joonis 18). Kuna aluse läbimõõt on suurem kui silindri kõrgus, siis

- nurk AOB. Kolmnurgast ABO sellest järeldub, et silindri kõrgus

Silindri aluse raadius

. .

Selgub, et

Asendame leitud andmed silindri mahu valemis:

;

Seega

Leiame suhte

Vastus:

2.4 Olümpiaadiülesannete näited koos koonus

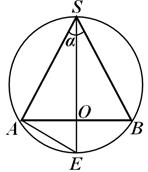
Näide 1. Raadiusega pallini R sisse on kirjutatud ringikujuline koonus; koonuse generatriksite vaheline nurk telglõikes on võrdne α-ga. Leidke kõrgus, mis moodustab koonuse aluse raadiuse.

Lahendus. Koonuse telge läbiv kuuli lõik on kuuli suur ring, milles

AB S(joon. 19), kus A IN- koonuse aluse läbimõõt. Jätkame koonuse kõrgust (telge). NII kuni see lõikub punktis suure ringiga E ja kaaluda E S V:

selles kolmnurgas

S.E. = 2R ,

S AE = 90° Ja A S E= .

A S = 2R

Nüüd alates

A OS leiame

A KOHTA = r = 2R

, NII = h= 2R

Vastus : SO= 2R

A S = 2R , A KOHTA =.

Näide 2. Koonuse kõrguse ja selle ümber oleva kuuli raadiuse suhe on võrdne k . Leidke nende kehade ruumalade suhe. Uuri välja, mille juures k ülesanne on mõttekas.

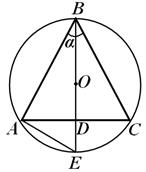
Lahendus. Vaatleme koonuse telglõike (joon. 20). Lase h- koonuse kõrgus, R- koonuse ümber piiratud sfääri raadius. Siis tingimusel,

=k, st. h = kR .

Väljendame raadiust r koonuse alus läbi R; olles kaalunud akorde AC Ja OLE, saame:

IN D

D E = A D D KOOS(sest AD=DC ,
- ristkülikukujuline, AD – kõrgus täisnurga tipust langenud).

(seega, k < 2).

V w =

; V k ==

Seega

, (0< k < 2).

Vastus:

, (0< k < 2).

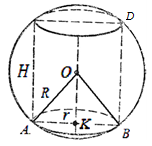
Näide 3. Tüvikoonuses on alumise ja ülemise aluse raadiused vastavalt võrdsed r 1 Ja r 2 , ja koonuse generatriks on alumise aluse tasapinna suhtes nurga all α (joonis 21). Leia sfääri raadius, millesse antud kärbikoonus on kantud.

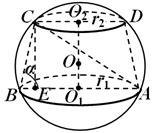
Lahendus. Tüvikoonuse telge läbivas palli lõigus saadakse suur kuuli ring, millesse on kantud trapets ABC D. Mõelgem

A päike, mis on samuti kirjutatud palli suurde ringi. Nurk selles kolmnurgas on teada KOOS B.A. = α . Siinuse teoreemi tõttu AC = 2R. Seega, et määrata R piisab leidmisest AC. Loobume asjast KOOS risti SE peal AB. Ilmselgelt

AE= r 1 + r 2 ,BE = r 1 - r 2,a CE = ( r 1 - r 2 )

Seega Pythagorase teoreemi järgi

= = = kust R =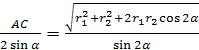

Vastus: R

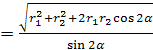3 Näited ühtse riigieksami ülesannetest

3.1 Näited ühtse riigieksami ülesannetest püramiidiga

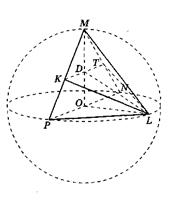
Näide 1. Segment P N , võrdne 8-ga, on sfääri läbimõõt. punktid M, L lamada sfääril nii, et püramiidi ruumala on P N M L suurim (joon. 22). Leidke kolmnurga K pindala L T, kus K ja T on PM servade keskpunktid ja N M vastavalt.

Lahendus. Lase KOHTA on sfääri keskpunkt ja R- selle raadius. Kuna R N = 2R= 8 ja punktid M Ja L lama siis sfääril VÕI = O L = O N = OM = R = 4. Sfääri lõiked tasapindade kaupa R LN Ja RM N- ringi raadius R = 4, kirjeldatud kolmnurkade kohta R LN Ja RM N , ja

RM N = R LN= 90°, kui sisse kirjutatud nurgad läbimõõdu põhjal R N .

Lase N- püramiidi kõrgus, ülalt alla lastud M, A h- kolmnurga kõrgus R LN , küljelt kinni hoitud R N . Alates punktist M asub sfääril ja tasapinnal R LN sisaldab siis sfääri keskpunkti N

R , ja N = R , Kui MO R NL . Samamoodi, alates punktist L asub siis sfääril h R , ja h = R , Kui L KOHTA R N .

Sellest ka püramiidi ruumala R N M L meil on

, .

Niisiis püramiid R N M L on suurim maht, kui kolmnurgad R LN Ja RM N ristkülikukujulised, võrdhaarsed ühise hüpotenuusiga R N, mis asub üksteisega risti asetsevates tasapindades. Kuna kolmnurgad L KOHTA N , L VÕI, L OM, ROM, N OM on kahel jalal võrdsed, siis kolmnurgad L M N Ja L HÄRRAõige küljega

NL =P L = PEAL

Sellest järeldub, et mediaanid L TO Ja L T need kolmnurgad on võrdsed ja

L TO =

= 2.

Kolmnurk TO L T võrdhaarne ja selle kõrgus LD on täisnurkse võrdhaarse kolmnurga mediaan L OM. Siit

LD =

= 2.

CT- kolmnurga keskjoon RM N ning seetõttu CT = 0,5R N =R . Seetõttu ala S TO L T =

CT LD = 4.

Vastus: 4

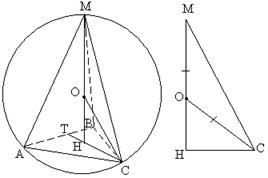
Näide 2. Tavalise kolmnurkse püramiidi korral on aluse külg 5 ja külgmised ribid on aluse suhtes 60 nurga all. O. Leidke püramiidi ümber piiratud sfääri raadius.

Lahendus. Lase ABCM näidatud püramiid (vt joonis 23) Kirjeldatud sfääri keskpunkt asub püramiidi kõrgusel, kuna püramiid on korrapärane.

Püramiidi kõrguse aluseks on kolmnurga keskpunkt ABC, st mediaanide lõikepunkt. Seejärel:

ST =

CH= = = .

Nüüd kaaluge kolmnurka MNS. Siin on nurk MSN külgserva vahelise nurgana on võrdne 60° PRL ja alus ABC. Nurk NMS võrdne 30-ga

. MO=OS nagu raadiused. Nii et see on kolmnurk MOS võrdhaarne. Nagu teate, on võrdkülgse kolmnurga aluse nurgad võrdsed. Seega OSM = Kohustuslik tervisekindlustus = 30, OSN = MSN - MCO = 60 - 30= 30.

Täisnurksest kolmnurgast OSN defineerime hüpotenuusi OS kasutades trigonomeetriliste funktsioonide seost täisnurkses kolmnurgas:

Vastus: O.C. =

3.2 Prismaga USE ülesannete näited

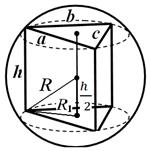
Näide 1. Prisma alus on külgedega kolmnurk a , b , c . Prisma kõrgus h (Joonis 25). Leia piiritletud sfääri raadius.

Lahendus. Kuna kera on ümbritsetud prisma ümber, on prisma sirge ja selle külgserv on võrdne selle kõrgusega. Prisma aluse ümber kirjeldatud ringi raadius arvutatakse valemiga

Vastus:

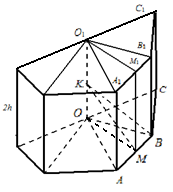
Näide 2. Palli raadius R . Kuulisse on kantud korrapärane n-nurkne prisma kõrgusega 2. h (Joonis 26). Leidke prisma aluse külg.

Lahendus. Lase TO– piiritletud sfääri keskpunkt. Meil on: K.B. = R , Okei = h. Lase OM

AB, Siis

O.B. =

(kolmnurgast OKB).

Kolmnurgast OMB leiame

a = 2M.B. = 2O.B.

Niisiis, a =

Vastus: a =

3.3 Näited ühtse riigieksami ülesannetest silindriga

Näide 1. Ringsilindri kõrgus on 10 võrra suurem kui aluse raadius ja kogupindala on 144

. Leia piiritletud sfääri raadius.

Lahendus. Piiratud sfääri raadius

(joonis 27).

Silindri pindala

, 144,

Lihtsustame seda väljendit:

Saame ruutvõrrandi

Leiame selle võrrandi juured

, ei sobi, kuna on negatiivne. Kõrgus

Leiame piiritletud sfääri raadiuse:

Vastus:

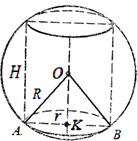
Näide 2. Sirge ringikujuline silinder on sisse kirjutatud kuuli (joonis 28). Mitu korda on kera ruumala suurem kui silindri ruumala, kui on teada, et kera raadiuse ja silindri põhja raadiuse suhe on poole suurem kui kera pinna suhe. kera silindri külgpinnale.

Lahendus. Kera ruumala suhe sissekirjutatud silindri ruumalasse

Tingimuste järgi on teada, et

; –

võrdkülgsed

Leiame sfääri ja sissekirjutatud silindri ruumalade suhte

Vastus: 16:9.

3.4 Koonusega ühtse riigieksami ülesannete näited

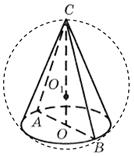
Näide 1. Koonuse aluse läbimõõt on 6 m, generatrix on aluse tasapinna suhtes 60° nurga all (joonis 29). Leidke koonuse ümber piiritletud sfääri pindala.

TAKSO võrdne nurgaga koonuse generaatori ja selle aluse pindala vahel. Sellepärast CAB= 60° ja võrdhaarne kolmnurk ABC -õige. Sellest järeldub

CA = AB = BC= 6 m.

Leiame koonuse ümber piiritletud sfääri keskpunkti asukoha. Sellise sfääri definitsiooni järgi on koonuse aluse ümbermõõt piiritletud sfääri lõik ja koonuse tipp asub sellel sfääril. Vastavalt selle mis tahes lõigu keskpunkti läbiva kera läbimõõdu omadusele sirgjoon CO risti koonuse aluse tasapinnaga ja seega ka keskpunktiga KOHTA 1 piiritletud sfäärist asub sirgel CO. Sellest järeldub, et keskus KOHTA 1 ümber koonuse ümbritsetud sfäärist on selle telglõike ümber ümbritsetud ringi keskpunkt.

Täisnurkses kolmnurgas

ABC R = O 1 C =

(m)

Leiame sfääri pindala:

(m2).

Vastus: 48

m 2.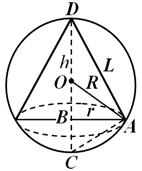

Näide 2. Raadiusega pallini R = 6 cm kõrgune kirjakoonus h (joonis 30). Väljendage koonuse ruumala ja külgpinda argumendi funktsioonina h .

Lahendus. Meil on:

Kus r - baasi raadius, L- koonuse moodustamine.

võttes arvesse, et r = VA – kõrgus, mis on langetatud täisnurga tipust hüpotenuusile, on meil: ja . Või r 2 ja

, .

Nüüd saame:

, .

Vastus:

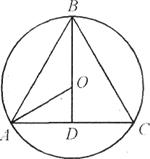
Näide 3. Kuuli on sisse kirjutatud koonus, mille generatriks on võrdne aluse läbimõõduga (joonis 31). Leidke koonuse pinna ja kuuli pinna suhe.

Lahendus. Kujutagem koonuse aksiaalset lõiku, mis läbib kuuli keskpunkti. Kuna koonuse aluse läbimõõt on võrdne generatriksiga, saame läbilõikes ringi sisse kirjutatud korrapärase kolmnurga (joonis 31). Olgu kuuli raadius võrdne R : Siis

AB =R

, A D =

Tähistame koonuse kogupinda tähisega S 1 ja palli pind läbi S 2. Meil on

kus S 1: S 2 = 9:16.

Vastus: S 1: S 2 = 9:16.

Järeldus

Uurimistöö käigus saime teada, et kirjeldatud valdkonnaga seotud ülesandeid pakutakse koolilastele ühtsel riigieksamil üsna sageli, seega on seda tüüpi ülesannete lahendamise oskus eksamite edukal sooritamisel väga oluline. Samuti esineb kirjeldatud alaga probleeme sageli erinevatel tasemetel matemaatikaolümpiaadidel. Asjakohased näited on toodud meie töös. Selles etapis piirdusime probleemide kaalumisega, mis on seotud piiritletud sfääri ja püramiidi, prisma, silindri ja koonuse kombinatsiooniga. Valitud ülesanded iseseisvaks tööks. Töö teostamise käigus kasutasime järgmisi meetodeid: töötamine teadusliku ja populaarteadusliku kirjandusega, info kogumine Internetis, analüüs, süstematiseerimine, klassifitseerimine ja töötlemine arvutis. Tulemused on praegu esitatud abstraktsel kujul. Edaspidi on plaanis tööd täiendada uute ülesannetega.

Bibliograafia

1. Abramovitš M.I., Starodubtsev M.T. Matemaatika (geomeetria ja trigonomeetrilised funktsioonid). Õpik ülikoolide ettevalmistusosakondadele - M: Kõrgkool, 1976. - 304 lk.

2. Voitovitš F.S. Geomeetriliste kehade kombinatsioonid: (kirjutatud ja piiritletud sfäärid): Raamat õpilastele. – Minsk: Narodnaja Asveta, 1992. – 160 lk.

3. Govorov V.M., Dybov P.T., Mirošin N.V. Ja teised.Matemaatika võistlusülesannete loetelu (koos metoodiliste juhiste ja lahendustega): õpik. – teine trükk – M: Nauka, 1986. – 384 lk.

4. Deništševa L.O., Bezrukova G.K., Boytšenko E.M. jt.Ühtne riigieksam, matemaatika, kontrollmõõtematerjalid - M: Haridus 2005. - 80 lk.

5. Deništševa L.O., Glazkov Yu.A., Krasnyanskaya K.A. jt Ühtne riigieksam. Matemaatika. Õppe- ja koolitusmaterjalid õpilaste ettevalmistamiseks / FIPI - M: Intellect-Center, 2008. - 240 lk.

6. Dorofejev G.V., Potapov K.M., Rozov N.Kh. Matemaatika käsiraamat ülikooli astujatele - M: Nauka 1972. - 528 lk.

7. Egerev V.K., Zaitsev V.V., Kordemsky B.A. 2500 matemaatikaülesannet lahendustega ülikoolidesse astujatele: - M: LLC kirjastus "ONICS 21st century": LLC kirjastus "Maailm ja haridus", 2002. - 912 lk.

8. Zvavich L.I., Rjazanovski A.R. Geomeetria tabelites - M: Bustard 2007. - 128 lk.

9. Klimin S.V., Strunkina T.V., Panteleeva E.I. jt.Ühtne riigieksam, kontrolltöö ülesanded - M: Haridus 2002. - 24 lk.

10. Modenov V.P., Dorofejev G.V., Novoselov S.I. ja teised.Matemaatika käsiraamat - M: Moskva Ülikooli kirjastus, 1972. - 404 lk.

11. Shuvalova E.Z., Kaplun V.I. Geomeetria: õpik ülikoolide ettevalmistusosakondadele - M: Kõrgkool, 1980. - 265 lk.

12. http://kvant.mirror1.mccme.ru/pdf/2000/06/kv0600solut.pdf

13. http://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D1%80%D1%82%D0%B0%D0%BB:%D0%9D%D0%B0%D1% 83%D0%BA%D0%B0

14. http://rgp.nm.ru/geometriia/praktika11/zadatcha119.html

Rakendus. Ülesanded iseseisvaks lahendamiseks

1. Püramiidis FABC servad ABF Ja ABC risti, B.F. :F.A. = 15:11. Sirge vahelise nurga puutuja B.C. ja lennuk ABF võrdub 5. Punkt M servast valitud B.C. Niisiis B M :M C = 4:11. Punkt T asub sirgjoonel F.A. ja punktidest võrdsel kaugusel M Ja IN. Püramiidi ümber piiratud sfääri keskpunkt FABC , asub äärel AB, selle sfääri pindala on 36

. Leidke püramiidi ruumala ASMT. (Vastus: 6)

2. Püramiidi alus FABCD on ristkülik ABCD . Lennuk A.F.C. tasapinnaga risti ABC , nurga puutuja FAC võrdub

, sirge vahelise nurga puutuja B.C. ja lennuk A.F.C. võrdne . Punkt M asub äärel B.C. , VM =B.C. . Punkt L asub sirgjoonel F.A. ja punktidest võrdsel kaugusel M Ja C . Püramiidi ruumala L IN D M võrdub 72. Püramiidi ümber piiritletud sfääri keskpunkt FABCD , asub selle aluse tasapinnal. Leidke selle sfääri raadius. (Vastus: 5)

3. Tavalise püramiidi lähedal FABC kirjeldab sfääri, mille kese asub aluse tasapinnal ABC püramiidid. Punkt M asub äärel AB Niisiis A M :M B=1:3. Punkt T asub sirgjoonel F.A. ja punktist võrdsel kaugusel M Ja IN. Püramiidi ruumala TVSM võrdub

. Leidke püramiidiga ümbritsetud sfääri raadius FABC . (Vastus: )

4. Joonelõik AB- sfääri läbimõõt. Punktid KOOS, D ABCD suurim. Leidke joontevahelise nurga koosinus CM Ja AB, Kui M– ribi keskosa BD . (Vastus:

)

5. Joonelõik R N , võrdne 8-ga, on sfääri läbimõõt. Punkt M, L lamada sfääril nii, et püramiidi maht R N M L suurim. Leidke kolmnurga pindala KLT , Kus K Ja T – ribide keskel RM Ja N M vastavalt. (Vastus: 4

)

6. Antud on sfäär raadiusega 6. Sfääri ristlõige tasapinna järgi on läbimõõduga ring CT. Lõiketasand eemaldatakse sfääri keskpunktist 5. Punkti kaugusel R on valitud sfääril ja punkt L RK L T suurim. Leidke sirge vaheline nurk L.M. ja lennuk PTK , Kui M keskribi RK. (Vastus: 30

)

7. Kesklinna kaudu KOHTA F on valitud sfääril ja punktid A , B , C , D – FABCD suurim. Punktid M, T, L – ribide keskel FB , CD Ja AD vastavalt. Kolmnurga pindala MLT võrdne 64-ga

. Leidke sfääri raadius. (Vastus: 2)

8. Kesklinna kaudu KOHTA sellest sfäärist tehakse lõik. Punkt F on valitud sfääril ja punktid A , B , C , D – järjestikku ristlõike ringil nii, et püramiidi ruumala FABCD suurim. Leidke sirge vahelise nurga siinus OLEN ja lennuk B.F.D. . (Vastus:

)

9. Antud on kera raadiusega 10. Selle sfääri tasapinnaline läbilõige on ring läbimõõduga AB. Lõiketasand eemaldatakse sfääri keskpunktist 8. Punkti kaugusel D on valitud sfääril ja punkt KOOS– ristlõike ümbermõõdul nii, et püramiidi ruumala ABC D suurim. Leidke näo piirkond ACD .(Vastus: 27

)

10. Püramiidi alus on ristkülik. Tasapind on tasapinnaga risti ABC, sirge vahelise nurga puutuja Päike ja lennuk FAC võrdub 2. Punkt M asub äärel Päike Ja MV =

Punkt L asub sirgjoonel F.A. ja punktidest võrdsel kaugusel M Ja KOOS. Püramiidi ümber piiratud sfääri keskpunkt F.A. IN CD, asub püramiidi aluse tasapinnal, selle sfääri raadius on 4. Leia püramiidi ruumala L.A. PRL. (Vastus: 48)

11. Palliks, raadius 2

ABCA 1 IN 1 KOOS 1 . Otse AC 1 Vormid tasapinnaga ABB (Vastus: 288)

12. Korrapärane kolmnurkne prisma on kantud sfääri ABCA 1 IN 1 KOOS 1, mille maht on 4,5. Otse VA 1 vormib tasapinnaga VSS 1 nurk45

. Leidke sfääri pindala. (Vastus: 11)

13. Raadiusega palliks

on sisse kirjutatud korrapärane kolmnurkne prisma ABCA 1 IN 1 KOOS 1 . Otse AB 1 vormib tasapinnaga ACC 1 nurk 45. Leia prisma ruumala. (Vastus: 36)

14. Arvutage korrapärase kolmnurkse prisma servad, teades raadiust R piiritletud kera ja kaldenurk α selle kuuli raadius, mis on tõmmatud prisma tipuni, seda tippu sisaldava külgpinnani. (Vastus: 2

)

15. Raadiusega pallini R sisse on kirjutatud parempoolne ringkoonus. Leidke koonuse külgpind, kui selle kõrgus on h . (Vastus:

)

16. Sfääri sisse on kirjutatud koonus. Koonuse aksiaalne ristlõikepindala on võrdne S. Selle kõrguse ja generaatori vaheline nurk on võrdne α . Leidke sfääri ruumala. (Vastus:

)

17. Määrake koonuse külgpind, teades raadiuse pikkust R selle ümber piiratud kera ja nurk α, mille all on kuuli keskpunktist nähtav koonuse generatrix. (Vastus:

)

18. Leidke kuuli sisse kirjutatud parempoolse koonuse kogupindala ja selle kuuli pindala suhe, kui koonuse telglõike tipus on nurk võrdne α Ja

. (Vastus:

)

19. Koonus on kuuli sisse kirjutatud nii, et selle kõrgus jagatakse kuuli keskpunktiga keskmise ja äärmise suhtega. Leidke nurk koonuse teljesuunalise lõigu tipus. Määrake, mitu korda on sfääri ruumala suurem kui koonuse ruumala. (Vastus:

; 4 korda )

Näide 2.Tavalise kolmnurkse püramiidi korral on aluse külg 5 ja külgmised ribid on aluse suhtes 60 nurga all. O. Leidke püramiidi ümber piiratud sfääri raadius.

Lahendus. Lase ABCM näidatud püramiid (vt joonis 23) Kirjeldatud sfääri keskpunkt asub püramiidi kõrgusel, kuna püramiid on korrapärane.

Püramiidi kõrguse aluseks on kolmnurga keskpunkt ABC, st mediaanide lõikepunkt. Seejärel:

CH= ST = CH= = = .

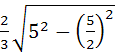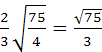Nüüd kaaluge kolmnurka MNS. Siin on nurk MSN külgserva vahelise nurgana on võrdne 60° PRL ja alus ABC. Nurk NMS võrdub 30. MO=OS nagu raadiused. Nii et see on kolmnurk MOS võrdhaarne. Nagu teate, on võrdkülgse kolmnurga aluse nurgad võrdsed. Seega

OSM = Kohustuslik tervisekindlustus = 30, OSN = MSN - MCO = 60 - 30= 30.

Täisnurksest kolmnurgast OSN defineerime hüpotenuusi OS kasutades trigonomeetriliste funktsioonide seost täisnurkses kolmnurgas:

OS= = .

Vastus: O.C.= .

3.2 Prismaga USE ülesannete näited

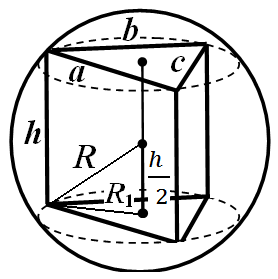
Näide 1.Prisma alus on külgedega kolmnurka, b, c. Prisma kõrgush(Joonis 25). Leia piiritletud sfääri raadius.

Lahendus. Kuna kera on ümbritsetud prisma ümber, on prisma sirge ja selle külgserv on võrdne selle kõrgusega. Prisma aluse ümber kirjeldatud ringi raadius arvutatakse valemiga

Vastus:

Näide 2.Palli raadiusR. Kuulisse on kantud korrapärane n-nurkne prisma kõrgusega 2.h(Joonis 26). Leidke prisma aluse külg.

Lahendus. Lase TO– piiritletud sfääri keskpunkt. Meil on: K.B.= R, Okei= h. Lase OMAB, Siis

O.B.=

(kolmnurgast OKB).

Kolmnurgast OMB leiame

a= 2M.B.= 2O.B..

Niisiis, a= .

Vastus: a= .

3.3 Näited ühtse riigieksami ülesannetest silindriga

Näide 1.Ringsilindri kõrgus on 10 võrra suurem kui aluse raadius ja kogupindala on 144. Leia piiritletud sfääri raadius.

Lahendus. Piiratud sfääri raadius

Silindri pindala

Lihtsustame seda väljendit:

Saame ruutvõrrandi

Leiame selle võrrandi juured

Juur ei sobi, kuna on negatiivne. Kõrgus

Leiame piiritletud sfääri raadiuse:

Vastus: .

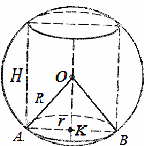
Näide 2.Sirge ringikujuline silinder on sisse kirjutatud kuuli (joonis 28). Mitu korda on kera ruumala suurem kui silindri ruumala, kui on teada, et kera raadiuse ja silindri põhja raadiuse suhe on poole suurem kui kera pinna suhe. kera silindri külgpinnale.

Lahendus. Kera ruumala suhe sissekirjutatud silindri ruumalasse

Tingimuste järgi on teada, et

võrdkülgsed

Leiame sfääri ja sissekirjutatud silindri ruumalade suhte

Vastus: 16:9.

3.4 Koonusega ühtse riigieksami ülesannete näited

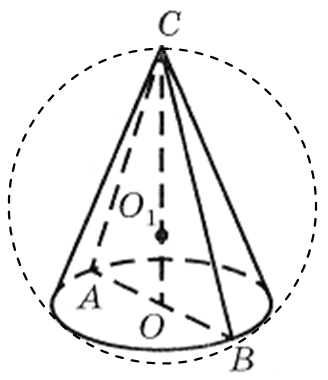
Näide 1.Koonuse aluse läbimõõt on 6 m, generatrix on aluse tasapinna suhtes 60° nurga all (joonis 29). Leidke koonuse ümber piiritletud sfääri pindala.

Lahendus. Lase KOOS - koonuse ülaosa KOHTA - selle aluse keskpunkt, DIA - koonuse aksiaalne osa. Kuna koonuse generatriks on aluse tasapinna suhtes 60° nurga all ja CO on koonuse kõrgus, seejärel sirgjoon AB - otseprojektsioon SA koonuse aluse tasapinnale. Seega TAKSO võrdne nurgaga koonuse generaatori ja selle aluse pindala vahel. Sellepärast CAB= 60° ja võrdhaarne kolmnurk ABC -õige. Sellest järeldub

CA = AB = BC= 6 m.

Leiame koonuse ümber piiritletud sfääri keskpunkti asukoha. Sellise sfääri definitsiooni järgi on koonuse aluse ümbermõõt piiritletud sfääri lõik ja koonuse tipp asub sellel sfääril. Vastavalt selle mis tahes lõigu keskpunkti läbiva kera läbimõõdu omadusele sirgjoon CO risti koonuse aluse tasapinnaga ja seega ka keskpunktiga KOHTA 1 piiritletud kera asub sirgel CO. Sellest järeldub, et keskus KOHTA 1 koonuse ümber ümbritsetud kera on ümber selle telglõike ümbritsetud ringi keskpunkt.

Täisnurkses kolmnurgas

ABCR= O 1 C= (m)

Näide 3.Kuuli on sisse kirjutatud koonus, mille generatriks on võrdne aluse läbimõõduga (joonis 31). Leidke koonuse pinna ja kuuli pinna suhe.

AB= R , AD =

Tähistame koonuse kogupinda tähisega S 1 ja palli pind läbi S 2. Meil on

kus S 1: S 2 = 9:16.

Vastus:S 1: S 2 = 9:16.

Järeldus

Bibliograafia

Abramovitš M.I., Starodubtsev M.T. Matemaatika (geomeetria ja trigonomeetrilised funktsioonid). Õpik ülikoolide ettevalmistusosakondadele - M: Kõrgkool, 1976. - 304 lk.

Voitovich F.S. Geomeetriliste kehade kombinatsioonid: (kirjutatud ja piiritletud sfäärid): Raamat õpilastele. – Minsk: Narodnaja Asveta, 1992. – 160 lk.

Govorov V.M., Dybov P.T., Mirošin N.V. Ja teised.Matemaatika võistlusülesannete loetelu (koos metoodiliste juhiste ja lahendustega): õpik. – teine trükk – M: Nauka, 1986. – 384 lk.

Deništševa L.O., Bezrukova G.K., Boychenko E.M. jt.Ühtne riigieksam, matemaatika, kontrollmõõtematerjalid - M: Haridus 2005. - 80 lk.

Deništševa L.O., Glazkov Yu.A., Krasnyanskaya K.A. jt Ühtne riigieksam. Matemaatika. Õppe- ja koolitusmaterjalid õpilaste ettevalmistamiseks / FIPI - M: Intellect-Center, 2008. - 240 lk.

Dorofejev G.V., Potapov K.M., Rozov N.Kh. Matemaatika käsiraamat ülikooli astujatele - M: Nauka 1972. - 528 lk.

Egerev V.K., Zaitsev V.V., Kordemsky B.A. 2500 matemaatikaülesannet lahendustega ülikoolidesse astujatele: - M: LLC kirjastus "ONICS 21st century": LLC kirjastus "Maailm ja haridus", 2002. - 912 lk.

Zvavich L.I., Rjazanovski A.R. Geomeetria tabelites - M: Bustard 2007. - 128 lk.

Klimin S.V., Strunkina T.V., Panteleeva E.I. jt.Ühtne riigieksam, kontrolltöö ülesanded - M: Haridus 2002. - 24 lk.

Modenov V.P., Dorofejev G.V., Novoselov S.I. ja teised.Matemaatika käsiraamat - M: Moskva Ülikooli kirjastus, 1972. - 404 lk.

Shuvalova E.Z., Kaplun V.I. Geomeetria: õpik ülikoolide ettevalmistusosakondadele - M: Kõrgkool, 1980. - 265 lk.

http :// kvant. peegel1. mccme. ru/ pdf/2000/06/ kv0600 lahus. pdf

http :// ru. wikipedia. org/ wiki/% D0%9 F% D0% OLE% D1%80% D1%82% D0% B0% D0% BB:% D0%9 D% D0% B0% D1%83% D0% B.A.% D0% B0

rgp . nm. ru/ geomeetria/ praktika11/ zadacha119. html

Rakendus. Ülesanded iseseisvaks lahendamiseks

Teema “Erinevad ülesanded hulktahukal, silindril, koonusel ja kuulil” on 11. klassi geomeetria kursuse üks raskemaid. Enne geomeetriliste ülesannete lahendamist tutvuvad nad tavaliselt teooria vastavate osadega, millele ülesannete lahendamisel viidatakse. S. Atanasyani ja teiste selleteemalisest õpikust (lk 138) võib leida vaid sfääri ümber kirjeldatud hulktahuka, sfääri sisse kirjutatud hulktahuka, polüeedrisse kantud sfääri ja sfääri ümber kirjeldatud sfääri definitsioonid. hulktahukas. Selle õpiku metoodilistes soovitustes (vt S. M. Sahakyani ja V. F. Butuzovi raamatut „Geomeetria õppimine 10.–11. klassis”, lk 159) on kirjas, milliseid kehade kombinatsioone ülesannete nr 629–646 lahendamisel arvesse võetakse, ja juhitakse tähelepanu. asjaolule, et „konkreetse probleemi lahendamisel tuleb eelkõige tagada, et õpilased saaksid hästi aru tingimuses märgitud kehade suhtelistest asenditest“. Järgnevalt on toodud ülesannete nr 638(a) ja nr 640 lahendus.

Arvestades kõike eeltoodut ja asjaolu, et õpilaste jaoks on kõige raskemad probleemid palli kombineerimine teiste kehadega, on vajalik vastavad teoreetilised põhimõtted süstematiseerida ja õpilastele edastada.

Definitsioonid.

1. Kuuli nimetatakse polüeedrisse sissekirjutatuks ja kuuli ümber kirjeldatavaks hulktahuks, kui kuuli pind puudutab hulktahuka kõiki tahke.

2. Kuuli nimetatakse ümber hulktahukaks piiritletuks ja kuuli sissekirjutatuks, kui kuuli pind läbib kõik hulktahuka tipud.

3. Kuuli nimetatakse silindrisse, tüvikoonusesse (koonusesse) ja silindrisse, tüvikoonusesse (koonusesse), kui kuuli pind puudutab aluseid (aluseid) ja kõik silindri generatriksid, tüvikoonus (koonus).

(Sellest definitsioonist järeldub, et kuuli suurring võib olla kantud nende kehade mis tahes telglõikesse).

4. Kuuli nimetatakse ümber silindri, tüvikoonuse (koonuse), kui aluste ringid (alusring ja tipp) kuuluvad kuuli pinnale.

(Sellest definitsioonist järeldub, et nende kehade mis tahes telglõike ümber saab kirjeldada kuuli suurema ringi ringjoont).

Üldised märkused palli keskpunkti asukoha kohta.

1. Hulktahukasse kantud kuuli kese asub polüeedri kõigi kahetahuliste nurkade poolitajate tasandite lõikepunktis. See asub ainult hulktahuka sees.

2. Hulktahuka ümber ümbritsetud kuuli keskpunkt asub hulktahuka kõigi servadega risti olevate ja nende keskpunkte läbivate tasapindade lõikepunktis. See võib asuda polüeedri sees, pinnal või väljaspool.

Kera ja prisma kombinatsioon.

1. Sirgesse prismasse kantud kuul.

1. teoreem. Kera saab sirge prisma sisse kirjutada siis ja ainult siis, kui prisma põhja saab kirjutada ringjoone ja prisma kõrgus on võrdne selle ringi läbimõõduga.

Järeldus 1. Parempoolsesse prismasse kantud sfääri keskpunkt asub prisma kõrguse keskpunktis, mis läbib alusesse kantud ringi keskpunkti.

Järeldus 2. Eelkõige saab kuuli kirjutada sirgjoontega: kolmnurkne, korrapärane, nelinurkne (milles aluse vastaskülgede summad on üksteisega võrdsed) tingimusel H = 2r, kus H on kuuli kõrgus. prisma, r on alusesse kantud ringi raadius.

2. Prisma ümber piiratud kera.

2. teoreem. Kera saab kirjeldada prisma ümber siis ja ainult siis, kui prisma on sirge ja selle aluse ümber saab kirjeldada ringjoont.

Järeldus 1. Ümber sirge prisma ümbritsetud sfääri keskpunkt asub prisma kõrguse keskpunktis, mis on tõmmatud läbi aluse ümber piiratud ringi keskpunkti.

Järeldus 2. Eelkõige võib palli kirjeldada: täisnurkse kolmnurkse prisma lähedal, korrapärase prisma lähedal, ristkülikukujulise rööptahuka lähedal, täisnurkse nelinurkse prisma lähedal, milles aluse vastasnurkade summa on 180 kraadi.

L.S.Atanasyani õpikust saab palli ja prisma kombinatsiooni jaoks välja pakkuda ülesanded nr 632, 633, 634, 637(a), 639(a,b).

Palli ja püramiidi kombinatsioon.

1. Püramiidi lähedal kirjeldatud pall.

3. teoreem. Palli saab kirjeldada ümber püramiidi siis ja ainult siis, kui saab kirjeldada ringi ümber selle aluse.

Järeldus 1.Ümber püramiidi ümbritsetud sfääri keskpunkt asub püramiidi põhjaga risti oleva sirge lõikepunktis, mis läbib selle aluse ümber ümbritsetud ringi keskpunkti ja tasandit, mis on risti mis tahes külgservaga, mis on tõmmatud läbi püramiidi keskosa. see serv.

Järeldus 2. Kui püramiidi külgservad on üksteisega võrdsed (või aluse tasapinna suhtes võrdselt kallutatud), siis saab sellise püramiidi ümber kirjeldada kuuli, mille keskpunkt asub sel juhul püramiidi (või selle laiendi) kõrgus tasapinnas paikneva külgserva sümmeetriateljega külgserv ja kõrgus.

Järeldus 3. Eriti palli saab kirjeldada: kolmnurkpüramiidi lähedal, tavalise püramiidi lähedal, nelinurkse püramiidi lähedal, mille vastasnurkade summa on 180 kraadi.

2. Püramiidi sisse kirjutatud pall.

4. teoreem. Kui püramiidi külgpinnad on aluse suhtes võrdselt kallutatud, saab sellisesse püramiidi sisse kirjutada palli.

Järeldus 1. Püramiidi, mille külgpinnad on aluse suhtes võrdselt kallutatud, kantud kuuli kese asub püramiidi kõrguse lõikepunktis püramiidi põhjas asuva mis tahes kahetahulise nurga lineaarnurga poolitajaga, mille külg millest on püramiidi tipust tõmmatud külgpinna kõrgus.

Järeldus 2. Tavalisse püramiidi saab sobitada palli.

L.S.Atanasyani õpikust saab palli ja püramiidi kombineerimiseks välja pakkuda ülesanded nr 635, 637(b), 638, 639(c), 640, 641.

Kombinatsioon pallist kärbitud püramiidiga.

1. Korrapärase kärbitud püramiidi ümber piiratud pall.

5. teoreem. Sfääri saab kirjeldada mis tahes korrapärase kärbitud püramiidi ümber. (See tingimus on piisav, kuid mitte vajalik)

2. Korrapärasesse kärbitud püramiidi sisse kirjutatud kuul.

6. teoreem. Kuuli saab kirjutada tavalisesse kärbitud püramiidi siis ja ainult siis, kui püramiidi apoteem on võrdne aluste apoteemide summaga.

L. S. Atanasyani õpikus (nr 636) on palli ja kärbitud püramiidi kombinatsiooni puhul vaid üks probleem.

Kombinatsioon palli ümarate kehadega.

7. teoreem. Kera võib kirjeldada silindri, tüvikoonuse (sirge ringikujulise) või koonuse ümber.

8. teoreem. Kuuli saab kirjutada (sirgesse ümmargusesse) silindrisse siis ja ainult siis, kui silinder on võrdkülgne.

9. teoreem. Saate palli sobitada mis tahes koonusesse (sirge ringikujuline).

10. teoreem. Kuuli saab kirjutada kärbikoonusesse (sirgesse ringikujuliseks) siis ja ainult siis, kui selle generaator on võrdne aluste raadiuste summaga.

L.S.Atanasyani õpikust saab välja pakkuda ülesanded nr 642, 643, 644, 645, 646 ümarate kehadega palli kombineerimiseks.

Selle teema materjali edukamaks õppimiseks on vaja tundidesse lisada suulisi ülesandeid:

1. Kuubi serv võrdub a-ga. Leidke kuulide raadiused: kirjutatud kuubikusse ja ümbritsetud selle ümber. (r = a/2, R = a3).

2. Kas on võimalik kirjeldada kera (palli) ümber: a) kuubi; b) ristkülikukujuline rööptahukas; c) kaldus rööptahukas, mille põhjas on ristkülik; d) sirge rööptahukas; e) kaldus rööptahukas? a) jah; b) jah; c) ei; d) ei; d) ei)

3. Kas vastab tõele, et sfääri saab kirjeldada mis tahes kolmnurkse püramiidi ümber? (jah)

4. Kas suvalise nelinurkse püramiidi ümber olevat kera on võimalik kirjeldada? (Ei, mitte ühegi nelinurkse püramiidi lähedal)

5. Millised omadused peavad olema püramiidil, et kirjeldada teda ümbritsevat kera? (Selle põhjas peaks olema hulknurk, mille ümber saab kirjeldada ringi)

6. Püramiid on sisse kirjutatud sfääri, mille külgserv on aluse suhtes risti. Kuidas leida kera keskpunkt? (Sfääri keskpunkt on kahe ruumipunktide geomeetrilise lookuse lõikepunkt. Esimene on risti, mis on tõmmatud püramiidi aluse tasapinnaga läbi selle ümberringi keskpunkti. Teine on tasapind risti etteantud külgservaga ja tõmmatud läbi selle keskosa)

7. Millistel tingimustel saab kirjeldada prisma ümber olevat kera, mille põhjas on trapets? (Esiteks peab prisma olema sirge ja teiseks peab trapets olema võrdhaarne, et selle ümber saaks kirjeldada ringjoont)

8. Milliseid tingimusi peab prisma täitma, et selle ümber saaks kirjeldada sfääri? (Prisma peab olema sirge ja selle alus peab olema hulknurk, mille ümber saab kirjeldada ringi)

9. Kolmnurkse prisma ümber kirjeldatakse kera, mille keskpunkt asub prismast väljaspool. Milline kolmnurk on prisma alus? (nüri kolmnurk)

10. Kas on võimalik kirjeldada kera ümber kaldprisma? (Ei, sa ei saa)

11. Millisel tingimusel paikneb täisnurkse kolmnurkse prisma ümber piiritletud sfääri keskpunkt prisma ühel külgpinnal? (Alus on täisnurkne kolmnurk)

12. Püramiidi alus on võrdhaarne trapets Püramiidi tipu ortogonaalprojektsioon aluse tasapinnale on trapetsist väljaspool asuv punkt. Kas sellise trapetsi ümber olevat kera on võimalik kirjeldada? (Jah, saab. Asjaolu, et püramiidi tipu ristprojektsioon asub väljaspool selle alust, ei oma tähtsust. Oluline on, et püramiidi põhjas asub võrdhaarne trapets – hulknurk, mille ümber saab ringjoont teha. kirjeldatud)

13. Korrapärase püramiidi lähedal kirjeldatakse kera. Kuidas asub selle keskpunkt püramiidi elementide suhtes? (Sfääri keskpunkt on risti, mis on tõmmatud aluse tasapinnaga läbi selle keskpunkti)

14. Mis tingimusel asub täisnurkse kolmnurkse prisma ümber kirjeldatud sfääri keskpunkt: a) prisma sees; b) väljaspool prismat? (Prisma põhjas: a) terav kolmnurk; b) nüri kolmnurk)

15. Kirjeldatakse kera ristkülikukujulise rööptahuka ümber, mille servad on 1 dm, 2 dm ja 2 dm. Arvutage sfääri raadius. (1,5 dm)

16. Millisesse tüvikoonusesse kera mahub? (Tärkkoonuses, mille telglõikesse saab sisse kirjutada ringjoone. Koonuse telglõik on võrdhaarne trapets, selle aluste summa peab olema võrdne tema külgmiste külgede summaga. Teisisõnu, koonuse aluste raadiuste summa peab olema võrdne generaatoriga)

17. Tüvikoonusesse on sisse kirjutatud kera. Millise nurga all on koonuse generatriks sfääri keskpunktist nähtav? (90 kraadi)

18. Milline omadus peab olema sirgel prismal, et sellesse saaks sisse kirjutatud kera? (Esiteks peab sirge prisma põhjas olema hulknurk, kuhu saab kirjutada ringi, ja teiseks peab prisma kõrgus olema võrdne alusesse kantud ringi läbimõõduga)

19. Too näide püramiidist, mis ei mahu sfääri külge? (Näiteks nelinurkne püramiid, mille põhjas on ristkülik või rööpkülik)

20. Sirge prisma põhjas on romb. Kas sellesse prismasse on võimalik kera mahutada? (Ei, see on võimatu, kuna üldiselt on võimatu kirjeldada ringi ümber rombi)

21. Mis tingimusel saab sfääri kirjutada täisnurksesse kolmnurkprismasse? (Kui prisma kõrgus on kaks korda suurem kui alusesse kantud ringi raadius)

22. Millisel tingimusel saab kera kirjutada korrapärasesse nelinurksesse tüvipüramiidi? (Kui antud püramiidi ristlõige on tasapind, mis läbib sellega risti oleva aluse külje keskkohta, on tegemist võrdhaarse trapetsiga, millesse saab kirjutada ringi)

23. Kolmnurksesse tüvipüramiidi on sisse kirjutatud kera. Milline püramiidi punkt on sfääri keskpunkt? (Sellesse püramiidi sisse kirjutatud sfääri keskpunkt on püramiidi ja aluse külgpindade poolt moodustatud kolme nurkade poolitamise tasandi ristumiskohas)

24. Kas silindri ümber olevat kera on võimalik kirjeldada (parem ringjoon)? (Jah, sa saad)

25. Kas on võimalik kirjeldada kera ümber koonuse, tüvikoonust (sirge ringikujuline)? (Jah, saate mõlemal juhul)

26. Kas sfääri saab kirjutada mis tahes silindrisse? Millised omadused peavad olema silindril, et sellesse kera mahutada? (Ei, mitte iga kord: silindri teljesuunaline osa peab olema ruudukujuline)

27. Kas kera saab kirjutada mis tahes koonusesse? Kuidas määrata koonusesse kirjutatud kera keskpunkti asukohta? (Jah, absoluutselt. Sissekirjutatud sfääri keskpunkt on koonuse kõrguse ja generatriksi kaldenurga poolitaja ristumiskohas aluse tasapinnaga)

Autor usub, et kolmest planeerimistunnist teemal “Erinevad probleemid polüeedril, silindril, koonusel ja kuulil” on soovitatav pühendada kaks õppetundi palli teiste kehadega kombineerimise probleemide lahendamisele. Eespool toodud teoreeme ei ole soovitatav tõestada, kuna tunnis pole piisavalt aega. Saate kutsuda õpilasi, kellel on selleks piisavad oskused, neid tõestama, näidates ära (õpetaja äranägemisel) tõendamise kursuse või kava.