Trigonomeetriliste funktsioonide integraalide tabel. Trigonomeetriliste funktsioonide integreerimine

Trigonomeetriliste funktsioonide integraalid.
Näited lahendustest

Selles õppetükis vaatleme trigonomeetriliste funktsioonide integraale, see tähendab, et integraalide täitmine on siinused, koosinused, puutujad ja kotangensid erinevates kombinatsioonides. Kõiki näiteid analüüsitakse üksikasjalikult, ligipääsetavad ja arusaadavad isegi teekannu jaoks.

Trigonomeetriliste funktsioonide integraalide edukaks uurimiseks peate hästi aru saama kõige lihtsamatest integraalidest ja valdama mõningaid integreerimisvõtteid. Nende materjalidega saate tutvuda loengutes Määramatu integraal. Näited lahendustest Ja .

Ja nüüd vajame: Integraalide tabel, Tuletisinstrumentide tabel Ja Trigonomeetriliste valemite kataloog. Kõik õppevahendid on leitavad lehelt Matemaatilised valemid ja tabelid. Soovitan kõik välja printida. Ma keskendun eriti trigonomeetrilistele valemitele, need peaksid olema teie silme ees– ilma selleta väheneb töö efektiivsus märgatavalt.

Kuid kõigepealt selle kohta, millised integraalid selles artiklis on Ei. Vormi integraale ei ole, - koosinus, siinus, korrutatuna mõne polünoomiga (harvemini midagi puutuja või kotangensiga). Sellised integraalid integreeritakse osade kaupa ja meetodi õppimiseks külastage õppetükki Integreerimine osade kaupa. Lahendusnäited Ka siin puuduvad “kaarega” integraalid – arktangens, arcsiinus jne, samuti on need kõige sagedamini integreeritud osade kaupa.

Trigonomeetriliste funktsioonide integraalide leidmisel kasutatakse mitmeid meetodeid:

(4) Kasutame tabelivalemit , ainus erinevus on see, et “X” asemel on meil keeruline avaldis.

Näide 2

Näide 3

Leidke määramatu integraal.

Žanri klassika neile, kes võistlusel uppuvad. Nagu ilmselt märkasite, pole integraalide tabelis puutuja ja kotangensi integraali, kuid sellegipoolest võib selliseid integraale leida.

(1) Kasutame trigonomeetrilist valemit

(2) Toome funktsiooni diferentsiaalmärgi alla.

(3) Kasutame tabeliintegraali .

Näide 4

Leidke määramatu integraal.

See on näide iseseisva lahenduse jaoks, täislahendus ja vastus on tunni lõpus.

Näide 5

Leidke määramatu integraal.

Meie kraadid tõusevad järk-järgult =).
Esiteks lahendus:

(1) Kasutame valemit

(2) Kasutame peamist trigonomeetrilist identiteeti , millest järeldub, et .

(3) Jagage lugeja nimetaja liikmega liigendiga.

(4) Kasutame määramatu integraali lineaarsusomadust.

(5) Integreerime tabeli abil.

Näide 6

Leidke määramatu integraal.

See on näide iseseisva lahenduse jaoks, täislahendus ja vastus on tunni lõpus.

Samuti on puutujate ja kotangentide integraalid, mis on kõrgemates võimsustes. Tunnis käsitletakse puutuja kuubi integraali Kuidas arvutada tasase figuuri pindala? Neljanda ja viienda astme puutuja (kotangens) integraalid saab lehelt Komplekssed integraalid.

Integrandi astme vähendamine

See tehnika töötab, kui integrandi funktsioonid on täidetud siinustega ja koosinustega isegi kraadid. Kraadi vähendamiseks kasutage trigonomeetrilisi valemeid , ja , ning viimast valemit kasutatakse sageli vastupidises suunas: .

Näide 7

Leidke määramatu integraal.

Lahendus:

Põhimõtteliselt pole siin midagi uut peale selle, et rakendasime valemit (integrandi astme alandamine). Pange tähele, et olen lahendust lühendanud. Kogemuste omandamisel on integraal leitav suuliselt, see säästab aega ja on ülesannete täitmisel täiesti vastuvõetav. Sel juhul on soovitatav reeglit mitte kirjeldada , kõigepealt võtame verbaalselt integraali 1, seejärel .

Näide 8

Leidke määramatu integraal.

See on näide iseseisva lahenduse jaoks, täislahendus ja vastus on tunni lõpus.

See on lubatud kraaditõus:

Näide 9

Leidke määramatu integraal.

Kõigepealt lahendus, siis kommentaarid:

(1) Valemi rakendamiseks valmistage integrand ette .

(2) Me tegelikult rakendame valemit.

(3) Teeme nimetaja ruudu ja võtame integraalimärgist välja konstandi. Oleks võinud natuke teisiti teha, aga minu meelest oli nii mugavam.

(4) Kasutame valemit

(5) Kolmandas liikmes vähendame jällegi kraadi, kuid kasutades valemit .

(6) Esitame sarnased terminid (siin jagasin terminid terminite kaupa ja tegi lisamise).

(7) Tegelikult võtame integraali, lineaarsuse reegli ja funktsiooni diferentsiaalmärgi alla liitmise meetod viiakse läbi suuliselt.

(8) Vastuse kammimine.

! Määramatus integraalis saab vastuse sageli kirjutada mitmel viisil

Äsja vaadeldud näites oleks võinud lõpliku vastuse kirjutada teisiti - avades sulgud ja isegi tehes seda enne avaldise integreerimist, see tähendab, et järgmine näite lõpp on täiesti vastuvõetav:

On täiesti võimalik, et see valik on veelgi mugavam, ma lihtsalt selgitasin seda nii, nagu olen harjunud seda ise lahendama). Siin on veel üks tüüpiline näide sõltumatu lahenduse kohta:

Näide 10

Leidke määramatu integraal.

Seda näidet saab lahendada kahel viisil ja see võib õnnestuda kaks täiesti erinevat vastust(täpsemalt näevad nad välja täiesti erinevad, kuid matemaatilisest vaatepunktist on nad samaväärsed). Tõenäoliselt ei näe te kõige ratsionaalsemat meetodit ja kannatate sulgude avamise ja muude trigonomeetriliste valemite kasutamisega. Kõige tõhusam lahendus antakse tunni lõpus.

Lõigu kokkuvõtteks järeldame: vormi mis tahes integraal , kus ja - isegi numbrid, lahendatakse integrandi astme vähendamise meetodiga.
Praktikas puutusin kokku integraalidega 8 ja 10 kraadiga ning nende kohutava segaduse pidin lahendama kraadi mitu korda langetades, mille tulemuseks olid pikad-pikad vastused.

Muutuja asendamise meetod

Nagu artiklis mainitud Muutuja muutmise meetod määramata integraalis, on asendusmeetodi kasutamise peamiseks eelduseks asjaolu, et integrandis on teatud funktsioon ja selle tuletis:
(funktsioonid ei pruugi tootes sisalduda)

Näide 11

Leidke määramatu integraal.

Vaatame tuletiste tabelit ja märkame valemeid, , see tähendab, et meie integrandis on funktsioon ja selle tuletis. Küll aga näeme, et diferentseerumise käigus muunduvad koosinus ja siinus vastastikku üksteiseks ning tekib küsimus: kuidas teostada muutuja muutust ja mida siinuse või koosinuse all mõeldakse?! Küsimuse saab lahendada teadusliku torkamisega: kui teeme asendamise valesti, siis ei tule sellest midagi head.

Üldine juhis: sarnastel juhtudel peate määrama nimetajas oleva funktsiooni.

Katkestame lahenduse ja teeme asendus

Nimetajas on kõik korras, kõik sõltub ainult , nüüd jääb üle välja selgitada, mis sellest saab.
Selleks leiame diferentsiaali:

Või lühidalt:
Saadud võrdsusest väljendame proportsioonireeglit kasutades meile vajaliku avaldise:

Niisiis:

Nüüd sõltub kogu meie integrand ainult sellest ja saame jätkata lahendamist

Valmis. Tuletan meelde, et asendamise eesmärk on integrandi lihtsustamine, sel juhul taandus kõik võimsusfunktsiooni integreerimisele vastavalt tabelile.

Pole juhus, et ma seda näidet nii üksikasjalikult kirjeldasin, seda tehti õppetunni materjalide kordamise ja tugevdamise eesmärgil Muutuja muutmise meetod määramata integraalis.

Ja nüüd kaks näidet teie enda lahenduseks:

Näide 12

Leidke määramatu integraal.

Näide 13

Leidke määramatu integraal.

Terviklahendused ja vastused tunni lõpus.

Näide 14

Leidke määramatu integraal.

Siin on jällegi integrandis siinus ja koosinus (tuletisega funktsioon), aga korrutises ja tekib dilemma - mida me siinuse või koosinuse all mõtleme?

Võite proovida asendada teadusliku meetodi abil ja kui miski ei tööta, määrake see teiseks funktsiooniks, kuid seal on:

Üldsuunis: peate määrama funktsiooni, mis piltlikult öeldes on "ebamugavas asendis".

Näeme, et selles näites õpilaskoosinus “kannatab” kraadi ja siinus istub vabalt, omaette.

Seetõttu teeme asendus:

Kui kellelgi on endiselt raskusi muutuja asendamise ja diferentsiaali leidmise algoritmiga, siis tuleks õppetunni juurde tagasi pöörduda Muutuja muutmise meetod määramata integraalis.

Näide 15

Leidke määramatu integraal.

Analüüsime integrandi, mida tuleks tähistada ?
Pidagem meeles meie juhiseid:
1) Funktsioon on kõige tõenäolisemalt nimetajas;
2) Funktsioon on "ebamugavas asendis".

Muide, need juhised ei kehti ainult trigonomeetriliste funktsioonide jaoks.

Siinus vastab mõlemale kriteeriumile (eriti teisele), nii et asendus soovitab ennast. Põhimõtteliselt saab vahetuse juba teostada, aga enne oleks tore välja mõelda, millega peale hakata? Esiteks "näpime ära" ühe koosinuse:

Me reserveerime oma "tuleviku" diferentsiaali jaoks

Ja me väljendame seda siinuse kaudu, kasutades põhilist trigonomeetrilist identiteeti:

Nüüd on siin asendus:

Üldreegel: kui integrandis on üks trigonomeetrilistest funktsioonidest (siinus või koosinus) sees kummaline kraadi, siis peate paaritu astme juurest ühe funktsiooni "ära hammustama" ja määrama selle taha teise funktsiooni. Me räägime ainult integraalidest, kus on koosinused ja siinused.

Vaadeldavas näites oli meil paaritu astmega koosinus, nii et võtsime astmest välja ühe koosinuse ja määrasime selle siinusena.

Näide 16

Leidke määramatu integraal.

Kraadid on tõusmas =).
See on näide, mille saate ise lahendada. Täislahendus ja vastus tunni lõpus.

Universaalne trigonomeetriline asendus

Universaalne trigonomeetriline asendus on muutuva asendusmeetodi tavaline juhtum. Võite proovida seda kasutada, kui te "ei tea, mida teha". Kuid tegelikult on selle rakendamiseks mõned juhised. Tüüpilised integraalid, mille puhul tuleb rakendada universaalset trigonomeetrilist asendust, on järgmised integraalid: , , , jne.

Näide 17

Leidke määramatu integraal.

Universaalne trigonomeetriline asendus rakendatakse sel juhul järgmiselt. Asendame: . Ma ei kasuta tähte , vaid tähte , see ei ole mingi reegel, see on lihtsalt see, et jällegi olen harjunud asju nii lahendama.

Siin on mugavam leida diferentsiaal; selleks väljendan võrdsusest:
Kinnitan mõlemale osale arctangensi:

Arktangens ja tangens tühistavad üksteist:

Seega:

Praktikas ei pea te seda nii üksikasjalikult kirjeldama, vaid lihtsalt kasutage valmis tulemust:

! Avaldis kehtib ainult siis, kui siinuste ja koosinuste all on integraali jaoks lihtsalt “X”. (millest me hiljem räägime) kõik on veidi teistmoodi!

Asendamisel muutuvad siinused ja koosinused järgmisteks murdudeks:
, , need võrdsused põhinevad tuntud trigonomeetrilistel valemitel: ,

Seega võiks lõplik kujundus välja näha selline:

Teeme universaalse trigonomeetrilise asendus:

Esitatakse põhilised trigonomeetrilised valemid ja põhiasendused. Välja on toodud trigonomeetriliste funktsioonide integreerimise meetodid - ratsionaalfunktsioonide integreerimine, sin x ja cos x astmefunktsioonide korrutis, polünoomi, eksponentsiaali ja siinuse või koosinuse korrutis, pöördtrigonomeetriliste funktsioonide integreerimine. Mõjutatud on mittestandardsed meetodid.

Sisu

Standardmeetodid trigonomeetriliste funktsioonide integreerimiseks

Üldine lähenemine

Esmalt tuleb vajadusel integrandi teisendada nii, et trigonomeetrilised funktsioonid sõltuksid ühest argumendist, mis on sama mis integratsioonimuutuja.

Näiteks kui integrand sõltub sin(x+a) Ja cos(x+b), siis peaksite tegema teisenduse:
cos (x+b) = cos (x+a - (a-b)) = cos (x+a) cos (b-a) + patt ( x+a ) patt (b-a).
Seejärel tee asendus z = x+a. Selle tulemusena sõltuvad trigonomeetrilised funktsioonid ainult integreerimismuutujast z.

Kui trigonomeetrilised funktsioonid sõltuvad ühest argumendist, mis langeb kokku integratsioonimuutujaga (oletame, et see on z), see tähendab, et integrand koosneb ainult sellistest funktsioonidest nagu sin z, cos z, tg z, ctg z, siis tuleb teha asendus
.
Selline asendus viib ratsionaalsete või irratsionaalsete funktsioonide integreerimiseni (kui on juured) ja võimaldab arvutada integraali, kui see on integreeritud elementaarfunktsioonidesse.

Tihti võib aga leida ka teisi meetodeid, mis võimaldavad integraali lühemalt hinnata, lähtudes integrandi spetsiifikast. Allpool on kokkuvõte peamistest sellistest meetoditest.

Sin x ja cos x ratsionaalsete funktsioonide integreerimise meetodid

Ratsionaalsed funktsioonid alates sin x Ja cos x on funktsioonid, mis on moodustatud sin x, cos x ja mis tahes konstandid, mis kasutavad liitmise, lahutamise, korrutamise, jagamise ja täisarvuni tõstmise tehteid. Need on tähistatud järgmiselt: R (sin x, cos x). See võib hõlmata ka puutujaid ja kotangente, kuna need moodustatakse siinuse jagamisel koosinusega ja vastupidi.
Ratsionaalfunktsioonide integraalid on kujul:
.

Ratsionaalsete trigonomeetriliste funktsioonide integreerimise meetodid on järgmised.
1) Asendamine viib alati ratsionaalse murru integraalini. Kuid mõnel juhul on asendusi (need on esitatud allpool), mis viivad lühemate arvutusteni.
2) Kui R (sin x, cos x) cos x → - cos x sin x.
3) Kui R (sin x, cos x) asendamisel korrutatud -1-ga sin x → - sin x, siis asendus t = cos x.
4) Kui R (sin x, cos x) ei muutu nagu samaaegse asendamise korral cos x → - cos x, Ja sin x → - sin x, siis asendus t = tg x või t = ctg x.

Näited:
, , .

Cos x ja sin x võimsusfunktsioonide korrutis

Vormi integraalid

on ratsionaalsete trigonomeetriliste funktsioonide integraalid. Seetõttu saab nende puhul rakendada eelmises jaotises kirjeldatud meetodeid. Allpool käsitletakse selliste integraalide eripäral põhinevaid meetodeid.

Kui m ja n on ratsionaalarvud, siis üks asendustest t = sin x või t = cos x integraal taandatakse diferentsiaalbinoomi integraaliks.

Kui m ja n on täisarvud, siis integreerimine toimub redutseerimisvalemite abil:

;
;
;
.

Näide:
.

Polünoomi ja siinuse või koosinuse korrutise integraalid

Vormi integraalid:
, ,
kus P(x) on x-i polünoom, integreeritakse osade kaupa. See annab järgmised valemid:

;
.

Näited:
, .

Polünoomi, eksponentsiaali ja siinuse või koosinuse korrutise integraalid

Vormi integraalid:
, ,
kus P(x) on polünoom punktis x, integreeritud Euleri valemiga
e iax = cos ax + isin ax(kus i 2 = - 1 ).
Selleks arvutage integraal eelmises lõigus kirjeldatud meetodil
.
Eraldades tulemusest tegeliku ja mõttelise osa, saadakse algintegraalid.

Näide:
.

Mittestandardsed meetodid trigonomeetriliste funktsioonide integreerimiseks

Allpool on toodud mitmed mittestandardsed meetodid, mis võimaldavad teil teostada või lihtsustada trigonomeetriliste funktsioonide integreerimist.

Sõltuvus (a sin x + b cos x)

Kui integrand sõltub ainult a sin x + b cos x, siis on kasulik rakendada valemit:
,
Kus.

Näiteks

Murdude lahutamine siinustest ja koosinustest lihtsamateks murdudeks

Mõelge integraalile
.
Lihtsaim integreerimismeetod on teisenduse abil murdosa jagamine lihtsamateks:
sin(a - b) = sin(x + a - (x + b)) = sin(x+a) cos(x+b) - cos(x+a) sin(x+b)

Esimese astme murdude integreerimine

Integraali arvutamisel
,
mugav on eraldada murdosa täisarvuline osa ja nimetaja tuletis
a 1 sin x + b 1 cos x = A (a sin x + b cos x) + B (a sin x + b cos x)′ .
Konstandid A ja B leitakse vasaku ja parema külje võrdlemisel.

Viited:
N.M. Gunter, R.O. Kuzmin, Kõrgema matemaatika ülesannete kogu, “Lan”, 2003.

Vaata ka:

Üksikasjalikult vaadeldakse näiteid integraalide lahenditest osade kaupa, mille integrand on polünoomi korrutis eksponentsiaaliga (e x astmega) või siinuse (sin x) või koosinusega (cos x).

Sisu

Vaata ka: Osade kaupa integreerimise meetod
Määramata integraalide tabel
Määramata integraalide arvutamise meetodid
Põhilised elementaarfunktsioonid ja nende omadused

Osade kaupa integreerimise valem

Selle jaotise näidete lahendamisel kasutatakse osade kaupa integreerimise valemit:
;
.

Näited integraalidest, mis sisaldavad polünoomi ja sin x, cos x või e x korrutist

Siin on selliste integraalide näited:
, , .

Selliste integraalide integreerimiseks tähistatakse polünoomi u-ga ja ülejäänud osa v dx-ga. Järgmisena rakendage osade kaupa integreerimise valemit.

Allpool on nende näidete üksikasjalik lahendus.

Integraalide lahendamise näited

Näide astendajaga, e x astmega

Määrake integraal:
.

Tutvustame eksponenti diferentsiaalmärgi all:
e - x dx = - e - x d(-x) = - d(e - x).

Integreerime osade kaupa.

Siin
.
Samuti integreerime ülejäänud integraali osade kaupa.
.
.
.
Lõpuks on meil:
.

Siinuse integraali defineerimise näide

Arvutage integraal:
.

Tutvustame siinuse diferentsiaalmärgi all:

Integreerime osade kaupa.

siin u = x 2, v = cos (2 x+3), du = ( x 2 )′ dx

Samuti integreerime ülejäänud integraali osade kaupa. Selleks sisestage diferentsiaalmärgi alla koosinus.

siin u = x, v = sin (2 x+3), du = dx

Lõpuks on meil:

Näide polünoomi ja koosinuse korrutisest

Arvutage integraal:
.

Tutvustame diferentsiaalmärgi all olevat koosinust:

Integreerime osade kaupa.

siin u = x 2 + 3 x + 5, v = patt 2 x, du = ( x 2 + 3 x + 5 )′ dx

Samuti on teil iseseisvalt lahendatavad probleemid, millele näete vastuseid.

Integrandi saab teisendada trigonomeetriliste funktsioonide korrutisest summaks

Vaatleme integraale, milles integrand on x-i esimese astme siinuste ja koosinuste korrutis erinevate teguritega, st vormi integraalid

Tuntud trigonomeetriliste valemite kasutamine

(2)
(3)
(4)
iga vormi (31) integraali korrutist saab teisendada algebraliseks summaks ja integreerida vastavalt valemitele

(5)

(6)

Näide 1. Otsi

Lahendus. Vastavalt valemile (2) kl

Näide 2. Otsi trigonomeetrilise funktsiooni integraal

Lahendus. Vastavalt valemile (3) kl

Näide 3. Otsi trigonomeetrilise funktsiooni integraal

Lahendus. Vastavalt valemile (4) kl saame integrandi järgmise teisenduse:

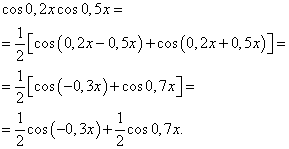
Rakendades valemit (6), saame

Integraal sama argumendi siinuse ja koosinuse astmete korrutisest

Vaatleme nüüd funktsioonide integraale, mis on sama argumendi siinuse ja koosinuse astmete korrutis, st.

(7)

Erijuhtudel on üks näitajatest ( m või n) võib olla null.

Selliste funktsioonide integreerimisel kasutatakse seda, et siinuse kaudu saab väljendada koosinuse ühtlast võimsust ja siinuse diferentsiaal on võrdne cos-iga x dx(või isegi siinuse võimsust saab väljendada koosinuse kaudu ja koosinuse diferentsiaal on võrdne - sin x dx ) .

Eristada tuleks kahte juhtumit: 1) vähemalt üks näitajatest m Ja n kummaline; 2) mõlemad näitajad on paaris.

Laske toimuda esimene juhtum, nimelt indikaator n = 2k+ 1 - paaritu. Siis, arvestades seda

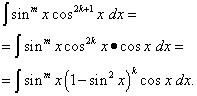
Integrand esitatakse nii, et üks osa sellest on ainult siinuse funktsioon ja teine on siinuse diferentsiaal. Nüüd kasutatakse muutuja asendust t= patt x lahendus taandub polünoomi integreerimisele t. Kui ainult kraad m on veider, siis teevad nad sama, isoleerides patuteguri x, väljendades ülejäänud integrandi kos x ja uskudes t=cos x. Seda tehnikat saab kasutada ka siis, kui siinuse ja koosinuse jagatisastmete integreerimine , Millal vähemalt üks näitajatest on paaritu . Kogu point on selles siinuse ja koosinuse astmete jagatis on nende korrutise erijuht : Kui trigonomeetriline funktsioon on integrandi nimetajas, on selle aste negatiivne. Kuid on ka osaliste trigonomeetriliste funktsioonide juhtumeid, kui nende võimsused on paaris. Nende kohta - järgmises lõigus.

Kui mõlemad näitajad m Ja n– isegi siis, kasutades trigonomeetrilisi valemeid

vähendada siinuse ja koosinuse eksponente, mille järel saadakse ülaltoodud sama tüüpi integraal. Seetõttu tuleks integratsiooni jätkata sama skeemi järgi. Kui üks paarisaste on negatiivne, see tähendab siinuse ja koosinuse paarisastmete jagatist, siis see skeem ei sobi . Seejärel kasutatakse muutuja muutust sõltuvalt sellest, kuidas integrandi saab teisendada. Sellist juhtumit käsitletakse järgmises lõigus.

Näide 4. Otsi trigonomeetrilise funktsiooni integraal

Lahendus. Koosinusaste on paaritu. Seetõttu kujutame ette

t= patt x(Siis dt=cos x dx ). Siis saame

Naastes vana muutuja juurde, leiame lõpuks

Näide 5. Otsi trigonomeetrilise funktsiooni integraal

Lahendus. Koosinusaste, nagu eelmises näites, on paaritu, kuid suurem. Kujutame ette

ja muutke muutujat t= patt x(Siis dt=cos x dx ). Siis saame

Avame sulgud

ja saame

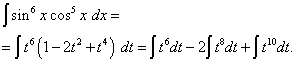
Naastes vana muutuja juurde, saame lahenduse

Näide 6. Otsi trigonomeetrilise funktsiooni integraal

Lahendus. Siinuse ja koosinuse eksponendid on paarisarvulised. Seetõttu teisendame integrandi funktsiooni järgmiselt:

Siis saame

Teises integraalis muudame muutuja seadistust t= sin2 x. Siis (1/2)dt= cos2 x dx . Seega

Lõpuks saame

Muutuja asendamise meetodi kasutamine

Muutuja asendamise meetod trigonomeetriliste funktsioonide integreerimisel saab seda kasutada juhtudel, kui integrand sisaldab ainult siinust või ainult koosinust, siinuse ja koosinuse korrutist, kus siinus või koosinus on esimesel astmel, puutuja või kotangens, samuti jagatis ühe ja sama argumendi isegi siinuse ja koosinuse astmed. Sel juhul on võimalik teha permutatsioone mitte ainult pattu x = t ja patt x = t, aga ka tg x = t ja ctg x = t .

Näide 8. Otsi trigonomeetrilise funktsiooni integraal

Lahendus. Muudame muutujat: , siis . Saadud integrandi saab hõlpsasti integreerida integraalide tabeli abil:

Näide 9. Otsi trigonomeetrilise funktsiooni integraal

Lahendus. Teisendame puutuja siinuse ja koosinuse suhteks:

Muudame muutujat: , siis . Saadud integrand on tabeli integraal miinusmärgiga:

Naastes algse muutuja juurde, saame lõpuks:

Näide 10. Otsi trigonomeetrilise funktsiooni integraal

Lahendus. Muudame muutujat: , siis .

Teisendame integrandi trigonomeetrilise identiteedi rakendamiseks :

Muudame muutujat, unustamata panna integraali ette miinusmärki (vt ülalt, mis võrdub dt). Järgmisena arvestame integrandi ja integreerime vastavalt tabelile:

Naastes algse muutuja juurde, saame lõpuks:

Leidke ise trigonomeetrilise funktsiooni integraal ja seejärel vaadake lahendust

Universaalne trigonomeetriline asendus

Universaalne trigonomeetriline asendus saab kasutada juhtudel, kui integrand ei kuulu eelmistes lõikudes käsitletud juhtumite alla. Põhimõtteliselt siis, kui siinus või koosinus (või mõlemad) on murdosa nimetajas. On tõestatud, et siinust ja koosinust saab asendada teise avaldisega, mis sisaldab poole algnurga puutujat järgmiselt:

Kuid pange tähele, et universaalne trigonomeetriline asendamine hõlmab sageli üsna keerukaid algebralisi teisendusi, seega on seda kõige parem kasutada siis, kui ükski teine meetod ei tööta. Vaatame näiteid, kus koos universaalse trigonomeetrilise asendusega kasutatakse asendust diferentsiaalmärgi all ja määramatute koefitsientide meetodit.

Näide 12. Otsi trigonomeetrilise funktsiooni integraal

Lahendus. Lahendus. Kasutame ära universaalne trigonomeetriline asendus. Siis
.

Korrutame lugeja ja nimetaja murrud arvuga , võtame need kaks välja ja asetame integraalimärgi ette. Siis

Antiderivaatide ("integraalide") tabel. Integraalide tabel. Tabelikujulised määramatud integraalid. (Kõige lihtsamad integraalid ja integraalid parameetriga). Osade kaupa integreerimise valemid. Newtoni-Leibnizi valem.

Antiderivaatide ("integraalide") tabel. Tabelikujulised määramatud integraalid. (Kõige lihtsamad integraalid ja integraalid parameetriga).
Toitefunktsiooni integraal.	Toitefunktsiooni integraal.
Integraal, mis taandub võimsusfunktsiooni integraaliks, kui x juhitakse diferentsiaalmärgi all.

	Eksponentsi integraal, kus a on konstantne arv.
Kompleksse eksponentsiaalfunktsiooni integraal.	Eksponentfunktsiooni integraal.

Naturaallogaritmiga võrdne integraal.	Integraal: "Pikk logaritm".
	Integraal: "Pikk logaritm".
Integraal: "Kõrge logaritm".	Integraal, kus x lugejas asetatakse diferentsiaalmärgi alla (märgi all olevat konstanti saab kas liita või lahutada), sarnaneb lõppkokkuvõttes naturaallogaritmiga võrdse integraaliga.
Integraal: "Kõrge logaritm".

Koosinusintegraal.	Siinuse integraal.
Integraal võrdub puutujaga.	Integraal võrdub kotangensiga.

Integraal, mis on võrdne nii arkosiini kui ka arkosiiniga
Integraal, mis on võrdne nii arkosiini kui ka arkosiiniga.	Integraal, mis on võrdne nii arktangensiga kui ka arkotangensiga.

Integraal võrdne kosekantsiga.	Integraal võrdub sekantiga.
Integraal võrdub kaarekujulisega.	Integraal võrdne arccosecantiga.
Integraal võrdub kaarekujulisega.	Integraal võrdub kaarekujulisega.

Integraal võrdub hüperboolse siinusega.	Integraal võrdub hüperboolse koosinusega.

Integraal on võrdne hüperboolse siinusega, kus sinhx on ingliskeelses versioonis hüperboolne siinus.	Integraal, mis on võrdne hüperboolse koosinusega, kus sinhx on ingliskeelses versioonis hüperboolne siinus.
Integraal, mis on võrdne hüperboolse puutujaga.	Integraal, mis on võrdne hüperboolse kotangensiga.
Integraal, mis on võrdne hüperboolse sekantiga.	Integraal, mis on võrdne hüperboolse kosekandiga.

Osade kaupa integreerimise valemid. Integratsioonireeglid.

Osade kaupa integreerimise valemid. Newtoni-Leibnizi valem.Integratsioonireeglid.
Toote (funktsiooni) integreerimine konstandiga:
Funktsioonide summa integreerimine:
määramata integraalid:
Osade kaupa integreerimise valem kindlad integraalid:
Newtoni-Leibnizi valem kindlad integraalid:	Kus F(a), F(b) on antiderivaatide väärtused vastavalt punktides b ja a.

Tuletisinstrumentide tabel. Tabelituletised. Toote tuletis. Jagatise tuletis. Kompleksfunktsiooni tuletis.

Kui x on sõltumatu muutuja, siis:

Tuletisinstrumentide tabel. Tabelituletised."tabelituletis" - jah, kahjuks just nii neid Internetist otsitakse
	Võimsusfunktsiooni tuletis

	Eksponent tuletis
Kompleksse eksponentsiaalfunktsiooni tuletis	Eksponentfunktsiooni tuletis

Logaritmilise funktsiooni tuletis	Naturaallogaritmi tuletis
	Funktsiooni naturaallogaritmi tuletis

Siinuse tuletis	Koosinuse tuletis
Koossekandi tuletis	Sekanti tuletis
Arsiini tuletis	Kaarkoosinuse tuletis
Arsiini tuletis	Kaarkoosinuse tuletis
Tangentne tuletis	Kootangensi tuletis
Arktangensi tuletis	Kaare kotangensi tuletis
Arktangensi tuletis	Kaare kotangensi tuletis
Arcsekanti tuletis	Arccosecanti tuletis
Arcsekanti tuletis	Arccosecanti tuletis

Hüperboolse siinuse tuletis Hüperboolse siinuse tuletis ingliskeelses versioonis	Hüperboolse koosinuse tuletis Hüperboolse koosinuse tuletis ingliskeelses versioonis
Hüperboolse puutuja tuletis	Hüperboolse kotangensi tuletis
Hüperboolse sekandi tuletis	Hüperboolse kosekandi tuletis

Eristamise reeglid. Toote tuletis. Jagatise tuletis. Kompleksfunktsiooni tuletis.
Toote (funktsiooni) tuletis konstandi abil:
Summa tuletis (funktsioonid):
Toote tuletis (funktsioonid):
Jagatise (funktsioonide) tuletis:
Kompleksfunktsiooni tuletis:

Logaritmide omadused. Logaritmide põhivalemid. Kümnend (lg) ja naturaallogaritmid (ln).

Põhiline logaritmiline identiteet
Näitame, kuidas vormi a b mis tahes funktsiooni saab muuta eksponentsiaalseks. Kuna funktsiooni kujul e x nimetatakse eksponentsiaalseks, siis
Iga funktsiooni kujul a b võib esitada kümne astmena

Naturaallogaritm ln (logaritm alusele e = 2,718281828459045...) ln(e)=1; ln(1)=0

Taylori sari. Taylori seeria funktsiooni laiendus.

Selgub, et enamus praktiliselt kokku puutunud matemaatilisi funktsioone saab esitada mis tahes täpsusega teatud punkti läheduses astmeridade kujul, mis sisaldavad muutuja astmeid kasvavas järjekorras. Näiteks punkti x=1 läheduses:

Sarja kasutamisel nn Taylori read segafunktsioone, mis sisaldavad näiteks algebralisi, trigonomeetrilisi ja eksponentsiaalfunktsioone, saab väljendada puhtalt algebraliste funktsioonidena. Seeriaid kasutades saate sageli kiiresti eristada ja integreerida.

Taylori seeria punkti a naabruses on kujul:

1) , kus f(x) on funktsioon, millel on kõigi järkude tuletised x = a. R n - Taylori seeria ülejäänud liige määratakse avaldise järgi

Rea k-s koefitsient (at x k) määratakse valemiga

3) Taylori seeria erijuhtum on Maclaurini (=McLareni) seeria (laienemine toimub punkti a=0 ümber)

juures a = 0

seeria liikmed määratakse valemiga

Taylori seeria kasutamise tingimused.

1. Funktsiooni f(x) laiendamiseks Taylori seeriaks intervallil (-R;R) on vajalik ja piisav, et ülejäänud liige Taylori (Maclaurin (=McLaren)) valemis. funktsioon kaldub nullini kui k →∞ määratud intervallil (-R;R).

2. On vaja, et antud funktsiooni jaoks oleks tuletised punktis, mille läheduses me konstrueerime Taylori seeria.

Taylori seeria omadused.

Kui f on analüütiline funktsioon, siis selle Taylori jada f definitsioonipiirkonna mis tahes punktis a koondub f-le mõnes a naabruses.

On lõpmatult diferentseeruvaid funktsioone, mille Taylori seeria koondub, kuid erineb samal ajal funktsioonist a mis tahes naabruses. Näiteks:

Taylori seeriaid kasutatakse funktsiooni lähendamiseks (lähendamine on teaduslik meetod, mis seisneb mõne objekti asendamises teistega, mis on ühes või teises mõttes originaalile lähedased, kuid lihtsamad) funktsiooni polünoomide abil. Eelkõige lineariseerimine ((sõnast linearis - lineaarne), üks suletud mittelineaarsete süsteemide ligikaudse kujutamise meetodeid, milles mittelineaarse süsteemi uurimine asendatakse lineaarse süsteemi analüüsiga, mis on mõnes mõttes samaväärne algse süsteemiga. .) võrrandid laienevad Taylori seeriaks ja lõigates ära kõik esimeses järjekorras olevad terminid.

Seega saab peaaegu iga funktsiooni etteantud täpsusega esitada polünoomina.

Näited mõnedest levinud võimsusfunktsioonide laiendustest Maclaurini seerias (=McLaren, Taylor punkti 0 läheduses) ja Taylor punkti 1 läheduses. Taylori ja McLareni seeria põhifunktsioonide laienduste esimesed liikmed.

Näited mõnedest Maclaurini seeria võimsusfunktsioonide laiendustest (= McLaren, Taylor punkti 0 läheduses)