Standardhälbe valem. Valemi standardhälve Excelis

$X$. Alustuseks tuletagem meelde järgmist määratlust:

Definitsioon 1

Rahvaarv- teatud tüüpi juhuslikult valitud objektide kogum, mille üle tehakse vaatlusi juhusliku suuruse konkreetsete väärtuste saamiseks, mis viiakse läbi konstantsetes tingimustes ühe antud tüüpi juhusliku muutuja uurimisel.

2. definitsioon

Üldine dispersioon- populatsioonivariandi väärtuste keskväärtusest kõrvalekallete ruudu aritmeetiline keskmine.

Olgu valiku $x_1,\ x_2,\dots ,x_k$ väärtustel vastavalt sagedused $n_1,\ n_2,\dots ,n_k$. Seejärel arvutatakse üldine dispersioon järgmise valemi abil:

Vaatleme erilist juhtumit. Olgu kõik valikud $x_1,\ x_2,\dots ,x_k$ erinevad. Sel juhul $n_1,\ n_2,\dots ,n_k=1$. Leiame, et sel juhul arvutatakse üldine dispersioon järgmise valemi abil:

Seda mõistet seostatakse ka üldise standardhälbe mõistega.

3. definitsioon

Üldine standardhälve

\[(\sigma )_g=\sqrt(D_g)\]

Valimi dispersioon

Olgu meile antud valimipopulatsioon juhusliku suuruse $X$ suhtes. Alustuseks tuletagem meelde järgmist määratlust:

4. definitsioon

Näidispopulatsioon-- osa üldpopulatsioonist valitud objektidest.

Definitsioon 5

Valimi dispersioon- valimi üldkogumi väärtuste aritmeetiline keskmine.

Olgu valiku $x_1,\ x_2,\dots ,x_k$ väärtustel vastavalt sagedused $n_1,\ n_2,\dots ,n_k$. Seejärel arvutatakse valimi dispersioon järgmise valemi abil:

Vaatleme erilist juhtumit. Olgu kõik valikud $x_1,\ x_2,\dots ,x_k$ erinevad. Sel juhul $n_1,\ n_2,\dots ,n_k=1$. Leiame, et sel juhul arvutatakse valimi dispersioon järgmise valemiga:

Selle kontseptsiooniga on seotud ka valimi standardhälbe mõiste.

Definitsioon 6

Näidis standardhälve-- ruutjuur üldisest dispersioonist:

\[(\sigma )_в=\sqrt(D_в)\]

Parandatud dispersioon

Parandatud dispersiooni $S^2$ leidmiseks on vaja valimi dispersioon korrutada murdosaga $\frac(n)(n-1)$, see tähendab

Seda mõistet seostatakse ka korrigeeritud standardhälbe mõistega, mis leitakse valemiga:

Juhul, kui variantide väärtused ei ole diskreetsed, vaid esindavad intervalle, siis üld- või näidisvariansside arvutamise valemites võetakse $x_i$ väärtuseks intervalli keskkoha väärtus. kuhu $x_i.$ kuulub.

Probleemi näide dispersiooni ja standardhälbe leidmiseks

Näide 1

Valimipopulatsioon määratakse järgmise jaotustabeli abil:

Pilt 1.

Leiame selle jaoks valimi dispersiooni, valimi standardhälbe, korrigeeritud dispersiooni ja korrigeeritud standardhälbe.

Selle probleemi lahendamiseks koostame esmalt arvutustabeli:

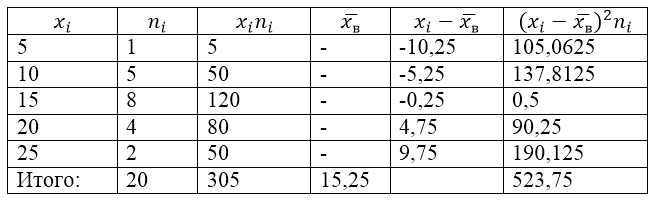
Joonis 2.

Tabeli väärtus $\overline(x_в)$ (proovi keskmine) leitakse järgmise valemiga:

\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)\]

\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)=\frac(305)(20)=15,25\]

Leiame valimi dispersiooni valemi abil:

Näidis standardhälve:

\[(\sigma )_в=\sqrt(D_в)\umbes 5,12\]

Parandatud dispersioon:

\[(S^2=\frac(n)(n-1)D)_в=\frac(20)(19)\cdot 26.1875\umbes 27.57\]

Parandatud standardhälve.

Standardhälve(sünonüümid: standardhälve, standardhälve, ruuthälve; seotud terminid: standardhälve, standardne levik) - tõenäosusteoorias ja statistikas on kõige levinum juhusliku suuruse väärtuste hajuvuse näitaja selle matemaatilise ootuse suhtes. Piiratud väärtuste valimite massiivi puhul kasutatakse matemaatilise ootuse asemel valimite komplekti aritmeetilist keskmist.

Entsüklopeediline YouTube

1 / 5
Standardhälvet mõõdetakse juhusliku suuruse enda mõõtühikutes ja seda kasutatakse aritmeetilise keskmise standardvea arvutamisel, usaldusvahemike koostamisel, hüpoteeside statistilisel kontrollimisel, juhuslike suuruste vahelise lineaarse seose mõõtmisel. Määratletakse juhusliku suuruse dispersiooni ruutjuurena.
Standardhälve:
s = n n − 1 σ 2 = 1 n − 1 ∑ i = 1 n (x i − x ¯) 2 ; (\displaystyle s=(\sqrt ((\frac (n)(n-1))\sigma ^(2)))=(\sqrt ((\frac (1)(n-1))\sum _( i=1)^(n)\left(x_(i)-(\bar (x))\right)^(2)));)
- Märkus. Väga sageli esineb lahknevusi MSD (Root Mean Square Deviation) ja STD (Standardhälve) nimetustes nende valemitega. Näiteks Pythoni programmeerimiskeele numPy moodulis kirjeldatakse funktsiooni std() kui "standardhälvet", samas kui valem kajastab standardhälvet (jagamine valimi juurega). Excelis on funktsioon STANDARDEVAL() erinev (jagamine n-1 juurega).
Standardhälve(juhusliku suuruse standardhälbe hinnang x võrreldes selle matemaatilise ootusega, mis põhineb selle dispersiooni erapooletul hinnangul) s (\displaystyle s):
σ = 1 n ∑ i = 1 n (x i − x ¯) 2 . (\displaystyle \sigma =(\sqrt ((\frac (1)(n))\sum _(i=1)^(n)\left(x_(i)-(\bar (x))\right) ^(2))).)
Kus σ 2 (\displaystyle \sigma ^(2))- dispersioon; x i (\displaystyle x_(i)) - i valiku element; n (\displaystyle n)- näidissuurus; - valimi aritmeetiline keskmine:
x ¯ = 1 n ∑ i = 1 n x i = 1 n (x 1 + … + x n) . (\displaystyle (\bar (x))=(\frac (1) (n))\sum _(i=1)^(n)x_(i)=(\frac (1) (n))(x_ (1)+\lpunktid +x_(n)).
Tuleb märkida, et mõlemad hinnangud on kallutatud. Üldjuhul on erapooletu hinnangu koostamine võimatu. Siiski on erapooletu dispersioonihinnangul põhinev hinnang järjepidev.
Vastavalt standardile GOST R 8.736-2011 arvutatakse standardhälve selle jaotise teise valemi abil. Palun kontrollige tulemusi.

Kolme sigma reegel

Kolme sigma reegel (3 σ (\displaystyle 3\sigma)) - peaaegu kõik normaalse jaotusega juhusliku suuruse väärtused asuvad intervallis (x ¯ − 3 σ ; x ¯ + 3 σ) (\displaystyle \left((\bar (x))-3\sigma ;(\bar (x))+3\sigma \right)). Täpsemalt – ligikaudu tõenäosusega 0,9973 asub normaalse jaotusega juhusliku suuruse väärtus määratud intervallis (eeldusel, et väärtus x ¯ (\displaystyle (\bar (x))) tõsi ja seda ei saadud proovi töötlemise tulemusena).
Kui tegelik väärtus x ¯ (\displaystyle (\bar (x))) on teadmata, siis ei tohiks te seda kasutada σ (\displaystyle \sigma ), A s. Seega muudetakse kolme sigma reegel kolme reegliks s .

Standardhälbe väärtuse tõlgendamine

Suurem standardhälbe väärtus näitab suuremat väärtuste levikut esitatud komplektis koos komplekti keskmise väärtusega; väiksem väärtus näitab vastavalt, et komplekti väärtused on rühmitatud keskmise väärtuse ümber.
Näiteks on meil kolm arvukomplekti: (0, 0, 14, 14), (0, 6, 8, 14) ja (6, 6, 8, 8). Kõigil kolmel komplektil on keskmised väärtused 7 ja standardhälbed vastavalt 7, 5 ja 1. Viimasel komplektil on väike standardhälve, kuna komplekti väärtused on rühmitatud keskmise väärtuse ümber; esimesel komplektil on suurim standardhälbe väärtus - komplektis olevad väärtused erinevad suuresti keskmisest väärtusest.
Üldises mõttes võib standardhälvet pidada määramatuse mõõdupuuks. Näiteks füüsikas kasutatakse standardhälvet mingi suuruse järjestikuste mõõtmiste jada vea määramiseks. See väärtus on väga oluline uuritava nähtuse usutavuse määramiseks võrreldes teooria ennustatud väärtusega: kui mõõtmiste keskmine väärtus erineb suuresti teoorias ennustatud väärtustest (suur standardhälve), siis tuleks saadud väärtused või nende saamise meetod uuesti üle kontrollida. tuvastatud portfelliriskiga.

Kliima

Oletame, et on kaks linna, mille keskmine ööpäevane maksimaalne temperatuur on sama, kuid üks asub rannikul ja teine tasandikul. On teada, et rannikul asuvates linnades on palju erinevaid maksimaalseid päevaseid temperatuure, mis on madalamad kui sisemaal asuvates linnades. Seetõttu on rannikulinna maksimaalsete ööpäevaste temperatuuride standardhälve väiksem kui teise linna puhul, hoolimata asjaolust, et selle väärtuse keskmine väärtus on sama, mis praktikas tähendab, et tõenäosus, et maksimaalne õhutemperatuur mis tahes päev aastas erineb sisemaal asuva linna keskmisest väärtusest kõrgem.

Sport

Oletame, et on mitu jalgpallimeeskonda, keda hinnatakse mõne parameetri alusel, näiteks löödud ja löödud väravate arv, väravavõimalused jne. Suure tõenäosusega on selle grupi parimal meeskonnal paremad väärtused rohkemate parameetrite järgi. Mida väiksem on meeskonna standardhälve iga esitatud parameetri puhul, seda prognoositavam on meeskonna tulemus; sellised meeskonnad on tasakaalus. Seevastu suure standardhälbega meeskonnal on raske tulemust ennustada, mis omakorda on seletatav tasakaalustamatusega, näiteks tugev kaitse, aga nõrk rünnak.
Meeskonna parameetrite standardhälbe kasutamine võimaldab ühel või teisel määral ennustada kahe meeskonna vahelise matši tulemust, hinnates meeskondade tugevaid ja nõrku külgi ning seega ka valitud võitlusmeetodeid.

Standardhälve

Kõige täiuslikum variatsiooni tunnus on keskmine ruuthälve, mida nimetatakse standardhälbeks (või standardhälbeks). Standardhälve() on võrdne atribuudi üksikute väärtuste keskmise ruuthälbe ruutjuurega aritmeetilisest keskmisest:

Standardhälve on lihtne:

Rühmitatud andmetele rakendatakse kaalutud standardhälvet:

Tavalise jaotustingimuste korral on keskmise ruudu ja keskmise lineaarhälbe vahel järgmine suhe: ~ 1,25.

Standardhälvet, mis on peamine absoluutne variatsioonimõõt, kasutatakse normaaljaotuse kõvera ordinaatväärtuste määramisel, valimi vaatluse korraldamise ja valimi karakteristikute täpsuse kindlakstegemisega seotud arvutustes, samuti proovide tunnuste täpsuse hindamisel. tunnuse varieerumise piirid homogeenses populatsioonis.

18. Dispersioon, selle liigid, standardhälve.

Juhusliku suuruse dispersioon- antud juhusliku suuruse leviku mõõt, st selle kõrvalekalle matemaatilisest ootusest. Statistikas kasutatakse sageli tähist või. Tavaliselt nimetatakse dispersiooni ruutjuurt standardhälve, standardhälve või tavaline levi.

Kogu dispersioon (σ 2) mõõdab tunnuse muutumist tervikuna kõigi selle kõikumise põhjustanud tegurite mõjul. Samas on tänu rühmitamismeetodile võimalik tuvastada ja mõõta rühmitamistunnusest tulenevat variatsiooni ja arvestamata tegurite mõjul tekkivat variatsiooni.

Gruppidevaheline dispersioon (σ 2 m.gr) iseloomustab süstemaatilist varieerumist ehk erinevusi uuritava tunnuse väärtuses, mis tekivad tunnuse – rühma aluseks oleva teguri – mõjul.

Standardhälve(sünonüümid: standardhälve, standardhälve, ruuthälve; seotud terminid: standardhälve, standardne levik) - tõenäosusteoorias ja statistikas on kõige levinum juhusliku suuruse väärtuste hajuvuse näitaja selle matemaatilise ootuse suhtes. Piiratud väärtuste valimite massiivi puhul kasutatakse matemaatilise ootuse asemel valimite komplekti aritmeetilist keskmist.

Standardhälvet mõõdetakse juhusliku suuruse enda mõõtühikutes ja seda kasutatakse aritmeetilise keskmise standardvea arvutamisel, usaldusvahemike koostamisel, hüpoteeside statistilisel kontrollimisel, juhuslike suuruste vahelise lineaarse seose mõõtmisel. Määratletakse juhusliku suuruse dispersiooni ruutjuurena.

Standardhälve:

Standardhälve(juhusliku suuruse standardhälbe hinnang x võrreldes selle matemaatilise ootusega, mis põhineb selle dispersiooni erapooletul hinnangul):

kus on dispersioon; - i valiku element; - näidissuurus; - valimi aritmeetiline keskmine:

Tuleb märkida, et mõlemad hinnangud on kallutatud. Üldjuhul on erapooletu hinnangu koostamine võimatu. Sel juhul on erapooletu dispersioonihinnangul põhinev hinnang järjepidev.

19. Režiimi ja mediaani olemus, ulatus ja määramise kord.

Lisaks statistikas võimsuskeskmistele kasutatakse muutuva tunnuse väärtuse ja jaotusridade sisemise struktuuri suhteliseks iseloomustamiseks struktuurseid keskmisi, mida esindavad peamiselt mood ja mediaan.

Mood- See on seeria kõige levinum variant. Moodi kasutatakse näiteks klientide seas kõige enam nõutavate rõivaste ja jalanõude suuruse määramisel. Diskreetse seeria režiim on kõrgeima sagedusega variant. Intervalli variatsiooniseeria režiimi arvutamisel on äärmiselt oluline kõigepealt määrata modaalne intervall (maksimaalse sageduse järgi) ja seejärel - atribuudi modaalväärtuse väärtus valemi abil:

§ - moe tähendus

§ - modaalse intervalli alumine piir

§ - intervalli väärtus

§ - modaalintervalli sagedus

§ - modaalile eelneva intervalli sagedus

§ - modaalile järgneva intervalli sagedus

Mediaan – see atribuudi väärtus ĸᴏᴛᴏᴩᴏᴇ asub järjestatud seeria aluses ja jagab selle seeria kaheks võrdseks osaks.

Mediaani määramiseks diskreetses seerias kui sagedused on saadaval, arvutage esmalt sageduste poolsumma ja seejärel määrake, milline variandi väärtus sellele langeb. (Kui sorteeritud seerias on paaritu arv tunnuseid, arvutatakse mediaanarv järgmise valemi abil:

M e = (n (tunnuste arv kokku) + 1)/2,

paarisarvu tunnuste korral on mediaan võrdne rea keskel asuva kahe tunnuse keskmisega).

Mediaani arvutamisel intervallide variatsiooniseeriate jaoks Esmalt määrake mediaanintervall, mille sees mediaan asub, ja seejärel määrake mediaani väärtus valemi abil:

§ – nõutav mediaan

§ - mediaani sisaldava intervalli alumine piir

§ - intervalli väärtus

§ - sageduste summa või seerialiikmete arv

§ - mediaanile eelnevate intervallide akumuleeritud sageduste summa

§ - mediaanintervalli sagedus

Näide. Leidke režiim ja mediaan.

Lahendus: selles näites on modaalne intervall vanuserühmas 25–30 aastat, kuna sellel intervallil on kõrgeim sagedus (1054).

Arvutame režiimi suuruse:

See tähendab, et õpilaste modaalne vanus on 27 aastat.

Arvutame mediaani. Keskmine intervall on vanuserühmas 25-30 aastat, kuna selle intervalli sees on valik, mis jagab elanikkonna kaheks võrdseks osaks (Σf i /2 = 3462/2 = 1731). Järgmisena asendame valemis vajalikud arvandmed ja saame mediaanväärtuse:

See tähendab, et pooled õpilastest on alla 27,4-aastased, teine pool aga üle 27,4-aastased.

Lisaks režiimile ja mediaanile kasutatakse selliseid näitajaid nagu kvartiilid, mis jagavad järjestatud seeriad 4 võrdseks osaks, detsiilid - 10 osaks ja protsentiilid - 100 osaks.

20. Valimivaatluse mõiste ja selle ulatus.

Valikuline vaatlus kehtib pideva järelevalve kasutamisel füüsiliselt võimatu suure andmemahu tõttu või ei ole majanduslikult otstarbekas. Füüsiline võimatus ilmneb näiteks reisijatevoogude, turuhindade ja pereeelarvete uurimisel. Majanduslik ebaotstarbekus ilmneb nende hävitamisega seotud kaupade kvaliteedi hindamisel, näiteks maitsmisel, telliste tugevuse kontrollimisel jne.

Vaatluseks valitud statistilised ühikud on näidispopulatsioon või näidis ja kogu nende massiiv - üldine elanikkond(GS). Kus ühikute arv proovis tähistama n ja kogu GS-is - N. Suhtumine n/N tavaliselt kutsutakse suhteline suurus või näidisosa.

Proovide vaatlustulemuste kvaliteet sõltub valimi esinduslikkus st selle kohta, kui esinduslik see GS-is on. Valimi esinduslikkuse tagamiseks on äärmiselt oluline järgida ühikute juhusliku valiku põhimõte, mis eeldab, et HS-ühiku valimisse kaasamist ei saa mõjutada ükski muu tegur peale juhuse.

Olemas 4 juhusliku valiku võimalust prooviks:
1. Tegelikult juhuslikult valik või "lotomeetod", kui statistilistele väärtustele määratakse seerianumbrid, mis registreeritakse teatud objektidele (näiteks tünnid), mis seejärel segatakse konteineris (näiteks kotis) ja valitakse juhuslikult. Praktikas kasutatakse seda meetodit juhuslike arvude generaatori või juhuslike arvude matemaatiliste tabelite abil.
2. Mehaaniline valik, mille järgi iga ( N/n)-nda üldkogumi väärtus. Näiteks kui see sisaldab 100 000 väärtust ja peate valima 1000, kaasatakse valimisse iga 100 000 / 1000 = 100. väärtus. Veelgi enam, kui neid ei järjestata, valitakse esimene saja hulgast juhuslikult ja teiste numbrid on saja võrra suuremad. Näiteks kui esimene ühik oli nr 19, siis järgmine peaks olema nr 119, siis nr 219, siis nr 319 jne. Kui rahvastikuüksused on järjestatud, siis valitakse kõigepealt nr 50, seejärel nr 150, siis nr 250 jne.
3. Väärtused valitakse heterogeensest andmemassiivist kihistunud(kihistatud) meetod, kui populatsioon jagatakse esmalt homogeenseteks rühmadeks, millele rakendatakse juhuslikku või mehaanilist valikut.
4. Spetsiaalne proovivõtumeetod on sari selektsioon, mille käigus nad valivad juhuslikult või mehaaniliselt mitte üksikuid väärtusi, vaid nende seeriaid (jadad mingist arvust mõne numbrini reas), mille raames teostatakse pidevat vaatlust.
Proovivaatluste kvaliteet sõltub ka sellest proovi tüüp: kordas või kordumatu. Kell uuesti valik Valimisse kaasatud statistilised väärtused või nende seeriad tagastatakse pärast kasutamist üldkogumisse, millel on võimalus sattuda uude valimisse. Veelgi enam, kõigil üldkogumi väärtustel on valimisse kaasamise tõenäosus sama. Kordumatu valik tähendab, et valimisse kaasatud statistilised väärtused või nende seeriad ei naase pärast kasutamist üldkogumisse ja seetõttu suureneb viimaste ülejäänud väärtuste puhul tõenäosus järgmisse valimisse sattuda.

Mittekorduv proovivõtt annab täpsemad tulemused ja seetõttu kasutatakse seda sagedamini. Kuid on olukordi, kus seda ei saa rakendada (reisijatevoogude, tarbijanõudluse jms uurimine) ja siis tehakse korduv valik.

21. Maksimaalne vaatlusviga, keskmine valimiviga, nende arvutamise kord.

Vaatleme üksikasjalikult ülaltoodud meetodeid valimi üldkogumi moodustamiseks ja tekkivaid esindusvigu. Õige juhuslikult valim põhineb populatsioonist üksuste juhuslikul valimisel ilma süstemaatiliste elementideta. Tehniliselt toimub tegelik juhuslik valik loosi teel (näiteks loteriid) või juhuslike arvude tabeli abil.

Õiget juhuslikku valikut "puhtal kujul" kasutatakse selektiivse vaatluse praktikas harva, kuid see on teiste valikutüüpide hulgas esialgne, rakendab selektiivse vaatluse põhiprintsiipe. Vaatleme mõningaid küsimusi valimimeetodi teooriast ja lihtsa juhusliku valimi veavalemi kohta.

Valimi kallutatus- ϶ᴛᴏ parameetri väärtuse erinevus üldkogumis ja selle valimi vaatluse tulemuste põhjal arvutatud väärtuse vahel. Oluline on märkida, et keskmise kvantitatiivse karakteristiku valimi võtmise vea määrab

Näitajat nimetatakse tavaliselt maksimaalseks diskreetimisveaks. Valimi keskmine on juhuslik suurus, mis võib saada erinevaid väärtusi, sõltuvalt sellest, millised ühikud valimisse kaasatakse. Seetõttu on valimivead ka juhuslikud muutujad ja võivad omandada erinevaid väärtusi. Sel põhjusel määratakse võimalike vigade keskmine - keskmine proovivõtuviga, mis sõltub:

· valimi suurus: mida suurem arv, seda väiksem on keskmine viga;

· uuritava tunnuse muutumise määr: mida väiksem on tunnuse varieeruvus ja sellest tulenevalt ka dispersioon, seda väiksem on keskmine valimiviga.

Kell juhuslik uuesti valik arvutatakse keskmine viga. Praktikas ei ole üldist dispersiooni täpselt teada, kuid tõenäosusteoorias on see tõestatud . Kuna piisavalt suure n väärtus on 1-le lähedane, võime eeldada, et . Seejärel tuleks arvutada keskmine valimiviga: . Kuid väikese valimi korral (koos n<30) коэффициент крайне важно учитывать, и среднюю ошибку малой выборки рассчитывать по формуле .

Kell juhuslik mittekorduv valim antud valemeid korrigeeritakse väärtusega . Siis on keskmine mittekorduv diskreetimisviga: Ja . Sest on alati väiksem kui , siis kordaja () on alati väiksem kui 1. See tähendab, et korduva valiku korral on keskmine viga alati väiksem kui korduva valiku korral. Mehaaniline proovivõtt kasutatakse siis, kui üldrahvastik on mingil viisil järjestatud (näiteks valijate nimekirjad tähestikulises järjekorras, telefoninumbrid, maja- ja korterinumbrid). Ühikute valimine toimub teatud intervalliga, mis on võrdne proovivõtuprotsendi pöördväärtusega. Seega valitakse 2% valimiga iga 50 ühikut = 1/0,02, 5% valimi korral iga 1/0,05 = 20 ühikut üldkogumist.

Võrdluspunkt valitakse erineval viisil: juhuslikult, intervalli keskelt, võrdluspunkti muutusega. Peaasi on vältida süstemaatilisi vigu. Näiteks 5% valimiga, kui esimene ühik on 13., siis järgmised on 33, 53, 73 jne.

Täpsuse poolest on mehaaniline valik lähedane tegelikule juhuslikule valimile. Sel põhjusel kasutatakse mehaanilise valimi keskmise vea määramiseks õigeid juhusliku valiku valemeid.

Kell tüüpiline valik küsitletav elanikkond on esialgselt jagatud homogeenseteks sarnasteks rühmadeks. Näiteks ettevõtete küsitlemisel on need majandusharud, allsektorid, rahvastiku uurimisel piirkonnad, sotsiaalsed või vanuserühmad. Järgmisena tehakse igast rühmast sõltumatu valik mehaaniliselt või puhtjuhuslikult.

Tüüpiline proovivõtt annab täpsemaid tulemusi kui muud meetodid. Üldkogumi tüpiseerimine tagab, et iga tüpoloogiline rühm on valimis esindatud, mis võimaldab välistada rühmadevahelise dispersiooni mõju keskmisele valimiveale. Seetõttu on tüüpvalimi vea leidmisel dispersioonide liitmise reegli ( () järgi äärmiselt oluline arvestada ainult grupi dispersioonide keskmist. Siis keskmine proovivõtuviga: korduva proovivõtmisega, mittekorduva proovivõtuga , Kus – valimi rühmasiseste dispersioonide keskmine.

Seeria (või pesa) valik kasutatakse, kui üldkogum jagatakse enne valikuuringu algust seeriateks või rühmadeks. Need seeriad hõlmavad valmistoodete pakendeid, õpilasrühmi ja brigaade. Uurimiseks valitakse seeriad mehaaniliselt või puhtjuhuslikult ning seeria raames viiakse läbi pidev ühikute kontroll. Sel põhjusel sõltub keskmine valimiviga ainult rühmadevahelisest (ridadevahelisest) dispersioonist, mis arvutatakse järgmise valemi abil: kus r on valitud seeriate arv; – i-nda seeria keskmine. Arvutatakse jadavalimise keskmine viga: korduva valimiga, mittekorduva valimiga , kus R on seeriate koguarv. Kombineeritud valik on valitud valikumeetodite kombinatsioon.

Iga valimivõtumeetodi keskmine valimiviga sõltub peamiselt valimi absoluutsest suurusest ja vähemal määral valimi protsendist. Oletame, et esimesel juhul tehakse 225 vaatlust 4500 ühiku suurusest populatsioonist ja teisel juhul 225 000 ühiku suurusest populatsioonist. Dispersioon on mõlemal juhul võrdne 25-ga. Siis on esimesel juhul 5% valiku korral valimiviga: Teisel juhul, 0,1% valikuga, on see võrdne:

Kui aga valimiprotsenti vähendati 50 korda, suurenes valimi võtmise viga veidi, kuna valimi suurus ei muutunud. Oletame, et valimi suurust suurendatakse 625 vaatluseni. Sel juhul on proovivõtu viga: Valimi suurendamine sama populatsiooni suurusega 2,8 korda vähendab valimi vea suurust rohkem kui 1,6 korda.

22.Meetodid ja meetodid valimipopulatsiooni moodustamiseks.

Statistikas kasutatakse erinevaid valimipopulatsioonide moodustamise meetodeid, mis on määratud uuringu eesmärkidega ja sõltuvad uurimisobjekti spetsiifikast.

Valimküsitluse läbiviimise peamiseks tingimuseks on vältida süstemaatiliste vigade tekkimist, mis tulenevad võrdse võimaluse põhimõtte rikkumisest üldkogumi iga valimisse sattumise üksuse osas. Süstemaatiliste vigade vältimine saavutatakse teaduslikult põhjendatud meetodite kasutamisega valimipopulatsiooni moodustamisel.

Üldkogumi hulgast üksuste valimiseks on järgmised meetodid: 1) individuaalne valik - valimisse valitakse üksikud üksused; 2) rühmavalik - valimisse kuuluvad kvalitatiivselt homogeensed uuritavad rühmad või ühikute seeriad; 3) kombineeritud valik on kombinatsioon individuaalsest ja rühmavalikust. Valimismeetodid on määratud valimi üldkogumi moodustamise reeglitega.

Näidis peaks olema:
- tegelikult juhuslik seisneb selles, et valimipopulatsioon moodustub üldkogumist üksikute üksuste juhusliku (tahtmatu) valiku tulemusena. Sel juhul määratakse valimikogumisse valitud üksuste arv tavaliselt aktsepteeritud valimi osakaalu alusel. Valimi osakaal on valimi üldkogumi n üksuste arvu ja üldkogumi N üksuste arvu suhe, ᴛ.ᴇ.
- mehaanilised seisneb selles, et valimipopulatsiooni üksuste valik tehakse üldkogumi hulgast, mis on jagatud võrdseteks intervallideks (rühmadeks). Sel juhul on intervalli suurus üldkogumis võrdne valimi osakaalu pöördarvuga. Seega valitakse 2% valimiga iga 50. ühik (1:0,02), 5% valimiga iga 20. ühik (1:0,05) jne. Kuid vastavalt aktsepteeritud valiku proportsioonile jagatakse üldpopulatsioon justkui mehaaniliselt võrdseteks rühmadeks. Igast rühmast valitakse valimi jaoks ainult üks ühik.
- tüüpiline - milles üldpopulatsioon jagatakse esmalt homogeenseteks tüüpilisteks rühmadeks. Seejärel kasutatakse igast tüüpilisest rühmast puhtjuhuslikku või mehaanilist valimit, et valida üksused valimipopulatsiooni. Tüüpilise valimi oluline tunnus on see, et see annab täpsemaid tulemusi võrreldes teiste valimipopulatsiooni üksuste valimise meetoditega;
- sari- milles üldpopulatsioon on jagatud võrdse suurusega rühmadeks - seeriad. Seeriad valitakse valimipopulatsiooni. Seeria sees toimub seeriasse kuuluvate ühikute pidev vaatlus;
- kombineeritud- proovide võtmine peaks olema kaheetapiline. Sel juhul jagatakse elanikkond esmalt rühmadesse. Järgmisena valitakse rühmad ja viimase sees üksikud üksused.
Statistikas eristatakse valimipopulatsioonis üksuste valimiseks järgmisi meetodeid:
- üks etapp valim - iga valitud üksus allutatakse koheselt uuringule vastavalt etteantud kriteeriumile (õige juhuslik ja jadavalim);
- mitmeastmeline valim - tehakse valik üksikute rühmade üldkogumi hulgast ja rühmade hulgast valitakse välja üksikud üksused (tüüpiline valim mehaanilise ühikute valimise meetodiga valimipopulatsiooni).
Lisaks on olemas:
- uuesti valik- vastavalt tagastatud palli skeemile. Sel juhul tagastatakse iga valimisse kuuluv üksus või seeria üldkogumisse ja seetõttu on tal võimalus uuesti valimisse kaasata;
- korda valikut- tagastamata palli skeemi järgi. Sellel on täpsemad tulemused sama valimi suurusega.
23. Äärmiselt olulise valimi suuruse määramine (Studentsi t-tabeli abil).

Valimiteooria üks teaduslikest põhimõtetest on tagada, et valitakse piisav arv ühikuid. Teoreetiliselt on selle printsiibi järgimise üliolulisust väljendatud tõenäosusteooria piirteoreemide tõestustes, mis võimaldavad kindlaks teha, milline maht ühikuid tuleks üldkogumist valida, et see oleks piisav ja tagaks valimi esinduslikkuse.

Valimi standardvea vähenemine ja seega ka hinnangu täpsuse suurenemine on alati seotud valimi suuruse suurenemisega, seetõttu tuleb juba valimivaatluse korraldamise etapis otsustada, milline suurus on valimi populatsioonist peaks olema, et tagada vaatlustulemuste nõutav täpsus. Äärmiselt olulise proovimahu arvutamisel kasutatakse maksimaalsete proovivõtuvigade (A) valemitest tuletatud valemeid, mis vastavad konkreetsele tüübile ja valikumeetodile. Seega on juhusliku korduva valimi suuruse (n) jaoks:

Selle valemi olemus seisneb selles, et äärmiselt oluliste arvude juhusliku korduva valimi võtmisel on valimi suurus otseselt võrdeline usalduskoefitsiendi ruuduga. (t2) ja variatsioonikarakteristiku dispersioon (?2) ning on pöördvõrdeline maksimaalse diskreetimisvea (A2) ruuduga. Eelkõige tuleks maksimaalse vea suurendamisel kahekordselt nõutavat valimi suurust vähendada neljakordselt. Kolmest parameetrist kaks (t ja?) määrab uurija. Samal ajal uurija, lähtudes eesmärgist

ja valikuuringu probleemid peavad lahendama küsimuse: millisesse kvantitatiivsesse kombinatsiooni on parem neid parameetreid kaasata, et tagada optimaalne valik? Ühel juhul võib ta olla rohkem rahul saadud tulemuste usaldusväärsusega (t) kui täpsuse mõõduga (?), teisel juhul - vastupidi. Maksimaalse valimivea väärtuse küsimuse lahendamine on keerulisem, kuna valimivaatluse kavandamise staadiumis uurijal see näitaja puudub, mistõttu on praktikas tavaks määrata maksimaalse valimivea väärtus. , tavaliselt 10% piires atribuudi eeldatavast keskmisest tasemest. Hinnangulise keskmise määramisele saab läheneda erineval viisil: kasutades sarnaste varasemate uuringute andmeid või kasutades valimi raami andmeid ja viies läbi väikese pilootvalimi.

Valimivaatluse kujundamisel on kõige keerulisem tuvastada valemis (5.2) kolmas parameeter - valimi üldkogumi dispersioon. Sel juhul on äärmiselt oluline kasutada kogu teadlasele kättesaadavat teavet, mis on saadud varasemate sarnaste ja pilootuuringute käigus.

Äärmiselt olulise valimi suuruse määramise küsimus muutub keerulisemaks, kui valikuuringu käigus uuritakse mitut valimiüksuste tunnust. Sel juhul on iga tunnuse keskmised tasemed ja nende varieeruvus reeglina erinevad ning sellega seoses on võimalik otsustada, millist erinevust millistest omadustest eelistada, ainult eesmärki ja eesmärke arvesse võttes. uuringust.

Valimivaatluse kavandamisel eeldatakse lubatud valimivea etteantud väärtust vastavalt konkreetse uuringu eesmärkidele ja vaatlustulemuste põhjal järelduste tegemise tõenäosusele.

Üldiselt võimaldab valimi keskmise maksimaalse vea valem määrata:

‣‣‣ üldkogumi näitajate võimalike kõrvalekallete suurust valimi üldkogumi näitajatest;

‣‣‣ nõutava täpsuse tagamiseks vajalik valimi suurus, mille juures võimaliku vea piirid ei ületa teatud määratud väärtust;

‣‣‣ tõenäosus, et valimi veal on määratud piir.

Õpilaste jaotus tõenäosusteoorias on see absoluutselt pidevate jaotuste üheparameetriline perekond.

24. Dünaamilised seeriad (intervall, hetk), dünaamiliste seeriate sulgemine.

Dünaamika seeria- need on statistiliste näitajate väärtused, mis on esitatud teatud kronoloogilises järjestuses.

Iga aegrida sisaldab kahte komponenti:

1) ajaperioodide näitajad(aastad, kvartalid, kuud, päevad või kuupäevad);

2) uuritavat objekti iseloomustavad näitajad perioodideks või vastavatel kuupäevadel, mida kutsutakse seeria tasemed.

Seeriatasemeid väljendatakse nii absoluutsete kui ka keskmiste või suhteliste väärtustena. Võttes arvesse sõltuvust näitajate olemusest, koostatakse absoluutsete, suhteliste ja keskmiste väärtuste dünaamilised seeriad. Suhteliste ja keskmiste väärtuste dünaamilised seeriad koostatakse tuletatud absoluutväärtuste seeriate põhjal. Dünaamikas on intervallide ja hetkede jada.

Dünaamilised intervallid sisaldab teatud ajaperioodide näitajate väärtusi. Intervallreas saab tasemeid summeerida, et saada nähtuse maht pikema perioodi jooksul ehk nn akumuleeritud summad.

Dünaamiline hetkesari peegeldab indikaatorite väärtusi teatud ajahetkel (kellaaeg). Hetkesarjade puhul võib uurijat huvitada vaid nähtuste erinevus, mis peegeldab seeria taseme muutumist teatud kuupäevade vahel, kuna tasemete summal pole siin tegelikku sisu. Kumulatiivseid kogusummasid siin ei arvutata.

Aegridade õige konstrueerimise kõige olulisem tingimus on seeriatasemete võrreldavus mis kuuluvad erinevatesse perioodidesse. Tasemed peavad olema esitatud homogeensetes kogustes ja nähtuse eri osade katvus peab olema võrdne.

Et vältida tegeliku dünaamika moonutamist, tehakse statistilistes uuringutes eelarvutused (dünaamikarea sulgemine), mis eelneb aegridade statistilisele analüüsile. Under dünaamika jada sulgemineÜldtunnustatud on mõista kombinatsiooni üheks seeriaks kahest või enamast seeriast, mille tasemed on arvutatud erineva metoodikaga või ei vasta territoriaalsetele piiridele jne. Dünaamikaseeria sulgemine võib tähendada ka dünaamikaseeriate absoluuttasemete viimist ühisele alusele, mis neutraliseerib dünaamikaseeriate tasemete võrreldamatuse.

25. Dünaamika ridade, koefitsientide, kasvu ja kasvumäärade võrreldavuse mõiste.

Dünaamika seeria- need on statistiliste näitajate jada, mis iseloomustavad loodus- ja ühiskonnanähtuste arengut aja jooksul. Venemaa riikliku statistikakomitee avaldatud statistikakogud sisaldavad suurt hulka dünaamika seeriaid tabeli kujul. Dünaamilised seeriad võimaldavad tuvastada uuritavate nähtuste arengumustreid.

Dynamics seeriad sisaldavad kahte tüüpi indikaatoreid. Aja indikaatorid(aastad, kvartalid, kuud jne) või ajapunktid (aasta alguses, iga kuu alguses jne). Rea taseme indikaatorid. Dünaamika seeriate tasemenäitajaid saab väljendada absoluutväärtustes (tootetoodang tonnides või rublades), suhtelistes väärtustes (linnaelanikkonna osakaal protsentides) ja keskmistes väärtustes (tööstustöötajate keskmine palk aasta lõikes). , jne.). Tabeli kujul sisaldab aegrida kahte veergu või kahte rida.

Aegridade õige koostamine eeldab mitme nõude täitmist:
1. kõik mitme dünaamika näitajad peavad olema teaduslikult põhjendatud ja usaldusväärsed;
2. dünaamikaseeria näitajad peavad olema ajas võrreldavad, ᴛ.ᴇ. tuleb arvutada samade ajavahemike või samade kuupäevade kohta;
3. mitme dünaamika näitajad peavad olema kogu territooriumil võrreldavad;
4. dünaamika jada näitajad peavad olema sisult võrreldavad, ᴛ.ᴇ. arvutatakse ühe metoodika järgi, samal viisil;
5. mitme dünaamika näitajad peaksid olema kõigi arvesse võetavate põllumajandusettevõtete puhul võrreldavad. Kõik dünaamikaseeria näitajad tuleb esitada samades mõõtühikutes.
Statistilised näitajad võivad iseloomustada kas uuritava protsessi tulemusi teatud ajaperioodi jooksul või uuritava nähtuse seisundit teatud ajahetkel, ᴛ.ᴇ. indikaatorid võivad olla intervallsed (perioodilised) ja hetkelised. Vastavalt sellele on dünaamikaseeriad algselt kas intervall või hetk. Momendidünaamika seeriad tulevad omakorda võrdsete ja ebavõrdsete ajavahemikega.

Algset dünaamikaseeriat saab teisendada keskmiste väärtuste ja suhteliste väärtuste seeriaks (ahel ja põhi). Selliseid aegridu nimetatakse tuletatud aegridadeks.

Dünaamika seeria keskmise taseme arvutamise metoodika on erinev, olenevalt dünaamika seeria tüübist. Näidete abil käsitleme dünaamika seeriate tüüpe ja keskmise taseme arvutamise valemeid.

Absoluutsed tõusud (Δy) näitavad, mitu ühikut on seeria järgnev tase muutunud võrreldes eelmisega (gr. 3. - ahel absoluutsed tõusud) või võrreldes algtasemega (gr. 4. - põhi absoluutsed tõusud). Arvutusvalemid saab kirjutada järgmiselt:

Kui seeria absoluutväärtused vähenevad, toimub vastavalt "vähendamine" või "vähendamine".

Absoluutsed kasvunäitajad viitavad sellele, et näiteks 1998.a. toote "A" tootmine kasvas võrreldes 1997. aastaga. 4 tuhande tonni võrra ja võrreldes 1994. aastaga ᴦ. - 34 tuhande tonni võrra; teiste aastate kohta vaata tabelit. 11,5 gr.
Postitatud aadressil ref.rf
3 ja 4.

Kasvumäär näitab, mitu korda on seeria tase muutunud võrreldes eelmisega (gr. 5 – kasvu või languse ahela koefitsiendid) või võrreldes algtasemega (gr. 6 – kasvu või languse põhikoefitsiendid). Arvutusvalemid saab kirjutada järgmiselt:

Kasvumäärad näidata, mitu protsenti on seeria järgmine tase võrreldes eelmisega (gr. 7 – ahela kasvumäärad) või võrreldes algtasemega (gr. 8 – põhikasvumäärad). Arvutusvalemid saab kirjutada järgmiselt:

Nii näiteks 1997.a. toote "A" tootmismaht võrreldes 1996. aastaga ᴦ. moodustas 105,5% (

Kasvumäär näidata, mitu protsenti aruandeperioodi tase tõusis võrreldes eelmisega (veerg 9 - ahela kasvumäärad) või võrreldes algtasemega (veerg 10 - põhikasvumäärad). Arvutusvalemid saab kirjutada järgmiselt:

T pr = T r - 100% või T pr = absoluutne kasv / eelmise perioodi tase * 100%

Nii näiteks 1996. a. võrreldes 1995. aastaga ᴦ. Toodet "A" toodeti rohkem 3,8% (103,8% - 100%) ehk (8:210)x100% võrra ja võrreldes 1994. aastaga ᴦ. - 9% võrra (109% - 100%).

Kui seeria absoluuttasemed vähenevad, on määr alla 100% ja vastavalt sellele toimub ka vähenemise määr (miinusmärgiga kasvutempo).

Absoluutväärtus 1% tõus(gr.
Postitatud aadressil ref.rf
11) näitab, mitu ühikut on vaja antud perioodil toota, et eelmise perioodi tase tõuseks 1%. Meie näites 1995. aastal ᴦ. oli vaja toota 2,0 tuhat tonni ja 1998 ᴦ. - 2,3 tuhat tonni, ᴛ.ᴇ. palju suurem.

1% kasvu absoluutväärtust saab määrata kahel viisil:

§ eelmise perioodi tase jagatud 100-ga;

§ ahela absoluutsed kasvud jagatakse vastavate ahela kasvumääradega.

1% kasvu absoluutväärtus =

Dünaamikas, eriti pika perioodi jooksul, on oluline kasvutempo ühine analüüs koos iga protsendi suurenemise või languse sisuga.

Pange tähele, et vaadeldav metoodika aegridade analüüsimiseks on rakendatav nii aegridade puhul, mille tasemed on väljendatud absoluutväärtustes (t, tuhat rubla, töötajate arv jne), kui ka aegridade puhul, mille tasemed väljendatakse suhteliste näitajatena (defektide %, kivisöe tuhasisaldus % jne) või keskmiste väärtustena (keskmine saagikus c/ha, keskmine palk jne).

Dünaamikaseeriate analüüsimisel on lisaks igaks aastaks arvutatud analüütilistele näitajatele, mis on arvutatud võrreldes eelmise või algtasemega, äärmiselt oluline arvutada perioodi keskmised analüütilised näitajad: rea keskmine tase, aasta keskmine absoluutne tase. suurenemine (vähenemine) ja keskmine aastane kasvumäär ja kasvutempo .

Eespool käsitleti dünaamikaseeria keskmise taseme arvutamise meetodeid. Vaadeldavas intervalldünaamika seerias arvutatakse seeria keskmine tase lihtsa aritmeetilise keskmise valemi abil:

Toote keskmine aastane tootmismaht aastatel 1994-1998. moodustas 218,4 tuhat tonni.

Aasta keskmine absoluutkasv arvutatakse samuti aritmeetilise keskmise valemi abil

Standardhälve – mõiste ja liigid. Kategooria "Keskmine ruuthälve" klassifikatsioon ja tunnused 2017, 2018.

Õppetund nr 4
Teema: “Kirjeldav statistika. Tunnuste mitmekesisuse näitajad kokku"
Karakteristiku mitmekesisuse peamised kriteeriumid statistilises populatsioonis on: piir, amplituud, standardhälve, võnketegur ja variatsioonikoefitsient. Eelmises õppetükis arutati, et keskmised väärtused annavad ainult uuritava tunnuse üldistatud omaduse koondmaterjalina ega võta arvesse selle üksikute variantide väärtusi: miinimum- ja maksimumväärtused, keskmisest kõrgemad, allapoole. keskmine jne.
Näide. Kahe erineva numbrijada keskmised väärtused: -100; -20; 100; 20 ja 0,1; -0,2; 0,1 on absoluutselt identsed ja võrdsedKOHTA.Nende suhteliste keskmiste järjestuste andmete hajuvusvahemikud on aga väga erinevad.
Loetletud tunnuse mitmekesisuse kriteeriumide kindlaksmääramisel võetakse eelkõige arvesse selle väärtust statistilise üldkogumi üksikutes elementides.
Tunnuse varieerumise mõõtmise indikaatorid on absoluutne Ja sugulane. Variatsiooni absoluutnäitajate hulka kuuluvad: varieeruvuse vahemik, piir, standardhälve, dispersioon. Variatsioonitegur ja võnketegur viitavad suhtelistele variatsioonimõõtudele.
Limiit (lim) – See on kriteerium, mille määravad variatsiooniseeria variandi äärmuslikud väärtused. Teisisõnu, see kriteerium on piiratud atribuudi minimaalse ja maksimaalse väärtusega:
Amplituud (am) või variatsiooni vahemik - See on äärmuslike võimaluste erinevus. Selle kriteeriumi arvutamiseks lahutatakse atribuudi maksimaalsest väärtusest selle minimaalne väärtus, mis võimaldab meil hinnata valiku hajumise astet:
Piiri ja amplituudi kui varieeruvuse kriteeriumide puuduseks on see, et need sõltuvad täielikult variatsioonirea karakteristiku äärmuslikest väärtustest. Sel juhul ei võeta seeriasiseseid atribuutide väärtuste kõikumisi arvesse.
Kõige täielikuma kirjelduse tunnuse mitmekesisusest statistilises populatsioonis annab standardhälve(sigma), mis on optsiooni keskmisest väärtusest kõrvalekaldumise üldine mõõt. Sageli nimetatakse standardhälvet standardhälve.
Standardhälve põhineb iga variandi võrdlusel antud üldkogumi aritmeetilise keskmisega. Kuna agregaadis on alati valikuid nii vähem kui ka rohkem, siis märgiga "" kõrvalekallete summa tühistatakse märgiga "" kõrvalekallete summa võrra, st. kõigi kõrvalekallete summa on null. Et vältida erinevuste märkide mõju, võetakse kõrvalekalded aritmeetilisest keskmisest ruudust, s.o. . Ruuthälvete summa ei võrdu nulliga. Muutuvust mõõtva koefitsiendi saamiseks võtke ruutude summa keskmine - seda väärtust nimetatakse hälbed:
Sisuliselt on dispersioon tunnuse üksikute väärtuste kõrvalekallete keskmine ruut selle keskmisest väärtusest. Dispersioon – standardhälbe ruut.
Dispersioon on mõõtmete suurus (nimetatakse). Seega, kui arvurea variandid on väljendatud meetrites, siis dispersioon annab ruutmeetreid; kui variandid on väljendatud kilogrammides, siis dispersioon annab selle mõõdu ruudu (kg 2) jne.
Standardhälve– dispersiooni ruutjuur:
, siis dispersiooni ja standardhälbe arvutamisel murdosa nimetaja asemeltuleb panna.
Standardhälbe arvutamise võib jagada kuueks etapiks, mis tuleb läbi viia kindlas järjekorras:
Standardhälbe rakendamine:
a) variatsiooniridade varieeruvuse hindamiseks ja aritmeetiliste keskmiste tüüpilisuse (representatiivsuse) võrdlevaks hindamiseks. See on vajalik diferentsiaaldiagnostikas sümptomite stabiilsuse määramisel.
b) rekonstrueerida variatsioonirida, s.o. alusel selle sageduskarakteristiku taastamine kolm sigma reeglit. Vaheajal (М±3σ) 99,7% seeria kõigist variantidest asuvad intervallis (М±2σ) - 95,5% ja vahemikus (М±1σ) - 68,3% rea variant(joonis 1).
c) "hüpikakna" valikute tuvastamiseks
d) määrata normi ja patoloogia parameetrid sigma hinnangute abil
e) variatsioonikoefitsiendi arvutamiseks
f) arvutada aritmeetilise keskmise keskmine viga.
Et iseloomustada mis tahes populatsiooni, millel onnormaaljaotuse tüüp , piisab kahe parameetri teadmisest: aritmeetilisest keskmisest ja standardhälbest.
Joonis 1. Kolme sigma reegel
Näide.
Pediaatrias kasutatakse standardhälvet laste füüsilise arengu hindamiseks, võrreldes konkreetse lapse andmeid vastavate standardnäitajatega. Standardiks võetakse tervete laste füüsilise arengu aritmeetiline keskmine. Näitajate võrdlemine standarditega toimub spetsiaalsete tabelite abil, milles on toodud standardid koos neile vastavate sigma skaaladega. Arvatakse, et kui lapse füüsilise arengu näitaja on normi piires (aritmeetiline keskmine) ±σ, siis lapse füüsiline areng (selle näitaja järgi) vastab normile. Kui indikaator jääb normi ±2σ piiresse, siis on normist väike kõrvalekalle. Kui näitaja ületab neid piire, erineb lapse füüsiline areng normist järsult (patoloogia on võimalik).
Lisaks absoluutväärtustes väljendatud variatsiooninäitajatele kasutatakse statistilistes uuringutes suhtelistes väärtustes väljendatud variatsiooninäitajaid. võnkekoefitsient - see on variatsioonivahemiku ja tunnuse keskmise väärtuse suhe. Variatsioonikoefitsient - see on standardhälbe ja tunnuse keskmise väärtuse suhe. Tavaliselt väljendatakse neid väärtusi protsentides.
Suhtelise variatsiooni näitajate arvutamise valemid:
Ülaltoodud valemitest on selge, et mida suurem on koefitsient V on nullile lähemal, seda väiksem on tunnuse väärtuste kõikumine. Rohkem V, seda muutuvam on märk.
Statistilises praktikas kasutatakse kõige sagedamini variatsioonikordajat. Seda ei kasutata mitte ainult varieeruvuse võrdlevaks hindamiseks, vaid ka populatsiooni homogeensuse iseloomustamiseks. Populatsioon loetakse homogeenseks, kui variatsioonikordaja ei ületa 33% (normaallähedaste jaotuste korral). Aritmeetiliselt neutraliseerib σ ja aritmeetilise keskmise suhe nende tunnuste absoluutväärtuse mõju ning protsentuaalne suhe muudab variatsioonikordaja dimensioonideta (nimeta) väärtuseks.
Saadud variatsioonikordaja väärtust hinnatakse vastavalt tunnuse mitmekesisuse astme ligikaudsele gradatsioonile:
nõrk - kuni 10%
Keskmine – 10–20%
Tugev - üle 20%
Variatsioonikoefitsiendi kasutamine on soovitatav juhtudel, kui on vaja võrrelda erineva suuruse ja mõõtmetega omadusi.
Variatsioonikoefitsiendi ja muude hajuvuskriteeriumide erinevus on selgelt näidatud näide.
Tabel 1
Tööstusettevõtete töötajate koosseis

Näites toodud statistiliste tunnuste põhjal saame teha järelduse ettevõtte töötajate vanuselise koosseisu ja haridustaseme suhtelise homogeensuse kohta, arvestades uuritava kontingendi madalat ametialast stabiilsust. On lihtne mõista, et katse hinnata neid sotsiaalseid suundumusi standardhälbe järgi viiks ekslikule järeldusele ning katse võrrelda raamatupidamistunnuseid "töökogemus" ja "vanus" raamatupidamisnäitajaga "haridus" oleks üldiselt nende omaduste heterogeensuse tõttu valed.
Mediaan ja protsentiilid
Järjekorraliste (asukoha) jaotuste puhul, kus rea keskkoha kriteeriumiks on mediaan, ei saa standardhälvet ja dispersiooni kasutada variandi dispersiooni tunnustena.
Sama kehtib ka avatud variatsiooniseeriate kohta. See asjaolu on tingitud asjaolust, et hälbeid, millest dispersioon ja σ arvutatakse, mõõdetakse aritmeetilisest keskmisest, mida ei arvutata avatud variatsiooniridades ja kvalitatiivsete tunnuste jaotuste jadades. Seetõttu kasutatakse jaotuste tihendatud kirjelduse jaoks teist hajumise parameetrit - kvantiil(sünonüüm - "protsentiil"), sobib kvalitatiivsete ja kvantitatiivsete omaduste kirjeldamiseks nende mis tahes jaotusvormis. Seda parameetrit saab kasutada ka kvantitatiivsete tunnuste teisendamiseks kvalitatiivseteks. Sel juhul määratakse sellised hinnangud sõltuvalt sellest, millisele kvantiili järjekorrale konkreetne valik vastab.
Biomeditsiiniliste uuringute praktikas kasutatakse kõige sagedamini järgmisi kvantiile:
– mediaan;
, – kvartiilid (kvartiilid), kus – alumine kvartiil, – ülemine kvartiil.
Kvantiilid jagavad variatsioonirea võimalike muutuste ala teatud intervallideks. Mediaan (kvantiil) on variant, mis on variatsioonirea keskel ja jagab selle seeria pooleks kaheks võrdseks osaks ( 0,5 Ja 0,5 ). Kvartiil jagab seeria neljaks osaks: esimene osa (alumine kvartiil) on optsioon, mis eraldab optsioonid, mille arvväärtused ei ületa 25% antud seeria maksimaalsest võimalikust; kvartiil eraldab optsioonid, mille arvväärtus on kuni 50% maksimaalsest võimalikust. Ülemine kvartiil () eraldab valikud kuni 75% maksimaalsetest võimalikest väärtustest.
Asümmeetrilise jaotuse korral muutuja aritmeetilise keskmise suhtes, selle iseloomustamiseks kasutatakse mediaani ja kvartiile. Sel juhul kasutatakse keskmise väärtuse kuvamiseks järgmist vormi - meh (;). Näiteks, on uuritav tunnus – „periood, mil laps hakkas iseseisvalt kõndima“ – jaotus õpperühmas asümmeetriliselt. Samal ajal vastab alumine kvartiil () kõndimise algusele - 9,5 kuud, mediaan - 11 kuud, ülemine kvartiil () - 12 kuud. Vastavalt sellele esitatakse määratud atribuudi keskmise trendi tunnuseks 11 (9,5; 12) kuud.
Õppetulemuste statistilise olulisuse hindamine
Andmete statistilise olulisuse all mõistetakse seda, mil määral need vastavad kuvatavale reaalsusele, s.t. statistiliselt olulised andmed on need, mis ei moonuta ja kajastavad õigesti objektiivset tegelikkust.
Uurimistulemuste statistilise olulisuse hindamine tähendab määramist, millise tõenäosusega on võimalik valimikogumilt saadud tulemusi üle kanda kogu üldkogumile. Statistilise olulisuse hindamine on vajalik, et mõista, kui suure osa nähtusest saab hinnata nähtust tervikuna ja selle mustreid.
Uurimistulemuste statistilise olulisuse hindamine koosneb:
1. esindusvead (keskmiste ja suhteliste väärtuste vead) - m;
2. keskmiste või suhteliste väärtuste usalduspiirid;
3. keskmiste või suhteliste väärtuste erinevuse usaldusväärsus vastavalt kriteeriumile t.
Aritmeetilise keskmise standardviga või esindusviga iseloomustab keskmise kõikumist. Tuleb märkida, et mida suurem on valimi suurus, seda väiksem on keskmiste väärtuste levik. Keskmise standardviga arvutatakse järgmise valemi abil:
Kaasaegses teaduskirjanduses kirjutatakse aritmeetiline keskmine koos representatiivsusveaga:
või koos standardhälbega:
Vaatleme näiteks andmeid riigi 1500 linnakliiniku kohta (üldrahvastik). Kliinikus teenindatavate patsientide keskmine arv on 18 150 inimest. Juhuslik valik 10% kohtadest (150 kliinikut) annab keskmiseks patsientide arvuks 20 051 inimest. Valimi võtmise viga, mis tuleneb ilmselt asjaolust, et valimisse ei kaasatud kõiki 1500 kliinikut, on võrdne nende keskmiste erinevusega - üldkeskmise ( M geen) ja proovi keskmine ( M valitud). Kui moodustame oma populatsioonist teise sama suurusega valimi, annab see erineva veaväärtuse. Kõik need valimi keskmised, piisavalt suurte valimitega, jaotuvad normaalselt üldkeskmise ümber, kusjuures üldkogumi sama arvu objektide valimi korduste arv on piisavalt suur. Keskmise standardviga m- see on valimi keskmiste vältimatu levik üldkeskmise ümber.
Juhul, kui uurimistulemused esitatakse suhtelistes kogustes (näiteks protsentides) - arvutatakse murdosa standardviga:
kus P on näitaja %, n on vaatluste arv.
Tulemus kuvatakse kujul (P ± m)%. Näiteks, paranemise protsent patsientide seas oli (95,2±2,5)%.
Juhul, kui populatsiooni elementide arv, siis keskväärtuse standardvigade arvutamisel ja murdosa nimetaja murdosa asemeltuleb panna.
Normaaljaotuse korral (valimi keskmiste jaotus on normaalne) teame, milline osa populatsioonist jääb mis tahes keskmist ümbritsevasse intervalli. Eriti:
Praktikas on probleem selles, et üldkogumi tunnused on meile tundmatud ning valim tehakse just nende hindamise eesmärgil. See tähendab, et kui teeme sama suurusega proovid nüldkogumikust, siis 68,3% juhtudest sisaldab intervall väärtust M(95,5% juhtudest on see intervallil ja 99,7% juhtudest intervallil).
Kuna tegelikult võetakse ainult üks valim, on see väide sõnastatud tõenäosuse alusel: tõenäosusega 68,3%, atribuudi keskmine väärtus üldkogumis asub intervallis, tõenäosusega 95,5%. - intervallis jne.
Praktikas ehitatakse valimi väärtuse ümber intervall nii, et etteantud (piisavalt suure) tõenäosusega usalduse tõenäosus –"kataks" selle parameetri tegeliku väärtuse üldpopulatsioonis. Seda intervalli nimetatakse usaldusvahemik.
Usalduse tõenäosusP – see on usaldusväärsuse aste, et usaldusvahemik sisaldab tegelikult üldkogumi parameetri tõelist (tundmatut) väärtust.
Näiteks kui usalduse tõenäosus R on 90%, see tähendab, et 90 proovi 100-st annavad populatsiooni parameetri õige hinnangu. Vastavalt sellele on vea tõenäosus, s.o. valimi üldkeskmise vale hinnang on võrdne protsentides: . Selle näite puhul tähendab see, et 10 proovi 100-st annavad vale hinnangu.
Ilmselgelt sõltub usalduse aste (usaldustõenäosus) intervalli suurusest: mida laiem on intervall, seda suurem on kindlus, et sellesse satub üldkogumi jaoks tundmatu väärtus. Praktikas kasutatakse vähemalt 95,5% usaldusväärsuse tagamiseks usaldusvahemiku koostamiseks vähemalt kahekordset valimiviga.
Keskmiste ja suhteliste väärtuste usalduspiiride määramine võimaldab meil leida nende kaks äärmist väärtust - minimaalne võimalik ja maksimaalne võimalik, mille piires võib uuritav näitaja esineda kogu populatsioonis. Selle põhjal usalduspiirid (või usaldusvahemik)- need on keskmiste või suhteliste väärtuste piirid, millest üle on juhuslike kõikumiste tõttu ebaoluline tõenäosus.
Usaldusvahemiku saab ümber kirjutada järgmiselt: , kus t– usalduskriteerium.
Aritmeetilise keskmise usalduspiirid üldkogumis määratakse järgmise valemiga:
M geen = M vali + t m M
suhtelise väärtuse jaoks:
R geen = P vali + t m R
Kus M geen Ja R geen- üldrahvastiku keskmiste ja suhteliste väärtuste väärtused; M vali Ja R vali- valimipopulatsioonist saadud keskmiste ja suhteliste väärtuste väärtused; m M Ja m P- keskmiste ja suhteliste väärtuste vead; t- usalduskriteerium (täpsuskriteerium, mis kehtestatakse uuringu planeerimisel ja võib olla võrdne 2 või 3-ga); t m- see on usaldusvahemik või Δ - näidisuuringus saadud indikaatori maksimaalne viga.
Tuleb märkida, et kriteeriumi väärtus t teatud määral seotud veavaba prognoosi tõenäosusega (p), väljendatuna %. Selle valib uurija ise, juhindudes vajadusest saada nõutava täpsusega tulemus. Seega veavaba prognoosi tõenäosuse 95,5% korral on kriteeriumi väärtus t on 2, 99,7% - 3 puhul.
Antud usaldusvahemiku hinnangud on vastuvõetavad ainult statistiliste üldkogumite puhul, kus on rohkem kui 30 vaatlust.Väiksema populatsiooni (väikesed valimid) korral kasutatakse t-kriteeriumi määramiseks spetsiaalseid tabeleid. Nendes tabelites asub soovitud väärtus populatsiooni suurusele vastava joone ristumiskohas (n-1), ja veerg, mis vastab teadlase valitud veavaba prognoosi tõenäosustasemele (95,5%; 99,7%). Meditsiiniuuringutes on mis tahes näitaja usalduspiiride kehtestamisel veavaba prognoosi tõenäosus 95,5% või rohkem. See tähendab, et valimikogumist saadud näitaja väärtus tuleb leida üldkogumist vähemalt 95,5% juhtudest.
10. Usaldusvahemiku mõiste, selle rakendamine.
1. MUUTUMISE ABSOLUUTSEID NÄITAJAID, KUIDAS VIIDATE
1) variatsioonikoefitsient
2) võnkekoefitsient
4) mediaan
2. VARIATSIOONI SUHTELISED NÄITAJAD SEOTUD
1) dispersioon
4) variatsioonikoefitsient
3. KRITEERIUM, MIS ON MÄÄRATUD VARIATSIOONSERIA OPTIONI ÄRIVÄÄRTUSTE ALUSEL
2) amplituud
3) hajutamine
4) variatsioonikoefitsient
4. Äärmusvalikud ERINEVUSED ON
2) amplituud
3) standardhälve
4) variatsioonikoefitsient
5. ISELOOMULIKU KESKMISEST VÄÄRTUSEST ON INDIVIDUAALVÄÄRTUSTE HÕLMETE KESKMINE RUUT
1) võnkekoefitsient
2) mediaan
3) hajutamine
6. VARIATION SSKAALA SUHE MÄRGI KESKMISSE VÄÄRTUSEGA ON
1) variatsioonikoefitsient
2) standardhälve
4) võnkekoefitsient
7. KESKMISE RUUTHÄLBE SUHE TUNNUSLIKU KESKMISSE VÄÄRTUSEGA ON
1) dispersioon
2) variatsioonikoefitsient
3) võnkekoefitsient
4) amplituud
8. VARIANT, MIS ON VARIATSIOONIDE SERIA KESKES JA JAGAB SELLE KAHEKS VÕRDSEKS OSAKS, ON
1) mediaan
3) amplituud
9. MEDITSIINILISES UURINGUS MIS TAHES INDIKAATORILE KINNITUSLIIME KEHTES ON AKTSEPTEERITUD VEATETA ENNUSTUSE TÕENÄOSUSEGA
10. KUI 90 PROOVI 100-st ANNAVAD POPULATSIOONI PARAMEETRI ÕIGE HINNANGUSE, TÄHENDAB SEE, ET KINNITUSE TÕENÄOSUS P VÕRDSED
11. KUI 10 PROOVI 100-st ANNAVAD VALE HINNANGUSE, ON VEA TÕENÄOSUS VÕRDNE
12. KESKMISTE VÕI SUHTELISTE VÄÄRTUSTE PIIRID, MILLE ÜLEMINE JUHUSLIKUTE VÕNKUMISTE PÄRAST ON VÄIKE TÕENÄOSUS – SEE ON
1) usaldusvahemik
2) amplituud
4) variatsioonikoefitsient
13. VÄIKSEKS VALIMIKS LOETAKSE, KELLES
1) n on väiksem kui 100 või sellega võrdne
2) n on väiksem kui 30 või sellega võrdne
3) n on väiksem kui 40 või sellega võrdne
4) n on nullilähedane
14. 95% KRITEERIUMI VÄÄRTUSE VEATEVABA PROGNOOSIDE TÕENÄOSUSE KOHTA t ON
15. 99% KRITEERIUMI VÄÄRTUSE VEATETA PROGNOOSIDE TÕENÄOSUSE KOHTA t ON
16. NORMAALSELE LÄHEDASTE JAOTUSTE PUHUL LOETAKSE RAHVASTIK HOMOGEENSEKS, KUI VARIatsiooniKOefitsient EI ÜLETA
17. VALIK, ERALDAMISVÕIMALUSED, MILLISTE ARVUVÄÄRTUSED EI ÜLE 25% ANNETUD SERIES MAKSIMAALSEST VÕIMALIKUST – SEE ON
2) alumine kvartiil
3) ülemine kvartiil
4) kvartiil
18. ANDMEID, MIS EI MOONUTA JA OBJEKTIIVSET REAALSUST ÕIGESTI Peegeldavad, nimetatakse
1) võimatu
2) võrdselt võimalik
3) usaldusväärne
4) juhuslik
19. VASTAVALT "KOLME SigMA" REEGLILE, KES TAVALINE JAOTUS
ASUTAKSE
1) 68,3% optsioon

Ootus ja dispersioon

Mõõdame juhuslikku suurust N korda, näiteks mõõdame tuule kiirust kümme korda ja tahame leida keskmist väärtust. Kuidas on keskmine väärtus seotud jaotusfunktsiooniga?

Veeretame täringuid palju kordi. Iga viskega täringule ilmuvate punktide arv on juhuslik suurus ja võib võtta mis tahes loomuliku väärtuse vahemikus 1 kuni 6. Kõikide täringuvisete jaoks arvutatud langenud punktide aritmeetiline keskmine on samuti juhuslik suurus, kuid suurte N see kaldub väga konkreetsele numbrile – matemaatilisele ootusele M x. Sel juhul M x = 3,5.

Kuidas sa selle väärtuse said? Laske sisse N testid, kord saad 1 punkti, kord 2 punkti jne. Siis kui N→ ∞ tulemuste arv, mille puhul visati üks punkt, samamoodi, seega

Mudel 4.5. Täringud

Oletame nüüd, et teame juhusliku suuruse jaotusseadust x, see tähendab, et me teame, et juhuslik muutuja x võib võtta väärtusi x 1 , x 2 , ..., x k tõenäosustega lk 1 , lk 2 , ..., p k.

Oodatud väärtus M x juhuslik muutuja x võrdub:

Vastus. 2,8.

Matemaatiline ootus ei ole alati mõne juhusliku muutuja mõistlik hinnang. Seega on keskmise palga hindamisel mõistlikum kasutada mediaani mõistet ehk sellist väärtust, et mediaanist madalamat ja suuremat palka saavate inimeste arv langeb kokku.

Mediaan juhuslikku muutujat nimetatakse arvuks x 1/2 on selline lk (x < x 1/2) = 1/2.

Teisisõnu, tõenäosus lk 1 et juhuslik suurus x saab olema väiksem x 1/2 ja tõenäosus lk 2 et juhuslik suurus x saab olema suurem x 1/2 on identsed ja võrdub 1/2-ga. Mediaani ei määrata kõigi jaotuste jaoks üheselt.

Pöördume tagasi juhusliku muutuja juurde x, mis võib võtta väärtusi x 1 , x 2 , ..., x k tõenäosustega lk 1 , lk 2 , ..., p k.

Dispersioon juhuslik muutuja x Juhusliku suuruse ruudus kõrvalekalde keskmist väärtust selle matemaatilisest ootusest nimetatakse:

Näide 2

Arvutage eelmise näite tingimustes juhusliku suuruse dispersioon ja standardhälve x.

Vastus. 0,16, 0,4.

Mudel 4.6. Sihtmärgi pihta laskmine

Näide 3

Leidke esimesel täringuviskel saadud punktide arvu tõenäosusjaotus, mediaan, matemaatiline ootus, dispersioon ja standardhälve.

Iga serv kukub võrdselt suure tõenäosusega välja, seega näeb jaotus välja järgmine:

Standardhälve On näha, et väärtuse hälve keskmisest väärtusest on väga suur.

Matemaatilise ootuse omadused:
- Sõltumatute juhuslike muutujate summa matemaatiline ootus on võrdne nende matemaatiliste ootuste summaga:
Näide 4

Leidke kahel täringul veeretatud punktide summa ja korrutise matemaatiline ootus.

Näites 3 leidsime, et ühe kuubi puhul M (x) = 3,5. Nii kahe kuubi jaoks

Dispersiooni omadused:
- Sõltumatute juhuslike suuruste summa dispersioon on võrdne dispersioonide summaga:
D x + y = D x + Dy.

Lase eest N veeretab täringut veeretatud y punktid. Siis

See tulemus ei kehti ainult täringuveeretuste puhul. Paljudel juhtudel määrab see empiiriliselt matemaatilise ootuse mõõtmise täpsuse. On näha, et mõõtmiste arvu suurenemisega N väärtuste levik keskmise ehk standardhälbe ümber väheneb proportsionaalselt

Juhusliku suuruse dispersioon on seotud selle juhusliku suuruse ruudu matemaatilise ootusega järgmise seosega:

Leiame selle võrdsuse mõlema poole matemaatilised ootused. A-prioor,

Võrdsuse parema poole matemaatiline ootus vastavalt matemaatiliste ootuste omadusele on võrdne

Standardhälve

Standardhälve võrdub dispersiooni ruutjuurega:
Piisavalt suure uuritava üldkogumi (n > 30) standardhälbe määramisel kasutatakse järgmisi valemeid:
Seotud Informatsioon.

Standardhälbe valem. Valemi standardhälve Excelis

Valimi dispersioon

Parandatud dispersioon

Probleemi näide dispersiooni ja standardhälbe leidmiseks

Entsüklopeediline YouTube

Kolme sigma reegel

Standardhälbe väärtuse tõlgendamine

Kliima

Sport