Seal on ainult “X” ja ainult abstsisstelg, kuid nüüd lisanduvad “Y” ja tegevusväli laieneb kogu koordinaattasandile. Edasi mõistetakse tekstis väljendit “lineaarne ebavõrdsus” kahemõõtmelises tähenduses, mis saab selgeks mõne sekundiga.
Lisaks analüütilisele geomeetriale on materjal asjakohane mitmete matemaatilise analüüsi ning majandusliku ja matemaatilise modelleerimise probleemide jaoks, seega soovitan seda loengut täie tõsidusega uurida.
Lineaarsed ebavõrdsused
Lineaarset ebavõrdsust on kahte tüüpi:
1) Range ebavõrdsused: .
2) Lax ebavõrdsused: .
Mis on nende ebavõrdsuste geomeetriline tähendus? Kui lineaarvõrrand defineerib sirge, siis lineaarne ebavõrdsus poollennuk.
Järgmise teabe mõistmiseks peate teadma tasapinna joonte tüüpe ja oskama sirgjooni konstrueerida. Kui teil on selles osas raskusi, lugege abi Funktsioonide graafikud ja omadused– lõik lineaarfunktsiooni kohta.
Alustame lihtsamatest lineaarsetest võrratustest. Iga vaese õpilase unistus on koordinaattasand, millel pole midagi:

Nagu teate, on x-telg antud võrrandiga - "y" on alati (mis tahes "x" väärtuse korral) võrdne nulliga
Mõelgem ebavõrdsusele. Kuidas seda mitteametlikult mõista? "Y" on alati (mis tahes "x" väärtuse korral) positiivne. Ilmselt määrab see ebavõrdsus ülemise pooltasandi - seal asuvad ju kõik positiivsete “mängudega” punktid.
Juhul, kui ebavõrdsus ei ole range, ülemisele pooltasandile lisaks telg ise on lisatud.
Samamoodi: ebavõrdsust rahuldavad kõik alumise pooltasandi punktid, alumisele pooltasandile + teljele vastab mitterange ebavõrdsus.
Sama proosaline lugu on y-teljega:
– ebavõrdsus määrab õige pooltasandi;
– ebavõrdsus määrab parempoolse pooltasandi, sealhulgas ordinaattelje;
– ebavõrdsus täpsustab vasakpoolset pooltasandit;
– ebavõrdsus määrab vasaku pooltasandi, sealhulgas ordinaattelje.
Teises etapis käsitleme ebavõrdsust, milles üks muutujatest puudub.
"Y" puudub:
Või pole "x"-i:
Seda ebavõrdsust saab käsitleda kahel viisil: palun kaaluge mõlemat lähenemisviisi. Pidagem meeles ja kinnistagem koolitegusid ebavõrdsusega, millest juba tunnis räägiti Funktsiooni domeen.
Näide 1
Lahendage lineaarsed võrratused:
Mida tähendab lineaarse ebavõrdsuse lahendamine?
Lineaarse ebavõrdsuse lahendamine tähendab pooltasandi leidmist, mille punktid seda ebavõrdsust rahuldavad (pluss joon ise, kui ebavõrdsus ei ole range). Lahendus, tavaliselt, graafiline.
Mugavam on kohe joonistada ja seejärel kõike kommenteerida: 
a) Lahenda ebavõrdsus
Meetod üks
Meetod meenutab väga lugu koordinaattelgedega, millest me eespool rääkisime. Idee on teisendada ebavõrdsust – jätta üks muutuja vasakule poole ilma konstantideta, antud juhul muutuja “x”.
Reegel: Ebavõrdsuses kanduvad terminid osast osasse märgimuutusega, samas kui ebavõrdsuse märk ISE ei muutu(näiteks kui oli märk "vähem kui", siis see jääb "vähem kui").
Liigutame "viie" märgivahetusega paremale:
Reegel POSITIIVNE ei muutu.
Nüüd tõmmake sirgjoon (sinine punktiirjoon). Sirge tõmmatakse punktiirjoonena, kuna ebavõrdsus range, ja sellele reale kuuluvad punktid lahendusse kindlasti ei kaasata.
Mida tähendab ebavõrdsus? "X" on alati (mis tahes "Y" väärtuse korral) väiksem kui . Ilmselgelt rahuldavad selle väite kõik vasaku pooltasandi punktid. Seda pooltasapinda saab põhimõtteliselt varjutada, kuid piirdun väikeste siniste nooltega, et mitte muuta joonist kunstiliseks paletiks.
Teine meetod
See on universaalne meetod. LUGEGE VÄGA HOOLIKALT!
Kõigepealt tõmbame sirge. Muide, selguse huvides on võrrand soovitatav esitada kujul .
Valige nüüd lennuki mis tahes punkt, ei kuulu otsesesse. Enamikul juhtudel on magus koht loomulikult. Asendame selle punkti koordinaadid ebavõrdsusega: ![]()
Vastu võetud vale ebavõrdsus(lihtsamalt öeldes ei saa see olla), see tähendab, et punkt ei rahulda ebavõrdsust.
Meie ülesande põhireegel:
ei rahulda ebavõrdsus siis KÕIK antud pooltasandi punktid ei rahulda see ebavõrdsus.
– kui mõni pooltasandi punkt (mis ei kuulu joone alla) rahuldab ebavõrdsus siis KÕIK antud pooltasandi punktid rahuldada see ebavõrdsus.
Saate testida: ükski joonest paremal olev punkt ei rahulda ebavõrdsust.
Mis järeldus punktiga tehtud katsest? Pole kuhugi minna, ebavõrdsust rahuldavad kõik teise - vasaku pooltasandi punktid (saate ka kontrollida).
b) Lahenda ebavõrdsus
Meetod üks
Teisendame ebavõrdsust:
Reegel: Ebavõrdsuse mõlemad pooled saab korrutada (jagada). NEGATIIVNE arv, ebavõrdsuse märgiga MUUTUV vastupidisele (näiteks kui oli märk "suurem või võrdne", muutub see "väiksem või võrdne").
Korrutame ebavõrdsuse mõlemad pooled järgmisega:
Tõmbame sirge (punane) ja joonestame pideva joone, kuna meil on ebavõrdsus mitte ranged, ja sirgjoon kuulub ilmselt lahenduse juurde.
Olles analüüsinud saadud ebavõrdsust, jõuame järeldusele, et selle lahendus on alumine pooltasand (+ sirge ise).
Varjutame või tähistame nooltega sobiva pooltasandi.
Teine meetod
Tõmbame sirge. Valime tasapinnal näiteks suvalise punkti (mis ei kuulu sirgele) ja asendame selle koordinaadid meie ebavõrdsusega: ![]()
Vastu võetud tõeline ebavõrdsus, mis tähendab, et punkt rahuldab ebavõrdsust ja üldiselt rahuldavad seda ebavõrdsust KÕIK alumise pooltasandi punktid.
Siin "tabame" katsepunktiga soovitud pooltasandit.
Probleemi lahendust tähistab punane joon ja punased nooled.
Isiklikult eelistan esimest lahendust, kuna teine on formaalsem.
Näide 2
Lahendage lineaarsed võrratused:
See on näide, mille saate ise lahendada. Proovige probleemi lahendada kahel viisil (muide, see on hea viis lahenduse kontrollimiseks). Tunni lõpus olev vastus sisaldab ainult lõplikku joonist.
Ma arvan, et pärast kõiki näidetes tehtud toiminguid peate nendega abielluma, pole raske lahendada kõige lihtsamat ebavõrdsust, nagu jne.
Vaatleme kolmandat üldjuhtumit, kui mõlemad muutujad esinevad ebavõrdsuses:
Teise võimalusena võib vaba termin "ce" olla null.
Näide 3
Leidke pooltasandid, mis vastavad järgmistele ebavõrdsustele:
Lahendus: Siin kasutatakse universaalset lahendusmeetodit punktiasendusega.
a) Koostame sirge võrrandi ja joon tuleks tõmmata punktiirjoonena, kuna ebavõrdsus on range ja sirget ennast lahendusse ei kaasata.
Valime tasapinna katsepunkti, mis ei kuulu näiteks antud sirgele, ja asendame selle koordinaadid meie ebavõrdsusega:
Vastu võetud vale ebavõrdsus, mis tähendab, et antud pooltasandi punkt ja KÕIK punktid ei rahulda ebavõrdsust. Ebavõrdsuse lahendus on veel üks pooltasapind, imetleme sinist välku: 
b) Lahendame ebavõrdsuse. Esiteks konstrueerime sirge. Seda pole raske teha, meil on kanooniline otsene proportsionaalsus. Me tõmbame joont pidevalt, kuna ebavõrdsus ei ole range.
Valime tasapinna suvalise punkti, mis ei kuulu sirgele. Tahaks uuesti päritolu kasutada, aga paraku see nüüd ei sobi. Seetõttu peate töötama koos teise sõbraga. Kasumlikum on võtta väikeste koordinaatide väärtustega punkt, näiteks . Asendame selle koordinaadid meie ebavõrdsusega:
Vastu võetud tõeline ebavõrdsus, mis tähendab, et antud pooltasandi punkt ja kõik punktid vastavad ebavõrdsusele . Soovitud pooltasand on tähistatud punaste nooltega. Lisaks sisaldab lahendus sirgjoont ennast.
Näide 4
Leidke võrratustele vastavad pooltasandid:
See on näide, mille saate ise lahendada. Terviklahendus, lõpliku kavandi ligikaudne näidis ja vastus tunni lõpus.
Vaatame pöördprobleemi:
Näide 5
a) Antud sirge. Defineeri pooltasapind, milles punkt asub, samas kui sirge ise peab olema lahendusse kaasatud.
b) Antud sirge. Defineeri pooltasand, milles punkt asub. Sirge ise ei sisaldu lahenduses.
Lahendus: Siin pole joonist vaja ja lahendus on analüütiline. Ei midagi keerulist:
a) Koostame abipolünoomi ![]() ja arvutage selle väärtus punktis:
ja arvutage selle väärtus punktis:
. Seega on soovitud ebavõrdsusel märk "vähem kui". Tingimuse järgi on sirgjoon lahendusesse kaasatud, nii et ebavõrdsus ei ole range:
b) Koostame polünoomi ja arvutame selle väärtuse punktis:
. Seega on soovitud ebavõrdsusel märk "suurem kui". Tingimuse järgi sirgjoont lahendusesse ei kaasata, seetõttu on ebavõrdsus range: .
Vastus:
Loov näide iseõppimiseks:
Näide 6
Antud punktid ja sirge. Loetletud punktide hulgast leia need, mis koos koordinaatide alguspunktiga asuvad antud sirge samal küljel.
Väike vihje: kõigepealt tuleb luua ebavõrdsus, mis määrab pooltasapinna, milles koordinaatide alguspunkt asub. Analüütiline lahendus ja vastus tunni lõpus.
Lineaarsete võrratuste süsteemid
Lineaarsete võrratuste süsteem on, nagu te mõistate, mitmest ebavõrdsusest koosnev süsteem. Lol, ma andsin definitsiooni välja =) Siil on siil, nuga on nuga. Kuid see on tõsi – see osutus lihtsaks ja ligipääsetavaks! Ei, tõsiselt, ma ei taha tuua ühtegi üldist näidet, nii et liigume otse pakiliste probleemide juurde:
Mida tähendab lineaarse ebavõrdsuse süsteemi lahendamine?
Lahendage lineaarsete võrratuste süsteem- see tähendab leida punktide kogum tasapinnal, mis rahuldavad igale süsteemi ebavõrdsus.
Lihtsaimate näidetena vaatleme ristkülikukujulise koordinaatsüsteemi koordinaatveerandi määravaid võrratussüsteeme (“vaeste õpilaste pilt” on tunni alguses):
Võrratuste süsteem defineerib esimese koordinaatveerandi (paremal üleval). Näiteks mis tahes punkti koordinaadid esimeses veerandis, ![]() jne. rahuldada igale selle süsteemi ebavõrdsus.
jne. rahuldada igale selle süsteemi ebavõrdsus.
Samamoodi:
– võrratuste süsteem määrab teise koordinaatveerandi (üleval vasakul);
– võrratuste süsteem defineerib kolmanda koordinaatveerandi (all vasakul);
– võrratuste süsteem defineerib neljanda koordinaatveerandi (all paremal).
Lineaarsete võrratuste süsteemil ei pruugi olla lahendusi st olla mitteliigeste. Jällegi kõige lihtsam näide: . On üsna ilmne, et “x” ei saa olla korraga rohkem kui kolm ja väiksem kui kaks.
Võrdsuste süsteemi lahenduseks võib olla näiteks sirgjoon: . Luik, jõevähk, ilma haugita, vankrit kahes erinevas suunas vedamas. Jah, asjad on endiselt alles – selle süsteemi lahendus on sirgjoon.
Kuid kõige tavalisem juhtum on see, kui süsteemi lahendus on mõni lennuki ala. Lahenduse piirkond Võib olla ei ole piiratud(näiteks koordinaatveerandid) või piiratud. Piiratud lahenduse piirkonda nimetatakse hulknurga lahendussüsteem.
Näide 7
Lahendage lineaarsete võrratuste süsteem
Praktikas peame enamikul juhtudel tegelema nõrga ebavõrdsusega, nii et nemad juhivad kogu ülejäänud tunni ringtantsu.
Lahendus: See, et ebavõrdsust on liiga palju, ei tohiks olla hirmutav. Kui palju ebavõrdsust võib süsteemis olla? Jah, nii palju kui soovite. Peamine on järgida lahendusala koostamise ratsionaalset algoritmi:
1) Kõigepealt käsitleme lihtsamaid võrratusi. Võrratused määravad esimese koordinaatveerandi, sealhulgas koordinaatide telgede piiri. See on juba palju lihtsam, kuna otsinguala on oluliselt kitsenenud. Joonisel märgime kohe vastavad pooltasandid nooltega (punased ja sinised nooled)
2) Teine kõige lihtsam ebavõrdsus on see, et siin pole Y-d. Esiteks konstrueerime sirge enda ja teiseks, pärast ebavõrdsuse teisendamist vormiks , selgub kohe, et kõik “X-id” on väiksemad kui 6. Märgistame vastava pooltasandi roheliste nooltega. Noh, otsinguala on muutunud veelgi väiksemaks - selline ristkülik, mis pole ülalt piiratud.
3) Viimases etapis lahendame ebavõrdsused "täis laskemoonaga": . Lahendusalgoritmi käsitlesime üksikasjalikult eelmises lõigus. Lühidalt: kõigepealt ehitame sirge, seejärel leiame katsepunkti abil meile vajaliku pooltasandi.
Tõuske püsti, lapsed, seiske ringis: 
Süsteemi lahendusala on hulknurk; joonisel on see karmiinpunase joonega piiritletud ja varjutatud. Natuke pingutasin üle =) Märkmikus piisab, kui lahendusala kas varjutada või lihtsa pliiatsiga julgemalt kontuurida.
Antud hulknurga suvaline punkt rahuldab IGA süsteemi ebavõrdsust (saate seda nalja pärast kontrollida).
Vastus: süsteemi lahendus on hulknurk.
Puhta koopia taotlemisel oleks hea mõte üksikasjalikult kirjeldada, milliseid punkte kasutasite sirgjoonte ehitamiseks (vt õppetundi Funktsioonide graafikud ja omadused) ja kuidas pooltasandid määrati (vt selle õppetüki esimest lõiku). Kuid praktikas krediteeritakse teile enamikul juhtudel just õige joonis. Arvutused ise saab teha mustandi alusel või isegi suuliselt.
Lisaks süsteemi lahenduspolügonile on praktikas, ehkki harvem, avatud piirkond. Proovige järgmist näidet ise mõista. Kuigi täpsuse huvides pole siin piinamist - ehitusalgoritm on sama, lihtsalt ala ei piirata.
Näide 8
Lahendage süsteem
Lahendus ja vastus on tunni lõpus. Tõenäoliselt on teil saadud piirkonna tippude jaoks erinevad tähed. See pole oluline, peamine on tipud õigesti leida ja ala õigesti konstrueerida.
Pole harvad juhud, kui probleemid nõuavad mitte ainult süsteemi lahendusdomeeni konstrueerimist, vaid ka domeeni tippude koordinaatide leidmist. Kahes eelmises näites olid nende punktide koordinaadid ilmselged, kuid praktikas pole kõik jääst kaugel:
Näide 9
Lahendage süsteem ja leidke saadud piirkonna tippude koordinaadid
Lahendus: kujutame joonisel selle süsteemi lahendusala. Ebavõrdsus määrab vasaku pooltasandi koos ordinaatteljega ja siin pole enam tasuta. Pärast lõpliku koopia/mustandi või sügavate mõtlemisprotsesside arvutusi saame järgmise lahenduste valdkonna: 
Selles artiklis vastan veel ühele oma tellijate küsimusele. Küsimused tulevad erineval viisil. Kõik need ei ole õigesti sõnastatud. Ja osa neist on sõnastatud nii, et kohe ei saa aru, mida autor küsida tahab. Seetõttu pean suure hulga saadetud küsimuste hulgast välja valima tõeliselt huvitavad, sellised “pärlid”, millele vastamine pole mitte ainult põnev, vaid ka kasulik, nagu mulle tundub, ka teistele lugejatele. Ja täna vastan ühele neist küsimustest. Kuidas kujutada ebavõrdsuse süsteemi lahenduste hulka?
See on tõesti hea küsimus. Sest matemaatika ülesannete graafilise lahendamise meetod on väga võimas meetod. Inimene on kujundatud nii, et tal on mugavam tajuda infot erinevate visuaalsete materjalide abil. Seega, kui valdate seda meetodit, siis uskuge mind, see on teie jaoks hädavajalik nii ühtse riigieksami ülesannete lahendamisel, eriti teise osa, muude eksamite kui ka optimeerimisprobleemide lahendamisel jne jne. .
Nii et siin see on. Kuidas saame sellele küsimusele vastata? Alustame lihtsast. Olgu võrratuste süsteem ainult üks muutuja.
| Näide 1. Joonistage võrratuste süsteemi lahenduste hulk: Title=" Renderdab QuickLaTeX.com">!} |
Lihtsustame seda süsteemi. Selleks lisage esimese võrratuse mõlemale poolele 7 ja jagage mõlemad pooled 2-ga, muutmata ebavõrdsuse märki, kuna 2 on positiivne arv. Lisame teise võrratuse mõlemale poolele 4 Selle tulemusena saame järgmise võrratuste süsteemi:
Title=" Renderdab QuickLaTeX.com">!}
Tavaliselt nimetatakse sellist probleemi ühemõõtmeliseks. Miks? Jah, sest selle paljude lahenduste kujutamiseks on see piisavalt otsekohene. Numbririda, kui täpne olla. Märgime sellele arvureale punktid 6 ja 8. Selge on see, et punkt 8 jääb punktist 6 paremale, sest arvureal on suuremad numbrid väiksematest paremal. Lisaks on punkt 8 varjutatud, kuna esimese võrratuse tähise kohaselt on see selle lahenduses kaasatud. Vastupidi, punkt 6 jääb varjutamata, kuna see ei sisaldu teise võrratuse lahenduses:
Märgistame nüüd noolega ülalpool väärtused, mis on väiksemad või võrdsed 8-ga, nagu nõuab süsteemi esimene ebavõrdsus, ja noolega allpool - väärtused, mis on suuremad kui 6, vastavalt süsteemi nõuetele. süsteemi teine ebavõrdsus:
Jääb üle vastata küsimusele, kus arvureal asuvad ebavõrdsuste süsteemi lahendid. Pidage meeles üks kord ja kõik. Süsteemi sümbol - lokkis sulg - asendab matemaatikas sidesõna "mina". See tähendab, et valemite keelt inimkeelde tõlkides võime öelda, et peame näitama väärtused, mis on suuremad kui 6 JA väiksemad või võrdsed 8-ga. See tähendab, et nõutav intervall asub märgitud ristumiskohas. intervallid:
Seega oleme kujutanud võrratussüsteemi lahendite kogumit arvteljel juhul, kui võrratuste süsteem sisaldab ainult ühte muutujat. See varjutatud intervall sisaldab kõiki väärtusi, mille puhul on täidetud kõik süsteemis kirjutatud ebavõrdsused.
Vaatleme nüüd keerukamat juhtumit. Olgu meie süsteem sisaldab ebavõrdsust kahe muutujaga ja . Sel juhul ei ole sellise süsteemi lahenduste kujutamiseks võimalik kasutada ainult sirgjoont. Me läheme kaugemale ühemõõtmelisest maailmast ja lisame sellele veel ühe mõõtme. Siin on vaja tervet lennukit. Vaatame olukorda konkreetse näite abil.
Niisiis, kuidas me saame kujutada tasapinnal ristkülikukujulises koordinaatsüsteemis kahe muutujaga antud võrratuste süsteemi lahenduste komplekti? Alustame kõige lihtsamast. Küsigem endalt, millise selle tasandi piirkonna määrab ebavõrdsus. Võrrand määrab teljega risti kulgeva sirge HÄRG läbi punkti (0;0). See tähendab, et see sirgjoon langeb teljega kokku OY. Noh, kuna meid huvitavad väärtused, mis on suuremad või võrdsed 0-ga, siis sobib kogu sirgjoonest paremal asuv pooltasapind:
Pealegi kõik punktid, mis asuvad teljel OY, sobivad ka meile, sest ebavõrdsus ei ole range.
Et mõista, millise ala koordinaattasandil kolmas ebavõrdsus määratleb, peate funktsiooni joonistama. See on alguspunkti ja näiteks punkti (1;1) läbiv sirge. See tähendab, et tegelikult on see sirgjoon, mis sisaldab esimese koordinaatveerandi moodustava nurga poolitajat.
Vaatame nüüd süsteemi kolmandat ebavõrdsust ja mõelgem. Millise piirkonna peame leidma? Vaatame: . Suurem või võrdusmärk. See tähendab, et olukord on sarnane eelmise näitega. Ainult siin ei tähenda "rohkem" "rohkem paremale", vaid "kõrgemale". Sest OY- see on meie vertikaaltelg. See tähendab, et kolmanda ebavõrdsusega tasapinnal määratletud ala on punktide kogum, mis asuvad joone kohal või sellel:
Esimese ebavõrdsusega on süsteem veidi vähem mugav. Kuid pärast seda, kui suutsime määrata kolmanda ebavõrdsusega määratletud piirkonna, on minu arvates juba selge, kuidas tegutseda.
Seda ebavõrdsust on vaja esitada nii, et vasakul on ainult muutuja ja paremal ainult muutuja. Selleks lahutage võrratuse mõlemast küljest ja jagage mõlemad pooled 2-ga, muutmata ebavõrdsuse märki, sest 2 on positiivne arv. Selle tulemusena saame järgmise ebavõrdsuse:
Jääb vaid tõmmata telge lõikuvale koordinaattasandile sirge OY punktis A(0;4) ja sirge punktis . Viimast õppisin selgeks sirge võrrandite paremad küljed võrdsustades ja võrrandi saades. Sellest võrrandist leitakse ristumispunkti koordinaat ja koordinaat, ma arvan, et arvasite ära, on võrdne koordinaadiga. Neile, kes pole veel arvanud, on see sellepärast, et meil on ühe lõikuva sirge võrrand: .
Niipea, kui oleme selle sirgjoone tõmmanud, saame soovitud ala kohe märkida. Ebavõrdsuse märk on siin "väiksem või võrdne". See tähendab, et soovitud ala asub kujutatud sirgjoone all või otse sellel:
Noh, viimane küsimus. Kus on soovitud piirkond, mis rahuldab süsteemi kõiki kolme ebavõrdsust? Ilmselgelt asub see kõigi kolme märgitud ala ristumiskohas. Jälle ristumine! Pidage meeles: süsteemimärk matemaatikas tähendab ristmikku. Siin see on, see ala:
Noh, viimane näide. Veel üldisemalt. Oletame nüüd, et meil pole süsteemis mitte ühte muutujat, mitte kahte, vaid koguni kolm!
Kuna muutujaid on kolm, vajame sellise ebavõrdsuse süsteemi lahenduste kogumi kujutamiseks lisaks kahele, millega eelmises näites töötasime, kolmandat mõõdet. See tähendab, et ronime tasapinnast välja ruumi ja kujutame kolmemõõtmelist ruumilist koordinaatsüsteemi: X, Y Ja Z. Mis vastab pikkusele, laiusele ja kõrgusele.
Alustuseks kujutame selles koordinaatsüsteemis võrrandiga määratud pinda. Vormilt on see väga sarnane tasapinnal oleva ringi võrrandiga, muutujaga on lisatud ainult üks liige. Lihtne on arvata, et see on võrrand sfäärist, mille keskpunkt on punktis (1;3;2), mille raadiuse ruut on 4. See tähendab, et raadius ise on 2.
Siis küsimus. Mida siis ebavõrdsus ise määrab? Neile, keda see küsimus hämmeldab, teen ettepaneku arutleda järgmiselt. Tõlkides valemikeelt inimkeelde, võib öelda, et nõutav on märkida kõik sfäärid, mille keskpunkt on punktis (1;3;2), mille raadiused on väiksemad või võrdsed 2-ga. need sfäärid asuvad kujutatud sfääri sees! See tähendab, et tegelikult määrab see ebavõrdsus kujutatud sfääri kogu sisemise piirkonna. Soovi korral määratletakse pall, mis on piiratud kujutatud sfääriga:
Võrrandiga x+y+z=4 defineeritud pind on tasapind, mis lõikub koordinaattelgedega punktides (0;0;4), (0;4;0) ja (4;0;0). Noh, on selge, et mida suurem arv on võrdusmärgist paremal, seda kaugemal koordinaatide keskpunktist asuvad selle tasapinna ja koordinaattelgede lõikepunktid. See tähendab, et teine võrratus määrab poolruumi, mis asub antud tasapinna kohal. Kasutades tavapärast terminit "kõrgem", mõtlen ma edasi koordinaatide väärtuste suurendamise suunas piki telge.
See tasapind lõikub kujutatud sfääriga. Sel juhul on ristmikuks ring. Saate isegi arvutada, millisel kaugusel koordinaatsüsteemi keskpunktist selle ringi keskpunkt asub. Muide, kes arvab, kuidas seda teha, kirjutage oma lahendused ja vastused kommentaaridesse. Seega määrab algne võrratuste süsteem ruumipiirkonna, mis asub sellest tasapinnast kaugemal koordinaatide suurenemise suunas, kuid on kujutatud sfääris:
Nii on kujutatud palju ebavõrdsuse süsteemi lahendusi. Kui süsteemis on muutujaid rohkem kui 3 (näiteks 4), ei ole lahenduste hulka enam võimalik selgelt kujutada. Sest selleks oleks vaja 4-mõõtmelist koordinaatsüsteemi. Aga normaalne inimene ei suuda ette kujutada, kuidas võiks paikneda 4 omavahel risti olevat koordinaattelge. Kuigi mul on sõber, kes väidab, et saab sellega hakkama ja seda lihtsalt. Ma ei tea, kas ta räägib tõtt, võib-olla ta räägib tõtt. Kuid sellegipoolest ei luba inimese normaalne kujutlusvõime seda teha.
Loodan, et tänane õppetund oli teile kasulik. Kontrollimaks, kui hästi olete sellest aru saanud, tehke allolevat kodutööd.
Joonistage võrratuste süsteemi lahenduste hulk:
ql-right-eqno"> title=" Renderdab QuickLaTeX.com">!}
Materjali koostas Sergei Valerievich
Kahe muutuja võrratuse lahendamine, ja veelgi enam kahe muutujaga võrratuste süsteemid, tundub üsna raske ülesanne olevat. Siiski on olemas lihtne algoritm, mis aitab sedalaadi pealtnäha väga keerukaid probleeme lihtsalt ja ilma suurema vaevata lahendada. Proovime selle välja mõelda.
Olgu meil ebavõrdsus kahe muutujaga, mis on ühte järgmistest tüüpidest:
y > f(x); y ≥ f(x); y< f(x); y ≤ f(x).
Sellise ebavõrdsuse lahenduste hulga kujutamiseks koordinaattasandil toimige järgmiselt.
1. Koostame funktsiooni y = f(x) graafiku, mis jagab tasandi kaheks piirkonnaks.
2. Valime saadud aladest suvalise ja arvestame selles suvalise punktiga. Kontrollime selle punkti algse ebavõrdsuse teostatavust. Kui testi tulemuseks on õige arvuline võrratus, siis järeldame, et algne võrratus on täidetud kogu piirkonnas, kuhu valitud punkt kuulub. Seega on ebavõrdsuse lahenduste hulk piirkond, kuhu valitud punkt kuulub. Kui kontrolli tulemuseks on vale numbriline võrratus, siis on võrratuse lahendite hulk teine piirkond, kuhu valitud punkt ei kuulu.
3.
Kui ebavõrdsus on range, siis piirkonna piirid ehk funktsiooni y = f(x) graafiku punktid ei kuulu lahenduste hulka ja piir on kujutatud punktiirjoonega. Kui ebavõrdsus ei ole range, kaasatakse piirkonna piirid, see tähendab funktsiooni y = f(x) graafiku punktid selle võrratuse lahenduste hulka ja see piir on sel juhul kujutatud. pideva joonena.
Vaatame nüüd mitmeid selle teemaga seotud probleeme.
Ülesanne 1.
Millise punktide hulga annab võrratus x · y ≤ 4?
Lahendus.
1) Koostame graafiku võrrandist x · y = 4. Selleks teisendame selle esmalt. Ilmselgelt ei muutu x sel juhul 0-ks, sest muidu oleks meil 0 · y = 4, mis on vale. See tähendab, et saame oma võrrandi jagada x-ga. Saame: y = 4/x. Selle funktsiooni graafik on hüperbool. See jagab kogu tasapinna kaheks piirkonnaks: hüperbooli kahe haru vahele jäävasse ja neist väljapoole jäävasse piirkonda.
2) Valime esimesest piirkonnast suvalise punkti, olgu selleks punkt (4; 2).
Kontrollime ebavõrdsust: 4 · 2 ≤ 4 – väär.
See tähendab, et selle piirkonna punktid ei rahulda algset ebavõrdsust. Siis võime järeldada, et ebavõrdsuse lahenduste hulk on teine piirkond, kuhu valitud punkt ei kuulu.
3) Kuna ebavõrdsus ei ole range, siis tõmbame piiripunktid ehk funktsiooni y = 4/x graafiku punktid pideva joonega.
Värvime kollaseks punktide komplekti, mis määratleb algse ebavõrdsuse (joonis 1).
2. ülesanne.
Joonistage süsteemi poolt koordinaattasandile määratud ala
( y > x 2 + 2;
(y + x > 1;
( x 2 + y 2 ≤ 9.
Lahendus.
Alustuseks koostame järgmiste funktsioonide graafikud (Joonis 2):
y = x 2 + 2 – parabool,
y + x = 1 – sirgjoon
x 2 + y 2 = 9 – ring.

1) y > x 2 + 2.
Võtame punkti (0; 5), mis asub funktsiooni graafiku kohal.
Kontrollime ebavõrdsust: 5 > 0 2 + 2 – tõene.
Järelikult rahuldavad kõik punktid, mis asuvad antud parabooli kohal y = x 2 + 2, süsteemi esimest võrratust. Värvime need kollaseks.
2) y + x > 1.
Võtame punkti (0; 3), mis asub funktsiooni graafiku kohal.
Kontrollime ebavõrdsust: 3 + 0 > 1 – tõene.
Järelikult rahuldavad kõik punktid, mis asuvad sirge y + x = 1 kohal, süsteemi teist võrratust. Värvime need rohelise varjundiga.
3) x 2 + y 2 ≤ 9.
Võtke punkt (0; -4), mis asub väljaspool ringi x 2 + y 2 = 9.
Kontrollime ebavõrdsust: 0 2 + (-4) 2 ≤ 9 – vale.
Seetõttu on kõik punktid, mis asuvad väljaspool ringi x 2 + y 2 = 9,  ei rahulda süsteemi kolmandat ebavõrdsust. Siis võime järeldada, et kõik punktid, mis asuvad ringi x 2 + y 2 = 9 sees, rahuldavad süsteemi kolmandat võrratust. Värvime need lilla varjundiga.
ei rahulda süsteemi kolmandat ebavõrdsust. Siis võime järeldada, et kõik punktid, mis asuvad ringi x 2 + y 2 = 9 sees, rahuldavad süsteemi kolmandat võrratust. Värvime need lilla varjundiga.
Ärge unustage, et kui ebavõrdsus on range, tuleks vastav piirijoon tõmmata punktiirjoonega. Saame järgmise pildi (Joonis 3).

(Joonis 4).
3. ülesanne.
Joonistage süsteemiga koordinaattasandile määratud ala:
(x 2 + y 2 ≤ 16;
(x ≥ -y;
(x 2 + y 2 ≥ 4.
Lahendus.
Alustuseks koostame järgmiste funktsioonide graafikud: 
x 2 + y 2 = 16 – ring,
x = -y – sirgjoon
x 2 + y 2 = 4 – ring (Joonis 5).
Vaatame nüüd iga ebavõrdsust eraldi.
1) x 2 + y 2 ≤ 16.
Võtke punkt (0; 0), mis asub ringi sees x 2 + y 2 = 16.
Kontrollime ebavõrdsust: 0 2 + (0) 2 ≤ 16 – tõene.
Seetõttu rahuldavad kõik punktid, mis asuvad ringi sees x 2 + y 2 = 16, süsteemi esimest võrratust.
Värvime need punase varjundiga. 
Võtame punkti (1; 1), mis asub funktsiooni graafiku kohal.
Kontrollime ebavõrdsust: 1 ≥ -1 – tõene.
Järelikult rahuldavad kõik punktid, mis asuvad sirgest x = -y kõrgemal, süsteemi teist võrratust. Värvime need sinise varjundiga.
3) x 2 + y 2 ≥ 4.
Võtke punkt (0; 5), mis asub väljaspool ringi x 2 + y 2 = 4.
Kontrollime ebavõrdsust: 0 2 + 5 2 ≥ 4 – tõene.
Järelikult rahuldavad kõik punktid, mis asuvad väljaspool ringi x 2 + y 2 = 4, süsteemi kolmandat võrratust. Värvime need siniseks.
Selles ülesandes ei ole kõik ebavõrdsused ranged, mis tähendab, et me tõmbame kõik piirid pideva joonega. Saame järgmise pildi (Joonis 6).
Otsinguala on ala, kus kõik kolm värvilist ala ristuvad üksteisega (Joonis 7).

Kas teil on endiselt küsimusi? Ei tea, kuidas lahendada kahe muutujaga võrratuste süsteemi?
Juhendajalt abi saamiseks -.
Esimene tund on tasuta!
blog.site, materjali täielikul või osalisel kopeerimisel on vaja linki algallikale.
, matemaatikaõpetaja, Munitsipaalharidusasutus "Upsha Põhikool"
Ebavõrdsuse graafiline lahenduskahe muutujaga
Sageli on vaja kujutada koordinaattasandil kahe muutuja võrratuse lahenduste komplekt. Tuletage meelde, et kahe muutujaga ebavõrdsuse lahendus on nende muutujate väärtuste paar, mis muudab antud ebavõrdsuse tõeliseks arvuliseks ebavõrdsuseks.
Näide 1
Mõelge ebavõrdsusele
Muutuvate väärtuste paar (-1; 1) muudab selle ebavõrdsuse
õige arvuline ebavõrdsus 2< 8, и является решением неравенства. Пара значений (2; 1) приводит к неверному числовому неравенству 11 < 8, и не является решением данного неравенства.
Vaatleme näidete abil, kuidas kahe muutujaga võrratuse lahendite hulk on kujutatud koordinaattasandil.
Näide 2
Kujutame koordinaattasandil ner lahendite hulkaautoritasu 2у+ Zx< 6.
Esiteks konstrueerime sirge
See jagab koordinaattasandi kõigi punktide hulga selle kohal asuvateks punktideks ja selle all asuvateks punktideks.
Võtame igast piirkonnast kontrollpunkt , Näiteks A (1; 1) ja B (1; 3)
Punktide koordinaadid A seda ebavõrdsust rahuldada 2у+ Zx< 6, т. е. 2 1 + 3 1 < 6.
Punktide koordinaadid IN ei rahulda seda ebavõrdsust 2∙3 + 3∙1< 6.
Kuna see ebavõrdsus võib sirgel märki muuta 2у+ 3x = 6, siis on ebavõrdsus rahuldatud punktide hulgaga piirkonnas, kus punkt A asub. Varjutame seda piirkonda.
Seega oleme kujutanud ebavõrdsuse lahenduste komplekti 2у+ Zx< 6.
Näide 3
Kujutame võrratuse x2 lahendite hulka + 2x + y2- 4у + 1 > 0koordinaattasandil.
Koostame esmalt graafiku võrrandist x2 + 2x + y2 - 4y + 1 = 0. Toome selles võrrandis esile ringi võrrandi: (x2 + 2x + 1) + (y2 - 4y + 4) = 4 või (x + 1) 2 + ( y - 2) 2 = 22.
See on võrrand ringist, mille keskpunkt on punktis 0 (-1; 2) ja raadius R = 2. Ehitame selle ringi.

Kuna see võrratus on range ja ringil endal asuvad punktid ebavõrdsust ei rahulda, konstrueerime ringi punktiirjoonega.
Lihtne on kontrollida, kas keskuse koordinaadid KOHTA ringid seda ebavõrdsust ei rahulda. Avaldis x2 + 2x + y2 - 4 a+ 1 muudab konstrueeritud ringil oma märki. Siis on ebavõrdsus rahuldatud punktidega, mis asuvad väljaspool ringi. Need punktid on varjutatud.
Näide 4
Kujutagem koordinaattasandil võrratuse lahendite hulka
(y - x2) (y- x - 3)< 0.
Esiteks joonistame võrrandi graafikule (y - x2) (y- x - 3) = 0. See on parabool juures= x2 ja sirgjoon y = x+ 3. Ehitame need read ja paneme tähele, et avaldise märgi muutmine (y - x2) (y- x - 3) esineb ainult neil ridadel. Punkti A (0; 5) jaoks määrame selle avaldise märgi: - 3) > 0 (st see ebavõrdsus ei kehti). Nüüd on lihtne märkida punktide kogum, mille puhul see ebavõrdsus on rahuldatud (need alad on varjutatud).
Ebavõrdsus on kaks arvu või matemaatilist avaldist, mis on ühendatud ühe märgiga: > (suurem kui range ebavõrdsuse korral),< (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).
Ebavõrdsus on lineaarne samadel tingimustel kui võrrand: see sisaldab muutujaid ainult esimesel astmel ja ei sisalda muutujate korrutisi.
Lineaarvõrratuste ja lineaarsete võrratuste süsteemide lahendus on lahutamatult seotud nende geomeetrilise tähendusega: lineaarvõrratuse lahendus on teatud pooltasand, milleks kogu tasapind on jagatud sirgjoonega, mille võrrand defineerib lineaarse ebavõrdsuse. . Jooniselt tuleb leida see pooltasapind ja joonvõrratuste süsteemi puhul mitme sirgjoonega piiratud tasandi osa.
Paljud majandusprobleemid, eriti lineaarse programmeerimise ülesanded, mille puhul on vaja leida funktsiooni maksimum või miinimum, taandatakse suure hulga muutujatega lineaarsete ebavõrdsuste süsteemide lahendamiseks.
Lineaarsete võrratuste süsteemide lahendamine mis tahes arvu tundmatutega
Kõigepealt vaatame tasapinna lineaarset ebavõrdsust. Vaatleme ühte ebavõrdsust kahe muutujaga ja :
![]() ,
,
kus on muutujate koefitsiendid (mõned arvud), on vaba liige (ka mõni arv).
Ühel võrratusel kahe tundmatuga, nagu võrrandil, on lõpmatu arv lahendeid. Selle ebavõrdsuse lahendus on arvupaar, mis seda ebavõrdsust rahuldab. Geomeetriliselt kujutatakse võrratuse lahendite kogumit pooltasapinnana, mida piirab sirgjoon
![]() ,
,
mida me nimetame piirijooneks.
Samm 1. Koostage sirge, mis piirab lahenduste hulka lineaarse võrratusega
Selleks peate teadma selle joone kahte punkti. Leiame koordinaatide telgedega lõikepunktid. Ristmiku ordinaat A võrdne nulliga (joonis 1). Selle joonise telgede arvväärtused viitavad näitele 1, mida analüüsime kohe pärast seda teoreetilist ekskursiooni.

Abstsissi leiame, lahendades sirge võrrandi telje kui süsteemi võrrandiga.
Leiame ristmiku teljega:

Asendades väärtuse esimesse võrrandisse, saame
Kus.
Seega leidsime punkti abstsissi A .
Leiame teljega lõikepunkti koordinaadid.
Abstsissi täpid B võrdne nulliga. Lahendame piirijoone võrrandi koordinaatide telje võrrandiga:
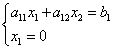
![]() ,
,
seega punkti koordinaadid B: .
Samm 2. Joonistage sirgjoon, mis piirab lahenduste hulka ebavõrdsusega. Punktide tundmine A Ja B piirijoone ja koordinaattelgede lõikepunkti, saame selle sirge tõmmata. Sirge (taas joonis 1) jagab kogu tasapinna kaheks osaks, mis asuvad sellest sirgest paremal ja vasakul (üleval ja all).
3. samm. Määrake, milline pooltasand on selle ebavõrdsuse lahendus. Selleks peate selle ebavõrdsusega asendama koordinaatide alguspunkti (0; 0). Kui lähtepunkti koordinaadid rahuldavad ebavõrdsust, siis on võrratuse lahendiks pooltasapind, millel koordinaatide alguspunkt asub. Kui koordinaadid ei rahulda ebavõrdsust, siis on võrratuse lahendiks pooltasapind, mis ei sisalda alguspunkti. Ebavõrdsuse lahenduse pooltasapinda tähistatakse tõmmetega sirgjoonelt pooltasapinnale, nagu joonisel 1.
Kui lahendame lineaarsete võrratuste süsteemi, siis sooritatakse iga samm iga süsteemi ebavõrdsuse jaoks.
Näide 1. Lahendage ebavõrdsus
Lahendus. Tõmbame sirgjoone
Asendades võrrandisse sirge, saame , ja asendades saame . Seetõttu on telgede lõikepunktide koordinaadid A(3; 0) , B(0; 2) . Tõmbame läbi nende punktide sirge (taas joonis 1).

Valime ebavõrdsuse lahenduste pooltasandi. Selleks asendame algpunkti koordinaadid (0; 0) ebavõrdsusega:
saame , s.t lähtepunkti koordinaadid rahuldavad seda ebavõrdsust. Järelikult on ebavõrdsuse lahenduseks koordinaatide alguspunkti sisaldav pooltasand, st vasakpoolne (aka alumine) pooltasand.
Kui see ebavõrdsus oleks range, see tähendab, et sellel oleks vorm
siis ei oleks piirijoone punktid lahendus, kuna need ei rahulda ebavõrdsust.
Vaatleme nüüd kahe tundmatuga lineaarse ebavõrdsuse süsteemi:

Iga selle süsteemi ebavõrdsus tasapinnal määratleb pooltasandi. Lineaarsete võrratuste süsteemi nimetatakse järjekindlaks, kui sellel on vähemalt üks lahend, ja ebajärjekindlaks, kui sellel pole lahendeid. Lineaarsete võrratuste süsteemi lahendus on suvaline arvupaar (), mis rahuldab kõik antud süsteemi ebavõrdsused.
Geomeetriliselt on lineaarsete võrratuste süsteemi lahendus punktide kogum, mis rahuldab süsteemi kõiki võrratusi, see tähendab saadud pooltasandite ühisosa. Seetõttu võib geomeetriliselt üldjuhul lahendust kujutada mõne hulknurga kujul, see võib olla sirge, lõiguga või isegi punktiga. Kui lineaarsete võrratuste süsteem on ebajärjekindel, siis pole tasapinnal ühtegi punkti, mis rahuldaks süsteemi kõiki võrratusi.
Näide 2.
Lahendus. Seega peame leidma selle ebavõrdsuse süsteemi lahenduste hulknurga. Ehitame esimese võrratuse ehk sirge piirjoone ja teise võrratuse ehk sirge piirjoone.
Teeme seda samm-sammult, nagu oli näidatud teoreetilises viites ja näites 1, eriti kuna näites 1 ehitasime ebavõrdsuse piirijoone, mis on selles süsteemis esimene.

Selle süsteemi ebavõrdsustele vastavate lahenduste pooltasandid on joonisel 2 varjutatud sissepoole. Lahenduse pooltasandite ühisosa on avatud nurk ABC. See tähendab, et tasapinna punktide kogum, mis moodustavad avatud nurga ABC, on nii süsteemi esimese kui ka teise võrratuse lahendus, see tähendab, et see on kahe lineaarse ebavõrdsuse süsteemi lahendus. Teisisõnu, selle hulga mis tahes punkti koordinaadid vastavad süsteemi mõlemale ebavõrdsusele.
Näide 3. Lahendage lineaarsete võrratuste süsteem
Lahendus. Ehitame süsteemi ebavõrdsustele vastavad piirijooned. Teeme seda, järgides iga ebavõrdsuse teoreetilises abis toodud samme. Nüüd määrame iga võrratuse lahenduste pooltasandid (joonis 3).

Antud süsteemi ebavõrdsustele vastavad lahenduste pooltasandid on sissepoole varjutatud. Lahenduste pooltasandite lõikekoht on kujutatud, nagu on näidatud joonisel, nelinurga kujul ABCE. Leidsime, et kahe muutujaga lineaarsete võrratuste süsteemi lahenduste hulknurk on nelinurk ABCE .
Kõik ülalkirjeldatu kahe tundmatuga lineaarsete võrratuste süsteemide kohta kehtib ka suvalise arvu tundmatute võrratuste süsteemide kohta, ainsa erinevusega, et ebavõrdsuse lahendus n tundmatu on tervik n arvud (), mis rahuldavad kõik ebavõrdsused ja piirjoone asemel on piiri hüpertasand n-mõõtmeline ruum. Lahenduseks on lahuse polühedron (simplex), mida piiravad hüpertasandid.
