Taylori seeria võimsusfunktsiooni laiendus. Positiivsed jadad, nende konvergents, funktsioonide laiendamine astmeridadeks

Funktsionaalsete seeriate hulgas on kõige olulisem koht võimsusseeriatel.

Võimseeria on seeria

mille terminid on kasvavate mittenegatiivsete täisarvude astmetena järjestatud astmefunktsioonid x, A c 0 , c 1 , c 2 , c n - konstantsed väärtused. Numbrid c 1 , c 2 , c n - seerialiikmete koefitsiendid, c 0 - vabaliige. Astumusrea tingimused on määratletud tervel arvureal.

Tutvume kontseptsiooniga astmeridade lähenemisalad. See on muutuvate väärtuste kogum x, mille jaoks seeria koondub. Võimsusridadel on üsna lihtne lähenemispiirkond. Reaalsete muutujate väärtuste jaoks x lähenemispiirkond koosneb kas ühest punktist või on teatud intervall (konvergentsivahemik) või langeb kokku kogu teljega Ox .

Väärtuste asendamisel võimsusreadesse x= 0 annab tulemuseks arvuseeria

c 0 +0+0+...+0+... ,

mis koondub.

Seetõttu, millal x= 0 mis tahes astmerida läheneb ja seetõttu selle lähenemisala ei saa olla tühi komplekt. Kõigi astmeridade lähenemispiirkonna struktuur on sama. Selle saab kindlaks teha järgmise teoreemi abil.

1. teoreem (Abeli ​​teoreem). Kui astmerida läheneb mingile väärtusele x = x 0, erineb nullist, siis see läheneb ja pealegi absoluutselt kõigi | x| < |x 0 | . Pange tähele: nii algväärtust “X on null” kui ka mis tahes “X” väärtust, mida võrreldakse algväärtusega, võetakse modulo – märki arvesse võtmata.

Tagajärg. Kui võimsusseeria lahkneb mingis väärtuses x = x 1, siis see erineb kõigi | väärtuste puhul x| > |x 1 | .

Nagu me juba varem teada saime, koondub mis tahes astmerida väärtusele x= 0. On astmeridu, mis koonduvad ainult siis, kui x= 0 ja muude väärtuste puhul lahknevad X. Jättes selle juhtumi vaatlusest välja, eeldame, et astmerida läheneb mingile väärtusele x = x 0, erineb nullist. Siis koondub see vastavalt Abeli ​​teoreemile intervalli ]-| kõikides punktides x 0 |, |x 0 |[ (intervall, mille vasak ja parem piir on x väärtused, mille juures astmerida koondub, võttes vastavalt miinus- ja plussmärgiga), sümmeetriline lähtekoha suhtes.

Kui võimsusjada teatud väärtuse juures lahkneb x = x 1, siis lahkneb see Abeli ​​teoreemi järelduvuse põhjal kõigis punktides väljaspool lõiku [-| x 1 |, |x 1 |] . Sellest järeldub, et iga astmerea jaoks on alguspunkti suhtes sümmeetriline intervall, nn konvergentsi intervall, mille igas punktis seeria koondub, piiridel võib see läheneda või lahkneda, ja mitte tingimata samal ajal, ja väljaspool lõiku seeria lahkneb. Number R nimetatakse astmeridade lähenemisraadiuseks.

Erijuhtudel astmeridade lähenemisintervall võib degenereeruda punktini (siis seeria koondub ainult siis, kui x= 0 ja seda peetakse R= 0) või esindavad tervet arvjoont (siis seeria koondub arvjoone kõikidesse punktidesse ja eeldatakse, et ).

Seega seisneb astmerea konvergentsipiirkonna määramine selle määramises lähenemisraadius R ja ridade konvergentsi uurimine lähenemisintervalli (at ) piiridel.

Teoreem 2. Kui kõik astmerea koefitsiendid, alates ühest kindlast, erinevad nullist, siis on selle lähenemisraadius võrdne piirväärtusega, mis on seotud astmete ühisliikmete koefitsientide absoluutväärtuste suhtega. sellele järgnevad sarjad, st.

Näide 1. Leidke astmeridade konvergentsi piirkond

Lahendus. Siin

Kasutades valemit (28), leiame selle seeria lähenemisraadiuse:

Uurime ridade konvergentsi lähenemisintervalli otstes. Näide 13 näitab, et see jada koondub punktis x= 1 ja lahkneb juures x= -1. Järelikult on lähenemispiirkond poolintervall.

Näide 2. Leidke astmeridade konvergentsi piirkond

Lahendus. Seeria koefitsiendid on positiivsed ja

Leiame selle suhte piiri, s.o. astmeridade lähenemisraadius:

Uurime jada konvergentsi intervalli otstes. Väärtuste asendamine x= -1/5 ja x= 1/5 selles reas annab:

Esimene neist seeriatest läheneb (vt näide 5). Kuid siis lõigu "Absoluutne konvergents" teoreemi kohaselt koondub ka teine ​​seeria ja selle koondumispiirkond on segment

Näide 3. Leidke astmeridade konvergentsi piirkond

Lahendus. Siin

Valemi (28) abil leiame jada lähenemisraadiuse:

Uurime väärtuste seeriate konvergentsi. Asendades need selles seerias, saame vastavalt

Mõlemad seeriad lahknevad seetõttu, et konvergentsi vajalik tingimus ei ole täidetud (nende ühised tingimused ei kipu punktis nullini). Seega see jada lähenemisintervalli mõlemas otsas lahkneb ja selle lähenemispiirkond on intervall.

Näide 5. Leidke astmeridade konvergentsi piirkond

Lahendus. Leiame seose, kus , ja :

Vastavalt valemile (28) selle jada lähenemisraadius

,

see tähendab, et seeria koondub ainult siis, kui x= 0 ja erineb teiste väärtuste puhul X.

Näited näitavad, et lähenemisintervalli lõpus käituvad jadad erinevalt. Näites 1 seeria lähenemisintervalli ühes otsas läheneb ja teises lahkneb; näites 2 koondub see mõlemas otsas; näites 3 see lahkneb mõlemas otsas.

Astumusrea lähenemisraadiuse valem saadakse eeldusel, et kõik seerialiikmete koefitsiendid, alates teatud punktist, erinevad nullist. Seetõttu on valemi (28) kasutamine lubatud ainult nendel juhtudel. Kui seda tingimust rikutakse, tuleks astmeridade lähenemisraadiust otsida d'Alemberti testi abil või muutuja asendamisel teisendada jada kujule, milles määratud tingimus on täidetud.

Näide 6. Leidke astmeridade konvergentsi intervall

Lahendus. See seeria ei sisalda paaritu kraadiga termineid X. Seetõttu muudame seeria, seade . Siis saame sarja

mille konvergentsiraadiuse leidmiseks saame rakendada valemit (28). Kuna , a , siis selle rea lähenemisraadius

Võrdsuselt saame Seega see seeria koondub intervallile .

Jõuridade summa. Astmete ridade diferentseerimine ja integreerimine

Olgu võimuseeria jaoks

lähenemisraadius R> 0, st. see seeria läheneb intervallile .

Siis iga väärtus X konvergentsivahemikust vastab rea teatud summale. Seetõttu on astmeridade summa funktsioon X konvergentsi intervallil. Tähistades seda f(x), saame kirjutada võrdsuse

mõista seda selles mõttes, et seeriate summa igas punktis X konvergentsi intervallist on võrdne funktsiooni väärtusega f(x) sel hetkel. Samas tähenduses ütleme, et astmerida (29) läheneb funktsioonile f(x) lähenemisvahemikul.

Väljaspool konvergentsivahemikku pole võrdusel (30) mõtet.

Näide 7. Leidke astmeridade summa

Lahendus. See on geomeetriline seeria, mille jaoks a= 1, a q= x. Seetõttu on selle summa funktsioon . Seeria läheneb, kui , ja on selle lähenemisintervall. Seega võrdsus

kehtib ainult väärtuste puhul, kuigi funktsioon määratletud kõigi väärtuste jaoks X, välja arvatud X= 1.

Võib tõestada, et astmeridade summa f(x) on pidev ja diferentseeruv lähenemisintervalli mis tahes intervallil, eriti jada lähenemisintervalli mis tahes punktis.

Esitame teoreemid astmeridade terminite kaupa diferentseerimise ja integreerimise kohta.

Teoreem 1. Lähenemisvahemikus olevat astmerida (30) saab liikme kaupa diferentseerida piiramatu arv kordi ning saadud astmeridade lähenemisraadius on sama kui algsel jada ja nende summad on vastavalt võrdsed .

Teoreem 2. Astmete rida (30) saab integreerida terminite kaupa piiramatu arv kordi vahemikus 0 kuni X, kui , ja saadud astmeridadel on sama lähenemisraadius kui algsel seerial ning nende summad on vastavalt võrdsed

Funktsioonide laiendamine võimsusridadesse

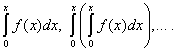
Olgu funktsioon antud f(x), mis vajab laiendamist võimsusreaks, s.o. esindama kujul (30):

Ülesanne on määrata koefitsiendid rida (30). Selleks, eristades võrdsust (30) termini kaupa, leiame järjekindlalt:

……………………………………………….. (31)

Eeldades võrdsustes (30) ja (31) X= 0, leiame

Asendades leitud avaldised võrdsusega (30), saame

(32)

Leiame mõne elementaarfunktsiooni Maclaurini seeria laienduse.

Näide 8. Laiendage funktsiooni Maclaurini seerias

Lahendus. Selle funktsiooni tuletised langevad kokku funktsiooni endaga:

Seetõttu, millal X= 0 meil on

Asendades need väärtused valemiga (32), saame soovitud laienduse:

(33)

See jada koondub tervele arvujoonele (selle lähenemisraadiusele).

Funktsionaalsete jadate teoorias on kesksel kohal jaotis, mis on pühendatud funktsiooni laiendamisele jadaks.

Seega on ülesanne püstitatud: antud funktsiooni jaoks me peame leidma sellise võimsusjada

mis lähenes teatud intervallile ja selle summa oli võrdne
, need.

= ..

Seda ülesannet nimetatakse funktsiooni astmereaks laiendamise probleem.

Vajalik tingimus astmereas oleva funktsiooni lagundatavuse jaoks kas selle diferentseeritavus on lõpmatu arv kordi – see tuleneb koonduvate astmeridade omadustest. See tingimus on reeglina täidetud elementaarfunktsioonide puhul nende määratluspiirkonnas.

Oletame, et funktsioon
omab mis tahes järjestust tuletisi. Kas seda on võimalik laiendada võimsusseeriaks?Kui jah, siis kuidas seda seeriat leida? Probleemi teist osa on lihtsam lahendada, nii et alustame sellest.

Oletame, et funktsioon
saab esitada punkti sisaldavas intervallis koonduvate astmeridade summana X 0 :

= .. (*)

Kus A 0 ,A 1 ,A 2 ,...,A P ,... – tundmatud (veel) koefitsiendid.

Paneme võrdsusse (*) väärtuse x = x 0 , siis saame

.

Eristagem astmerida (*) termini kaupa

= ..

ja siin uskudes x = x 0 , saame

.

Järgmise diferentseerimisega saame seeria

= ..

uskudes x = x 0 , saame
, kus
.

Pärast P- saame mitu eristamist

Eeldusel viimases võrdsuses x = x 0 , saame
, kus

Niisiis, koefitsiendid on leitud

,
,
, …,
,….,

asendades mille seeriasse (*), saame

Saadud seeriat nimetatakse Taylori kõrvalfunktsiooni jaoks
.

Seega oleme selle kindlaks teinud kui funktsiooni saab laiendada astmeseeriaks astmetes (x - x 0 ), siis on see laiendus ainulaadne ja sellest tulenev seeria on tingimata Taylori seeria.

Pange tähele, et Taylori seeria võib saada mis tahes funktsiooni jaoks, millel on punktis mis tahes järgu tuletised x = x 0 . Aga see ei tähenda, et funktsiooni ja saadud jada vahele saab panna võrdusmärgi, s.t. et jada summa on võrdne algfunktsiooniga. Esiteks saab selline võrdus olla mõttekas ainult konvergentsi piirkonnas ja funktsiooni jaoks saadud Taylori jada võib lahkneda ja teiseks, kui Taylori jada koondub, siis ei pruugi selle summa kattuda algfunktsiooniga.

3.2. Piisavad tingimused funktsiooni lagunemiseks Taylori seerias

Sõnastagem väide, mille abil ülesanne lahendatakse.

Kui funktsioon
mõnes punkti x naabruses 0 on tuletised kuni (n+ 1) järjekorras, siis selles naabruses on meilvalemTaylor

KusR n (X)-Taylori valemi ülejäänud termin - on kujul (Lagrange'i vorm)

Kus punktξ asub x ja x vahel 0 .

Pange tähele, et Taylori seeria ja Taylori valemi vahel on erinevus: Taylori valem on lõplik summa, st. P - fikseeritud number.

Tuletage meelde, et seeria summa S(x) saab määratleda osasummade funktsionaalse jada piirina S P (x) mingi intervalliga X:

.

Selle järgi tähendab funktsiooni laiendamine Taylori seeriaks sellise seeria leidmist, mis sobib mis tahes XX

Kirjutame Taylori valemi kujul kus

Märka seda
defineerib saadud vea, asenda funktsioon f(x) polünoom S n (x).

Kui
, See
, need. funktsioon on laiendatud Taylori seeriaks. Vastupidi, kui
, See
.

Nii me tõestasime Taylori seeria funktsiooni lagundatavuse kriteerium.

Funktsiooni jaoksf(x) laieneb Taylori seeriaks, on vajalik ja piisav, et sellel intervallil
, KusR n (x) on Taylori seeria ülejäänud termin.

Kasutades sõnastatud kriteeriumi, on võimalik saada piisavfunktsiooni lagundatavuse tingimused Taylori seerias.

Kui sissemingi punkti x naabruskond 0 funktsiooni kõigi tuletiste absoluutväärtused on piiratud sama arvuga M≥ 0, st.

, To selles naabruses laieneb funktsioon Taylori seeriaks.

Eeltoodust järeldub algoritmfunktsiooni laiendaminef(x) Taylori seerias punkti läheduses X 0 :

1. Funktsioonide tuletiste leidmine f(x):

f(x), f'(x), f"(x), f'"(x), f (n) (x),…

2. Arvutage funktsiooni väärtus ja selle tuletiste väärtused punktis X 0

f(x 0 ), f’(x 0 ), f”(x 0 ), f’”(x 0 ), f (n) (x 0 ),…

3. Kirjutame formaalselt Taylori jada ja leiame saadud astmeridade konvergentsipiirkonna.

4. Kontrollime piisavate tingimuste täitmist, s.o. mille jaoks kehtestame X lähenemispiirkonnast, ülejäänud tähtaeg R n (x) kipub nulli as
või
.

Funktsioonide laiendamist Taylori seeriasse selle algoritmi abil nimetatakse funktsiooni laiendamine Taylori seeriasse definitsiooni järgi või otsene lagunemine.

Kuidas lisada veebisaidile matemaatilisi valemeid?

Kui teil on kunagi vaja veebilehele lisada üks või kaks matemaatilist valemit, on lihtsaim viis seda teha artiklis kirjeldatud viisil: matemaatilised valemid sisestatakse saidile hõlpsasti piltide kujul, mille Wolfram Alpha genereerib automaatselt. . Lisaks lihtsusele aitab see universaalne meetod parandada saidi nähtavust otsingumootorites. See on töötanud pikka aega (ja ma arvan, et töötab igavesti), kuid on juba moraalselt vananenud.

Kui kasutate oma saidil regulaarselt matemaatilisi valemeid, siis soovitan kasutada MathJaxi – spetsiaalset JavaScripti teeki, mis kuvab MathML-i, LaTeX-i või ASCIIMathML-i märgistust kasutavates veebibrauserites matemaatilisi tähistusi.

MathJaxi kasutamise alustamiseks on kaks võimalust: (1) lihtsa koodi abil saate kiiresti ühendada oma veebisaidiga MathJaxi skripti, mis laaditakse automaatselt õigel ajal kaugserverist (serverite loend); (2) laadige MathJaxi skript alla kaugserverist oma serverisse ja ühendage see oma saidi kõigi lehtedega. Teine meetod – keerulisem ja aeganõudvam – kiirendab teie saidi lehtede laadimist ning kui MathJaxi emaserver muutub mingil põhjusel ajutiselt kättesaamatuks, ei mõjuta see teie saiti kuidagi. Vaatamata nendele eelistele valisin esimese meetodi, kuna see on lihtsam, kiirem ja ei nõua tehnilisi oskusi. Järgige minu eeskuju ja juba 5 minuti pärast saate oma saidil kasutada kõiki MathJaxi funktsioone.

Saate ühendada MathJaxi teegi skripti kaugserverist, kasutades kahte MathJaxi põhiveebisaidilt või dokumentatsioonilehelt võetud koodivalikut:

Üks neist koodivalikutest tuleb kopeerida ja kleepida oma veebilehe koodi, eelistatavalt siltide vahele ja või kohe pärast märgendit. Esimese variandi järgi laadib MathJax kiiremini ja aeglustab lehte vähem. Kuid teine ​​valik jälgib ja laadib automaatselt MathJaxi uusimad versioonid. Kui sisestate esimese koodi, tuleb seda perioodiliselt värskendada. Kui sisestate teise koodi, laaditakse lehed aeglasemalt, kuid te ei pea pidevalt MathJaxi värskendusi jälgima.

Lihtsaim viis MathJaxi ühendamiseks on Bloggeris või WordPressis: lisage saidi juhtpaneelile vidin, mis on mõeldud kolmanda osapoole JavaScripti koodi sisestamiseks, kopeerige sellesse ülaltoodud allalaadimiskoodi esimene või teine ​​versioon ja asetage vidin lähemale. malli algusesse (muide, see pole üldse vajalik, kuna MathJaxi skript laaditakse asünkroonselt). See on kõik. Nüüd õppige MathML-i, LaTeX-i ja ASCIIMathML-i märgistussüntaksit ning olete valmis oma saidi veebilehtedele matemaatilisi valemeid sisestama.

Iga fraktal on konstrueeritud kindla reegli järgi, mida rakendatakse järjekindlalt piiramatu arv kordi. Iga sellist aega nimetatakse iteratsiooniks.

Mengeri käsna konstrueerimise iteratiivne algoritm on üsna lihtne: algne kuubik küljega 1 jagatakse selle tahkudega paralleelsete tasapindade abil 27 võrdseks kuubiks. Sellest eemaldatakse üks keskne kuubik ja 6 selle külge külgnevat kuubikut. Tulemuseks on komplekt, mis koosneb ülejäänud 20 väiksemast kuubikust. Tehes sama iga kuubikuga, saame komplekti, mis koosneb 400 väiksemast kuubikust. Seda protsessi lõputult jätkates saame Mengeri käsna.

Kui funktsioonil f(x) on teatud intervalli, mis sisaldab punkti a, kõigi järkude tuletised, saab sellele rakendada Taylori valemit:
,
Kus r n– seeria nn jääk liige või jääk, seda saab hinnata Lagrange'i valemi abil:
, kus arv x on x ja a vahel.

f(x)=

punktis x 0 = reaelementide arv 3 4 5 6 7

Kasutage elementaarfunktsioonide laiendust e x , cos(x), sin(x), ln(1+x), (1+x) m

Funktsioonide sisestamise reeglid:

Kui mõne väärtuse eest X r n→0 kl n→∞, siis piirväärtuses muutub Taylori valem selle väärtuse jaoks koonduvaks Taylori sari:
,
Seega saab funktsiooni f(x) vaadeldavas punktis x laiendada Taylori seeriaks, kui:
1) tal on kõikide järjekordade tuletised;
2) konstrueeritud jada selles punktis koondub.

Kui a = 0, saame rea nimega Maclaurini seeria:
,
Maclaurini seeria kõige lihtsamate (elementaarsete) funktsioonide laiendamine:
Eksponentfunktsioonid
, R=∞
Trigonomeetrilised funktsioonid
, R=∞
, R=∞
, (-π/2< x < π/2), R=π/2
Funktsioon actgx ei laiene x astmetes, sest ctg0=∞
Hüperboolsed funktsioonid


Logaritmilised funktsioonid
, -1