Murdarvu kalkulaator loodud kiireks arvutamiseks murdarvudega, see aitab teil hõlpsasti murde lisada, korrutada, jagada või lahutada.
Kaasaegsed koolilapsed alustavad murdude õppimist juba 5. klassis ja harjutused nendega muutuvad iga aastaga keerulisemaks. Koolis õpitavad matemaatilised terminid ja kogused võivad meile täiskasvanuelus harva kasulikud olla. Murrud, erinevalt logaritmidest ja astmetest, leidub aga igapäevaelus (kauguste mõõtmine, kauba kaalumine jne) üsna sageli. Meie kalkulaator on mõeldud kiireks toiminguks murdarvudega.
Esiteks määratleme, mis on murrud ja mis need on. Murrud on ühe arvu ja teise arvu suhe; see on arv, mis koosneb ühiku täisarvust murdude.
Murdude tüübid:
- Tavaline
- Kümnend
- Segatud
Näide tavalised murrud:
Ülemine väärtus on lugeja, alumine on nimetaja. Kriips näitab, et ülemine arv jagub alumise arvuga. Kui kriips on horisontaalne, saate selle kirjutamisvormingu asemel kirjutada teisiti. Võite panna näiteks kaldjoone:
1/2, 3/7, 19/5, 32/8, 10/100, 4/1
Kümnendkohad on kõige populaarsem murdude tüüp. Need koosnevad täisarvulisest osast ja murdosast, mis on eraldatud komaga.
Kümnendmurdude näide:
0,2 või 6,71 või 0,125
Koosneb täisarvust ja murdosast. Selle murru väärtuse väljaselgitamiseks tuleb liita täisarv ja murd.
Näide segafraktsioonidest:

Meie veebisaidil olev murdude kalkulaator suudab võrgus kiiresti sooritada mis tahes matemaatilisi tehteid murdudega:
- Lisand
- Lahutamine
- Korrutamine
- Jaoskond
Arvutamiseks peate sisestama väljadele numbrid ja valima toimingu. Murdude jaoks peate sisestama lugeja ja nimetaja; täisarvu ei tohi kirjutada (kui murd on tavaline). Ärge unustage klõpsata nuppu "Võrdne".
Mugav on see, et kalkulaator pakub kohe näite lahendamise protsessi murdarvudega, mitte ainult valmis vastuse. Tänu üksikasjalikule lahendusele saate seda materjali kasutada kooliprobleemide lahendamiseks ja käsitletava materjali paremaks valdamiseks.
Peate tegema näidisarvutuse:
Pärast indikaatorite sisestamist vormiväljadele saame:

Enda arvutuse tegemiseks sisestage andmed vormi.
Murdarvu kalkulaator
Sisestage kaks murdu:| + - * : | |||||||
Seotud jaotised.
Murrud on tavalised arvud ja neid saab ka liita ja lahutada. Kuid kuna neil on nimetaja, nõuavad nad keerukamaid reegleid kui täisarvude puhul.
Vaatleme kõige lihtsamat juhtumit, kui on kaks samade nimetajatega murdu. Seejärel:
Samade nimetajatega murdude liitmiseks tuleb lisada nende lugejad ja nimetaja muutmata jätta.
Samade nimetajatega murdude lahutamiseks peate esimese murru lugejast lahutama teise lugeja ja jätma nimetaja jälle muutmata.
Igas avaldises on murdude nimetajad võrdsed. Murdude liitmise ja lahutamise määratluse järgi saame:
Nagu näete, pole see midagi keerulist: lihtsalt liidame või lahutame lugejad ja kõik.
Kuid isegi sellistes lihtsates tegevustes õnnestub inimestel vigu teha. Kõige sagedamini unustatakse ära, et nimetaja ei muutu. Näiteks nende lisamisel hakkavad need ka kokku tulema ja see on põhimõtteliselt vale.
Nimetajate lisamise halvast harjumusest vabanemine on üsna lihtne. Proovige sama asja lahutamisel. Selle tulemusena on nimetaja null ja murdosa kaotab (äkitselt!) oma tähenduse.
Seetõttu pidage kindlasti meeles: liitmisel ja lahutamisel nimetaja ei muutu!
Paljud inimesed teevad vigu ka mitme negatiivse murru lisamisel. Märkidega on segadus: kuhu panna miinus ja kuhu pluss.
Seda probleemi on ka väga lihtne lahendada. Piisab meeles pidada, et miinus enne murdosa märki saab alati üle kanda lugejasse - ja vastupidi. Ja muidugi ärge unustage kahte lihtsat reeglit:
- Pluss miinusega annab miinuse;
- Kaks negatiivset teevad jaatava.
Vaatame seda kõike konkreetsete näidetega:
Ülesanne. Leidke väljendi tähendus:
Esimesel juhul on kõik lihtne, kuid teisel lisame murdude lugejatele miinused:

Mida teha, kui nimetajad on erinevad
Erinevate nimetajatega murde ei saa otse lisada. Vähemalt see meetod on mulle tundmatu. Algseid murde saab aga alati ümber kirjutada, et nimetajad muutuksid samaks.
Murdude teisendamiseks on palju viise. Neist kolme käsitletakse õppetükis “Murdude taandamine ühisnimetajale”, mistõttu me siinkohal neil pikemalt ei peatu. Vaatame mõnda näidet:
Ülesanne. Leidke väljendi tähendus:
Esimesel juhul taandame murrud ühise nimetajani, kasutades “risti” meetodit. Teises otsime NOC-i. Pange tähele, et 6 = 2 · 3; 9 = 3 · 3. Nende laienduste viimased tegurid on võrdsed ja esimesed on suhteliselt esmased. Seetõttu LCM(6; 9) = 2 3 3 = 18.

Mida teha, kui murd sisaldab täisarvu
Võin teile meeldida: erinevad nimetajad murdarvudes pole just kõige suurem pahe. Palju rohkem vigu tekib, kui kogu osa on liitmismurdudes esile tõstetud.
Loomulikult on selliste murdude jaoks olemas oma liitmis- ja lahutamisalgoritmid, kuid need on üsna keerulised ja nõuavad pikka uurimist. Kasutage parem allolevat lihtsat diagrammi:
- Teisendage kõik täisarvu sisaldavad murrud ebaõigeteks murdudeks. Saame normaalterminid (isegi erinevate nimetajatega), mis arvutatakse eelpool käsitletud reeglite järgi;
- Tegelikult arvutage saadud murdude summa või erinevus. Selle tulemusena leiame praktiliselt vastuse;
- Kui see on kõik, mida ülesandes nõuti, teostame pöördteisendust, s.o. Vabaneme valest murdest, tõstes esile kogu osa.
Vale murdude juurde liikumise ja kogu osa esiletõstmise reegleid kirjeldatakse üksikasjalikult õppetükis “Mis on numbriline murd”. Kui te ei mäleta, korrake seda kindlasti. Näited:
Ülesanne. Leidke väljendi tähendus:
Siin on kõik lihtne. Iga avaldise sees olevad nimetajad on võrdsed, seega jääb üle vaid teisendada kõik murrud valedeks ja lugeda. Meil on:
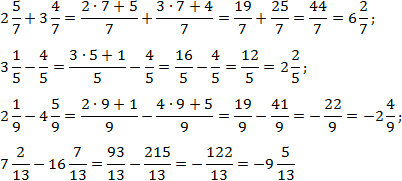
Arvutuste lihtsustamiseks jätsin viimastes näidetes mõned ilmsed sammud vahele.
Väike märkus kahe viimase näite kohta, kus lahutatakse murrud, millel on esile tõstetud täisarvuline osa. Miinus enne teist murdu tähendab, et lahutatakse kogu murd, mitte ainult selle osa.
Lugege see lause uuesti läbi, vaadake näiteid – ja mõelge selle üle. See on koht, kus algajad teevad tohutul hulgal vigu. Neile meeldib selliseid probleeme testides anda. Samuti kohtate neid mitu korda selle õppetunni testides, mis avaldatakse peagi.
Kokkuvõte: üldine arvutusskeem
Kokkuvõtteks annan üldise algoritmi, mis aitab teil leida kahe või enama murru summa või erinevuse:
- Kui ühel või mitmel murdul on täisarvuline osa, teisendage need murdudeks ebaõigeteks;
- Viige kõik murrud teile sobival viisil ühisele nimetajale (muidugi, kui probleemide kirjutajad seda ei teinud);
- Saadud arvud liita või lahutada vastavalt sarnaste nimetajatega murdude liitmise ja lahutamise reeglitele;
- Kui võimalik, lühendage tulemust. Kui murdosa on vale, valige kogu osa.
Pidage meeles, et parem on kogu osa esile tõsta ülesande lõpus, vahetult enne vastuse kirja panemist.
Viiendal sajandil eKr sõnastas Vana-Kreeka filosoof Zenon Eleast oma kuulsad apooriad, millest kuulsaim on "Achilleuse ja kilpkonna" apooria. See kõlab järgmiselt:Oletame, et Achilleus jookseb kümme korda kiiremini kui kilpkonn ja on sellest tuhat sammu maas. Aja jooksul, mis kulub Achilleuse läbimiseks, roomab kilpkonn sada sammu samas suunas. Kui Achilleus jookseb sada sammu, roomab kilpkonn veel kümme sammu jne. Protsess jätkub lõpmatuseni, Achilleus ei jõua kilpkonnale kunagi järele.
See arutluskäik sai loogiliseks šokiks kõigile järgnevatele põlvkondadele. Aristoteles, Diogenes, Kant, Hegel, Hilbert... Nad kõik pidasid ühel või teisel viisil Zenoni apooriat. Šokk oli nii tugev, et " ... arutelud jätkuvad tänini, teadusringkonnad pole paradokside olemuses veel ühisele seisukohale jõudnud ... teema uurimisse kaasati matemaatilist analüüsi, hulgateooriat, uusi füüsikalisi ja filosoofilisi käsitlusi. ; ükski neist ei saanud probleemi üldtunnustatud lahenduseks..."[Wikipedia, "Zeno's Aporia". Kõik saavad aru, et neid lollitatakse, aga keegi ei saa aru, milles pettus seisneb.
Matemaatilisest vaatenurgast näitas Zenon oma apooriates selgelt üleminekut kvantiteedilt . See üleminek eeldab rakendust püsivate asemel. Minu arusaamist mööda pole muutuvate mõõtühikute kasutamise matemaatilist aparaati kas veel välja töötatud või pole seda Zenoni apooria puhul rakendatud. Meie tavapärase loogika rakendamine viib meid lõksu. Me rakendame mõtlemise inertsi tõttu vastastikusele väärtusele konstantseid ajaühikuid. Füüsilisest vaatenurgast näeb see välja nagu aeg aeglustub, kuni see täielikult peatub hetkel, mil Achilleus kilpkonnale järele jõuab. Kui aeg peatub, ei suuda Achilleus enam kilpkonnast üle joosta.
Kui pöörame oma tavapärase loogika ümber, loksub kõik paika. Achilleus jookseb ühtlase kiirusega. Tema tee iga järgmine lõik on kümme korda lühem kui eelmine. Sellest tulenevalt on selle ületamiseks kulunud aeg kümme korda väiksem kui eelmisel. Kui rakendame selles olukorras "lõpmatuse" mõistet, siis oleks õige öelda: "Achilleus jõuab kilpkonnale lõpmatult kiiresti järele."
Kuidas seda loogilist lõksu vältida? Jääge konstantsetesse ajaühikutesse ja ärge lülituge vastastikustele ühikutele. Zenoni keeles näeb see välja järgmine:
Aja jooksul, mis kulub Achilleuse tuhande sammu jooksmiseks, roomab kilpkonn sada sammu samas suunas. Järgmise esimesega võrdse ajaintervalli jooksul jookseb Achilleus veel tuhat sammu ja kilpkonn roomab sada sammu. Nüüd on Achilleus kilpkonnast kaheksasada sammu ees.
See lähenemine kirjeldab adekvaatselt tegelikkust ilma loogiliste paradoksideta. Kuid see pole probleemi täielik lahendus. Einsteini väide valguse kiiruse vastupandamatusest on väga sarnane Zenoni apooriaga "Achilleus ja kilpkonn". Seda probleemi tuleb veel uurida, ümber mõelda ja lahendada. Ja lahendust tuleb otsida mitte lõpmata suurtes arvudes, vaid mõõtühikutes.
Veel üks Zenoni huvitav apooria räägib lendavast noolest:
Lendav nool on liikumatu, kuna ta on igal ajahetkel puhkeolekus ja kuna ta on igal ajahetkel puhkab, siis on ta alati puhkeolekus.
Selles apoorias ületatakse loogiline paradoks väga lihtsalt - piisab, kui selgitada, et igal ajahetkel on lendav nool paigal erinevates ruumipunktides, mis tegelikult on liikumine. Siin tuleb märkida veel üks punkt. Ühe maanteel oleva auto foto järgi on võimatu kindlaks teha ei selle liikumise fakti ega kaugust selleni. Et teha kindlaks, kas auto liigub, vajate kahte fotot, mis on tehtud ühest ja samast punktist erinevatel ajahetkedel, kuid te ei saa määrata nende kaugust. Auto kauguse määramiseks on vaja kahte pilti, mis on tehtud ühel ajahetkel erinevatest ruumipunktidest, kuid nende järgi ei saa liikumise fakti kindlaks teha (loomulikult vajate arvutusteks siiski lisaandmeid, trigonomeetria aitab teid ). Erilist tähelepanu tahan juhtida see, et kaks ajapunkti ja kaks punkti ruumis on erinevad asjad, mida ei tohiks segi ajada, sest need annavad uurimistööks erinevaid võimalusi.
Kolmapäeval, 4. juulil 2018
Vikipeedias on väga hästi kirjeldatud komplekti ja multikomplekti erinevusi. Vaatame.
Nagu näete, "komplektis ei saa olla kahte identset elementi", kuid kui komplektis on identsed elemendid, nimetatakse sellist komplekti "multiseks". Mõistlikud olendid ei mõista kunagi sellist absurdset loogikat. See on rääkivate papagoide ja treenitud ahvide tase, kellel puudub mõistus sõnast “täiesti”. Matemaatikud tegutsevad tavaliste koolitajatena, kuulutades meile oma absurdseid ideid.
Kunagi olid silla ehitanud insenerid silda katsetades silla all paadis. Kui sild kokku kukkus, suri keskpärane insener oma loomingu rusude all. Kui sild koormusele vastu pidas, ehitas andekas insener teisi sildu.
Pole tähtis, kuidas matemaatikud peituvad fraasi "mind me, I'm in the house" taha või õigemini: "matemaatika uurib abstraktseid mõisteid", on üks nabanöör, mis seob neid lahutamatult reaalsusega. See nabanöör on raha. Rakendagem matemaatilist hulgateooriat matemaatikute endi suhtes.
Õppisime väga hästi matemaatikat ja nüüd istume kassa taga ja anname palka välja. Nii et matemaatik tuleb meie juurde oma raha pärast. Loeme talle kogu summa välja ja laotame oma lauale erinevatesse hunnikutesse, millesse paneme sama nimiväärtusega arveid. Seejärel võtame igast hunnikust ühe arve ja anname matemaatikule tema "matemaatilise palgakomplekti". Selgitagem matemaatikule, et ta saab ülejäänud arved alles siis, kui ta tõestab, et ilma identsete elementideta hulk ei võrdu identsete elementidega hulgaga. Siit saab alguse lõbus.
Esiteks hakkab tööle saadikute loogika: "Seda võib teistele rakendada, aga mulle mitte!" Siis hakkavad nad meile kinnitama, et sama nimiväärtusega vekslitel on erinevad arvenumbrid, mis tähendab, et neid ei saa pidada samadeks elementideks. Olgu, loeme palgad müntidesse – müntidel pole numbreid. Siin hakkab matemaatik paaniliselt meenutama füüsikat: erinevatel müntidel on erinev kogus mustust, kristallstruktuur ja aatomite paigutus on igal mündil unikaalne...
Ja nüüd on mul kõige huvitavam küsimus: kus on piir, millest kaugemale muutuvad multikomplekti elemendid hulga elementideks ja vastupidi? Sellist joont pole olemas – kõike otsustavad šamaanid, teadus ei ole siin lähedalgi valetamisele.
Vaata siia. Valime välja sama alaga jalgpallistaadionid. Väljade pindalad on samad – see tähendab, et meil on multikomplekt. Aga kui vaadata nende samade staadioninimesid, siis saame neid palju, sest nimed on erinevad. Nagu näete, on sama elementide komplekt nii hulk kui ka multikomplekt. Kumb on õige? Ja siin tõmbab matemaatik-šamaan-teramees varrukast trumpide ässa ja hakkab meile rääkima kas komplektist või multikomplektist. Igal juhul veenab ta meid, et tal on õigus.
Et mõista, kuidas tänapäeva šamaanid hulgateooriaga opereerivad, sidudes selle reaalsusega, piisab, kui vastata ühele küsimusele: mille poolest erinevad ühe hulga elemendid teise hulga elementidest? Ma näitan teile, ilma igasuguse "mõeldava mitte ühe tervikuna" või "ei ole mõeldav ühtse tervikuna".
Pühapäev, 18. märts 2018
Arvu numbrite summa on šamaanide tants tamburiiniga, millel pole matemaatikaga mingit pistmist. Jah, matemaatikatundides õpetatakse meid leidma arvu numbrite summat ja seda kasutama, aga seepärast ongi nad šamaanid, et õpetada järeltulijatele nende oskusi ja tarkust, muidu surevad šamaanid lihtsalt välja.
Kas vajate tõestust? Avage Wikipedia ja proovige leida leht "Arvu numbrite summa". Teda pole olemas. Matemaatikas pole valemit, mille abil saaks leida mis tahes arvu numbrite summa. Numbrid on ju graafilised sümbolid, millega me numbreid kirjutame, ja matemaatika keeles kõlab ülesanne järgmiselt: "Leia mis tahes arvu tähistavate graafiliste sümbolite summa." Matemaatikud ei suuda seda ülesannet lahendada, kuid šamaanid saavad sellega hõlpsasti hakkama.
Mõelgem välja, mida ja kuidas teeme, et leida antud arvu numbrite summa. Ja nii, olgu meil number 12345. Mida tuleb teha, et leida selle arvu numbrite summa? Vaatleme kõiki samme järjekorras.
1. Kirjutage number paberile. Mida me oleme teinud? Oleme teisendanud numbri graafiliseks numbrisümboliks. See ei ole matemaatiline tehe.
2. Lõikasime ühe saadud pildi mitmeks üksikuid numbreid sisaldavaks pildiks. Pildi lõikamine ei ole matemaatiline tehe.
3. Teisendage üksikud graafilised sümbolid numbriteks. See ei ole matemaatiline tehe.
4. Lisage saadud numbrid. Nüüd on see matemaatika.
Arvu 12345 numbrite summa on 15. Need on šamaanide õpetatavad “lõikamis- ja õmbluskursused”, mida matemaatikud kasutavad. Kuid see pole veel kõik.
Matemaatilisest seisukohast pole vahet, millisesse arvusüsteemi me arvu kirjutame. Seega on erinevates numbrisüsteemides sama numbri numbrite summa erinev. Matemaatikas märgitakse numbrisüsteem numbrist paremal oleva alaindeksina. Suure numbriga 12345 ei taha ma oma pead petta, mõelgem numbrile 26 artiklist. Kirjutame selle arvu kahend-, kaheksand-, kümnend- ja kuueteistkümnendsüsteemis. Me ei vaata iga sammu mikroskoobi all, me oleme seda juba teinud. Vaatame tulemust.
Nagu näete, on erinevates numbrisüsteemides sama numbri numbrite summa erinev. Sellel tulemusel pole matemaatikaga mingit pistmist. See on sama, kui määraksite ristküliku pindala meetrites ja sentimeetrites, saaksite täiesti erinevad tulemused.
Null näeb kõigis numbrisüsteemides välja ühesugune ja sellel pole numbrite summat. See on veel üks argument selle kasuks, et. Küsimus matemaatikutele: kuidas on matemaatikas määratud midagi, mis ei ole arv? Mis, matemaatikute jaoks ei eksisteeri midagi peale numbrite? Ma võin seda lubada šamaanidele, kuid mitte teadlastele. Tegelikkus ei seisne ainult numbrites.
Saadud tulemust tuleks pidada tõestuseks, et arvusüsteemid on arvude mõõtühikud. Me ei saa ju võrrelda numbreid erinevate mõõtühikutega. Kui samad toimingud sama suuruse erinevate mõõtühikutega annavad pärast nende võrdlemist erinevaid tulemusi, siis pole sellel matemaatikaga mingit pistmist.
Mis on tõeline matemaatika? See on siis, kui matemaatilise tehte tulemus ei sõltu arvu suurusest, kasutatavast mõõtühikust ja sellest, kes selle toimingu sooritab.
Oh! Kas see pole mitte naiste tualett?
- Noor naine! See on laboratoorium hingede indefiilse pühaduse uurimiseks nende taevasse tõusmise ajal! Halo peal ja nool üles. Mis tualett veel?
Naine... Halo peal ja nool alla on isased.
Kui selline disainikunstiteos vilksatab teie silme ees mitu korda päevas,
Siis pole üllatav, et äkki leiate oma autost kummalise ikooni:
Mina isiklikult pingutan selle nimel, et kakaval inimesel oleks näha miinus nelja kraadi (üks pilt) (mitmest pildist koosnev kompositsioon: miinusmärk, number neli, kraadide tähistus). Ja ma ei arva, et see tüdruk on loll, kes füüsikat ei tunne. Tal on lihtsalt tugev stereotüüp graafiliste piltide tajumisest. Ja matemaatikud õpetavad seda meile kogu aeg. Siin on näide.
1A ei ole "miinus neli kraadi" ega "üks a". See on "kakav mees" või number "kakskümmend kuus" kuueteistkümnendsüsteemis. Need inimesed, kes pidevalt selles numbrisüsteemis töötavad, tajuvad numbrit ja tähte automaatselt ühe graafilise sümbolina.
Tunni sisuSarnaste nimetajatega murdude lisamine
Murdude liitmist on kahte tüüpi:
- Sarnaste nimetajatega murdude lisamine
- Erinevate nimetajatega murdude liitmine
Esiteks õpime sarnase nimetajaga murdude liitmist. Siin on kõik lihtne. Samade nimetajatega murdude liitmiseks tuleb lisada nende lugejad ja nimetaja muutmata jätta. Näiteks liidame murrud ja . Lisage lugejad ja jätke nimetaja muutmata:

Seda näidet on lihtne mõista, kui meenutada pitsat, mis on jagatud neljaks osaks. Kui lisate pitsale pitsa, saate pizza:

Näide 2. Lisage fraktsioonid ja .

Vastuseks osutus vale murd. Kui ülesande lõpp saabub, on kombeks valedest murdudest lahti saada. Ebaõigest murdosast vabanemiseks peate valima kogu selle osa. Meie puhul on kogu osa kergesti eraldatav - kaks jagatud kahega võrdub ühega:

Seda näidet saab hõlpsasti mõista, kui meenutame pitsat, mis on jagatud kaheks osaks. Kui lisate pitsale rohkem pitsat, saate ühe terve pitsa:

Näide 3. Lisage fraktsioonid ja .
Jällegi liidame lugejad kokku ja jätame nimetaja muutmata:
![]()
Seda näidet on lihtne mõista, kui meenutame pitsat, mis on jagatud kolmeks osaks. Kui lisate pitsale rohkem pitsat, saate pizza:

Näide 4. Leidke avaldise väärtus 
See näide on lahendatud täpselt samamoodi nagu eelmised. Lugejad tuleb lisada ja nimetaja jätta muutmata:
Proovime oma lahendust joonise abil kujutada. Kui lisate pitsale pitsad ja lisate rohkem pitsasid, saate 1 terve pitsa ja rohkem pitsasid.

Nagu näete, pole samade nimetajatega murdude liitmises midagi keerulist. Piisab, kui mõistad järgmisi reegleid:
- Sama nimetajaga murdude liitmiseks tuleb lisada nende lugejad ja nimetaja muutmata jätta;
Erinevate nimetajatega murdude liitmine
Nüüd õpime, kuidas lisada erinevate nimetajatega murde. Murdude liitmisel peavad murdude nimetajad olema samad. Kuid need ei ole alati ühesugused.
Näiteks võib murde lisada, kuna neil on samad nimetajad.
Kuid murde ei saa kohe lisada, kuna neil murdudel on erinevad nimetajad. Sellistel juhtudel tuleb murded taandada sama (ühise) nimetajani.
Murdude samale nimetajale taandamiseks on mitu võimalust. Täna vaatleme neist ainult ühte, kuna teised meetodid võivad algajale tunduda keerulised.
Selle meetodi olemus seisneb selles, et esmalt otsitakse mõlema murru nimetajate LCM-i. Seejärel jagatakse LCM esimese murru nimetajaga, et saada esimene lisategur. Nad teevad sama teise murdosaga – LCM jagatakse teise murdosa nimetajaga ja saadakse teine lisategur.
Seejärel korrutatakse murdude lugejad ja nimetajad nende lisateguritega. Nende toimingute tulemusel muutuvad erineva nimetajaga murrud samade nimetajatega murdudeks. Ja me juba teame, kuidas selliseid murde lisada.
Näide 1. Liidame kokku murrud ja
Kõigepealt leiame mõlema murru nimetajate väikseima ühiskordse. Esimese murru nimetaja on arv 3 ja teise murru nimetaja on arv 2. Nende arvude vähim ühiskordne on 6
LCM (2 ja 3) = 6
Nüüd pöördume tagasi murdude ja . Esiteks jagage LCM esimese murru nimetajaga ja hankige esimene lisategur. LCM on arv 6 ja esimese murru nimetaja on arv 3. Jagage 6 3-ga, saame 2.
Saadud arv 2 on esimene lisakordaja. Kirjutame selle esimese murruni. Selleks tehke murru kohale väike kaldus joon ja kirjutage üles selle kohal leitud lisategur:
Teeme sama teise murdosaga. Jagame LCM-i teise murru nimetajaga ja saame teise lisateguri. LCM on arv 6 ja teise murdosa nimetaja on arv 2. Jagage 6 2-ga, saame 3.
Saadud arv 3 on teine lisakordaja. Kirjutame selle teise murruni. Jällegi teeme teise murru kohale väikese kaldus joone ja kirjutame üles selle kohal leitud lisateguri:
Nüüd on meil kõik lisamiseks valmis. Jääb üle korrutada murdude lugejad ja nimetajad nende lisateguritega:

Vaadake hoolikalt, milleni oleme jõudnud. Jõudsime järeldusele, et erineva nimetajaga murrud muutusid samade nimetajatega murdudeks. Ja me juba teame, kuidas selliseid murde lisada. Toome selle näite lõpuni:

See lõpetab näite. Selgub, et lisada.
Proovime oma lahendust joonise abil kujutada. Kui lisate pitsale pitsa, saate ühe terve pitsa ja veel kuuendiku pitsast:

Murdude taandamist samale (ühis)nimetajale saab kujutada ka pildi abil. Vähendades murde ja ühise nimetaja, saime murrud ja . Neid kahte fraktsiooni esindavad samad pitsatükid. Ainus erinevus seisneb selles, et seekord jagatakse need võrdseteks osadeks (vähendatud samale nimetajale).

Esimene joonis kujutab murdosa (neli tükki kuuest) ja teine joonis kujutab murdosa (kolm tükki kuuest). Lisades need tükid saame (seitse tükki kuuest). See murd on vale, seetõttu tõstsime esile kogu selle osa. Tulemuseks saime (ühe terve pitsa ja teise kuuenda pitsa).
Pange tähele, et oleme seda näidet liiga üksikasjalikult kirjeldanud. Haridusasutustes pole kombeks nii detailselt kirjutada. Peate suutma kiiresti leida mõlema nimetaja ja nende lisategurite LCM-i, samuti kiiresti korrutama leitud lisategurid lugejate ja nimetajatega. Kui oleksime koolis, peaksime selle näite kirjutama järgmiselt:

Kuid mündil on ka teine külg. Kui te matemaatika õppimise esimestel etappidel üksikasjalikke märkmeid ei tee, hakkavad ilmnema omalaadsed küsimused. “Kust see arv tuleb?”, “Miks muutuvad murrud järsku täiesti erinevateks murdudeks? «.
Erinevate nimetajatega murdude lisamise hõlbustamiseks võite kasutada järgmisi samm-sammulisi juhiseid.
- Leia murdude nimetajate LCM;
- Jagage LCM iga murdosa nimetajaga ja hankige iga murdosa jaoks lisategur;
- Korrutage murdude lugejad ja nimetajad nende lisateguritega;
- Lisa murrud, millel on samad nimetajad;
- Kui vastus osutub valeks murruks, valige selle kogu osa;
Näide 2. Leidke avaldise väärtus  .
.
Kasutame ülaltoodud juhiseid.
Samm 1. Leidke murdude nimetajate LCM
Leidke mõlema murru nimetajate LCM. Murdude nimetajad on numbrid 2, 3 ja 4

2. samm. Jagage LCM iga murdosa nimetajaga ja hankige iga murdosa jaoks lisategur
Jagage LCM esimese murru nimetajaga. LCM on arv 12 ja esimese murru nimetaja on arv 2. Jagage 12 2-ga, saame 6. Saime esimese lisateguri 6. Kirjutame selle esimese murru kohale:
Nüüd jagame LCM-i teise murru nimetajaga. LCM on arv 12 ja teise murru nimetaja on arv 3. Jagage 12 3-ga, saame 4. Saame teise lisateguri 4. Kirjutame selle teise murru kohale:
Nüüd jagame LCM-i kolmanda murru nimetajaga. LCM on arv 12 ja kolmanda murru nimetaja on arv 4. Jagage 12 4-ga, saame 3. Saame kolmanda lisateguri 3. Kirjutame selle kolmanda murru kohale:
Etapp 3. Korrutage murdude lugejad ja nimetajad nende lisateguritega
Korrutame lugejad ja nimetajad nende lisateguritega:
4. samm. Lisage samade nimetajatega murded
Jõudsime järeldusele, et erineva nimetajaga murrud muutusid samade (ühiste) nimetajatega murdudeks. Jääb vaid need murded lisada. Lisage see:

Lisand ei mahtunud ühele reale, nii et teisaldasime ülejäänud avaldise järgmisele reale. See on matemaatikas lubatud. Kui avaldis ühele reale ei mahu, liigutatakse see järgmisele reale ning esimese rea lõppu ja uue rea algusesse on vaja panna võrdusmärk (=). Võrdsusmärk teisel real näitab, et see on esimesel real olnud avaldise jätk.
5. samm. Kui vastus osutub valeks murdarvuks, siis valige kogu selle osa
Meie vastus osutus valeks murdarvuks. Peame esile tõstma terve osa sellest. Toome esile:

Saime vastuse
Sarnaste nimetajatega murdude lahutamine
Murdude lahutamist on kahte tüüpi:
- Sarnaste nimetajatega murdude lahutamine
- Erinevate nimetajatega murdude lahutamine
Esiteks õpime, kuidas lahutada murde sarnaste nimetajatega. Siin on kõik lihtne. Ühest murrust teise lahutamiseks peate esimese murru lugejast lahutama teise murru lugeja, kuid jätma nimetaja samaks.
Näiteks leiame avaldise väärtuse. Selle näite lahendamiseks peate esimese murru lugejast lahutama teise murru lugeja ja jätma nimetaja muutmata. Teeme ära:

Seda näidet on lihtne mõista, kui meenutada pitsat, mis on jagatud neljaks osaks. Kui lõikad pitsast pitsad, saad pitsad:

Näide 2. Leidke avaldise väärtus.
Jällegi lahutage esimese murru lugejast teise murru lugeja ja jätke nimetaja muutmata:

Seda näidet on lihtne mõista, kui meenutame pitsat, mis on jagatud kolmeks osaks. Kui lõikad pitsast pitsad, saad pitsad:

Näide 3. Leidke avaldise väärtus 
See näide on lahendatud täpselt samamoodi nagu eelmised. Esimese murru lugejast tuleb lahutada ülejäänud murdude lugejad:

Nagu näete, pole samade nimetajatega murdude lahutamises midagi keerulist. Piisab, kui mõistad järgmisi reegleid:
- Ühest murrust teise lahutamiseks peate esimese murru lugejast lahutama teise murru lugeja ja jätma nimetaja muutmata;
- Kui vastus osutub valeks murdarvuks, peate esile tõstma kogu selle osa.
Erinevate nimetajatega murdude lahutamine
Näiteks võite murdosast lahutada murdosa, kuna murdudel on samad nimetajad. Kuid te ei saa murdosast murda lahutada, kuna neil murdudel on erinevad nimetajad. Sellistel juhtudel tuleb murded taandada sama (ühise) nimetajani.
Ühine nimetaja leitakse samal põhimõttel, mida kasutasime erinevate nimetajatega murdude liitmisel. Kõigepealt leidke mõlema murru nimetajate LCM. Seejärel jagatakse LCM esimese murru nimetajaga ja saadakse esimene lisategur, mis kirjutatakse esimese murru kohale. Samamoodi jagatakse LCM teise murru nimetajaga ja saadakse teine lisategur, mis kirjutatakse teise murru kohale.
Seejärel korrutatakse fraktsioonid nende lisateguritega. Nende toimingute tulemusena teisendatakse erineva nimetajaga murrud samade nimetajatega murdudeks. Ja me juba teame, kuidas selliseid murde lahutada.
Näide 1. Leidke väljendi tähendus:
Nendel murdudel on erinevad nimetajad, seega peate need taandama samale (ühise) nimetajale.
Kõigepealt leiame mõlema murru nimetajate LCM-i. Esimese murru nimetaja on arv 3 ja teise murru nimetaja on arv 4. Nende arvude vähim ühiskordne on 12
LCM (3 ja 4) = 12
Nüüd pöördume tagasi murdude ja
Leiame esimese murru jaoks lisateguri. Selleks jagage LCM esimese murru nimetajaga. LCM on arv 12 ja esimese murru nimetaja on arv 3. Jagage 12 3-ga, saame 4. Kirjutage esimese murru kohale neli:
Teeme sama teise murdosaga. Jagage LCM teise murru nimetajaga. LCM on arv 12 ja teise murru nimetaja on arv 4. Jagage 12 4-ga, saame 3. Kirjutage teise murru kohale kolm:
Nüüd oleme lahutamiseks valmis. Jääb üle korrutada fraktsioonid nende lisateguritega:

Jõudsime järeldusele, et erineva nimetajaga murrud muutusid samade nimetajatega murdudeks. Ja me juba teame, kuidas selliseid murde lahutada. Toome selle näite lõpuni:

Saime vastuse
Proovime oma lahendust joonise abil kujutada. Kui lõikad pitsast pitsa, saad pizza

See on lahenduse üksikasjalik versioon. Kui oleksime koolis, peaksime selle näite lühemalt lahendama. Selline lahendus näeks välja järgmine:

Murdude taandamist ühisele nimetajale saab kujutada ka pildi abil. Nende murdude taandamisel ühiseks nimetajaks saime murrud ja . Neid murde esindavad samad pitsaviilud, kuid seekord jagatakse need võrdseteks osadeks (vähendatud samale nimetajale):

Esimesel pildil on murdosa (kaheksa tükki kaheteistkümnest) ja teisel pildil murdosa (kolm tükki kaheteistkümnest). Lõikates kaheksast tükist kolm tükki, saame kaheteistkümnest viis tükki. Murd kirjeldab neid viit tükki.
Näide 2. Leidke avaldise väärtus 
Nendel murdudel on erinevad nimetajad, nii et kõigepealt peate need taandama samale (ühisnimetajale).
Leiame nende murdude nimetajate LCM.
Murdude nimetajateks on arvud 10, 3 ja 5. Nende arvude vähim ühiskordne on 30
LCM(10; 3; 5) = 30
Nüüd leiame iga murdosa jaoks täiendavaid tegureid. Selleks jagage LCM iga murdosa nimetajaga.
Leiame esimese murru jaoks lisateguri. LCM on arv 30 ja esimese murru nimetaja on arv 10. Jagage 30 10-ga, saame esimese lisateguri 3. Kirjutame selle esimese murru kohale:
Nüüd leiame teise murru jaoks lisateguri. Jagage LCM teise murru nimetajaga. LCM on arv 30 ja teise murru nimetaja on arv 3. Jagage 30 3-ga, saame teise lisateguri 10. Kirjutame selle teise murru kohale:
Nüüd leiame kolmanda murru jaoks lisateguri. Jagage LCM kolmanda murru nimetajaga. LCM on arv 30 ja kolmanda murru nimetaja on arv 5. Jagage 30 5-ga, saame kolmanda lisateguri 6. Kirjutame selle kolmanda murru kohale:
Nüüd on kõik lahutamiseks valmis. Jääb üle korrutada fraktsioonid nende lisateguritega:
Jõudsime järeldusele, et erineva nimetajaga murrud muutusid samade (ühiste) nimetajatega murdudeks. Ja me juba teame, kuidas selliseid murde lahutada. Lõpetame selle näite.
Näite jätk ei mahu ühele reale, seega liigume jätku järgmisele reale. Ärge unustage uuel real võrdusmärki (=):

Vastuseks osutus tavaline murd ja kõik tundub meile sobivat, kuid see on liiga tülikas ja kole. Peaksime selle lihtsamaks tegema. Mida saaks teha? Saate seda murdosa lühendada.
Murru vähendamiseks peate jagama selle lugeja ja nimetaja (GCD) arvudest 20 ja 30.
Niisiis, leiame numbrite 20 ja 30 gcd:

Nüüd pöördume tagasi oma näite juurde ja jagame murru lugeja ja nimetaja leitud gcd-ga, see tähendab 10-ga

Saime vastuse
Murru korrutamine arvuga
Murru korrutamiseks arvuga peate korrutama antud murdosa lugeja selle arvuga ja jätma nimetaja samaks.
Näide 1. Korrutage murdarvuga 1.
Korrutage murdosa lugeja arvuga 1
![]()
Salvestusest võib aru saada, et võtab pool 1 korda. Näiteks kui võtad pizza üks kord, saad pizza

Korrutamise seadustest teame, et kui korrutis ja tegur vahetada, siis korrutis ei muutu. Kui avaldis on kirjutatud kujul , on korrutis ikkagi võrdne . Jällegi töötab täisarvu ja murdarvu korrutamise reegel:
![]()
Seda tähistust võib mõista nii, et see võtab poole ühest. Näiteks kui on 1 terve pitsa ja me võtame sellest poole, siis saame pitsa:

Näide 2. Leidke avaldise väärtus
Korrutage murdosa lugeja 4-ga
![]()
Vastus oli vale murd. Toome esile kogu selle osa:
![]()
Väljendit võib mõista nii, et see võtab kaks veerandit 4 korda. Näiteks kui võtad 4 pitsat, saad kaks tervet pitsat

Ja kui vahetame kordaja ja kordaja, saame avaldise . See on samuti võrdne 2-ga. Seda väljendit võib mõista nii, et neljast tervest pitsast võetakse kaks pitsat:

Murdude korrutamine
Murdude korrutamiseks peate korrutama nende lugejad ja nimetajad. Kui vastus osutub valeks murdarvuks, peate esile tõstma kogu selle osa.
Näide 1. Leidke avaldise väärtus.
![]()
Saime vastuse. Soovitav on seda osa vähendada. Fraktsiooni saab vähendada 2 võrra. Seejärel saab lõpplahus järgmise kuju:

Väljendit võib mõista kui pizza võtmist poole pitsa pealt. Oletame, et meil on pool pitsat:
Kuidas sellest poolest kaks kolmandikku võtta? Kõigepealt peate selle poole jagama kolmeks võrdseks osaks:

Ja võtke nendest kolmest tükist kaks:

Teeme pitsat. Pidage meeles, kuidas pitsa kolmeks osaks jagatuna välja näeb:

Üks tükk sellest pitsast ja kahel meie võetud tükil on samad mõõtmed:

Teisisõnu, me räägime sama suurusega pitsast. Seetõttu on avaldise väärtus

Näide 2. Leidke avaldise väärtus
Korrutage esimese murru lugeja teise murru lugejaga ja esimese murru nimetaja teise murru nimetajaga:

Vastus oli vale murd. Toome esile kogu selle osa:
![]()
Näide 3. Leidke avaldise väärtus
Korrutage esimese murru lugeja teise murru lugejaga ja esimese murru nimetaja teise murru nimetajaga:
![]()
Vastuseks osutus tavaline murd, aga hea oleks, kui seda lühendaks. Selle murdosa vähendamiseks peate jagama selle murru lugeja ja nimetaja arvude 105 ja 450 suurima ühisjagajaga (GCD).
Niisiis, leiame numbrite 105 ja 450 gcd:

Nüüd jagame oma vastuse lugeja ja nimetaja nüüd leitud gcd-ga, see tähendab 15-ga
Täisarvu esitamine murruna
Mis tahes täisarvu saab esitada murdarvuna. Näiteks numbrit 5 saab esitada kui . See ei muuda viie tähendust, kuna väljend tähendab "arvu viis jagatud ühega" ja see, nagu me teame, võrdub viiega:
Vastastikused numbrid
Nüüd tutvume väga huvitava matemaatika teemaga. Seda nimetatakse "tagurpidi numbriteks".
Definitsioon. Tagurpidi numbrilea on arv, mis korrutatunaa annab ühe.
Asendame selles definitsioonis muutuja asemel a number 5 ja proovige definitsiooni lugeda:
Tagurpidi numbrile 5 on arv, mis korrutatuna 5 annab ühe.
Kas on võimalik leida arvu, mis 5-ga korrutades annab ühe? Selgub, et see on võimalik. Kujutagem ette viit murdosana:
Seejärel korrutage see murdosa iseendaga, vahetage lihtsalt lugeja ja nimetaja. Teisisõnu, korrutame murdosa iseendaga, ainult tagurpidi:
Mis selle tulemusena saab? Kui jätkame selle näite lahendamist, saame ühe:
![]()
See tähendab, et arvu 5 pöördväärtus on arv , sest kui korrutate 5-ga, saate ühe.
Arvu pöördarvu võib leida ka mis tahes muu täisarvu kohta.
Samuti saate leida mis tahes muu murru pöördarvu. Selleks keerake see lihtsalt ümber.
Murru jagamine arvuga
Oletame, et meil on pool pitsat:
Jagame selle kahe vahel võrdselt. Kui palju pizzat iga inimene saab?

Näha on, et peale poole pitsa jagamist saadi kaks võrdset tükki, millest igaüks moodustab pitsa. Nii et igaüks saab pitsa.
Murdude jagamine toimub pöördarvude abil. Vastastikused numbrid võimaldavad asendada jagamise korrutamisega.
Murru jagamiseks arvuga tuleb murdosa korrutada jagaja pöördväärtusega.
Seda reeglit kasutades paneme kirja meie poole pitsa jagamise kaheks osaks.
Seega peate murdosa jagama arvuga 2. Siin on dividend murdosa ja jagaja on arv 2.
Murru jagamiseks arvuga 2 peate selle murdosa korrutama jagaja 2 pöördarvuga. Jagaja 2 pöördarvuks on murd. Nii et peate korrutama
- Korrutame 7 nimetajaga (2), saame 14,
- lisage ülemine osa (1) 14-le, saate 15,
- ja asendage nimetaja.
- tulemus on 15/2.
- Murd on õige, st. lugeja on nimetajast väiksem. Siis saab vastuseks pärast ülesannet saadud segaarv.
- Murd on ebakorrektne, st. lugeja on nimetajast suurem. Siis on vaja veidi teisendada. Vale murd tuleks muuta segaarvuks ehk teisisõnu eraldada kogu osa. Seda tehakse järgmiselt:
Täisarvu lisamiseks murrule piisab toimingute seeria või õigemini arvutuste tegemisest.
Näiteks on teil 7 - täisarv; peate selle lisama murdarvule 1/2.
Toimime järgmiselt:
Sel lihtsal viisil saate lisada murdarvudele täisarvu.
Ja selleks, et eraldada täisarv murdosast, peate jagama lugeja nimetajaga ja ülejäänud osa - ja siis tuleb murdosa.
Täisarvu lisamine õigele harilikule murrule ei ole keeruline ja mõnikord hõlmab lihtsalt segamurru moodustamist, mille käigus täisarvu osa asetatakse murdosast vasakule, näiteks segatakse selline murd:
Enamasti põhjustab aga täisarvu lisamine murrule vale murdosa, mille lugeja on nimetajast suurem. See toiming sooritatakse järgmiselt: täisarv esitatakse valemurruna, mille nimetaja on liidetaval murrul, ja seejärel lisatakse lihtsalt mõlema murru lugejad. Näites näeb see välja järgmine:
5+1/8 = 5*8/8+1/8 = 40/8+1/8 = 41/8
Ma arvan, et see on väga lihtne.
Näiteks on meil murdosa 1/4 (see on sama, mis 0,25, see tähendab veerand täisarvust).
Ja sellele kvartalile saab lisada mis tahes täisarvu, näiteks 3. Saad kolm ja veerand:
3.25. Või murdosa väljendatakse järgmiselt: 3 1/4
Selle näite abil saate lisada mis tahes täisarvuga murde.
Peate tõstma täisarvu murdosani, mille nimetaja on 10 (6/10). Järgmisena viige olemasolev murd ühise nimetajani 10 (35=610). Noh, tehke nii nagu tavaliste murdude 610+610=1210 puhul kokku 12.
Selleks on kaks võimalust.
1). Murru saab teisendada täisarvuks ja liita. Näiteks 1/2 on 0,5; 1/4 võrdub 0,25; 2/5 on 0,4 jne.
Võtke täisarv 5, millele peate lisama murdosa 4/5. Teisendame murdosa: 4/5 on 4 jagatud 5-ga ja saame 0,8. Lisab 0,8 5-le ja saame 5,8 või 5 4/5.
2). Teine meetod: 5 + 4/5 = 29/5 = 5 4/5.
Murdude liitmine on lihtne matemaatiline tehe, näiteks tuleb liita täisarv 3 ja murdosa 1/7. Nende kahe arvu liitmiseks peab teil olema sama nimetaja, seega peate korrutama kolm seitsmega ja jagama selle arvuga, siis saate 21/7+1/7, nimetaja üks, lisage 21 ja 1, saate vastuseks 22/ 7 .
Lihtsalt võtke ja lisage sellele murdarvule täisarv. Oletame, et vajate 6 + 1/2 = 6 1/2. Noh, kui see on kümnendmurd, saate seda teha järgmiselt: 6+1,2=7,2.
Murru ja täisarvu liitmiseks tuleb lisada täisarvule murd ja kirjutada need üles kompleksarvuna, näiteks täisarvuga hariliku murru liitmisel saame: 1/2 +3 = 3 1/ 2; kümnendmurru liitmisel: 0,5 +3 =3,5.
Murd iseenesest ei ole täisarv, sest selle kogus ei ulatu selleni ja seetõttu pole vaja täisarvu selleks murdeks teisendada. Seetõttu jääb täisarv täisarvuks ja demonstreerib täielikult täisväärtust ning sellele lisatakse murdosa, mis näitab, kui palju sellest täisarvust on puudu enne järgmise täispunkti lisamist.
Akadeemiline eeskuju.
10 + 7/3 = 10 tervet ja 7/3.
Kui loomulikult on täisarvud, siis need liidetakse täisarvudega.
12 + 5 7/9 = 17 ja 7/9.
See sõltub sellest, milline täisarv ja milline murdosa.
Kui mõlemad terminid on positiivsed, tuleks see murd lisada täisarvule. Tulemuseks on segaarv. Lisaks võib olla 2 juhtumit.
Juhtum 1.
4/9 + 10 = 10 4/9 (kümme koma neli üheksandikku).

Juhtum 2.

Pärast seda peate lisama täisarvule vale murdosa ja lisama saadud summale selle murdosa. Samamoodi lisatakse segaarvule tervik.
1) 11/4 + 5 = 2 3/4 + 5 = 7 3/4 (7 punkti kolmveerand).
2) 5 1/2 + 6 = 11 1/2 (11 punkti üks).
Kui üks tingimustest või mõlemad negatiivne, siis teostame liitmise vastavalt erinevate või identsete märkidega numbrite liitmise reeglitele. Täisarv esitatakse selle arvu ja 1 suhtena ning seejärel korrutatakse nii lugeja kui ka nimetaja arvuga, mis on võrdne selle murdosa nimetajaga, millele täisarv liidetakse.
3) 1/5 + (-2) = 1/5 + -2/1 = 1/5 + -10/5 = -9/5 = -1 4/5 (miinus 1 punkt neli viiendikku).
4) -13/3 + (-4) = -13/3 + -4/1 = -13/3 + -12/3 = -25/3 = -8 1/3 (miinus 8 punkti üks kolmandik).
Kommenteeri.
Pärast negatiivsete arvudega tutvumist peaksid 6. klassi õpilased nendega tehteid õppides mõistma, et positiivse täisarvu liitmine negatiivsele murdule on sama, mis naturaalarvust murdu lahutamine. Seda toimingut tehakse teadaolevalt järgmiselt:

Tegelikult tuleb murd- ja täisarvu liitmiseks lihtsalt olemasolev täisarv murduks teisendada ja see on sama lihtne kui pirnide koorimine. Peate lihtsalt võtma murdosa nimetaja (näites) ja muutma selle täisarvu nimetajaks, korrutades selle nimetajaga ja jagades. Siin on näide:
2+2/3 = 2*3/3+2/3 = 6/3+2/3 = 8/3
