Looge suhe ja arvutage piirmäär.
Kust see tuli? tuletiste ja diferentseerimisreeglite tabel? Tänu ainsale piirile. See näib olevat maagia, kuid tegelikkuses on see salakavalus ja ei mingit pettust. Õppetunnis Mis on tuletis? Hakkasin vaatama konkreetseid näiteid, kus definitsiooni kasutades leidsin lineaar- ja ruutfunktsiooni tuletised. Kognitiivse soojenduse eesmärgil jätkame häirimist tuletisinstrumentide tabel, lihvides algoritmi ja tehnilisi lahendusi:
Näide 1
Sisuliselt peate tõestama astmefunktsiooni tuletise erijuhtumit, mis tavaliselt kuvatakse tabelis: .
Lahendus tehniliselt vormistatud kahel viisil. Alustame esimese, juba tuttava lähenemisega: redel algab plangiga ja tuletisfunktsioon algab punktis tuletisega.
Mõelgem mõned(konkreetne) punkt kuuluv määratlusvaldkond funktsioon, milles on tuletis. Määrame siinkohal juurdekasvu (muidugi ulatuse piireso/o
- mina) ja koostage funktsiooni vastav samm:
Arvutame limiidi:
Ebakindlus 0:0 kõrvaldatakse standardtehnikaga, mida peetakse tagasi esimesel sajandil eKr. Korrutage lugeja ja nimetaja konjugaadi avaldisega 
:
Sellise piiri lahendamise tehnikat käsitletakse üksikasjalikult sissejuhatavas tunnis. funktsioonide piiride kohta.
Kuna kvaliteediks saate valida MIS TAHES intervalli punkti, siis pärast asendamist saame:
Vastus
Rõõmustagem veel kord logaritmide üle:
Näide 2
Leia funktsiooni tuletis tuletise definitsiooni abil
Lahendus: Vaatame sama ülesande edendamiseks teistsugust lähenemist. See on täpselt sama, kuid disaini poolest ratsionaalsem. Idee on lahenduse alguses olevast alamindeksist lahti saada ja kasutada tähe asemel tähte.
Mõelgem meelevaldne punkt, mis kuulub määratlusvaldkond funktsioon (intervall) ja määra selle juurdekasv. Kuid siin, muide, nagu enamikul juhtudel, saate teha ilma reservatsioonideta, kuna logaritmiline funktsioon on definitsioonipiirkonna mis tahes punktis diferentseeritav.
Siis on funktsiooni vastav juurdekasv:
Leiame tuletise:
Disaini lihtsust tasakaalustab segadus, mis võib algajatel (ja mitte ainult) tekkida. Oleme ju harjunud, et täht “X” limiidis muutub! Kuid siin on kõik teisiti: - antiikkuju ja - elav külaline, kes sammub reipalt mööda muuseumi koridori. See tähendab, et "x" on "nagu konstant".
Kommenteerin määramatuse kõrvaldamist samm-sammult:
(1) Kasutame logaritmi omadust.
(2) Sulgudes jagage lugeja nimetaja liikmega.
(3) Nimetajas me kunstlikult korrutame ja jagame x-ga, et seda ära kasutada tähelepanuväärne piir 
, samas kui as lõpmatult väike paistab silma.
Vastus: tuletise määratluse järgi:
Või lühidalt:
Teen ettepaneku ise koostada veel kaks tabelivalemit:
Näide 3
Sel juhul on mugav koostatud juurdekasvu koheselt ühise nimetajani taandada. Ülesande ligikaudne näidis tunni lõpus (esimene meetod).
Näide 3:Lahendus
: kaaluge mõnda punkti
, mis kuulub funktsiooni määratluspiirkonda
. Määrame siinkohal juurdekasvu
ja koostage funktsiooni vastav samm:
Leiame tuletise punktist
:
Kuna kui a
saate valida mis tahes punkti
funktsiooni domeen
, See
Ja
Vastus
:
tuletise määratluse järgi
Näide 4
Leia tuletis definitsiooni järgi
Ja siin tuleb kõike taandada imeline piir. Lahendus vormistatakse teisel viisil.
Hulk muid tabelituletised. Täieliku nimekirja leiab kooliõpikust või näiteks Fichtenholtzi 1. köitest. Ma ei näe erilist mõtet diferentseerimisreeglite tõendite kopeerimisel raamatutest – need genereeritakse samuti valemiga.
Näide 4:Lahendus
, mis kuulub
ja määrake selle juurdekasv
Leiame tuletise:
Kasutades imelist piiri
Vastus
:
a-prioor
Näide 5
Leia funktsiooni tuletis tuletise definitsiooni abil
Lahendus: kasutame esimest kujundusstiili. Vaatleme mõnda punkti, mis kuulub , ja täpsustame argumendi juurdekasvu selles. Siis on funktsiooni vastav juurdekasv:
Võib-olla pole mõned lugejad veel täielikult mõistnud põhimõtet, mille järgi tuleb juurdekasvu teha. Võtke punkt (arv) ja leidke selles funktsiooni väärtus: 
, see tähendab funktsiooni selle asemel"X" tuleks asendada. Nüüd võtame ka väga konkreetse arvu ja asendame selle funktsiooniga selle asemel"iksa": . Paneme erinevuse kirja ja see on vajalik pane täielikult sulgudesse.
Kompileeritud funktsiooni juurdekasv Võib olla kasulik kohe lihtsustada. Milleks? Hõlbustada ja lühendada lahendust täiendava piirini.
Kasutame valemeid, avame sulud ja vähendame kõike, mida saab vähendada: 
Kalkun on roogitud, praega pole probleeme:
Kuna saame väärtuseks valida mis tahes reaalarvu, teeme asendus ja saame 
.
Vastus: a-prioor.
Kontrollimiseks leiame tuletise kasutades diferentseerimisreeglid ja tabelid:
Õiget vastust on alati kasulik ja meeldiv ette teada, seega on parem pakutud funktsioon "kiirelt" eristada, kas mõtteliselt või mustandis, kohe lahenduse alguses.
Näide 6
Leia funktsiooni tuletis tuletise definitsiooni järgi
See on näide, mille saate ise lahendada. Tulemus on ilmne:
Näide 6:Lahendus
: kaaluge mõnda punkti
, mis kuulub
ja määrake selles sisalduva argumendi juurdekasv
. Siis on funktsiooni vastav juurdekasv:
Arvutame tuletise:
Seega: 
Sest nagu
siis saate valida mis tahes reaalarvu
Ja
Vastus
:
a-prioor.
Läheme tagasi stiili nr 2 juurde:
Näide 7
Uurime kohe, mis juhtuma peaks. Kõrval keeruliste funktsioonide diferentseerimise reegel:
Lahendus: vaatleme suvalist punkti, mis kuulub punktile , määrake sellele argumendi juurdekasv ja koostage funktsiooni juurdekasv:
Leiame tuletise: 
(1) Kasutamine trigonomeetriline valem 
.
(2) Siinuse all avame sulud, koosinuse all esitame sarnased terminid.
(3) Siinuse all taandame liikmeid, koosinuse all jagame lugeja nimetaja liikmega.
(4) Siinuse veidruse tõttu võtame “miinuse” välja. Koosinuse all märgime, et termin .
(5) Kasutamiseks teostame nimetajas kunstlikku korrutamist esimene imeline piir. Seega on ebakindlus kõrvaldatud, teeme tulemuse korda.
Vastus: a-prioor
Nagu näete, seisneb vaadeldava probleemi põhiraskus limiidi enda keerukuses + pakendi kerges unikaalsuses. Praktikas kasutatakse mõlemat disainimeetodit, seega kirjeldan mõlemat lähenemist võimalikult üksikasjalikult. Need on samaväärsed, kuid minu subjektiivse mulje järgi on mannekeenidel soovitatavam jääda valiku 1 juurde, kus on “X-null”.
Näide 8
Definitsiooni kasutades leidke funktsiooni tuletis
Näide 8:Lahendus
: kaaluge suvalist punkti
, mis kuulub
, määrake selle juurdekasv
ja koostage funktsiooni juurdekasv:
Leiame tuletise:
Kasutame trigonomeetrilist valemit
ja esimene tähelepanuväärne piir:
Vastus
:
a-prioor
Vaatame probleemi haruldasemat versiooni:
Näide 9
Leia funktsiooni tuletis punktis, kasutades tuletise definitsiooni.
Esiteks, mis peaks olema lõpptulemus? Number
Arvutame vastuse standardsel viisil: 
Lahendus: selguse seisukohalt on see ülesanne palju lihtsam, kuna valem arvestab selle asemel konkreetset väärtust.
Määrame punkti juurdekasvu ja koostame vastava funktsiooni juurdekasvu:
Arvutame tuletise punktis:
Kasutame väga haruldast puutuja erinevuse valemit 
ja veel kord taandame lahenduse esimene imeline piir:
Vastus: tuletise määratluse järgi punktis.
Probleemi pole nii keeruline "üldiselt" lahendada - piisab, kui asendada või lihtsalt sõltuvalt disainimeetodist. Sel juhul on selge, et tulemus ei ole arv, vaid tuletatud funktsioon.
Näide 10
Definitsiooni kasutades leidke funktsiooni tuletis 
punktis (millest üks võib osutuda lõpmatuks), mida olen juba üldiselt kirjeldanud teoreetiline tund tuletise kohta.
Mõned tükkhaaval antud funktsioonid on diferentseeruvad ka graafiku “ristmike” punktides, näiteks on catdogil punktis ühine tuletis ja ühine puutuja (x-telg). Kõver, kuid eristatav ! Huvilised saavad selles äsja lahendatud näite abil ise veenduda.
©2015-2019 sait
Kõik õigused kuuluvad nende autoritele. See sait ei pretendeeri autorlusele, kuid pakub tasuta kasutamist.
Lehe loomise kuupäev: 2017-06-11
Artikli sisu
DERIVAAT– funktsiooni tuletis y = f(x), antud teatud intervalliga ( a, b) punktis x Seda intervalli nimetatakse piiriks, milleni funktsiooni juurdekasvu suhe kaldub f siinkohal argumendi vastavale juurdekasvule, kui argumendi juurdekasv kipub olema null.
Tuletis on tavaliselt tähistatud järgmiselt:
Laialdaselt kasutatakse ka muid nimetusi:
Vahetu kiirus.
Olgu punkt M liigub sirgjooneliselt. Kaugus s liikuv punkt, mis loetakse mingist algasendist M 0 , oleneb ajast t, st. s on aja funktsioon t: s= f(t). Lase mingil ajahetkel t liikuv punkt M oli eemal s algasendist M 0 ja mõnel järgmisel hetkel t+D t leidis end olukorrast M 1 - distantsil s+D s algsest positsioonist ( vaata pilti.).
Seega teatud aja jooksul D t vahemaa s muudetud summa D võrra s. Sel juhul ütlevad nad, et ajaintervalli D jooksul t suurusjärk s sai juurdekasvu D s.
Keskmine kiirus ei saa kõigil juhtudel täpselt iseloomustada punkti liikumiskiirust M teatud ajahetkel t. Kui näiteks keha intervalli D alguses t liikus väga kiiresti ja lõpus väga aeglaselt, siis ei suuda keskmine kiirus peegeldada punkti liikumise näidatud tunnuseid ja anda aimu selle tegelikust liikumise kiirusest hetkel t. Tegeliku kiiruse täpsemaks väljendamiseks keskmise kiiruse abil peate võtma lühema ajaperioodi D t. Kõige täielikumalt iseloomustab punkti liikumiskiirust hetkel t piir, milleni keskmine kiirus D-s kaldub t® 0. Seda piirangut nimetatakse praeguseks kiiruseks:
Seega nimetatakse liikumiskiirust antud hetkel tee juurdekasvu suhte D piiriks s aja juurdekasvuks D t, kui ajakasv kipub olema null. Sest
Tuletise geomeetriline tähendus. Funktsiooni graafiku puutuja.
Puutujate konstrueerimine on üks neist probleemidest, mis viis diferentsiaalarvutuse sünnini. Esimene avaldatud Leibnizi diferentsiaalarvutusega seotud töö kandis pealkirja Uus maksimumide ja miinimumide ning puutujate meetod, mille puhul ei ole takistuseks murd- ega irratsionaalsed suurused, ning selle jaoks spetsiaalne arvutus.
Olgu kõver funktsiooni graafik y =f(x) ristkülikukujulises koordinaatsüsteemis ( cm. riis.).
Mingil väärtusel x funktsioon on oluline y =f(x). Need väärtused x Ja y kõvera punkt vastab M 0(x, y). Kui argument x anda juurdekasv D x, siis argumendi uus väärtus x+D x vastab uuele funktsiooni väärtusele y+ D y = f(x + D x). Kõvera vastav punkt on punkt M 1(x+D x,y+D y). Kui joonistad sekanti M 0M 1 ja tähistatud j-ga nurk, mille moodustab põik telje positiivse suunaga Ox, on jooniselt kohe selge, et .
Kui nüüd D x kipub nulli, siis punkt M 1 liigub mööda kõverat, lähenedes punktile M 0 ja nurk j muutub D-ga x. Kell Dx® 0 kaldub nurk j teatud piirini a ja punkti läbiv sirge M 0 ja x-telje positiivse suunaga komponent, nurk a, on soovitud puutuja. Selle kalle on:
Seega f´( x) = tga
need. tuletisväärtus f´( x) antud argumendi väärtuse jaoks x võrdub funktsiooni graafiku puutuja poolt moodustatud nurga puutujaga f(x) vastavas punktis M 0(x,y) positiivse telje suunaga Ox.
Funktsioonide eristatavus.
Definitsioon. Kui funktsioon y = f(x) on punktis tuletis x = x 0, siis on funktsioon selles punktis diferentseeritav.
Tuletist omava funktsiooni pidevus. Teoreem.
Kui funktsioon y = f(x) on mingil hetkel eristatav x = x 0, siis on see selles punktis pidev.
Seega ei saa funktsioonil olla tuletist katkestuspunktides. Vastupidine järeldus on vale, s.t. sellest, et mingil hetkel x = x 0 funktsioon y = f(x) on pidev, ei tähenda, et see on selles punktis diferentseeritav. Näiteks funktsioon y = |x| jätkuv kõigile x(–Ґ x x = 0 ei oma tuletist. Siinkohal pole graafikul puutujat. On parem- ja vasak puutuja, kuid need ei lange kokku.
Mõned teoreemid diferentseeruvate funktsioonide kohta. Teoreem tuletise juurtest (Rolle teoreem). Kui funktsioon f(x) on lõigul pidev [a,b], on selle segmendi kõigis sisemistes punktides ja otstes eristatav x = a Ja x = b läheb nulli ( f(a) = f(b) = 0), siis segmendi [ a,b] on vähemalt üks punkt x= Koos, a c b, milles tuletis fў( x) läheb nulli, st. fў( c) = 0.
Lõpliku juurdekasvu teoreem (Lagrange'i teoreem). Kui funktsioon f(x) on pidev intervallil [ a, b] ja on eristatav selle segmendi kõigis sisemistes punktides, seejärel segmendi sees [ a, b] on vähemalt üks punkt Koos, a c b see
f(b) – f(a) = fў( c)(b– a).
Teoreem kahe funktsiooni juurdekasvu suhte kohta (Cauchy teoreem). Kui f(x) Ja g(x) – segmendil kaks pidevat funktsiooni [a, b] ja diferentseeruvad selle segmendi kõigis sisemistes punktides ja gў( x) ei kao kuhugi selle segmendi sees, siis segmendi sees [ a, b] on selline punkt x = Koos, a c b see
Erinevate tellimuste tuletised.
Laske funktsioonil y =f(x) on mõnel intervallil diferentseeruv [ a, b]. Tuletisväärtused f ў( x), sõltuvad üldiselt x, st. tuletis f ў( x) on ka funktsioon x. Selle funktsiooni eristamisel saame funktsiooni nn teise tuletise f(x), mis on tähistatud f ўў ( x).
Tuletis n- funktsiooni järjekord f(x) nimetatakse tuletise (esimest järku) tuletiseks n- 1- th ja seda tähistatakse sümboliga y(n) = (y(n– 1))ў.
Erinevate tellimuste diferentsiaalid.
Funktsioonide diferentsiaal y = f(x), Kus x– sõltumatu muutuja, jah dy = f ў( x)dx, mõni funktsioon x, aga alates x sõltuda võib ainult esimene tegur f ў( x), teine tegur ( dx) on sõltumatu muutuja juurdekasv x ja ei sõltu selle muutuja väärtusest. Sest dy on funktsioon alates x, siis saame määrata selle funktsiooni diferentsiaali. Funktsiooni diferentsiaali diferentsiaali nimetatakse selle funktsiooni teist diferentsiaaliks või teist järku diferentsiaaliks ja seda tähistatakse d 2y:
d(dx) = d 2y = f ўў( x)(dx) 2 .
Diferentsiaal n- esimest järku nimetatakse diferentsiaali esimeseks diferentsiaaliks n- 1- järjekord:
d n a = d(dn–1y) = f(n)(x)dx(n).
Osaline tuletis.
Kui funktsioon ei sõltu mitte ühest, vaid mitmest argumendist x i(i varieerub vahemikus 1 kuni n,i= 1, 2,… n),f(x 1,x 2,… x n), siis võetakse diferentsiaalarvutuses kasutusele osatuletise mõiste, mis iseloomustab mitme muutuja funktsiooni muutumise kiirust, kui muutub näiteks ainult üks argument, x i. 1. järku osatuletis suhtes x i on defineeritud kui tavaline tuletis ja eeldatakse, et kõik argumendid v.a x i, hoidke püsivaid väärtusi. Osatuletiste puhul võetakse kasutusele tähistus
Sel viisil defineeritud 1. järku osatuletistel (samade argumentide funktsioonidena) võivad omakorda olla ka osatuletised, need on teist järku osatuletised jne. Selliseid erinevatest argumentidest võetud tuletisi nimetatakse segateks. Sama järku pidevad segatuletised ei sõltu diferentseerumisjärjekorrast ja on omavahel võrdsed.
Anna Chugainova
Olgu funktsioon y = f(x) defineeritud intervallis X. Tuletis funktsiooni y = f(x) punktis x o nimetatakse piiriks
=
.
Kui see piir piiratud, siis kutsutakse funktsioon f(x). eristatav punktis x o; Pealegi osutub see sel hetkel tingimata pidevaks.
Kui vaadeldav piirväärtus on võrdne (või - ), siis eeldusel, et funktsioon punktis X o on pidev, siis ütleme, et funktsioonil f(x) on punkt X o lõpmatu tuletis.
Tuletist tähistatakse sümbolitega
y , f (x o), , .
Tuletise leidmist nimetatakse eristamist funktsioonid. Tuletise geomeetriline tähendus tuletis on kõvera y=f(x) puutuja kalle antud punktis X o ; füüsiline tähendus - on see, et tee tuletis aja suhtes on liikuva punkti hetkkiirus sirgjoonelise liikumise ajal s = s(t) hetkel t o .
Kui Koos on konstantne arv ja u = u(x), v = v(x) on mõned diferentseeruvad funktsioonid, siis kehtivad järgmised diferentseerimisreeglid:
1) (c) " = 0, (cu) " = cu";
2) (u+v)" = u"+v";
3) (uv)" = u"v+v"u;
4) (u/v)" = (u"v-v"u)/v 2;
5) kui y = f(u), u = (x), s.o. y = f((x)) - keeruline funktsioon või superpositsioon, mis koosneb diferentseeruvatest funktsioonidest ja f, siis , või
6) kui funktsiooni y = f(x) korral on pöördvõrdeline diferentseeruv funktsioon x = g(y) ja 0, siis .
Tuletise definitsiooni ja diferentseerimisreeglite põhjal on võimalik koostada põhiliste elementaarfunktsioonide tabelituletisi loetelu.
1. (u )" = u 1 u" ( R).
2. (a u)" = a u lna u".
3. (e u)" = e u u".
4. (log a u)" = u"/(u ln a).
5. (ln u)" = u"/u.
6. (sin u)" = cos u u".
7. (cos u)" = - sin u u".
8. (tg u)" = 1/ cos 2 u u".
9. (ctg u)" = - u" / sin 2 u.
10. (arcsin u)" = u" / .
11. (arccos u)" = - u" / .
12. (arctg u)" = u"/(1 + u 2).
13. (arcctg u)" = - u"/(1 + u 2).
Arvutame astmeeksponentsiaalse avaldise y=u v , (u>0) tuletise, kus u Ja v funktsiooni olemus alates X, millel on antud punktis tuletised sina",v".
Võttes võrrandi y=u v logaritmid, saame ln y = v ln u.
Tuletiste võrdsustamine suhtes X saadud võrdsuse mõlemalt küljelt, kasutades reegleid 3, 5 ja logaritmilise funktsiooni tuletise valemit, saame:
y"/y = vu"/u +v" ln u, kust y" = y (vu"/u +v" ln u).
(u v)"=u v (vu"/u+v" ln u), u > 0.
Näiteks kui y = x sin x, siis y" = x sin x (sin x/x + cos x ln x).
Kui funktsioon y = f(x) on punktis diferentseeruv x, st. on selles punktis lõplik tuletis y", siis = y"+, kus 0 juures х 0; seega y = y" х + x.
Funktsiooni juurdekasvu põhiosa, lineaarne x suhtes, nimetatakse diferentsiaal funktsioonid ja seda tähistatakse dy-ga: dy = y" х. Kui paneme sellesse valemisse y=x, saame dx = x"х = 1х =х, seega dy=y"dx, st sümbol for Tuletise tähistust võib pidada murdarvuks.
Funktsiooni juurdekasv y on kõvera ordinaadi juurdekasv ja diferentsiaal d y on puutuja ordinaatne juurdekasv.
Leiame funktsiooni y=f(x) jaoks selle tuletise y = f (x). Selle tuletise tuletist nimetatakse teist järku tuletis funktsioonid f(x), või teine tuletis, ja on määratud 
.
Järgmised on määratletud ja tähistatud samal viisil:
kolmandat järku tuletis
-
,
neljandat järku tuletis -
ja üldiselt n-ndat järku tuletis
-
.
Näide 3.15. Arvutage funktsiooni y=(3x 3 -2x+1)sin x tuletis.
Lahendus. Reegli 3 järgi y"=(3x 3 -2x+1)"sin x + (3x 3 -2x+1)(sin x)" = = (9x 2 -2)sin x + (3x 3 -2x +1)cos x.
Näide 3.16 . Leidke y", y = tan x + .
Lahendus. Kasutades summa ja jagatise eristamise reegleid, saame: y"=(tgx + )" = (tgx)" + ()" = + 
=
.
Näide 3.17. Leidke kompleksfunktsiooni y= , u=x 4 +1 tuletis.
Lahendus. Kompleksfunktsiooni diferentseerimise reegli järgi saame: y" x =y " u u" x =()" u (x 4 +1)" x =(2u +. Kuna u=x 4 +1, siis (2 x 4 + 2+ 
.
Tuletis on matemaatilise analüüsi kõige olulisem mõiste. See iseloomustab argumendi funktsiooni muutumist x mingil hetkel. Pealegi on tuletis ise argumendi funktsioon x
Funktsiooni tuletis punktis on funktsiooni ja argumendi juurdekasvu suhte piir (kui see on olemas ja on lõplik), eeldusel, et viimane kipub olema null.
Kõige sagedamini kasutatavad on järgmised tuletismärkimine :
Näide 1. Kasu lõikama tuletise määratlus, leidke funktsiooni tuletis
Lahendus. Tuletise definitsioonist tuleneb selle arvutamiseks järgmine skeem.
Anname argumendile juurdekasvu (delta) ja leiame funktsiooni juurdekasvu:
Leiame funktsiooni juurdekasvu ja argumendi juurdekasvu suhte:
Arvutame selle suhte piiri eeldusel, et argumendi juurdekasv kipub nulli, st ülesande avalduses nõutud tuletis:
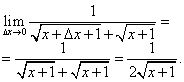
Tuletise füüsiline tähendus
TO tuletise mõiste viis Galileo Galilei uurimuseni kehade vaba langemise seadusest ja laiemas mõttes – punkti ebaühtlase sirgjoonelise liikumise hetkekiiruse probleemist.
Lase kivikesel üles tõsta ja seejärel puhkeseisundist vabastada. Tee s ajas läbitud t, on aja funktsioon, see tähendab. s = s(t). Kui punkti liikumisseadus on antud, saab määrata mis tahes ajavahemiku keskmise kiiruse. Laske sellel hetkel olla kivikeses asendis A, ja hetkel - asendis B. Teatud aja jooksul (alates t punkt on läbinud tee . Seetõttu on selle ajaperioodi keskmine liikumiskiirus, mida tähistame , on
.
Vabalt langeva keha liikumine on aga selgelt ebaühtlane. Kiirus v sügis kasvab pidevalt. Ja keskmisest kiirusest ei piisa enam erinevatel marsruudilõikudel liikumiskiiruse iseloomustamiseks. Mida lühem on ajavahemik, seda täpsem on see omadus. Seetõttu võetakse kasutusele järgmine mõiste: sirgjoonelise liikumise hetkekiirus (või kiirus antud ajahetkel t) nimetatakse keskmiseks kiiruspiiranguks:
(eeldusel, et see piir on olemas ja on piiratud).
Seega selgub, et hetkekiirus on funktsiooni juurdekasvu suhte piir s(t) argumendi juurdekasvuni t at See on tuletis, mis üldkujul on kirjutatud järgmiselt:.
.
Näidatud probleemi lahendus on tuletise füüsiline tähendus . Niisiis, funktsiooni tuletis y=f(x) punktis x nimetatakse funktsiooni juurdekasvu piiriks (kui see on olemas ja on lõplik) argumendi juurdekasvuni, eeldusel, et viimane kaldub nullini.
Näide 2. Leia funktsiooni tuletis
Lahendus. Tuletise definitsioonist tuleneb selle arvutamise järgmine skeem.
1. samm. Suurendame argumenti ja leiame
2. samm. Leidke funktsiooni juurdekasv:
3. samm. Leidke funktsiooni ja argumendi juurdekasvu suhe:
4. samm. Arvutage selle suhte piirväärtus , st tuletis:
Tuletise geomeetriline tähendus
Olgu funktsioon defineeritud intervallil ja punkt M funktsiooni graafikul vastab argumendi väärtusele ja punktile R- tähendus. Joonistame punktid läbi M Ja R sirge joon ja helistage sellele sekant. Tähistagem sekandi ja telje vahelise nurgaga. Ilmselt sõltub see nurk sellest.
Kui on olemas
punkti läbimist nimetatakse sekandi piirasendiks HÄRRA kell (või kell ).
Funktsiooni graafiku puutuja punktis M nimetatakse sekandi piirpositsiooniks HÄRRA, või, mis on sama aadressil .
Definitsioonist järeldub, et puutuja olemasoluks piisab piiri olemasolust
,
ja piir on võrdne telje puutuja kaldenurgaga.
Nüüd anname puutuja täpse definitsiooni.
Tangent funktsiooni graafikule punktis on punkti läbiv sirge, millel on kalle, s.t. sirge, mille võrrand
Sellest määratlusest järeldub, et funktsiooni tuletis on võrdne selle funktsiooni graafiku puutuja kaldega punktis, kus on abstsiss x. See on tuletise geomeetriline tähendus.