7.1. Ristkorrutise määratlus
Kolm mittetasatasandilist vektorit a, b ja c, mis on võetud näidatud järjekorras, moodustavad parempoolse kolmiku, kui kolmanda vektori c lõpust on näha lühim pööre esimesest vektorist a teise vektorisse b. olema vastupäeva ja vasakukäeline kolmik, kui päripäeva (vt joonis . 16).
Vektorite a ja vektori b vektorkorrutist nimetatakse vektoriks c, mis:
1. Risti vektoritega a ja b, st c ^ a ja c ^ b ;
2. Selle pikkus on arvuliselt võrdne vektoritele a ja konstrueeritud rööpküliku pindalagab nagu külgedel (vt joon. 17), st.
3. Vektorid a, b ja c moodustavad paremakäelise kolmiku.


Ristkorrutist tähistatakse a x b või [a,b]. Järgmised seosed ühikvektorite i vahel tulenevad otseselt vektorkorrutise definitsioonist, j Ja k(vt joonis 18):
i x j = k, j x k = i, k x i = j.
Tõestame seda näiteks i xj =k.
1) k ^ i, k ^ j ;
2) |k |=1, kuid | i x j| = |i | |J | sin(90°)=1;
3) vektorid i, j ja k moodustavad parempoolse kolmiku (vt joon. 16).
7.2. Ristkorrutise omadused
1. Faktorite ümberkorraldamisel muudab vektorkorrutis märki, s.o. ja xb =(b xa) (vt joonis 19).
Vektorid a xb ja b xa on kollineaarsed, neil on samad moodulid (rööpküliku pindala jääb muutumatuks), kuid on vastupidise suunaga (vastupidise orientatsiooni kolmikud a, b, a xb ja a, b, b x a). See on axb = -(b xa).
2. Vektorkorrutisel on skalaarteguri suhtes kombineeriv omadus, st l (a xb) = (l a) x b = a x (l b).

Olgu l >0. Vektor l (a xb) on risti vektoritega a ja b. Vektor ( l a)x b on samuti risti vektoritega a ja b(vektorid a, l kuid lebavad samas tasapinnas). See tähendab, et vektorid l(a xb) ja ( l a)x b kollineaarne. On ilmne, et nende suunad langevad kokku. Neil on sama pikkus:
Sellepärast l(a xb)= l a xb. Seda tõestatakse sarnasel viisil l<0.
3. Kaks nullist erinevat vektorit a ja b on kollineaarsed siis ja ainult siis, kui nende vektorkorrutis on võrdne nullvektoriga, st a ||b<=>ja xb = 0.

Täpsemalt i *i =j *j =k *k =0 .
4. Vektorkorrutisel on jaotusomadus:
(a+b) xc = a xc + b xs.
Võtame vastu ilma tõenditeta.
7.3. Ristkorrutise väljendamine koordinaatidena
Kasutame vektorite i ristkorrutistabelit, j ja k:

kui lühima tee suund esimesest vektorist teise kattub noole suunaga, siis on korrutis võrdne kolmanda vektoriga, kui see ei lange kokku, võetakse kolmas vektor miinusmärgiga.
Olgu antud kaks vektorit a =a x i +a y j+a z k ja b = b x i+b a j+b z k. Leiame nende vektorite vektorkorrutise, korrutades need polünoomidena (vastavalt vektorkorrutise omadustele):

![]()
Saadud valemi saab kirjutada veelgi lühidalt:

kuna võrdsuse (7.1) parem pool vastab kolmandat järku determinandi laiendusele esimese rea elementide osas Võrdsust (7.2) on lihtne meelde jätta.
7.4. Mõned risttoote rakendused
Vektorite kollineaarsuse tuvastamine

Rööpküliku ja kolmnurga pindala leidmine
Vastavalt vektorite vektorkorrutisele A ja b |a xb | =|a | * |b |sin g, st S paari = |a x b |. Ja seetõttu D S =1/2|a x b |.
Punkti suhtes mõjuva jõumomendi määramine
Punkti A rakendatakse jõudu F = AB lase sel minna KOHTA- mingi punkt ruumis (vt joonis 20).

Füüsikast on teada, et jõumoment F punkti suhtes KOHTA nimetatakse vektoriks M, mis läbib punkti KOHTA Ja:
1) risti punkte läbiva tasapinnaga O, A, B;
2) arvuliselt võrdne jõu korrutisega käe kohta
3) moodustab parempoolse kolmiku vektoritega OA ja A B.
Seetõttu M = OA x F.
Lineaarse pöörlemiskiiruse leidmine
Kiirus v nurkkiirusega pöörleva jäiga keha punkt M wümber fikseeritud telje, määratakse Euleri valemiga v =w xr, kus r =OM, kus O on telje mingi fikseeritud punkt (vt joonis 21).

Enne vektorkorrutise mõiste andmist pöördugem vektorite a →, b →, c → järjestatud kolmiku orientatsiooni küsimuse juurde kolmemõõtmelises ruumis.
Alustuseks paneme ühest punktist kõrvale vektorid a → , b → , c →. Kolmiku a → , b → , c → orientatsioon võib olla parem- või vasakpoolne, olenevalt vektori c → enda suunast. Kolmiku a → , b → , c → tüüp määratakse selle järgi, millises suunas tehakse lühim pööre vektorist a → punkti b → vektori c → lõpust.
Kui sooritada lühim pööre vastupäeva, siis vektorite kolmik a → , b → , c → nimetatakse õige, kui päripäeva – vasakule.
Järgmiseks võtame kaks mittekollineaarset vektorit a → ja b →. Joonistame siis vektorid A B → = a → ja A C → = b → punktist A. Koostame vektori A D → = c →, mis on samaaegselt risti nii A B → kui ka A C →. Seega saame vektori enda A D → = c → koostamisel teha kahte asja, andes sellele kas ühe suuna või vastupidi (vt joonist).

Vektorite järjestatud kolmik a → , b → , c → võib, nagu saime teada, olenevalt vektori suunast olla parem- või vasakpoolne.
Ülaltoodust saame tutvustada vektorkorrutise definitsiooni. See määratlus on antud kahe vektori jaoks, mis on määratletud kolmemõõtmelise ruumi ristkülikukujulises koordinaatsüsteemis.
Definitsioon 1
Kahe vektori a → ja b → vektorkorrutis me nimetame sellist vektorit, mis on määratletud kolmemõõtmelise ruumi ristkülikukujulises koordinaatsüsteemis, nii et:
- kui vektorid a → ja b → on kollineaarsed, on see null;
- see on risti nii vektori a → kui ka vektori b → suhtes, st. ∠ a → c → = ∠ b → c → = π 2 ;
- selle pikkus määratakse valemiga: c → = a → · b → · sin ∠ a → , b → ;
- vektorite kolmik a → , b → , c → on sama orientatsiooniga kui antud koordinaatsüsteem.
Vektorite a → ja b → vektorkorrutis on järgmise tähistusega: a → × b →.
Vektorkorrutise koordinaadid
Kuna igal vektoril on koordinaatide süsteemis teatud koordinaadid, saame kasutusele võtta teise vektori korrutise definitsiooni, mis võimaldab leida selle koordinaadid vektorite antud koordinaatide abil.
2. definitsioon
Kolmemõõtmelise ruumi ristkülikukujulises koordinaatsüsteemis kahe vektori a → = (a x ; a y ; a z) ja b → = (b x ; b y ; b z) vektorkorrutis nimetatakse vektoriks c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , kus i → , j → , k → on koordinaatvektorid.
Vektorkorrutist saab esitada kolmandat järku ruutmaatriksi determinandina, kus esimene rida sisaldab vektorvektorid i → , j → , k → , teine rida sisaldab vektori a → koordinaate ja kolmas rida. sisaldab vektori b → koordinaate antud ristkülikukujulises koordinaatsüsteemis, maatriksi determinant näeb välja selline: c → = a → × b → = i → j → k → a x a y a z b x b y b z
Laiendades selle determinandi esimese rea elementidele, saame võrdsuse: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → - a x a z b x b z · j → + a = a · y b x b → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →
Ristkorrutise omadused
Teada on, et vektorkorrutis koordinaatides esitatakse maatriksi determinandina c → = a → × b → = i → j → k → a x a y a z b x b y b z , siis alusel maatriksdeterminandi omadused kuvatakse järgmised vektorprodukti omadused:
- antikommutatiivsus a → × b → = - b → × a → ;
- jaotus a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → või a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
- assotsiatiivsus λ a → × b → = λ a → × b → või a → × (λ b →) = λ a → × b →, kus λ on suvaline reaalarv.
Nendel omadustel on lihtsad tõendid.
Näitena saame tõestada vektorkorrutise antikommutatiivse omaduse.
Antikommutatiivsuse tõend
Definitsiooni järgi a → × b → = i → j → k → a x a y a z b x b y b z ja b → × a → = i → j → k → b x b y b z a x a y a z . Ja kui maatriksi kaks rida vahetatakse, peaks maatriksi determinandi väärtus muutuma vastupidiseks, seetõttu a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , mis ja tõestab, et vektorkorrutis on antikommutatiivne.
Vektortoode – näited ja lahendused
Enamasti on probleeme kolme tüüpi.
Esimest tüüpi ülesannetes on tavaliselt antud kahe vektori pikkused ja nendevaheline nurk ning tuleb leida vektorkorrutise pikkus. Sel juhul kasutage järgmist valemit c → = a → · b → · sin ∠ a → , b → .
Näide 1
Leia vektorite a → ja b → vektorkorrutise pikkus, kui tead a → = 3, b → = 5, ∠ a →, b → = π 4.
Lahendus
Määrates vektorite a → ja b → vektorkorrutise pikkuse, lahendame ülesande: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .
Vastus: 15 2 2 .
Teist tüüpi ülesannetel on seos vektorite koordinaatidega, nendes vektorkorrutisega, selle pikkusega jne. otsitakse antud vektorite teadaolevate koordinaatide kaudu a → = (a x; a y; a z) Ja b → = (b x ; b y ; b z) .
Seda tüüpi probleemide puhul saate lahendada palju ülesandevalikuid. Näiteks ei saa määrata vektorite a → ja b → koordinaate, vaid nende laiendusi vormi koordinaatvektoriteks b → = b x · i → + b y · j → + b z · k → ja c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → või vektoreid a → ja b → saab määrata nende alguse koordinaatidega ja lõpp-punktid.
Mõelge järgmistele näidetele.
Näide 2
Ristkülikukujulises koordinaatsüsteemis on antud kaks vektorit: a → = (2; 1; - 3), b → = (0; - 1; 1). Leidke nende ristprodukt.
Lahendus
Teise definitsiooni järgi leiame kahe vektori vektorkorrutise antud koordinaatides: a → × b → = (a y · b z - a z · b y) · i → + (a z · b x - a x · b z) · j → + ( a x · b y - a y · b x) · k → = = (1 · 1 - (- 3) · (- 1)) · i → + ((- 3) · 0 - 2 · 1) · j → + (2 · (- 1) - 1 · 0) · k → = = - 2 i → - 2 j → - 2 k → .
Kui kirjutada vektorkorrutis läbi maatriksi determinandi, siis selle näite lahendus näeb välja selline: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .
Vastus: a → × b → = - 2 i → - 2 j → - 2 k → .
Näide 3
Leia vektorite i → - j → ja i → + j → + k → vektorkorrutise pikkus, kus i →, j →, k → on ristkülikukujulise Descartesiuse koordinaatsüsteemi ühikvektorid.
Lahendus
Kõigepealt leiame antud vektorkorrutise i → - j → × i → + j → + k → koordinaadid antud ristkülikukujulises koordinaatsüsteemis.
On teada, et vektoritel i → - j → ja i → + j → + k → on vastavalt koordinaadid (1; - 1; 0) ja (1; 1; 1). Leiame maatriksi determinandi abil vektorkorrutise pikkuse, siis saame i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .
Seetõttu on vektorkorrutisel i → - j → × i → + j → + k → antud koordinaatsüsteemis koordinaadid (- 1 ; - 1 ; 2).
Vektorkorrutise pikkuse leiame valemi abil (vt vektori pikkuse leidmise osa): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6.
Vastus: i → - j → × i → + j → + k → = 6 . .
Näide 4
Ristkülikukujulises Descartes'i koordinaatsüsteemis on antud kolme punkti A (1, 0, 1), B (0, 2, 3), C (1, 4, 2) koordinaadid. Leia mõni vektor, mis on samaaegselt risti A B → ja A C →.
Lahendus
Vektoritel A B → ja A C → on järgmised koordinaadid (- 1 ; 2 ; 2) ja (0 ; 4 ; 1). Olles leidnud vektorite A B → ja A C → vektorkorrutise, on ilmne, et see on definitsiooni järgi risti vektor nii A B → kui ka A C → suhtes, st see on meie probleemi lahendus. Leiame selle A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .
Vastus: - 6 i → + j → - 4 k → . - üks risti vektoritest.
Kolmandat tüüpi ülesanded on suunatud vektorite vektorkorrutise omaduste kasutamisele. Pärast mille rakendamist saame antud probleemile lahenduse.
Näide 5
Vektorid a → ja b → on risti ja nende pikkused on vastavalt 3 ja 4. Leidke vektorkorrutise 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → pikkus. + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → .
Lahendus
Vektorkorrutise jaotusomaduse järgi saame kirjutada 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →
Assotsiatiivsuse omaduse järgi võtame arvulised koefitsiendid välja viimase avaldise vektori korrutiste märgist: 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → = = 3 · a → × a → + 3 · (- 2) · a → × b → + (- 1) · b → × a → + (- 1) · (- 2) · b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →
Vektorkorrutised a → × a → ja b → × b → on võrdsed 0-ga, kuna a → × a → = a → · a → · sin 0 = 0 ja b → × b → = b → · b → · sin 0 = 0, siis 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b → = - 6 · a → × b → - b → × a → . .
Vektorkorrutise antikommutatiivsusest järeldub - 6 · a → × b → - b → × a → = - 6 · a → × b → - (- 1) · a → × b → = - 5 · a → × b → . .
Vektorkorrutise omadusi kasutades saame võrrandi 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .
Tingimuse järgi on vektorid a → ja b → risti, see tähendab, et nendevaheline nurk on võrdne π 2-ga. Nüüd jääb üle vaid asendada leitud väärtused vastavatesse valemitesse: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → · sin (a → , b →) = 5 · 3 · 4 · sin π 2 = 60 .
Vastus: 3 a → - b → × a → - 2 b → = 60.
Vektorite vektorkorrutise pikkus definitsiooni järgi on võrdne a → × b → = a → · b → · sin ∠ a → , b → . Kuna on juba teada (koolikursusest), et kolmnurga pindala on võrdne poolega selle kahe külje pikkuste korrutisest nende külgede vahelise nurga siinusega. Järelikult on vektorkorrutise pikkus võrdne rööpküliku pindalaga - kahekordse kolmnurgaga, nimelt külgede korrutisega vektorite a → ja b → kujul, mis on paigutatud ühest punktist siinuse võrra. nendevaheline nurk sin ∠ a →, b →.
See on vektorkorrutise geomeetriline tähendus.

Vektorkorrutise füüsiline tähendus
Mehaanikas, ühes füüsika harust, saate tänu vektorkorrutisele määrata jõu momendi ruumipunkti suhtes.
3. määratlus
Punktile B rakendatud jõu F → punkti A suhtes punkti A suhtes saame aru järgmisest vektorkorrutisest A B → × F →.
Kui märkate tekstis viga, tõstke see esile ja vajutage Ctrl+Enter
Nurk vektorite vahel
Kahe vektori vektorkorrutise kontseptsiooni juurutamiseks peame esmalt mõistma sellist mõistet kui nende vektorite vahelist nurka.
Olgu meile antud kaks vektorit $\overline(α)$ ja $\overline(β)$. Võtame ruumis mingi punkti $O$ ja joonistame sealt vektorid $\overline(α)=\overline(OA)$ ja $\overline(β)=\overline(OB)$, seejärel nurga $AOB$ nimetatakse nende vektorite vaheliseks nurgaks (joonis 1).
Tähistus: $∠(\overline(α),\overline(β))$
Vektorite vektorkorrutise mõiste ja leidmise valem
Definitsioon 1
Kahe vektori vektorkorrutis on vektor, mis on risti mõlema antud vektoriga ja selle pikkus võrdub nende vektorite pikkuste korrutisega nende vektori vahelise nurga siinusega ning ka sellel kahe algse vektoriga vektoril on sama orientatsiooniga nagu Descartes'i koordinaatsüsteem.
Tähistus: $\overline(α)х\overline(β)$.
Matemaatiliselt näeb see välja selline:
- $|\overline(α)х\overline(β)|=|\overline(α)||\overline(β)|sin∠(\overline(α),\overline(β))$
- $\overline(α)х\overline(β)⊥\overline(α)$, $\overline(α)х\overline(β)⊥\overline(β)$
- $(\overline(α)х\overline(β),\overline(α),\overline(β))$ ja $(\overline(i),\overline(j),\overline(k))$ on sama suunitlusega (joonis 2)
Ilmselt võrdub vektorite väliskorrutis nullvektoriga kahel juhul:
- Kui ühe või mõlema vektori pikkus on null.
- Kui nende vektorite vaheline nurk on võrdne $180^\circ$ või $0^\circ$ (kuna antud juhul siinus on null).
Et selgelt näha, kuidas vektorite vektorkorrutis leitakse, vaadake järgmisi lahendusnäiteid.
Näide 1
Leidke vektori $\overline(δ)$ pikkus, mis on vektorite vektorkorrutise tulemus, koordinaatidega $\overline(α)=(0,4,0)$ ja $\overline(β) =(3,0,0 )$.
Lahendus.
Kujutame neid vektoreid Descartes'i koordinaatruumis (joonis 3):
Joonis 3. Vektorid ristkoordinaadiruumis. Autor24 - õpilastööde veebivahetus
Näeme, et need vektorid asuvad vastavalt $Ox$ ja $Oy$ telgedel. Seetõttu on nende vaheline nurk $90^\circ$. Leiame nende vektorite pikkused:
$|\overline(α)|=\sqrt(0+16+0)=4$
$|\overline(β)|=\sqrt(9+0+0)=3$
Seejärel saame 1. definitsiooni järgi mooduli $|\overline(δ)|$
$|\overline(δ)|=|\overline(α)||\overline(β)|sin90^\circ=4\cdot 3\cdot 1=12$
Vastus: 12 dollarit.
Ristkorrutise arvutamine vektori koordinaatide järgi
Definitsioon 1 hõlmab kohe meetodit vektori korrutise leidmiseks kahe vektori jaoks. Kuna vektoril on lisaks väärtusele ka suund, siis pole seda võimalik leida ainult skalaarsuuruse abil. Kuid peale selle on ka võimalus koordinaatide abil meile antud vektoreid leida.
Olgu meile antud vektorid $\overline(α)$ ja $\overline(β)$, millel on vastavalt $(α_1,α_2,α_3)$ ja $(β_1,β_2,β_3)$ koordinaadid. Seejärel saab ristkorrutise vektori (nimelt selle koordinaadid) leida järgmise valemi abil:
$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\α_1&α_2&α_3\\β_1&β_2&β_3\end(vmatrix)$
Vastasel juhul saame determinanti laiendades järgmised koordinaadid
$\overline(α)х\overline(β)=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3, α_1 β_2-α_2 β_1)$
Näide 2
Leia koordinaatidega $(0,3,3)$ ja $(-1,2,6)$ kollineaarsete vektorite $\overline(α)$ ja $\overline(β)$ vektorkorrutise vektor.
Lahendus.
Kasutame ülaltoodud valemit. Saame
$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\0&3&3\\-1&2&6\end(vmatrix)=(18 -6)\overline(i)-(0+3)\overline(j)+(0+3)\overline(k)=12\overline(i)-3\overline(j)+3\overline(k) )=(12,-3,3)$
Vastus: $(12,-3,3)$.
Vektorite vektorkorrutise omadused
Kolme suvalise segatud vektori $\overline(α)$, $\overline(β)$ ja $\overline(γ)$, samuti $r∈R$ puhul kehtivad järgmised omadused:
Näide 3
Leidke rööpküliku pindala, mille tippude koordinaadid on $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ ja $(3,8,0) $.
Lahendus.
Esmalt kujutame seda rööpkülikut koordinaatruumis (joonis 5):
Joonis 5. Parallelogramm koordinaatruumis. Autor24 - õpilastööde veebivahetus
Näeme, et selle rööpküliku kaks külge on konstrueeritud kasutades kollineaarseid vektoreid koordinaatidega $\overline(α)=(3,0,0)$ ja $\overline(β)=(0,8,0)$. Neljandat omadust kasutades saame:
$S=|\overline(α)х\overline(β)|$
Leiame vektori $\overline(α)х\overline(β)$:
$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\3&0&0\\0&8&0\end(vmatrix)=0\overline (i)-0\overline(j)+24\overline(k)=(0,0,24)$
Seega
$S=|\overline(α)х\overline(β)|=\sqrt(0+0+24^2)=24$
Ilmselgelt on vektorkorrutise puhul oluline vektorite võtmise järjekord, pealegi
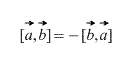
Samuti tuleneb definitsioonist otse, et mis tahes skalaarteguri k (arv) puhul kehtib järgmine:
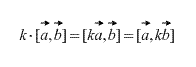
Kollineaarsete vektorite ristkorrutis on võrdne nullvektoriga. Pealegi on kahe vektori ristkorrutis null siis ja ainult siis, kui need on kollineaarsed. (Juhul kui üks neist on nullvektor, tuleb meeles pidada, et nullvektor on definitsiooni järgi mis tahes vektoriga kollineaarne).

Vektorproduktil on jaotusvara, see on

Vektorkorrutise väljendamine vektorite koordinaatide kaudu.
Olgu antud kaks vektorit

(kuidas leida vektori koordinaate selle alguse ja lõpu koordinaatide järgi – vt artiklit Vektorite punktkorrutis, punkt Punktkorrutise alternatiivne määratlus või kahe koordinaatidega määratud vektori punktkorrutise arvutamine.)

Miks on vaja vektortoodet?
Ristkorrutise kasutamiseks on palju võimalusi, näiteks nagu ülalpool kirjutatud, saab kahe vektori ristkorrutise arvutamisel teada, kas need on kollineaarsed.

Või saab seda kasutada nendest vektoritest koostatud rööpküliku pindala arvutamiseks. Definitsiooni põhjal on saadud vektori pikkuseks antud rööpküliku pindala.
Samuti on tohutul hulgal rakendusi elektri ja magnetismi valdkonnas.Online vektortoote kalkulaator.
Selle kalkulaatori abil kahe vektori skalaarkorrutise leidmiseks peate esimesele reale sisestama esimese vektori koordinaadid ja teisele reale teise vektori koordinaadid. Vektorite koordinaate saab arvutada nende alguse ja lõpu koordinaatide järgi (vt artiklit Vektorite punktkorrutis, punkt Punktkorrutise alternatiivne määratlus või kahe vektori punktkorrutise arvutamine nende koordinaatidega.)
Vektorkunstiteos on pseudovektor, mis on risti kahest tegurist koosneva tasapinnaga, mis on kolmemõõtmelise eukleidilise ruumi vektorite binaartehte “vektori korrutamine” tulemus. Vektorkorrutis ei oma kommutatiivsuse ja assotsiatiivsuse omadusi (see on antikommutatiivne) ja erinevalt vektorite skalaarkorrutisest on vektor. Laialdaselt kasutatav paljudes inseneri- ja füüsikarakendustes. Näiteks nurkimpulss ja Lorentzi jõud kirjutatakse matemaatiliselt vektorkorrutisena. Ristkorrutis on kasulik vektorite perpendikulaarsuse "mõõtmiseks" - kahe vektori ristkorrutise moodul on võrdne nende moodulite korrutisega, kui need on risti, ja väheneb nullini, kui vektorid on paralleelsed või antiparalleelsed.
Vektorkorrutist saab defineerida erineval viisil ja teoreetiliselt saab mis tahes mõõtmega n ruumis arvutada n-1 vektori korrutise, saades seeläbi ühe vektori, mis on nendega risti. Kuid kui korrutis on piiratud mittetriviaalsete vektortulemustega binaarkorrutistega, siis on traditsiooniline vektorkorrutis defineeritud ainult kolme- ja seitsmemõõtmelistes ruumides. Vektorkorrutise tulemus, nagu ka skalaarkorrutis, sõltub Eukleidilise ruumi meetrikast.
Erinevalt kolmemõõtmelise ristkülikukujulise koordinaatsüsteemi koordinaatidest skalaarkorrutisvektorite arvutamise valemist sõltub ristkorrutise valem ristkülikukujulise koordinaatsüsteemi orientatsioonist või teisisõnu selle "kiraalsusest".
Definitsioon:
Vektorite a ja vektori b vektorkorrutis ruumis R3 on vektor c, mis vastab järgmistele nõuetele:
vektori c pikkus võrdub vektorite a ja b pikkuste ning nendevahelise nurga φ siinuse korrutisega:
|c|=|a||b|sin φ;
vektor c on ortogonaalne vektori a ja b suhtes;
vektor c on suunatud nii, et vektorite abc kolmik on paremakäeline;
ruumi R7 puhul on vajalik vektorite a, b, c kolmiku assotsiatiivsus.
Määramine:
c===a × b

Riis. 1. Rööpküliku pindala on võrdne vektorkorrutise mooduliga
Ristkorrutise geomeetrilised omadused:
Kahe nullist erineva vektori kollineaarsuse vajalik ja piisav tingimus on, et nende vektorkorrutis on võrdne nulliga.
Risttoodete moodul võrdub pindalaga S rööpkülik, mis on konstrueeritud ühisele algpunktile taandatud vektoritele a Ja b(vt joonis 1).
Kui e- vektoritega risti asetsev ühikvektor a Ja b ja valiti nii, et kolm a,b,e- õige ja S on neile konstrueeritud rööpküliku pindala (taandatud ühise alguseni), siis kehtib vektorkorrutise valem:
=S e
Joonis 2. Rööptahuka ruumala, kasutades vektorit ja vektorite skalaarkorrutist; punktiirjooned näitavad vektori c projektsioone punktile a × b ja vektori a projektsioone punktile b × c, esimene samm on leida skalaarkorrutised
Kui c- mõni vektor, π
- mis tahes tasapind, mis sisaldab seda vektorit, e- tasapinnas asuv ühikvektor π
ja ortogonaalne c,g- tasapinnaga ortogonaalne ühikvektor π
ja suunatud nii, et vektorite kolmik ekg on õige, siis iga lennukis lamamise puhul π
vektor a valem on õige:
=Pr e a |c|g
kus Pr e a on vektori e projektsioon a-le
|c|-vektori c moodul
Vektor- ja skalaarkorrutise kasutamisel saate arvutada rööptahuka ruumala, mis on ehitatud ühisele algpunktile taandatud vektoritele a, b Ja c. Sellist kolme vektori korrutist nimetatakse segatud.
V=|a (b×c)|
Joonisel on näha, et seda mahtu saab leida kahel viisil: geomeetriline tulemus säilib ka siis, kui “skalaar” ja “vektor” korrutised on vahetatud:
V=a×b c=a b×c
Ristkorrutise suurus sõltub algsete vektorite vahelise nurga siinusest, nii et ristkorrutist võib tajuda vektorite „perpendikulaarsuse“ astmena, nii nagu skalaarkorrutist võib vaadelda „paralleelsuse“ astmena. ”. Kahe ühikvektori vektorkorrutis on võrdne 1-ga (ühikvektor), kui algsed vektorid on risti, ja 0-ga (nullvektor), kui vektorid on paralleelsed või antiparalleelsed.
Ristkorrutise avaldis Descartes'i koordinaatides
Kui kaks vektorit a Ja b mis on määratletud nende ristkülikukujuliste Descartes'i koordinaatidega või täpsemalt ortonormaalsel alusel
a=(a x,a y,a z)
b=(b x ,b y,b z)
ja koordinaatsüsteem on paremakäeline, siis on nende vektorkorrutis kuju
=(a y b z -a z b y ,a z b x -a x b z ,a x b y -a y b x)
Selle valemi meeldejätmiseks:
i =∑ε ijk a j b k
Kus ε ijk- Levi-Civita sümbol.
