Løsning af lineære ligningssystemer ved hjælp af Gauss-metoden. Enkeltdelingsordning

Når man løser et ligningssystem

Den enkleste version af den Gaussiske metode resulterer i store fejl. Årsagen er udseendet af store koefficienter, hvis afrunding resulterer i en stor absolut fejl D ~ 0,5. Til gengæld opnås store koefficienter efter at have divideret med en lille førende koefficient .

Konklusion: For at reducere virkningen af afrundingsfejl skal du vælge et førende element, der ikke bare er forskelligt fra 0, men også stort nok.

Første modifikation af Gauss' metode– søg efter strenge. I algoritmen skal det førende element vælges fra betingelsen.

Manglende modifikation. Antag, at x i findes med fejlen D. Så, når man søger efter enhver x s, er det nødvendigt, ifølge den omvendte formel, at gange . I dette tilfælde vil fejlen D også ganges med . Hvis værdien er stor, vil fejlen stige.

Konklusion: det er nødvendigt at sikre, at det førende element ikke bare er stort, men det største modulo i sin linje. Så, når man normaliserer den forreste linje, vil alle andre koefficienter ifølge formel (5) være mindre end 1 i absolut værdi, og fejlene vil være formindske.

Anden modifikation af Gauss-metoden– søg efter kolonner. Dette krav kan opfyldes, hvis de ukendte x i udelukkes i tilfældig rækkefølge, og der søges på den forreste linje efter , leverer . Dette vil være det næste førende element. Efter at have bestemt det førende element, skift k-te og r-te kolonner.

Opmærksomhed. Med en sådan udskiftning ændres nummereringen af de ukendte x i. For at sikre en sådan udskiftning er det nødvendigt at indtaste et array p 1 ,...p n med de reelle tal for de ukendte under programmering. I begyndelsen af det fremadrettede slag er alle p i = i den sædvanlige nummerering. Efter at have fundet det førende element, skift p k og p r. Under det omvendte slag beregnes de omnummererede x i ved hjælp af formel (7). Efter at have beregnet alle de ukendte, skal vi sætte y]:=x[i] og et array y[i] vil være den endelige løsning på problemet.

Den tredje modifikation af Gauss-metoden– fuld søgning. Det leverede element vælges som leder. I dette tilfælde byttes de k-te og r-te kolonner, p k og p r, samt m-te og k-te rækker. Denne modifikation giver maksimal nøjagtighed, men er også den mest komplekse.

Anvendelse af Gauss-metoden til at løse forskellige lineære algebraproblemer

1. Matrix inversion. Lad det være nødvendigt at beregne den inverse matrix af kvadratmatricen A. Lad os betegne X = A –1. Som bekendt er AX = I, hvor I er identitetsmatrixen, hvor 1'er er placeret langs diagonalen, og de resterende elementer er 0. Med andre ord er den i-te søjle i matrix I lig med

(1 er på i-pladsen). Lad x (i) være den i-te kolonne i matrixen X. Så har vi i kraft af matrixmultiplikationsreglen (rækken ganges med kolonnen) A x (i) = e (i). Det betyder, at for at invertere matrixen skal vi løse n systemer af lineære ligninger med identiske matricer og forskellige højresider:

Åh = e (1) ; Åh = e (2) ; …; Åh = e (n) . (2.1)

Efter at have løst disse systemer finder vi ud af, at de fundne løsninger x (1), x (2), ..., x (n) er søjler i matrixen A –1.

2. Beregning af determinanter. I processen med at konvertere matrix A til trekantet form ved hjælp af Gauss-metoden udførte vi følgende handlinger med den:

1) omarrangerede rækker eller kolonner afhængigt af ændringen af metoden;

2) dividere den førende linje med et ikke-nul førende element;

3) en forreste række ganget med et bestemt tal blev tilføjet til rækkerne i matrixen.

Som det er kendt under sådanne transformationer undergår determinanten af matrixen tilsvarende ændringer:

1) skifter tegn;

2) er divideret med det samme element;

3) ændres ikke.

Efter det fremadrettede træk vil matrix A blive reduceret til den øverste trekantede form med dem på hoveddiagonalen. Determinanten for en sådan matrix er naturligvis lig med 1. Under hensyntagen til de ændringer, som determinanten af matrix A undergik under transformationsprocessen, har vi følgende formel:

det A = (–1) s × a 11 × a 22 ×…× a n n ,

hvor a j j er ledende elementer, s er antallet af permutationer af rækker og/eller kolonner, når der søges efter ledende elementer.

TEST SPØRGSMÅL OG OPGAVER

1. Manuelt implementere Gauss-metoden (med søgning i rækker, kolonner, gennem hele matrixen - afhængigt af opgavemuligheden) for et givet ligningssystem

og udfør følgende opgaver

1) Løs dette ligningssystem

2) Beregn determinanten af matrixen for dette system ( Gaussisk metode– se s 2 ).

3) Inverter matrixen af dette system ( Gaussisk metode– se s 1 ).

Brug i fremtiden resultatet af at løse dette problem som et testeksempel.

2. Lav et program til løsning af et lineært system ved hjælp af Gauss-metoden (med søgning i rækker, kolonner, gennem hele matrixen - afhængig af opgavens version) og udfør matrixinversion ved hjælp af dette program.

Vi fortsætter med at overveje systemer af lineære ligninger. Denne lektion er den tredje om emnet. Hvis du har en vag idé om, hvad et system af lineære ligninger generelt er, hvis du har lyst til en tekande, så anbefaler jeg at starte med det grundlæggende på siden. Dernæst er det nyttigt at studere lektionen.

Gauss-metoden er nem! Hvorfor? Den berømte tyske matematiker Johann Carl Friedrich Gauss modtog i sin levetid anerkendelse som den største matematiker gennem tiderne, et geni og endda kaldenavnet "Kongen af matematik." Og alt genialt, som du ved, er enkelt! For øvrigt får ikke kun sutter penge, men også genier - Gauss’ portræt var på 10-dansk-sedlen (før euroens indførelse), og Gauss smiler stadig mystisk til tyskerne fra almindelige frimærker.

Gauss-metoden er enkel ved, at VIDEN OM EN FEMTE-KLASSE ELEV ER NOG til at mestre den. Du skal vide, hvordan du adderer og multiplicerer! Det er ikke tilfældigt, at lærere ofte overvejer metoden til sekventiel udelukkelse af ukendte i skolens matematikvalgfag. Det er et paradoks, men eleverne finder den gaussiske metode den sværeste. Intet overraskende - det handler om metoden, og jeg vil prøve at tale om metodens algoritme i en tilgængelig form.

Lad os først systematisere lidt viden om systemer af lineære ligninger. Et system af lineære ligninger kan:

1) Få en unik løsning. 2) Har uendeligt mange løsninger. 3) Har ingen løsninger (vær ikke-fælles).

Gauss-metoden er det mest kraftfulde og universelle værktøj til at finde en løsning nogen systemer af lineære ligninger. Som vi husker, Cramers regel og matrixmetode er uegnede i tilfælde, hvor systemet har uendeligt mange løsninger eller er inkonsistent. Og metoden til sekventiel eliminering af ukendte Alligevel vil lede os til svaret! I denne lektion vil vi igen overveje Gauss-metoden for case nr. 1 (den eneste løsning på systemet), en artikel er afsat til situationerne i punkt nr. 2-3. Jeg bemærker, at selve metodens algoritme fungerer ens i alle tre tilfælde.

Lad os vende tilbage til det enkleste system fra lektionen Hvordan løser man et system af lineære ligninger? og løse det ved hjælp af Gauss-metoden.

Det første skridt er at skrive ned udvidet systemmatrix: . Jeg tror, at alle kan se, efter hvilket princip koefficienterne er skrevet. Den lodrette linje inde i matrixen har ingen matematisk betydning - den er blot en gennemstregning for at lette designet.

Reference : Jeg anbefaler dig at huske betingelser lineær algebra. System Matrix er en matrix kun sammensat af koefficienter for ukendte, i dette eksempel systemets matrix: . Udvidet systemmatrix – dette er den samme matrix af systemet plus en kolonne med frie termer, i dette tilfælde: . For kortheds skyld kan enhver af matricerne simpelthen kaldes en matrix.

Efter at den udvidede systemmatrix er skrevet, er det nødvendigt at udføre nogle handlinger med den, som også kaldes elementære transformationer.

Følgende elementære transformationer findes:

1) Strenge matricer Kan omarrangere nogle steder. For eksempel, i den overvejede matrix, kan du smertefrit omarrangere den første og anden række:

2) Hvis der er (eller har optrådt) proportionale (som et specialtilfælde - identiske) rækker i matrixen, skal du slette fra matrixen alle disse rækker undtagen én. Overvej for eksempel matrixen . I denne matrix er de sidste tre rækker proportionale, så det er nok kun at forlade en af dem: .

3) Hvis der optræder en nulrække i matricen under transformationer, så skal den også være det slette. Jeg vil ikke tegne, selvfølgelig, nullinjen er den linje, hvori alle nuller.

4) Matrixrækken kan være gange (dividere) til ethvert nummer ikke-nul. Overvej for eksempel matrixen. Her er det tilrådeligt at dividere den første linje med -3, og gange den anden linje med 2: . Denne handling er meget nyttig, fordi den forenkler yderligere transformationer af matrixen.

5) Denne transformation volder de fleste vanskeligheder, men faktisk er der heller ikke noget kompliceret. Til en række af en matrix kan du tilføje endnu en streng ganget med et tal, forskellig fra nul. Lad os se på vores matrix ud fra et praktisk eksempel: . Først vil jeg beskrive transformationen meget detaljeret. Gang den første linje med –2: , Og til den anden linje lægger vi den første linje ganget med –2: . Nu kan den første linje deles "tilbage" med –2: . Som du kan se, er den linje, der tilføjes LI – har ikke ændret sig. Altid linjen, SOM ER TILFØJET, ændres UT.

I praksis skriver de det selvfølgelig ikke så detaljeret, men skriver det kort: Endnu en gang: til anden linje tilføjet den første linje ganget med –2. En linje multipliceres normalt mundtligt eller på et udkast, hvor mentalberegningsprocessen foregår sådan her:

"Jeg omskriver matrixen og omskriver den første linje: »

"Første kolonne. I bunden skal jeg have nul. Derfor multiplicerer jeg den øverste med –2: , og lægger den første til den anden linje: 2 + (–2) = 0. Jeg skriver resultatet i den anden linje: »

"Nu den anden kolonne. Øverst gange jeg -1 med -2: . Jeg tilføjer den første til den anden linje: 1 + 2 = 3. Jeg skriver resultatet i den anden linje: »

"Og den tredje kolonne. Øverst gange jeg -5 med -2:. Jeg tilføjer den første til den anden linje: –7 + 10 = 3. Jeg skriver resultatet i den anden linje: »

Forstå venligst dette eksempel omhyggeligt og forstå den sekventielle beregningsalgoritme, hvis du forstår dette, så er den Gaussiske metode praktisk talt i din lomme. Men vi vil selvfølgelig stadig arbejde på denne transformation.

Elementære transformationer ændrer ikke løsningen af ligningssystemet

! OPMÆRKSOMHED: betragtes som manipulationer ikke kan bruge, hvis du bliver tilbudt en opgave, hvor matricerne er givet "af sig selv." For eksempel med "klassisk" operationer med matricer Du må under ingen omstændigheder omarrangere noget inde i matricerne! Lad os vende tilbage til vores system. Det er praktisk talt taget i stykker.

Lad os nedskrive systemets udvidede matrix og ved hjælp af elementære transformationer reducere den til trinvis udsigt:

(1) Den første linje blev lagt til den anden linje, ganget med –2. Og igen: hvorfor gange vi den første linje med –2? For at få nul i bunden, hvilket betyder at slippe af med en variabel i den anden linje.

(2) Divider den anden linje med 3.

Formålet med elementære transformationer – reducer matrixen til trinvis form: . I designet af opgaven markerer de bare "trappen" med en simpel blyant og cirkler også tallene, der er placeret på "trinene". Selve begrebet "trinvist" er ikke helt teoretisk i videnskabelig og pædagogisk litteratur kaldes det ofte trapezformet udsigt eller trekantet udsigt.

Som et resultat af elementære transformationer opnåede vi tilsvarende oprindelige ligningssystem:

Nu skal systemet "afvikles" i den modsatte retning - fra bund til top kaldes denne proces omvendt af Gauss-metoden.

I den nederste ligning har vi allerede et færdigt resultat: .

Lad os overveje den første ligning af systemet og erstatte den allerede kendte værdi af "y" i den:

Lad os overveje den mest almindelige situation, når den Gaussiske metode kræver løsning af et system af tre lineære ligninger med tre ukendte.

Eksempel 1

Løs ligningssystemet ved hjælp af Gauss-metoden:

Lad os skrive systemets udvidede matrix:

Nu vil jeg straks tegne det resultat, som vi kommer frem til under løsningen: Og jeg gentager, vores mål er at bringe matrixen til en trinvis form ved hjælp af elementære transformationer. Hvor skal man begynde?

Se først nummeret øverst til venstre: Burde næsten altid være her enhed. Generelt vil –1 (og nogle gange andre tal) duge, men på en eller anden måde er det traditionelt sket, at man normalt er placeret der. Hvordan organiserer man en enhed? Vi ser på den første kolonne - vi har en færdig enhed! Transformation en: skift første og tredje linje:

Nu vil den første linje forblive uændret indtil slutningen af løsningen. Nu fint.

Enheden i øverste venstre hjørne er organiseret. Nu skal du have nuller på disse steder:

Vi får nuller ved at bruge en "svær" transformation. Først behandler vi den anden linje (2, –1, 3, 13). Hvad skal der gøres for at få nul i den første position? Behøver til den anden linje lægges den første linje ganget med –2. Mentalt eller på et udkast, gange den første linje med –2: (–2, –4, 2, –18). Og vi udfører konsekvent (igen mentalt eller på et udkast) tilføjelse, til den anden linje lægger vi den første linje, allerede ganget med –2:

Vi skriver resultatet i anden linje:

Vi behandler den tredje linje på samme måde (3, 2, –5, –1). For at få et nul i den første position, skal du til den tredje linje læg den første linje ganget med –3. Mentalt eller på et udkast, gange den første linje med –3: (–3, –6, 3, –27). OG til den tredje linje lægger vi den første linje ganget med –3:

Vi skriver resultatet i tredje linje:

I praksis udføres disse handlinger normalt mundtligt og nedskrives i ét trin:

Det er ikke nødvendigt at tælle alt på én gang og på samme tid. Rækkefølgen af beregninger og "indskrivning" af resultaterne konsekvent og normalt er det sådan her: først omskriver vi den første linje og puster langsomt på os selv - KONSISTENT og OPMÆRKSOMT:
Og jeg har allerede diskuteret den mentale proces af selve beregningerne ovenfor.

I dette eksempel er dette let at gøre, vi dividerer den anden linje med –5 (da alle tal der er delelige med 5 uden en rest). Samtidig dividerer vi den tredje linje med –2, for jo mindre tallene er, jo enklere er løsningen:

På den sidste fase af elementære transformationer skal du få endnu et nul her:

For det til den tredje linje lægger vi den anden linje ganget med –2:
Prøv selv at finde ud af denne handling - gang mentalt den anden linje med –2 og udfør tilføjelsen.

Den sidste handling, der udføres, er resultatets frisure, divider den tredje linje med 3.

Som et resultat af elementære transformationer blev et ækvivalent system af lineære ligninger opnået: Fedt nok.

Nu kommer det omvendte af Gauss-metoden ind. Ligningerne "vinder af" fra bund til top.

I den tredje ligning har vi allerede et klar resultat:

Lad os se på den anden ligning: . Betydningen af "zet" er allerede kendt, således:

Og endelig den første ligning:. "Igrek" og "zet" er kendt, det er bare et spørgsmål om små ting:

Svar:

Som det allerede er blevet bemærket flere gange, for ethvert ligningssystem er det muligt og nødvendigt at kontrollere den fundne løsning, heldigvis er dette nemt og hurtigt.

Eksempel 2

Dette er et eksempel på en uafhængig løsning, et eksempel på det endelige design og et svar i slutningen af lektionen.

Det skal bemærkes, at din forløbet af beslutningen falder muligvis ikke sammen med min beslutningsproces, og dette er et træk ved Gauss-metoden. Men svarene skal være de samme!

Eksempel 3

Løs et system af lineære ligninger ved hjælp af Gauss-metoden

Vi ser på det øverste venstre "trin". Vi burde have en der. Problemet er, at der slet ikke er nogen enheder i den første kolonne, så en omarrangering af rækkerne løser ikke noget. I sådanne tilfælde skal enheden organiseres ved hjælp af en elementær transformation. Dette kan normalt gøres på flere måder. Jeg gjorde dette: (1) Til den første linje lægger vi den anden linje ganget med –1. Det vil sige, at vi mentalt gangede anden linje med –1 og tilføjede første og anden linje, mens den anden linje ikke ændrede sig.

Nu øverst til venstre er der “minus én”, hvilket passer os ret godt. Enhver, der ønsker at få +1, kan udføre en ekstra bevægelse: gange den første linje med –1 (skift fortegn).

(2) Den første linje ganget med 5 blev tilføjet til den anden linje. Den første linje ganget med 3 blev tilføjet til den tredje linje.

(3) Den første linje blev ganget med –1, i princippet er dette for skønhed. Tegnet på den tredje linje blev også ændret, og det blev flyttet til andenpladsen, så vi på det andet "trin" havde den nødvendige enhed.

(4) Den anden linje blev tilføjet til den tredje linje, ganget med 2.

(5) Den tredje linje blev divideret med 3.

Et dårligt tegn, der indikerer en fejl i beregninger (mere sjældent en tastefejl) er en "dårlig" bundlinje. Det vil sige, hvis vi fik noget som , nedenfor, og i overensstemmelse hermed, , så kan vi med en høj grad af sandsynlighed sige, at der er lavet en fejl under elementære transformationer.

Vi lader det omvendte, i design af eksempler omskriver de ofte ikke selve systemet, men ligningerne er "taget direkte fra den givne matrix." Det omvendte slag, jeg minder dig om, virker fra bund til top. Ja, her er en gave:

Svar: .

Eksempel 4

Løs et system af lineære ligninger ved hjælp af Gauss-metoden

Dette er et eksempel for dig at løse på egen hånd, det er noget mere kompliceret. Det er okay, hvis nogen bliver forvirrede. Fuld løsning og prøvedesign i slutningen af lektionen. Din løsning kan være anderledes end min løsning.

I den sidste del vil vi se på nogle funktioner i den Gaussiske algoritme. Den første funktion er, at nogle gange mangler nogle variabler i systemligningerne, for eksempel: Hvordan skriver man den udvidede systemmatrix korrekt? Jeg har allerede talt om dette punkt i klassen. Cramers regel. Matrix metode. I systemets udvidede matrix sætter vi nuller i stedet for manglende variable: Forresten er dette et ret nemt eksempel, da den første kolonne allerede har et nul, og der er færre elementære transformationer at udføre.

Den anden funktion er denne. I alle de betragtede eksempler placerede vi enten -1 eller +1 på "trinene". Kan der være andre tal der? I nogle tilfælde kan de. Overvej systemet: .

Her på øverste venstre "trin" har vi en toer. Men vi bemærker det faktum, at alle tallene i den første kolonne er delelige med 2 uden en rest - og den anden er to og seks. Og de to øverst til venstre vil passe til os! I det første trin skal du udføre følgende transformationer: læg den første linje ganget med –1 til den anden linje; til den tredje linje læg den første linje ganget med –3. På denne måde får vi de nødvendige nuller i den første kolonne.

Eller et andet konventionelt eksempel: . Her passer de tre på det andet “trin” også os, da 12 (stedet hvor vi skal have nul) er deleligt med 3 uden en rest. Det er nødvendigt at udføre følgende transformation: tilføj den anden linje til den tredje linje, ganget med -4, som et resultat af hvilket nul, vi har brug for, vil blive opnået.

Gauss' metode er universel, men der er en særegenhed. Du kan trygt lære at løse systemer ved hjælp af andre metoder (Cramers metode, matrixmetode) bogstaveligt talt første gang - de har en meget streng algoritme. Men for at føle dig sikker på Gauss-metoden, bør du "sætte tænderne i" og løse mindst 5-10 ti systemer. Derfor kan der i starten være forvirring og fejl i beregninger, og det er der ikke noget usædvanligt eller tragisk i.

Regnfuldt efterårsvejr uden for vinduet.... Derfor til alle, der ønsker at løse et mere komplekst eksempel på egen hånd:

Eksempel 5

Løs et system med 4 lineære ligninger med fire ubekendte ved hjælp af Gauss-metoden.

Sådan en opgave er ikke så sjælden i praksis. Jeg tror, at selv en tekande, der har studeret denne side grundigt, vil forstå algoritmen til intuitivt at løse et sådant system. Grundlæggende er alt det samme – der er bare flere handlinger.

Tilfælde, hvor systemet ikke har nogen løsninger (inkonsekvente) eller har uendeligt mange løsninger, diskuteres i lektionen Inkompatible systemer og systemer med en fælles løsning. Der kan du rette den betragtede algoritme for Gauss-metoden.

Jeg ønsker dig succes!

Løsninger og svar:

Eksempel 2: Løsning : Lad os nedskrive systemets udvidede matrix og ved hjælp af elementære transformationer bringe det til en trinvis form.
Elementære transformationer udført: (1) Den første linje blev lagt til den anden linje, ganget med –2. Den første linje blev lagt til den tredje linje, ganget med –1. Opmærksomhed! Her kan du blive fristet til at trække den første fra den tredje linje. Jeg anbefaler stærkt ikke at trække den fra - risikoen for fejl stiger meget. Bare fold den! (2) Tegnet på den anden linje blev ændret (multipliceret med –1). Anden og tredje linje er blevet byttet om. Bemærk , at vi på "trinene" ikke kun er tilfredse med en, men også med -1, hvilket er endnu mere bekvemt. (3) Den anden linje blev tilføjet til den tredje linje, ganget med 5. (4) Tegnet på den anden linje blev ændret (multipliceret med –1). Den tredje linje blev divideret med 14.

Baglæns:

Svar : .

Eksempel 4: Løsning : Lad os nedskrive den udvidede matrix af systemet og ved hjælp af elementære transformationer bringe det til en trinvis form:

Udførte konverteringer: (1) En anden linje blev tilføjet til den første linje. Således er den ønskede enhed organiseret i øverste venstre "trin". (2) Den første linje ganget med 7 blev tilføjet til den anden linje. Den første linje ganget med 6 blev tilføjet til den tredje linje.

Med det andet "trin" bliver alt værre , "kandidaterne" til det er tallene 17 og 23, og vi har brug for enten en eller -1. Transformationer (3) og (4) vil være rettet mod at opnå den ønskede enhed (3) Den anden linje blev lagt til den tredje linje, ganget med –1. (4) Den tredje linje blev lagt til den anden linje, ganget med –3. Det påkrævede element på det andet trin er modtaget. . (5) Den anden linje blev tilføjet til den tredje linje, ganget med 6. (6) Den anden linje blev ganget med –1, den tredje linje blev divideret med -83.

Baglæns:

Svar :

Eksempel 5: Løsning : Lad os nedskrive systemets matrix og ved hjælp af elementære transformationer bringe det til en trinvis form:

Udførte konverteringer: (1) Den første og anden linje er blevet skiftet. (2) Den første linje blev lagt til den anden linje, ganget med –2. Den første linje blev lagt til den tredje linje, ganget med –2. Den første linje blev lagt til den fjerde linje, ganget med –3. (3) Den anden linje blev tilføjet til den tredje linje, ganget med 4. Den anden linje blev tilføjet til den fjerde linje, ganget med –1. (4) Tegnet på den anden linje blev ændret. Den fjerde linje blev delt med 3 og placeret i stedet for den tredje linje. (5) Den tredje linje blev lagt til den fjerde linje, ganget med –5.

Baglæns:

Svar :

Gauss metode perfekt til at løse systemer af lineære algebraiske ligninger (SLAE'er). Det har en række fordele sammenlignet med andre metoder:

for det første er der ingen grund til først at undersøge ligningssystemet for konsistens;
for det andet kan Gauss-metoden løse ikke kun SLAE'er, hvor antallet af ligninger falder sammen med antallet af ukendte variable, og systemets hovedmatrix er ikke-singular, men også ligningssystemer, hvor antallet af ligninger ikke er sammenfaldende med antallet af ukendte variable eller determinanten af hovedmatrixen er lig med nul;
for det tredje fører den Gaussiske metode til resultater med et relativt lille antal beregningsoperationer.

Kort oversigt over artiklen.

Først giver vi de nødvendige definitioner og introducerer notationer.

Dernæst vil vi beskrive Gauss-metodens algoritme for det enkleste tilfælde, det vil sige for systemer med lineære algebraiske ligninger, hvor antallet af ligninger falder sammen med antallet af ukendte variable og determinanten for systemets hovedmatrix er ikke lig med nul. Når man løser sådanne ligningssystemer, er essensen af Gauss-metoden tydeligst synlig, som er den sekventielle eliminering af ukendte variable. Derfor kaldes Gauss-metoden også metoden til sekventiel eliminering af ukendte. Vi vil vise detaljerede løsninger af flere eksempler.

Afslutningsvis vil vi overveje løsningen ved Gauss-metoden af systemer af lineære algebraiske ligninger, hvis hovedmatrix er enten rektangulær eller ental. Løsningen til sådanne systemer har nogle funktioner, som vi vil undersøge i detaljer ved hjælp af eksempler.

Sidenavigation.

Grundlæggende definitioner og notationer.

Overvej et system af p lineære ligninger med n ukendte (p kan være lig med n):

Hvor er ukendte variable, er tal (reelle eller komplekse) og er frie led.

Hvis , så kaldes systemet af lineære algebraiske ligninger homogen, Ellers - heterogen.

Sættet af værdier af ukendte variable, for hvilke alle systemets ligninger bliver identiteter, kaldes SLAU's beslutning.

Hvis der er mindst én løsning til et system af lineære algebraiske ligninger, så kaldes det samling, Ellers - ikke-fælles.

Hvis en SLAE har en unik løsning, så kaldes den bestemte. Hvis der er mere end én løsning, kaldes systemet usikker.

De siger, at systemet er skrevet ind koordinatform, hvis det har formen
.

Dette system i matrixform poster har formen , hvor - SLAE'ens hovedmatrix - matrixen for kolonnen med ukendte variable - matrixen af frie led.

Tilføjer vi en matrix-søjle af frie led til matrix A som (n+1). kolonne, får vi den såkaldte udvidet matrix systemer af lineære ligninger. Typisk er en udvidet matrix betegnet med bogstavet T, og kolonnen med frie udtryk er adskilt af en lodret linje fra de resterende kolonner, dvs.

Den kvadratiske matrix A kaldes degenerere, hvis dens determinant er nul. Hvis , så kaldes matrix A ikke-degenereret.

Følgende punkt skal bemærkes.

Hvis du udfører følgende handlinger med et system af lineære algebraiske ligninger

skift to ligninger,
gange begge sider af enhver ligning med et vilkårligt og ikke-nul reelt (eller komplekst) tal k,
til begge sider af enhver ligning lægges de tilsvarende dele af en anden ligning, ganget med et vilkårligt tal k,

så får du et tilsvarende system, der har de samme løsninger (eller, ligesom det originale, ikke har nogen løsninger).

For en udvidet matrix af et system af lineære algebraiske ligninger vil disse handlinger betyde at udføre elementære transformationer med rækkerne:

bytte to linjer,
multiplicerer alle elementer i en hvilken som helst række af matrix T med et ikke-nul tal k,
tilføjelse til elementerne i en række i en matrix af de tilsvarende elementer i en anden række ganget med et vilkårligt tal k.

Nu kan vi gå videre til beskrivelsen af Gauss-metoden.

Løsning af systemer af lineære algebraiske ligninger, hvor antallet af ligninger er lig med antallet af ukendte, og systemets hovedmatrix er ikke-singular, ved hjælp af Gauss-metoden.

Hvad ville vi gøre i skolen, hvis vi fik til opgave at finde en løsning på et ligningssystem? .

Nogle ville gøre det.

Bemærk, at ved at tilføje venstre side af den første til venstre side af den anden ligning, og højre side til højre, kan du slippe af med de ukendte variable x 2 og x 3 og straks finde x 1:

Vi erstatter den fundne værdi x 1 =1 i systemets første og tredje ligning:

Hvis vi multiplicerer begge sider af den tredje ligning i systemet med -1 og lægger dem til de tilsvarende dele af den første ligning, slipper vi af med den ukendte variabel x 3 og kan finde x 2:

Vi erstatter den resulterende værdi x 2 = 2 i den tredje ligning og finder den resterende ukendte variabel x 3:

Andre ville have gjort anderledes.

Lad os løse systemets første ligning med hensyn til den ukendte variabel x 1 og erstatte det resulterende udtryk i systemets anden og tredje ligning for at udelukke denne variabel fra dem:

Lad os nu løse den anden ligning i systemet for x 2 og erstatte det opnåede resultat i den tredje ligning for at eliminere den ukendte variabel x 2 fra den:

Fra systemets tredje ligning er det klart, at x 3 =3. Fra den anden ligning finder vi , og fra den første ligning får vi .

Kendte løsninger, ikke?

Det mest interessante her er, at den anden løsningsmetode i det væsentlige er metoden til sekventiel eliminering af ukendte, det vil sige den Gaussiske metode. Da vi udtrykte de ukendte variable (første x 1, på næste trin x 2) og substituerede dem i de resterende ligninger i systemet, udelukkede vi dem derved. Vi udførte eliminering, indtil der kun var en ukendt variabel tilbage i den sidste ligning. Processen med sekventiel eliminering af ukendte kaldes direkte Gauss-metode. Efter at have gennemført det fremadrettede træk, har vi mulighed for at beregne den ukendte variabel fundet i den sidste ligning. Med dens hjælp finder vi den næste ukendte variabel fra næstsidste ligning og så videre. Processen med sekventielt at finde ukendte variable, mens man går fra den sidste ligning til den første, kaldes omvendt af Gauss-metoden.

Det skal bemærkes, at når vi udtrykker x 1 i form af x 2 og x 3 i den første ligning og derefter erstatter det resulterende udtryk i den anden og tredje ligning, fører følgende handlinger til det samme resultat:

En sådan procedure gør det faktisk også muligt at eliminere den ukendte variabel x 1 fra systemets anden og tredje ligning:

Nuancer med eliminering af ukendte variable ved hjælp af Gauss-metoden opstår, når systemets ligninger ikke indeholder nogle variable.

For eksempel i SLAU i den første ligning er der ingen ukendt variabel x 1 (med andre ord, koefficienten foran den er nul). Derfor kan vi ikke løse den første ligning i systemet for x 1 for at eliminere denne ukendte variabel fra de resterende ligninger. Vejen ud af denne situation er at bytte om på systemets ligninger. Da vi overvejer systemer af lineære ligninger, hvis determinanter af hovedmatricerne er forskellige fra nul, er der altid en ligning, hvor den variable, vi har brug for, er til stede, og vi kan omarrangere denne ligning til den position, vi har brug for. For vores eksempel er det nok at bytte systemets første og anden ligning , så kan du løse den første ligning for x 1 og udelukke den fra de resterende ligninger i systemet (selvom x 1 ikke længere er til stede i den anden ligning).

Vi håber du forstår kernen.

Lad os beskrive Gaussisk metode algoritme.

Antag, at vi skal løse et system af n lineære algebraiske ligninger med n ukendte variable på formen , og lad determinanten af dens hovedmatrix være forskellig fra nul.

Det vil vi antage, da vi altid kan opnå dette ved at omarrangere systemets ligninger. Lad os fjerne den ukendte variabel x 1 fra alle systemets ligninger, begyndende med den anden. For at gøre dette lægger vi den første, ganget med , til den anden ligning i systemet, til den tredje ligning lægger vi den første, ganget med , og så videre, til den n'te ligning lægger vi den første, ganget med . Ligningssystemet efter sådanne transformationer vil antage formen

hvor og .

Vi ville være nået frem til det samme resultat, hvis vi havde udtrykt x 1 i form af andre ukendte variable i systemets første ligning og substitueret det resulterende udtryk i alle andre ligninger. Variablen x 1 er således udelukket fra alle ligninger, startende fra den anden.

Dernæst fortsætter vi på lignende måde, men kun med en del af det resulterende system, som er markeret i figuren

For at gøre dette lægger vi den anden, ganget med , til den tredje ligning i systemet, til den fjerde ligning lægger vi den anden, ganget med , og så videre, til den n'te ligning lægger vi den anden, ganget med . Ligningssystemet efter sådanne transformationer vil antage formen

hvor og . Variablen x 2 er således udelukket fra alle ligninger, startende fra den tredje.

Dernæst fortsætter vi med at eliminere den ukendte x 3, mens vi handler på samme måde med den del af systemet, der er markeret i figuren

Så vi fortsætter den direkte progression af den Gaussiske metode, indtil systemet tager formen

Fra dette øjeblik begynder vi det omvendte af Gauss-metoden: vi beregner x n fra den sidste ligning som , ved hjælp af den opnåede værdi af x n finder vi x n-1 fra den næstsidste ligning, og så videre finder vi x 1 fra den første ligning .

Lad os se på algoritmen ved hjælp af et eksempel.

Eksempel.

Gauss metode.

Løsning.

Koefficienten a 11 er ikke-nul, så lad os fortsætte til den direkte progression af Gauss-metoden, det vil sige til udelukkelse af den ukendte variabel x 1 fra alle systemets ligninger undtagen den første. For at gøre dette skal du til venstre og højre side af den anden, tredje og fjerde ligning tilføje venstre og højre side af den første ligning ganget med hhv. Og:

Den ukendte variabel x 1 er blevet elimineret, lad os gå videre til at eliminere x 2 . Til venstre og højre side af systemets tredje og fjerde ligning lægger vi venstre og højre side af den anden ligning ganget med hhv. Og :

For at fuldføre den fremadgående progression af den Gaussiske metode skal vi eliminere den ukendte variabel x 3 fra den sidste ligning i systemet. Lad os lægge til venstre og højre side af henholdsvis den fjerde ligning venstre og højre side af den tredje ligning ganget med :

Du kan begynde det omvendte af Gauss-metoden.

Fra den sidste ligning vi har ,
fra den tredje ligning får vi,
fra den anden,
fra den første.

For at kontrollere kan du erstatte de opnåede værdier af de ukendte variabler i det originale ligningssystem. Alle ligninger bliver til identiteter, hvilket indikerer, at løsningen ved hjælp af Gauss-metoden blev fundet korrekt.

Svar:

Lad os nu give en løsning på det samme eksempel ved at bruge den Gaussiske metode i matrixnotation.

Eksempel.

Find løsningen på ligningssystemet Gauss metode.

Løsning.

Systemets udvidede matrix har formen . Øverst i hver kolonne er de ukendte variable, der svarer til matricens elementer.

Den direkte tilgang til den Gaussiske metode involverer her at reducere den udvidede matrix af systemet til en trapezformet form ved hjælp af elementære transformationer. Denne proces ligner elimineringen af ukendte variabler, som vi gjorde med systemet i koordinatform. Nu vil du se dette.

Lad os transformere matricen, så alle elementer i den første kolonne, startende fra den anden, bliver nul. For at gøre dette tilføjer vi til elementerne i den anden, tredje og fjerde linje de tilsvarende elementer i den første linje ganget med , og følgelig:

Dernæst transformerer vi den resulterende matrix, så i den anden kolonne alle elementer, startende fra den tredje, bliver nul. Dette ville svare til at eliminere den ukendte variabel x 2 . For at gøre dette tilføjer vi til elementerne i den tredje og fjerde række de tilsvarende elementer i den første række af matricen, ganget med hhv. Og :

Det er tilbage at udelukke den ukendte variabel x 3 fra den sidste ligning i systemet. For at gøre dette tilføjer vi til elementerne i den sidste række i den resulterende matrix de tilsvarende elementer i den næstsidste række ganget med :

Det skal bemærkes, at denne matrix svarer til et system af lineære ligninger

som blev opnået tidligere efter et fremadgående træk.

Det er tid til at vende tilbage. I matrixnotation involverer det omvendte af Gauss-metoden transformation af den resulterende matrix, således at matrixen markeret i figuren

blev diagonal, det vil sige tog formen

hvor er nogle tal.

Disse transformationer ligner de fremadgående transformationer af Gauss-metoden, men udføres ikke fra den første linje til den sidste, men fra den sidste til den første.

Tilføj til elementerne i den tredje, anden og første linje de tilsvarende elementer i den sidste linje, ganget med , ved og ved henholdsvis:

Tilføj nu til elementerne i den anden og første linje de tilsvarende elementer i den tredje linje, ganget med og med henholdsvis:

I det sidste trin af den omvendte Gauss-metode tilføjer vi til elementerne i den første række de tilsvarende elementer i den anden række ganget med:

Den resulterende matrix svarer til ligningssystemet , hvorfra vi finder de ukendte variable.

Svar:

BEMÆRK.

Når man bruger Gauss-metoden til at løse systemer af lineære algebraiske ligninger, bør omtrentlige beregninger undgås, da dette kan føre til helt forkerte resultater. Vi anbefaler ikke at afrunde decimaler. Det er bedre at gå fra decimalbrøker til almindelige brøker.

Eksempel.

Løs et system af tre ligninger ved hjælp af Gauss-metoden .

Løsning.

Bemærk, at i dette eksempel har de ukendte variable en anden betegnelse (ikke x 1, x 2, x 3, men x, y, z). Lad os gå videre til almindelige brøker:

Lad os udelukke det ukendte x fra systemets anden og tredje ligning:

I det resulterende system er den ukendte variabel y fraværende i den anden ligning, men y er til stede i den tredje ligning, så lad os bytte den anden og tredje ligning:

Dette fuldender den direkte progression af Gauss-metoden (det er ikke nødvendigt at udelukke y fra den tredje ligning, da denne ukendte variabel ikke længere eksisterer).

Lad os starte det omvendte træk.

Fra den sidste ligning finder vi ,
fra næstsidste

fra den første ligning vi har

Svar:

X = 10, y = 5, z = -20.

Løsning af systemer af lineære algebraiske ligninger, hvor antallet af ligninger ikke falder sammen med antallet af ukendte eller systemets hovedmatrix er ental ved hjælp af Gauss-metoden.

Ligningssystemer, hvis hovedmatrix er rektangulær eller kvadratisk ental, har muligvis ingen løsninger, kan have en enkelt løsning eller kan have et uendeligt antal løsninger.

Nu vil vi forstå, hvordan Gauss-metoden giver os mulighed for at etablere kompatibiliteten eller inkonsistensen af et system af lineære ligninger, og i tilfælde af dets kompatibilitet bestemme alle løsninger (eller en enkelt løsning).

I princippet forbliver processen med at eliminere ukendte variabler i tilfælde af sådanne SLAE'er den samme. Det er dog værd at gå i detaljer om nogle situationer, der kan opstå.

Lad os gå videre til den vigtigste fase.

Så lad os antage, at systemet af lineære algebraiske ligninger, efter at have fuldført fremadgående progression af Gauss-metoden, har formen og ikke en eneste ligning blev reduceret til (i dette tilfælde ville vi konkludere, at systemet er inkompatibelt). Et logisk spørgsmål opstår: "Hvad skal man gøre nu"?

Lad os nedskrive de ukendte variable, der kommer først i alle ligninger i det resulterende system:

I vores eksempel er disse x 1, x 4 og x 5. På venstre side af systemets ligninger efterlader vi kun de led, der indeholder de skrevne ukendte variable x 1, x 4 og x 5, de resterende led overføres til højre side af ligningerne med det modsatte fortegn:

Lad os give de ukendte variable, der er på højre side af ligningerne vilkårlige værdier, hvor - vilkårlige tal:

Herefter indeholder højresiden af alle ligninger af vores SLAE tal, og vi kan gå videre til det modsatte af Gauss-metoden.

Fra den sidste ligning i systemet vi har, fra den næstsidste ligning vi finder, fra den første ligning får vi

Løsningen til et ligningssystem er et sæt værdier af ukendte variable

Giver tal forskellige værdier, vil vi få forskellige løsninger til ligningssystemet. Det vil sige, at vores ligningssystem har uendeligt mange løsninger.

Svar:

Hvor - vilkårlige tal.

For at konsolidere materialet vil vi analysere i detaljer løsningerne af flere flere eksempler.

Eksempel.

Løs et homogent system af lineære algebraiske ligninger Gauss metode.

Løsning.

Lad os udelukke den ukendte variabel x fra systemets anden og tredje ligning. For at gøre dette, til venstre og højre side af den anden ligning, tilføjer vi henholdsvis venstre og højre side af den første ligning, ganget med , og til venstre og højre side af den tredje ligning tilføjer vi venstre og højre side af den tredje ligning. højre side af den første ligning ganget med:

Lad os nu udelukke y fra den tredje ligning af det resulterende ligningssystem:

Den resulterende SLAE svarer til systemet .

Vi efterlader i venstre side af systemligningerne kun led, der indeholder de ukendte variable x og y, og flytter led med den ukendte variabel z til højre:

Den Gaussiske metode, også kaldet metoden til sekventiel eliminering af ukendte, er som følger. Ved hjælp af elementære transformationer bringes et system af lineære ligninger til en sådan form, at dets matrix af koefficienter viser sig at være trapezformet (det samme som trekantet eller trinformet) eller tæt på trapezformet (direkte slag af Gauss-metoden, herefter - simpelthen lige slag). Et eksempel på et sådant system og dets løsning er i figuren ovenfor.

I et sådant system indeholder den sidste ligning kun én variabel, og dens værdi kan entydigt findes. Værdien af denne variabel erstattes derefter med den foregående ligning ( omvendt af Gauss-metoden , så bare omvendt), hvorfra den forrige variabel findes, og så videre.

I et trapezformet (trekantet) system, som vi ser, indeholder den tredje ligning ikke længere variabler y Og x, og den anden ligning er variablen x .

Efter at systemets matrix har taget en trapezformet form, er det ikke længere svært at forstå problemet med systemets kompatibilitet, bestemme antallet af løsninger og selv finde løsningerne.

Fordele ved metoden:

når man løser systemer af lineære ligninger med mere end tre ligninger og ukendte, er Gauss-metoden ikke så besværlig som Cramer-metoden, da løsning med Gauss-metoden kræver færre beregninger;
Gauss-metoden kan løse ubestemte systemer af lineære ligninger, det vil sige have en generel løsning (og vi vil analysere dem i denne lektion), og ved hjælp af Cramer-metoden kan vi kun konstatere, at systemet er ubestemt;
du kan løse systemer af lineære ligninger, hvor antallet af ukendte ikke er lig med antallet af ligninger (vi vil også analysere dem i denne lektion);
Metoden er baseret på elementære (skole) metoder - metoden til at substituere ukendte og metoden til at tilføje ligninger, som vi kom ind på i den tilsvarende artikel.

For at alle skal forstå den enkelhed, hvormed trapezformede (trekantede, trin) systemer af lineære ligninger løses, præsenterer vi en løsning til et sådant system ved hjælp af omvendt bevægelse. En hurtig løsning på dette system blev vist på billedet i begyndelsen af lektionen.

Eksempel 1. Løs et system af lineære ligninger ved hjælp af inverse:

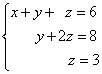
Løsning. I dette trapezformede system er variablen z kan entydigt findes fra den tredje ligning. Vi erstatter dens værdi i den anden ligning og får værdien af variablen y:

Nu kender vi værdierne af to variable - z Og y. Vi erstatter dem i den første ligning og får værdien af variablen x:

Fra de foregående trin skriver vi løsningen til ligningssystemet:

For at opnå et sådant trapezformet system af lineære ligninger, som vi løste meget enkelt, er det nødvendigt at bruge et fremadgående slag forbundet med elementære transformationer af systemet af lineære ligninger. Det er heller ikke særlig svært.

Elementære transformationer af et system af lineære ligninger

Ved at gentage skolemetoden med algebraisk at lægge et systems ligninger til, fandt vi ud af, at til en af systemets ligninger kan vi tilføje endnu en ligning af systemet, og hver af ligningerne kan ganges med nogle tal. Som et resultat får vi et system af lineære ligninger svarende til denne. I den indeholdt en ligning allerede kun én variabel, og erstatter værdien af denne med andre ligninger, og vi kommer til en løsning. En sådan tilføjelse er en af typerne af elementær transformation af systemet. Ved brug af Gauss-metoden kan vi bruge flere typer transformationer.

Animationen ovenfor viser, hvordan ligningssystemet gradvist bliver til et trapezformet. Det vil sige den, du så i den allerførste animation og overbeviste dig selv om, at det er nemt at finde værdierne for alle ukendte fra den. Hvordan man udfører en sådan transformation og selvfølgelig eksempler vil blive diskuteret yderligere.

Når man løser systemer af lineære ligninger med et vilkårligt antal ligninger og ukendte i ligningssystemet og i systemets udvidede matrix Kan:

omarranger linjer (dette blev nævnt i begyndelsen af denne artikel);
hvis andre transformationer resulterer i lige store eller proportionale rækker, kan de slettes, undtagen én;
fjern "nul" rækker, hvor alle koefficienter er lig med nul;
gange eller dividere enhver streng med et bestemt tal;
til en hvilken som helst linje tilføje en anden linje, ganget med et bestemt tal.

Som et resultat af transformationerne får vi et system af lineære ligninger svarende til denne.

Algoritme og eksempler på løsning af et system af lineære ligninger med en kvadratisk matrix af systemet ved hjælp af Gauss-metoden

Lad os først overveje at løse systemer af lineære ligninger, hvor antallet af ubekendte er lig med antallet af ligninger. Matrixen for et sådant system er kvadratisk, det vil sige, at antallet af rækker i det er lig med antallet af kolonner.

Eksempel 2. Løs et system af lineære ligninger ved hjælp af Gauss-metoden

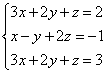
Når vi løste systemer af lineære ligninger ved hjælp af skolemetoder, gangede vi en af ligningerne led for led med et vist tal, således at koefficienterne for den første variabel i de to ligninger var modsatte tal. Når man tilføjer ligninger, elimineres denne variabel. Gauss-metoden fungerer på samme måde.

For at forenkle udseendet af løsningen lad os skabe en udvidet matrix af systemet:

I denne matrix er koefficienterne for de ukendte placeret til venstre før den lodrette linje, og de frie led er placeret til højre efter den lodrette linje.

For at gøre det lettere at dividere koefficienter for variable (for at opnå division med enhed) Lad os bytte den første og anden række af systemmatricen. Vi opnår et system svarende til dette, da i et system af lineære ligninger kan ligningerne ombyttes:

Brug af den nye første ligning fjerne variablen x fra den anden og alle efterfølgende ligninger. For at gøre dette tilføjer vi til den anden række i matrixen den første række ganget med (i vores tilfælde med ), til den tredje række - den første række ganget med (i vores tilfælde med ).

Dette er muligt pga

Hvis der var mere end tre ligninger i vores system, så skulle vi tilføje til alle efterfølgende ligninger den første linje, ganget med forholdet mellem de tilsvarende koefficienter, taget med et minustegn.

Som et resultat får vi en matrix svarende til dette system af et nyt ligningssystem, hvor alle ligninger, startende fra den anden ikke indeholder en variabel x :

For at forenkle den anden linje i det resulterende system skal du gange det med og få matrixen for et ligningssystem svarende til dette system:

Hold nu den første ligning af det resulterende system uændret, ved hjælp af den anden ligning eliminerer vi variablen y fra alle efterfølgende ligninger. For at gøre dette tilføjer vi den anden række til den tredje række i systemmatricen, ganget med (i vores tilfælde med ).

Hvis der var mere end tre ligninger i vores system, så skulle vi tilføje en anden linje til alle efterfølgende ligninger, ganget med forholdet mellem de tilsvarende koefficienter taget med et minustegn.

Som et resultat får vi igen matrixen af et system svarende til dette system af lineære ligninger:

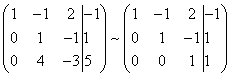
Vi har opnået et ækvivalent trapezformet system af lineære ligninger:

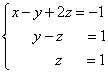
Hvis antallet af ligninger og variable er større end i vores eksempel, så fortsætter processen med sekventiel eliminering af variable, indtil systemmatrixen bliver trapezformet, som i vores demo-eksempel.

Vi finder løsningen "fra slutningen" - det omvendte træk. For det ud fra den sidste ligning vi bestemmer z:
.
Ved at indsætte denne værdi i den foregående ligning, vi finder y:

Fra den første ligning vi finder x:

Svar: Løsningen til dette ligningssystem er .

: i dette tilfælde vil det samme svar blive givet, hvis systemet har en unik løsning. Hvis systemet har et uendeligt antal løsninger, så vil dette være svaret, og det er emnet for den femte del af denne lektion.

Løs selv et system af lineære ligninger ved hjælp af Gauss-metoden, og se derefter på løsningen

Her har vi igen et eksempel på et konsistent og bestemt system af lineære ligninger, hvor antallet af ligninger er lig med antallet af ukendte. Forskellen fra vores demo-eksempel fra algoritmen er, at der allerede er fire ligninger og fire ukendte.

Eksempel 4. Løs et system af lineære ligninger ved hjælp af Gauss-metoden:

Nu skal du bruge den anden ligning til at eliminere variablen fra efterfølgende ligninger. Lad os udføre det forberedende arbejde. For at gøre det mere bekvemt med forholdet mellem koefficienter, skal du få en i anden kolonne i den anden række. For at gøre dette skal du trække den tredje fra den anden linje og gange den resulterende anden linje med -1.

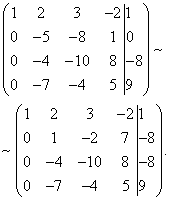
Lad os nu udføre den faktiske eliminering af variablen fra den tredje og fjerde ligning. For at gøre dette skal du tilføje den anden linje, ganget med , til den tredje linje, og den anden, ganget med , til den fjerde linje.

Nu, ved at bruge den tredje ligning, eliminerer vi variablen fra den fjerde ligning. For at gøre dette skal du lægge den tredje linje til den fjerde linje ganget med . Vi opnår en udvidet trapezformet matrix.

Vi fik et ligningssystem, som det givne system svarer til:

Følgelig er de resulterende og givne systemer kompatible og bestemte. Vi finder den endelige løsning "fra slutningen". Fra den fjerde ligning kan vi direkte udtrykke værdien af variablen "x-fire":

Vi erstatter denne værdi i systemets tredje ligning og får

Endelig værdisubstitution

Den første ligning giver

hvor finder vi "x først":

Svar: dette ligningssystem har en unik løsning .

Du kan også tjekke systemets løsning på en lommeregner ved hjælp af Cramers metode: i dette tilfælde vil det samme svar blive givet, hvis systemet har en unik løsning.

Løsning af anvendte problemer ved hjælp af Gauss-metoden ved hjælp af eksemplet med et problem på legeringer

Systemer af lineære ligninger bruges til at modellere virkelige objekter i den fysiske verden. Lad os løse et af disse problemer - legeringer. Lignende problemer er problemer med blandinger, omkostningerne eller andelen af individuelle varer i en gruppe af varer og lignende.

Eksempel 5. Tre stykker legering har en samlet masse på 150 kg. Den første legering indeholder 60% kobber, den anden - 30%, den tredje - 10%. Desuden er der i den anden og tredje legering tilsammen 28,4 kg mindre kobber end i den første legering, og i den tredje legering er der 6,2 kg mindre kobber end i den anden. Find massen af hvert stykke af legeringen.

Løsning. Vi sammensætter et system af lineære ligninger:

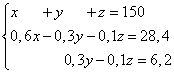
Hvis vi multiplicerer anden og tredje ligning med 10, får vi et ækvivalent system af lineære ligninger:

Vi opretter en udvidet matrix af systemet:

OBS, lige ud. Ved at addere (i vores tilfælde fratrække) en række ganget med et tal (vi anvender det to gange), sker følgende transformationer med systemets udvidede matrix:

Den direkte flytning er slut. Vi opnåede en udvidet trapezformet matrix.

Vi anvender det omvendte træk. Vi finder løsningen fra slutningen. Det ser vi.

Fra den anden ligning finder vi

Fra den tredje ligning -

Du kan også tjekke systemets løsning på en lommeregner ved hjælp af Cramers metode: i dette tilfælde vil det samme svar blive givet, hvis systemet har en unik løsning.

Enkelheden i Gauss' metode fremgår af, at det tog den tyske matematiker Carl Friedrich Gauss kun 15 minutter at opfinde den. Ud over den metode, der er opkaldt efter ham, kendes ordsproget "Vi bør ikke forveksle det, der virker utroligt og unaturligt for os med det absolut umulige" fra Gauss' værker - en slags kort instruktion om at gøre opdagelser.

I mange anvendte problemer er der måske ikke en tredje begrænsning, det vil sige en tredje ligning, så skal du løse et system af to ligninger med tre ubekendte ved hjælp af Gauss-metoden, eller omvendt er der færre ubekendte end ligninger. Vi vil nu begynde at løse sådanne ligningssystemer.

Ved hjælp af Gauss-metoden kan du bestemme, om et hvilket som helst system er kompatibelt eller inkompatibelt n lineære ligninger med n variabler.

Gauss-metoden og lineære ligningssystemer med et uendeligt antal løsninger

Det næste eksempel er et konsistent, men ubestemt system af lineære ligninger, det vil sige med et uendeligt antal løsninger.

Efter at have udført transformationer i systemets udvidede matrix (omarrangere rækker, gange og dividere rækker med et bestemt tal, tilføje en anden til en række), kunne rækker i formen vises

Hvis i alle ligninger har formen

Frie led er lig med nul, det betyder, at systemet er ubestemt, det vil sige, at det har et uendeligt antal løsninger, og ligninger af denne type er "overflødige", og vi udelukker dem fra systemet.

Eksempel 6.

Løsning. Lad os skabe en udvidet matrix af systemet. Derefter, ved hjælp af den første ligning, eliminerer vi variablen fra efterfølgende ligninger. For at gøre dette skal du tilføje den første til den anden, tredje og fjerde linje ganget med:

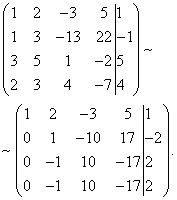
Lad os nu tilføje den anden linje til den tredje og fjerde.

Som et resultat kommer vi til systemet

De sidste to ligninger blev til formens ligninger. Disse ligninger er opfyldt for enhver værdi af de ukendte og kan kasseres.

For at opfylde den anden ligning kan vi vælge vilkårlige værdier for og , så vil værdien for blive bestemt unikt: . Fra den første ligning findes værdien for også unikt: .

Både det givne og det sidste system er konsistente, men usikre, og formlerne

for vilkårlige og give os alle løsninger af et givet system.

Gauss metode og systemer af lineære ligninger uden løsninger

Det næste eksempel er et inkonsekvent system af lineære ligninger, det vil sige et, der ikke har nogen løsninger. Svaret på sådanne problemer er formuleret på denne måde: systemet har ingen løsninger.

Som allerede nævnt i forbindelse med det første eksempel, efter at have udført transformationer, kunne rækker af formen vises i systemets udvidede matrix

svarende til en ligning af formen

Hvis der blandt dem er mindst én ligning med et frit led, der ikke er nul (dvs. ), så er dette ligningssystem inkonsekvent, det vil sige, det har ingen løsninger, og dets løsning er komplet.

Eksempel 7. Løs systemet af lineære ligninger ved hjælp af Gauss-metoden:

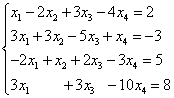
Løsning. Vi sammensætter en udvidet matrix af systemet. Ved at bruge den første ligning udelukker vi variablen fra efterfølgende ligninger. For at gøre dette skal du lægge den første linje ganget med til den anden linje, den første linje ganget med den tredje linje og den første linje ganget med den fjerde linje.

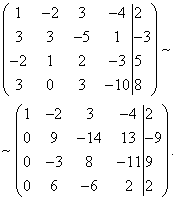
Nu skal du bruge den anden ligning til at eliminere variablen fra efterfølgende ligninger. For at opnå heltalsforhold mellem koefficienter bytter vi anden og tredje række i systemets udvidede matrix.

For at udelukke den tredje og fjerde ligning skal du lægge den anden ganget med , til den tredje linje, og den anden ganget med , til den fjerde linje.

Nu, ved at bruge den tredje ligning, eliminerer vi variablen fra den fjerde ligning. For at gøre dette skal du lægge den tredje linje til den fjerde linje ganget med .

Det givne system svarer derfor til følgende:

Det resulterende system er inkonsekvent, da dets sidste ligning ikke kan opfyldes af nogen værdier af de ukendte. Derfor har dette system ingen løsninger.

2. Ændringer af Gauss-metoden

Gaussisk metode med valg af hovedelementet. Gauss-metodens hovedbegrænsning er antagelsen om, at alle elementer, som opdelingen udføres i ved hvert fremadgående trin, ikke er lig med nul. Disse elementer kaldes hovedelementer og er placeret på hoveddiagonalen af matrix A.

Hvis hovedelementet på et eller andet trin i fremadgående bevægelse er 0, så er yderligere løsning af systemet umulig. Hvis hovedelementet har en lille værdi, tæt på nul, er en stærk stigning i fejl mulig på grund af en kraftig stigning i den absolutte værdi af koefficienterne opnået som følge af division. I sådanne situationer bliver den Gaussiske metode ustabil.

Gauss-metoden med valget af hovedelementet giver os mulighed for at udelukke forekomsten af sådanne tilfælde.

Ideen med denne metode er som følger. Ved et eller andet k'te trin i den fremadgående bevægelse er det ikke den næste nummererede variabel x k, der er udelukket fra ligningerne, men den variabel, hvis koefficient er den største i absolut værdi. Dette sikrer, at der ikke er nogen division med nul, og at metoden forbliver stabil.

Hvis i det k. trin ¹ vælges som hovedelement, så skal rækkerne med tallene k og p og kolonnerne med tallene k og q i matrix A¢ byttes om.

Omarrangering af rækkerne påvirker ikke løsningen, da det svarer til at vende ligningerne i systemet, men at omarrangere kolonnerne betyder, at man ændrer nummereringen af variablerne. Derfor skal information om alle omarrangerede kolonner bevares, så efter at det omvendte træk er gennemført, kan den oprindelige nummerering af variablerne gendannes.

Der er to enklere modifikationer af Gauss-metoden:

Med valg af hovedelementet for kolonne;

Med valg af hovedelementet for linje.

I det første tilfælde vælges det største element i absolut værdi af den k. række (blandt elementerne i = ) som hovedelement. I den anden - det største element i absolut værdi af den kth kolonne (blandt elementerne, i = ). Den første tilgang er mest udbredt, da nummereringen af variabler ikke ændres her.

Det skal bemærkes, at disse modifikationer kun gælder for fremadgående bevægelse af den Gaussiske metode. Det omvendte træk udføres uden ændringer, men efter at have opnået en løsning, kan det være nødvendigt at genoprette den oprindelige nummerering af variablerne.

LU nedbrydning. I moderne computersoftware implementeres den Gaussiske metode ved hjælp af LU-nedbrydning, som forstås som at repræsentere koefficientmatricen A som produktet A = LU af to matricer L og U, hvor L er den nederste trekantede matrix, U er den øverste trekantede matrix

Hvis LU-udvidelsen opnås, reduceres løsningen af det oprindelige ligningssystem (2) til den sekventielle løsning af de følgende to ligningssystemer med trekantede koefficientmatricer

lineær algebraisk ligning numerisk

hvor Y = er en vektor af hjælpevariable.

Denne tilgang giver dig mulighed for gentagne gange at løse systemer af lineære ligninger med forskellige højre sider B. I dette tilfælde udføres den mest arbejdskrævende del (LU-nedbrydning af matrix A) kun én gang. Denne procedure svarer til den fremadgående kørsel af Gauss-metoden og har et kompleksitetsestimat på O(n 3). Yderligere løsning af ligningssystemer (6) og (7) kan udføres flere gange (for forskellige B), og løsningen af hver af dem svarer til det omvendte af Gauss-metoden og har et beregningsmæssigt kompleksitetsestimat på O(n 2 ).

For at opnå LU-nedbrydningen kan du bruge følgende algoritme.

1. For det oprindelige system (1), udfør den fremadgående progression af Gauss-metoden og opnå et system af trekantede ligninger (5).

2. Bestem elementerne i matricen U efter reglen

u ij = C ij (i = ; j = )

3. Beregn elementerne i matrix L efter reglerne

Beregningsformler for løsning af system (6) har følgende form:

y1 = b1/111;

Beregningsformler til løsning af system (7)

(i = n - 1, n - 2, …, 1).

Samtidig er det faktisk en ret arbejdskrævende proces at finde den inverse matrix, og dens programmering kan næppe kaldes en elementær opgave. Derfor anvendes i praksis oftere numeriske metoder til løsning af systemer af lineære ligninger. Numeriske metoder til løsning af lineære ligningssystemer omfatter følgende: Gauss-metoden, Cramer-metoden, iterative metoder. I Gauss-metoden arbejder man for eksempel med...

35437 x4=0,58554 5 x1=1,3179137 x2=-1,59467 x3=0,35371 x4=0,58462 6 x1=1,3181515 x2=-1,59506 x3=0,35455 forskellige komp tion og integration 5.1 Numeriske differentieringsmetoder 5.1. 1 Beskrivelsesmetode Lad os antage, at i et naboskab af punktet xi er funktionen F (x) differentiabel et tilstrækkeligt antal gange. ...

I Turbo Pascal 7.0 til løsning af systemer af lineære algebraiske ligninger ved hjælp af den simple iterationsmetode. 1.2 Matematisk formulering af opgaven Lad A være en ikke-singular matrix, og vi skal løse et system, hvor de diagonale elementer i matrix A er ikke-nul. 1.3 Gennemgang af eksisterende numeriske metoder til løsning af problemet Gauss-metoden I Gauss-metoden bruger SLAE-matricen ækvivalent...

numre). Dernæst, ved hjælp af formlerne (2), findes xn-1, xn-2,..., x1 successivt for henholdsvis i=n-1, n-2,...,1. Således er løsningen af ligninger af type (1) beskrevet ved en metode kaldet sweep-metoden, som reduceres til beregninger ved hjælp af tre simple formler: at finde de såkaldte sweep-koefficienter δi, λi ved hjælp af formlerne (3) for i=1 ,2,...,n (direkte sweep) og derefter ukendt xi af...