Online metode til usikre koefficienter med detaljeret løsning. Usikker koefficientmetode

Metoden er anvendelig til at minimere logiske algebrafunktioner af et hvilket som helst antal variable.

Lad os overveje tilfældet med tre variable. En boolsk funktion i DNF kan repræsenteres i form af alle slags konjunktive udtryk, der kan indgå i DNF:

hvor kО(0,1) er koefficienter. Metoden består i at udvælge koefficienter på en sådan måde, at den resulterende DNF er minimal.

Hvis vi nu sætter alle mulige værdier af variablerne fra 000 til 111, får vi 2 n (2 3 = 8) ligninger til bestemmelse af koefficienterne k:

I betragtning af de mængder, som funktionen har en nulværdi for, bestem koefficienterne, der er lig med 0, og streg dem ud fra ligningerne, hvis højre side indeholder 1. Af de resterende koefficienter i hver ligning er én koefficient lig med én, hvilket bestemmer konjunktionen af den laveste rang. De resterende koefficienter er lig med 0. Altså enhedskoefficienterne k bestemme den passende minimumsform.

Eksempel. Minimer en given funktion

hvis værdierne er kendt: ; ; ; ; ; ; ; .

Løsning.

Efter at have streget nulkoefficienterne ud får vi:

=1;

=1.

Lad os sætte lighedstegn mellem en koefficient, der svarer til konjunktionen af den laveste rang og vender de sidste fire ligninger til 1, og i den første ligning er det tilrådeligt at sidestille koefficienten til 1. De resterende koefficienter er sat til 0.

Svar: type minimeret funktion.

Det skal bemærkes, at metoden med ubestemte koefficienter er effektiv, når antallet af variable er lille og ikke overstiger 5-6.

Multidimensionel terning

Lad os overveje en grafisk repræsentation af en funktion i form af en flerdimensionel terning. Hver top n-dimensionel terning kan sættes i overensstemmelse med enhedens bestanddel.

Delmængden af markerede hjørner er en afbildning på n-dimensionel terning af en boolsk funktion fra n variable i SDNF.

For at vise funktionen fra n variabler præsenteret i enhver DNF, er det nødvendigt at etablere en overensstemmelse mellem dens minitermer og elementer n-dimensionel terning.

En miniterm af (n-1) rang kan betragtes som resultatet af sammenklæbning af to minitermer n-th rang, dvs.

På n-dimensional terning dette svarer til at erstatte to hjørner, der kun adskiller sig i koordinatværdier x i, der forbinder disse hjørner med en kant (en kant siges at dække de hjørner, der falder ind på den).

Således miniterms ( n Den -1) orden svarer til kanterne af en n-dimensionel terning.

Tilsvarende korrespondancen af miniterms ( n-2) ordens ansigter n-dimensionel terning, som hver dækker fire hjørner (og fire kanter).

Elementer n-dimensionel terning, karakteriseret ved S målinger kaldes S- terninger

Så hjørner er 0-terninger, kanter er 1-terninger, flader er 2-terninger osv.

For at opsummere kan vi sige, at minitermen ( n-S) rang i DNF for funktionen n viste variabler S-en terning, hver S-cube dækker alle de terninger af lavere dimension, som kun er forbundet med dens hjørner.

Eksempel. I fig. givet kortlægningen

Her minitermer og svarer til 1-terninger ( S=3-2=1), og miniterm x 3 vist til 2-terninger ( S=3-1=2).

Så enhver DNF er kortlagt til n-dimensionel terning i sin helhed S-kuber, der dækker alle hjørner svarende til de konstituerende enheder (0-terning).

Bestanddele. For variabler x 1,x 2,…x n udtryk kaldes enhedens bestanddel, og - en bestanddel af nul (betyder enten eller).

Denne bestanddel af én (nul) bliver kun til én (nul) med et tilsvarende sæt variabelværdier, som opnås, hvis alle variable tages lig med én (nul), og deres negationer lig med nul (én).

For eksempel: den konstituerende ene svarer til mængden (1011), og den konstituerende nul - sæt (1001).

Da SD(K)NF er en disjunktion (konjunktion) af bestanddelene af en (nul), kan det hævdes, at den boolske funktion, den repræsenterer f(x 1, x 2, …, x n) bliver kun til én (nul) for sæt af variabelværdier x 1, x 2, …, x n, svarende til disse repræsentanter. På andre sæt skifter denne funktion til 0 (én).

Det modsatte udsagn er også sandt, som det er baseret på måde at repræsentere evt Boolesk funktion angivet af tabellen.

For at gøre dette er det nødvendigt at skrive disjunktioner (konjunktioner) af bestanddelene af en (nul), svarende til sæt af værdier af variable, på hvilke funktionen har en værdi lig med en (nul).

For eksempel en funktion givet af en tabel

korrespondere

De resulterende udtryk kan konverteres til en anden form baseret på egenskaberne for logikkens algebra.

Det omvendte udsagn er også sandt: hvis nogle samling S-kuber dækker mængden af alle toppunkter svarende til enhedsværdier af funktionen, derefter disjunktionen svarende til disse S-kuber af minitermer er udtryk for denne funktion i DNF.

De siger, at sådan en samling S-kuber (eller deres tilsvarende minitermer) danner en dækning af funktionen. Ønsket om en minimal form forstås intuitivt som søgen efter en sådan dækning, antallet S-hvoraf der ville være færre kuber, og deres dimensioner S- mere. Dækningen svarende til minimumsformen kaldes minimumsdækningen.

For eksempel til funktionen på= belægningen tilpasser sig en ikke-minimal form.

Hilsen alle, kære venner!

Nå, tillykke! Vi har sikkert nået hovedmaterialet i integrationen af rationelle brøker - metode til usikre koefficienter. Stor og mægtig.) Hvad er hans majestæt og magt? Og det ligger i dens alsidighed. Det giver mening at tjekke det ud, ikke? Jeg advarer dig om, at der vil være flere lektioner om dette emne. Fordi emnet er meget langt, og materialet er ekstremt vigtigt.)

Jeg vil med det samme sige, at i dagens lektion (og også de efterfølgende) vil vi ikke beskæftige os så meget med integration, men... løse systemer af lineære ligninger! Ja Ja! Så dem der har problemer med systemer, gentager matricerne, determinanter og Cramers metode. Og til de kammerater, der har problemer med matricer, opfordrer jeg dig i værste fald til at genopfriske din hukommelse om i det mindste "skole"-metoderne til at løse systemer - substitutionsmetoden og term-for-term addition/subtraktion metoden.

For at begynde vores bekendtskab, lad os spole filmen lidt tilbage. Lad os kort vende tilbage til tidligere lektioner og analysere alle de fraktioner, som vi integrerede før. Direkte, uden nogen metode med ubestemte koefficienter! Her er de, disse fraktioner. Jeg sorterede dem i tre grupper.

Gruppe 1

I nævneren - lineær funktion enten alene eller til en vis grad. Med et ord er nævneren produktet identisk parentes af formularen (ha).

For eksempel:

(x+4) 1 = (x+4)

(x-10) 2 = (x-10)(x-10)

(2x+5) 3 = (2x+5)(2x+5)(2x+5)

Og så videre. Lad i øvrigt ikke parentesen forvirre dig (4x+5) eller (2x+5) 3 med koefficient k inde. Disse er stadig i deres kerne parenteser af formularen (ha). Fordi dette er det meste k fra sådanne beslag kan du altid tage den udenfor.

Sådan her:

Det er alt.) Og det er lige meget, hvad der præcist står i tælleren - bare dx eller en slags polynomium. Vi har altid udvidet tælleren i parentesens potenser (x-a), forvandlede den store fraktion til summen af små, placerede (hvor nødvendigt) en parentes under differentialet og integrerede.

Gruppe 2

Hvad har disse fraktioner til fælles?

Og det fælles er, at i alle nævnere er der kvadratisk trinomiumøkse 2 + bx+ c. Men ikke kun, nemlig i et enkelt eksemplar. Og her er det lige meget, om hans diskriminant er positiv eller negativ.

Sådanne brøker blev altid integreret på en af to måder - enten ved at udvide tælleren til potenser af nævneren eller ved at isolere det perfekte kvadrat i nævneren og derefter erstatte variablen. Det hele afhænger af den specifikke integrand.

Gruppe 3

Disse var de værste fraktioner at integrere. Nævneren indeholder et uopløseligt kvadratisk trinomium, og endda til den grad n. Men igen, i et enkelt eksemplar. For udover trinomiet er der ingen andre faktorer i nævneren. Sådanne fraktioner blev integreret over . Enten direkte eller reduceret til det efter isolering af det perfekte kvadrat i nævneren og efterfølgende udskiftning af variablen.

Men desværre er hele den rige variation af rationelle fraktioner ikke begrænset til kun disse tre betragtede grupper.

Men hvad nu hvis nævneren er forskellige beslag? For eksempel noget som:

(x-1)(x+1)(x+2)

Eller samtidig en parentes (ha) og et kvadratisk trinomium, noget lignende (x-10)(x 2 -2x+17)? Og i andre lignende tilfælde? Det er netop i sådanne tilfælde, at det kommer til undsætning metode til usikre koefficienter!

Jeg siger med det samme: for nu vil vi kun arbejde med korrekt i fraktioner. Dem, hvis tællergrad er strengt mindre end nævnergraden. Hvordan man håndterer uægte brøker er beskrevet detaljeret i brøker. Det er nødvendigt at vælge hele delen (polynomiet). Ved at dividere tælleren med nævneren med et hjørne eller ved at dekomponere tælleren - som du ønsker det. Og selv eksemplet er analyseret. Og du vil på en eller anden måde integrere polynomiet. Ikke lille allerede.) Men vi løser også eksempler på uægte brøker!

Og nu begynder vi at stifte bekendtskab. I modsætning til de fleste lærebøger om højere matematik vil vi ikke begynde vores bekendtskab med en tør og tung teori om algebras grundlæggende sætning, Bezouts sætning, om nedbrydningen af en rationel brøk til summen af de simpleste (mere om disse brøker senere) og anden træthed, men vi starter med et simpelt eksempel .

For eksempel skal vi finde følgende ubestemte integral:

Kig først på integranden. Nævneren er produktet af tre parenteser:

(x-1)(x+3)(x+5)

Og alle beslagene forskellige. Derfor virker vores gamle teknologi med udvidelsen af tælleren med nævnerens potens ikke længere denne gang: hvilken parentes skal fremhæves i tælleren? (x-1)? (x+3)? Det er ikke klart... At vælge et komplet kvadrat i nævneren er heller ikke en god idé: der er et polynomium der tredje grader (hvis du gange alle parenteser). Hvad skal man gøre?

Når man ser på vores fraktion, opstår der et helt naturligt ønske... Direkte uimodståeligt! Fra vores store fraktion, som ubehageligt integrere, på en eller anden måde lave tre små. I hvert fald sådan her:

Hvorfor skal du lede efter netop denne art? Og alt sammen fordi i denne form er vores første brøk allerede praktisk til integration! Lad os opsummere nævneren for hver lille brøk og - fremad.)

Er det overhovedet muligt at opnå en sådan nedbrydning? Gode nyheder! Den tilsvarende sætning i matematik siger - Ja du kan! En sådan nedbrydning eksisterer og er unik.

Men der er et problem: koefficienterne EN, I Og MED Vi Farvel vi ved det ikke. Og nu bliver vores hovedopgave netop identificere dem. Find ud af, hvad vores bogstaver er lig med EN, I Og MED. Deraf navnet - metode usikker koefficienter Lad os begynde vores fantastiske rejse!

Så vi har en lighed, der får os til at danse:

Lad os bringe alle tre brøker til højre til en fællesnævner og tilføje:

Nu kan vi roligt kassere nævnerne (da de er ens) og blot sætte lighedstegn mellem tællerne. Alt er som det plejer

Næste skridt åbne alle beslag(koefficienter EN, I Og MED Farvel bedre at lade det ligge udenfor):

Og nu (vigtigt!) stiller vi hele vores struktur op til højre efter anciennitet af grader: først samler vi alle vilkårene med x 2 i en bunke, derefter bare med x og til sidst samler vi de frie vilkår. Faktisk præsenterer vi simpelthen lignende og grupperer termerne efter potenser af x.

Sådan her:

Lad os nu forstå resultatet. Til venstre er vores oprindelige polynomium. Anden grad. Tælleren for vores integrand. Også til højre et eller andet polynomium af anden grad. Næse ukendte koefficienter. Denne ligestilling skal være gældende hvornår alle gyldige værdier af x. Brøkerne til venstre og højre var de samme (ifølge vores tilstand)! Det betyder, at de tæller og (dvs. vores polynomier) er også de samme. Derfor koefficienterne ved samme potens af x disse polynomier skal have vær ligeværdig!

Vi starter med højeste grad. Fra pladsen. Lad os se, hvilken slags koefficienter vi har x 2 venstre og højre. Til højre har vi summen af koefficienterne A+B+C, og til venstre er en toer. Sådan er vores første ligning født.

Vi skriver ned:

A+B+C = 2

Spise. Den første ligning er klar.)

Dernæst følger vi en faldende bane - vi ser på termer med X til første potens. Til højre ved X har vi 8A+4B+2C. Bøde. Og hvad har vi med X'et til venstre? Hm... Til venstre er der slet ikke noget led med et X! Der er kun 2x 2 - 3. Hvad skal man gøre? Meget simpelt! Det betyder, at koefficienten for x til venstre er lig med nul! Vi kan skrive vores venstre side sådan:

Og hvad? Vi har fuld ret.) Derfor ser den anden ligning sådan ud:

8 EN+4 B+2 C = 0

Nå, det er praktisk talt alt. Det er tilbage at sidestille de gratis vilkår:

15A-5B-3C = -3

Med et ord, ligning af koefficienter for de samme potenser af x sker i henhold til følgende skema:

Alle vores tre ligestilling skal være opfyldt samtidigt. Derfor sammensætter vi et system ud fra vores skrevne ligninger:

Systemet er ikke det sværeste for en flittig elev – tre ligninger og tre ubekendte. Beslut som du ønsker. Du kan bruge Cramer-metoden gennem matricer med determinanter, du kan bruge Gauss-metoden, du kan endda bruge den sædvanlige skolesubstitution.

Til at begynde med vil jeg løse dette system, som kulturelever normalt løser sådanne systemer. Nemlig Cramer-metoden.

Vi begynder løsningen med at tegne en systemmatrix. Lad mig minde dig om, at denne matrix kun er en plade, der består af koefficienter for ukendte.

Her er hun:

Først og fremmest, lad os beregne determinant for systemmatricen. Eller kort sagt, systemdeterminant. Det er normalt angivet med det græske bogstav ∆ ("delta"):

Godt, systemdeterminanten er ikke nul (-48≠0) . Fra teorien om systemer af lineære ligninger betyder dette faktum, at vores system er konsistent og har en unik løsning.

Næste trin er at beregne determinanter for ukendte ∆A, ∆B, ∆C. Lad mig minde dig om, at hver af disse tre determinanter opnås fra systemets hoveddeterminant ved at erstatte kolonnerne med koefficienter for de tilsvarende ukendte med en kolonne med frie udtryk.

Så vi laver determinanterne og beregner:

Jeg vil ikke forklare i detaljer teknikken til beregning af tredjeordens determinanter her. Og spørg ikke. Dette vil være en fuldstændig afvigelse fra emnet.) De, der er på emnet, forstår, hvad vi taler om. Og måske har du allerede gættet præcis, hvordan jeg beregnede disse tre determinanter.)

Det er det, alt er klar.)

Sådan løser kultiverede elever normalt systemer. Men... Ikke alle elever er venner med og kvalificerede. Desværre. For nogle forbliver disse simple begreber om højere matematik for evigt som kinesisk læsefærdighed og et mystisk monster i tågen...

Nå, især for sådanne ukulturerede studerende, foreslår jeg en mere velkendt løsning - metode til sekventiel eliminering af ukendte. Faktisk er dette en avanceret "skole" substitutionsmetode. Der vil kun være flere trin.) Men essensen er den samme. Den første ting jeg vil gøre er at fjerne variablen MED. For at gøre dette vil jeg udtrykke MED fra den første ligning og indsæt den i den anden og tredje:

Vi forenkler, bringer lignende og får et nyt system, allerede med to ukendt:

Nu, i dette nye system, er det også muligt at udtrykke en af variablerne i form af en anden. Men de mest opmærksomme elever vil nok bemærke, at koefficienterne foran variablen B – modsat. To og minus to. Derfor vil det være meget praktisk at lægge begge ligninger sammen for at eliminere variablen I og efterlad kun brevet EN.

Vi tilføjer venstre og højre del, mentalt forkorte 2B Og -2B og løs kun ligningen relativt EN:

Spise. Den første koefficient blev fundet: A = -1/24.

Bestem den anden koefficient I. For eksempel fra den øverste ligning:

Herfra får vi:

Store. Den anden koefficient blev også fundet: B = -15/8 . Der er stadig et brev tilbage MED. For at bestemme det bruger vi den øverste ligning, hvor vi udtrykker det igennem EN Og I:

Så:

OK, det hele er forbi nu. Ukendte odds fundet! Det er lige meget, om det er gennem Cramer eller gennem udskiftning. Hoved, Højre fundet.)

Derfor vil vores nedbrydning af en stor brøkdel til summen af små se sådan ud:

Og lad dig ikke forvirre af de resulterende fraktionskoefficienter: i denne procedure (metoden med ubestemte koefficienter) er dette det mest almindelige fænomen. :)

Nu er det meget tilrådeligt at kontrollere, om vi fandt vores koefficienter korrekt EN, B Og MED. Derfor tager vi nu kladden og husker ottende klasse - vi lægger alle tre små brøker tilbage.

Hvis vi får den oprindelige store fraktion, så er alt fint. Nej - det betyder, at slå mig og lede efter en fejl.

Fællesnævneren vil naturligvis være 24(x-1)(x+3)(x+5).

Gå:

Ja!!! Vi fik den oprindelige fraktion. Hvilket skulle tjekkes. Alt er godt. Så vær venlig ikke at slå mig.)

Lad os nu vende tilbage til vores oprindelige integral. Han er ikke blevet nemmere i denne tid, ja. Men nu hvor vores fraktion er blevet dekomponeret til en sum af små, er det blevet en sand fornøjelse at integrere den!

Se selv! Vi indsætter vores ekspansion i det originale integral.

Vi får:

Vi bruger linearitetens egenskaber og deler vores store integral op i en sum af små, og placerer alle konstanter uden for integraltegnene.

Vi får:

Og de resulterende tre små integraler er allerede nemme at tage .

Vi fortsætter integrationen:

Det er alt.) Og i denne lektion, spørg mig ikke, hvor logaritmerne i svaret kom fra! Enhver, der husker, ved og vil forstå alt. Og for dem, der ikke kan huske, følger vi linkene. Jeg sætter dem ikke bare der.

Endeligt svar:

Her er sådan en smuk treenighed: tre logaritmer - en kujon, en rutineret og en dunce. :) Og prøv, gæt sådan et tricky svar med det samme! Kun metoden med ubestemte koefficienter hjælper, ja. Faktisk kigger vi på dette til dette formål. Hvad, hvordan og hvor.

Som en træningsøvelse foreslår jeg, at du øver metoden og integrerer følgende fraktion:

Øv, find integralet, find det ikke svært! Svaret burde være noget som dette:

Metoden med ubestemte koefficienter er en stærk ting. Det sparer selv i den mest håbløse situation, når man alligevel konverterer en brøkdel. Og her kan nogle opmærksomme og interesserede læsere have en række spørgsmål:

- Hvad skal man gøre, hvis polynomiet i nævneren slet ikke er faktoriseret?

- HVORDAN skal man se efter nedbrydningen af enhver stor rationel fraktion til summen af små? I nogen form? Hvorfor netop dette og ikke det?

- Hvad skal man gøre, hvis der er flere faktorer i udvidelsen af nævneren? Eller parentes i potenser som (x-1) 2? I hvilken form skal vi lede efter nedbrydning?

- Hvad skal man gøre, hvis nævneren udover simple parenteser af formen (x-a) samtidig indeholder et uopløseligt kvadratisk trinomium? Lad os sige x 2 +4x+5? I hvilken form skal vi lede efter nedbrydning?

Nå, tiden er inde til grundigt at forstå, hvor benene vokser fra. I de næste lektioner.)

Metoden er anvendelig til at minimere logiske algebrafunktioner af et hvilket som helst antal variable.

Lad os overveje tilfældet med tre variable. En boolsk funktion i DNF kan repræsenteres i form af alle slags konjunktive udtryk, der kan indgå i DNF:

hvor kО(0,1) er koefficienter. Metoden består i at udvælge koefficienter på en sådan måde, at den resulterende DNF er minimal.

Hvis vi nu sætter alle mulige værdier af variablerne fra 000 til 111, får vi 2 n (2 3 = 8) ligninger til bestemmelse af koefficienterne k:

Eksempel. Minimer en given funktion

hvis værdierne er kendt:
;
;
;
;
;
;
;
.

Løsning.

Efter at have streget nulkoefficienterne ud får vi:

=1;

=1.

Lad os sidestille koefficienten med enhed , svarende til konjunktionen af den laveste rang og dreje de sidste fire ligninger til 1, og i den første ligning er det tilrådeligt at sidestille koefficienten til 1 . De resterende koefficienter er sat til 0.

Svar: type minimeret funktion.

Det skal bemærkes, at metoden med ubestemte koefficienter er effektiv, når antallet af variable er lille og ikke overstiger 5-6.

Multidimensionel terning

Lad os overveje en grafisk repræsentation af en funktion i form af en flerdimensionel terning. Hver top n-dimensionel terning kan sættes i overensstemmelse med enhedens bestanddel.

Delmængden af markerede hjørner er en afbildning på n-dimensionel terning af en boolsk funktion fra n variable i SDNF.

For at vise funktionen fra n variabler præsenteret i enhver DNF, er det nødvendigt at etablere en overensstemmelse mellem dens minitermer og elementer n-dimensionel terning.

Minitermin af (n-1) rang
kan betragtes som resultatet af limning af to minitermer n-th rang, dvs.

På n-dimensional terning dette svarer til at erstatte to hjørner, der kun adskiller sig i koordinatværdier x jeg, der forbinder disse hjørner med en kant (en kant siges at dække de hjørner, der falder ind på den).

Således minitermer ( n Den -1) orden svarer til kanterne af en n-dimensionel terning.

Tilsvarende korrespondancen af miniterms ( n-2) ordens ansigter n-dimensionel terning, som hver dækker fire hjørner (og fire kanter).

Elementer n-dimensionel terning, karakteriseret ved S målinger kaldes S- terninger

Så hjørner er 0-terninger, kanter er 1-terninger, flader er 2-terninger osv.

For at opsummere kan vi sige, at minitermen ( n-S) rang i DNF for funktionen n viste variabler S-en terning, hver S-cube dækker alle de terninger af lavere dimension, der kun er forbundet med dens hjørner.

Eksempel. I fig. givet kortlægningen

Her er minivilkår
Og
svarer til 1-terninger ( S=3-2=1), og miniterm x 3 vist til 2-terninger ( S=3-1=2).

Så enhver DNF er kortlagt til n-dimensionel terning i sin helhed S-kuber, der dækker alle hjørner svarende til de konstituerende enheder (0-terning).

Bestanddele. For variabler x 1 ,x 2 ,…x n udtryk
kaldes enhedens bestanddel, og
- bestanddel af nul ( betyder enten , eller ).

Denne bestanddel af én (nul) bliver kun til én (nul) med ét tilsvarende sæt variabelværdier, som opnås, hvis alle variable tages lig med én (nul), og deres negationer lig med nul (én).

For eksempel: konstituerende enhed
svarer til mængden (1011), og bestanddelen er nul
- sæt (1001).

Da SD(K)NF er en disjunktion (konjunktion) af bestanddelene af én (nul), kan det hævdes, at den boolske funktion, den repræsenterer f(x 1 , x 2 ,…, x n) bliver kun til én (nul) for sæt af variabelværdier x 1 , x 2 ,…, x n, svarende til disse repræsentanter. På andre sæt skifter denne funktion til 0 (én).

Det modsatte udsagn er også sandt, som det er baseret på måde at repræsentere evt Boolesk funktion angivet af tabellen.

For at gøre dette er det nødvendigt at skrive disjunktioner (konjunktioner) af bestanddelene af en (nul), svarende til sæt værdier af variabler, hvor funktionen har en værdi lig med en (nul).

For eksempel en funktion givet af en tabel

korrespondere

De resulterende udtryk kan konverteres til en anden form baseret på egenskaberne for logikkens algebra.

For eksempel til funktionen på=
belægningen svarer til en ikke-minimum form:

ris a) på=,

et overtræk på ris b) på=
, ris c) på=
minimal.

Ris. Funktionsdækning på=:

a) ikke-minimal; b), c) minimum.

Viser en funktion på n-målt klart og enkelt med n3. En firedimensionel terning kan afbildes som vist i fig., der viser funktionen af fire variable og dens minimumsdækning svarende til udtrykket på=

Brug af denne metode når n>4 kræver så komplekse formationer, at det mister alle sine fordele.

En rationel funktion er en brøkdel af formen, hvis tæller og nævner er polynomier eller produkter af polynomier.

Eksempel 1. Trin 2.

Vi multiplicerer de ubestemte koefficienter med polynomier, der ikke er i denne individuelle brøk, men som er i andre resulterende brøker:

Vi åbner parenteserne og sætter lighedstegn mellem tælleren for den oprindelige integrand med det resulterende udtryk:

På begge sider af ligheden leder vi efter led med samme potens af x og sammensætter et ligningssystem ud fra dem:

Vi annullerer alle x'erne og får et ækvivalent system af ligninger:

Således er den endelige udvidelse af integranden til en sum af simple brøker:

Eksempel 2. Trin 2. På trin 1 opnåede vi følgende dekomponering af den oprindelige fraktion til summen af simple fraktioner med ubestemte koefficienter i tællere:

Nu begynder vi at lede efter usikre koefficienter. For at gøre dette, sidestiller vi tælleren for den oprindelige brøk i funktionsudtrykket med tælleren for udtrykket opnået efter at have reduceret summen af brøker til en fællesnævner:

Nu skal du oprette og løse et ligningssystem. For at gøre dette sidestiller vi variablens koefficienter i den tilsvarende grad i tælleren for det oprindelige udtryk for funktionen og lignende koefficienter i udtrykket opnået i det foregående trin:

Vi løser det resulterende system:

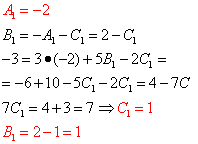
Så herfra

Eksempel 3. Trin 2. På trin 1 opnåede vi følgende dekomponering af den oprindelige fraktion til summen af simple fraktioner med ubestemte koefficienter i tællere:

Vi begynder at lede efter usikre koefficienter. For at gøre dette, sidestiller vi tælleren for den oprindelige brøk i funktionsudtrykket med tælleren for udtrykket opnået efter at have reduceret summen af brøker til en fællesnævner:

Som i tidligere eksempler sammensætter vi et ligningssystem:

Vi reducerer x'erne og får et ækvivalent system af ligninger:

Ved at løse systemet får vi følgende værdier af de usikre koefficienter:

Vi opnår den endelige dekomponering af integranden til summen af simple brøker:

Eksempel 4. Trin 2. På trin 1 opnåede vi følgende dekomponering af den oprindelige fraktion til summen af simple fraktioner med ubestemte koefficienter i tællere:

Vi ved allerede fra tidligere eksempler, hvordan man kan sidestille tælleren for den oprindelige brøk med udtrykket i tælleren, der opnås efter at have dekomponeret brøken i summen af simple brøker og bringe denne sum til en fællesnævner. Derfor præsenterer vi kun for kontrolformål det resulterende ligningssystem:

Ved at løse systemet får vi følgende værdier af de usikre koefficienter:

Vi opnår den endelige dekomponering af integranden til summen af simple brøker:

Eksempel 5. Trin 2. På trin 1 opnåede vi følgende dekomponering af den oprindelige fraktion til summen af simple fraktioner med ubestemte koefficienter i tællere:

Vi reducerer uafhængigt denne sum til en fællesnævner, og sidestiller dette udtryks tæller med tælleren for den oprindelige brøk. Resultatet skal være følgende ligningssystem:

Ved at løse systemet får vi følgende værdier af de usikre koefficienter:

Vi opnår den endelige dekomponering af integranden til summen af simple brøker:

Eksempel 6. Trin 2. På trin 1 opnåede vi følgende dekomponering af den oprindelige fraktion til summen af simple fraktioner med ubestemte koefficienter i tællere:

Vi udfører de samme handlinger med dette beløb som i de foregående eksempler. Resultatet skal være følgende ligningssystem:

Ved at løse systemet får vi følgende værdier af de usikre koefficienter:

Vi opnår den endelige dekomponering af integranden til summen af simple brøker:

Eksempel 7. Trin 2. På trin 1 opnåede vi følgende dekomponering af den oprindelige fraktion til summen af simple fraktioner med ubestemte koefficienter i tællere:

Efter visse handlinger med den resulterende mængde skal følgende ligningssystem opnås:

Ved at løse systemet får vi følgende værdier af de usikre koefficienter:

Vi opnår den endelige dekomponering af integranden til summen af simple brøker:

Eksempel 8. Trin 2. På trin 1 opnåede vi følgende dekomponering af den oprindelige fraktion til summen af simple fraktioner med ubestemte koefficienter i tællere:

Lad os foretage nogle ændringer i de handlinger, der allerede er blevet bragt til automatik for at opnå et ligningssystem. Der findes en kunstig teknik, der i nogle tilfælde hjælper med at undgå unødvendige beregninger. Ved at bringe summen af brøker til en fællesnævner, opnår vi og sidestiller tælleren for dette udtryk med tælleren for den oprindelige brøk, vi opnår.

Ligestilling (I) er identitet. Ved at reducere det til heltalsform opnår vi ligheden mellem 2 polynomier. Men en sådan lighed er altid kun opfyldt under betingelse af term-for-term lighed af disse polynomier.

Ved at sidestille koefficienterne for de samme potenser af x på venstre og højre side af ligheden får vi et system af lineære ligninger for ukendte koefficienter, der skal løses.

Da ekspansion (I) altid eksisterer for enhver egentlig rationel fraktion, er det resulterende system altid konsistent.

Denne metode til at finde koefficienter kaldes metoden med usikre koefficienter (en metode til at sammenligne koefficienter).

Lad os give et eksempel på dekomponering af en rationel funktion i elementære brøker.

Eksempel 6.6.27. Opdel brøker i elementære brøker.

erstatte den sidste ligning med den anden

Dermed,
.

x=2 ;

x=3 .

Bør; .

Delværdimetoden kræver mindre arbejdskraft og fortjener derfor særlig opmærksomhed ved integration af rationelle brøker.

Hvis nævnerens rødder kun er reelle, er det tilrådeligt at bruge denne metode til at bestemme ukendte koefficienter.

I andre tilfælde kan begge metoder kombineres for at bestemme ukendte koefficienter.

Kommentar. Metoden med delværdier bruges også i andre tilfælde, men her skal identiteten differentieres.

For at integrere rigtige rationelle brøker er det således nok at være i stand til at:

1) integrere elementære fraktioner;

2) nedbryde rationelle brøker til elementære.

3. Integration af rationelle brøker

Skema til integration af rationelle brøker:

At integrere rationelle brøker ;

Hvor P(x) og Q(x) er polynomier med reelle koefficienter, udføres tre trin sekventielt.

Første skridt. Hvis brøken er uegentlig, dvs. graden af tælleren P(x) er større end eller lig med graden af nævneren Q(x), isoleres hele delen af den rationelle brøk ved at dividere tælleren med nævneren iht. til reglen for at dividere et polynomium med et polynomium. Herefter kan den rationelle brøk skrives som en sum:

1) den valgte heltalsdel – polynomiet M(x);

2) korrekt restfraktion :

Andet trin.

Korrekt restfraktion nedbrydes i efterfølgende fraktioner.

For at gøre dette skal du finde rødderne af ligningen Q(x)=0 og dekomponere nævneren Q(x) i faktorer af første og anden grad med reelle koefficienter:

I denne udvidelse af nævneren svarer 1. grads faktorer til reelle rødder, og faktorerne i 2. grad svarer til parallelle konjugerede rødder.

Koefficienten for en større grad af x i nævneren Q(x) kan betragtes som lig med 1, da dette altid kan opnås ved at dividere P(x) og Q(x) med den.

Herefter nedbrydes den rigtige restfraktion i simpleste (elementære) fraktioner.

Tredje trin. Find integralerne af den valgte heltalsdel og alle elementære brøker (ved hjælp af metoderne beskrevet ovenfor), som derefter tilføjes.

Eksempel 6.6.28.

Under integraltegnet er der en ukorrekt rationel brøk, da graden af tælleren er lig med graden af nævneren, så vi vælger heltalsdelen.