и секущей плоскостью, которая параллельна ее основанию.
Или другими словами: усеченная пирамида — это такой многогранник, который образован пирамидой и ее сечением, параллельным основанию.
Сечение, которое параллельно основанию пирамиды делит пирамиду на 2 части. Часть пирамиды меж ее основанием и сечением — это усеченная пирамида .
Это сечение для усеченной пирамиды оказывается 1-ним из оснований этой пирамиды.
Расстояние меж основаниями усеченной пирамиды является высотой усеченной пирамиды .
Усеченная пирамида будет правильной , когда пирамида, из которой она была получена, тоже была правильной.
Высота трапеции боковой грани правильной усеченной пирамиды является апофемой правильной усеченной пирамиды.
Свойства усеченной пирамиды.
1. Каждая боковая грань правильной усеченной пирамиды является равнобокими трапециями одной величины.
2. Основания усеченной пирамиды являются подобными многоугольниками.
3. Боковые ребра правильной усеченной пирамиды имеют равную величину и один наклонен по отношению к основанию пирамиды.
4. Боковые грани усеченной пирамиды являются трапециями.
5. Двугранные углы при боковых ребрах правильной усеченной пирамиды имеют равную величину.
6. Отношение площадей оснований: S 2 /S 1 = k 2 .
Формулы для усеченной пирамиды.
Для произвольной пирамиды:
Объем усеченной пирамиды равен 1/3 произведения высоты h (OS ) на сумму площадей верхнего основания S 1 (abcde ), нижнего основания усеченной пирамиды S 2 (ABCDE ) и средней пропорциональной между ними.
Объем пирамиды:
где S 1 , S 2 — площади оснований,
h — высота усеченной пирамиды.
Площадь боковой поверхности ![]() равняется сумме площадей боковых граней усеченной пирамиды.
равняется сумме площадей боковых граней усеченной пирамиды.
Для правильной усеченной пирамиды:
Правильная усеченная пирамида — многогранник, который образован правильной пирамидой и ее сечением, которое параллельно основанию.
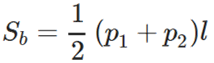
Площадь боковой поверхности правильной усеченной пирамиды равна ½ произведения суммы периметров ее оснований и апофемы.
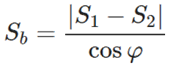
где S 1 , S 2 — площади оснований,
φ — двугранный угол у основания пирамиды.
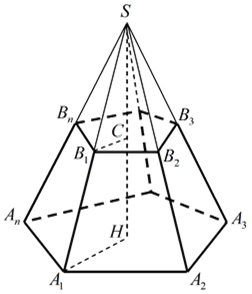
CH является высотой усеченной пирамиды, P 1 и P 2 — периметрами оснований, S 1 и S 2 — площадями оснований, S бок — площадью боковой поверхности, S полн — площадью полной поверхности:
Сечение пирамиды плоскостью, параллельной основанию.
Сечение пирамиды плоскостью, которое параллельно ее основанию (перпендикулярной высоте) разделяет высоту и боковые ребра пирамиды на пропорциональные отрезки.
Сечение пирамиды плоскостью, которое параллельно ее основанию (перпендикулярной высоте) - это многоугольник, который подобен основанию пирамиды, при этом коэффициент подобия этих многоугольников соответствует отношению их расстояний от вершины пирамиды.
Площади сечений, которые параллельны основанию пирамиды, относятся как квадраты их расстояний от вершины пирамиды.
Следующий уникальный калькулятор служит для перевода экзотических единиц длины в…
Следующий онлайн калькулятор о фунтах. Ранее он был очень популярен,…
Следующий онлайн калькулятор может вычислить уровень жидкости в цилиндрической таре…
Следующий онлайн калькулятор переводит температуры между разными шкалами. Помните калькулятор…
Следующий калькулятор интересен тем, что он переводит древние российские денежные…
Следующий калькулятор будет очень полезен тем, кто решил купить или…
Следующий калькулятор работает очень просто, вам нужно ввести всего одно…
Следующий онлайн калькулятор считает рост человека благодаря русской системе мер…
Следующий онлайн калькулятор может вычислить габариты экрана телевизоров, компьютеров, проекторов,…
Перед вами 2 калькулятора: один поможет вам подобрать формат снимков…
Следующие 2 калькуляторы переводят заданное число плиток в квадратные метры…
Перед вами 2 онлайн-калькулятора. Они переводят меры площади из метрической…
Следующий необычный калькулятор переводит меры длины из русской системы в…
Перед вами 2 калькулятора, которые предназначены для перевода мер длины…
Следующий простенький калькулятор переводит введенную вами toC из кельвинов в…
Следующий калькулятор предназначен для перевода кг в фунты. Также есть…
Многогранник, у которого одна из граней – многоугольник, а все остальные грани – треугольники с общей вершиной, называется пирамидой.
Эти треугольники, из которых составлена пирамида, называют боковыми гранями , а оставшийся многоугольник – основанием пирамиды.
В основании пирамиды лежит геометрическая фигура – n-угольник. В таком случае пирамиду называют еще n-угольной .
Треугольную пирамиду, все ребра которой равны, называют тетраэдром.
Ребра пирамиды, которые не принадлежат основанию, называются боковыми , а их общая точка – это вершина пирамиды. Другие ребра пирамиды обычно называют сторонами основания .
Пирамиду называют правильной , если у нее в основании лежит правильный многоугольник, а все боковые ребра равны между собой.
Расстояние от вершины пирамиды до плоскости основания называется высотой пирамиды. Можно сказать, что высота пирамиды есть отрезок, перпендикулярный основанию, концы которого находятся в вершине пирамиды и на плоскости основания.
Для любой пирамиды имеют место следующие формулы:
1) S полн = S бок + S осн , где
S полн – площадь полной поверхности пирамиды;
S бок – площадь боковой поверхности, т.е. сумма площадей всех боковых граней пирамиды;
S осн – площадь основания пирамиды.
2) V = 1/3 S осн · Н , где
V – объем пирамиды;
Н – высота пирамиды.
Для правильной пирамиды имеет место:
S бок = 1/2 P осн h , где
P осн – периметр основания пирамиды;
h – длина апофемы, то есть длина высоты боковой грани, опущенной из вершины пирамиды.
Часть пирамиды, заключенная между двумя плоскостями – плоскостью основания и секущей плоскостью, проведенной параллельно основанию, называют усеченной пирамидой .
Основание пирамиды и сечение пирамиды параллельной плоскостью называются основаниями усеченной пирамиды. Остальные грани называют боковыми . Расстояние между плоскостями оснований называют высотой усеченной пирамиды. Ребра, которые не принадлежат основаниям, называются боковыми .
Кроме того, основания усеченной пирамиды подобные n-угольники . Если основания усеченной пирамиды – правильные многоугольники, а все боковые ребра равны между собой, то такая усеченная пирамида называется правильной .
Для произвольной усеченной пирамиды имеют место следующие формулы:
1) S полн = S бок + S 1 + S 2 , где
S полн – площадь полной поверхности;
S бок – площадь боковой поверхности, т.е. сумма площадей всех боковых граней усеченной пирамиды, которые представляют собой трапеции;
S 1 , S 2 – площади оснований;
2) V = 1/3(S 1 + S 2 + √(S 1 · S 2))H , где
V – объем усеченной пирамиды;
H – высота усеченной пирамиды.
Для правильной усеченной пирамиды также имеем:
S бок = 1/2(P 1 + P 2) · h, где
P 1 , P 2 – периметры оснований;
h – апофема (высота боковой грани, представляющей собой трапецию).
Рассмотрим несколько задач на усеченную пирамиду.
Задача 1.
В треугольной усеченной пирамиде с высотой, равной 10, стороны одного из оснований равны 27, 29 и 52. Определите объем усеченной пирамиды, если периметр другого основания равен 72.
Решение.
Рассмотрим усеченную пирамиду АВСА 1 В 1 С 1 , изображенную на рисунке1.
1. Объем усеченной пирамиды может быть найден по формуле
V = 1/3H · (S 1 + S 2 + √(S 1 · S 2)), где S 1 – площадь одного из оснований, можно найти по формуле Герона
S = √(p(p – a)(p – b)(p – c)),
т.к. в задаче даны длины трех сторон треугольника.
Имеем: p 1 = (27 + 29 + 52)/2 = 54.
S 1 = √(54(54 – 27)(54 – 29)(54 – 52)) = √(54 · 27 · 25 · 2) = 270.
2. Пирамида усеченная, а значит, в основаниях лежат подобные многоугольники. В нашем случае треугольник АВС подобен треугольнику А 1 В 1 С 1 . Кроме того, коэффициент подобия можно найти как отношение периметров рассматриваемых треугольников, а отношение их площадей будет равно квадрату коэффициента подобия. Таким образом, имеем:
S 1 /S 2 = (P 1) 2 /(P 2) 2 = 108 2 /72 2 = 9/4. Отсюда S 2 = 4S 1 /9 = 4 · 270/9 = 120.
Итак, V = 1/3 · 10(270 + 120 + √(270 · 120)) = 1900.
Ответ: 1900.
Задача 2.
В треугольной усеченной пирамиде через сторону верхнего основания проведена плоскость параллельно противоположному боковому ребру. В каком отношении разделился объем усеченной пирамиды, если соответственные стороны оснований относятся как 1: 2?
Решение.
Рассмотрим АВСА 1 В 1 С 1 – усеченную пирамиду, изображенную на рис. 2.
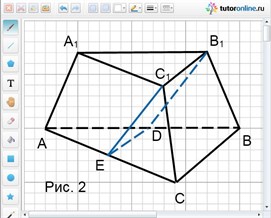
Так как в основаниях стороны относятся как 1: 2, то площади оснований относятся как 1: 4 (треугольник АВС подобен треугольнику А 1 В 1 С 1).
Тогда объем усеченной пирамиды равен:
V = 1/3h · (S 1 + S 2 + √(S 1 · S 2)) = 1/3h · (4S 2 + S 2 + 2S 2) = 7/3 · h · S 2 , где S 2 – площадь верхнего основания, h – высота.
Но объем призмы АDEA 1 B 1 C 1 составляет V 1 = S 2 · h и, значит,
V 2 = V – V 1 = 7/3 · h · S 2 - h · S 2 = 4/3 · h · S 2 .
Итак, V 2: V 1 = 3: 4.
Ответ: 3: 4.
Задача 3.
Стороны оснований правильной четырехугольной усеченной пирамиды равны 2 и 1, а высота равна 3. Через точку пересечения диагоналей пирамиды параллельно основаниям пирамиды проведена плоскость, делящая пирамиду на две части. Найти объем каждой из них.
Решение.
Рассмотрим усеченную пирамиду АВСDА 1 В 1 С 1 D 1 , изображенную на рис. 3.
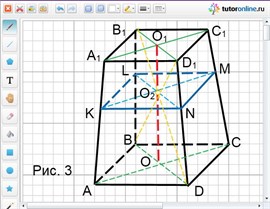
Обозначим О 1 О 2 = х, тогда ОО₂ = О 1 О – О 1 О 2 = 3 – х.
Рассмотрим треугольник В 1 О 2 D 1 и треугольник ВО 2 D:
угол В 1 О 2 D 1 равен углу ВО 2 D как вертикальные;
угол ВDO 2 равен углу D 1 B 1 O 2 и угол O 2 ВD равен углу B 1 D 1 O 2 как накрест лежащие при B 1 D 1 || BD и секущих B₁D и BD₁ соответственно.
Следовательно, треугольник В 1 О 2 D 1 подобен треугольнику ВО 2 D и имеет место отношение сторон:
В1D 1 /ВD = О 1 О 2 /ОО 2 или 1/2 = х/(х – 3), откуда х = 1.
Рассмотрим треугольник В 1 D 1 В и треугольник LО 2 B: угол В – общий, а так же имеется пара односторонних углов при B 1 D 1 || LM, значит, треугольник В 1 D 1 В подобен треугольнику LО 2 B, откуда В 1 D: LO 2 = OO 1: OO 2 = 3: 2, т.е.
LO 2 = 2/3 · B 1 D 1 , LN = 4/3 · B 1 D 1 .
Тогда S KLMN = 16/9 · S A 1 B 1 C 1 D 1 = 16/9.
Итак, V 1 = 1/3 · 2(4 + 16/9 + 8/3) = 152/27.
V 2 = 1/3 · 1 · (16/9 + 1 + 4/3) = 37/27.
Ответ: 152/27; 37/27.
www.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
