В класическата Нютонова механика размерите на телата и времевите интервали между събитията се считат за абсолютни стойности. Това означава, че можем да говорим за дължина на тела, без да посочваме дали това тяло е в покой или се движи. линейните мащаби (дължината на сегментите) и интервалите от време остават непроменени при преминаване от 1-ва референтна система към друга, т.е. не зависят от избора на референтна система.Тези идеи отразяват концепцията на Нютон за абсолютността на пространството и времето.
2.Кинематика
Това е раздел по механика, кат. Те изучават начини за описание на движението на телата, без да се интересуват от причините, които пораждат това движение.
3. Траектория
Това е линия в пространството, по която се движи частицата (геометричното местоположение на краищата на радиус вектора на частицата)
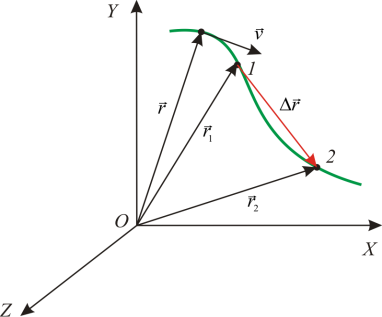
4.Преместване
д r = r 2 – r 1 за определен период от време Г Tе вектор, начертан от началната до крайната позиция на частицата (от точката 1 точно 2 ).
5. Вектор на средната скорост< v>.
Вектор на средната скорост< v> е вектор, равен на отношението на изместването на частиците към времето D Tза което е ангажирано:
Вектор на средната скорост < v> съвпада по посока с вектора на преместване дr.
6. Моментална скоростvчастици (или просто скорост) е вектор, равен на производната на радиус вектора rпо време:
Мигновена скорост vнасочена тангенциално към траекторията по посока на движението на частицата .SI:m/s
7. Ускорениесе нарича вектор, равен на производната по време на скоростта vчастици:
8. Закон за движението
се нарича времева зависимост на координатите на частиците:
Съществува проста връзка между векторния и координатния метод за описание на движението. Всеки вектор може да бъде определен чрез неговите проекции върху координатните оси. Например радиус векторът на частица:
Където аз, й, к– единични вектори на координатните оси.
9. Скорост с координатния метод за описване на движение
Скорост v, като всеки вектор, може да бъде представен чрез проекции върху оста на DSC:
Тези., скоростvчастиците могат да бъдат представени в следната форма: 
Вижда се, че компонентите на скоростта, изразени чрез функциите х(T), г(T), z(T), са равни
10.Ускорение с координатен метод за определяне на движениеУскорение а, като всеки вектор, може да бъде представен чрез проекции върху оста на DSC:
Тези., скоростvчастици могат да бъдат представени в следната форма
11.Пътекас(или Д с) е равно на разстоянието, измерено по траекторията и изминато от частицата по време на нейното движение (дължина на траекторията). Пътят е скаларна величина, неотрицателна и ненамаляваща.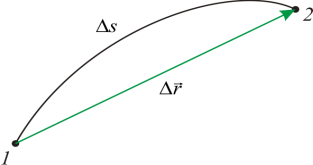 
12. Общо ускорение на частиците
аможе да се представи като сбор от два компонента, перпендикулярни един на друг:
Модул за пълно ускорение: 
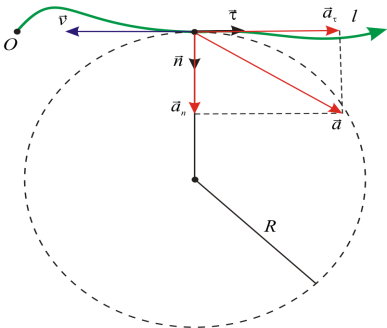
13.Тангенциално (тангенциално) ускорение
вектор а Tнасочена тангенциално към траекторията на частицата; при което а T v, ако движението е ускорено; а T v, ако движението е бавно. Тангенциалното ускорение на частица характеризира промяната в скоростта на частицата по модул (ако а t = 0, движението е равномерно).
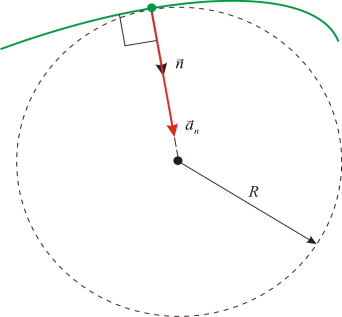
14.нормален (центростремителен)
ускорение
вектор а нвинаги перпендикулярна на допирателната към траекторията на движение, т.е. а н ^vИ а н ^а T.
Нормалното ускорение характеризира промяната на скоростта в посока (за линейно движение, когато Р = ¥, а н = 0)
15.Абсолютно твърдо тяло
в механиката наричат тяло, при движението на което разстоянията между произволни две негови точки остават непроменени. Така твърдото тяло не се деформира под въздействието на външни сили.
16. Брой степени на свобода на тялотое броят на независимите променливи (количества), които трябва да бъдат зададени, за да се определи позицията на тялото в пространството. Пример.Броят на степените на свобода на материална точка е 3 (три независими променливи (координати) х, г, z).
17.Ъглова скорост на тялото
Нека тялото се върти около ос З, реализирани за кратък период от време дтелементарен завой дй.Ъглова скорост на тялотонаречен вектор
вектор wсъвпада по посока с вектора дй, т.е. насочен по оста на въртене на тялото, така че да образува десен винт с посоката на въртене.Проекция на вектора wна ос Зи неговия модул: 
Мерна единица w
– радиани в секунда
(рад/сек)
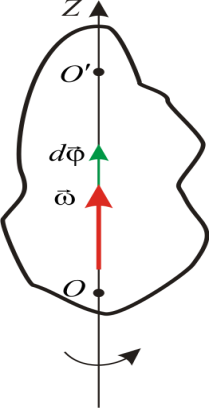
Фразата линейна скорост се използва, когато се разглежда криволинейното движение на тяло и иска да подчертае разликата между скоростта $v\ $ и престъпната скорост $\omega $. Най-често се пропуска думата линеен и се казва просто скорост.
Вектор на средната скорост
Определение
Съотношението на движението ($\Delta \overline(r)$) към периода от време, през който е настъпило това движение, се нарича Средната скорост($\left\langle \overline(v)\right\rangle $) движения:
\[\left\langle \overline(v)\right\rangle =\frac(\Delta \overline(r))(\Delta t)\left(1\right),\]
където $\Delta \overline(r)$ е промяната в радиус вектора на материална точка във времето $\Delta t$ (фиг. 1).
Векторът на средната скорост $\left\langle \overline(v)\right\rangle $ има същата посока като вектора $\Delta \overline(r)$, тъй като $\Delta t>0$. Дължината на сегмента, изобразяващ вектора на средната скорост (фиг. 1), не е свързана с дължината на вектора $\Delta \overline(r)$.
Средната скорост характеризира скоростта, с която се движи дадена точка. Тази характеристика се отнася за определен период от време.
Ако едно тяло се движи по крива, тогава пътят ($\Delta s$) е по-голям от модула на изместване ($\Delta r$) за същия период от време, тъй като дължината на дъгата винаги е по-малка от дължината на хордата, която го свива (фиг. 1). Пътят и преместването съвпадат при движение по права линия в една посока. Средната скорост на пътя се определя като:
\[\left\langle v\right\rangle (\rm =)\frac(\Delta s)(\Delta t)\left(2\right).\]
Средната скорост характеризира скоростта на движение на материална точка за краен период от време
Мигновена скорост
Определение
Чрез намаляване на периода от време, през който се разглежда движението на частицата ($\Delta t\до 0$), получаваме характеристика на движението на точка в даден момент от времето. Стойността е равна на:
\[\overline(v)=(\mathop(\lim )_(\Delta t\to 0) \left\langle \overline(v)\right\rangle =\ )(\mathop(\lim )_(\ Delta t\до 0) \frac(\Delta \overline(r))(\Delta t)=\frac(d\overline(r))(dt)\left(3\right),\ )\]
Наречен моментна скоростили просто скорост.
При изчисляване на скоростта по формула (3) е очевидно, че намаляването на интервала от време $\Delta t$ води до факта, че в крайна сметка следващите получени стойности на средната скорост ще се различават малко една от друга. Следователно, когато намират моментната скорост, те спират на крайна стойност $\Delta t,\ $но малка, за да могат да получат необходимата точност на стойността на скоростта.
Преминаването към границата (3) има геометричен смисъл. Векторът $\Delta \overline(r)$ е насочен по хордата, свързваща две точки от траекторията; сближаването на тези точки води до факта, че този вектор заема позицията на допирателна към траекторията на движение в дадена точка . Оказва се, че векторът на скоростта е насочен тангенциално към траекторията на движение. При праволинейно движение векторът на скоростта е насочен по права линия.
Скоростта на движение се определя по подобен начин:
Ако траекторията на материална точка е гладка крива, тогава колкото по-къса е дъгата, толкова по-близо е по дължина до дължината на хордата. При преминаването към границата при $\ \Delta t\to 0$ можем да приемем, че $\Delta s\to \Delta r$. следователно
Добавяне на скорост
Скоростта е векторна величина. Ако една материална точка участва в няколко движения, тогава нейната скорост се намира като векторна сума от скоростите на всяко от движенията:
\[\overline(v)=\sum\limits_i((\overline(v))_i\left(6\right).)\]
В някои случаи е удобно да се мисли за сложно движение като суперпозиция на няколко прости движения. Тогава равенството (6) може да се разглежда като правило за разлагане на вектора на скоростта на компоненти.
Скорост и ускорение на движение
Когато се движи неравномерно, материалната точка има ускорение ($\overline(a)$). Ускорението е първата производна на скоростта спрямо времето:
\[\overline(a)=\frac(d\overline(v))(dt)\left(7\right).\]
От израз (7) следва, че знаейки ускорението на точка, скоростта се намира като:
\[\overline(v)=\int\limits^(t_2)_(t_1)(\overline(a)dt)\left(8\right).\]
Ъглови и линейни скорости
При движение в кръг заедно със скоростта на движение по траекторията ($v$ - линейна скорост) се въвежда и ъгловата скорост ($\omega $), която характеризира скоростта на изменение на ъгъла на завъртане $\varphi $:
\[\omega =\frac(d\varphi )(dt)\left(9\right).\]
Връзката между линейните и ъгловите скорости се дава от израза:
Примери за задачи с решения
Пример 1
Упражнение.Промяната в радиус вектора, който определя позицията на материалната точка, се дава от уравнението: $\overline(r\ )\left(t\right)=t^4\overline(i)+3t^2\overline( j),$ където $\ overline(i)$ и $\overline(j)$ са единичните вектори на осите X и Y (фиг. 2). Каква е моментната скорост на точката в момент $t=1$c?
Решение.Нека дефинираме скоростта на частиците като:
\[\overline(v)=(\frac(d\overline(r))(dt) \left(1.1\right).\ )\]
Заместваме във формула (1.1) уравнението за радиус вектора $\overline(r\ )\left(t\right)=t^4\overline(i)+3t^2\overline(j),$ получаваме:
\[\overline(v)=\frac(d)(dt)\left(t^4\overline(i)+3t^2\overline(j)\right)=4t^3\overline(i)+6t \overline(j)\ \left(1.2\right).\]
От уравнение (1.2) виждаме, че:
\[\left\( \begin(array)(c) v_x=4t^3 \\ v_y=6t \end(array) \right.\left(1.3\right).\]
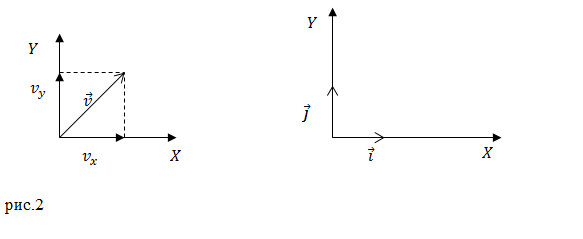
Следвайки теоремата на Питагор, намираме модула на скоростта като:
Нека изчислим скоростта, като заместим времето $t=1$c в получената формула:
Отговор.$v$=7,2 $\frac(m)(s)$
Пример 2
Упражнение.Материалната точка се движи по права линия. Ускорението на тази точка нараства в съответствие с графиката (фиг. 3). Каква ще бъде скоростта на точката в момент $t_1?$
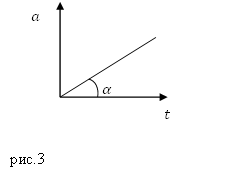
Решение.В графиката на фиг.3 ускорението е изобразено като права линия, идваща от началото на координатите; въз основа на фиг.3 записваме аналитичния израз за ускорение като:
където $k=tg\ \alpha $.
Намираме скоростта на точката като:
Отговор.$v=\frac(tg\ \alpha \cdot t^2_1)(2)$
Намалявайки неограничено периода от време t, през който м.т. се е движил в пространството в границата, когато t 0, получаваме моментната скорост, т.е.
Векторът на моментната скорост е равен на границата на съотношението на увеличението на радиус вектора mt към периода от време, през който е настъпило това увеличение, когато T 0 или равно на първата производна на радиус вектора по отношение на времето.
Векторът на моментната скорост в даден момент е насочен тангенциално към траекторията в дадена точка (фиг. 9).
Наистина, при t 0, когато точка M 2 се доближи до M 1, хордата (секущата) 
, се доближава до дължината на дъговия сегмент s и в границата s = , а секансът става допирателна. Това ясно се потвърждава от експерименти. Например, искрите при заточване на инструмент винаги са насочени тангенциално към шлифовъчното колело. Тъй като скоростта е векторна величина, нейният модул
.
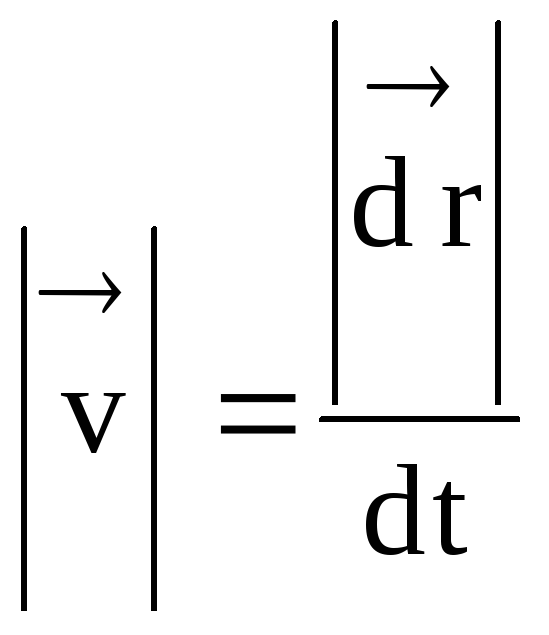В някои видове ускорители (например циклотрони и др.) Частиците се движат многократно по затворена траектория без спиране. Следователно във всяка точка на траекторията абсолютната стойност на вектора на моментната скорост трябва да се различава от нула. Това заключение се потвърждава не само от уравнение (15), но също така е в съответствие с концепцията за средна скаларна скорост (формула 11). Ако в уравнение (11) отидем до границата при t 0, тогава ще трябва да разгледаме такива малки участъци от пътя по траекторията s, които не се различават от модула на елементарния вектор на изместване . Тогава, въз основа на уравнение (11), можем да получим стойността на моментната скаларна скорост 
съвпадащ с големината на вектора на моментната скорост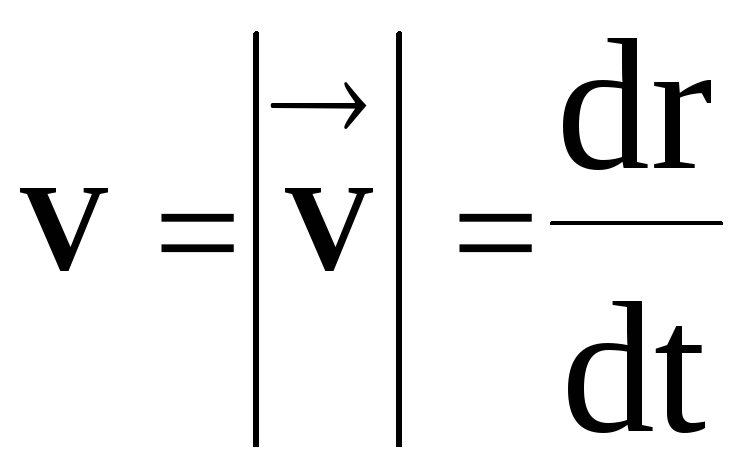 
,
тъй като r = s при t 0.
Едно уравнение на вектора на моментната скорост (15) може да бъде заменено с еквивалентна система от три скаларни уравнения, проекции на вектора на скоростта върху координатните оси
v x = dx/dt, v y = dy/dt, v z = dz/dt. (16)
Векторът на моментната скорост е свързан с неговите проекции върху координатните оси чрез израза
,
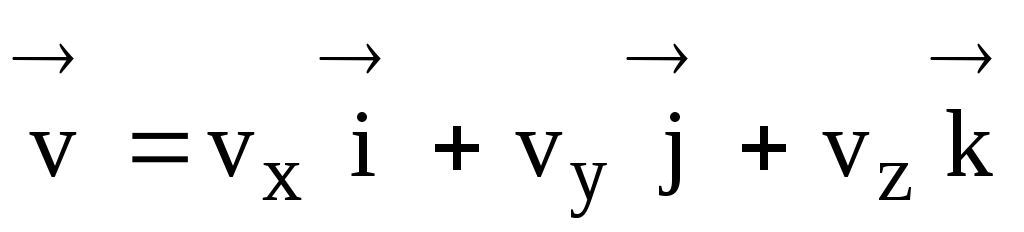(17)
Където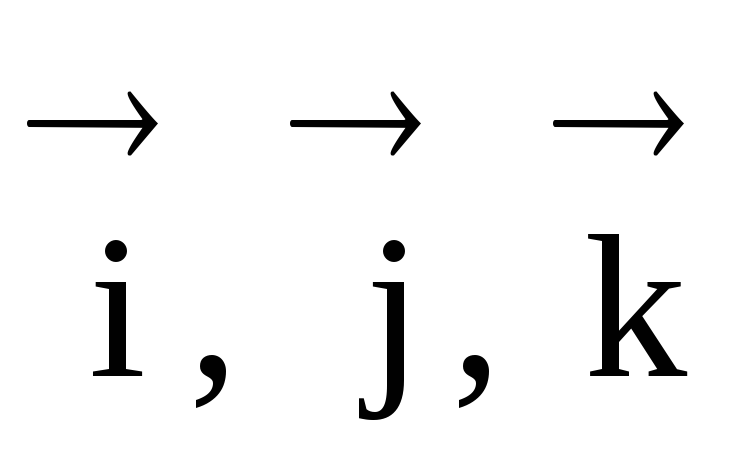 
– единични вектори, насочени съответно по осите X, Y, Z.
Модуло
.
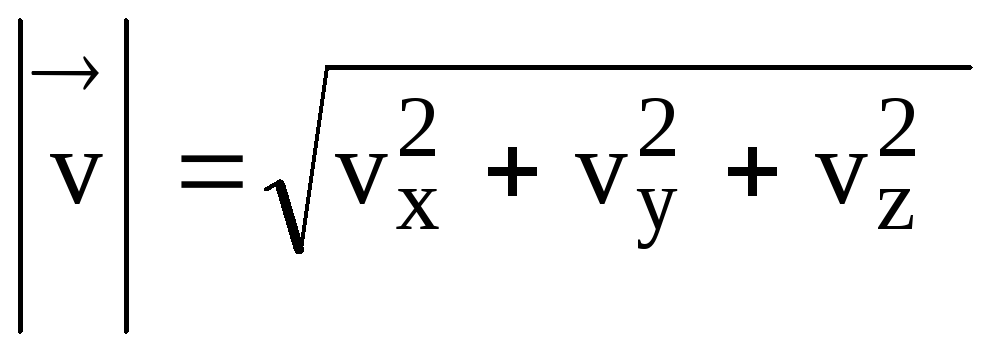(18)
По този начин векторът на скоростта характеризира скоростта на промяна на движението в пространството по величина и посока във времето. Скоростта е функция на времето.
1.12. Средно ускорение
При движение на тела скоростта в общия случай може да се променя както по големина, така и по посока.
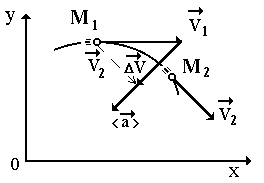
Нека m.t. в някакъв момент от време t 1 е в точка M 1 и се движи със скорост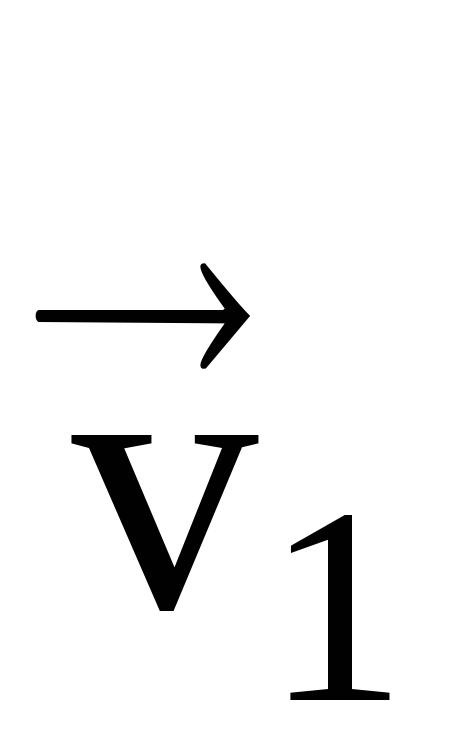 
, а в момент t 2 - в точка M 2 - със скорост 
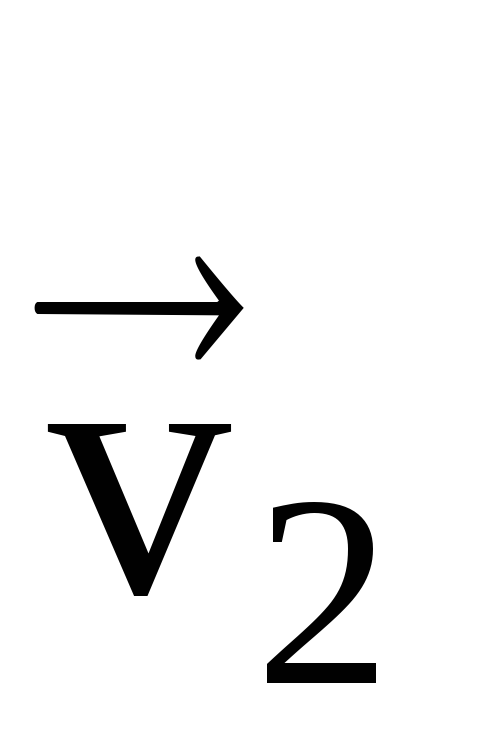(фиг. 10).
Нека преместим вектора 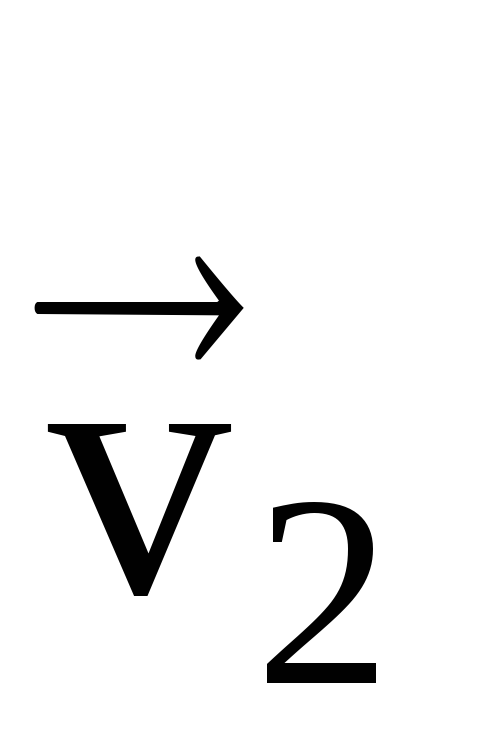успореден на себе си до точката M 1, така че началните точки на векторите да съвпадат 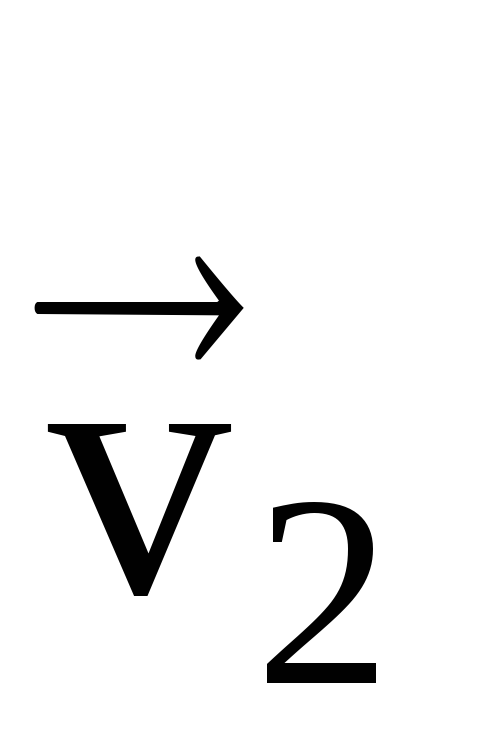И .
След това векторната разлика 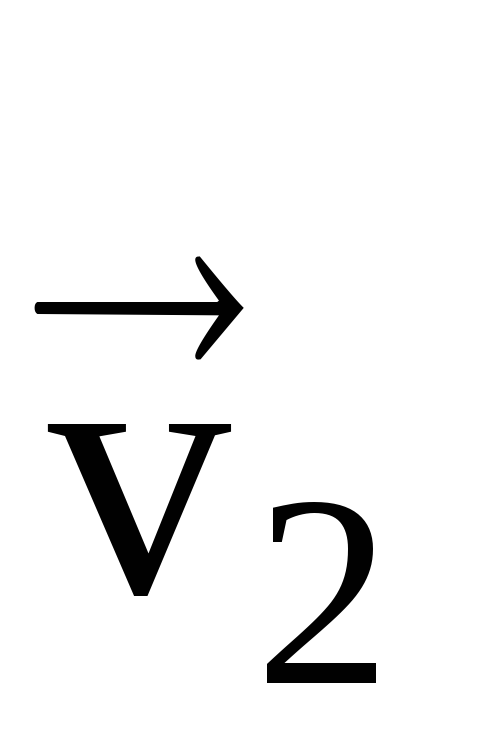И е векторът на изменение (приращение) на скоростта за период от време t = t 2 – t 1, т.е.
.
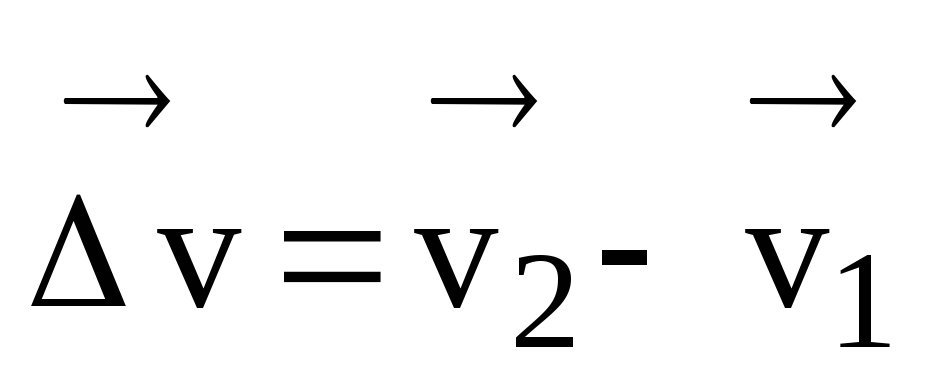(19)
Средният вектор на ускорението е равен на отношението на вектора на промяна на скоростта към периода от време, през който е настъпила тази промяна.
следователно
.
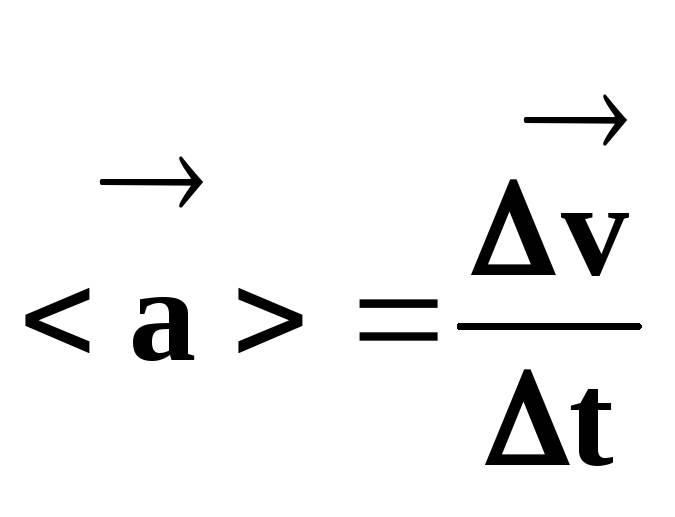(20)
Векторът на средното ускорение съвпада с посоката на вектора на промяна на скоростта и е насочен вътре в кривината на траекторията.
Едно векторно уравнение (1.20) съответства на система от три скаларни уравнения за проекции на вектора на средното ускорение върху координатните оси
Векторен модул за средно ускорение
.
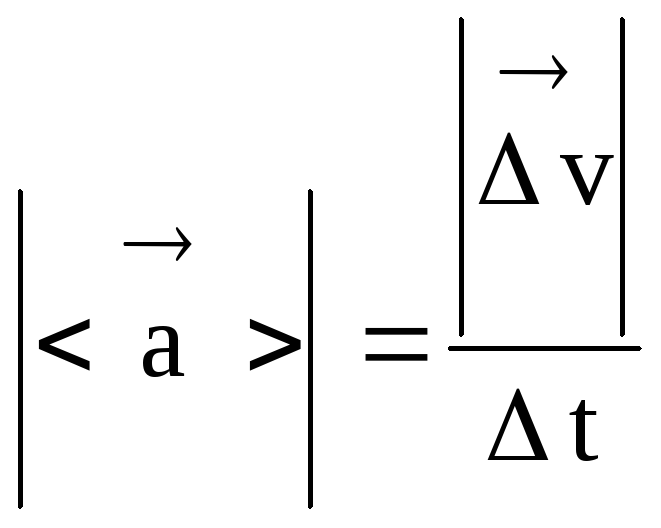(22)
Единицата SI за ускорение е метър в секунда на квадрат.
Ако големината на скоростта (или величината на вектора на скоростта) не се променя, движението е равномерно, когато големината на скоростта се променя, то е неравномерно.
УниформаНаречен движение, при което тялото изминава едни и същи пътища за всякакви равни интервали от време. В този случай големината на скоростта остава непроменена (в посоката, в която скоростта може да се промени, ако движението е криволинейно).
НаправоНаречен движение, при което траекторията е права линия. В този случай посоката на скоростта остава непроменена (големината на скоростта може да се промени, ако движението не е равномерно).
Униформа правасе нарича движение, което е едновременно равномерно и праволинейно. В този случай както величината, така и посоката остават непроменени.
В общия случай, когато тялото се движи, както големината, така и посоката на вектора на скоростта се променят. За да се характеризира колко бързо настъпват тези промени, се използва специално количество - ускорение.
Ускорение – това е количество, равно на съотношението на промяната в скоростта на тялото към продължителността на периода от време, през който е настъпила тази промяна в скоростта. Средното ускорение въз основа на това определение е m/s²:
Незабавно ускорениеНаречен физическа величина, равна на границата, към която клони средното ускорение за интервал∆t → 0, m/s²:
Тъй като скоростта може да се променя както по големина, така и по посока по траекторията, векторът на ускорението има два компонента.
Компонентът на вектора на ускорението a, насочен по допирателната към траекторията в дадена точка, се нарича тангенциално ускорение, което характеризира промяната на вектора на скоростта по величина.
Компонентът на вектора на ускорението a, насочен по нормалата към допирателната в дадена точка от траекторията, се нарича нормално ускорение. Той характеризира промяната в посоката на вектора на скоростта при криволинейно движение. Естествено, когато тялото се движи по траектория, която е права линия, нормалното ускорение е нула.
Праволинейното движение се нарича равномерно променливо, ако за някакъв период от време скоростта на тялото се променя с една и съща величина. В този случай отношението
∆V/ ∆t е едно и също за всички времеви интервали. Следователно големината и посоката на ускорението остават непроменени: a = const.
При праволинейно движение векторът на ускорението е насочен по линията на движение. Ако посоката на ускорението съвпада с посоката на вектора на скоростта, тогава величината на скоростта ще се увеличи. В този случай движението се нарича равномерно ускорено. Ако посоката на ускорението е противоположна на посоката на вектора на скоростта, тогава величината на скоростта ще намалее. В този случай движението се нарича равномерно бавно. В природата съществува естествено равномерно ускорено движение – това е свободно падане.
Свободно падане- Наречен падането на тяло, ако единствената сила, действаща върху него, е гравитацията. Експериментите, проведени от Галилей, показват, че по време на свободно падане всички тела се движат с еднакво ускорение на гравитацията и се означават с буквата ĝ. Близо до земната повърхност ĝ = 9,8 m/s². Ускорението на свободното падане се причинява от гравитацията от Земята и е насочено вертикално надолу. Строго погледнато, такова движение е възможно само във вакуум. Падането във въздуха може да се счита за приблизително безплатно.
Траекторията на свободно падащо тяло зависи от посоката на вектора на началната скорост. Ако тялото е хвърлено вертикално надолу, тогава траекторията е вертикален сегмент, а движението се нарича равномерно променливо. Ако тялото е хвърлено вертикално нагоре, тогава траекторията се състои от два вертикални сегмента. Първо, тялото се издига, движейки се еднакво бавно. В точката на максимално изкачване скоростта става нула, след което тялото се спуска, движейки се равномерно ускорено.
Ако векторът на началната скорост е насочен под ъгъл към хоризонта, тогава движението се извършва по парабола. Така се движат хвърлена топка, диск, спортист, изпълняващ дълъг скок, летящ куршум и др.