Формула за стандартно отклонение. Стандартно отклонение на формула в excel

$X$. Като начало нека си припомним следното определение:

Определение 1

Население-- съвкупност от произволно избрани обекти от даден тип, върху които се извършват наблюдения с цел получаване на конкретни стойности на случайна величина, извършвани при постоянни условия при изследване на една случайна величина от даден тип.

Определение 2

Обща вариация-- средноаритметичната стойност на квадратите на отклоненията на стойностите на варианта на популацията от тяхната средна стойност.

Нека стойностите на опция $x_1,\ x_2,\dots ,x_k$ имат съответно честоти $n_1,\ n_2,\dots ,n_k$. След това общата дисперсия се изчислява по формулата:

Нека разгледаме частен случай. Нека всички опции $x_1,\ x_2,\dots ,x_k$ са различни. В този случай $n_1,\ n_2,\dots ,n_k=1$. Откриваме, че в този случай общата дисперсия се изчислява по формулата:

Тази концепция също се свързва с концепцията за общо стандартно отклонение.

Определение 3

Общо стандартно отклонение

\[(\sigma )_g=\sqrt(D_g)\]

Дисперсия на извадката

Нека ни бъде дадена примерна популация по отношение на случайна променлива $X$. Като начало нека си припомним следното определение:

Определение 4

Извадкова популация-- част от избрани обекти от генералната съвкупност.

Определение 5

Дисперсия на извадката-- средно аритметично на стойностите на извадката от съвкупността.

Нека стойностите на опция $x_1,\ x_2,\dots ,x_k$ имат съответно честоти $n_1,\ n_2,\dots ,n_k$. След това дисперсията на извадката се изчислява по формулата:

Нека разгледаме частен случай. Нека всички опции $x_1,\ x_2,\dots ,x_k$ са различни. В този случай $n_1,\ n_2,\dots ,n_k=1$. Откриваме, че в този случай дисперсията на извадката се изчислява по формулата:

Също така свързана с тази концепция е концепцията за стандартно отклонение на извадката.

Определение 6

Примерно стандартно отклонение-- корен квадратен от общата дисперсия:

\[(\sigma )_в=\sqrt(D_в)\]

Коригирана дисперсия

За да се намери коригираната дисперсия $S^2$, е необходимо дисперсията на извадката да се умножи по частта $\frac(n)(n-1)$, т.е.

Тази концепция се свързва и с концепцията за коригирано стандартно отклонение, което се намира по формулата:

В случай, че стойностите на вариантите не са дискретни, а представляват интервали, тогава във формулите за изчисляване на общите или извадковите дисперсии стойността на $x_i$ се приема за стойност на средата на интервала до на който $x_i.$ принадлежи.

Пример за задача за намиране на дисперсията и стандартното отклонение

Пример 1

Извадката от съвкупността се определя от следната таблица на разпределение:

Снимка 1.

Нека намерим за него дисперсията на извадката, стандартното отклонение на извадката, коригираната дисперсия и коригираното стандартно отклонение.

За да разрешим този проблем, първо правим таблица за изчисление:

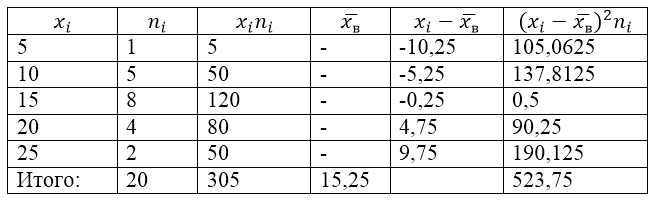
Фигура 2.

Стойността $\overline(x_в)$ (извадково средно) в таблицата се намира по формулата:

\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)\]

\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)=\frac(305)(20)=15,25\]

Нека намерим дисперсията на примера, използвайки формулата:

Примерно стандартно отклонение:

\[(\sigma )_в=\sqrt(D_в)\приблизително 5,12\]

Коригирана дисперсия:

\[(S^2=\frac(n)(n-1)D)_в=\frac(20)(19)\cdot 26.1875\приблизително 27.57\]

Коригирано стандартно отклонение.

Стандартно отклонение(синоними: стандартно отклонение, стандартно отклонение, квадратно отклонение; свързани термини: стандартно отклонение, стандартен спред) - в теорията на вероятностите и статистиката, най-често срещаният индикатор за дисперсията на стойностите на случайна променлива спрямо нейното математическо очакване. При ограничени масиви от извадки от стойности вместо математическото очакване се използва средноаритметичното от набора от извадки.

Енциклопедичен YouTube

  • 1 / 5

    Стандартното отклонение се измерва в мерни единици на самата случайна променлива и се използва при изчисляване на стандартната грешка на средната аритметична стойност, при конструиране на доверителни интервали, при статистическа проверка на хипотези, при измерване на линейната зависимост между случайни променливи. Дефинира се като корен квадратен от дисперсията на случайна променлива.

    Стандартно отклонение:

    s = n n − 1 σ 2 = 1 n − 1 ∑ i = 1 n (x i − x ¯) 2 ; (\displaystyle s=(\sqrt ((\frac (n)(n-1))\sigma ^(2)))=(\sqrt ((\frac (1)(n-1))\sum _( i=1)^(n)\left(x_(i)-(\bar (x))\right)^(2)));)
    • Забележка: Много често има несъответствия в имената на MSD (средно квадратно отклонение) и STD (стандартно отклонение) с техните формули. Например в модула numPy на езика за програмиране Python функцията std() е описана като „стандартно отклонение“, докато формулата отразява стандартното отклонение (деление на корена на извадката). В Excel функцията STANDARDEVAL() е различна (деление по корен от n-1).

    Стандартно отклонение(оценка на стандартното отклонение на случайна променлива хспрямо неговото математическо очакване въз основа на безпристрастна оценка на неговата дисперсия) s (\displaystyle s):

    σ = 1 n ∑ i = 1 n (x i − x ¯) 2 . (\displaystyle \sigma =(\sqrt ((\frac (1)(n))\sum _(i=1)^(n)\left(x_(i)-(\bar (x))\right) ^(2))).)

    Където σ 2 (\displaystyle \sigma ^(2))- дисперсия; x i (\displaystyle x_(i)) - азелемент на селекцията; n (\displaystyle n)- размер на извадката; - средно аритметично от извадката:

    x ¯ = 1 n ∑ i = 1 n x i = 1 n (x 1 + … + x n) . (\displaystyle (\bar (x))=(\frac (1)(n))\sum _(i=1)^(n)x_(i)=(\frac (1)(n))(x_ (1)+\lточки +x_(n)).)

    Трябва да се отбележи, че и двете оценки са пристрастни. В общия случай е невъзможно да се изгради безпристрастна оценка. Въпреки това оценката, базирана на безпристрастната оценка на дисперсията, е последователна.

    В съответствие с GOST R 8.736-2011 стандартното отклонение се изчислява по втората формула на този раздел. Моля, проверете резултатите.

    Правилото на трите сигми

    Правилото на трите сигми (3 σ (\displaystyle 3\sigma )) - почти всички стойности на нормално разпределена случайна променлива лежат в интервала (x ¯ − 3 σ ; x ¯ + 3 σ) (\displaystyle \left((\bar (x))-3\sigma ;(\bar (x))+3\sigma \right)). По-строго - с приблизително вероятност 0,9973, стойността на нормално разпределена случайна променлива се намира в посочения интервал (при условие, че стойността x ¯ (\displaystyle (\bar (x)))вярно, а не получено в резултат на обработка на пробата).

    Ако истинската стойност x ¯ (\displaystyle (\bar (x)))е неизвестен, тогава не трябва да използвате σ (\displaystyle \sigma ), А с. Така правилото на трите сигми се трансформира в правилото на трите с .

    Интерпретация на стойността на стандартното отклонение

    По-голямата стойност на стандартното отклонение показва по-голямо разпространение на стойностите в представения набор със средната стойност на набора; по-малка стойност, съответно, показва, че стойностите в набора са групирани около средната стойност.

    Например, имаме три набора от числа: (0, 0, 14, 14), (0, 6, 8, 14) и (6, 6, 8, 8). И трите набора имат средни стойности, равни на 7, и стандартни отклонения, съответно равни на 7, 5 и 1. Последният набор има малко стандартно отклонение, тъй като стойностите в набора са групирани около средната стойност; първият набор има най-голямата стойност на стандартното отклонение - стойностите в рамките на набора се различават значително от средната стойност.

    В общ смисъл стандартното отклонение може да се счита за мярка за несигурност. Например във физиката стандартното отклонение се използва за определяне на грешката на серия от последователни измервания на някаква величина. Тази стойност е много важна за определяне на правдоподобността на изследваното явление в сравнение със стойността, предвидена от теорията: ако средната стойност на измерванията се различава значително от стойностите, предвидени от теорията (голямо стандартно отклонение), тогава получените стойности или методът за получаването им трябва да бъдат проверени отново. идентифицирани с портфейлния риск.

    Климат

    Да предположим, че има два града с еднаква средна максимална дневна температура, но единият е разположен на брега, а другият в равнината. Известно е, че градовете, разположени на брега, имат много различни максимални дневни температури, които са по-ниски от градовете, разположени във вътрешността. Следователно стандартното отклонение на максималните дневни температури за крайбрежен град ще бъде по-малко, отколкото за втория град, въпреки факта, че средната стойност на тази стойност е същата, което на практика означава, че вероятността максималната температура на въздуха на всеки ден от годината ще бъде по-висока разлика от средната стойност, по-висока за град, разположен във вътрешността на страната.

    спорт

    Да приемем, че има няколко футболни отбора, които са оценени по някакъв набор от параметри, например брой отбелязани и допуснати голове, шансове за гол и т.н. Най-вероятно е най-добрият отбор в тази група да има по-добри стойности по повече параметри. Колкото по-малко е стандартното отклонение на екипа за всеки от представените параметри, толкова по-предвидим е резултатът на отбора; От друга страна, отбор с голямо стандартно отклонение трудно може да предвиди резултата, което от своя страна се обяснява с дисбаланс, например силна защита, но слаба атака.

    Използването на стандартното отклонение на параметрите на отбора позволява в една или друга степен да се прогнозира резултатът от мач между два отбора, като се оценяват силните и слабите страни на отборите и следователно избраните методи на борба.

    Стандартно отклонение

    Най-съвършената характеристика на вариацията е средното квадратично отклонение, което се нарича стандарт (или стандартно отклонение). Стандартно отклонение() е равен на корен квадратен от средното квадратно отклонение на отделните стойности на атрибута от средното аритметично:

    Стандартното отклонение е просто:

    Претегленото стандартно отклонение се прилага към групирани данни:

    Следното съотношение има място между средно квадратично и средно линейно отклонение при нормални условия на разпределение: ~ 1,25.

    Стандартното отклонение, което е основната абсолютна мярка за вариация, се използва при определяне на ординатните стойности на крива на нормално разпределение, при изчисления, свързани с организацията на наблюдението на извадката и установяване на точността на характеристиките на извадката, както и при оценката на граници на вариация на характеристика в хомогенна популация.

    18. Дисперсия, нейните видове, стандартно отклонение.

    Дисперсия на случайна променлива- мярка за разпространението на дадена случайна величина, т.е. нейното отклонение от математическото очакване. В статистиката често се използва обозначението или. Обикновено се нарича корен квадратен от дисперсията стандартно отклонение, стандартно отклонениеили стандартен спред.

    Обща дисперсия (σ 2) измерва вариацията на черта в нейната цялост под въздействието на всички фактори, които са причинили тази вариация. В същото време, благодарение на метода на групиране, е възможно да се идентифицира и измери вариацията, дължаща се на груповата характеристика и вариацията, възникваща под въздействието на неотчетени фактори.

    Междугрупова дисперсия (σ 2 м.гр) характеризира системната вариация, т.е. разликите в стойността на изследваната черта, които възникват под влиянието на чертата - факторът, който формира основата на групата.

    Стандартно отклонение(синоними: стандартно отклонение, стандартно отклонение, квадратно отклонение; свързани термини: стандартно отклонение, стандартен спред) - в теорията на вероятностите и статистиката, най-често срещаният индикатор за дисперсията на стойностите на случайна променлива спрямо нейното математическо очакване. При ограничени масиви от извадки от стойности вместо математическото очакване се използва средноаритметичното от набора от извадки.

    Стандартното отклонение се измерва в мерни единици на самата случайна променлива и се използва при изчисляване на стандартната грешка на средната аритметична стойност, при конструиране на доверителни интервали, при статистическа проверка на хипотези, при измерване на линейната зависимост между случайни променливи. Дефинира се като корен квадратен от дисперсията на случайна променлива.

    Стандартно отклонение:

    Стандартно отклонение(оценка на стандартното отклонение на случайна променлива хспрямо неговото математическо очакване въз основа на безпристрастна оценка на неговата дисперсия):

    къде е дисперсията; - азелемент на селекцията; - размер на извадката; - средно аритметично от извадката:

    Трябва да се отбележи, че и двете оценки са пристрастни. В общия случай е невъзможно да се изгради безпристрастна оценка. В този случай оценката, базирана на безпристрастната оценка на дисперсията, е последователна.

    19. Същност, обхват и ред за определяне на мода и медиана.

    В допълнение към средните мощности в статистиката, за относителното характеризиране на стойността на варираща характеристика и вътрешната структура на сериите на разпределение се използват структурни средни стойности, които са представени главно от мода и медиана.

    Мода- Това е най-разпространеният вариант на сериала. Модата се използва например при определяне на размера на дрехите и обувките, които са най-търсени сред клиентите. Режимът за дискретна серия е вариантът с най-висока честота. При изчисляване на режима за серия от интервални вариации е изключително важно първо да се определи модалният интервал (по максимална честота), а след това - стойността на модалната стойност на атрибута, като се използва формулата:

    § - значение на модата

    § - долна граница на модалния интервал

    § - интервална стойност

    § - модална интервална честота

    § - честота на интервала, предхождащ модала

    § - честота на интервала след модала

    Медиана -тази стойност на атрибута, ĸᴏᴛᴏᴩᴏᴇ лежи в основата на класираната серия и разделя тази серия на две равни по брой части.

    За определяне на медианата в дискретна серияако има налични честоти, първо изчислете полусумата на честотите и след това определете коя стойност на варианта попада върху нея. (Ако сортираната серия съдържа нечетен брой характеристики, тогава средното число се изчислява по формулата:

    M e = (n (общ брой функции) + 1)/2,

    в случай на четен брой характеристики, медианата ще бъде равна на средната стойност на двете характеристики в средата на реда).

    При изчисляване на медианата за интервални вариационни серииПърво определете средния интервал, в който се намира медианата, и след това определете стойността на медианата, като използвате формулата:

    § - необходимата медиана

    § - долна граница на интервала, който съдържа медианата

    § - интервална стойност

    § - сбор от честоти или брой членове на серията

    § - сумата от натрупаните честоти на интервалите, предхождащи медианата

    § - честота на медианния интервал

    Пример. Намерете модата и медианата.

    Решение: В този пример модалният интервал е във възрастовата група от 25-30 години, тъй като този интервал има най-висока честота (1054).

    Нека изчислим величината на модата:

    Това означава, че модалната възраст на студентите е 27 години.

    Нека изчислим медианата. Медианният интервал е във възрастовата група 25-30 години, тъй като в рамките на този интервал има опция͵ която разделя населението на две равни части (Σf i /2 = 3462/2 = 1731). След това заместваме необходимите числени данни във формулата и получаваме средната стойност:

    Това означава, че половината от студентите са на възраст под 27,4 години, а другата половина са над 27,4 години.

    В допълнение към модата и медианата се използват показатели като квартили, разделящи класираната серия на 4 равни части, децили - 10 части и персентили - на 100 части.

    20. Понятието извадково наблюдение и неговия обхват.

    Селективно наблюдениесе прилага при използване на непрекъснато наблюдение физически невъзможнопоради голямо количество данни или не е икономически целесъобразно. Физическата невъзможност възниква например при изследване на пътникопотоци, пазарни цени и семейни бюджети. Икономическа нецелесъобразност възниква при оценка на качеството на стоките, свързани с тяхното унищожаване, например дегустация, тестване на тухли за здравина и др.

    Избраните за наблюдение статистически единици са извадкова популацияили пробаи целият им масив - общо население(GS). При което брой единици в извадкатаобозначавам н, и през целия HS - н. Поведение n/Nобикновено се нарича относителен размерили примерен дял.

    Качеството на резултатите от пробното наблюдение зависи от представителност на извадката, тоест доколко е представителен в GS. За да се гарантира представителността на извадката, е изключително важно да се спазват принцип на случаен избор на единици, което предполага, че включването на HS единица в извадката не може да бъде повлияно от друг фактор освен случайност.

    Съществува 4 начина за произволен изборза проба:

    1. Всъщност произволноселекция или „метод на лото“, когато на статистическите стойности се присвояват серийни номера, записани върху определени обекти (например бъчви), които след това се смесват в контейнер (например в торба) и се избират на случаен принцип. На практика този метод се осъществява с помощта на генератор на произволни числа или математически таблици на произволни числа.
    2. Механичниизбор, според който всеки ( N/n)-та стойност на генералната съвкупност. Например, ако съдържа 100 000 стойности и трябва да изберете 1000, тогава всяка 100 000 / 1000 = 100-та стойност ще бъде включена в извадката. Освен това, ако не са класирани, тогава първият се избира на случаен принцип от първите сто, а числата на останалите ще бъдат със сто по-високи. Например, ако първата единица е № 19, тогава следващата трябва да бъде № 119, след това № 219, след това № 319 и т.н. Ако единиците на съвкупността са класирани, първо се избира номер 50, след това номер 150, след това номер 250 и т.н.
    3. Извършва се избор на стойности от разнороден масив от данни стратифицирани(стратифициран) метод, когато популацията първо се разделя на хомогенни групи, към които се прилага случаен или механичен подбор.
    4. Специален метод за вземане на проби е сериенселекция, при която произволно или механично избират не отделни стойности, а техните серии (последователности от някакво число до някакво число в редица), в рамките на които се извършва непрекъснато наблюдение.

    Качеството на извадковите наблюдения също зависи от тип проба: повтаря сеили неповторимо.При повторна селекцияСтатистическите стойности или техните серии, включени в извадката, се връщат към общата популация след употреба, като имат шанс да бъдат включени в нова извадка. Освен това всички стойности в общата съвкупност имат еднаква вероятност за включване в извадката. Неповторима селекцияозначава, че статистическите стойности или техните серии, включени в извадката, не се връщат в общата популация след употреба и следователно за останалите стойности на последната вероятността да бъдат включени в следващата извадка се увеличава.

    Неповтарящото се вземане на проби дава по-точни резултати и следователно се използва по-често. Но има ситуации, когато не може да се приложи (проучване на пътникопотоци, потребителско търсене и т.н.) и тогава се извършва повторна селекция.

    21. Максимална извадкова грешка при наблюдение, средна извадкова грешка, ред за изчисляването им.

    Нека разгледаме подробно изброените по-горе методи за формиране на извадкова съвкупност и възникващите грешки в представителността. Съвсем произволноизвадката се основава на произволно избиране на единици от съвкупността без никакви систематични елементи. Технически действителният случаен подбор се извършва чрез теглене на жребий (например лотарии) или използване на таблица със случайни числа.

    Правилният случаен подбор „в чист вид“ рядко се използва в практиката на селективното наблюдение, но е първоначалният сред другите видове подбор, той реализира основните принципи на селективното наблюдение. Нека разгледаме някои въпроси от теорията на метода за вземане на проби и формулата за грешка за проста случайна извадка.

    Пристрастност при вземане на проби- ϶ᴛᴏ разликата между стойността на параметъра в генералната съвкупност и неговата стойност, изчислена от резултатите от извадковото наблюдение. Важно е да се отбележи, че за средната количествена характеристика грешката на извадката се определя от

    Индикаторът обикновено се нарича максимална грешка на извадката. Средната стойност на извадката е случайна променлива, която може да приема различни стойности в зависимост от това кои единици са включени в извадката. Следователно грешките на извадката също са случайни променливи и могат да приемат различни стойности. Поради тази причина се определя средната стойност на възможните грешки - средна извадкова грешка, което зависи от:

    · размер на извадката: колкото по-голямо е числото, толкова по-малка е средната грешка;

    · степента на промяна в изследваната характеристика: колкото по-малка е вариацията на характеристиката и, следователно, дисперсията, толкова по-малка е средната извадкова грешка.

    При случаен повторен изборизчислява се средната грешка. На практика общата дисперсия не е известна точно, но в теорията на вероятностите е доказано, че . Тъй като стойността за достатъчно голямо n е близка до 1, можем да приемем, че . Тогава трябва да се изчисли средната извадкова грешка: . Но в случаите на малка извадка (с n<30) коэффициент крайне важно учитывать, и среднюю ошибку малой выборки рассчитывать по формуле .

    При произволно неповтарящо се вземане на пробидадените формули се коригират със стойността. Тогава средната неповтаряща се извадкова грешка е: И . защото винаги е по-малко от , тогава множителят () винаги е по-малък от 1. Това означава, че средната грешка при повторен избор винаги е по-малка, отколкото при повторен избор. Механично вземане на пробисе използва, когато генералната съвкупност е подредена по някакъв начин (например списъци с избиратели по азбучен ред, телефонни номера, номера на къщи и апартаменти). Изборът на единици се извършва на определен интервал, който е равен на обратната стойност на процента на извадката. И така, при 2% извадка се избират всеки 50 единици = 1/0,02, при 5% извадка, всеки 1/0,05 = 20 единици от общата съвкупност.

    Референтната точка се избира по различни начини: произволно, от средата на интервала, с промяна на референтната точка. Основното е да се избягват систематични грешки. Например при 5% извадка, ако първата единица е 13-та, то следващите са 33, 53, 73 и т.н.

    По отношение на точността, механичният подбор е близък до действителното произволно вземане на проби. Поради тази причина, за да се определи средната грешка на механичното вземане на проби, се използват подходящи формули за произволен избор.

    При типична селекцияизследваната популация е предварително разделена на хомогенни сходни групи. Например, когато се изследват предприятията, това са отрасли, подотрасли; когато се изследва населението, това са региони, социални или възрастови групи. След това се прави независим избор от всяка група механично или чисто на случаен принцип.

    Типичното вземане на проби дава по-точни резултати от другите методи. Типизирането на генералната съвкупност гарантира, че всяка типологична група е представена в извадката, което прави възможно елиминирането на влиянието на междугруповата вариация върху средната извадкова грешка. Следователно, когато се намира грешката на типична извадка според правилото за добавяне на дисперсии (), е изключително важно да се вземе предвид само средната стойност на груповите дисперсии. След това средната грешка при вземане на проби: с повторно вземане на проби, с неповтарящо се вземане на проби , Където – средната стойност на дисперсиите в рамките на групата в извадката.

    Сериен избор (или гнездо).използва се, когато съвкупността е разделена на серии или групи преди началото на извадковото изследване. Тези серии включват опаковане на готови продукти, студентски групи и бригади. Сериите за изследване се избират механично или чисто произволно, като в рамките на серията се извършва непрекъснат преглед на единици. Поради тази причина средната извадкова грешка зависи само от дисперсията между групите (между сериите), която се изчислява по формулата: където r е броят на избраните серии; – средно от i-тата серия. Средната грешка на серийното вземане на проби се изчислява: с многократно вземане на проби, с неповтарящо се вземане на проби , където R е общият брой серии. Комбиниранселекцията е комбинация от разгледаните методи за селекция.

    Средната извадкова грешка за всеки метод на извадка зависи главно от абсолютния размер на извадката и в по-малка степен от процента на извадката. Нека приемем, че са направени 225 наблюдения в първия случай от популация от 4500 единици, а във втория от популация от 225 000 единици. Дисперсиите и в двата случая са равни на 25. Тогава в първия случай, с 5% селекция, грешката на извадката ще бъде: Във втория случай, с 0,1% избор, той ще бъде равен на:

    Въпреки това, когато процентът на извадката беше намален с 50 пъти, грешката на извадката се увеличи леко, тъй като размерът на извадката не се промени. Да приемем, че размерът на извадката е увеличен до 625 наблюдения. В този случай грешката на извадката е: Увеличаването на извадката с 2,8 пъти със същия размер на популацията намалява размера на грешката на извадката с повече от 1,6 пъти.

    22. Методи и методи за формиране на извадкова съвкупност.

    В статистиката се използват различни методи за формиране на извадкови съвкупности, което се определя от целите на изследването и зависи от спецификата на обекта на изследване.

    Основното условие за провеждане на извадково изследване е да се предотврати появата на систематични грешки, произтичащи от нарушаване на принципа на равните възможности за всяка единица от генералната съвкупност, която да бъде включена в извадката. Предотвратяването на систематични грешки се постига чрез използването на научно обосновани методи за формиране на извадкова съвкупност.

    Съществуват следните методи за избор на единици от генералната съвкупност: 1) индивидуален подбор - за извадката се избират отделни единици; 2) групов подбор - извадката включва качествено хомогенни групи или серии от изследвани единици; 3) комбиниран подбор е комбинация от индивидуален и групов подбор. Методите за подбор се определят от правилата за формиране на извадкова съвкупност.

    Пробата трябва да бъде:

    • всъщност произволносе състои в това, че извадковата съвкупност се формира в резултат на случаен (непреднамерен) подбор на отделни единици от генералната съвкупност. В този случай броят на единиците, избрани в извадката от популацията, обикновено се определя въз основа на приетата пропорция на извадката. Пропорцията на извадката е съотношението на броя на единиците в извадката от съвкупността n към броя на единиците в генералната съвкупност N, ᴛ.ᴇ.
    • механиченсе състои в това, че подборът на единици в извадковата съвкупност се извършва от генералната съвкупност, разделена на равни интервали (групи). В този случай размерът на интервала в популацията е равен на реципрочната стойност на извадковия дял. И така, при 2% проба се избира всяка 50-та единица (1:0,02), при 5% проба, всяка 20-та единица (1:0,05) и т.н. Въпреки това, в съответствие с приетата пропорция на подбор, генералната популация е като че ли механично разделена на равни групи. От всяка група се избира само една единица за извадката.
    • типичен –при което генералната съвкупност първо се разделя на хомогенни типични групи. След това от всяка типична група се използва чисто произволна или механична извадка за индивидуален избор на единици в извадковата популация. Важна характеристика на типичната извадка е, че тя дава по-точни резултати в сравнение с други методи за подбор на единици в извадката;
    • сериен- при които генералната съвкупност е разделена на групи с еднакъв размер - серии. Сериите се избират в извадката. В рамките на серията се извършва непрекъснато наблюдение на единиците, включени в серията;
    • комбинирани- вземането на проби трябва да бъде двуетапно. В този случай населението първо се разделя на групи. След това се избират групи, а в рамките на последните се избират отделни единици.

    В статистиката се разграничават следните методи за избор на единици в извадкова съвкупност:

    • единичен етапвземане на проби - всяка избрана единица незабавно се подлага на изследване по зададен критерий (правилно произволно и серийно вземане на проби);
    • многоетапенизвадка - прави се селекция от генералната съвкупност на отделни групи и отделни единици се избират от групите (типична извадка с механичен метод за избиране на единици в извадката).

    Освен това има:

    • повторна селекция- по схемата на върната топка. В този случай всяка единица или серия, включена в извадката, се връща към генералната съвкупност и следователно има шанс да бъде включена отново в извадката;
    • повторете избора- по схемата на невърната топка. Има по-точни резултати със същия размер на извадката.

    23. Определяне на изключително важния размер на извадката (използване на t-таблицата на Student).

    Един от научните принципи в теорията на пробите е да се гарантира, че са избрани достатъчен брой единици. Теоретично изключителното значение на спазването на този принцип е представено в доказателствата на гранични теореми в теорията на вероятностите, които позволяват да се установи какъв обем единици трябва да се избере от съвкупността, така че да е достатъчен и да гарантира представителността на извадката.

    Намаляването на стандартната грешка на извадката и следователно увеличаването на точността на оценката винаги е свързано с увеличаване на размера на извадката, следователно, още на етапа на организиране на извадково наблюдение е необходимо да се реши какъв е размерът на извадковата съвкупност трябва да бъде, за да се осигури необходимата точност на резултатите от наблюдението. Изчисляването на изключително важния обем на извадката се конструира с помощта на формули, получени от формулите за максималните грешки на извадката (A), съответстващи на определен тип и метод на подбор. И така, за произволен повторен размер на извадката (n) имаме:

    Същността на тази формула е, че при произволно повтарящо се вземане на проби от изключително важни числа, размерът на извадката е право пропорционален на квадрата на коефициента на доверие (t2)и дисперсия на вариационната характеристика (?2) и е обратно пропорционална на квадрата на максималната извадкова грешка (?2). По-специално, с увеличаване на максималната грешка с коефициент два, необходимият размер на извадката трябва да бъде намален с коефициент четири. От трите параметъра два (t и?) се задават от изследователя. В същото време изследователят въз основа на целта

    и проблемите на извадковото изследване трябва да решат въпроса: в каква количествена комбинация е по-добре да се включат тези параметри, за да се осигури оптимален вариант? В един случай той може да бъде по-доволен от надеждността на получените резултати (t), отколкото от мярката за точност (?), в друг - обратното. По-трудно е да се реши въпросът относно стойността на максималната грешка на извадката, тъй като изследователят не разполага с този показател на етапа на проектиране на наблюдението на извадката, следователно на практика е обичайно да се определя стойността на максималната грешка на извадката , обикновено в рамките на 10% от очакваното средно ниво на атрибута. Към установяването на прогнозната средна стойност може да се подходи по различни начини: използване на данни от подобни предишни проучвания или използване на данни от рамката на извадката и провеждане на малка пилотна извадка.

    Най-трудното нещо за установяване при проектирането на извадково наблюдение е третият параметър във формула (5.2) – дисперсията на извадковата съвкупност. В този случай е изключително важно да се използва цялата налична за изследователя информация, получена в предишни подобни и пилотни проучвания.

    Въпросът за определяне на изключително важния размер на извадката става по-сложен, ако извадковото изследване включва изследване на няколко характеристики на извадкови единици. В този случай средните нива на всяка от характеристиките и тяхната вариация като правило са различни и в тази връзка решаването на коя вариация на коя от характеристиките да се даде предпочитание е възможно само като се вземат предвид целта и целите на анкетата.

    При проектирането на извадково наблюдение се приема предварително определена стойност на допустимата извадкова грешка в съответствие с целите на конкретно изследване и вероятността от заключения въз основа на резултатите от наблюдението.

    Като цяло формулата за максималната грешка на средната стойност на извадката ни позволява да определим:

    ‣‣‣ големината на възможните отклонения на показателите на генералната съвкупност от показателите на извадката;

    ‣‣‣ необходимия размер на извадката за осигуряване на необходимата точност, при която границите на възможна грешка не надвишават определена определена стойност;

    ‣‣‣ вероятността грешката в извадката да има определена граница.

    Студентско разпределениев теорията на вероятностите това е еднопараметрично семейство от абсолютно непрекъснати разпределения.

    24. Динамична серия (интервал, момент), затваряща динамична серия.

    Серия Dynamics- това са стойностите на статистическите показатели, които са представени в определена хронологична последователност.

    Всеки времеви ред съдържа два компонента:

    1) показатели за периоди от време(години, тримесечия, месеци, дни или дати);

    2) показатели, характеризиращи изследвания обектза периоди от време или на съответни дати, които се извикват нива на серията.

    Серийните нива се изразяват както в абсолютни, така и в средни или относителни стойности. Като се вземе предвид зависимостта от характера на показателите, се изграждат динамични серии от абсолютни, относителни и средни стойности. Динамичните серии от относителни и средни стойности се изграждат въз основа на получени серии от абсолютни стойности. Има интервални и моментни серии от динамика.

    Динамични интервални сериисъдържа стойностите на показателите за определени периоди от време. В интервални серии нивата могат да се сумират, като се получи обемът на явлението за по-дълъг период или така наречените акумулирани суми.

    Серия от динамични моментиотразява стойностите на индикаторите в определен момент от време (дата от време). В моментните серии изследователят може да се интересува само от разликата в явленията, която отразява промяната в нивото на серията между определени дати, тъй като сумата от нивата тук няма реално съдържание. Кумулативните суми не се изчисляват тук.

    Най-важното условие за правилното изграждане на динамичните редове е съпоставимост на нивата на сериятапринадлежащи към различни периоди. Нивата трябва да бъдат представени в хомогенни количества и трябва да има еднаква пълнота на покриване на различните части на явлението.

    За да се избегне изкривяване на реалната динамика, при статистическите изследвания се извършват предварителни изчисления (затваряне на динамичните редове), които предхождат статистическия анализ на динамичните редове. Под затваряне на поредицата от динамикаОбщоприето е да се разбира комбинацията в една серия от две или повече серии, чиито нива се изчисляват по различна методология или не съответстват на териториалните граници и т.н. Затварянето на динамичните серии може също така да означава привеждане на абсолютните нива на динамичните серии до обща основа, което неутрализира несравнимостта на нивата на динамичните серии.

    25. Концепцията за съпоставимост на динамичните редове, коефициенти, растеж и темпове на растеж.

    Серия Dynamics- това са поредица от статистически показатели, характеризиращи развитието на природните и социалните явления във времето. Статистическите колекции, публикувани от Държавния комитет по статистика на Русия, съдържат голям брой динамични серии в таблична форма. Динамичните серии позволяват да се идентифицират моделите на развитие на изследваните явления.

    Динамичните серии съдържат два вида индикатори. Индикатори за време(години, тримесечия, месеци и т.н.) или точки във времето (в началото на годината, в началото на всеки месец и т.н.). Индикатори за ниво на ред. Индикаторите на нивата на динамичните серии могат да бъдат изразени в абсолютни стойности (производство на продукт в тонове или рубли), относителни стойности (дял на градското население в%) и средни стойности (средна заплата на работниците в индустрията по години и т.н.). В таблична форма времевият ред съдържа две колони или два реда.

    Правилното изграждане на времеви редове изисква изпълнението на редица изисквания:

    1. всички показатели на редица динамики трябва да бъдат научно обосновани и надеждни;
    2. индикаторите на поредица от динамики трябва да бъдат сравними във времето, ᴛ.ᴇ. трябва да се изчисляват за едни и същи периоди от време или на едни и същи дати;
    3. показателите за редица динамики трябва да са сравними на територията;
    4. индикаторите на поредица от динамика трябва да бъдат сравними по съдържание, ᴛ.ᴇ. изчислени по една и съща методика;
    5. показателите за редица динамики трябва да бъдат сравними в целия диапазон от взети под внимание стопанства. Всички показатели на серия от динамика трябва да бъдат дадени в едни и същи мерни единици.

    Статистическите показатели могат да характеризират или резултатите от процеса, който се изучава за определен период от време, или състоянието на явлението, което се изследва в определен момент от времето, ᴛ.ᴇ. показателите могат да бъдат интервални (периодични) и моментни. Съответно, първоначално динамичните серии са или интервални, или моментни. Сериите от моментна динамика от своя страна идват с равни и неравни времеви интервали.

    Оригиналната динамична серия може да се трансформира в серия от средни стойности и серия от относителни стойности (верижни и основни). Такива времеви редове се наричат ​​производни времеви редове.

    Методологията за изчисляване на средното ниво в динамичните серии е различна в зависимост от вида на динамичните серии. Използвайки примери, ще разгледаме видовете динамични серии и формули за изчисляване на средното ниво.

    Абсолютни увеличения (Δy) показват колко единици се е променило следващото ниво на серията в сравнение с предишното (гр. 3. - верижни абсолютни увеличения) или в сравнение с първоначалното ниво (гр. 4. - основни абсолютни увеличения). Формулите за изчисление могат да бъдат записани, както следва:

    Когато абсолютните стойности на серията намаляват, ще има съответно „намаляване“ или „намаляване“.

    Абсолютните показатели за растеж показват, че например през 1998г. производството на продукт "А" нараства спрямо 1997г. с 4 хил. тона, а спрямо 1994 г. ᴦ. - с 34 хиляди тона; за други години виж таблицата. 11,5 гр.
    Публикувано на реф.рф
    3 и 4.

    Скорост на растежпоказва колко пъти нивото на серията се е променило спрямо предходното (гр. 5 - верижни коефициенти на растеж или спад) или спрямо първоначалното ниво (гр. 6 - основни коефициенти на растеж или спад). Формулите за изчисление могат да бъдат записани, както следва:

    Темпове на растежпоказват какъв процент е следващото ниво от серията в сравнение с предходното (колона 7 - темпове на растеж на веригата) или в сравнение с първоначалното ниво (гр. 8 - основни темпове на растеж). Формулите за изчисление могат да бъдат записани, както следва:

    Така например през 1997 г. обем на производство на продукт „А” спрямо 1996 г. ᴦ. възлиза на 105,5% (

    Скорост на растежпокажете с какъв процент се е увеличило нивото на отчетния период в сравнение с предходния (колона 9 - верижни темпове на растеж) или в сравнение с първоначалното ниво (колона 10 - основни темпове на растеж). Формулите за изчисление могат да бъдат записани, както следва:

    T pr = T r - 100% или T pr = абсолютен ръст / ниво от предходния период * 100%

    Така например през 1996 г. спрямо 1995 г. ᴦ. Изделие „А” е произведено повече с 3,8% (103,8% - 100%) или (8:210) х 100%, а спрямо 1994 г. ᴦ. - с 9% (109% - 100%).

    Ако абсолютните нива в серията намаляват, тогава скоростта ще бъде по-малка от 100% и съответно ще има скорост на намаление (скорост на нарастване със знак минус).

    Абсолютна стойност от 1% увеличение(гр.
    Публикувано на реф.рф
    11) показва колко единици трябва да бъдат произведени за даден период, така че нивото от предходния период да се увеличи с 1%. В нашия пример през 1995 г. ᴦ. е необходимо да се произведат 2,0 хил. тона, а през 1998 г. ᴦ. - 2,3 хиляди тона, ᴛ.ᴇ. много по-голям.

    Абсолютната стойност на 1% растеж може да се определи по два начина:

    § нивото на предходния период, разделено на 100;

    § верижните абсолютни увеличения се разделят на съответните верижни темпове на растеж.

    Абсолютна стойност от 1% увеличение =

    В динамика, особено за дълъг период, е важен съвместен анализ на темпа на растеж със съдържанието на всеки процент увеличение или намаление.

    Имайте предвид, че разглежданата методология за анализиране на времеви редове е приложима както за времеви редове, чиито нива са изразени в абсолютни стойности (t, хиляди рубли, брой служители и т.н.), така и за времеви редове, нивата на които се изразяват в относителни показатели (% дефекти, % пепелно съдържание на въглища и др.) или средни стойности (среден добив в c/ha, средна работна заплата и др.).

    Наред с разглежданите аналитични показатели, изчислени за всяка година в сравнение с предходното или изходно ниво, при анализа на динамичните редове е изключително важно да се изчислят средните аналитични показатели за периода: средното ниво на реда, средногодишното абсолютно нарастване (намаляване) и средния годишен темп на растеж и темп на растеж .

    Методите за изчисляване на средното ниво на серия от динамика бяха обсъдени по-горе. В серията с интервална динамика, която разглеждаме, средното ниво на серията се изчислява с помощта на простата средноаритметична формула:

    Средногодишен обем на производството на продукта за 1994-1998г. възлиза на 218,4 хил. тона.

    Средногодишният абсолютен прираст също се изчислява по формулата за средно аритметично

    Стандартно отклонение – понятие и видове. Класификация и характеристики на категорията "Средноквадратично отклонение" 2017, 2018г.

    Урок No4

    Тема: „Описателна статистика. Индикатори за разнообразие на признаци в съвкупността"

    Основните критерии за разнообразието на даден признак в статистическа съвкупност са: граница, амплитуда, стандартно отклонение, коефициент на колебание и коефициент на вариация. В предишния урок беше обсъдено, че средните стойности предоставят само обобщена характеристика на характеристиката, която се изучава в съвкупност, и не вземат предвид стойностите на нейните отделни варианти: минимални и максимални стойности, над средното, под средно и т.н.

    Пример. Средни стойности на две различни числови последователности: -100; -20; 100; 20 и 0,1; -0,2; 0,1 са абсолютно еднакви и равниОТНОСНО.Въпреки това диапазоните на разсейване на тези данни за относителна средна последователност са много различни.

    Определянето на изброените критерии за разнообразието на дадена характеристика се извършва преди всичко, като се вземе предвид нейната стойност в отделни елементи на статистическата съвкупност.

    Индикаторите за измерване на вариациите на даден признак са абсолютенИ роднина. Абсолютните показатели за вариация включват: диапазон на вариация, граница, стандартно отклонение, дисперсия. Коефициентът на вариация и коефициентът на колебание се отнасят до относителни мерки за вариация.

    Лимит (lim)–Това е критерий, който се определя от екстремните стойности на вариант в серия от варианти. С други думи, този критерий е ограничен от минималните и максималните стойности на атрибута:

    Амплитуда (Am)или диапазон на вариация –Това е разликата между екстремните варианти. Изчисляването на този критерий се извършва чрез изваждане на минималната му стойност от максималната стойност на атрибута, което ни позволява да оценим степента на разсейване на опцията:

    Недостатъкът на границата и амплитудата като критерии за променливост е, че те напълно зависят от екстремните стойности на характеристиката в вариационната серия. В този случай колебанията в стойностите на атрибутите в рамките на серия не се вземат предвид.

    Най-пълното описание на разнообразието на признак в статистическа съвкупност се предоставя от стандартно отклонение(сигма), което е обща мярка за отклонението на опция от нейната средна стойност. Често се нарича стандартно отклонение стандартно отклонение.

    Стандартното отклонение се основава на сравнение на всяка опция със средната аритметична стойност на дадена популация. Тъй като в съвкупността винаги ще има опции както по-малко, така и повече от него, сумата от отклонения със знак "" ще се анулира от сумата от отклонения със знак "", т.е. сумата от всички отклонения е нула. За да се избегне влиянието на знаците на разликите, се вземат отклонения от средноаритметичното на квадрат, т.е. . Сумата от квадратите на отклоненията не е равна на нула. За да получите коефициент, който може да измерва променливостта, вземете средната стойност на сумата от квадрати - тази стойност се нарича отклонения:

    По същество дисперсията е средният квадрат на отклоненията на отделните стойности на дадена характеристика от нейната средна стойност. дисперсия – квадрат на стандартното отклонение.

    Дисперсията е размерно количество (наименувано). Така че, ако вариантите на числова серия са изразени в метри, тогава дисперсията дава квадратни метри; ако опциите са изразени в килограми, тогава дисперсията дава квадрата на тази мярка (kg 2) и т.н.

    Стандартно отклонение– корен квадратен от дисперсията:

    , тогава при изчисляване на дисперсията и стандартното отклонение в знаменателя на дробта, вместотрябва да се постави.

    Изчисляването на стандартното отклонение може да бъде разделено на шест етапа, които трябва да се извършват в определена последователност:

    Приложение на стандартното отклонение:

    а) за преценка на променливостта на вариационните серии и сравнителна оценка на типичността (представителността) на средните аритметични стойности. Това е необходимо при диференциална диагноза при определяне на стабилността на симптомите.

    б) да се реконструира вариационната серия, т.е. възстановяване на неговата честотна характеристика въз основа на три сигма правила. В интервала (М±3σ) 99,7% от всички варианти на серията са разположени в интервала (М±2σ) - 95,5% и в диапазона (М±1σ) - 68,3% редов вариант(Фиг. 1).

    в) за идентифициране на „изскачащи“ опции

    г) да се определят параметрите на нормата и патологията с помощта на сигма оценки

    д) да се изчисли коефициентът на вариация

    е) да се изчисли средната грешка на средноаритметичното.

    За да се характеризира всяка популация, която иманормален тип разпределение , достатъчно е да знаете два параметъра: средно аритметично и стандартно отклонение.

    Фигура 1. Правило на трите сигми

    Пример.

    В педиатрията стандартното отклонение се използва за оценка на физическото развитие на децата чрез сравняване на данните за конкретно дете със съответните стандартни показатели. За стандарт се приема средноаритметичното на физическото развитие на здрави деца. Сравнението на показателите със стандартите се извършва с помощта на специални таблици, в които стандартите са дадени заедно със съответните им сигма скали. Смята се, че ако показателят за физическото развитие на детето е в рамките на стандарта (средно аритметично) ±σ, тогава физическото развитие на детето (според този показател) съответства на нормата. Ако индикаторът е в рамките на стандарта ±2σ, тогава има леко отклонение от нормата. Ако индикаторът надхвърли тези граници, тогава физическото развитие на детето се различава рязко от нормата (възможна е патология).

    В допълнение към вариационните показатели, изразени в абсолютни стойности, статистическите изследвания използват вариационни показатели, изразени в относителни стойности. Коефициент на трептене -това е отношението на диапазона на вариация към средната стойност на признака. Коефициентът на вариация -това е отношението на стандартното отклонение към средната стойност на характеристиката. Обикновено тези стойности се изразяват в проценти.

    Формули за изчисляване на показателите за относителна вариация:

    От горните формули става ясно, че колкото по-голям е коеф V е по-близо до нула, толкова по-малка е вариацията в стойностите на характеристиката. Колкото повече V, толкова по-променлив е знакът.

    В статистическата практика най-често се използва коефициентът на вариация. Използва се не само за сравнителна оценка на вариацията, но и за характеризиране на хомогенността на популацията. Популацията се счита за хомогенна, ако коефициентът на вариация не надвишава 33% (за разпределения, близки до нормалните). Аритметично съотношението на σ и средноаритметичното неутрализира влиянието на абсолютната стойност на тези характеристики, а процентното съотношение прави коефициента на вариация безразмерна (неназована) стойност.

    Получената стойност на коефициента на вариация се оценява в съответствие с приблизителните градации на степента на разнообразие на признака:

    Слаб - до 10%

    Средно - 10 - 20%

    Силен - повече от 20%

    Използването на коефициента на вариация е препоръчително в случаите, когато е необходимо да се сравнят характеристики, които са различни по размер и размер.

    Разликата между коефициента на вариация и други критерии за разсейване е ясно демонстрирана пример.

    маса 1

    Състав на работниците в промишленото предприятие

    Въз основа на статистическите характеристики, дадени в примера, можем да направим заключение за относителната хомогенност на възрастовия състав и образователното ниво на служителите на предприятието, като се има предвид ниската професионална стабилност на анкетирания контингент. Лесно е да се види, че опитът да се преценят тези социални тенденции чрез стандартното отклонение би довел до погрешно заключение, а опитът да се сравнят счетоводните характеристики „трудов опит“ и „възраст“ със счетоводния показател „образование“ като цяло би бил неправилно поради разнородността на тези характеристики.

    Медиана и процентили

    За ординални (рангови) разпределения, където критерият за средата на реда е медианата, стандартното отклонение и дисперсията не могат да служат като характеристики на дисперсията на варианта.

    Същото важи и за отворените вариационни серии. Това обстоятелство се дължи на факта, че отклоненията, от които се изчисляват дисперсията и σ, се измерват от средната аритметична стойност, която не се изчислява в отворени вариационни серии и в серии от разпределения на качествени характеристики. Следователно, за компресирано описание на разпределения се използва друг параметър на разсейване - квантил(синоним - "перцентил"), подходящ за описание на качествени и количествени характеристики във всякаква форма на тяхното разпределение. Този параметър може да се използва и за преобразуване на количествени характеристики в качествени. В този случай такива рейтинги се присвояват в зависимост от това на кой ред от квантил отговаря дадена опция.

    В практиката на биомедицинските изследвания най-често се използват следните квантили:

    - Медиана;

    , – квартили (четвърти), където – долен квартил, – горен квартил.

    Квантилите разделят областта на възможните промени в вариационна серия на определени интервали. Медиана (квантил) е опция, която е в средата на вариационна серия и разделя тази серия наполовина на две равни части ( 0,5 И 0,5 ). Квартил разделя серия на четири части: първата част (долен квартил) е опция, която разделя опции, чиито числени стойности не надвишават 25% от максимално възможните в дадена серия; квартил разделя опции с числена стойност от до 50% от максимално възможния. Горният квартил () разделя опциите до 75% от максимално възможните стойности.

    При асиметрично разпределение променлива спрямо средната аритметична стойност, медианата и квартилите се използват за нейното характеризиране.В този случай се използва следната форма за показване на средната стойност - мех (;). Например, изследваният признак – „периодът, в който детето започва да ходи самостоятелно” – има асиметрично разпределение в изследваната група. В същото време долният квартил () съответства на началото на ходенето - 9,5 месеца, медианата - 11 месеца, горният квартил () - 12 месеца. Съответно, характеристиката на средния тренд на посочения признак ще бъде представена като 11 (9,5; 12) месеца.

    Оценка на статистическата значимост на резултатите от изследването

    Статистическата значимост на данните се разбира като степента, в която те съответстват на показаната реалност, т.е. статистически значими данни са тези, които не изкривяват и правилно отразяват обективната реалност.

    Оценяването на статистическата значимост на резултатите от изследването означава да се определи с каква вероятност е възможно резултатите, получени от извадката от съвкупността, да се прехвърлят към цялата популация. Оценката на статистическата значимост е необходима, за да се разбере каква част от дадено явление може да се използва, за да се прецени явлението като цяло и неговите модели.

    Оценката на статистическата значимост на резултатите от изследването се състои от:

    1. грешки на представителността (грешки на средни и относителни стойности) - м;

    2. доверителни граници на средни или относителни стойности;

    3. надеждност на разликата в средните или относителните стойности според критерия T.

    Стандартна грешка на средноаритметичната стойностили грешка в представителносттахарактеризира колебанията на средната стойност. Трябва да се отбележи, че колкото по-голям е размерът на извадката, толкова по-малък е разпределението на средните стойности. Стандартната грешка на средната стойност се изчислява по формулата:

    В съвременната научна литература средноаритметичната стойност се записва заедно с грешката на представителност:

    или заедно със стандартното отклонение:

    Като пример, разгледайте данните за 1500 градски клиники в страната (общо население). Средният брой обслужени пациенти в клиниката е 18 150 души. Случайният избор на 10% от обектите (150 клиники) дава среден брой пациенти, равен на 20 051 души. Грешката на извадката, очевидно поради факта, че не всички 1500 клиники са включени в извадката, е равна на разликата между тези средни стойности - общата средна ( Мген) и средно извадка ( Мизбран). Ако формираме друга извадка със същия размер от нашата популация, това ще даде различна стойност на грешката. Всички тези извадкови средни с достатъчно големи извадки се разпределят нормално около генералната средна с достатъчно голям брой повторения на извадката от същия брой обекти от генералната съвкупност. Стандартна грешка на средната стойност м- това е неизбежното разпръскване на извадковите средни около генералното средно.

    В случай, че резултатите от изследването са представени в относителни количества (например проценти) - изчислени стандартна грешка на дроб:

    където P е показателят в %, n е броят на наблюденията.

    Резултатът се показва като (P ± m)%. Например,процентът на възстановяване сред пациентите е (95,2±2,5)%.

    В случай, че броят на елементите на съвкупността, тогава при изчисляване на стандартните грешки на средната и дробта в знаменателя на дробта, вместотрябва да се постави.

    За нормално разпределение (разпределението на извадковите средни стойности е нормално), знаем каква част от съвкупността попада във всеки интервал около средната стойност. В частност:

    На практика проблемът е, че характеристиките на генералната съвкупност са ни непознати и извадката се прави именно с цел да ги оценим. Това означава, че ако направим проби с еднакъв размер нот общата популация, тогава в 68,3% от случаите интервалът ще съдържа стойността М(в 95,5% от случаите ще бъде на интервала и в 99,7% от случаите – на интервала).

    Тъй като всъщност е взета само една извадка, това твърдение е формулирано по отношение на вероятността: с вероятност от 68,3%, средната стойност на атрибута в популацията се намира в интервала, с вероятност от 95,5% - в интервала и т.н.

    На практика се изгражда интервал около стойността на извадката, така че с дадена (достатъчно висока) вероятност, вероятност за доверие –ще „покрие“ истинската стойност на този параметър в общата популация. Този интервал се нарича доверителен интервал.

    Вероятност за довериеП – това е степента на увереност, че доверителният интервал действително ще съдържа истинската (неизвестна) стойност на параметъра в популацията.

    Например, ако вероятността за доверие Ре 90%, това означава, че 90 проби от 100 ще дадат правилната оценка на параметъра в популацията. Съответно вероятността от грешка, т.е. неправилна оценка на общата средна стойност за извадката е равна в проценти: . За този пример това означава, че 10 проби от 100 ще дадат неправилна оценка.

    Очевидно степента на доверие (вероятността на доверие) зависи от размера на интервала: колкото по-широк е интервалът, толкова по-висока е увереността, че неизвестна стойност за популацията ще попадне в него. На практика най-малко два пъти грешката на извадката се използва за конструиране на доверителен интервал, за да се осигури поне 95,5% увереност.

    Определянето на доверителните граници на средните и относителните стойности ни позволява да намерим двете им екстремни стойности - минималната възможна и максималната възможна, в рамките на които изследваният показател може да се появи в цялата популация. Въз основа на това, доверителни граници (или доверителен интервал)- това са границите на средни или относителни стойности, извън които поради случайни колебания има незначителна вероятност.

    Доверителният интервал може да бъде пренаписан като: , където T– критерий за доверие.

    Доверителните граници на средноаритметичната стойност в популацията се определят по формулата:

    М ген = М изберете + t m М

    за относителна стойност:

    Р ген = П изберете + t m Р

    Където М генИ Р ген- стойности на средни и относителни стойности за генералната съвкупност; М изберетеИ Р изберете- стойности на средни и относителни стойности, получени от извадката; м МИ м П- грешки на средни и относителни стойности; T- критерий за доверие (критерий за точност, който се установява при планиране на изследването и може да бъде равен на 2 или 3); t m- това е доверителен интервал или Δ - максималната грешка на показателя, получена при извадково изследване.

    Трябва да се отбележи, че стойността на критерия Tдо известна степен свързана с вероятността за безгрешна прогноза (p), изразена в %. Избира се от самия изследовател, ръководен от необходимостта да получи резултата с необходимата степен на точност. По този начин, за вероятността за безгрешна прогноза от 95,5%, стойността на критерия Tе 2, за 99,7% - 3.

    Дадените оценки на доверителния интервал са приемливи само за статистически популации с повече от 30 наблюдения. При по-малък размер на популацията (малки извадки) се използват специални таблици за определяне на критерия t. В тези таблици желаната стойност се намира в пресечната точка на линията, съответстваща на размера на популацията (n-1)и колона, съответстваща на нивото на вероятност за прогноза без грешки (95,5%; 99,7%), избрана от изследователя. В медицинските изследвания, когато се установяват граници на доверие за всеки индикатор, вероятността за безгрешна прогноза е 95,5% или повече. Това означава, че стойността на показателя, получена от извадковата съвкупност, трябва да бъде намерена в генералната съвкупност в поне 95,5% от случаите.

      Въпроси по темата на урока:

      Уместност на показателите за разнообразие на признаци в статистическа популация.

      Обща характеристика на абсолютните вариационни показатели.

      Стандартно отклонение, изчисление, приложение.

      Относителни мерки на вариация.

      Медиана, квартилен резултат.

      Оценка на статистическата значимост на резултатите от изследването.

      Стандартна грешка на средноаритметичната стойност, формула за изчисление, пример за използване.

      Изчисляване на пропорцията и нейната стандартна грешка.

      Концепцията за доверителна вероятност, пример за използване.

    10. Концепцията за доверителен интервал, неговото приложение.

      Тестови задачи по темата със стандартни отговори:

    1. АБСОЛЮТНИТЕ ПОКАЗАТЕЛИ НА ВАРИАЦИЯТА СЕ ОТНАСЯТ КЪМ

    1) коефициент на вариация

    2) коефициент на трептене

    4) медиана

    2. ОТНОСИТЕЛНИТЕ ПОКАЗАТЕЛИ НА ВАРИАЦИЯТА СЕ СВЪРЗВАТ

    1) дисперсия

    4) коефициент на вариация

    3. КРИТЕРИИ, КОИТО СЕ ОПРЕДЕЛЯТ ОТ ЕКСТРЕМАЛНИТЕ СТОЙНОСТИ НА ОПЦИЯ В СЕРИЯ ИЗМЕНЕНИЯ

    2) амплитуда

    3) дисперсия

    4) коефициент на вариация

    4. РАЗЛИКАТА НА ЕКСТРЕМНИТЕ ВАРИАНТИ Е

    2) амплитуда

    3) стандартно отклонение

    4) коефициент на вариация

    5. СРЕДНИЯТ КВАДРАТ НА ОТКЛОНЕНИЯТА НА ИНДИВИДУАЛНИТЕ СТОЙНОСТИ НА ХАРАКТЕРИСТИКА ОТ НЕЙНИТЕ СРЕДНИ СТОЙНОСТИ Е

    1) коефициент на трептене

    2) медиана

    3) дисперсия

    6. СЪОТНОШЕНИЕТО НА СКАЛАТА НА ВАРИАЦИЯТА КЪМ СРЕДНАТА СТОЙНОСТ НА ХАРАКТЕРА Е

    1) коефициент на вариация

    2) стандартно отклонение

    4) коефициент на трептене

    7. СЪОТНОШЕНИЕТО НА СРЕДНОТО КВАДРАТНО ОТКЛОНЕНИЕ КЪМ СРЕДНАТА СТОЙНОСТ НА ХАРАКТЕРИСТИКАТА Е

    1) дисперсия

    2) коефициент на вариация

    3) коефициент на трептене

    4) амплитуда

    8. ОПЦИЯТА, КОЯТО Е В СРЕДАТА НА ВАРИАЦИОННАТА СЕРИЯ И Я РАЗДЕЛЯ НА ДВЕ РАВНИ ЧАСТИ Е

    1) медиана

    3) амплитуда

    9. В МЕДИЦИНСКИТЕ ИЗСЛЕДВАНИЯ, ПРИ УСТАНОВЯВАНЕ НА ДОВЕРИТЕЛНИ ГРАНИЦИ ЗА ВСЯК ИНДИКАТОР, СЕ ПРИЕМА ВЕРОЯТНОСТТА ЗА БЕЗГРЕШНА ПРОГНОЗА

    10. АКО 90 ПРОБИ ОТ 100 ДАВАТ ПРАВИЛНАТА ОЦЕНКА НА ПАРАМЕТЪР В ПОПУЛАЦИЯТА, ТОВА ОЗНАЧАВА, ЧЕ ВЕРОЯТНОСТТА ЗА ДОВЕРИЕ ПРАВЕН

    11. АКО 10 ПРОБИ ОТ 100 ДАВАТ НЕПРАВИЛНА ОЦЕНКА, ВЕРОЯТНОСТТА ЗА ГРЕШКА Е РАВНА

    12. ГРАНИЦИ НА СРЕДНИ ИЛИ ОТНОСИТЕЛНИ СТОЙНОСТИ, ПРЕДВИЖДАНЕТО НА КОИТО ПОРАДИ СЛУЧАЙНИ КОЛЕБАНИЯ ИМА МАЛКА ВЕРОЯТНОСТ – ТОВА Е

    1) доверителен интервал

    2) амплитуда

    4) коефициент на вариация

    13. ЗА МАЛКА ИЗВАДКА СЕ СЧИТА ТАЗИ ПОПУЛАЦИЯ, В КОЯТО

    1) n е по-малко или равно на 100

    2) n е по-малко или равно на 30

    3) n е по-малко или равно на 40

    4) n е близо до 0

    14. ЗА ВЕРОЯТНОСТ ЗА БЕЗГРЕШНА ПРОГНОЗА 95% КРИТЕРИЙНА СТОЙНОСТ TЕ

    15. ЗА ВЕРОЯТНОСТ ЗА БЕЗГРЕШНА ПРОГНОЗА 99% КРИТЕРИЙНА СТОЙНОСТ TЕ

    16. ЗА РАЗПРЕДЕЛЕНИЯ, БЛИЗКИ ДО НОРМАЛНОТО, ПОПУЛАЦИЯТА СЕ СЧИТА ЗА ХОМОГЕННА, АКО КОЕФИЦИЕНТЪТ НА ВАРИАЦИЯ НЕ ПРЕВИШАВА

    17. ОПЦИЯ, РАЗДЕЛИТЕЛНИ ОПЦИИ, ЧИИСТО ЧИСЛОВИТЕ СТОЙНОСТИ НЕ ПРЕВИШАВАТ 25% ОТ МАКСИМАЛНО ВЪЗМОЖНИТЕ В ДАДЕНА СЕРИЯ – ТОВА Е

    2) долен квартил

    3) горен квартил

    4) квартил

    18. ДАННИ, КОИТО НЕ ИЗКРИВЯВАТ И ПРАВИЛНО ОТРАЗЯВАТ ОБЕКТИВНАТА РЕАЛНОСТ, СЕ НАРИЧАТ

    1) невъзможно

    2) еднакво възможно

    3) надежден

    4) случаен

    19. СЪГЛАСНО ПРАВИЛОТО НА "ТРИ Сигми", С НОРМАЛНО РАЗПРЕДЕЛЕНИЕ НА ХАРАКТЕРИСТИКА В ВРЪХ
    ЩЕ БЪДАТ ЛОКАЛИЗАЦИИ

    1) 68,3% опция

    Очакване и дисперсия

    Нека измерим случайна променлива нпъти, например, измерваме скоростта на вятъра десет пъти и искаме да намерим средната стойност. Как средната стойност е свързана с функцията на разпределение?

    Ще хвърлим заровете голям брой пъти. Броят на точките, които ще се появят на заровете с всяко хвърляне, е случайна променлива и може да приеме произволна естествена стойност от 1 до 6. Средната аритметична стойност на изпуснатите точки, изчислена за всички хвърляния на зарове, също е случайна променлива, но за големи нклони към много конкретно число - математическо очакване Mx. В такъв случай Mx = 3,5.

    Как получихте тази стойност? Нека влезе нтестове, веднъж получавате 1 точка, веднъж получавате 2 точки и т.н. Тогава когато н→ ∞ брой резултати, при които е хвърлена една точка, По същия начин, Следователно

    Модел 4.5. Зарове

    Нека сега приемем, че знаем закона за разпределение на случайната променлива х, тоест знаем, че случайната променлива хможе да приема стойности х 1 , х 2 , ..., x kс вероятности стр 1 , стр 2 , ..., p k.

    Очаквана стойност Mxслучайна величина хравно на:

    Отговор. 2,8.

    Математическото очакване не винаги е разумна оценка на някаква случайна променлива. Така че, за да се оцени средната заплата, е по-разумно да се използва понятието медиана, тоест такава стойност, че броят на хората, получаващи заплата, по-ниска от средната, и по-висока, съвпадат.

    Медианаслучайна променлива е число х 1/2 е такова, че стр (х < х 1/2) = 1/2.

    С други думи, вероятността стр 1, че случайната променлива хще бъде по-малък х 1/2 и вероятност стр 2, че случайната променлива хще бъде по-голяма х 1/2 са еднакви и равни на 1/2. Медианата не се определя еднозначно за всички разпределения.

    Да се ​​върнем към случайната променлива х, които могат да приемат стойности х 1 , х 2 , ..., x kс вероятности стр 1 , стр 2 , ..., p k.

    Дисперсияслучайна величина хСредната стойност на квадрата на отклонението на случайна променлива от нейното математическо очакване се нарича:

    Пример 2

    При условията на предишния пример изчислете дисперсията и стандартното отклонение на случайната променлива х.

    Отговор. 0,16, 0,4.

    Модел 4.6. Стрелба по мишена

    Пример 3

    Намерете вероятностното разпределение на броя точки, получени при първото хвърляне на зара, медианата, математическото очакване, дисперсията и стандартното отклонение.

    Всеки ръб е еднакво вероятно да изпадне, така че разпределението ще изглежда така:

    Стандартно отклонение Вижда се, че отклонението на стойността от средната стойност е много голямо.

    Свойства на математическото очакване:

    • Математическото очакване на сумата от независими случайни променливи е равно на сумата от техните математически очаквания:

    Пример 4

    Намерете математическото очакване на сбора и произведението на точките, хвърлени на два зара.

    В пример 3 открихме, че за един куб М (х) = 3,5. И така за две кубчета

    Дисперсионни свойства:

    • Дисперсията на сумата от независими случайни променливи е равна на сумата от дисперсиите:

    D x + г = D x + Dy.

    Нека за нхвърля на зара хвърлен гточки. Тогава

    Този резултат е верен не само за хвърляния на зарове. В много случаи той определя точността на емпиричното измерване на математическото очакване. Вижда се, че с увеличаване на броя на измерванията нразпространението на стойностите около средната стойност, т.е. стандартното отклонение, намалява пропорционално

    Дисперсията на случайна променлива е свързана с математическото очакване на квадрата на тази случайна променлива чрез следната връзка:

    Нека намерим математическите очаквания на двете страни на това равенство. A-приори,

    Математическото очакване на дясната страна на равенството, според свойството на математическите очаквания, е равно на

    Стандартно отклонение

    Стандартно отклонениеравен на корен квадратен от дисперсията:
    При определяне на стандартното отклонение за достатъчно голям обем от изследваната популация (n > 30) се използват следните формули:

    Свързана информация.