Сред функционалните редове най-важно място заемат степенните редове.
Степенен ред е ред
чиито членове са степенни функции, подредени в нарастващи неотрицателни цели числа х, А ° С 0 , ° С 1 , ° С 2 , ° С n - постоянни стойности. Числа ° С 1 , ° С 2 , ° С n - коефициенти на членовете на серията, ° С 0 - безплатен член. Членовете на степенния ред са определени на цялата числова ос.
Нека се запознаем с концепцията области на сходимост на степенния ред.Това е набор от променливи стойности х, за които серията се събира. Степеновите редове имат доста проста област на сближаване. За стойности на реални променливи хобластта на конвергенция се състои или от една точка, или е определен интервал (интервал на конвергенция), или съвпада с цялата ос вол .
При заместване на стойностите в степенната серия х= 0 ще доведе до числова серия
° С 0 +0+0+...+0+... ,
който се сближава.
Следователно, когато х= 0 всеки степенен ред се сближава и следователно, нейната зона на конвергенцияне може да бъде празното множество. Структурата на областта на сближаване на всички степенни редове е еднаква. Може да се установи с помощта на следната теорема.
Теорема 1 (теорема на Абел). Ако степенен ред се сближава при някаква стойност х = х 0, различен от нула, тогава той се сближава и, освен това, абсолютно, за всички стойности на | х| < |х 0 | . Моля, обърнете внимание: както началната стойност „X е нула“, така и всяка стойност на „X“, която се сравнява с началната стойност, се вземат по модул - без да се взема предвид знакът.
Последица. Ако степенните редове се разминаватна някаква стойност х = х 1, тогава той се разминава за всички стойности на | х| > |х 1 | .
Както вече разбрахме по-рано, всеки степенен ред се сближава при стойността х= 0. Има степенни редове, които се събират само когато х= 0 и се разминават за други стойности х. Като изключим този случай от разглеждане, приемаме, че степенният ред се сближава при някаква стойност х = х 0, различно от нула. Тогава, съгласно теоремата на Абел, тя се събира във всички точки от интервала ]-| х 0 |, |х 0 |[ (интервал, чиито лява и дясна граница са стойностите x, при които степенната редица се сближава, взети съответно със знак минус и знак плюс), симетричен спрямо началото.
Ако степенният ред се разминава при определена стойност х = х 1, тогава, въз основа на следствието от теоремата на Абел, тя се разминава във всички точки извън сегмента [-| х 1 |, |х 1 |] . От това следва, че за всеки степенен ред съществува интервал, симетричен спрямо началото, т.нар интервал на конвергенция, във всяка точка от които редицата се събира, на границите може да се събира или може да се разминава и не е задължително едновременно, а извън отсечката редицата се разминава. Номер Рсе нарича радиус на сходимост на степенния ред.
В специални случаи интервал на сходимост на степенни редовеможе да се изроди до точка (тогава серията се сближава само когато х= 0 и се счита, че Р= 0) или представлява цялата числова линия (тогава редът се събира във всички точки на числовата линия и се приема, че ).
По този начин определянето на областта на сближаване на степенен ред се състои в определяне на неговата радиус на конвергенция Ри изследване на сходимостта на серията в границите на интервала на сходимост (при ).
Теорема 2. Ако всички коефициенти на степенна серия, започвайки от определена, са различни от нула, тогава нейният радиус на конвергенция е равен на границата при съотношението на абсолютните стойности на коефициентите на общите членове на сериалите, които го следват, т.е.
Пример 1. Намерете областта на сходимост на степенния ред
Решение. Тук
Използвайки формула (28), намираме радиуса на конвергенция на тази серия:
Нека изследваме сходимостта на реда в краищата на интервала на сходимост. Пример 13 показва, че този ред се събира при х= 1 и се отклонява при х= -1. Следователно областта на конвергенция е полуинтервалът.
Пример 2. Намерете областта на сходимост на степенния ред
Решение. Коефициентите на реда са положителни и
Нека намерим границата на това отношение, т.е. радиус на сходимост на степенния ред:
Нека изследваме сходимостта на редицата в краищата на интервала. Подмяна на стойности х= -1/5 и х= 1/5 в този ред дава:
Първата от тези серии се сближава (виж Пример 5). Но тогава, по силата на теоремата в раздела „Абсолютна конвергенция“, вторият ред също се сближава и областта на нейното сближаване е сегментът
Пример 3. Намерете областта на сходимост на степенния ред
Решение. Тук
Използвайки формула (28), намираме радиуса на сходимост на серията:
Нека проучим сходимостта на реда за стойности на . Замествайки ги в тази серия, получаваме съответно
И двата реда се разминават, защото необходимото условие за сходимост не е изпълнено (техните общи членове не клонят към нула при ). И така, в двата края на интервала на конвергенция тази редица се разминава и областта на нейната конвергенция е интервалът.
Пример 5. Намерете областта на сходимост на степенния ред
Решение. Намираме връзката, където , и 
:
Според формула (28), радиусът на конвергенция на тази серия
,
т.е. серията се сближава само когато х= 0 и се разминава за други стойности х.
Примерите показват, че в края на интервала на конвергенция редовете се държат различно. В пример 1 в единия край на интервала на сближаване се сближава, а в другия се разминава; в пример 3 се разминава в двата края.
Формулата за радиуса на сходимост на степенен ред се получава при предположението, че всички коефициенти на членовете на реда, започващи от определена точка, са различни от нула. Следователно използването на формула (28) е допустимо само в тези случаи. Ако това условие е нарушено, тогава радиусът на сходимост на степенния ред трябва да се търси с помощта на теста на d'Alembert или чрез замяна на променливата, трансформиране на реда във форма, в която определеното условие е изпълнено.
Пример 6. Намерете интервала на сходимост на степенния ред
Решение. Тази серия не съдържа термини с нечетни степени х. Затова трансформираме поредицата, настройка . Тогава получаваме сериала
за да намерим чийто радиус на конвергенция можем да приложим формула (28). Тъй като , a , тогава радиусът на сходимост на тази серия
Следователно от равенството, което получаваме, този ред се събира на интервала.
Сума от степенни редове. Диференциране и интегриране на степенни редовеНека за степенния ред
радиус на конвергенция Р> 0, т.е. тази серия се събира на интервала.
След това всяка стойност хот интервала на сходимост съответства на определен сбор от реда. Следователно сборът от степенните редове е функция на хна интервала на конвергенция. Означавайки го с f(х), можем да запишем равенството
разбирайки го в смисъл, че сумата от серията във всяка точка хот интервала на сходимост е равна на стойността на функцията f(х) в този момент. В същия смисъл ще кажем, че степенният ред (29) сходен към функцията f(х) върху интервала на конвергенция.
Извън интервала на конвергенция равенството (30) няма смисъл.
Пример 7. Намерете сумата от степенния ред
Решение. Това е геометрична серия, за която а= 1, а р= х. Следователно неговата сума е функция 
. Серия се сближава, ако , и е нейният интервал на сближаване. Следователно равенство
е валиден само за стойности, въпреки че функцията 
определени за всички стойности х, с изключение х= 1.
Може да се докаже, че сумата от степенния ред f(х) е непрекъснат и диференцируем на всеки интервал в рамките на интервала на сближаване, по-специално във всяка точка от интервала на сближаване на реда.
Нека представим теореми за член по член диференциране и интегриране на степенни редове.
Теорема 1. Степенен ред (30) в интервала на неговата сходимост може да се диференцира член по член неограничен брой пъти, като получените степенни редове имат същия радиус на сходимост като оригиналния ред и сумите им съответно са равни на .
Теорема 2. Степенен ред (30) може да се интегрира член по член неограничен брой пъти в диапазона от 0 до х, ако , и получените степенни редове имат същия радиус на сходимост като оригиналния ред и сумите им съответно са равни
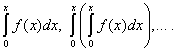
Нека функцията е дадена f(х), който трябва да бъде разширен в степенен ред, т.е. представя във формата (30):
Задачата е да се определят коефициентите 
ред (30). За да направим това, диференцирайки равенство (30) термин по термин, ние последователно намираме:
……………………………………………….. (31)
Приемайки в равенства (30) и (31) х= 0, намираме
Замествайки намерените изрази в равенство (30), получаваме
(32)
Нека намерим разширение в редица на Маклорен на някои елементарни функции.
Пример 8. Разгънете функцията в редица на Маклорен
Решение. Производните на тази функция съвпадат със самата функция:
Следователно, когато х= 0 имаме
Замествайки тези стойности във формула (32), получаваме желаното разширение:
(33)
Този ред се събира на цялата числова ос (нейния радиус на сходимост).
В теорията на функционалните серии централно място заема разделът, посветен на разлагането на функция в серия.
Така се поставя задачата: за дадена функция трябва да намерим такъв степенен ред
който се сближава на определен интервал и сумата му е равна на 
,
тези.
=
..
Тази задача се нарича проблемът за разширяване на функция в степенен ред.
Необходимо условие за разложимостта на функция в степенен реде неговата диференцируемост безкраен брой пъти - това следва от свойствата на сходните степенни редове. Това условие е изпълнено, като правило, за елементарни функции в тяхната област на дефиниране.
Така че нека приемем, че функцията 
има производни от всякакъв ред. Възможно ли е да го разширим в степенна серия. Ако е така, как можем да намерим тази серия? Втората част от проблема е по-лесна за решаване, така че нека започнем с нея.
Да приемем, че функцията 
може да се представи като сбор от степенен ред, събиращ се в интервала, съдържащ точката х 0 :
=
..
(*)
Където А 0 ,А 1 ,А 2 ,...,А П ,... – неизвестни (все още) коефициенти.
Нека поставим в равенство (*) стойността х = х 0 , тогава получаваме
.
Нека диференцираме степенните редове (*) член по член
=
..
и вярвайки тук х = х 0 , получаваме
.
При следващото диференциране получаваме редицата
=
..
вярвайки х = х 0 ,
получаваме 
, където 
.
След П-кратна диференциация, която получаваме
Приемайки в последното равенство х = х 0 ,
получаваме 
, където
И така, коефициентите са намерени
,
,
,
…,
,….,
замествайки което в серията (*), получаваме
Получената серия се нарича до Тейлърза функция
.
Така установихме, че ако функцията може да бъде разширена в степенен ред по степени (x - x 0 ), тогава това разширение е уникално и получената серия непременно е серия на Тейлър.
Имайте предвид, че серията на Тейлър може да бъде получена за всяка функция, която има производни от всякакъв ред в точката х = х 0 . Но това не означава, че между функцията и получената серия може да се постави знак за равенство, т.е. че сумата от редицата е равна на оригиналната функция. Първо, такова равенство може да има смисъл само в областта на конвергенция и серията на Тейлър, получена за функцията, може да се разминава, и второ, ако серията на Тейлър се сближава, тогава нейната сума може да не съвпада с оригиналната функция.
3.2. Достатъчни условия за разложимостта на функция в ред на ТейлърНека формулираме твърдение, с помощта на което ще бъде решена задачата.
Ако функцията
в някаква околност на точка x 0 има производни до (н+
1) от ред включително, тогава в този квартал имамеформулаТейлър
КъдетоР н (х)-остатъчният член на формулата на Тейлър – има формата (форма на Лагранж)
Където точкаξ се намира между x и x 0 .
Имайте предвид, че има разлика между реда на Тейлър и формулата на Тейлър: формулата на Тейлър е крайна сума, т.е. П -фиксиран номер.
Припомнете си, че сумата от сер С(х) може да се дефинира като граница на функционална последователност от частични суми С П (х) на някакъв интервал х:
.
Според това, да се разшири функция в серия на Тейлър означава да се намери серия такава, че за всяко хх
Нека запишем формулата на Тейлър във формата където
забележи това 
дефинира грешката, която получаваме, заменете функцията f(х)
полином С н (х).
Ако 
, Че 
,тези. функцията се разширява в серия на Тейлър. Обратно, ако 
, Че 
.
Така доказахме критерий за разложимостта на функция в ред на Тейлър.
За да може функциятаf(x) се разширява в серия на Тейлър, е необходимо и достатъчно на този интервал
, КъдетоР н (х) е остатъчният член на реда на Тейлър.
Използвайки формулирания критерий, може да се получи достатъчноусловия за разложимостта на функция в ред на Тейлър.
Ако внякаква околност на точка x 0 абсолютните стойности на всички производни на функцията са ограничени до едно и също число М≥ 0, т.е.
, To в тази близост функцията се разширява в серия на Тейлър.
От горното следва алгоритъмразширяване на функциятаf(х) в серията Тейлърв близост до точка х 0 :
1. Намиране на производни на функции f(х):
f(x), f’(x), f”(x), f’”(x), f (н) (х),…
2. Изчислете стойността на функцията и стойностите на нейните производни в точката х 0
f(x 0 ), f’(x 0 ), f”(x 0 ), f’”(x 0 ), е (н) (х 0 ),…
3. Формално записваме редицата на Тейлър и намираме областта на сходимост на получената степенна редица.
4. Проверяваме изпълнението на достатъчни условия, т.е. установяваме за кои хот областта на конвергенция, остатъчен член Р н (х)
клони към нула при 
или
.
Развиването на функции в ред на Тейлър с помощта на този алгоритъм се нарича разширяване на функция в ред на Тейлър по дефиницияили директно разграждане.
Как да вмъкнете математически формули в уебсайт?
Ако някога трябва да добавите една или две математически формули към уеб страница, тогава най-лесният начин да направите това е както е описано в статията: математическите формули лесно се вмъкват в сайта под формата на снимки, които се генерират автоматично от Wolfram Alpha . В допълнение към простотата, този универсален метод ще помогне за подобряване на видимостта на сайта в търсачките. Работи отдавна (и мисля, че ще работи завинаги), но вече е морално остарял.
Ако редовно използвате математически формули на вашия сайт, тогава ви препоръчвам да използвате MathJax - специална JavaScript библиотека, която показва математически нотации в уеб браузъри, използвайки MathML, LaTeX или ASCIIMathML маркиране.
Има два начина да започнете да използвате MathJax: (1) като използвате прост код, можете бързо да свържете MathJax скрипт към вашия уебсайт, който автоматично ще бъде зареден от отдалечен сървър в точното време (списък със сървъри); (2) изтеглете скрипта MathJax от отдалечен сървър на вашия сървър и го свържете към всички страници на вашия сайт. Вторият метод - по-сложен и отнемащ време - ще ускори зареждането на страниците на вашия сайт и ако родителският MathJax сървър стане временно недостъпен по някаква причина, това няма да се отрази по никакъв начин на вашия собствен сайт. Въпреки тези предимства избрах първия метод, тъй като е по-прост, по-бърз и не изисква технически умения. Следвайте примера ми и само след 5 минути ще можете да използвате всички функции на MathJax на вашия сайт.
Можете да свържете скрипта на библиотеката MathJax от отдалечен сървър, като използвате две опции за код, взети от основния уебсайт на MathJax или от страницата с документация:
Една от тези опции за код трябва да бъде копирана и поставена в кода на вашата уеб страница, за предпочитане между таговете и/или непосредствено след тага. Според първата опция MathJax се зарежда по-бързо и забавя страницата по-малко. Но втората опция автоматично следи и зарежда най-новите версии на MathJax. Ако поставите първия код, той ще трябва да се актуализира периодично. Ако поставите втория код, страниците ще се зареждат по-бавно, но няма да е необходимо постоянно да следите актуализациите на MathJax.
Най-лесният начин за свързване на MathJax е в Blogger или WordPress: в контролния панел на сайта добавете уиджет, предназначен да вмъква JavaScript код на трета страна, копирайте в него първата или втората версия на кода за изтегляне, представен по-горе, и поставете уиджета по-близо до началото на шаблона (между другото, това изобщо не е необходимо, тъй като скриптът MathJax се зарежда асинхронно). Това е всичко. Сега научете синтаксиса за маркиране на MathML, LaTeX и ASCIIMathML и сте готови да вмъквате математически формули в уеб страниците на вашия сайт.
Всеки фрактал се конструира според определено правило, което се прилага последователно неограничен брой пъти. Всяко такова време се нарича итерация.
Итеративният алгоритъм за конструиране на гъба на Менгер е доста прост: оригиналният куб със страна 1 е разделен от равнини, успоредни на лицата му, на 27 равни куба. От него се отстраняват един централен куб и 6 куба, съседни на него по стените. Резултатът е комплект, състоящ се от останалите 20 по-малки кубчета. Като направим същото с всяко от тези кубчета, получаваме комплект, състоящ се от 400 по-малки кубчета. Продължавайки този процес безкрайно, получаваме гъба Menger.
Ако функцията f(x) има производни от всички порядъци на определен интервал, съдържащ точка a, тогава към нея може да се приложи формулата на Тейлър:
,
Където r n– така нареченият остатъчен член или остатък от серията, може да се оцени с помощта на формулата на Лагранж:
, където числото x е между x и a.
f(x)=
в точка x 0 = Брой елементи на реда 3 4 5 6 7
Използвайте разширението на елементарни функции e x , cos(x), sin(x), ln(1+x), (1+x) m
Правила за въвеждане на функции:
Ако за някаква стойност х r n→0 при н→∞, тогава в границата формулата на Тейлър става сходяща за тази стойност Серия Тейлър:
,
По този начин функцията f(x) може да бъде разширена в серия на Тейлър в разглежданата точка x, ако:
1) има производни от всички поръчки;
2) построеният ред се събира в тази точка.
Когато a = 0, получаваме серия, наречена серия на Маклорен:
,
Разширение на най-простите (елементарни) функции в серията Maclaurin:
Експоненциални функции
, R=∞
Тригонометрични функции 
, R=∞ 
, R=∞
, (-π/2< x < π/2), R=π/2
Функцията actgx не се разширява по степени на x, защото ctg0=∞
Хиперболични функции
Логаритмични функции
, -1