Правила за прости дроби. Изваждане на смесени дроби

Калкулатор на дробипредназначен за бързо изчисляване на операции с дроби, той ще ви помогне лесно да добавяте, умножавате, разделяте или изваждате дроби.

Съвременните ученици започват да изучават дроби още в 5-ти клас и всяка година упражненията с тях стават все по-сложни. Математическите термини и величини, които учим в училище, рядко могат да ни бъдат полезни в живота на възрастните. Дробите обаче, за разлика от логаритмите и степените, се срещат доста често в ежедневието (измерване на разстояния, претегляне на стоки и др.). Нашият калкулатор е предназначен за бързи операции с дроби.

Първо, нека да дефинираме какво представляват дробите и какви са те. Дробите са съотношението на едно число към друго; това е число, състоящо се от цял брой дроби от единица.

Видове дроби:

Обикновен
десетична
Смесени

Пример обикновени дроби:

Горната стойност е числителят, долната е знаменателят. Тирето ни показва, че горното число се дели на долното число. Вместо този формат на писане, когато тирето е хоризонтално, можете да пишете различно. Можете да поставите наклонена линия, например:

1/2, 3/7, 19/5, 32/8, 10/100, 4/1

Десетични знациса най-популярният вид дроби. Състоят се от цяла и дробна част, разделени със запетая.

Пример за десетични дроби:

0,2 или 6,71 или 0,125

Състои се от цяло число и дробна част. За да разберете стойността на тази дроб, трябва да съберете цялото число и дробта.

Пример за смесени дроби:

Калкулаторът за дроби на нашия уебсайт може бързо да извършва всякакви математически операции с дроби онлайн:

Допълнение
Изваждане
Умножение
дивизия

За да извършите изчислението, трябва да въведете числа в полетата и да изберете действие. За дроби трябва да попълните числителя и знаменателя, може да не се изписва цялото число (ако дробта е обикновена). Не забравяйте да кликнете върху бутона "равно".

Удобно е, че калкулаторът веднага предоставя процеса за решаване на пример с дроби, а не само готов отговор. Благодарение на подробното решение можете да използвате този материал за решаване на училищни задачи и за по-добро усвояване на преминатия материал.

Трябва да извършите примерното изчисление:

След въвеждане на индикаторите в полетата на формуляра получаваме:

За да направите собствена калкулация, въведете данните във формата.

Калкулатор на дроби

Въведете две дроби:

		+ - * :

Свързани раздели.

Дробите са обикновени числа и могат да се събират и изваждат. Но тъй като имат знаменател, те изискват по-сложни правила, отколкото за цели числа.

Нека разгледаме най-простия случай, когато има две дроби с еднакви знаменатели. След това:

За да добавите дроби с еднакви знаменатели, трябва да добавите техните числители и да оставите знаменателя непроменен.

За да извадите дроби с еднакви знаменатели, трябва да извадите числителя на втората от числителя на първата дроб и отново да оставите знаменателя непроменен.

Във всеки израз знаменателите на дробите са равни. По дефиниция за събиране и изваждане на дроби получаваме:

Както можете да видите, няма нищо сложно: просто събираме или изваждаме числителите и това е.

Но дори и в такива прости действия хората успяват да направят грешки. Най-често се забравя, че знаменателят не се променя. Например, когато ги добавяте, те също започват да се добавят и това е фундаментално погрешно.

Да се отървете от лошия навик да добавяте знаменатели е доста лесно. Опитайте същото, когато изваждате. В резултат на това знаменателят ще бъде нула и дробта (внезапно!) ще загуби значението си.

Затова запомнете веднъж завинаги: при събиране и изваждане знаменателят не се променя!

Много хора също правят грешки, когато събират няколко отрицателни дроби. Има объркване със знаците: къде да поставите минус и къде да поставите плюс.

Този проблем също е много лесен за решаване. Достатъчно е да запомните, че минусът пред знака на дроб винаги може да бъде прехвърлен в числителя - и обратно. И разбира се, не забравяйте две прости правила:

Плюс с минус дава минус;
Две отрицания правят утвърдително.

Нека разгледаме всичко това с конкретни примери:

Задача. Намерете значението на израза:

В първия случай всичко е просто, но във втория въвеждаме минуси в числителите на дробите:

Какво да направите, ако знаменателите са различни

Не можете директно да събирате дроби с различни знаменатели. Поне на мен този метод е непознат. Оригиналните дроби обаче винаги могат да бъдат пренаписани, така че знаменателите да станат еднакви.

Има много начини за преобразуване на дроби. Три от тях се разглеждат в урока „Привеждане на дроби към общ знаменател“, така че тук няма да се спираме на тях. Нека да разгледаме някои примери:

Задача. Намерете значението на израза:

В първия случай редуцираме дробите до общ знаменател по метода „кръстосан“. Във втория ще търсим НОК. Забележете, че 6 = 2 · 3; 9 = 3 · 3. Последните множители в тези разлагания са равни, а първите са относително прости. Следователно, LCM(6, 9) = 2 3 3 = 18.

Какво да направите, ако една дроб има цяла част

Мога да ви зарадвам: различните знаменатели в дробите не са най-голямото зло. Много повече грешки възникват, когато цялата част е осветена в събираемите фракции.

Разбира се, има собствени алгоритми за добавяне и изваждане за такива дроби, но те са доста сложни и изискват дълго проучване. По-добре използвайте простата диаграма по-долу:

Преобразувайте всички дроби, съдържащи цяло число, в неправилни. Получаваме нормални термини (дори с различни знаменатели), които се изчисляват по правилата, обсъдени по-горе;
Всъщност изчислете сумата или разликата на получените дроби. В резултат на това практически ще намерим отговора;
Ако това е всичко, което се изисква в задачата, извършваме обратната трансформация, т.е. Отърваваме се от неправилна дроб, като подчертаваме цялата част.

Правилата за преминаване към неправилни дроби и подчертаване на цялата част са описани подробно в урока „Какво е числова дроб“. Ако не си спомняте, не забравяйте да го повторите. Примери:

Задача. Намерете значението на израза:

Тук всичко е просто. Знаменателите във всеки израз са равни, така че всичко, което остава, е да преобразувате всички дроби в неправилни и да преброите. Ние имаме:

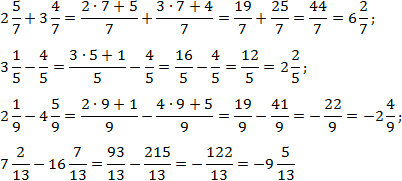
За да опростя изчисленията, пропуснах някои очевидни стъпки в последните примери.

Малка забележка към последните два примера, където се изваждат дроби с осветена цяла част. Минусът преди втората дроб означава, че се изважда цялата дроб, а не само цялата й част.

Прочетете отново това изречение, погледнете примерите - и помислете върху него. Това е мястото, където начинаещите правят огромен брой грешки. Те обичат да дават такива задачи на тестове. Ще ги срещнете няколко пъти и в тестовете за този урок, които ще бъдат публикувани скоро.

Резюме: обща изчислителна схема

В заключение ще дам общ алгоритъм, който ще ви помогне да намерите сумата или разликата на две или повече дроби:

Ако една или повече дроби имат цяла част, преобразувайте тези дроби в неправилни;
Приведете всички дроби към общ знаменател по всеки удобен за вас начин (освен ако, разбира се, авторите на проблемите не са направили това);
Събиране или изваждане на получените числа по правилата за събиране и изваждане на дроби с еднакви знаменатели;
Ако е възможно, съкратете резултата. Ако фракцията е неправилна, изберете цялата част.

Не забравяйте, че е по-добре да подчертаете цялата част в самия край на задачата, непосредствено преди да запишете отговора.

През пети век пр. н. е. древногръцкият философ Зенон от Елея формулира своите известни апории, най-известната от които е апорията „Ахил и костенурката“. Ето как звучи:

Да кажем, че Ахил тича десет пъти по-бързо от костенурката и е на хиляда стъпки зад нея. През времето, необходимо на Ахил да измине това разстояние, костенурката ще пропълзи стотина стъпки в същата посока. Когато Ахил пробяга сто крачки, костенурката пълзи още десет крачки и т.н. Процесът ще продължи безкрайно, Ахил никога няма да настигне костенурката.

Това разсъждение се превърна в логичен шок за всички следващи поколения. Аристотел, Диоген, Кант, Хегел, Хилберт... Всички те разглеждаха по един или друг начин апориите на Зенон. Шокът беше толкова силен, че " ... дискусиите продължават и до днес; научната общност все още не е успяла да стигне до общо мнение относно същността на парадоксите ... в изследването на въпроса са включени математически анализ, теория на множествата, нови физически и философски подходи ; нито едно от тях не стана общоприето решение на проблема...„[Уикипедия, „Апория на Зенон“. Всички разбират, че ги заблуждават, но никой не разбира в какво се състои измамата.

От математическа гледна точка Зенон в своята апория ясно демонстрира прехода от количество към . Този преход предполага прилагане вместо постоянни. Доколкото разбирам, математическият апарат за използване на променливи мерни единици или все още не е разработен, или не е приложен към апориите на Зенон. Прилагането на обичайната ни логика ни вкарва в капан. Ние, поради инерцията на мисленето, прилагаме постоянни единици време към реципрочната стойност. От физическа гледна точка това изглежда като забавяне на времето, докато спре напълно в момента, в който Ахил настигне костенурката. Ако времето спре, Ахил вече не може да изпревари костенурката.

Ако обърнем обичайната си логика, всичко си идва на мястото. Ахил тича с постоянна скорост. Всеки следващ сегмент от пътя му е десет пъти по-кратък от предишния. Съответно времето, прекарано за преодоляването му, е десет пъти по-малко от предишното. Ако приложим концепцията за „безкрайност“ в тази ситуация, тогава би било правилно да кажем „Ахил ще настигне костенурката безкрайно бързо“.

Как да избегнем този логически капан? Останете в постоянни единици за време и не преминавайте към реципрочни единици. На езика на Зенон това изглежда така:

За времето, необходимо на Ахил да направи хиляда крачки, костенурката ще пропълзи стотина крачки в същата посока. През следващия интервал от време, равен на първия, Ахил ще направи още хиляда стъпки, а костенурката ще пропълзи сто стъпки. Сега Ахил е на осемстотин стъпки пред костенурката.

Този подход описва адекватно реалността без никакви логически парадокси. Но това не е пълно решение на проблема. Твърдението на Айнщайн за неустоимостта на скоростта на светлината е много подобно на апорията на Зенон „Ахил и костенурката“. Все още трябва да изучаваме, преосмисляме и решаваме този проблем. И решението трябва да се търси не в безкрайно големи числа, а в мерни единици.

Друга интересна апория на Зенон разказва за летяща стрела:

Летящата стрела е неподвижна, тъй като във всеки момент от времето тя е в покой, и тъй като е в покой във всеки момент от времето, тя винаги е в покой.

В тази апория логическият парадокс се преодолява много просто – достатъчно е да се изясни, че във всеки момент една летяща стрела е в покой в различни точки на пространството, което всъщност е движение. Тук трябва да се отбележи още един момент. От една снимка на автомобил на пътя е невъзможно да се определи нито фактът на неговото движение, нито разстоянието до него. За да определите дали колата се движи, ви трябват две снимки, направени от една и съща точка в различни точки във времето, но не можете да определите разстоянието от тях. За да определите разстоянието до кола, имате нужда от две снимки, направени от различни точки в пространството в един момент във времето, но от тях не можете да определите факта на движение (разбира се, все още имате нужда от допълнителни данни за изчисления, тригонометрията ще ви помогне ). Това, на което искам да обърна специално внимание е, че две точки във времето и две точки в пространството са различни неща, които не бива да се бъркат, защото дават различни възможности за изследване.

Сряда, 4 юли 2018 г

Разликите между набор и мултимножество са описани много добре в Wikipedia. Да видим.

Както можете да видите, „не може да има два еднакви елемента в набор“, но ако има идентични елементи в набор, такъв набор се нарича „мултисет“. Разумните същества никога няма да разберат такава абсурдна логика. Това е нивото на говорещите папагали и дресираните маймуни, които нямат интелигентност от думата „напълно“. Математиците действат като обикновени обучители, проповядвайки ни своите абсурдни идеи.

Имало едно време инженерите, които построили моста, били в лодка под моста, докато тествали моста. Ако мостът се срути, посредственият инженер загина под развалините на своето творение. Ако мостът можеше да издържи натоварването, талантливият инженер построи други мостове.

Колкото и да се крият математиците зад фразата „имайте предвид, аз съм в къщата“ или по-скоро „математиката изучава абстрактни понятия“, има една пъпна връв, която ги свързва неразривно с реалността. Тази пъпна връв е пари. Нека приложим математическата теория на множествата към самите математици.

Учихме много добре математика и сега седим на касата и даваме заплати. И така, един математик идва при нас за парите си. Ние му преброяваме цялата сума и я поставяме на масата си в различни купчини, в които поставяме банкноти от една и съща деноминация. След това вземаме по една банкнота от всяка купчина и даваме на математика неговия „математически набор от заплата“. Нека обясним на математика, че той ще получи останалите сметки едва когато докаже, че множество без еднакви елементи не е равно на множество с еднакви елементи. Тук започва забавлението.

На първо място ще работи логиката на депутатите: „Това може да се приложи към другите, но не и към мен!“ След това ще започнат да ни уверяват, че банкнотите с една и съща номинална стойност имат различни номера на банкнотите, което означава, че не могат да се считат за едни и същи елементи. Добре, да броим заплатите в монети - на монетите няма цифри. Тук математикът ще започне трескаво да си спомня физиката: различните монети имат различно количество мръсотия, кристалната структура и разположението на атомите е уникално за всяка монета...

И сега имам най-интересния въпрос: къде е линията, отвъд която елементите на мултимножество се превръщат в елементи на множество и обратно? Такава линия не съществува - всичко се решава от шаманите, тук науката дори не лъже.

Вижте тук. Избираме футболни стадиони с еднаква площ. Площите на полетата са еднакви - което означава, че имаме мултимножество. Но ако погледнем имената на същите тези стадиони, получаваме много, защото имената са различни. Както можете да видите, едно и също множество от елементи е както множество, така и мултимножество. Кое е правилното? И ето че математикът-шаман-шарпист вади асо коз от ръкава си и започва да ни говори или за множество, или за мултимножество. При всички случаи той ще ни убеди, че е прав.

За да разберем как съвременните шамани оперират с теорията на множествата, обвързвайки я с реалността, е достатъчно да отговорим на един въпрос: как елементите на едно множество се различават от елементите на друго множество? Ще ви покажа, без никакво „мислимо като неединно цяло“ или „немислимо като единно цяло“.

Неделя, 18 март 2018 г

Сумата от цифрите на едно число е танц на шамани с тамбура, който няма нищо общо с математиката. Да, в уроците по математика ни учат да намираме сумата от цифрите на числото и да го използваме, но те затова са шамани, за да учат потомците на своите умения и мъдрост, иначе шаманите просто ще измрат.

Имате ли нужда от доказателство? Отворете Wikipedia и се опитайте да намерите страницата „Сума от цифри на число“. Тя не съществува. Няма формула в математиката, която може да се използва за намиране на сумата от цифрите на произволно число. В края на краищата числата са графични символи, с които пишем числа, а на езика на математиката задачата звучи така: „Намерете сумата от графични символи, представляващи произволно число.“ Математиците не могат да решат този проблем, но шаманите могат да го направят лесно.

Нека да разберем какво и как правим, за да намерим сумата от цифрите на дадено число. И така, нека имаме числото 12345. Какво трябва да се направи, за да се намери сборът от цифрите на това число? Нека разгледаме всички стъпки по ред.

1. Запишете числото на лист хартия. какво направихме Ние преобразувахме числото в графичен числов символ. Това не е математическа операция.

2. Нарежете една получена картина на няколко картинки, съдържащи отделни числа. Изрязването на картина не е математическа операция.

3. Преобразувайте отделни графични символи в числа. Това не е математическа операция.

4. Съберете получените числа. Сега това е математика.

Сумата от цифрите на числото 12345 е 15. Това са „курсовете по кроене и шиене“ от шаманите, които математиците използват. Но това не е всичко.

От математическа гледна точка няма значение в коя бройна система записваме едно число. Така че в различни системи с числа сумата от цифрите на едно и също число ще бъде различна. В математиката числовата система се обозначава като долен индекс отдясно на числото. С голямото число 12345, не искам да си заблуждавам главата, нека разгледаме числото 26 от статията за. Нека запишем това число в двоична, осмична, десетична и шестнадесетична бройни системи. Няма да разглеждаме всяка стъпка под микроскоп; вече сме го направили. Нека да видим резултата.

Както можете да видите, в различните бройни системи сумата от цифрите на едно и също число е различна. Този резултат няма нищо общо с математиката. Това е същото, както ако определите площта на правоъгълник в метри и сантиметри, ще получите напълно различни резултати.

Нулата изглежда еднакво във всички бройни системи и няма сбор от цифри. Това е още един аргумент в полза на факта, че. Въпрос към математиците: как в математиката се обозначава нещо, което не е число? Какво, за математиците не съществува нищо освен числата? Това мога да го позволя за шаманите, но не и за учените. Реалността не е само в числа.

Полученият резултат трябва да се счита за доказателство, че бройните системи са мерни единици за числа. В крайна сметка не можем да сравняваме числа с различни мерни единици. Ако едни и същи действия с различни мерни единици на една и съща величина водят до различни резултати след сравняването им, то това няма нищо общо с математиката.

Какво е истинска математика? Това е, когато резултатът от математическа операция не зависи от размера на числото, използваната мерна единица и от това кой извършва това действие.

Знак на вратата Той отваря вратата и казва:

о! Това не е ли женската тоалетна?
- Млада жена! Това е лаборатория за изследване на бездефилната святост на душите по време на възнесението им на небето! Ореол отгоре и стрелка нагоре. Каква друга тоалетна?

Жена... Ореолът отгоре и стрелката надолу са мъжки.

Ако такова произведение на дизайнерското изкуство мига пред очите ви няколко пъти на ден,

Тогава не е изненадващо, че изведнъж намирате странна икона в колата си:

Лично аз полагам усилия да видя минус четири градуса при акащ човек (една снимка) (композиция от няколко картинки: знак минус, число четири, обозначение на градуса). И не мисля, че това момиче е глупачка, която не знае физика. Тя просто има силен стереотип за възприемане на графични изображения. И математиците ни учат на това през цялото време. Ето един пример.

1А не е „минус четири градуса“ или „едно а“. Това е "какащ човек" или числото "двадесет и шест" в шестнадесетичен запис. Тези хора, които постоянно работят в тази бройна система, автоматично възприемат число и буква като един графичен символ.

Съдържание на урока

Събиране на дроби с еднакви знаменатели

Съществуват два вида събиране на дроби:

Събиране на дроби с еднакви знаменатели
Събиране на дроби с различни знаменатели

Първо, нека научим събирането на дроби с еднакви знаменатели. Тук всичко е просто. За да добавите дроби с еднакви знаменатели, трябва да добавите техните числители и да оставите знаменателя непроменен. Например, нека съберем дробите и . Добавете числителите и оставете знаменателя непроменен:

Този пример лесно може да бъде разбран, ако си спомним пицата, която е разделена на четири части. Ако добавите пица към пица, получавате пица:

Пример 2.Добавете дроби и .

Отговорът се оказа неправилна дроб. Когато дойде краят на задачата, обичайно е да се отървете от неправилните дроби. За да се отървете от неправилна дроб, трябва да изберете цялата част от нея. В нашия случай цялата част се изолира лесно - две делено на две е равно на едно:

Този пример може лесно да бъде разбран, ако си спомним за пица, която е разделена на две части. Ако добавите още пица към пицата, получавате една цяла пица:

Пример 3. Добавете дроби и .

Отново събираме числителите и оставяме знаменателя непроменен:

Този пример лесно може да бъде разбран, ако си спомним пицата, която е разделена на три части. Ако добавите още пица към пицата, получавате пица:

Пример 4.Намерете стойността на израз

Този пример се решава по абсолютно същия начин като предишните. Числителите трябва да се добавят, а знаменателят да се остави непроменен:

Нека се опитаме да изобразим нашето решение с помощта на чертеж. Ако добавите пица към една пица и добавите още пици, получавате 1 цяла пица и повече пици.

Както можете да видите, няма нищо сложно в събирането на дроби с еднакви знаменатели. Достатъчно е да разберете следните правила:

За да добавите дроби с еднакъв знаменател, трябва да добавите техните числители и да оставите знаменателя непроменен;

Събиране на дроби с различни знаменатели

Сега нека научим как да събираме дроби с различни знаменатели. При събиране на дроби знаменателите на дробите трябва да са еднакви. Но те не винаги са еднакви.

Например, дроби могат да се събират, защото имат еднакви знаменатели.

Но дробите не могат да се добавят веднага, тъй като тези дроби имат различни знаменатели. В такива случаи дробите трябва да се сведат до един и същ (общ) знаменател.

Има няколко начина за намаляване на дробите до един и същи знаменател. Днес ще разгледаме само един от тях, тъй като другите методи може да изглеждат сложни за начинаещ.

Същността на този метод е, че първо се търси LCM на знаменателите на двете дроби. След това LCM се разделя на знаменателя на първата дроб, за да се получи първият допълнителен фактор. Те правят същото и с втората дроб - LCM се разделя на знаменателя на втората дроб и се получава втори допълнителен множител.

След това числителите и знаменателите на дробите се умножават по техните допълнителни множители. В резултат на тези действия дроби с различни знаменатели се преобразуват в дроби с еднакви знаменатели. И вече знаем как да събираме такива дроби.

Пример 1. Нека съберем дробите и

Първо, намираме най-малкото общо кратно на знаменателите на двете дроби. Знаменателят на първата дроб е числото 3, а знаменателят на втората дроб е числото 2. Най-малкото общо кратно на тези числа е 6

LCM (2 и 3) = 6

Сега да се върнем към дробите и . Първо, разделете LCM на знаменателя на първата дроб и вземете първия допълнителен фактор. LCM е числото 6, а знаменателят на първата дроб е числото 3. Разделяме 6 на 3, получаваме 2.

Полученото число 2 е първият допълнителен множител. Записваме го до първата дроб. За да направите това, направете малка наклонена линия над фракцията и запишете допълнителния фактор, намерен над нея:

Правим същото с втората фракция. Разделяме LCM на знаменателя на втората дроб и получаваме втория допълнителен множител. LCM е числото 6, а знаменателят на втората дроб е числото 2. Разделяме 6 на 2, получаваме 3.

Полученото число 3 е вторият допълнителен множител. Записваме го до втората дроб. Отново правим малка наклонена линия над втората дроб и записваме допълнителния фактор, намерен над нея:

Сега имаме всичко готово за добавяне. Остава да умножим числителите и знаменателите на дробите с техните допълнителни множители:

Погледнете внимателно до какво сме стигнали. Стигнахме до извода, че дроби с различни знаменатели се превръщат в дроби с еднакви знаменатели. И вече знаем как да събираме такива дроби. Нека вземем този пример до края:

Това завършва примера. Оказва се да добавите .

Нека се опитаме да изобразим нашето решение с помощта на чертеж. Ако добавите пица към пица, получавате една цяла пица и още една шеста от пица:

Намаляването на дроби до един и същи (общ) знаменател също може да бъде изобразено с помощта на картина. Намалявайки дробите и до общ знаменател, получаваме дробите и . Тези две фракции ще бъдат представени от едни и същи парчета пица. Единствената разлика ще бъде, че този път те ще бъдат разделени на равни части (приведени към един знаменател).

Първият чертеж представлява дроб (четири части от шест), а вторият чертеж представлява дроб (три части от шест). Добавяйки тези парчета, получаваме (седем парчета от шест). Тази дроб е неправилна, затова подчертахме цялата й част. В резултат на това получихме (една цяла пица и още една шеста пица).

Моля, обърнете внимание, че сме описали този пример твърде подробно. В учебните заведения не е прието да се пише толкова подробно. Трябва да можете бързо да намерите LCM на двата знаменателя и допълнителните множители към тях, както и бързо да умножите намерените допълнителни множители по вашите числители и знаменатели. Ако бяхме в училище, трябваше да напишем този пример по следния начин:

Но има и друга страна на монетата. Ако не си водите подробни бележки в първите етапи на изучаване на математика, тогава започват да се появяват въпроси от този сорт. „Откъде идва това число?“, „Защо дробите изведнъж се превръщат в напълно различни дроби? «.

За да улесните добавянето на дроби с различни знаменатели, можете да използвате следните инструкции стъпка по стъпка:

Намерете LCM на знаменателите на дробите;
Разделете LCM на знаменателя на всяка дроб и получете допълнителен фактор за всяка дроб;
Умножете числителите и знаменателите на дробите с техните допълнителни множители;
Съберете дроби с еднакви знаменатели;
Ако отговорът се окаже неправилна дроб, изберете цялата й част;

Пример 2.Намерете стойността на израз .

Нека използваме инструкциите, дадени по-горе.

Стъпка 1. Намерете LCM на знаменателите на дробите

Намерете LCM на знаменателите на двете дроби. Знаменателите на дробите са числата 2, 3 и 4

Стъпка 2. Разделете LCM на знаменателя на всяка дроб и получете допълнителен фактор за всяка дроб

Разделете LCM на знаменателя на първата дроб. LCM е числото 12, а знаменателят на първата дроб е числото 2. Разделяме 12 на 2, получаваме 6. Получихме първия допълнителен множител 6. Записваме го над първата дроб:

Сега разделяме LCM на знаменателя на втората дроб. LCM е числото 12, а знаменателят на втората дроб е числото 3. Разделяме 12 на 3, получаваме 4. Получаваме втория допълнителен множител 4. Записваме го над втората дроб:

Сега разделяме LCM на знаменателя на третата дроб. LCM е числото 12, а знаменателят на третата дроб е числото 4. Разделяме 12 на 4, получаваме 3. Получаваме третия допълнителен множител 3. Записваме го над третата дроб:

Стъпка 3. Умножете числителите и знаменателите на дробите по техните допълнителни множители

Умножаваме числителите и знаменателите по техните допълнителни множители:

Стъпка 4. Добавете дроби с еднакви знаменатели

Стигнахме до извода, че дроби с различни знаменатели се превръщат в дроби с еднакви (общи) знаменатели. Всичко, което остава, е да съберем тези дроби. Добавете го:

Добавката не се побираше на един ред, така че преместихме оставащия израз на следващия ред. Това е позволено в математиката. Когато израз не се побира на един ред, той се премества на следващия ред, като е необходимо да се постави знак за равенство (=) в края на първия ред и в началото на новия ред. Знакът за равенство на втория ред показва, че това е продължение на израза, който беше на първия ред.

Стъпка 5. Ако отговорът се окаже неправилна дроб, тогава изберете цялата част от нея

Нашият отговор се оказа неправилна дроб. Трябва да подчертаем цяла част от него. Подчертаваме:

Получихме отговор

Изваждане на дроби с еднакви знаменатели

Има два вида изваждане на дроби:

Изваждане на дроби с еднакви знаменатели
Изваждане на дроби с различни знаменатели

Първо, нека научим как да изваждаме дроби с еднакви знаменатели. Тук всичко е просто. За да извадите друга от една дроб, трябва да извадите числителя на втората дроб от числителя на първата дроб, но да оставите знаменателя същия.

Например, нека намерим стойността на израза. За да решите този пример, трябва да извадите числителя на втората дроб от числителя на първата дроб и да оставите знаменателя непроменен. Нека направим това:

Този пример лесно може да бъде разбран, ако си спомним пицата, която е разделена на четири части. Ако режете пици от пица, получавате пици:

Пример 2.Намерете стойността на израза.

Отново от числителя на първата дроб извадете числителя на втората дроб и оставете знаменателя непроменен:

Този пример лесно може да бъде разбран, ако си спомним пицата, която е разделена на три части. Ако режете пици от пица, получавате пици:

Пример 3.Намерете стойността на израз

Този пример се решава точно по същия начин като предишните. От числителя на първата дроб трябва да извадите числителите на останалите дроби:

Както можете да видите, няма нищо сложно в изваждането на дроби с еднакви знаменатели. Достатъчно е да разберете следните правила:

За да извадите друга от една дроб, трябва да извадите числителя на втората дроб от числителя на първата дроб и да оставите знаменателя непроменен;
Ако отговорът се окаже неправилна дроб, тогава трябва да подчертаете цялата част от нея.

Изваждане на дроби с различни знаменатели

Например, можете да извадите дроб от дроб, защото дробите имат еднакви знаменатели. Но не можете да извадите дроб от дроб, тъй като тези дроби имат различни знаменатели. В такива случаи дробите трябва да се сведат до един и същ (общ) знаменател.

Общият знаменател се намира по същия принцип, който използвахме при събиране на дроби с различни знаменатели. Първо, намерете LCM на знаменателите на двете дроби. Тогава LCM се разделя на знаменателя на първата дроб и се получава първият допълнителен множител, който се записва над първата дроб. По същия начин LCM се разделя на знаменателя на втората дроб и се получава втори допълнителен множител, който се записва над втората дроб.

След това дробите се умножават по техните допълнителни множители. В резултат на тези операции дроби с различни знаменатели се преобразуват в дроби с еднакви знаменатели. И вече знаем как да изваждаме такива дроби.

Пример 1.Намерете значението на израза:

Тези дроби имат различни знаменатели, така че трябва да ги намалите до един и същи (общ) знаменател.

Първо намираме LCM на знаменателите на двете дроби. Знаменателят на първата дроб е числото 3, а знаменателят на втората дроб е числото 4. Най-малкото общо кратно на тези числа е 12

LCM (3 и 4) = 12

Сега да се върнем към дробите и

Нека намерим допълнителен фактор за първата дроб. За да направите това, разделете LCM на знаменателя на първата дроб. LCM е числото 12, а знаменателят на първата дроб е числото 3. Разделяме 12 на 3, получаваме 4. Напишете четири над първата дроб:

Правим същото с втората фракция. Разделете LCM на знаменателя на втората дроб. LCM е числото 12, а знаменателят на втората дроб е числото 4. Разделяме 12 на 4, получаваме 3. Напишете тройка върху втората дроб:

Сега сме готови за изваждане. Остава да умножим дробите по техните допълнителни множители:

Стигнахме до извода, че дроби с различни знаменатели се превръщат в дроби с еднакви знаменатели. И вече знаем как да изваждаме такива дроби. Нека вземем този пример до края:

Получихме отговор

Нека се опитаме да изобразим нашето решение с помощта на чертеж. Ако изрежете пица от пица, ще получите пица

Това е подробната версия на решението. Ако бяхме в училище, щяхме да решаваме този пример по-кратко. Такова решение би изглеждало така:

Намаляването на дроби до общ знаменател също може да бъде изобразено с помощта на картина. Намалявайки тези дроби до общ знаменател, получаваме дробите и . Тези фракции ще бъдат представени от едни и същи парчета пица, но този път ще бъдат разделени на равни части (намалени до същия знаменател):

Първата снимка показва дроб (осем части от дванадесет), а втората картина показва дроб (три части от дванадесет). Като изрежем три парчета от осем парчета, получаваме пет парчета от дванадесет. Дробта описва тези пет части.

Пример 2.Намерете стойността на израз

Тези дроби имат различни знаменатели, така че първо трябва да ги намалите до един и същи (общ) знаменател.

Нека намерим LCM на знаменателите на тези дроби.

Знаменателите на дробите са числата 10, 3 и 5. Най-малкото общо кратно на тези числа е 30

LCM(10, 3, 5) = 30

Сега намираме допълнителни множители за всяка дроб. За да направите това, разделете LCM на знаменателя на всяка дроб.

Нека намерим допълнителен фактор за първата дроб. LCM е числото 30, а знаменателят на първата дроб е числото 10. Разделяме 30 на 10, получаваме първия допълнителен множител 3. Записваме го над първата дроб:

Сега намираме допълнителен фактор за втората дроб. Разделете LCM на знаменателя на втората дроб. LCM е числото 30, а знаменателят на втората дроб е числото 3. Разделяме 30 на 3, получаваме втория допълнителен множител 10. Записваме го над втората дроб:

Сега намираме допълнителен фактор за третата дроб. Разделете LCM на знаменателя на третата дроб. LCM е числото 30, а знаменателят на третата дроб е числото 5. Разделяме 30 на 5, получаваме третия допълнителен множител 6. Записваме го над третата дроб:

Сега всичко е готово за изваждане. Остава да умножим дробите по техните допълнителни множители:

Стигнахме до извода, че дроби с различни знаменатели се превръщат в дроби с еднакви (общи) знаменатели. И вече знаем как да изваждаме такива дроби. Нека завършим този пример.

Продължението на примера няма да се побере на един ред, затова преместваме продължението на следващия ред. Не забравяйте за знака за равенство (=) на новия ред:

Отговорът се оказа обикновена дроб и изглежда, че всичко ни подхожда, но е твърде тромаво и грозно. Трябва да го направим по-просто. Какво може да се направи? Можете да съкратите тази фракция.

За да намалите дроб, трябва да разделите числителя и знаменателя на (НОД) на числата 20 и 30.

И така, намираме gcd на числата 20 и 30:

Сега се връщаме към нашия пример и разделяме числителя и знаменателя на дробта на намерения gcd, тоест на 10

Получихме отговор

Умножение на дроб по число

За да умножите дроб по число, трябва да умножите числителя на дробта по това число и да оставите знаменателя същия.

Пример 1. Умножете дроб по числото 1.

Умножете числителя на дробта по числото 1

Записът може да се разбира като отнемащ половин 1 път. Например, ако вземете пици 1 път, получавате пици

От законите на умножението знаем, че ако умножаемото и множителят се разменят, произведението няма да се промени. Ако изразът е записан като , тогава произведението пак ще бъде равно на . Отново правилото за умножение на цяло число и дроб работи:

Тази нотация може да се разбира като вземане на половината от едно. Например, ако има 1 цяла пица и вземем половината от нея, тогава ще имаме пица:

Пример 2. Намерете стойността на израз

Умножете числителя на дробта по 4

Отговорът беше неправилна дроб. Нека подчертаем цялата част от него:

Изразът може да се разбира като вземане на две четвърти 4 пъти. Например, ако вземете 4 пици, ще получите две цели пици

И ако разменим множителя и множителя, получаваме израза . То също ще бъде равно на 2. Този израз може да се разбира като вземане на две пици от четири цели пици:

Умножение на дроби

За да умножите дроби, трябва да умножите техните числители и знаменатели. Ако отговорът се окаже неправилна дроб, трябва да подчертаете цялата част от нея.

Пример 1.Намерете стойността на израза.

Получихме отговор. Препоръчително е тази фракция да се намали. Дробта може да се намали с 2. Тогава окончателното решение ще приеме следната форма:

Изразът може да се разбира като вземане на пица от половин пица. Да кажем, че имаме половин пица:

Как да вземем две трети от тази половина? Първо трябва да разделите тази половина на три равни части:

И вземете две от тези три части:

Ще направим пица. Припомнете си как изглежда пицата, разделена на три части:

Едно парче от тази пица и двете парчета, които взехме, ще имат еднакви размери:

С други думи, говорим за пица с еднакъв размер. Следователно стойността на израза е

Пример 2. Намерете стойността на израз

Умножете числителя на първата дроб по числителя на втората дроб и знаменателя на първата дроб по знаменателя на втората дроб:

Отговорът беше неправилна дроб. Нека подчертаем цялата част от него:

Пример 3.Намерете стойността на израз

Отговорът се оказа обикновена дроб, но би било добре да бъде съкратен. За да намалите тази дроб, трябва да разделите числителя и знаменателя на тази дроб на най-големия общ делител (НОД) на числата 105 и 450.

И така, нека намерим gcd на числата 105 и 450:

Сега разделяме числителя и знаменателя на нашия отговор на gcd, който намерихме сега, тоест на 15

Представяне на цяло число като дроб

Всяко цяло число може да бъде представено като дроб. Например числото 5 може да бъде представено като . Това няма да промени значението на пет, тъй като изразът означава "числото пет, разделено на едно", а това, както знаем, е равно на пет:

Реципрочни числа

Сега ще се запознаем с една много интересна тема по математика. Нарича се "обратни числа".

Определение. Обратно на номера е число, което, когато се умножи поа дава едно.

Нека заместим в тази дефиниция вместо променливата аномер 5 и се опитайте да прочетете определението:

Обратно на номер 5 е число, което, когато се умножи по 5 дава едно.

Възможно ли е да се намери число, което, умножено по 5, дава единица? Оказва се, че е възможно. Нека си представим пет като дроб:

След това умножете тази дроб сама по себе си, просто разменете числителя и знаменателя. С други думи, нека умножим дробта сама по себе си, само с главата надолу:

Какво ще се случи в резултат на това? Ако продължим да решаваме този пример, получаваме един:

Това означава, че обратното на числото 5 е числото , тъй като когато умножите 5 по, получавате едно.

Реципрочната стойност на число може да се намери и за всяко друго цяло число.

Можете също така да намерите реципрочната стойност на всяка друга дроб. За да направите това, просто го обърнете.

Деление на дроб на число

Да кажем, че имаме половин пица:

Нека го разделим по равно между две. Колко пица ще получи всеки човек?

Вижда се, че след разделянето на половината пица се получават две еднакви парчета, всяко от които представлява пица. Така че всеки получава пица.

Разделянето на дроби се извършва с помощта на реципрочни числа. Реципрочните числа ви позволяват да замените делението с умножение.

За да разделите дроб на число, трябва да умножите дробта по обратното на делителя.

Използвайки това правило, ще запишем разделянето на нашата половина пица на две части.

И така, трябва да разделите дроба на числото 2. Тук дивидентът е дробта, а делителят е числото 2.

За да разделите дроб на числото 2, трябва да умножите тази дроб по реципрочната стойност на делителя 2. Реципрочната стойност на делителя 2 е дробта. Така че трябва да умножите по

За да добавите цяло число към дроб, е достатъчно да извършите поредица от действия или по-скоро изчисления.

Например, имате 7 - цяло число, което трябва да добавите към дробта 1/2.

Процедираме по следния начин:

Умножаваме 7 по знаменателя (2), получаваме 14,
добавете горната част (1) към 14, получавате 15,
и заместете знаменателя.
резултатът е 15/2.

По този лесен начин можете да добавяте цели числа към дроби.

И за да изолирате цяло число от дроб, трябва да разделите числителя на знаменателя, а остатъка - и ще има дроб.

Операцията за добавяне на цяло число към правилна обикновена дроб не е сложна и понякога просто включва образуването на смесена дроб, в която цялата част се поставя отляво на дробната част, например такава дроб ще бъде смесена:

По-често обаче добавянето на цяло число към дроб води до неправилна дроб, в която числителят е по-голям от знаменателя. Тази операция се извършва по следния начин: цялото число се представя като неправилна дроб със същия знаменател като добавяната дроб и след това просто се събират числителите на двете дроби. В пример ще изглежда така:

5+1/8 = 5*8/8+1/8 = 40/8+1/8 = 41/8

Мисля, че е много просто.

Например, имаме частта 1/4 (това е същото като 0,25, тоест една четвърт от цялото число).

И към тази четвърт можете да добавите произволно цяло число, например 3. Получавате три и четвърт:

3.25. Или в дроб се изразява по следния начин: 3 1/4

Въз основа на този пример можете да събирате всякакви дроби с произволни цели числа.

Трябва да повдигнете цяло число до дроб със знаменател 10 (6/10). След това приведете съществуващата дроб към общ знаменател 10 (35=610). Е, извършете операцията като с обикновените дроби 610+610=1210 за общо 12.

Има два начина да направите това.

1). Една дроб може да се преобразува в цяло число и може да се извърши събиране. Например 1/2 е 0,5; 1/4 е равно на 0,25; 2/5 е 0,4 и т.н.

Вземете цяло число 5, към което трябва да добавите дробта 4/5. Нека трансформираме дробта: 4/5 е 4 делено на 5 и получаваме 0,8. Добавяме 0,8 към 5 и получаваме 5,8 или 5 4/5.

2). Втори метод: 5 + 4/5 = 29/5 = 5 4/5.

Добавянето на дроби е проста математическа операция, например трябва да съберете цяло число 3 и дроб 1/7. За да съберете тези две числа, трябва да имате един знаменател, така че трябва да умножите три по седем и да разделите на тази цифра, тогава получавате 21/7+1/7, знаменател едно, съберете 21 и 1, получавате отговора 22/7 .

Просто вземете и добавете цяло число към тази дроб. Да кажем, че имате нужда от 6 + 1/2 = 6 1/2. Е, ако това е десетична дроб, тогава можеш да го направиш така: 6+1,2=7,2.

За да съберете дроб и цяло число, трябва да добавите дробта към цялото число и да ги запишете като комплексно число, например, когато събираме обикновена дроб с цяло число, получаваме: 1/2 +3 = 3 1/ 2; при събиране на десетична дроб: 0,5 +3 =3,5.

Дробта сама по себе си не е цяло число, тъй като нейното количество не достига до нея и следователно не е необходимо цялото число да се преобразува в тази дроб. Следователно цялото число остава цяло число и напълно демонстрира пълната стойност, а частта се добавя към него и демонстрира колко липсва това цяло число, преди да се добави следващата пълна точка.

Академичен пример.

10 + 7/3 = 10 цяло и 7/3.

Ако, разбира се, има цели числа, тогава те се сумират с цели числа.

12 + 5 7/9 = 17 и 7/9.

Зависи кое цяло число и коя дроб.

Ако и двата термина са положителни, тази дроб трябва да се добави към цялото число. Резултатът ще бъде смесено число. Освен това може да има 2 случая.

Случай 1.

Дробта е правилна, т.е. числителят е по-малък от знаменателя. Тогава полученото след заданието смесено число ще бъде отговорът.

4/9 + 10 = 10 4/9 (десет цяло и четири девети).

Случай 2.

Дробта е неправилна, т.е. числителят е по-голям от знаменателя. Тогава е необходимо малко преобразуване. Една неправилна дроб трябва да се превърне в смесено число, с други думи, цялата част трябва да бъде изолирана. Това се прави по следния начин:

След това трябва да добавите цялата част от неправилната дроб към цялото число и да добавите нейната дробна част към получената сума. По същия начин цяло се добавя към смесено число.

1) 11/4 + 5 = 2 3/4 + 5 = 7 3/4 (7 точки три четвърти).

2) 5 1/2 + 6 = 11 1/2 (11 точка едно).

Ако един от термините или и двата отрицателен, след което извършваме събирането по правилата за събиране на числа с различни или еднакви знаци. Цяло число се представя като отношението на това число към 1, след което и числителят, и знаменателят се умножават по число, равно на знаменателя на дробта, към която се добавя цялото число.

3) 1/5 + (-2)= 1/5 + -2/1 = 1/5 + -10/5 = -9/5 = -1 4/5 (минус 1 точка четири пети).

4) -13/3 + (-4) = -13/3 + -4/1 = -13/3 + -12/3 = -25/3 = -8 1/3 (минус 8 точка една трета).

Коментирайте.

След като се запознаят с отрицателните числа, когато изучават действия с тях, учениците от 6. клас трябва да разберат, че добавянето на цяло положително число към отрицателна дроб е същото като изваждане на дроб от естествено число. Известно е, че това действие се изпълнява по следния начин:

Всъщност, за да добавите дроб и цяло число, просто трябва да преобразувате съществуващото цяло число в дроб и това е толкова лесно, колкото да махнете крушите. Просто трябва да вземете знаменателя на дробта (в примера) и да го направите знаменател на цяло число, като го умножите по този знаменател и разделите, ето пример:

2+2/3 = 2*3/3+2/3 = 6/3+2/3 = 8/3