Създайте съотношение и изчислете лимита.
Откъде дойде? таблица с производни и правила за диференциране? Благодарение на единствения лимит. Изглежда като магия, но в действителност е ловкост, а не измама. На урока Какво е дериват?Започнах да разглеждам конкретни примери, където, използвайки определението, намерих производните на линейна и квадратична функция. За целите на когнитивната загрявка ще продължим да безпокоим таблица с производни, усъвършенстване на алгоритъма и техническите решения:
Пример 1
По същество трябва да докажете специален случай на производна на степенна функция, който обикновено се появява в таблицата: .
Решениетехнически формализиран по два начина. Нека започнем с първия, вече познат подход: стълбата започва с дъска, а производната функция започва с производната в точка.
Нека помислим някои(конкретна) точка, принадлежаща на област на дефиницияфункция, в която има производна. Нека зададем увеличението в тази точка (разбира се, без да надхвърлямео/о
-аз)и съставете съответното увеличение на функцията:
Нека изчислим лимита:
Несигурността 0:0 се елиминира чрез стандартна техника, разглеждана още през първи век пр.н.е. Умножете числителя и знаменателя по спрегнатия израз ![]() :
:
Техниката за решаване на такава граница е разгледана подробно във въвеждащия урок. за границите на функциите.
Тъй като можете да изберете ВСЯКА точка от интервала като качество, тогава, като направим замяната, получаваме:
Отговор
Още веднъж да се порадваме на логаритмите:
Пример 2
Намерете производната на функция, като използвате определението за производна
Решение: Нека разгледаме различен подход за популяризиране на същата задача. Той е абсолютно същият, но по-рационален по отношение на дизайна. Идеята е да се отървете от индекса в началото на решението и да използвате буквата вместо буквата.
Нека помислим произволенточка, принадлежаща на област на дефиницияфункция (интервал) и задайте приращението в нея. Но тук, между другото, както в повечето случаи, можете да направите без никакви резерви, тъй като логаритмичната функция е диференцируема във всяка точка от областта на дефиницията.
Тогава съответното увеличение на функцията е:
Нека намерим производната:
Простотата на дизайна е балансирана от объркването, което може да възникне за начинаещи (и не само). В крайна сметка сме свикнали с факта, че буквата „X“ се променя в лимита! Но тук всичко е различно: - антична статуя и - жив посетител, бързо крачещ по коридора на музея. Тоест "x" е "като константа".
Ще коментирам премахването на несигурността стъпка по стъпка:

(1) Използваме свойството на логаритъма.
(2) В скоби разделете числителя на знаменателя термин по термин.
(3) В знаменателя ние изкуствено умножаваме и делим на „x“, за да се възползваме от забележителен лимит ![]() , докато като безкрайно малъкоткроява.
, докато като безкрайно малъкоткроява.
Отговор: по дефиниция на производна:
Или накратко:
Предлагам сами да изградите още две формули за таблици:
Пример 3
В този случай е удобно веднага да намалите компилираното увеличение до общ знаменател. Приблизителна извадка на задачата в края на урока (първи метод).
Пример 3:Решение
: помислете за някакъв момент
, принадлежащи към областта на дефиниране на функцията
. Нека зададем увеличението в тази точка
и съставете съответното нарастване на функцията:
Нека намерим производната в точката
:
Тъй като като a
можете да изберете всяка точка
функционална област
, Че
И
Отговор
:
по дефиниция на производна
Пример 4
Намерете производна по дефиниция
И тук всичко трябва да се сведе до прекрасен лимит. Решението се формализира по втория начин.
Редица други таблични производни. Пълният списък може да бъде намерен в училищния учебник или, например, 1-ви том на Фихтенхолц. Не виждам много смисъл да копирам доказателства за правилата за диференциране от книги - те също се генерират от формулата.
Пример 4:Решение
, принадлежи на
и задайте увеличението в него
Нека намерим производната:
Използване на чудесен лимит
Отговор
:
а-приорен
Пример 5
Намерете производната на функция, като използвате определението за производна
Решение: използваме първия стил на дизайн. Нека разгледаме някаква точка, принадлежаща на , и уточним увеличението на аргумента в нея. Тогава съответното увеличение на функцията е:
Може би някои читатели все още не са разбрали напълно принципа, по който трябва да се правят увеличения. Вземете точка (число) и намерете стойността на функцията в нея: ![]() , тоест във функцията вместо„X“ трябва да се замени. Сега също вземаме много конкретно число и също го заместваме във функцията вместо"икса": . Записваме разликата и тя е необходима постави в скоби напълно.
, тоест във функцията вместо„X“ трябва да се замени. Сега също вземаме много конкретно число и също го заместваме във функцията вместо"икса": . Записваме разликата и тя е необходима постави в скоби напълно.
Увеличаване на компилираната функция Може да бъде полезно незабавното опростяване. За какво? Улеснете и съкратете решението до по-нататъшна граница.
Използваме формули, отваряме скобите и съкращаваме всичко, което може да се съкрати: 
Пуйката е изкормена, няма проблем с печеното:
Тъй като можем да изберем всяко реално число като стойност, правим замяната и получаваме ![]() .
.
Отговор: ![]() а-приорен.
а-приорен.
За целите на проверката, нека намерим производната с помощта правила и таблици за диференциране:
Винаги е полезно и приятно да знаете правилния отговор предварително, така че е по-добре да разграничите предложената функция по „бърз“ начин, мислено или в чернова, в самото начало на решението.
Пример 6
Намерете производната на функция по дефиниция на производната
Това е пример, който можете да решите сами. Резултатът е очевиден:
Пример 6:Решение
: помислете за някакъв момент
, принадлежи на
и задайте увеличението на аргумента в него
. Тогава съответното увеличение на функцията е:

Нека изчислим производната:

По този начин: ![]()
Защото като
тогава можете да изберете всяко реално число
И
Отговор
:
а-приорен.
Да се върнем към стил #2:
Пример 7
![]()
Нека разберем веднага какво трябва да се случи. от правило за диференциране на сложни функции:
Решение: разгледайте произволна точка, принадлежаща на , задайте нарастването на аргумента в нея и съставете увеличението на функцията:
Нека намерим производната: 
(1) Използвайте тригонометрична формула ![]() .
.
(2) Под синуса отваряме скобите, под косинуса представяме подобни членове.
(3) Под синус намаляваме членовете, под косинус разделяме числителя на знаменателя член по член.
(4) Поради нечетността на синуса изваждаме „минуса“. Под косинуса показваме, че терминът .
(5) Извършваме изкуствено умножение в знаменателя, за да използваме първата прекрасна граница. Така несигурността е елиминирана, нека подредим резултата.
Отговор: а-приорен
Както можете да видите, основната трудност на разглеждания проблем се основава на сложността на самия лимит + лека уникалност на опаковката. На практика се срещат и двата метода на проектиране, така че описвам и двата подхода възможно най-подробно. Еквивалентни са, но все пак по мое субективно впечатление е по-препоръчително за манекените да се придържат към вариант 1 с „X-нула“.
Пример 8
Използвайки определението, намерете производната на функцията
Пример 8:Решение
: разгледайте произволна точка
, принадлежи на
, нека зададем увеличението в него
и съставете увеличението на функцията:
Нека намерим производната:

Използваме тригонометричната формула
и първото забележително ограничение:

Отговор
:
а-приорен
Нека да разгледаме по-рядка версия на проблема:
Пример 9
Намерете производната на функцията в точката, като използвате определението за производна.
Първо, какъв трябва да бъде крайният резултат? Номер
Нека изчислим отговора по стандартния начин: 
Решение: от гледна точка на яснота, тази задача е много по-проста, тъй като вместо това формулата взема предвид конкретна стойност.
Нека зададем увеличението в точката и съставим съответното увеличение на функцията:
Нека изчислим производната в точката:
Използваме много рядка формула за тангенс разлика ![]() и още веднъж намаляваме решението до първата прекрасна граница:
и още веднъж намаляваме решението до първата прекрасна граница:
Отговор: по дефиниция на производна в точка.
Проблемът не е толкова труден за решаване „като цяло“ - достатъчно е да се замени с или просто в зависимост от метода на проектиране. В този случай е ясно, че резултатът няма да бъде число, а производна функция.
Пример 10
Използвайки определението, намерете производната на функцията ![]() в точка (една от които може да се окаже безкрайна), която вече описах в общи линии теоретичен урок за производната.
в точка (една от които може да се окаже безкрайна), която вече описах в общи линии теоретичен урок за производната.
Някои зададени на части функции също могат да бъдат диференцирани в точките на „съединяване“ на графиката, например catdog има обща производна и обща допирателна (ос x) в точката. Крива, но диференцируема по ! Тези, които се интересуват, могат да проверят това сами, като използват току-що решения пример.
©2015-2019 сайт
Всички права принадлежат на техните автори. Този сайт не претендира за авторство, но предоставя безплатно използване.
Дата на създаване на страницата: 2017-06-11
Съдържанието на статията
ПРОИЗВОДНО– производна на функцията г = f(х), дадени на определен интервал ( а, b) в точка хот този интервал се нарича границата, към която клони съотношението на нарастването на функцията fв този момент към съответното увеличение на аргумента, когато увеличението на аргумента клони към нула.
Производната обикновено се обозначава по следния начин:
Други обозначения също са широко използвани:
Незабавна скорост.
Нека точката Мсе движи по права линия. Разстояние сподвижна точка, считано от някаква начална позиция М 0 , зависи от времето T, т.е. сима функция на времето T: с= f(T). Нека в някакъв момент от времето Tподвижна точка Мбеше на разстояние сот изходна позиция М 0 и в някой следващ момент T+D Tсе оказа в положение М 1 - на разстояние с+D сот начална позиция ( виж снимка.).
Така за определен период от време Д Tразстояние ссе променя със сумата D с. В този случай те казват, че през интервала от време D Tвеличина сполучено увеличение D с.
Средната скорост не може във всички случаи точно да характеризира скоростта на движение на дадена точка Мв даден момент T. Ако, например, тялото в началото на интервала D Tсе движи много бързо и накрая много бавно, тогава средната скорост няма да може да отрази посочените характеристики на движението на точката и да даде представа за истинската скорост на движението й в момента T. За да изразите по-точно истинската скорост, като използвате средната скорост, трябва да вземете по-кратък период от време D T. Най-пълно характеризира скоростта на движение на дадена точка в момента Tграницата, към която клони средната скорост при D T® 0. Тази граница се нарича текуща скорост:
По този начин скоростта на движение в даден момент се нарича граница на коефициента на нарастване на пътя D скъм нарастване на времето D T, когато нарастването на времето клони към нула. защото
Геометричен смисъл на производната. Тангента към графиката на функция.
Конструирането на допирателни линии е един от онези проблеми, довели до раждането на диференциалното смятане. Първата публикувана работа, свързана с диференциалното смятане, написана от Лайбниц, беше озаглавена Нов метод за максимуми и минимуми, както и допирателни, за които нито дробните, нито ирационалните величини са пречка, и специален вид смятане за това.
Нека кривата е графиката на функцията г =f(х) в правоъгълна координатна система ( см. ориз.).
На някаква стойност хфункцията има значение г =f(х). Тези ценности хИ гточката на кривата съответства М 0(х, г). Ако аргументът хдайте увеличение D х, след това новата стойност на аргумента х+D хсъответства на новата стойност на функцията y+д г = f(х + д х). Съответстващата точка на кривата ще бъде точката М 1(х+D х,г+D г). Ако начертаете секуща М 0М 1 и означен с j ъгълът, образуван от напречна с положителната посока на оста вол, от фигурата веднага става ясно, че .
Ако сега Д хклони към нула, тогава точката М 1 се движи по кривата, приближавайки се до точката М 0 и ъгъл й промени с D х. При Dx® 0 ъгъл j клони към определена граница a и правата, минаваща през точката М 0 и компонентът с положителна посока на оста x, ъгъл a, ще бъде желаната тангенс. Наклонът му е:
следователно f´( х) = tga
тези. производна стойност f´( х) за дадена стойност на аргумент хе равен на тангенса на ъгъла, образуван от допирателната към графиката на функцията f(х) в съответната точка М 0(х,г) с положителна посока на оста вол.
Диференцируемост на функциите.
Определение. Ако функцията г = f(х) има производна в точката х = х 0, тогава функцията е диференцируема в тази точка.
Непрекъснатост на функция с производна. Теорема.
Ако функцията г = f(х) е диференцируем в даден момент х = х 0, тогава той е непрекъснат в тази точка.
Следователно функцията не може да има производна в точките на прекъсване. Неправилен е обратният извод, т.е. от факта, че в един момент х = х 0 функция г = f(х) е непрекъснат, не означава, че е диференцируем в тази точка. Например функцията г = |х| непрекъснато за всички х(–Ґ x x = 0 няма производна. В тази точка няма допирателна към графиката. Има дясна допирателна и лява, но те не съвпадат.
Някои теореми за диференцируеми функции. Теорема за корените на производната (теорема на Рол).Ако функцията f(х) е непрекъснат на сегмента [а,b], е диференцируем във всички вътрешни точки на този сегмент и в краищата х = аИ х = bотива на нула ( f(а) = f(b) = 0), след това вътре в сегмента [ а,b] има поне една точка х= с, а c b, в която производната fў( х) отива на нула, т.е. fў( ° С) = 0.
Теорема за крайно нарастване (теорема на Лагранж).Ако функцията f(х) е непрекъснат на интервала [ а, b] и е диференцируем във всички вътрешни точки на този сегмент, след това вътре в сегмента [ а, b] има поне една точка с, а c b това
f(b) – f(а) = fў( ° С)(b– а).
Теорема за съотношението на нарастванията на две функции (теорема на Коши).Ако f(х) И ж(х) – две непрекъснати на отсечката функции [а, b] и диференцируеми във всички вътрешни точки на този сегмент, и жў( х) не изчезва никъде в този сегмент, след това в сегмента [ а, b] има такава точка х = с, а c b това
Производни от различни поръчки.
Нека функцията г =f(х) е диференцируем на някакъв интервал [ а, b]. Производни стойности f ў( х), най-общо казано, зависят от х, т.е. производна f ў( х) също е функция на х. При диференцирането на тази функция получаваме така наречената втора производна на функцията f(х), което е означено f ўў ( х).
Производна н-ти ред на функция f(х) се нарича производна (първи ред) на производната н- 1- и се обозначава със символа г(н) = (г(н– 1))ў.
Диференциали от различни поръчки.
Функционален диференциал г = f(х), Където х– независима променлива, да dy = f ў( х)dx, някаква функция от х, но от хсамо първият фактор може да зависи f ў( х), вторият фактор ( dx) е нарастването на независимата променлива хи не зависи от стойността на тази променлива. защото dyима функция от х, тогава можем да определим диференциала на тази функция. Диференциалът на диференциала на функция се нарича втори диференциал или диференциал от втори ред на тази функция и се обозначава д 2г:
д(dx) = д 2г = f ўў( х)(dx) 2 .
Диференциал н-от първи ред се нарича първи диференциал на диференциала н- 1- ти ред:
d n y = д(d n–1г) = f(н)(х)dx(н).
Частична производна.
Ако една функция зависи не от един, а от няколко аргумента x i(азварира от 1 до н,аз= 1, 2,… н),f(х 1,х 2,… x n), тогава в диференциалното смятане се въвежда концепцията за частична производна, която характеризира скоростта на промяна на функция на няколко променливи, когато се променя само един аргумент, например, x i. Частична производна от 1-ви ред по отношение на x iсе определя като обикновена производна и се приема, че всички аргументи освен x i, поддържат постоянни стойности. За частни производни се въвежда обозначението
Дефинираните по този начин частни производни от първи ред (като функции на едни и същи аргументи) могат от своя страна също да имат частни производни, това са частни производни от втори ред и т.н. Такива производни, взети от различни аргументи, се наричат смесени. Непрекъснатите смесени производни от един и същи ред не зависят от реда на диференциране и са равни една на друга.
Анна Чугайнова
Нека функцията y = f(x) е дефинирана в интервала X. Производнафункция y = f(x) в точка x o се нарича граница
=
![]() .
.
Ако това ограничение краен,тогава се извиква функцията f(x). диференцируемив точката х о; Нещо повече, оказва се, че е задължително непрекъснат в тази точка.
Ако разглежданата граница е равна на (или - ), тогава при условие, че функцията в точката х ое непрекъсната, ще кажем, че функцията f(x) има в точката х о безкрайна производна.
Производната се обозначава със символите
y , f (x o), , .
Намирането на производната се нарича диференциацияфункции. Геометрично значение на производнатае, че производната е наклонът на допирателната към кривата y=f(x) в дадена точка х о ; физически смисъл -е, че производната на пътя по отношение на времето е моментната скорост на движеща се точка по време на праволинейно движение s = s(t) в момента t o .
Ако се постоянно число и u = u(x), v = v(x) са някои диференцируеми функции, тогава следните правила за диференциране са валидни:
1) (c) " = 0, (cu) " = cu";
2) (u+v)" = u"+v";
3) (uv)" = u"v+v"u;
4) (u/v)" = (u"v-v"u)/v 2;
5) ако y = f(u), u = (x), т.е. y = f((x)) - сложна функцияили суперпозиция, съставен от диференцируеми функции и f, тогава , или
6) ако за функция y = f(x) има обратна диференцируема функция x = g(y) и 0, тогава .
Въз основа на дефиницията на производната и правилата за диференциране е възможно да се състави списък от таблични производни на основните елементарни функции.
1. (u )" = u 1 u" ( Р).
2. (a u)" = a u lna u".
3. (e u)" = e u u".
4. (log a u)" = u"/(u ln a).
5. (ln u)" = u"/u.
6. (sin u)" = cos u u".
7. (cos u)" = - sin u u".
8. (tg u)" = 1/ cos 2 u u".
9. (ctg u)" = - u" / sin 2 u.
10. (arcsin u)" = u" / .
11. (arccos u)" = - u" / .
12. (arctg u)" = u"/(1 + u 2).
13. (arcctg u)" = - u"/(1 + u 2).
Нека изчислим производната на степенно-експоненциалния израз y=u v , (u>0), където uИ vсъщността на функцията от х, имащи производни в дадена точка ти",v".
Като логаритмираме равенството y=u v , получаваме ln y = v ln u.
Приравняване на производни по отношение на хот двете страни на полученото равенство, използвайки правила 3, 5 и формулата за производната на логаритмична функция, ще имаме:
y"/y = vu"/u +v" ln u, откъдето y" = y (vu"/u +v" ln u).
(u v)"=u v (vu"/u+v" ln u), u > 0.
Например, ако y = x sin x, тогава y" = x sin x (sin x/x + cos x ln x).
Ако функцията y = f(x) е диференцируема в точката х, т.е. има крайна производна в тази точка y", тогава = y"+, където 0 при х 0; следователно y = y" х + x.
Извиква се основната част от нарастването на функцията, линейна спрямо x диференциал функциии се означава с dy: dy = y" х. Ако поставим y=x в тази формула, получаваме dx = x"х = 1х =х, следователно dy=y"dx, т.е. за Производната нотация може да се разглежда като дроб.
Увеличаване на функцията ге нарастването на ординатата на кривата, а диференциалът d ге нарастването на ординатата на тангентата.
Нека намерим за функцията y=f(x) нейната производна y = f (x). Производната на тази производна се нарича производна от втори редфункции f(x), или втора производна,и е обозначен ![]() .
.
Следните се определят и обозначават по същия начин:
производна от трети ред
-
![]() ,
,
производна от четвърти ред -
![]()
и най-общо казано производна от n-ти ред
-
![]() .
.
Пример 3.15. Изчислете производната на функцията y=(3x 3 -2x+1)sin x.
Решение.По правило 3, y"=(3x 3 -2x+1)"sin x + (3x 3 -2x+1)(sin x)" = = (9x 2 -2)sin x + (3x 3 -2x +1)cos x.
Пример 3.16 . Намерете y", y = tan x + .
Решение.Използвайки правилата за диференциране на сумата и частното, получаваме: y"=(tgx + )" = (tgx)" + ()" = + ![]() =
=
![]()
![]() .
.
Пример 3.17. Намерете производната на комплексната функция y= , u=x 4 +1.
Решение.Съгласно правилото за диференциране на сложна функция получаваме: y" x =y " u u" x =()" u (x 4 +1)" x =(2u +. Тъй като u=x 4 +1, тогава (2 х 4 + 2+ ![]() .
.
Производната е най-важната концепция в математическия анализ. Той характеризира промяната във функцията на аргумента хв някакъв момент. Освен това самата производна е функция на аргумента х
Производна на функция в точка е границата (ако съществува и е крайна) на съотношението на нарастването на функцията към нарастването на аргумента, при условие че последното клони към нула.
Най-често използваните са следните производна нотация :
Пример 1.Възползвам се дефиниция на производна, намерете производната на функцията
Решение. От дефиницията на производната следва следната схема за нейното изчисляване.
Нека дадем на аргумента увеличение (делта) и да намерим увеличението на функцията:
Нека намерим съотношението на нарастването на функцията към нарастването на аргумента:

Нека изчислим границата на това съотношение, при условие че увеличението на аргумента клони към нула, т.е. производната, изисквана в постановката на проблема:
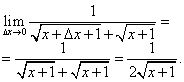
Физическо значение на производната
ДА СЕ концепция за производна довежда до изследването на Галилео Галилей на закона за свободното падане на телата, а в по-широк смисъл – на проблема за моментната скорост на неравномерното праволинейно движение на точка.
Оставете камъчето да бъде повдигнато и след това освободено от покой. Пътека спреминат във времето T, е функция на времето, т.е. s = s(T). Ако е даден законът за движение на точка, тогава може да се определи средната скорост за всеки период от време. Нека в момента камъчето е в позицията А, и в момента - на позиция б. За определен период от време (от Tдо) точка е изминала пътя. Следователно средната скорост на движение за този период от време, която означаваме с , е
![]() .
.
Движението на свободно падащо тяло обаче очевидно е неравномерно. Скорост vпадането непрекъснато се увеличава. И средната скорост вече не е достатъчна, за да характеризира скоростта на движение на различни участъци от маршрута. Колкото по-кратък е периодът от време, толкова по-точна е тази характеристика. Затова се въвежда следното понятие: моментната скорост на праволинейно движение (или скоростта в даден момент от време T) се нарича средно ограничение на скоростта при:
![]()
(при условие, че тази граница съществува и е крайна).
Така се оказва, че моментната скорост е границата на съотношението на увеличението на функцията с(T) към увеличението на аргумента Tв Това е производната, която в общ вид се записва по следния начин:.
![]() .
.
Решението на посочения проблем е физическо значение на производната . И така, производната на функцията y=f(х) в точка хсе нарича граница (ако съществува и е крайна) на приращението на функция към приращението на аргумента, при условие че последният клони към нула.
Пример 2.Намерете производната на функция
![]()
Решение. От дефиницията на производната следва следната схема за нейното изчисляване.
Стъпка 1. Нека увеличим аргумента и да намерим

Стъпка 2. Намерете нарастването на функцията:

Стъпка 3. Намерете съотношението на увеличението на функцията към увеличението на аргумента:

Стъпка 4. Изчислете границата на това съотношение при , тоест производната:
Геометрично значение на производната
Нека функцията е дефинирана на интервал и точката Мна графиката на функцията съответства на стойността на аргумента, а точката Р– значение. Нека начертаем точките МИ Рправа линия и я наречете секуща. Нека означим с ъгъла между секанса и оста. Очевидно този ъгъл зависи от .
Ако съществува
![]()
минаваща през точката се нарича гранично положение на секанса Г-Нв (или в ).
Тангента към графиката на функция в точка Мнаречено гранично положение на секанса Г-Нпри , или, което е същото при .
От дефиницията следва, че за съществуването на допирателна е достатъчно да има граница
![]() ,
,
а границата е равна на ъгъла на наклона на допирателната към оста.
Сега нека дадем точна дефиниция на допирателната.
Допирателнакъм графиката на функция в точка е права линия, минаваща през точката и имаща наклон, т.е. права линия, чието уравнение
От това определение следва, че производна на функция е равен на наклона на допирателната към графиката на тази функция в точката с абсцисата х. Това е геометричното значение на производната.
