Първата забележителна граница често се използва за изчисляване на граници, съдържащи синус, аркуссинус, тангенс, арктангенс и произтичащите несигурности на нула, разделена на нула.
Формула
Формулата за първата забележителна граница е: $$ \lim_(\alpha\to 0) \frac(\sin\alpha)(\alpha) = 1 $$
Отбелязваме, че за $ \alpha\to 0 $ получаваме $ \sin\alpha \to 0 $, следователно имаме нули в числителя и знаменателя. Следователно формулата на първата забележителна граница е необходима, за да разкрие несигурностите $ \frac(0)(0) $.
За да се приложи формулата, трябва да бъдат изпълнени две условия:
- Изразите, съдържащи се в синуса и знаменателя на дробта, са еднакви
- Изразите в синуса и знаменателя на дроб клонят към нула
внимание! $ \lim_(x\to 0) \frac(\sin(2x^2+1))(2x^2+1) \neq 1 $ Въпреки че изразите под синуса и в знаменателя са еднакви, обаче $ 2x ^2+1 = 1 $, за $ x\to 0 $. Второто условие не е изпълнено, така че НЕ МОЖЕТЕ да приложите формулата!
Последици
Доста рядко в задачите можете да видите чисто първо чудесно ограничение, в което веднага да запишете отговора. На практика всичко изглежда малко по-сложно, но за такива случаи ще бъде полезно да знаете последствията от първото забележително ограничение. Благодарение на тях можете бързо да изчислите необходимите лимити.
$$ \lim_(\alpha\to 0) \frac(\alpha)(\sin\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(\sin(a\alpha))(\sin(b\alpha)) = \frac(a)(b) $$
$$ \lim_(\alpha\to 0) \frac(tg\alpha)(\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(\arcsin\alpha)(\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(arctg\alpha)(\alpha) = 1 $$
Примери за решения
Нека разгледаме първата забележителна граница, примери за нейното решение за изчисляване на граници, съдържащи тригонометрични функции и несигурност $ \bigg[\frac(0)(0)\bigg] $
| Пример 1 |
| Изчислете $ \lim_(x\to 0) \frac(\sin2x)(4x) $ |
| Решение |
|
Нека погледнем границата и забележим, че тя съдържа синус. След това заместваме $ x = 0 $ в числителя и знаменателя и получаваме нулата на несигурността, разделена на нула: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \frac(0)(0 ) $$ Вече два знака, че трябва да приложим чудесна граница, но има малък нюанс: не можем веднага да приложим формулата, тъй като изразът под знака синус се различава от израза в знаменателя. И имаме нужда те да бъдат равни. Следователно, използвайки елементарни трансформации на числителя, ще го превърнем в $2x$. За да направим това, ще извадим двете от знаменателя на дробта като отделен фактор. Изглежда така: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \lim_(x\to 0) \frac(\sin2x)(2\cdot 2x) = $$ $$ = \frac(1)(2) \lim_(x\to 0) \frac(\sin2x)(2x) = \frac(1)(2)\cdot 1 = \frac(1)(2) $$ Моля имайте предвид, че в края $ \lim_(x\to 0) \frac(\sin2x)(2x) = 1 $ беше получено съгласно формулата. Ако не можете да разрешите проблема си, изпратете го до нас. Ние ще предоставим подробно решение. Ще можете да видите напредъка на изчислението и да получите информация. Това ще ви помогне да получите оценката си от вашия учител навреме! |
| отговор |
| $$ \lim_(x\to 0) \frac(\sin2x)(4x) =\frac(1)(2) $$ |
| Пример 2 |
| Намерете $ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) $ |
| Решение |
|
Както винаги, първо трябва да знаете вида на несигурността. Ако е нула, разделена на нула, тогава обръщаме внимание на наличието на синус: $$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = \frac(0) (0) = $$ Тази несигурност ни позволява да използваме формулата на първата забележителна граница, но изразът от знаменателя не е равен на аргумента на синуса? Следователно формулата не може да се приложи директно. Необходимо е дробта да се умножи и раздели на аргумента на синуса: $$ = \lim_(x\to 0) \frac((x^3+2x)\sin(x^3+2x))((2x -x^4)(x ^3+2x)) = $$ Сега записваме свойствата на границите: $$ = \lim_(x\to 0) \frac((x^3+2x))(2x -x^4)\cdot \lim_(x \to 0) \frac(\sin(x^3+2x))((x^3+2x)) = $$ Второто ограничение отговаря точно на формулата и е равно към едно: $$ = \lim_(x\to 0 ) \frac(x^3+2x)(2x-x^4)\cdot 1 = \lim_(x\to 0) \frac(x^3+2x )(2x-x^4) = $$ Заместваме отново $ x = 0 $ в дроб и получаваме несигурността $ \frac(0)(0) $. За да го премахнете, достатъчно е да извадите $ x $ извън скобите и да го намалите с: $$ = \lim_(x\to 0) \frac(x(x^2+2))(x(2-x^ 3)) = \ lim_(x\to 0) \frac(x^2+2)(2-x^3) = $$ $$ = \frac(0^2 + 2)(2 - 0^3) = \frac(2 )(2) = 1 $$ |
| отговор |
| $$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = 1 $$ |
| Пример 4 |
| Изчислете $ \lim_(x\to0) \frac(\sin2x)(tg3x) $ |
| Решение |
|
Нека започнем изчислението със замяната $ x=0 $. В резултат на това получаваме несигурността $ \frac(0)(0) $. Границата съдържа синус и тангенс, което подсказва за възможно развитие на ситуацията, използвайки формулата на първата забележителна граница. Нека трансформираме числителя и знаменателя на дробта във формула и следствие: $$ \lim_(x\to0) \frac(\sin2x)(tg3x) = \frac(0)(0) = \lim_(x\to0) \frac(\frac(\sin2x)(2x)\cdot 2x )(\frac(tg3x)(3x)\cdot 3x) = $$ Сега виждаме, че в числителя и знаменателя има изрази, които отговарят на формулата и последствията. Аргументът на синуса и аргумента на тангенса са еднакви за съответните знаменатели $$ = \lim_(x\to0) \frac(1\cdot 2x)(1\cdot 3x) = \frac(2)(3) $$ |
| отговор |
| $$ \lim_(x\to0) \frac(\sin2x)(tg2x) = \frac(2)(3) $$ |
Статията: „Първата забележителна граница, примери за решения“ говори за случаите, в които е препоръчително да използвате тази формула и нейните последствия.
Доказателство:
Нека първо докажем теоремата за случая на последователността 
Според биномната формула на Нютон:
Ако приемем, че получим
От това равенство (1) следва, че с нарастването на n броят на положителните членове от дясната страна се увеличава. Освен това, когато n нараства, числото намалява, така че стойностите 
се увеличават. Следователно последователността 
нарастваща и (2)*Показваме, че е ограничена. Заменете всяка скоба от дясната страна на равенството с една, дясната страна ще се увеличи и получаваме неравенството
Нека засилим полученото неравенство, замествайки 3,4,5, ..., стоящи в знаменателите на дробите, с числото 2: Намираме сумата в скоби по формулата за сумата на членовете на геометрична прогресия: Следователно 
(3)*
И така, последователността е ограничена отгоре и неравенствата (2) и (3) са изпълнени: 
Следователно, въз основа на теоремата на Вайерщрас (критерий за сходимост на последователност), последователността 
монотонно нараства и е ограничен, което означава, че има граница, означена с буквата e. Тези. 
Знаейки, че втората забележителна граница е вярна за естествените стойности на x, ние доказваме втората забележителна граница за реално x, тоест доказваме, че 
. Нека разгледаме два случая:
1. Нека всяка стойност на x е затворена между две положителни цели числа: , където е цялата част от x. => =>
Ако , тогава Следователно, според ограничението 
Имаме
Въз основа на критерия (за границата на междинна функция) за съществуването на граници 
2. Нека . Тогава нека направим заместването − x = t
От тези два случая следва, че 
за реално х.
Последици:
9 .) Сравнение на безкрайно малки. Теоремата за замяна на безкрайно малките с еквивалентни в предела и теоремата за основната част от безкрайно малките.
Нека функциите a( х) и b( х) – б.м. при х ® х 0 .
ДЕФИНИЦИИ.
1)а( х) наречен безкрайно малък по-висок порядък от b (х) Ако
Запишете: a( х) = o(b( х)) .
2)а( х) и b( х)се наричат безкрайно малки от същия порядък, Ако
където CÎℝ и В¹ 0 .
Запишете: a( х) = О(б( х)) .
3)а( х) и b( х) се наричат еквивалент , Ако
Запишете: a( х) ~ b( х).
4)а( х) наречено безкрайно малко от порядък k относително
абсолютно безкрайно малък b( х),
ако е безкрайно малъка( х)и(б( х))к имат същия ред, т.е. Ако
където CÎℝ и В¹ 0 .
ТЕОРЕМА 6 (относно замяната на безкрайно малки с еквивалентни).
Некаа( х), b( х), а 1 ( х), b 1 ( х)– б.м. при х ® х 0 . Акоа( х) ~ a 1 ( х), b( х) ~ b 1 ( х),
това 
Доказателство: Нека a( х) ~ a 1 ( х), b( х) ~ b 1 ( х), Тогава
ТЕОРЕМА 7 (за основната част от безкрайно малкото).
Некаа( х)и b( х)– б.м. при х ® х 0 , и b( х)– б.м. по-висок порядък ота( х).
= , a тъй като b( х) – по-висок ред от a( х), тогава, т.е. 
от ясно е, че а( х) + b( х) ~ a( х)
10) Непрекъснатост на функция в точка (на езика на епсилон-делта, геометрични граници) Едностранна непрекъснатост. Непрекъснатост на интервал, на отсечка. Свойства на непрекъснатите функции.
1. Основни определения
Нека f(х) е дефинирана в някаква околност на точката х 0 .
ДЕФИНИЦИЯ 1. Функция f(х) наречен непрекъснато в точка х 0 ако равенството е вярно
Бележки.
1) По силата на теорема 5 §3, равенството (1) може да бъде записано във формата
Условие (2) – дефиниция на непрекъснатост на функция в точка на езика на едностранните граници.
2) Равенство (1) може да се запише и като:
Те казват: „ако една функция е непрекъсната в точка х 0, тогава знакът на границата и функцията могат да бъдат разменени."
ДЕФИНИЦИЯ 2 (на език e-d).
Функция f(х) наречен непрекъснато в точка х 0 Ако"e>0 $d>0 такива, Какво
ако хОU( х 0 , d) (т.е. | х – х 0 | < d),
след това f(х)ÎU( f(х 0), e) (т.е. | f(х) – f(х 0) | < e).
Нека х, х 0 Î г(f) (х 0 – фиксиран, х –произволен)
Да означим: D х= х – х 0 – увеличение на аргумента
г f(х 0) = f(х) – f(х 0) – нарастване на функция в точка x 0
ОПРЕДЕЛЕНИЕ 3 (геометрично).
Функция f(х) включено наречен непрекъснато в точка
х 0
ако в този момент безкрайно малко увеличение в аргумента съответства на безкрайно малко увеличение във функцията, т.е.
Нека функцията f(х) е дефинирана на интервала [ х 0 ; х 0 + d) (на интервала ( х 0 – d; х 0 ]).
ОПРЕДЕЛЕНИЕ. Функция f(х) наречен непрекъснато в точка
х 0 точно
(наляво
), ако равенството е вярно
Очевидно е, че f(х) е непрекъсната в точката х 0 Û f(х) е непрекъсната в точката х 0 дясно и ляво.
ОПРЕДЕЛЕНИЕ. Функция f(х) наречен непрекъснато за интервал д ( а; b) ако е непрекъсната във всяка точка от този интервал.
Функция f(х) се нарича непрекъснат на сегмента [а; b] ако е непрекъснат на интервала (а; b) и има еднопосочна непрекъснатост в граничните точки(т.е. непрекъснато в точката аотдясно, в точката b- наляво).
11) Точки на прекъсване, тяхната класификация
ОПРЕДЕЛЕНИЕ. Ако функцията f(х) определени в някаква околност на точка x 0 , но не е непрекъснат в този момент, тогава f(х) наречено прекъснато в точка x 0 , и самата точка х 0 наречена точка на прекъсване функции f(х) .
Бележки.
1) f(х) могат да бъдат определени в непълна околност на точката х 0 .
След това разгледайте съответната едностранна непрекъснатост на функцията.
2) От дефиницията на Þ точка х 0 е точката на прекъсване на функцията f(х) в два случая:
а) U( х 0 , г)О г(f), но за f(х) равенството не е валидно
б) U * ( х 0 , г)О г(f) .
За елементарни функции е възможен само случай b).
Нека х 0 – точка на прекъсване на функцията f(х) .
ОПРЕДЕЛЕНИЕ. Точка х 0 наречен точка на прекъсване аз нещо като if функция f(х)има крайни граници отляво и отдясно в тази точка.
Ако тези граници са равни, тогава точка х 0 наречен подвижна точка на прекъсване , иначе – точка на скок .
ОПРЕДЕЛЕНИЕ. Точка х 0 наречен точка на прекъсване II нещо като ако поне една от едностранните граници на функцията f(х)в този момент е равен¥ или не съществува.
12) Свойства на функции, непрекъснати на интервал (теореми на Вайерщрас (без доказателство) и Коши
Теорема на Вайерщрас
Тогава нека функцията f(x) е непрекъсната на интервала
1)f(x) е ограничено до
2) f(x) приема най-малката и най-голямата си стойност в интервала
Определение: Стойността на функцията m=f се нарича най-малката, ако m≤f(x) за всяко x€ D(f).
Казва се, че стойността на функцията m=f е най-голяма, ако m≥f(x) за всеки x € D(f).
Функцията може да приема най-малката/най-голямата стойност в няколко точки от сегмента.
f(x 3)=f(x 4)=макс
Теорема на Коши.
Нека функцията f(x) е непрекъсната на сегмента и x е числото, съдържащо се между f(a) и f(b), тогава има поне една точка x 0 € такава, че f(x 0)= g
Сега със спокойна душа да преминем към разглеждането прекрасни граници.
прилича на .
Вместо променливата x могат да присъстват различни функции, основното е, че те клонят към 0.
Необходимо е да се изчисли лимитът
Както можете да видите, това ограничение е много подобно на първото забележително, но това не е съвсем вярно. Като цяло, ако забележите грях в лимита, тогава трябва незабавно да помислите дали е възможно да използвате първия забележителен лимит.
Според нашето правило № 1 заместваме нула вместо x:
Получаваме несигурност.
Сега нека се опитаме сами да организираме първия прекрасен лимит. За да направите това, нека направим проста комбинация:
Така че организираме числителя и знаменателя, за да подчертаем 7x. Сега познатата прекрасна граница вече се появи. Препоръчително е да го подчертаете, когато решавате:
Нека заместим решението на първия забележителен пример и ще получим:
Опростяване на дробта:
Отговор: 7/3.
Както можете да видите, всичко е много просто.
Прилича на 
, където e = 2,718281828... е ирационално число.
Вместо променливата x могат да присъстват различни функции, основното е, че те са склонни към .
Необходимо е да се изчисли лимитът
Тук виждаме наличието на степен под знака на граница, което означава, че е възможно да се използва втора забележителна граница.
Както винаги, ще използваме правило № 1 - заменете x вместо:
Вижда се, че при x основата на степента е , а показателят е 4x > , т.е. получаваме несигурност от формата:
Нека използваме втората прекрасна граница, за да разкрием нашата несигурност, но първо трябва да я организираме. Както можете да видите, трябва да постигнем присъствие в индикатора, за което повдигаме основата на степен 3x и в същото време на степен 1/3x, така че изразът да не се променя:
Не забравяйте да подчертаете нашия чудесен лимит:
Такива са наистина прекрасни граници!
Ако все още имате въпроси относно първата и втората чудесни граници, тогава не се колебайте да ги попитате в коментарите.
Ще отговорим максимално на всички.
Можете също да работите с учител по тази тема.
Имаме удоволствието да ви предложим услугите за избор на квалифициран учител във вашия град. Нашите партньори бързо ще изберат за вас добър учител при изгодни условия.
Няма достатъчно информация? - Ти можеш!
Можете да записвате математически изчисления в бележници. Много по-приятно е да пишете индивидуално в тетрадки с лого (http://www.blocnot.ru).
Има няколко забележителни лимита, но най-известните са първият и вторият забележителни лимити. Забележителното при тези лимити е, че те се използват широко и с тяхна помощ можете да намерите други лимити, открити в много проблеми. Това ще направим в практическата част на този урок. За да се решат проблемите, като се сведат до първата или втората забележителна граница, няма нужда да се разкриват съдържащите се в тях несигурности, тъй като стойностите на тези граници отдавна са изведени от велики математици.
Първата забележителна границасе нарича границата на съотношението на синуса на безкрайно малка дъга към същата дъга, изразено в радианова мярка:
Нека да преминем към решаване на проблеми на първата забележителна граница. Забележка: ако има тригонометрична функция под знака за граница, това е почти сигурен знак, че този израз може да бъде намален до първата забележителна граница.
Пример 1.Намерете границата.
Решение. Вместо това заместване хнула води до несигурност:
.
Знаменателят е синус, следователно изразът може да бъде приведен до първата забележителна граница. Да започнем трансформацията:
.
Знаменателят е синус от три X, но числителят има само едно X, което означава, че трябва да получите три X в числителя. за какво? Да представя 3 х = аи вземете израза.
И стигаме до вариант на първата забележителна граница:
защото няма значение коя буква (променлива) в тази формула стои вместо X.
Умножаваме X по три и веднага разделяме:
.
В съответствие с първото забелязано забележително ограничение, заместваме дробния израз:
Сега най-накрая можем да решим тази граница:
.
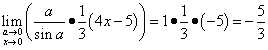Пример 2.Намерете границата.
Решение. Директното заместване отново води до несигурността „нула, разделена на нула“:
.
За да получим първата забележителна граница, е необходимо х под знака за синус в числителя и само х в знаменателя да имат еднакъв коефициент. Нека този коефициент е равен на 2. За да направите това, представете си текущия коефициент за x, както е показано по-долу, извършвайки операции с дроби, получаваме:
.
Пример 3.Намерете границата.
Решение. При заместване отново получаваме несигурността „нула, разделена на нула“:
.
Вероятно вече разбирате, че от оригиналния израз можете да получите първата прекрасна граница, умножена по първата прекрасна граница. За да направим това, разлагаме квадратите на x в числителя и синуса в знаменателя на еднакви множители и за да получим еднакви коефициенти за x и синуса, разделяме x в числителя на 3 и веднага умножаваме от 3. Получаваме:
.
Пример 4.Намерете границата.
Решение. Отново получаваме несигурността „нула, разделена на нула“:
.
Можем да получим съотношението на първите две забележителни граници. Разделяме и числителя, и знаменателя на x. След това, така че коефициентите за синуси и xes да съвпадат, умножаваме горното x по 2 и веднага разделяме на 2, а долното x умножаваме по 3 и веднага делим на 3. Получаваме:
Пример 5.Намерете границата.
Решение. И отново несигурността на „нула, разделена на нула“:
Спомняме си от тригонометрията, че тангенсът е отношението на синус към косинус, а косинусът на нулата е равен на едно. Извършваме трансформациите и получаваме:
.
Пример 6.Намерете границата.
Решение. Тригонометричната функция под знака на граница отново предполага използването на първата забележителна граница. Представяме го като отношение на синус към косинус.
Терминът „забележителна граница“ се използва широко в учебниците и учебните помагала за обозначаване на важни идентичности, които значително помагат опростете работата сиза намиране на граници.
Но да да може да донесевашата граница на забележителното, трябва да я разгледате добре, защото те не се срещат в пряка форма, а често под формата на последствия, оборудвани с допълнителни условия и фактори. Все пак първо теория, после примери и ще успеете!
Първата прекрасна граница
Хареса ли ти Добавяне към отметки
Първата забележителна граница е написана както следва (несигурност на формата $0/0$):
$$ \lim\limits_(x\to 0)\frac(\sin x)(x)=1.
$$
$$ \lim\limits_(x\to 0)\frac(x)(\sin x)=1.$$ $$ \lim\limits_(x\to 0)\frac(\sin (ax))(\sin (bx))=\frac(a)(b).
Пример 1. $$ $$ \lim\limits_(x\to 0)\frac(\tan x)(x)=1.
$$ $$ \lim\limits_(x\to 0)\frac(\arcsin x)(x)=1.$$ $$ \lim\limits_(x\to 0)\frac(\arctan x)(x)=1.
$$ $$ \lim\limits_(x\to 0)\frac(1-\cos x)(x^2/2)=1.
$$
Примери за решения: 1 чудесен лимит
Изчислете границата $$\lim\limits_(x\to 0)\frac(\sin 3x)(8x).$$ Решение. $3/8$.
Пример 2. Първата стъпка винаги е една и съща - заместваме граничната стойност $x=0$ във функцията и получаваме:
$$ $$ \lim\limits_(x\to 0)\frac(\arcsin x)(x)=1.$$\left[ \frac(\sin 0)(0) \right] = \left[\frac(0)(0)\right].$$
Получихме несигурност от формата $\left[\frac(0)(0)\right]$, която трябва да бъде разкрита. Ако се вгледате внимателно, оригиналната граница е много подобна на първата забележителна, но не съвпада с нея. Нашата задача е да го доведем до сходство. Нека го трансформираме по следния начин - погледнете израза под синуса, направете същото в знаменателя (относително казано, умножете и разделете на $3x$), след това намалете и опростете:
$$ \lim\limits_(x\to 0)\frac(\sin 3x)(8x) = \lim\limits_(x\to 0)\frac(\sin 3x)(3x)\frac(3x)(8x )=\lim\limits_(x\to 0)\frac(\sin (3x))(3x)\frac(3)(8)=\frac(3)(8). $$
По-горе е точно първата забележителна граница: $$ \lim\limits_(x\to 0)\frac(\sin (3x))(3x) = \lim\limits_(y\to 0)\frac(\sin ( y ))(y)=1, \text( направи условна замяна ) y=3x. $$
Решение. $9/16$.
Пример 3. отговор:
$$ $$ \lim\limits_(x\to 0)\frac(\arcsin x)(x)=1.Изчислете границата $$\lim\limits_(x\to 0)\frac(1-\cos 3x)(\tan 2x\cdot \sin 4x).$$
$$\left[ \frac(\sin (0+0))(0-0)\right] = \left[\frac(0)(0)\right].$$
Получихме несигурност от формата $\left[\frac(0)(0)\right]$. Умножете и разделете на $2x^3+3x$:
$$ \lim\limits_(x\to 0)\frac(\sin (2x^3+3x))(5x-x^5)=\lim\limits_(x\to 0)\frac(\sin (2x) ^3+3x))((2x^3+3x)) \cdot \frac(2x^3+3x)(5x-x^5)=\lim\limits_(x\to 0) 1 \cdot \frac( 2x^3+3x)(5x-x^5)= \left[\frac(0)(0)\right] = $$
Отново имаме несигурност, но в този случай това е само част. Нека намалим числителя и знаменателя с $x$:
$$ =\lim\limits_(x\to 0) \frac(2x^2+3)(5-x^4)= \left[\frac(0+3)(5-0)\right] =\ frac(3)(5). $$
Решение. $3/5$.
Второ прекрасно ограничение
Втората забележителна граница е написана по следния начин (несигурност на формата $1^\infty$):
$$ \lim\limits_(x\to \infty) \left(1+\frac(1)(x)\right)^(x)=e, \quad \text(or) \quad \lim\limits_( x\до 0) \left(1+x\right)^(1/x)=e.
$$
Последици от второто забележително ограничение$$ \lim\limits_(x\to \infty) \left(1+\frac(a)(x)\right)^(bx)=e^(ab).
Пример 4. $$ $$ \lim\limits_(x\to 0)\frac(\ln (1+x))(x)=1.
$$ $$ \lim\limits_(x\to 0)\frac(\arcsin x)(x)=1.$$ $$ \lim\limits_(x\to 0)\frac(e^x -1)(x)=1.
$$ $$ \lim\limits_(x\to 0)\frac(a^x-1)(x \ln a)=1, a>0, a \ne 1. $$ $$ \lim\limits_( x\до 0)\frac((1+x)^(a)-1)(ax)=1.
$$
Примери за решения: 2 прекрасни ограничения
Намерете границата $$\lim\limits_(x\to \infty)\left(1-\frac(2)(3x)\right)^(x+3).$$
Нека проверим вида на несигурността, заместваме $x=\infty$ във функцията и получаваме:
Решение.$$\left[ \left(1-\frac(2)(\infty)\right)^(\infty) \right] = \left.$$
Пример 5. Получихме несигурност от формата $\left$. Ограничението може да се сведе до второто забележително нещо. Нека преобразуваме:
$$ $$ \lim\limits_(x\to 0)\frac(\arcsin x)(x)=1.$$ \lim\limits_(x\to \infty)\left(1-\frac(2)(3x)\right)^(x+3) = \lim\limits_(x\to \infty)\left( 1+\frac(1)((-3x/2))\right)^(\frac(-3x/2)(-3x/2)(x+3))= $$ $$ = \lim\limits_ (x\to \infty)\left(\left(1+\frac(1)((-3x/2))\right)^((-3x/2))\right)^\frac(x+3 )(-3x/2)= $$
$$ \lim\limits_(x\to \infty)\left(\frac(x^3+2x^2+1)(x^3+x-7)\right)^(x) = \lim\limits_ (x\to \infty)\left(\frac(x^3+(x-7)-(x-7)+2x^2+1)(x^3+x-7)\right)^(x ) = \lim\limits_(x\to \infty)\left(\frac((x^3+x-7)+(-x+7+2x^2+1))(x^3+x-7 )\right)^(x) = $$ $$ = \lim\limits_(x\to \infty)\left(1+\frac(2x^2-x+8)(x^3+x-7) \вдясно)^(x) = \lim\limits_(x\до \infty)\вляво(\вляво(1+\frac(2x^2-x+8)(x^3+x-7)\вдясно) ^(\frac(x^3+x-7)(2x^2-x+8))\right)^(x \frac(2x^2-x+8)(x^3+x-7)) = $$
Изразът в скобите всъщност е втората забележителна граница $\lim\limits_(t\to \infty) \left(1+\frac(1)(t)\right)^(t)=e$, само $t= \ frac(x^3+x-7)(2x^2-x+8) \to \infty$, следователно
$$ = \lim\limits_(x\to \infty)\left(e\right)^(x \frac(2x^2-x+8)(x^3+x-7))= \lim\limits_ (x\to \infty)e^( \frac(2x^2-x+8)(x^2+1-7/x))= \lim\limits_(x\to \infty)e^( \frac (2-1/x+8/x^2)(1+1/x^2-7/x^3))=e^(2). $$