Инструкции. За да решите онлайн, трябва да изберете вида на уравнението и да зададете размерността на съответните матрици.
където A, B, C са посочените матрици, X е желаната матрица. Матричните уравнения от вида (1), (2) и (3) се решават чрез обратната матрица A -1. Ако е даден изразът A·X - B = C, тогава е необходимо първо да се съберат матриците C + B и да се намери решение за израза A·X = D, където D = C + B(). Ако е даден изразът A*X = B 2, тогава матрицата B трябва първо да бъде повдигната на квадрат. Препоръчително е също така да се запознаете с основните операции върху матрици.Пример №1. Упражнение. Намерете решението на матричното уравнение
Решение. Да обозначим:
Тогава матричното уравнение ще бъде записано във формата: A·X·B = C.
Детерминантата на матрица A е равна на detA=-1
Тъй като A е неособена матрица, има обратна матрица A -1 . Умножете двете страни на уравнението отляво по A -1: Умножете двете страни на това уравнение отляво по A -1 и отдясно по B -1: A -1 ·A·X·B·B -1 = A -1 ·C·B -1 . Тъй като A A -1 = B B -1 = E и E X = X E = X, тогава X = A -1 C B -1
Обратна матрица A -1: ![]()
Нека намерим обратната матрица B -1.
Транспонирана матрица B T:
Обратна матрица B -1: ![]()
Търсим матрицата X по формулата: X = A -1 ·C·B -1 ![]()
Отговор:
Пример №2. Упражнение.Решаване на матрично уравнение ![]()
Решение. Да обозначим:
Тогава матричното уравнение ще бъде записано във формата: A·X = B.
Детерминантата на матрица A е detA=0
Тъй като A е сингулярна матрица (детерминантата е 0), следователно уравнението няма решение.
Пример №3. Упражнение. Намерете решението на матричното уравнение
Решение. Да обозначим:
Тогава матричното уравнение ще бъде записано във формата: X A = B.
Детерминантата на матрица A е detA=-60
Тъй като A е неособена матрица, има обратна матрица A -1 . Нека умножим двете страни на уравнението отдясно по A -1: X A A -1 = B A -1, откъдето намираме, че X = B A -1
Нека намерим обратната матрица A -1 .
Транспонирана матрица A T: 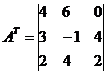
Обратна матрица A -1: 
Търсим матрицата X по формулата: X = B A -1 
Отговор: > 
С помощта на онлайн калкулатора на матрицата можете гънка, изваждам, умножават се, транспонирамматрици, пресм обратенматрица, псевдообратноматрица, рангматрици, детерминантматрица, m-норма и l-норма на матрицата, повдигнете матрицата на мощност, умножете матрицата по число, направи разлагане на скелетаматрици, премахване на линейно зависими редове от матрицаили линейно зависими колони, поведение, ръководене Гаусово изключване, решаване на матрично уравнение AX=B, направете LU декомпозиция на матрица,изчисляване на ядрото (нулево пространство) на матрица, направи Ортогонализация на Грам-Шмид и ортогонализация на Грам-Шмид.
Онлайн матричният калкулатор работи не само с десетични числа, но и с дроби. За да въведете дроби, трябва да въведете оригиналните матрици и да въведете числа във формуляра аили а/b, Където аИ bцели числа или десетични знаци ( bположително число). Например 12/67, -67,78/7,54, 327,6, -565.
Бутонът в горния ляв ъгъл на матрицата отваря меню (фиг. 1) за трансформиране на оригиналната матрица (създаване на единична матрица, нулева матрица или изчистване на съдържанието на клетки).

По време на изчисленията празна клетка се третира като нула.
За операции с единична матрица (т.е. транспониране, инверсия, псевдоинверсия, скелетно разлагане и т.н.), първо изберете конкретна матрица, като използвате бутона за избор.
Бутоните Fn1, Fn2 и Fn3 превключват различни групи функции.
Като щракнете върху изчислените матрици, се отваря меню (фиг. 2), което ви позволява да запишете тази матрица в оригиналните матрици и , както и да преобразувате елементите на матрицата на място в обикновена дроб, смесена дроб или десетично число.
Изчислете сбор, разлика, произведение на матрици онлайн
сума, разлика или произведение на матрици. За да се изчисли сумата или разликата на матриците, е необходимо те да са с еднаква размерност, а за да се изчисли произведението на матриците, броят на колоните на първата матрица трябва да е равен на броя на редовете на втората матрица.
За да изчислите сумата, разликата или произведението на матрици:
Онлайн обратно изчисление на матрица
Онлайн матричен калкулатор може да се използва за изчисляване на обратната матрица. За да съществува обратна матрица, оригиналната матрица трябва да бъде неособена квадратна матрица.
За да изчислите обратната матрица:
За подробно изчисляване на обратната матрица стъпка по стъпка, използвайте този калкулатор за обратна матрица. Вижте теорията за изчисляване на обратната матрица.
Изчислете детерминантата на матрица онлайн
Можете да използвате онлайн матричен калкулатор, за да изчислите детерминантата на матрица. За да съществува матрична детерминанта, оригиналната матрица трябва да бъде неособена квадратна матрица.
За да изчислите детерминантата на матрица:
За подробно изчисление на детерминантата на матрица стъпка по стъпка, използвайте този калкулатор, за да изчислите детерминантата на матрица. Вижте теорията за изчисляване на детерминанта на матрица.
Изчислете ранга на матрицата онлайн
Онлайн матричен калкулатор може да се използва за изчисляване на ранга на матрица.
За да изчислите ранга на матрица:
За да изчислите подробно ранга на матрицата стъпка по стъпка, използвайте този калкулатор за ранг на матрицата. Вижте теорията за изчисляване на ранга на матрица.
Онлайн изчисляване на псевдообратна матрица
Онлайн матричен калкулатор може да се използва за изчисляване на псевдообратната матрица. Псевдообратно на дадена матрица винаги съществува.
За да изчислите псевдообратната матрица:
Премахване на линейно зависими матрични редове или колони онлайн
Онлайн матричният калкулатор ви позволява да премахвате линейно зависими редове или колони от матрица, т.е. създайте пълна рангова матрица.
За да премахнете линейно зависими матрични редове или колони:
Разлагане на скелетна матрица онлайн
За извършване на декомпозиция на скелетна матрица онлайн
Решаване на матрично уравнение или система от линейни уравнения AX=B онлайн
С помощта на онлайн матричен калкулатор можете да решите матричното уравнение AX=B по отношение на матрицата X. В специалния случай, ако матрицата B е вектор-колона, тогава X ще бъде решение на системата от линейни уравнения AX= б.
За да решите матричното уравнение:
Моля, обърнете внимание, че матриците и трябва да имат еднакъв брой редове.
Елиминиране по Гаус или редуциране на матрица до триъгълна (стъпкова) форма онлайн
Онлайн матричният калкулатор извършва елиминиране на Гаус както за квадратни матрици, така и за правоъгълни матрици от всякакъв ранг. Първо се изпълнява обичайният метод на Гаус. Ако на даден етап водещият елемент е равен на нула, тогава се избира друга опция за елиминиране на Гаус чрез избиране на най-големия водещ елемент в колоната.
За елиминиране на Гаус или намаляване на матрицата до триъгълна форма
LU декомпозиция или LUP декомпозиция на матрица онлайн
Този матричен калкулатор ви позволява да извършвате LU декомпозиция на матрица (A=LU) или LUP декомпозиция на матрица (PA=LU), където L е долна триъгълна матрица, U е горна триъгълна (трапецовидна) матрица, P е a пермутационна матрица. Първо, програмата извършва LU декомпозиция, т.е. такова разлагане, при което P=E, където E е идентичната матрица (т.е. PA=EA=A). Ако това не е възможно, тогава се извършва LUP декомпозиция. Матрица A може да бъде или квадратна, или правоъгълна матрица от произволен ранг.
За LU(LUP) разлагане:
Конструиране на ядрото (нулево пространство) на матрица онлайн
С помощта на матричен калкулатор можете да конструирате нулевото пространство (ядро) на матрица.
Да се конструира нулевото пространство (ядрото) на матрицата.
>Здравейте на всички!!! Има ли формула, чрез която можете да премахнете мащабирането от матрица, без да знаете коефициентите на мащабиране???
Веднага си спомнихме полярното разлагане. Е, матрицата M е представена като O * P. Където O е ортогонална, а P е положително определена, симетрична - тоест матрица на компресия или разширение. Тук ще вземем матрицата O.
Възниква въпросът. И ако разширим M от другата страна, получаваме P’ * O’. Разлагане в различен ред, с различни априорни матрици. Защо не вземете O'? Борих се с въпроса около пет минути, докато не си спомних как бях провалил учениците по този въпрос. Матрица O’ всъщност съвпада с матрица O. Ако наскоро сте завършили университет или все още учите, можете дори да опитате да докажете този факт.
И така, полярно разширение:
За да се намери положителният квадратен корен на матрица, положителната наука предлага изчисляване на собствените стойности. За всяка собствена стойност намерете нейното собствено подпространство, след което внимателно извадете действителния корен квадратен от оператора.
Докато си представях какво ще се случи с матрица, близка до матрицата на идентичността, потръпнах. Всичко ще умре поради неточностите на поплавъка, редиците на матриците ще паднат - обещава да се случи пълен колапс.
Защо благородните донове не опитат итерации, за които се знае, че са божествени?
Тук коренът на число се намира с помощта на метода на Нютон. Последователност a_(i+1) = 0,5 * (a_i + x / a_i); гордо се свежда до корен квадратен от x. Като тест взех нечия библиотека за mat3x3 и заковах матричен аналог.
Директният аналог на метода на Нютон бързо се събира в 3-4 итерации, тестовете преминават като полъх. Резултатът е полярно разлагане за матрици; ефективността на алгоритъма е очевидна от елементарната спектрална теория на операторите. Очевидно след половин час скърцане на мозъка ми.
И така, открихме полярното разлагане. Въпросът е – защо? И тук съм принуден да премина към основното на моя доклад. Преподаването е зло. Времето, което прекарахте в припомняне на теорията на спектралните оператори, беше успешно пропиляно.
Декомпозицията Scale Shear Rotate се търси наведнъж. Ние прилагаме процеса на ортогонализиране и ортогонализиране към матрицата. По колони. Получаваме отлична матрица. И защо резултатът ще бъде по-лош? Нищо!
Видях публикация с код в Pascal, който изчислява същото разлагане Scale Shear Rotate, и изведнъж разбрах, че нямам аргументи за полярно разлагане. Което изисква кой знае каква компютърна технология.
Разбира се, има дребни забележки, почти заяждания. Например, допирателното пространство е по-лесно да се разглежда като ортонормално. Изчислително по-просто. Обикновено разглеждаме dPosition/du, нормалата, а третият вектор се взема перпендикулярно на тази двойка. Ясно е, че методът е асиметричен по отношение на текстурните координати; коя от тях е първа и коя е напълно неясно. Изглежда правилно да се приложи полярното разлагане към матрицата на локалната трансформация.
Може да забележите разликата между „правилното“ полярно разлагане и „неправилния“ процес на ортогонализиране на колони. Вероятно няма да забележите. И картината със сигурност няма да стане по-добра.
P.S. Също така е много готино да съхранявате анимации в Scale Shear Rotate. Три вектора, един кватернион. Срязването е почти винаги 0, мащабът е почти винаги 1, постоянните следи могат да бъдат изхвърлени. А където има непостоянни песни, има начин да ги изтръгнете чрез специализиране на шаблона. Или нещо друго.
1)
Нека първо разгледаме реалните матрици. Да предположим, че коренът е извлечен от матрицата $%A$%, т.е. има матрица $%B$% такава, че $%B \cdot B=A$%. Нека приемем също, че матрицата $%B$% може да се редуцира до диагонална форма, т.е. има матрица $%S$% такава, че $%S^(-1)BS=B"$%, където $%B"$% е диагонална матрица. От равенствата $%B"B"=S^(-1)BSS^(-1)BS=S^(-1)BBS=S^(-1)AS$% следва, че $%A"=S ^ (-1)AS$% също е диагонална матрица, т.е. матриците $%A$% и $%B$% се редуцират до диагонална форма чрез същата трансформация, тъй като елементите на първичните матрици са собствените стойности на негрундираните, то от горните съображения следват следните заключения.
1.1) Ако матрицата $%A$% е симетрична положително определена матрица, тогава коренът се извлича от нея под формата на реална матрица.
1.2) Алгоритъмът за изчисляване на корена на такава матрица е следният: решете проблема със собствените стойности, извлечете корените от собствените стойности, съставете диагонална матрица от тях, приложете към нея трансформация, обратна на трансформацията, която преобразува матрицата $%A$% в диагонална форма.
1.3) Броят на различните матрици $%B$% е равен на $%2^n$%, тъй като За всяка собствена стойност има 2 коренни стойности - положителна и отрицателна.
2) За сложна матрица разсъжденията ще останат валидни, ако заменим симетрията с унитарност. Изискването за положителна определеност естествено ще отпадне.
3)
Решение за общия случай.Да приемем, че трансформацията $%S$% привежда матрицата $%B$% не в диагонална, а в горна триъгълна форма, т.е. матрицата $%B"$% е горно триъгълна. Такова преобразуване съществува за всяка квадратна матрица. Лесно е да се провери, че матрицата $%A"$% също ще се окаже горно триъгълна и диагоналните елементи на матрица $%A"$% ще бъдат квадрати, съответстващи на диагонални елементи на матрицата $%B"$%. Това ви позволява да намерите всички диагонални елементи на матрицата $%B"$%, като вземете корена на диагоналните елементи на матрицата $%A"$%, и след това, по веригата, намерете всички останали елементи на матрица $%B"$%. От тук се получават следните изводи.
3.1) Коренът се извлича от всяка сложна матрица; в общия случай такива корени са $%2^n$%, но сред тях може да има съвпадащи (множество).
3.2) Алгоритъмът за изчисляване на корените е следният: преобразувайте матрицата $%A$% в горна триъгълна форма, намерете матрицата $%B"$% с помощта на формулирания алгоритъм и направете обратното преобразуване.
3.3) Необходимо и достатъчно условие за реалността на корените на реална матрица е диагоналните елементи да не са отрицателни след преобразуване на матрицата в триъгълна форма. Неотрицателността на детерминантата е необходимо, но не достатъчно условие.
Допълнение 1 (отговор на коментар). Имахте предвид „към триъгълен изглед“. Като цяло, в параграфи. 1, 2 всичко е абсолютно ясно, но точка 3 явно трябва да се помисли още. Въпросът е, че методът на Гаус не може да се сведе до трансформацията $%S^(-1)AS$%, и доказателството се основава на това. Тези. доказателството е приложимо само за онези матрици, които могат да бъдат редуцирани до триъгълна форма чрез трансформацията $%S^(-1)AS$%.
Допълнение 2. Изглежда, че в параграф 3 като цяло всичко е правилно, просто трябва да използвате трансформацията на матрицата $%A$% във формата на Йордан - за тази трансформация винаги има матрица, получена от решаването на проблема със собствените стойности. Проблемът е, че квадратът на йорданова матрица не е йорданова матрица (въпреки че е триъгълна и дори двудиагонална). Строгото обосноваване на алгоритъма изисква доказателство на следната теорема: „Ако $%A"=B"^2$% и $%A"$% е матрица на Йордан, тогава $%B"$% е триъгълна матрица. " Твърдението изглежда вярно, но все още не знам как да го докажа.
