Определение: Числовата функция е съответствие, което свързва всяко число x от даден набор с едно число y.

Обозначаване:

където x е независимата променлива (аргумент), y е зависимата променлива (функция). Наборът от стойности на x се нарича домейн на функцията (обозначава се D(f)). Наборът от стойности на y се нарича диапазон от стойности на функцията (обозначен с E(f)). Графиката на функция е набор от точки в равнината с координати (x, f(x))

Методи за задаване на функция.

1. аналитичен метод (с използване на математическа формула);
2. табличен метод (с помощта на таблица);
3. описателен метод (с използване на словесно описание);
4. графичен метод (с помощта на графика).

Основни свойства на функцията.

1. Четни и нечетни

Функция се извиква дори ако
– областта на дефиниране на функцията е симетрична спрямо нулата
f(-x) = f(x)

Графиката на четната функция е симетрична спрямо оста 0 г

Функция се нарича странна ако
– областта на дефиниране на функцията е симетрична спрямо нулата
– за всяко x от областта на дефиницията f(-x) = –f(x)

Графиката на нечетна функция е симетрична спрямо началото.

2. Честота

Функция f(x) се нарича периодична с период if за всяко x от областта на дефиниция f(x) = f(x+T) = f(x-T) .

Графиката на периодична функция се състои от неограничено повтарящи се идентични фрагменти.

3. Монотонност (нарастваща, намаляваща)

Функцията f(x) нараства върху множеството P, ако за всяко x 1 и x 2 от това множество, така че x 1

Функцията f(x) намалява в множеството P ако за всяко x 1 и x 2 от това множество, така че x 1 f(x 2) .

4. Крайности

Точката X max се нарича максимална точка на функцията f(x), ако за всички x от някаква околност на X max неравенството f(x) f(X max) е изпълнено.

Стойността Y max =f(X max) се нарича максимум на тази функция.

X max – максимална точка
На макс - максимум

Точка X min се нарича минимална точка на функцията f(x), ако за всички x от някакъв околност на X min е изпълнено неравенството f(x) f(X min).

Стойността Y min =f(X min) се нарича минимум на тази функция.

X min – минимална точка
Y min – минимум

X min , X max – точки на екстремум
Y min , Y max – екстремуми.

5. Нули на функцията

Нулата на функция y = f(x) е стойността на аргумента x, при която функцията става нула: f(x) = 0.

X 1, X 2, X 3 – нули на функцията y = f(x).

Задачи и тестове по темата "Основни свойства на функция"

• Функционални свойства - Числени функции 9 клас

  Уроци: 2 Задачи: 11 Тестове: 1

• Свойства на логаритмите - Показателни и логаритмични функции 11 клас

  Уроци: 2 Задачи: 14 Тестове: 1

• Функция квадратен корен, нейните свойства и графика - Функция квадратен корен. Свойства на корен квадратен 8 клас

  Уроци: 1 Задачи: 9 Тестове: 1

• Степенни функции, техните свойства и графики - Степени и корени. Степенни функции 11 клас

  Уроци: 4 Задачи: 14 Тестове: 1

• Функции - Важни теми за преглед на Единния държавен изпит по математика

  Задачи: 24

След като сте изучавали тази тема, трябва да можете да намерите областта на дефиниране на различни функции, да определите интервалите на монотонност на функция с помощта на графики и да изследвате функциите за четност и нечетност. Нека разгледаме решаването на подобни проблеми, като използваме следните примери.

Примери.

1. Намерете областта на дефиниция на функцията.

Решение:областта на дефиниране на функцията се намира от условието

Функции и техните свойства

Функцията е едно от най-важните математически понятия.функция Те наричат ​​такава зависимост на променливата y от променливата x, при която всяка стойност на променливата x съответства на една единствена стойност на променливата y.

Променлива хНаречен независима променлива или аргумент.Променлива приНаречен зависима променлива. Те също така казватпроменливата y е функция на променливата x. Стойностите на зависимата променлива се наричатстойности на функцията.

Ако зависимостта на променливатапри от променливах е функция, тогава може да се напише накратко, както следва:г= f( х ). (Прочети:при равно наf отх .) Символf( х) обозначават стойността на функцията, съответстваща на стойността на аргумента, равен нах .

Всички стойности на независимата променлива формаобласт на функция . Всички стойности, които зависимата променлива приемафункционален диапазон .

Ако дадена функция е посочена с формула и нейната област на дефиниране не е посочена, тогава се счита, че областта на дефиниция на функцията се състои от всички стойности на аргумента, за които формулата има смисъл.

Методи за определяне на функция:

1. аналитичен метод (функцията се определя с помощта на математическа формула;

2. табличен метод (функцията се определя с помощта на таблица)

3.описателен метод (функцията се определя чрез словесно описание)

4. графичен метод (функцията се определя с помощта на графика).

Функционална графика наименувайте множеството от всички точки на координатната равнина, чиито абсциси са равни на стойностите на аргумента и ординатите - съответните функционални стойности.

ОСНОВНИ СВОЙСТВА НА ФУНКЦИИТЕ

1. Функционални нули

Нула на функция е стойността на аргумента, при която стойността на функцията е равна на нула.

2. Интервали на постоянен знак на функция

Интервалите с постоянен знак на функция са набори от стойности на аргументи, при които стойностите на функцията са само положителни или само отрицателни.

3. Нарастваща (намаляваща) функция.

Повишаване на в определен интервал, функция е функция, за която по-голяма стойност на аргумента от този интервал съответства на по-голяма стойност на функцията.

функция y = f ( х ) Наречен повишаване на на интервала (A; b ), ако има х 1 И х 2 от този интервал, така чех 1 < х 2 , неравенството е вярноf ( х 1 )< f ( х 2 ).

Спускане в определен интервал, функция е функция, при която на по-голяма стойност на аргумента от този интервал съответства по-малка стойност на функцията.

функция при = f ( х ) Наречен намаляващина интервала (A; b ) , ако има такива х 1 И х 2 от този интервал, така че х 1 < х 2 , неравенството е вярноf ( х 1 )> f ( х 2 ).

4. Четна (нечетна) функция

Равномерна функция - функция, чиято област на дефиниция е симетрична по отношение на началото на координатите и за всяках от областта на дефиницията равенствотоf (- х ) = f ( х ) . Графиката на четна функция е симетрична спрямо ординатата.

Например y = x 2 - равномерна функция.

Странна функция- функция, чиято област на дефиниция е симетрична по отношение на началото на координатите и за всяка хот областта на дефиницията равенството е вярно f (- х ) = - f (х ). Графиката на нечетна функция е симетрична спрямо началото.

Например: y = x 3 - странна функция .

Функция от общ вид не е четна или нечетна (y = x 2 +x ).

Свойства на някои функции и техните графики

1. Линейна функция наречена функция на формата , Където к И b – числа.

Областта на дефиниране на линейна функция е множествоР реални числа.

Графика на линейна функцияпри = kx + b ( к ≠ 0) е права линия, минаваща през точката (0;b ) и успоредна на праватапри = kx .

Права, не успоредна на остаOU, е графиката на линейна функция.

Свойства на линейна функция.

1. Кога к > 0 функция при = kx + b

2. Кога к < 0 функция y = kx + b намаляващи в областта на дефиницията.

г = kx + b ( к ≠ 0 ) е цялата числова ос, т.е. няколкоР реални числа.

При к = 0 набор от функционални стойностиy = kx + b се състои от едно числоb .

3. Кога b = 0 и к = 0 функцията не е нито четна, нито нечетна.

При к = 0 линейната функция има форматаy = b и при b ≠ 0 равно е.

При к = 0 и b = 0 линейната функция има форматаy = 0 и е едновременно четно и нечетно.

Графика на линейна функцияy = b е права линия, минаваща през точката (0; b ) и успоредна на остаоИмайте предвид, че когато b = 0 графика на функциятаy = b съвпадат с оста о .

5. Кога к > 0 имаме това при> 0, ако и при< 0 ако . При к < 0 имаме, че y > 0 акои при< 0, если .

2. Функция г = х 2

Рреални числа.

Даване на променливах няколко стойности от домейна на функцията и изчисляване на съответните стойностиприспоред формулата г = х 2 , изобразяваме графиката на функцията.

Графика на функция г = х 2 Наречен парабола.

Свойства на функцията y = x 2 .

1. Ако х= 0, тогава y = 0, т.е. Параболата има обща точка с координатните оси (0; 0) - началото на координатите.

2. Ако x ≠ 0 , Че при > 0, т.е. всички точки на параболата, с изключение на началото, лежат над оста x.

3. Набор от стойности на функциятапри = х 2 е функцията за обхватпри = х 2 намалява.

х

3.Функция

Домейнът на тази функция е функцията spanг = | х | намалява.

7. Функцията приема най-малката си стойност в точкатаХ,то е равно на 0. Няма най-голяма стойност.

6. функция

Обхват на дефиницията на функцията: .

Функционален диапазон: .

Графиката е хипербола.

1. Функционални нули.

y ≠ 0, без нули.

2. Интервали на постоянство на знаците,

Ако к > 0, тогава при> 0 при х > 0; при < 0 при х < О.

Ако к < 0, то при < 0 при х > 0; при> 0 при х < 0.

3. Интервали на нарастване и намаляване.

Ако к > 0, тогава функцията намалява като .

Ако к < 0, то функция возрастает при .

4.Четна (нечетна) функция.

Функцията е странна.

Квадрат тричлен

Уравнение на формата брадва 2 + bx + ° С = 0, където а , bИ с - някои числа иа≠ 0, наречено квадрат.

В квадратно уравнениебрадва 2 + bx + ° С = 0 коефициент АНаречен първият коефициент b - втори коефициенти, с - безплатен член.

Формулата за корените на квадратно уравнение е:

.

Изразът се нарича дискриминанта квадратно уравнение и се означава сд .

Ако д = 0, тогава има само едно число, което удовлетворява уравнението брадва 2 + bx + ° С = 0. Въпреки това се съгласихме да кажем, че в този случай квадратното уравнение има два равни реални корена и самото число Наречен двоен корен.

Ако д < 0, то квадратное уравнение не имеет действительных корней.

Ако д > 0, тогава квадратното уравнение има два различни реални корена.

Нека е дадено квадратно уравнениебрадва 2 + bx + ° С = 0. Тъй като а≠ 0, след което разделяме двете страни на това уравнение наа, получаваме уравнението . Вярвайки И , стигаме до уравнението , в което първият коефициент е равен на 1. Това уравнение се наричададено.

Формулата за корените на горното квадратно уравнение е:

.

Уравнения на формата

А х 2 + bx = 0, брадва 2 + s = 0, А х 2 = 0

са наречени непълни квадратни уравнения. Непълните квадратни уравнения се решават чрез разлагане на лявата страна на уравнението.

Теорема на Виета .

Сумата от корените на квадратно уравнение е равна на съотношението на втория коефициент към първия, взето с обратен знак, а произведението на корените е съотношението на свободния член към първия коефициент, т.е.

Обратна теорема.

Ако сумата от произволни две числах 1 И х 2 равна на , а произведението им е равно, тогава тези числа са корените на квадратното уравнениео 2 + b x + c = 0.

Функция на формата о 2 + b x + cНаречен квадратен тричлен. Корените на тази функция са корените на съответното квадратно уравнениео 2 + b x + c = 0.

Ако дискриминантът на квадратичен трином е по-голям от нула, тогава този трином може да бъде представен като:

о 2 + b x + c = a(x-x 1 )(x-x 2 )

Където х 1 И х 2 - корени на тричлена

Ако дискриминантът на квадратичен трином е нула, тогава този трином може да бъде представен като:

о 2 + b x + c = a(x-x 1 ) 2

Където х 1 - корен на тричлена.

Например, 3x 2 - 12x + 12 = 3 (x - 2) 2 .

Уравнение на формата о 4 + b х 2 + s= 0 се извиква биквадратен. Използване на замяна на променлива с помощта на формулатах 2 = г тя се свежда до квадратно уравнениеА г 2 + от + s = 0.

Квадратична функция

Квадратична функция е функция, която може да бъде записана с формула от форматаг = брадва 2 + bx + ° С , Където х - независима променлива,а , b И ° С – някои числа иа ≠ 0.

Свойствата на функцията и вида на нейната графика се определят главно от стойностите на коефициентаа и дискриминант.

Свойства на квадратична функция

Домейн:Р;

Диапазон от стойности:

при А > 0 [- д/(4 а); ∞)

при А < 0 (-∞; - д/(4 а)];

Дори странно:

при b = 0 четна функция

при b ≠ Функцията 0 не е нито четна, нито нечетна

при д> 0 две нули: ,

при д= 0 една нула:

при д < 0 нулей нет

Интервали на постоянство на знака:

ако a > 0, д> 0, тогава

ако a > 0, д= 0, тогава

дако a > 0, д < 0, то

ако< 0, д> 0, тогава

ако< 0, д= 0, тогава

ако< 0, д < 0, то

- Интервали на монотонност

за a > 0

при а< 0

Графиката на квадратична функция епарабола – крива, симетрична спрямо права линия , минаваща през върха на параболата (върхът на параболата е пресечната точка на параболата с оста на симетрия).

За да начертаете графика на квадратична функция, трябва:

1) намерете координатите на върха на параболата и я маркирайте в координатната равнина;

2) конструирайте още няколко точки, принадлежащи на параболата;

3) свържете маркираните точки с гладка линия.

Координатите на върха на параболата се определят по формулите:

; .

Преобразуване на графики на функции

1. Разтягане графични изкустваy = x 2 по остапри V|a| пъти (при|a| < 1 е компресия на 1/|a| веднъж).

Ако и< 0, произвести, кроме того, зеркальное отражение графика отно­сительно оси х (клоновете на параболата ще бъдат насочени надолу).

Резултат: графика на функцияy = ах 2 .

2. Паралелен трансфер функционална графикаy = ах 2 по остах На| м | (вдясно, когато

м > 0 и наляво, когатоT< 0).

Резултат: функционална графикаy = a(x - t) 2 .

3. Паралелен трансфер функционална графика по остапри На| н | (нагоре къмp> 0 и надолу приП< 0).

Резултат: функционална графикаy = a(x - t) 2 + стр.

Квадратни неравенства

Неравенства на форматао 2 + b x + c > 0 ио 2 + bx + c< 0, къдетох - променлива,а , b Ис - някои числа иа≠ 0 се наричат ​​неравенства от втора степен с една променлива.

Решаването на неравенство от втора степен в една променлива може да се разглежда като намиране на интервалите, в които съответната квадратична функция приема положителни или отрицателни стойности.

За решаване на неравенства от видао 2 + bx + c > 0 ио 2 + bx + c< 0 продължете както следва:

1) намерете дискриминанта на квадратния трином и разберете дали триномът има корени;

2) ако тричленът има корени, тогава ги маркирайте на остах и през маркираните точки схематично е начертана парабола, чиито клонове са насочени нагоре къмА > 0 или надолу, когатоА< 0; ако триномът няма корени, тогава схематично изобразете парабола, разположена в горната полуравнина наА > 0 или по-ниско приА < 0;

3) намерени на остах интервали, за които точките на параболата са разположени над остах (ако неравенството е решеноо 2 + bx + c > 0) или под остах (ако неравенството е решеноо 2 + bx + c < 0).

Пример:

Нека решим неравенството .

Помислете за функцията

Неговата графика е парабола, чиито клонове са насочени надолу (тъй като ).

Нека разберем как е разположена графиката спрямо остаХ. Нека решим уравнението за това . Разбираме товаx = 4. Уравнението има един корен. Това означава, че параболата докосва остаХ.

Чрез схематично изобразяване на парабола откриваме, че функцията приема отрицателни стойности за всякаХ, освен 4.

Отговорът може да бъде написан така:х - всяко число, което не е равно на 4.

Решаване на неравенства по интервалния метод

диаграма на решението

1. Намерете нули функция от лявата страна на неравенството.

2. Маркирайте позицията на нулите върху числовата ос и определете тяхната кратност (Акок аз е четен, тогава нулата е с четна кратност, акок аз нечетното си е нечетно).

3. Намерете признаците на функцията в интервалите между неговите нули, започвайки от най-десния интервал: в този интервал функцията от лявата страна на неравенството винаги е положителна за дадената форма на неравенства. При преминаване от дясно на ляво през нулата на функция от един интервал към съседен, трябва да се вземе предвид:

ако нулата е нечетна кратност, знакът на функцията се променя,

ако нулата е четна кратност, знакът на функцията се запазва.

4. Запишете отговора.

Пример:

(x + 6) (x + 1) (Х - 4) < 0.

Намерени нули на функцията. Те са равни:х 1 = -6; х 2 = -1; х 3 = 4.

Нека отбележим нулите на функцията върху координатната праваf ( х ) = (x + 6) (x + 1) (Х - 4).

Нека намерим знаците на тази функция във всеки от интервалите (-∞; -6), (-6; -1), (-1; 4) и

От фигурата става ясно, че множеството от решения на неравенството е обединението на интервалите (-∞; -6) и (-1; 4).

Отговор: (-∞ ; -6) и (-1; 4).

Разгледаният метод за решаване на неравенства се наричаинтервален метод.

Домейнът на дефиниция и диапазонът от стойности на функция.В елементарната математика функциите се изучават само върху множеството от реални числа Р.Това означава, че аргументът на функцията може да приема само тези реални стойности, за които е дефинирана функцията, т.е. също така приема само реални стойности. Няколко хвсички валидни валидни стойности на аргумент х, за които функцията г= f(х)дефиниран, наречен област на функцията. Няколко Yвсички реални стойности г, което функцията приема, се извиква функционален диапазон. Сега можем да дадем по-точна дефиниция на функцията: правило(закон) за съответствие между множествата X и Y, според която за всеки елемент от множествотоX може да намери един и само един елемент от множеството Y, наречен функция.

От това определение следва, че една функция се счита за дефинирана, ако:

Указва се домейнът на функцията х ;

Обхватът на функцията е посочен Y ;

Известно е правилото (закона) за съответствие и то такова, че за всеки

Само една функционална стойност може да бъде намерена за стойност на аргумент.

Това изискване за уникалност на функцията е задължително.

Монотонна функция.Ако за всеки две стойности на аргумента х 1 и х 2 от условието х 2 > х 1 следва f(х 2) > f(х 1), след това функцията f(х) е наречен повишаване на; ако има х 1 и х 2 от условието х 2 > х 1 следва f(х 2) < f(х 1), след това функцията f(х) е наречен намаляващи. Извиква се функция, която само нараства или само намалява монотонен.

Ограничени и неограничени функции.Функцията се извиква ограничен, ако има такова положително число Мкакво | f(х) | Мза всички стойности х.Ако такова число не съществува, тогава функцията е неограничен.

ПРИМЕРИ.

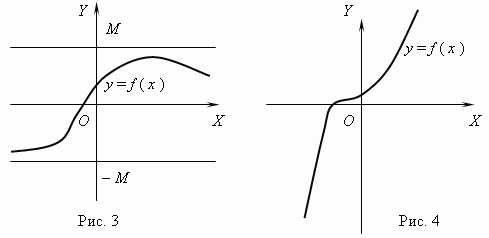
Функцията, показана на фиг. 3, е ограничена, но не монотонна. Функцията на фиг. 4 е точно обратното, монотонна, но неограничена. (Моля, обяснете това!).

Непрекъснати и прекъснати функции.функция г = f (х) е наречен непрекъснато в точкатах = а, ако:

1) функцията е дефинирана, когато х = а, т.е. f (а) съществува;

2) съществува краенлимит лим f (х) ;

х→а

(вижте ограниченията на функциите)

3) f (а) = lim f (х) .

х→а

Ако поне едно от тези условия не е изпълнено, тогава функцията се извиква експлозивенв точката х = а.

Ако функцията е непрекъсната по време на всеки точки от неговата област на дефиниране, тогава се нарича непрекъсната функция.

Четни и нечетни функции.Ако за всякакви х f(- х) = f (х), тогава функцията се извиква дори;ако се случи: f(- х) = - f (х), тогава функцията се извиква странно. Графика на четна функция симетричен спрямо оста Y(фиг. 5), графика на нечетна функция Simметрика по отношение на произхода(фиг. 6).

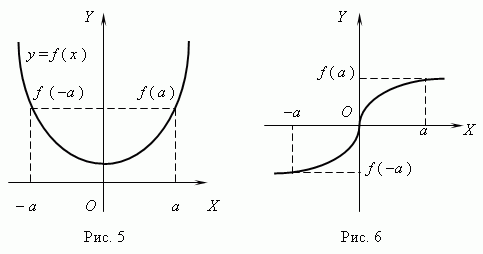
Периодична функция.функция f (х) - периодичен, ако има такова нещо ненулевномер Tза какво всякакви хот областта на дефиниране на функцията е валидно следното: f (х + T) = f (х). Това най-малкономерът се нарича период на функцията. Всички тригонометрични функции са периодични.

Пример 1. Докажете този грях хима период от 2.

Решение: Ние знаем, че грехът ( x+ 2н) = грях х, Където н= 0, ± 1, ± 2, …

Следователно допълнение 2 нне към аргумента синус

Променя значението си. Има ли друг номер с това

Същият имот?

Нека се преструваме, че П- такова число, т.е. равенство:

грях( x+ P) = грях х,

Валиден за всяка стойност х. Но тогава има

Място и време х= / 2, т.е.

Грях(/2 + П) = грях / 2 = 1.

Но според формулата за редукция sin ( / 2 + П) = cos П. Тогава

От последните две равенства следва, че cos П= 1, но ние

Знаем, че това е вярно само когато П = 2н. От най-малката

Ненулево число от 2 не 2, тогава това число

И има менструален грях х. По подобен начин може да се докаже, че 2от не , така че това е периодът sin 2 х.

Функционални нули.Извиква се стойността на аргумента, при която функцията е равна на 0 нула (root) функция. Една функция може да има няколко нули, например функцията г = х (х + 1) (х-3) има три нули: х= 0, х= -1, х= 3. Геометрично нулева функция - това е абсцисата на пресечната точка на графиката на функцията с оста х .

Фигура 7 показва графика на функция с нули: х= а, х = bИ х= ° С.

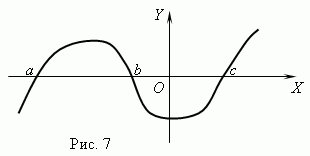
Асимптота.Ако графиката на функция се приближава неограничено до определена права, докато се отдалечава от началото, тогава тази права се нарича асимптота.

Поддържането на вашата поверителност е важно за нас. Поради тази причина разработихме Политика за поверителност, която описва как използваме и съхраняваме вашата информация. Моля, прегледайте нашите практики за поверителност и ни уведомете, ако имате въпроси.

Събиране и използване на лична информация

Личната информация се отнася до данни, които могат да бъдат използвани за идентифициране или контакт с конкретно лице.

Може да бъдете помолени да предоставите вашата лична информация по всяко време, когато се свържете с нас.

По-долу са дадени някои примери за видовете лична информация, която можем да събираме и как можем да използваме тази информация.

Каква лична информация събираме:

• Когато подадете заявление на сайта, ние може да съберем различна информация, включително вашето име, телефонен номер, имейл адрес и др.

Как използваме вашата лична информация:

• Личната информация, която събираме, ни позволява да се свържем с вас с уникални оферти, промоции и други събития и предстоящи събития.
• От време на време може да използваме вашата лична информация, за да изпращаме важни известия и съобщения.
• Може също така да използваме лична информация за вътрешни цели, като например извършване на одити, анализ на данни и различни изследвания, за да подобрим услугите, които предоставяме, и да ви предоставим препоръки относно нашите услуги.
• Ако участвате в теглене на награди, конкурс или подобна промоция, ние може да използваме предоставената от вас информация за администриране на такива програми.

Разкриване на информация на трети лица

Ние не разкриваме информацията, получена от вас, на трети страни.

Изключения:

• При необходимост - в съответствие със закона, съдебна процедура, в съдебно производство и/или въз основа на публични искания или искания от държавни органи на територията на Руската федерация - да разкриете вашата лична информация. Може също така да разкрием информация за вас, ако преценим, че такова разкриване е необходимо или подходящо за целите на сигурността, правоприлагането или други обществено значими цели.
• В случай на реорганизация, сливане или продажба, можем да прехвърлим личната информация, която събираме, на съответната трета страна приемник.

Защита на личната информация

Ние вземаме предпазни мерки – включително административни, технически и физически – за да защитим вашата лична информация от загуба, кражба и злоупотреба, както и неоторизиран достъп, разкриване, промяна и унищожаване.

Зачитане на вашата поверителност на фирмено ниво

За да гарантираме, че вашата лична информация е защитена, ние съобщаваме стандартите за поверителност и сигурност на нашите служители и стриктно прилагаме практиките за поверителност.

Този учебен материал е само за справка и се отнася до широк кръг от теми. Статията предоставя преглед на графики на основни елементарни функции и разглежда най-важния въпрос - как да изградите графика правилно и БЪРЗО. В хода на изучаване на висша математика без познаване на графиките на основните елементарни функции ще бъде трудно, така че е много важно да запомните как изглеждат графиките на парабола, хипербола, синус, косинус и т.н. и да запомните някои от значенията на функциите. Ще говорим и за някои свойства на основните функции.

Не претендирам за изчерпателност и научна изчерпателност на материалите, акцентът ще бъде поставен преди всичко върху практиката - тези неща, с които човек се среща буквално на всяка крачка, във всяка тема от висшата математика. Графики за манекени? Може да се каже и това.

Поради многобройни искания от читатели съдържание, върху което може да се кликне:

Освен това има супер кратко резюме по темата
– овладейте 16 вида диаграми, като изучавате ШЕСТ страници!

Сериозно, шест, дори аз бях изненадан. Това резюме съдържа подобрена графика и се предлага срещу номинална такса, може да се види демо версия. Удобно е да отпечатате файла, така че графиките да са винаги под ръка. Благодаря за подкрепата на проекта!

И да започнем веднага:

Как правилно да конструираме координатни оси?

На практика контролните работи почти винаги се попълват от учениците в отделни тетрадки, подредени в квадрат. Защо се нуждаете от карирана маркировка? В крайна сметка работата по принцип може да се извърши на листове А4. И клетката е необходима само за висококачествено и точно проектиране на чертежи.

Всеки чертеж на функционална графика започва с координатни оси.

Чертежите могат да бъдат двуизмерни и триизмерни.

Нека първо разгледаме двумерния случай Декартова правоъгълна координатна система:

1) Начертайте координатни оси. Оста се нарича ос х , а оста е у-ос . Винаги се опитваме да ги нарисуваме спретнат и не крив. Стрелките също не трябва да приличат на брадата на татко Карло.

2) Подписваме осите с големи букви „X“ и „Y“. Не забравяйте да обозначите осите.

3) Задайте скалата по осите: нарисувайте нула и две единици. При рисуване най-удобният и често използван мащаб е: 1 единица = 2 клетки (чертеж вляво) – при възможност се придържайте към него. От време на време обаче се случва чертежът да не се побира на листа на тетрадката - тогава намаляваме мащаба: 1 единица = 1 клетка (чертеж вдясно). Рядко, но се случва, че мащабът на чертежа трябва да бъде намален (или увеличен) още повече

НЯМА НУЖДА от „картечница“ …-5, -4, -3, -1, 0, 1, 2, 3, 4, 5, ….Защото координатната равнина не е паметник на Декарт, а ученикът не е гълъб. Ние поставяме нулаИ две единици по осите. Понякога вместоединици, удобно е да „маркирате“ други стойности, например „две“ по абсцисната ос и „три“ по ординатната ос - и тази система (0, 2 и 3) също ще дефинира уникално координатната мрежа.

По-добре е да прецените приблизителните размери на чертежа ПРЕДИ да конструирате чертежа. Така, например, ако задачата изисква начертаване на триъгълник с върхове , , , тогава е напълно ясно, че популярният мащаб 1 единица = 2 клетки няма да работи. Защо? Нека да разгледаме точката - тук ще трябва да измерите петнадесет сантиметра надолу и, очевидно, рисунката няма да се побере (или едва се побере) на лист от тетрадка. Затова веднага избираме по-малък мащаб: 1 единица = 1 клетка.

Между другото, за сантиметри и клетки от тетрадка. Вярно ли е, че 30 клетки от тетрадка съдържат 15 сантиметра? За забавление измерете 15 сантиметра в тетрадката си с линийка. В СССР това може би е било вярно... Интересно е да се отбележи, че ако измерите същите тези сантиметри хоризонтално и вертикално, резултатите (в клетките) ще бъдат различни! Строго погледнато, съвременните тетрадки не са карирани, а правоъгълни. Това може да изглежда глупост, но рисуването, например, на кръг с компас в такива ситуации е много неудобно. Честно казано, в такива моменти започвате да мислите за правотата на другаря Сталин, който беше изпратен в лагери за халтура в производството, да не говорим за местната автомобилна индустрия, падащи самолети или експлодиращи електроцентрали.

Говорейки за качество, или кратка препоръка за канцеларски материали. Днес повечето от продаваните тетрадки са меко казано пълна глупост. Поради причината, че се мокрят и то не само от гел химикалки, но и от химикалки! Те спестяват пари на хартия. За попълване на тестове препоръчвам да използвате тетрадки от Архангелската целулозно-хартиена фабрика (18 листа, квадрат) или „Pyaterochka“, въпреки че е по-скъпо. Препоръчително е да изберете гел химикал, дори най-евтиният китайски гел пълнител е много по-добър от химикалка, която или размазва, или къса хартията. Единствената „конкурентна“ химикалка, която мога да си спомня, е Erich Krause. Тя пише ясно, красиво и последователно – независимо дали с пълно ядро ​​или с почти празно.

Допълнително: Визията за правоъгълна координатна система през очите на аналитичната геометрия е разгледана в статията Линейна (не)зависимост на векторите. Основа на векторите, подробна информация за координатните квартали можете да намерите във втория параграф на урока Линейни неравенства.

3D калъф

Тук е почти същото.

1) Начертайте координатни оси. Стандартен: прилагане на ос – насочена нагоре, ос – насочена надясно, ос – насочена надолу наляво строгопод ъгъл от 45 градуса.

2) Маркирайте осите.

3) Задайте скалата по осите. Мащабът по оста е два пъти по-малък от мащаба по другите оси. Също така имайте предвид, че в десния чертеж използвах нестандартен "прорез" по оста (тази възможност вече беше спомената по-горе). От моя гледна точка това е по-точно, по-бързо и по-естетически приятно - няма нужда да търсите средата на клетката под микроскоп и да „извайвате“ единица, близка до началото на координатите.

Когато правите 3D чертеж, отново дайте приоритет на мащаба
1 единица = 2 клетки (чертеж вляво).

За какво са всички тези правила? Правилата са създадени за да се нарушават. Това ще направя сега. Факт е, че следващите чертежи на артикула ще бъдат направени от мен в Excel и координатните оси ще изглеждат неправилни от гледна точка на правилния дизайн. Бих могъл да начертая всички графики на ръка, но всъщност е страшно да ги нарисувам, тъй като Excel не желае да ги начертае много по-точно.

Графики и основни свойства на елементарни функции

Линейна функция е дадена от уравнението. Графиката на линейните функции е директен. За да се построи права линия, е достатъчно да се познават две точки.

Пример 1

Постройте графика на функцията. Нека намерим две точки. Изгодно е да изберете нула като една от точките.

Ако, тогава

Да вземем друга точка, например 1.

Ако, тогава

При изпълнение на задачи координатите на точките обикновено се обобщават в таблица:

А самите стойности се изчисляват устно или на чернова, калкулатор.

Намерени са две точки, нека направим чертежа:

Когато изготвяме чертеж, ние винаги подписваме графиките.

Би било полезно да си припомним специални случаи на линейна функция:

Забележете как поставих подписите, подписите не трябва да позволяват несъответствия при изучаване на чертежа. В този случай беше изключително нежелателно да се постави подпис до точката на пресичане на линиите или долу вдясно между графиките.

1) Линейна функция от формата () се нарича пряка пропорционалност. Например, . Графиката на правата пропорционалност винаги минава през началото. Така конструирането на права линия е опростено - достатъчно е да се намери само една точка.

2) Уравнение от формата определя права линия, успоредна на оста, по-специално, самата ос е дадена от уравнението. Графиката на функцията се начертава веднага, без да се откриват точки. Това означава, че записът трябва да се разбира по следния начин: „y винаги е равно на –4 за всяка стойност на x.“

3) Уравнение от формата определя права линия, успоредна на оста, по-специално, самата ос е дадена от уравнението. Графиката на функцията също се начертава веднага. Записът трябва да се разбира по следния начин: „x винаги, за всяка стойност на y, е равно на 1.“

Някои ще попитат, защо да помним 6 клас?! Така е, може би е така, но през годините на практика срещнах добра дузина студенти, които бяха объркани от задачата да построят графика като или.

Изграждането на права линия е най-често срещаното действие при правене на чертежи.

Правата е разгледана подробно в курса по аналитична геометрия, а интересуващите се могат да се обърнат към статията Уравнение на права на равнина.

Графика на квадратна, кубична функция, графика на полином

Парабола. Графика на квадратична функция () представлява парабола. Помислете за известния случай:

Нека си припомним някои свойства на функцията.

И така, решението на нашето уравнение: – в тази точка се намира върхът на параболата. Защо това е така може да научите от теоретичната статия за производната и урока за екстремуми на функцията. Междувременно нека изчислим съответната стойност „Y“:

Така върхът е в точката

Сега намираме други точки, докато нагло използваме симетрията на параболата. Трябва да се отбележи, че функцията – не е дори, но въпреки това никой не е отменил симетрията на параболата.

В какъв ред да намерите останалите точки, мисля, че ще стане ясно от финалната маса:

Този алгоритъм на изграждане образно може да се нарече „совалка” или принципът „напред и назад” при Анфиса Чехова.

Да направим чертежа:

От разгледаните графики идва на ум още една полезна функция:

За квадратична функция () следното е вярно:

Ако , тогава клоновете на параболата са насочени нагоре.

Ако , тогава клоновете на параболата са насочени надолу.

Задълбочени знания за кривата могат да се получат в урока Хипербола и парабола.

Кубична парабола е дадена от функцията. Ето рисунка, позната от училище:

Нека изброим основните свойства на функцията

Графика на функция

Представлява един от клоновете на парабола. Да направим чертежа:

Основни свойства на функцията:

В този случай оста е вертикална асимптота за графиката на хипербола при .

Би било ГРУБА грешка, ако при съставяне на чертеж небрежно позволите графиката да се пресече с асимптота.

Също така едностранните граници ни казват, че хиперболата не се ограничава отгореИ не се ограничава отдолу.

Нека разгледаме функцията в безкрайност: , тоест, ако започнем да се движим по оста наляво (или надясно) до безкрайност, тогава „игрите“ ще бъдат в подредена стъпка безкрайно близоприближават нулата и съответно клоновете на хиперболата безкрайно близоприближете се до оста.

Така че оста е хоризонтална асимптота за графиката на функция, ако „x“ клони към плюс или минус безкрайност.

Функцията е странно, и следователно хиперболата е симетрична спрямо началото. Този факт е очевиден от чертежа, освен това лесно се проверява аналитично: .

Графиката на функция от формата () представлява два клона на хипербола.

Ако , тогава хиперболата се намира в първата и третата координатна четвърт(вижте снимката по-горе).

Ако , тогава хиперболата се намира във втората и четвъртата координатна четвърт.

Посоченият модел на пребиваване на хипербола е лесен за анализ от гледна точка на геометрични трансформации на графики.

Пример 3

Конструирайте десния клон на хиперболата

Използваме метода на точково конструиране и е изгодно да изберете стойностите така, че да се делят на цяло:

Да направим чертежа:

Няма да е трудно да се конструира лявото разклонение на хиперболата; странността на функцията ще помогне тук. Грубо казано, в таблицата на точковата конструкция ние мислено добавяме минус към всяко число, поставяме съответните точки и рисуваме втория клон.

Подробна геометрична информация за разглежданата права можете да намерите в статията Хипербола и парабола.

Графика на експоненциална функция

В този раздел веднага ще разгледам експоненциалната функция, тъй като в проблемите на висшата математика в 95% от случаите се появява експоненциалната.

Нека ви напомня, че това е ирационално число: , това ще се изисква при изграждането на графика, която всъщност ще изградя без церемонии. Три точки вероятно са достатъчни:

Нека засега оставим графиката на функцията, повече за нея по-късно.

Основни свойства на функцията:

Функционалните графики и т.н. изглеждат фундаментално еднакви.

Трябва да кажа, че вторият случай се среща по-рядко в практиката, но се среща, затова сметнах за необходимо да го включа в тази статия.

Графика на логаритмична функция

Помислете за функция с натурален логаритъм.
Нека направим чертеж точка по точка:

Ако сте забравили какво е логаритъм, моля, вижте учебниците си в училище.

Основни свойства на функцията:

Домейн:

Диапазон от стойности: .

Функцията не е ограничена отгоре: , макар и бавно, но клонът на логаритъма се издига до безкрайност.
Нека разгледаме поведението на функцията близо до нула вдясно: . Така че оста е вертикална асимптота за графиката на функция като "x" клони към нула отдясно.

Задължително е да знаете и запомните типичната стойност на логаритъма: .

По принцип графиката на логаритъма при основа изглежда по същия начин: , , (десетичен логаритъм при основа 10) и т.н. Освен това, колкото по-голяма е основата, толкова по-плоска ще бъде графиката.

Няма да разглеждаме случая; не помня последния път, когато съм правил графика с такава основа. А логаритъмът изглежда е много рядък гост в задачите на висшата математика.

В края на този параграф ще кажа още един факт: Експоненциална функция и логаритмична функция– това са две взаимно обратни функции. Ако погледнете внимателно графиката на логаритъма, можете да видите, че това е същият показател, просто е разположен малко по-различно.

Графики на тригонометрични функции

Откъде започват тригонометричните мъки в училище? вярно От синуса

Нека начертаем функцията

Тази линия се нарича синусоида.

Нека ви напомня, че „пи“ е ирационално число: , а в тригонометрията ви заслепява очите.

Основни свойства на функцията:

Тази функция е периодиченс точка . Какво означава? Нека да разгледаме сегмента. Вляво и вдясно от нея безкрайно се повтаря точно една и съща част от графиката.

Домейн: , тоест за всяка стойност на „x“ има синусова стойност.

Диапазон от стойности: . Функцията е ограничен: , тоест всички „игри“ се намират строго в сегмента .
Това не се случва: или, по-точно, случва се, но тези уравнения нямат решение.