Частта от окръжност, ограничена от две точки, се нарича. Как се различава кръгът от кръга: обяснение

кръг е плоска затворена линия, всички точки на която са на еднакво разстояние от определена точка (точка O), която се нарича център на окръжността.
(Кръгът е геометрична фигура, състояща се от всички точки, разположени на дадено разстояние от дадена точка.)

кръг е част от равнината, ограничена от окръжност. Точка O се нарича още център на окръжността.

Разстоянието от точка на окръжност до нейния център, както и отсечката, свързваща центъра на окръжността с нейната точка, се нарича радиус кръг/кръг.
Вижте как кръгът и обиколката се използват в нашия живот, изкуство, дизайн.

Акорд - гръцки - струна, която свързва нещо заедно
Диаметър - "измерване чрез"

КРЪГЛА ФОРМА

Ъглите могат да се появяват във все по-големи количества и съответно да придобиват все по-голям завой – докато напълно изчезнат и равнината стане кръг.Това е много прост и в същото време много сложен случай, за който бих искал да говоря подробно. Тук трябва да се отбележи, че както простотата, така и сложността се дължат на липсата на ъгли. Кръгът е прост, защото натискът на неговите граници, в сравнение с правоъгълните форми, е изравнен - разликите тук не са толкова големи. Сложен е, защото горната част неусетно прелива в лявото и дясното, а лявото и дясното в дъното.

В. Кандински

В Древна Гърция кръгът и обиколката се смятали за венец на съвършенството. Наистина във всяка точка кръгът е подреден по един и същи начин, което му позволява да се движи сам. Това свойство на кръга направи колелото възможно, тъй като оста и главината на колелото трябва да са в контакт през цялото време.

Много полезни свойства на кръга се изучават в училище. Една от най-красивите теореми е следната: начертайте права през дадена точка, пресичаща дадена окръжност, след това произведението на разстоянията от тази точка до пресечните точки на окръжност с права линия не зависят от това как точно е начертана правата линия. Тази теорема е на около две хиляди години.

На фиг. Фигура 2 показва две окръжности и верига от окръжности, всяка от които се допира до тези две окръжности и две съседни във веригата. Швейцарският геометър Якоб Щайнер доказа следното твърдение преди около 150 години: ако веригата е затворена за определен избор от третия кръг, то тя ще бъде затворена и за всеки друг избор от третия кръг. От това следва, че ако веригата не е затворена веднъж, тогава тя няма да бъде затворена за никакъв избор на третия кръг. На художника, който рисуваизобразена верига, човек трябва да се потруди, за да работи, или да се обърне към математик, за да изчисли местоположението на първите два кръга, при които веригата е затворена.

Първо споменахме колелото, но още преди колелото хората са използвали обли трупи- ролки за транспортиране на тежки товари.

Възможно ли е да се използват ролки с друга форма освен кръгла? немскиинженер Франц Рело откри, че ролките, чиято форма е показана на фиг., имат същото свойство. 3. Тази фигура се получава чрез начертаване на дъги от окръжности с центрове във върховете на равностранен триъгълник, свързващ два други върха. Ако начертаем две успоредни допирателни към тази фигура, тогава разстоянието междуте ще бъдат равни на дължината на страната на оригиналния равностранен триъгълник, така че такива ролки не са по-лоши от кръглите. По-късно са изобретени други фигури, които могат да служат като ролки.

Енц. "Аз изследвам света. Математика", 2006г

Всеки триъгълник има и освен това само един, кръг от девет точки. товаокръжност, минаваща през следните три тройки точки, чиито позиции са определени за триъгълника: основите на неговите височини D1 D2 и D3, основите на неговите медиани D4, D5 и D6средните точки на D7, D8 и D9 на прави сегменти от точката на пресичане на неговите височини H до неговите върхове.

Този кръг, намерен през 18 век. от великия учен Л. Ойлер (поради което често се нарича и кръгът на Ойлер), е преоткрит през следващия век от учител в провинциална гимназия в Германия. Името на този учител е Карл Фойербах (той е брат на известния философ Лудвиг Фойербах).Освен това К. Фойербах установи, че кръг от девет точки има още четири точки, които са тясно свързани с геометрията на всеки даден триъгълник. Това са точките на контакта му с четири кръга от специален тип. Една от тези окръжности е вписана, останалите три са вписани. Те са вписани в ъглите на триъгълника и външно се допират до страните му. Точките на допиране на тези окръжности с окръжността от девет точки D10, D11, D12 и D13 се наричат точки на Фойербах. Така кръгът от девет точки всъщност е кръгът от тринадесет точки.

Този кръг е много лесен за конструиране, ако знаете двете му свойства. Първо, центърът на окръжността от девет точки се намира в средата на сегмента, свързващ центъра на описаната окръжност на триъгълника с точка Н - неговия ортоцентър (точката на пресичане на неговите височини). Второ, радиусът му за даден триъгълник е равен на половината от радиуса на описаната около него окръжност.

Енц. справочник за млади математици, 1989г

Виждаме кръгови форми и кръгове навсякъде: това е колелото на колата, линията на хоризонта и дискът на Луната. Математиците започнаха да изучават геометричните фигури - кръг върху равнина - много отдавна.

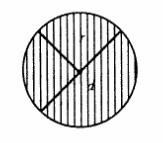
Окръжност с център и радиус е набор от точки в равнина, разположени на разстояние не по-голямо от . Кръгът е ограничен от кръг, състоящ се от точки, разположени точно на разстояние от центъра. Отсечките, свързващи центъра с точките на окръжността, имат дължина и се наричат още радиуси (на окръжност, кръг). Частите от окръжността, на които тя е разделена от два радиуса, се наричат кръгови сектори (фиг. 1). Хорда - отсечка, свързваща две точки от окръжност - разделя окръжността на две отсечки, а окръжността на две дъги (фиг. 2). Перпендикуляр, изтеглен от центъра към хордата, разделя нея и дъгите, граничещи с нея, наполовина. Акордът е по-дълъг, колкото по-близо е разположен до центъра; най-дългите хорди - хордите, минаващи през центъра - се наричат диаметри (на кръг, кръг).

Ако една права линия е отдалечена от центъра на окръжността на разстояние , тогава при тя не се пресича с окръжността, при пресича окръжността по хорда и се нарича секанс, при при има една обща точка с окръжност и окръжността и се нарича допирателна. Допирателната се характеризира с факта, че е перпендикулярна на радиуса, начертан до точката на допиране. Две допирателни могат да бъдат начертани към окръжност от точка извън нея и техните отсечки от дадена точка до точките на допиране са равни.

Дъгите на окръжност, подобно на ъглите, могат да се измерват в градуси и фракции. Част от целия кръг се приема като градус. Централният ъгъл (фиг. 3) се измерва в същия брой градуси като дъгата, върху която лежи; вписан ъгъл се измерва с половин дъга. Ако върхът на ъгъл лежи вътре в кръга, тогава този ъгъл в градуси е равен на половината от сумата на дъгите и (фиг. 4, а). Ъгъл с връх извън окръжността (фиг. 4,b), изрязващ дъги и върху окръжността, се измерва с полуразликата на дъгите и. И накрая, ъгълът между допирателната и хордата е равен на половината от дъгата на окръжност, затворена между тях (фиг. 4, c).

Кръгът и кръгът имат безкраен брой оси на симетрия.

От теоремите за измерване на ъглите и подобието на триъгълниците следват две теореми за пропорционалните отсечки в окръжност. Теоремата за акордите казва, че ако една точка лежи вътре в окръжност, тогава произведението от дължините на сегментите от акордите, минаващи през нея, е постоянно. На фиг. 5,а. Теоремата за секанса и тангенса (което означава дължините на сегментите на части от тези прави) гласи, че ако една точка лежи извън окръжността, тогава произведението на секанса и неговата външна част също е непроменено и е равно на квадрата на тангенса ( Фиг. 5, б).

Още в древни времена хората се опитват да решават проблеми, свързани с кръга - да измерват дължината на кръг или неговата дъга, площта на кръг или сектор, сегмент. Първият от тях има чисто „практично“ решение: можете да поставите конец по протежение на кръг, след което да го развиете и да го приложите към линийка, или да маркирате точка върху кръга и да я „търкаляте“ по линийката (можете , напротив, „разточете“ кръг с линийка). По един или друг начин измерванията показаха, че съотношението на обиколката към нейния диаметър е еднакво за всички кръгове. Това съотношение обикновено се обозначава с гръцка буква ("пи" е началната буква на гръцката дума perimetron, което означава "кръг").

Древногръцките математици обаче не са били доволни от такъв емпиричен, експериментален подход за определяне на обиколката на кръг: кръгът е линия, т.е. според Евклид „дължина без ширина“ и такива нишки не съществуват. Ако търкаляме кръг по линийка, тогава възниква въпросът: защо получаваме обиколката, а не някаква друга стойност? Освен това този подход не ни позволи да определим площта на кръга.

Решението беше намерено, както следва: ако разгледаме правилните -gons, вписани в окръжност, тогава като , клонящи към безкрайност, в границата те клонят към . Следователно е естествено да се въведат следните, вече строги дефиниции: дължината на окръжност е границата на последователността от периметри на правилни триъгълници, вписани в окръжност, а площта на окръжността е границата на последователността от техните области. Този подход е приет и в съвременната математика и по отношение не само на кръга и кръга, но и на други извити области или области, ограничени от криволинейни контури: вместо правилни многоъгълници, последователности от начупени линии с върхове на криви или контури на области се разглеждат и границата се взема, когато дължината клони към най-големите връзки на прекъснатата линия към нула.

Дължината на кръгова дъга се определя по подобен начин: дъгата се разделя на равни части, точките на разделяне се свързват с прекъсната линия, а дължината на дъгата се приема за равна на границата на периметрите на такава прекъснати линии като , клонящи към безкрайност. (Подобно на древните гърци, ние не изясняваме самата концепция за граница - тя вече не се отнася до геометрията и е доста строго въведена едва през 19 век.)

От дефиницията на самото число формулата за обиколката следва:

За дължината на дъга можем да напишем подобна формула: тъй като за две дъги и с общ централен ъгъл съображенията за подобие предполагат пропорцията , а от нея пропорцията , след преминаване до границата получаваме независимостта (на радиус на дъгата) на отношението . Това съотношение се определя само от централния ъгъл и се нарича радианова мярка на този ъгъл и всички съответстващи дъги с център в. Това дава формулата за дължината на дъгата:

където е радианова мярка на дъгата.

Написаните формули за и са просто пренаписани дефиниции или означения, но с тяхна помощ получаваме формули за площите на кръг и сектор, които далеч не са просто означения:

За да изведете първата формула, достатъчно е да отидете до границата във формулата за площта на правилен триъгълник, вписан в кръг:

По дефиниция лявата страна клони към площта на кръга, а дясната страна клони към числото

и , Основи на неговите медиани и , Среди и отсечки от точката на пресичане на неговите височини до неговите върхове.

Този кръг, намерен през 18 век. от великия учен Л. Ойлер (поради което често се нарича и кръгът на Ойлер), е преоткрит през следващия век от учител в провинциална гимназия в Германия. Името на този учител е Карл Фойербах (той е брат на известния философ Лудвиг Фойербах). Освен това К. Фойербах установи, че кръг от девет точки има още четири точки, които са тясно свързани с геометрията на всеки даден триъгълник. Това са точките на контакта му с четири кръга от специален тип (фиг. 2). Една от тези окръжности е вписана, останалите три са вписани. Те са вписани в ъглите на триъгълника и външно се допират до страните му. Допирните точки на тези окръжности с окръжност от девет точки се наричат точки на Фойербах. Така кръгът от девет точки всъщност е кръгът от тринадесет точки.

Този кръг е много лесен за конструиране, ако знаете двете му свойства. Първо, центърът на окръжността от девет точки се намира в средата на сегмента, свързващ центъра на окръжността, описана около триъгълника, с точка - неговия ортоцентър (точката на пресичане на неговите височини). Второ, радиусът му за даден триъгълник е равен на половината от радиуса на описаната около него окръжност.

И кръг- геометрични фигури, свързани помежду си. има граница начупена линия (крива) кръг,

Определение. Окръжността е затворена крива, всяка точка от която е на еднакво разстояние от точка, наречена център на окръжността.

За да се построи окръжност, се избира произволна точка O, която се приема за център на окръжността и се начертава затворена линия с помощта на компас.

Ако точка O от центъра на окръжността е свързана с произволни точки от окръжността, тогава всички получени сегменти ще бъдат равни един на друг и такива сегменти се наричат радиуси, съкратени с латинската малка или главна буква „er“ ( rили Р). Можете да начертаете толкова радиуси в кръг, колкото точки има в обиколката.

Отсечка, свързваща две точки от окръжност и минаваща през нейния център, се нарича диаметър. Диаметърсе състои от две радиуси, лежащи на една и съща права линия. Диаметърът се обозначава с латинската малка или главна буква „de“ ( dили г).

правило. Диаметъредна окръжност е равна на две от нейните радиуси.

d = 2r
D=2R

Обиколката на окръжност се изчислява по формулата и зависи от радиуса (диаметъра) на окръжността. Формулата съдържа числото ¶, което показва колко пъти обиколката е по-голяма от диаметъра си. Числото ¶ има безкраен брой десетични знаци. За изчисленията е взето ¶ = 3,14.

Обиколката на кръга се обозначава с латинската главна буква "tse" ( В). Обиколката на кръга е пропорционална на неговия диаметър. Формули за изчисляване на обиколката на кръг въз основа на неговия радиус и диаметър:

C = ¶d
C = 2¶r

Примери
Дадено е: d = 100 cm.
Обиколка: С=3,14*100см=314см
Дадено е: d = 25 mm.
Обиколка: C = 2 * 3,14 * 25 = 157 mm

Циркулярна секуща и окръжна дъга

Всеки секанс (права линия) пресича окръжност в две точки и я разделя на две дъги. Размерът на дъгата на окръжност зависи от разстоянието между центъра и секущата и се измерва по затворена крива от първата точка на пресичане на секущата с окръжността до втората.

дъгикръговете са разделени секущана голяма и малка, ако секансът не съвпада с диаметъра, и на две равни дъги, ако секансът минава по диаметъра на окръжността.

Ако секансът минава през центъра на кръг, тогава неговият сегмент, разположен между точките на пресичане с кръга, е диаметърът на кръга или най-голямата хорда на кръга.

Колкото секущата е разположена по-далече от центъра на окръжността, толкова по-малка е градусната мярка на по-малката дъга на окръжността и толкова по-голяма е по-голямата дъга на окръжността, а сегментът на секущата, т.нар. акорд, намалява, когато секансът се отдалечава от центъра на кръга.

Определение. Окръжност е част от равнина, разположена вътре в окръжност.

Центърът, радиусът и диаметърът на окръжност са едновременно център, радиус и диаметър на съответната окръжност.

Тъй като кръгът е част от равнина, един от неговите параметри е площта.

правило. Площ на кръг ( С) е равно на произведението на квадрата на радиуса ( r 2) към числото ¶.

Примери
Дадено е: r = 100 cm
Площ на кръга:
S = 3,14 * 100 cm * 100 cm = 31 400 cm 2 ≈ 3 m 2
Дадено: d = 50 мм
Площ на кръга:
S = ¼ * 3,14 * 50 mm * 50 mm = 1963 mm 2 ≈ 20 cm 2

Ако начертаете два радиуса в окръжност до различни точки от окръжността, тогава се образуват две части на окръжността, които се наричат сектори. Ако нарисувате хорда в кръг, тогава частта от равнината между дъгата и хордата се нарича кръгов сегмент.

кръг- геометрична фигура, състояща се от всички точки на равнината, разположени на дадено разстояние от дадена точка.

Тази точка (О) се нарича център на кръга.
Радиус на кръга- това е сегмент, свързващ центъра с всяка точка от окръжността. Всички радиуси имат еднаква дължина (по дефиниция).
Акорд- сегмент, свързващ две точки от окръжност. Нарича се хорда, минаваща през центъра на окръжност диаметър. Центърът на кръг е средата на произволен диаметър.
Всякакви две точки от окръжност я разделят на две части. Всяка от тези части се нарича дъга от окръжност. Дъгата се нарича полукръг, ако отсечката, свързваща краищата му, е диаметър.
Дължината на единичен полукръг се означава с π .
Сумата от градусните мерки на две дъги на окръжност с общи краища е равна на 360º.
Частта от равнината, ограничена от окръжност, се нарича навсякъде наоколо.
Кръгов сектор- част от окръжност, ограничена от дъга и два радиуса, свързващи краищата на дъгата с центъра на окръжността. Дъгата, която ограничава сектора, се нарича дъга на сектора.
Две окръжности с общ център се наричат концентричен.
Две окръжности, пресичащи се под прав ъгъл, се наричат ортогонален.

Относителното положение на права линия и окръжност

Ако разстоянието от центъра на окръжността до правата линия е по-малко от радиуса на окръжността ( г), тогава правата и окръжността имат две общи точки. В този случай линията се извиква секущапо отношение на кръга.
Ако разстоянието от центъра на окръжността до правата линия е равно на радиуса на окръжността, то правата и окръжността имат само една обща точка. Тази линия се нарича допирателна към окръжността, а общата им точка се нарича точка на допир между права и окръжност.
Ако разстоянието от центъра на окръжността до правата линия е по-голямо от радиуса на окръжността, тогава правата линия и окръжността нямат допирни точки

Централни и вписани ъгли

Централен ъгъле ъгъл, чийто връх е в центъра на окръжността.
Вписан ъгъл- ъгъл, чийто връх лежи върху окръжност и чиито страни пресичат окръжността.

Теорема за вписания ъгъл

Вписан ъгъл се измерва с половината от дъгата, върху която той се намира.

Следствие 1.
Вписаните ъгли, обхващащи една и съща дъга, са равни.

Следствие 2.
Вписан ъгъл, сключен от полукръг, е прав ъгъл.

Теорема за произведението на отсечки от пресичащи се хорди.

Ако две хорди на окръжност се пресичат, тогава произведението на сегментите на едната хорда е равно на произведението на сегментите на другата хорда.

Основни формули

Обиколка:

C = 2∙π∙R

Дължина на кръговата дъга:

R = С/(2∙π) = D/2

Диаметър:

D = C/π = 2∙R

Дължина на кръговата дъга:

l = (π∙R) / 180∙α,
Къде α - градусна мярка за дължината на кръгова дъга)

Площ на кръга:

S = π∙R 2

Площ на кръговия сектор:

S = ((π∙R 2) / 360)∙α

Уравнение на окръжност

В правоъгълна координатна система уравнението на окръжност с радиус е rс център в точката В(x o; y o) има формата:

(x - x o) 2 + (y - y o) 2 = r 2

Уравнението на окръжност с радиус r с център в началото има формата:

x 2 + y 2 = r 2

Окръжност с център $O$ и радиус $R$ е набор от точки в равнината, отдалечени от $O$ на разстояние не по-голямо от $R.$ Окръжност е ограничена от окръжност, състояща се от точки, отстранени от центъра $ O$ точно на разстояние $R .$ Отсечките, свързващи центъра с точките на окръжността, имат дължина $R$ и се наричат още радиуси (на окръжност, кръг). Частите от окръжността, на които тя е разделена от два радиуса, се наричат кръгови сектори (фиг. 1). Хорда - отсечка, свързваща две точки от окръжност - разделя окръжността на две отсечки, а окръжността на две дъги (фиг. 2). Перпендикуляр, изтеглен от центъра към хордата, разделя нея и дъгите, граничещи с нея, наполовина. Акордът е по-дълъг, колкото по-близо е разположен до центъра; най-дългите хорди - хордите, минаващи през центъра - се наричат диаметри (на кръг, кръг).

Ако права линия се намира на разстояние $d,$ от центъра на окръжността, то при $d > R$ тя не се пресича с окръжността, при $d

Дъгите на окръжност, подобно на ъглите, могат да се измерват в градуси и фракции. Един градус се приема за $1/360$ от целия кръг. Централният ъгъл $AOB$ (фиг. 3) се измерва в същия брой градуси като дъгата $AB,$, върху която той лежи; вписаният ъгъл $ACB$ се измерва с половината дъга $AB.$ Ако върхът $P$ на ъгъл $APB$ лежи вътре в окръжността, то този ъгъл в градуси е равен на половината от сбора на дъгите $AB$ и $A′B′$ (фиг. 4, а ). Ъгълът с върха $P$ извън окръжността (фиг. 4, б), изрязващ дъгите $AB$ и $A′B′,$ върху окръжността, се измерва с полуразликата на дъгите $A ′B′$ и $AB.$ И накрая, ъгълът между допирателната и хордата е равен на половината от дъгата на окръжност, затворена между тях (фиг. 4, в).

Кръгът и кръгът имат безкраен брой оси на симетрия.

От теоремите за измерване на ъглите и подобието на триъгълниците следват две теореми за пропорционалните отсечки в окръжност. Теоремата за хордите казва, че ако точка $M$ лежи вътре в окръжност, тогава произведението от дължините на отсечките $AM⋅BM$ на хордите, минаващи през нея, е константа. На фиг. 5, и $AM⋅BM=A′M′⋅B′M.$ Теоремата за секущата и допирателната (което означава дължините на отсечките - части от тези прави) гласи, че ако точката $M$ лежи извън окръжността, тогава произведението на секанса $ MA$ към външната му част $MB$ също не се променя и е равно на квадрата на допирателната $MC$ (фиг. 5, b).

Дори в древни времена те се опитват да решат проблеми, свързани с кръга - да измерят дължината на кръг или неговата дъга, площта на кръг или сектор, сегмент. Първият от тях има чисто „практично“ решение: можете да поставите нишка по протежение на кръг, след което да го развиете и да го прикрепите към линийка или да маркирате точка върху кръга и да я „навиете“ по линийката (можете , напротив, „разточете“ кръг с линийка). По един или друг начин, измерванията показаха, че отношението на обиколката $L$ към нейния диаметър $d=2R$ е еднакво за всички кръгове. Това съотношение обикновено се обозначава с гръцката буква $π$ („пи” е началната буква на гръцката дума perimetron, което означава „кръг”).

Решението беше намерено по следния начин: ако разгледаме правилните $n$-ъгълници $M_n,$, вписани в окръжност $K$, тогава тъй като $n,$ клони към безкрайност, $M_n$ в границата клони към $K.$ Следователно е естествено да се въведат следните, вече строги определения: обиколката $L$ е границата на последователността от периметри $P_n$ на правилни $n$-ъгълници, вписани в окръжността, а площта на окръжността $S$ е границата на последователността $S_n$ от техните области. Този подход е приет и в съвременната математика и по отношение не само на кръга и кръга, но и на други извити области или области, ограничени от криволинейни контури: вместо правилни многоъгълници, последователности от начупени линии с върхове на криви или контури на области се разглеждат и границата се взема, когато дължината клони към най-големите връзки на прекъснатата линия към нула.

Дължината на кръгова дъга се определя по подобен начин: дъгата се разделя на n равни части, точките на разделяне се свързват с прекъсната линия, а дължината на дъгата $L$ се задава равна на границата на периметрите $l_n$ от такива начупени линии като $n,$ клони към безкрайност. (Подобно на древните гърци, ние не изясняваме самата концепция за граница - тя вече не се отнася до геометрията и е доста строго въведена едва през 19 век.)

От самата дефиниция на числото π следва формулата за обиколката:

За дължината на дъгата можем да напишем подобна формула: тъй като за две дъги $Γ$ и $Γ′$ с общ централен ъгъл съображенията за подобие предполагат пропорцията $l_n:l′_n=R:R′,$ и от това е пропорцията $l_n: R=l′_n:R′,$ след преминаване до границата получаваме независимостта (от радиуса на дъгата) на връзката $l/R=l′/R′=α.$ Тази връзка се определя само от централния ъгъл $AOB$ и се нарича радиан, който измерва този ъгъл и всички дъги, съответстващи на него с център в $O.$ Така получаваме формула за дължината на дъгата:

където $α$ е радианова мярка на дъгата.

Написаните формули за $L$ и $l$ са просто пренаписани дефиниции или означения, но с тяхна помощ получаваме формули за площите на кръг и сектор, които далеч не са просто означения:

$S=πR^2,$ $S=\frac(1)(2)αR^2.$

За да извлечете първата формула, достатъчно е да отидете до границата във формулата за площта на правилен n-ъгълник, вписан в кръг:

$S_n=\frac(1)(2)P_nh_n.$

По дефиниция лявата страна клони към площта на кръга $S,$, а дясната страна клони към числото

$\frac(1)(2)LR=\frac(1)(2)⋅2πR⋅R =πR^2$

(апотемата $h_n,$ разбира се клони към $R$). Формулата за площта на сектора $s$ се извежда по абсолютно същия начин:

$s=\lim S_n=\lim (\frac(1)(2)l_nh_n)=$ $\frac(1)(2)\lim l_n⋅\lim h_n=$ $\frac(1)(2)lR =$ $\frac(1)(2)αR^2$

($\lim $- четете „лимит“). Така се решава задачата за определяне на площта на сегмент с хорда $AB,$, тъй като тя се представя като разлика или сума (фиг. 1, 2) на площите на съответния сектор и триъгълник $AOB. $