$X$. في البداية، أذكر التعريف التالي:
التعريف 1
سكان- مجموعة من الكائنات المختارة عشوائياً من نوع معين، والتي يتم إجراء الملاحظات عليها من أجل الحصول على قيم محددة لمتغير عشوائي، يتم إجراؤها في ظل ظروف ثابتة عند دراسة متغير عشوائي واحد من نوع معين.
التعريف 2
التباين العام- الوسط الحسابي لمربعات انحرافات قيم متغير السكان عن قيمتها المتوسطة.
دع قيم الخيار $x_1,\ x_2,\dots ,x_k$ لها ترددات $n_1,\n_2,\dots ,n_k$ على التوالي. ثم يتم حساب التباين العام باستخدام الصيغة:
دعونا نفكر في حالة خاصة. اجعل جميع الخيارات $x_1,\ x_2,\dots ,x_k$ مختلفة. في هذه الحالة $n_1,\ n_2,\dots ,n_k=1$. ونجد أنه في هذه الحالة يتم حساب التباين العام باستخدام الصيغة:
ويرتبط هذا المفهوم أيضًا بمفهوم الانحراف المعياري العام.
التعريف 3
الانحراف المعياري العام
\[(\sigma )_g=\sqrt(D_g)\]
تباين العينة
دعونا نعطي عينة من السكان فيما يتعلق بالمتغير العشوائي $X$. في البداية، أذكر التعريف التالي:
التعريف 4
عينة السكان- جزء من كائنات مختارة من عامة السكان.
التعريف 5
تباين العينة- الوسط الحسابي لقيم مجتمع العينة.
دع قيم الخيار $x_1,\ x_2,\dots ,x_k$ لها ترددات $n_1,\n_2,\dots ,n_k$ على التوالي. ثم يتم حساب تباين العينة باستخدام الصيغة:
دعونا نفكر في حالة خاصة. اجعل جميع الخيارات $x_1,\ x_2,\dots ,x_k$ مختلفة. في هذه الحالة $n_1,\ n_2,\dots ,n_k=1$. ونجد أنه في هذه الحالة يتم حساب تباين العينة باستخدام الصيغة:
ويرتبط أيضًا بهذا المفهوم مفهوم الانحراف المعياري للعينة.
التعريف 6
الانحراف المعياري للعينة- الجذر التربيعي للتباين العام :
\[(\سيجما )_в=\sqrt(D_в)\]
التباين المصحح
للعثور على التباين المصحح $S^2$، من الضروري ضرب تباين العينة بالكسر $\frac(n)(n-1)$، أي
ويرتبط هذا المفهوم أيضًا بمفهوم الانحراف المعياري المصحح والذي يوجد بالصيغة:
في الحالة التي تكون فيها قيم المتغيرات غير منفصلة، ولكنها تمثل فترات، ثم في صيغ حساب التباينات العامة أو تباينات العينة، يتم اعتبار قيمة $x_i$ هي قيمة منتصف الفاصل الزمني إلى الذي ينتمي إليه $x_i.$.
مثال على مشكلة إيجاد التباين والانحراف المعياري
مثال 1
يتم تحديد مجتمع العينة من خلال جدول التوزيع التالي:
الصورة 1.
دعونا نجد لها تباين العينة والانحراف المعياري للعينة والتباين المصحح والانحراف المعياري المصحح.
لحل هذه المشكلة، نقوم أولاً بعمل جدول حسابي:
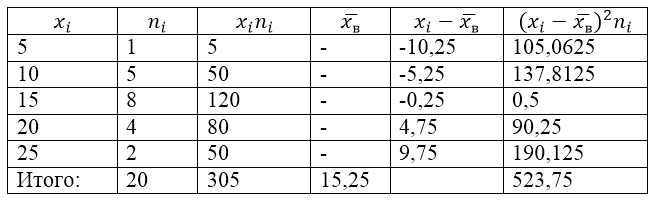
الشكل 2.
تم العثور على القيمة $\overline(x_в)$ (متوسط العينة) في الجدول بواسطة الصيغة:
\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)\]
\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)=\frac(305)(20)=15.25\]
دعونا نجد تباين العينة باستخدام الصيغة:
الانحراف المعياري للعينة:
\[(\sigma )_в=\sqrt(D_в)\حوالي 5.12\]
التباين المصحح:
\[(S^2=\frac(n)(n-1)D)_в=\frac(20)(19)\cdot 26.1875\حوالي 27.57\]
تصحيح الانحراف المعياري.
الانحراف المعياري(مرادفات: الانحراف المعياري, الانحراف المعياري, انحراف مربع; المصطلحات ذات الصلة: الانحراف المعياري, انتشار قياسي) - في نظرية الاحتمالات والإحصاء، المؤشر الأكثر شيوعا لتشتت قيم المتغير العشوائي نسبة إلى توقعه الرياضي. مع صفائف محدودة من عينات القيم، بدلا من التوقع الرياضي، يتم استخدام الوسط الحسابي لمجموعة العينات.
يوتيوب الموسوعي
-
1 / 5
يتم قياس الانحراف المعياري بوحدات قياس المتغير العشوائي نفسه ويستخدم عند حساب الخطأ المعياري للوسط الحسابي، عند بناء فترات الثقة، عند اختبار الفرضيات إحصائيا، عند قياس العلاقة الخطية بين المتغيرات العشوائية. يتم تعريفه على أنه الجذر التربيعي لتباين متغير عشوائي.
الانحراف المعياري:
s = n n − 1 σ 2 = 1 n − 1 ∑ i = 1 n (x i − x ¯) 2 ; (\displaystyle s=(\sqrt ((\frac (n)(n-1))\sigma ^(2)))=(\sqrt ((\frac (1)(n-1))\sum _( i=1)^(n)\left(x_(i)-(\bar (x))\right)^(2)));)- ملاحظة: في كثير من الأحيان توجد اختلافات في أسماء MSD (الانحراف الجذري لمتوسط المربع) وSTD (الانحراف المعياري) مع صيغهما. على سبيل المثال، في وحدة numPy في لغة البرمجة Python، توصف الدالة std() بأنها "الانحراف المعياري"، بينما تعكس الصيغة الانحراف المعياري (القسمة على جذر العينة). في Excel، تختلف الدالة STANDARDEVAL() (القسمة على جذر n-1).
الانحراف المعياري(تقدير الانحراف المعياري للمتغير العشوائي سمقارنة بتوقعها الرياضي المبني على تقدير غير متحيز لتباينها) س (\displaystyle s):
σ = 1 n ∑ i = 1 n (x i − x ¯) 2 . (\displaystyle \sigma =(\sqrt ((\frac (1)(n))\sum _(i=1)^(n)\left(x_(i)-(\bar (x))\right) ^(2))).)أين σ 2 (\displaystyle \sigma ^(2))- تشتت؛ س ط (\displaystyle x_(i)) - أناالعنصر الرابع من الاختيار؛ ن (\displaystyle n)- حجم العينة؛
- الوسط الحسابي للعينة:x ¯ = 1 n ∑ i = 1 n x i = 1 n (x 1 + … + x n) . (\displaystyle (\bar (x))=(\frac (1)(n))\sum _(i=1)^(n)x_(i)=(\frac (1)(n))(x_ (1)+\ldots +x_(n)).)
وتجدر الإشارة إلى أن كلا التقديرين متحيزان. في الحالة العامة، من المستحيل بناء تقدير غير متحيز. ومع ذلك، فإن التقدير المبني على تقدير التباين غير المتحيز ثابت.
وفقًا لـ GOST R 8.736-2011، يتم حساب الانحراف المعياري باستخدام الصيغة الثانية من هذا القسم. يرجى التحقق من النتائج.
وفقًا لـ GOST R 8.736-2011، يتم حساب الانحراف المعياري باستخدام الصيغة الثانية من هذا القسم. يرجى التحقق من النتائج. (قاعدة ثلاثة سيجما 3 σ (\displaystyle 3\سيجما ) ) - تقع جميع قيم المتغير العشوائي الموزع بشكل طبيعي تقريبًا في الفاصل الزمني(x ¯ − 3 σ ; x ¯ + 3 σ) (\displaystyle \left((\bar (x))-3\sigma ;(\bar (x))+3\sigma \right)) . بشكل أكثر صرامة - مع احتمال تقريبي 0.9973، تقع قيمة المتغير العشوائي الموزع بشكل طبيعي في الفاصل الزمني المحدد (شريطة أن تكون القيمةس ¯ (\displaystyle (\bar (x)))
صحيح، ولم يتم الحصول عليه نتيجة لمعالجة العينات). . بشكل أكثر صرامة - مع احتمال تقريبي 0.9973، تقع قيمة المتغير العشوائي الموزع بشكل طبيعي في الفاصل الزمني المحدد (شريطة أن تكون القيمةإذا كانت القيمة الحقيقية غير معروف، فلا يجب عليك استخدامهσ (\displaystyle \sigma ) ، أس ، أ .
. وهكذا تتحول قاعدة الثلاثة سيجما إلى قاعدة الثلاثة
تفسير قيمة الانحراف المعياري
على سبيل المثال، لدينا ثلاث مجموعات أرقام: (0، 0، 14، 14)، (0، 6، 8، 14) و (6، 6، 8، 8). جميع المجموعات الثلاث لها قيم متوسطة تساوي 7، والانحرافات المعيارية، على التوالي، تساوي 7 و 5 و 1. المجموعة الأخيرة لها انحراف معياري صغير، حيث يتم تجميع القيم في المجموعة حول القيمة المتوسطة؛ المجموعة الأولى لديها أكبر قيمة للانحراف المعياري - القيم داخل المجموعة تتباعد بشكل كبير عن القيمة المتوسطة.
وبمعنى عام، يمكن اعتبار الانحراف المعياري مقياسا لعدم اليقين. على سبيل المثال، في الفيزياء، يتم استخدام الانحراف المعياري لتحديد خطأ سلسلة من القياسات المتعاقبة لبعض الكمية. هذه القيمة مهمة جداً لتحديد مدى معقولية الظاهرة قيد الدراسة بالمقارنة مع القيمة التي تنبأت بها النظرية: إذا كان متوسط قيمة القياسات يختلف كثيراً عن القيم التي تنبأت بها النظرية (انحراف معياري كبير)، ثم يجب إعادة فحص القيم التي تم الحصول عليها أو طريقة الحصول عليها. المحددة بمخاطر المحفظة.
مناخ
لنفترض أن هناك مدينتين لهما نفس متوسط درجة الحرارة اليومية القصوى، لكن إحداهما تقع على الساحل والأخرى على السهل. من المعروف أن المدن الواقعة على الساحل لديها العديد من درجات الحرارة القصوى المختلفة أثناء النهار والتي تكون أقل من المدن الواقعة في الداخل. ولذلك فإن الانحراف المعياري لدرجات الحرارة القصوى اليومية لمدينة ساحلية سيكون أقل منه للمدينة الثانية، على الرغم من أن متوسط قيمة هذه القيمة هو نفسه، وهو ما يعني عمليا أن احتمال أن تكون درجة حرارة الهواء القصوى على في أي يوم من أيام السنة، ستكون القيمة أعلى تختلف عن متوسط القيمة، وتكون أعلى بالنسبة لمدينة تقع في الداخل.
رياضة
لنفترض أن هناك العديد من فرق كرة القدم التي يتم تصنيفها بناءً على مجموعة من المعايير، على سبيل المثال، عدد الأهداف المسجلة والمستقبلة، وفرص التسجيل، وما إلى ذلك. ومن المرجح أن يتمتع أفضل فريق في هذه المجموعة بقيم أفضل على المزيد من المعلمات. كلما كان الانحراف المعياري للفريق أصغر لكل من المعلمات المقدمة، كلما كانت نتيجة الفريق متوازنة بشكل أكبر؛ في المقابل، يصعب على الفريق الذي لديه انحراف معياري كبير التنبؤ بالنتيجة، وهو ما يفسر بدوره وجود خلل في التوازن، على سبيل المثال، دفاع قوي ولكن هجوم ضعيف.
إن استخدام الانحراف المعياري لمعلمات الفريق يجعل من الممكن، بدرجة أو بأخرى، التنبؤ بنتيجة المباراة بين فريقين، وتقييم نقاط القوة والضعف لدى الفريقين، وبالتالي أساليب القتال المختارة.
الانحراف المعياري
إن الخاصية المثالية للتباين هي متوسط انحراف المربع، والذي يسمى المعيار (أو الانحراف المعياري). الانحراف المعياري() يساوي الجذر التربيعي لمتوسط الانحراف المربع للقيم الفردية للسمة من الوسط الحسابي:
الانحراف المعياري بسيط:
يتم تطبيق الانحراف المعياري المرجح على البيانات المجمعة:
تحدث النسبة التالية بين متوسط الانحرافات المربعة ومتوسط الانحرافات الخطية في ظل ظروف التوزيع الطبيعي: ~ 1.25.
يُستخدم الانحراف المعياري، باعتباره المقياس المطلق الرئيسي للتباين، في تحديد القيم الإحداثية لمنحنى التوزيع الطبيعي، وفي الحسابات المتعلقة بتنظيم مراقبة العينة وتحديد دقة خصائص العينة، وكذلك في تقييم حدود الاختلاف في خاصية ما في مجتمع متجانس.
18. التباين أنواعه والانحراف المعياري.
تباين متغير عشوائي- مقياس انتشار متغير عشوائي معين، أي انحرافه عن التوقع الرياضي. في الإحصائيات، غالبًا ما يتم استخدام التدوين أو. عادة ما يسمى الجذر التربيعي للتباين الانحراف المعياري, الانحراف المعياريأو انتشار قياسي.
التباين الكلي (σ 2) يقيس تباين السمة بأكملها تحت تأثير جميع العوامل التي تسببت في هذا التباين. وفي الوقت نفسه، وبفضل طريقة التجميع، من الممكن تحديد وقياس التباين الناتج عن خاصية التجميع والتباين الناشئ تحت تأثير العوامل غير المحسوبة.
التباين بين المجموعات (σ 2 م.ج) يميز التباين المنهجي، أي الاختلافات في قيمة السمة المدروسة التي تنشأ تحت تأثير السمة - العامل الذي يشكل أساس المجموعة.
الانحراف المعياري(مرادفات: الانحراف المعياري, الانحراف المعياري, انحراف مربع; المصطلحات ذات الصلة: الانحراف المعياري, انتشار قياسي) - في نظرية الاحتمالات والإحصاء، المؤشر الأكثر شيوعا لتشتت قيم المتغير العشوائي نسبة إلى توقعه الرياضي. مع صفائف محدودة من قيم العينة، يتم استخدام المتوسط الحسابي لمجموعة العينات بدلاً من التوقع الرياضي.
يتم قياس الانحراف المعياري بوحدات قياس المتغير العشوائي نفسه ويستخدم عند حساب الخطأ المعياري للوسط الحسابي، عند بناء فترات الثقة، عند اختبار الفرضيات إحصائيا، عند قياس العلاقة الخطية بين المتغيرات العشوائية. يتم تعريفه على أنه الجذر التربيعي لتباين متغير عشوائي.
الانحراف المعياري:
الانحراف المعياري(تقدير الانحراف المعياري للمتغير العشوائي سبالنسبة إلى توقعاتها الرياضية بناءً على تقدير غير متحيز لتباينها):
أين التشتت؟ - أناالعنصر الرابع من الاختيار؛ - حجم العينة؛ - الوسط الحسابي للعينة:
وتجدر الإشارة إلى أن كلا التقديرين متحيزان. في الحالة العامة، من المستحيل بناء تقدير غير متحيز. وفي هذه الحالة، يكون التقدير المبني على تقدير التباين غير المتحيز متسقًا.
19. جوهر ونطاق وإجراءات تحديد الوضع والوسيط.
بالإضافة إلى متوسطات القوة في الإحصائيات، للتوصيف النسبي لقيمة خاصية متباينة والبنية الداخلية لسلسلة التوزيع، يتم استخدام المتوسطات الهيكلية، والتي تتمثل بشكل أساسي بـ الموضة والوسيط.
موضة- هذا هو الشكل الأكثر شيوعًا في السلسلة. تُستخدم الموضة، على سبيل المثال، في تحديد مقاسات الملابس والأحذية الأكثر طلبًا بين العملاء. وضع السلسلة المنفصلة هو المتغير ذو التردد الأعلى. عند حساب الوضع لسلسلة تباين الفاصل الزمني، من المهم للغاية تحديد الفاصل الزمني المشروط أولاً (بأقصى تردد)، ثم - قيمة القيمة المشروطة للسمة باستخدام الصيغة:
§ - معنى الموضة
§ - الحد الأدنى للفاصل المشروط
§ - قيمة الفاصل
§ - تردد الفاصل الزمني
§ - تردد الفاصل الزمني الذي يسبق المشروط
§ - تردد الفاصل الزمني التالي للشكل
الوسيط -تكمن قيمة السمة ĸᴏᴛᴏᴩᴏᴇ في أساس السلسلة المرتبة وتقسم هذه السلسلة إلى جزأين متساويين في العدد.
لتحديد الوسيط في سلسلة منفصلةإذا كانت الترددات متاحة، قم أولاً بحساب نصف مجموع الترددات، ثم حدد قيمة المتغير الذي يقع عليها. (إذا كانت السلسلة المصنفة تحتوي على عدد فردي من الخصائص، فسيتم حساب الرقم المتوسط باستخدام الصيغة:
M e = (n (إجمالي عدد الميزات) + 1)/2,
وفي حالة وجود عدد زوجي من المعالم، سيكون الوسيط مساويًا لمتوسط المعلمتين الموجودتين في منتصف الصف).
عند حساب الوسيط لسلسلة التغيير الفاصلأولاً، حدد الفاصل الزمني المتوسط الذي يقع فيه الوسيط، ثم حدد قيمة الوسيط باستخدام الصيغة:
§ - الوسيط المطلوب
§ - الحد الأدنى للفاصل الذي يحتوي على الوسيط
§ - قيمة الفاصل
§ - مجموع الترددات أو عدد مصطلحات السلسلة
§ - مجموع الترددات المتراكمة للفترات التي تسبق الوسيط
§ - تردد الفاصل الزمني المتوسط
مثال. العثور على الوضع والوسيط.
حل: في هذا المثال، الفاصل الزمني يقع ضمن الفئة العمرية 25-30 سنة، حيث أن هذا الفاصل الزمني له أعلى تكرار (1054).
دعونا نحسب حجم الوضع:
وهذا يعني أن العمر النموذجي للطلاب هو 27 عامًا.
دعونا نحسب الوسيط. يقع الفاصل الزمني المتوسط في الفئة العمرية من 25 إلى 30 عامًا، حيث يوجد ضمن هذا الفاصل خيار ͵ الذي يقسم السكان إلى جزأين متساويين (Σf i /2 = 3462/2 = 1731). بعد ذلك، نستبدل البيانات الرقمية اللازمة في الصيغة ونحصل على قيمة الوسيط:
وهذا يعني أن نصف الطلاب أقل من 27.4 عامًا، والنصف الآخر أكبر من 27.4 عامًا.
بالإضافة إلى الوضع والوسيط، يتم استخدام مؤشرات مثل الربعيات، وتقسيم السلسلة المرتبة إلى 4 أجزاء متساوية، والعشريات - 10 أجزاء والنسب المئوية - إلى 100 جزء.
20. مفهوم الملاحظة بالعينة ونطاقها.
مراقبة انتقائيةينطبق عند استخدام المراقبة المستمرة مستحيل جسديابسبب كمية كبيرة من البيانات أو غير مجدية اقتصاديا. وتحدث الاستحالة المادية، على سبيل المثال، عند دراسة تدفقات الركاب وأسعار السوق وميزانيات الأسرة. يحدث عدم الجدوى الاقتصادية عند تقييم جودة السلع المرتبطة بتدميرها، على سبيل المثال، التذوق، واختبار الطوب للقوة، وما إلى ذلك.
الوحدات الإحصائية المختارة للمراقبة هي عينة السكانأو عينة، ومصفوفتهم بأكملها - عامه السكان(ع). حيث عدد الوحدات في العينةدل ن، وفي جميع أنحاء النظام المنسق بأكمله - ن. سلوك ن / نعادة ما يسمى الحجم النسبيأو حصة العينة.
تعتمد جودة نتائج مراقبة العينة على تمثيل العينةأي على مدى تمثيلها في قطاع غزة. ولضمان تمثيل العينة، من المهم للغاية الالتزام بها مبدأ الاختيار العشوائي للوحدات، والذي يفترض أن إدراج وحدة النظام المنسق في العينة لا يمكن أن يتأثر بأي عامل آخر غير الصدفة.
موجود 4 طرق للاختيار العشوائيلأخذ عينات:
- في الواقع عشوائيةالاختيار أو "طريقة اليانصيب"، عندما يتم تعيين أرقام تسلسلية للقيم الإحصائية، المسجلة على كائنات معينة (على سبيل المثال، البراميل)، والتي يتم بعد ذلك خلطها في حاوية (على سبيل المثال، في كيس) واختيارها بشكل عشوائي. عمليًا، يتم تنفيذ هذه الطريقة باستخدام مولد أرقام عشوائية أو جداول رياضية للأرقام العشوائية.
- ميكانيكيالاختيار وفقا لكل ( لا/ن)-القيمة الرابعة لعامة السكان. على سبيل المثال، إذا كانت تحتوي على 100000 قيمة، وتحتاج إلى تحديد 1000، فسيتم تضمين كل 100000 / 1000 = القيمة رقم 100 في العينة. علاوة على ذلك، إذا لم يتم ترتيبهم، فسيتم اختيار الأول عشوائيًا من المائة الأولى، وستكون أعداد الآخرين أعلى بمائة. فمثلاً إذا كانت الوحدة الأولى رقم 19 فالتالية يجب أن تكون رقم 119 ثم رقم 219 ثم رقم 319 وهكذا. وفي حالة ترتيب الوحدات السكانية، يتم اختيار رقم 50 أولاً، ثم رقم 150، ثم رقم 250، وهكذا.
- يتم اختيار القيم من مجموعة بيانات غير متجانسة طبقيةالطريقة (الطبقية)، عندما يتم تقسيم السكان أولاً إلى مجموعات متجانسة يتم تطبيق الاختيار العشوائي أو الميكانيكي عليها.
- وهناك طريقة خاصة لأخذ العينات مسلسلالاختيار، حيث لا يختارون بشكل عشوائي أو ميكانيكي القيم الفردية، ولكن سلسلتهم (تسلسلات من رقم ما إلى رقم ما على التوالي)، والتي يتم من خلالها إجراء المراقبة المستمرة.
تعتمد جودة ملاحظات العينة أيضًا على نوع العينة: معادأو غير قابل للتكرار.في إعادة الاختياريتم إرجاع القيم الإحصائية أو سلاسلها المتضمنة في العينة إلى عامة السكان بعد استخدامها، مع وجود فرصة لإدراجها في عينة جديدة. علاوة على ذلك، فإن جميع القيم في عموم السكان لها نفس احتمالية إدراجها في العينة. اختيار لا يتكرريعني أن القيم الإحصائية أو سلسلتها المتضمنة في العينة لا تعود إلى عموم السكان بعد استخدامها، وبالتالي بالنسبة للقيم المتبقية للأخيرة يزداد احتمال إدراجها في العينة التالية.
يعطي أخذ العينات غير المتكررة نتائج أكثر دقة، وبالتالي يتم استخدامه في كثير من الأحيان. ولكن هناك حالات لا يمكن فيها تطبيقها (دراسة تدفقات الركاب، وطلب المستهلكين، وما إلى ذلك) ثم يتم إجراء الاختيار المتكرر.
21. الحد الأقصى لخطأ المعاينة، ومتوسط خطأ المعاينة، وإجراءات حسابها.
دعونا نفكر بالتفصيل في الطرق المذكورة أعلاه لتشكيل مجتمع العينة والأخطاء التمثيلية التي تنشأ. عشوائية بشكل صحيحتعتمد عملية أخذ العينات على اختيار وحدات من المجتمع بشكل عشوائي دون أي عناصر منهجية. من الناحية الفنية، يتم الاختيار العشوائي الفعلي عن طريق القرعة (على سبيل المثال، اليانصيب) أو باستخدام جدول أرقام عشوائية.
ونادرا ما يستخدم الاختيار العشوائي السليم “في شكله النقي” في ممارسة الملاحظة الانتقائية، ولكنه الأصل بين أنواع الاختيار الأخرى، فهو يطبق المبادئ الأساسية للملاحظة الانتقائية. دعونا نفكر في بعض الأسئلة المتعلقة بنظرية طريقة أخذ العينات وصيغة الخطأ لعينة عشوائية بسيطة.
أخذ العينات التحيز- ϶ᴛᴏ الفرق بين قيمة المعلمة في عموم السكان وقيمتها المحسوبة من نتائج ملاحظة العينة. ومن المهم ملاحظة أنه بالنسبة للخاصية الكمية المتوسطة، يتم تحديد خطأ أخذ العينات
يُطلق على المؤشر عادةً اسم الحد الأقصى لخطأ أخذ العينات. متوسط العينة هو متغير عشوائي يمكن أن يأخذ قيمًا مختلفة بناءً على الوحدات المضمنة في العينة. ولذلك، فإن أخطاء أخذ العينات هي أيضًا متغيرات عشوائية ويمكن أن تأخذ قيمًا مختلفة. ولهذا السبب، يتم تحديد متوسط الأخطاء المحتملة - متوسط خطأ أخذ العينات، والذي يعتمد على:
· حجم العينة: كلما زاد العدد، قل متوسط الخطأ.
· درجة التغير في الخاصية محل الدراسة: كلما قل تباين الخاصية، وبالتالي التشتت، قل متوسط خطأ المعاينة.
في إعادة الاختيار العشوائييتم حساب متوسط الخطأ. من الناحية العملية، التباين العام غير معروف بالضبط، ولكن في نظرية الاحتمالات ثبت ذلك
. وبما أن قيمة n كبيرة بما فيه الكفاية قريبة من 1، يمكننا أن نفترض ذلك. ومن ثم ينبغي حساب متوسط خطأ المعاينة: . ولكن في حالات عينة صغيرة (مع ن<30) коэффициент крайне важно учитывать, и среднюю ошибку малой выборки рассчитывать по формуле 
.في أخذ العينات العشوائية غير التكراريةيتم تعديل الصيغ المعطاة بالقيمة. ومن ثم فإن متوسط خطأ أخذ العينات غير التكراري هو:
و 
. لأن دائمًا أقل من، فإن المضاعف () دائمًا أقل من 1. وهذا يعني أن متوسط الخطأ في الاختيار المتكرر يكون دائمًا أقل من التحديد المتكرر. أخذ العينات الميكانيكيةيتم استخدامه عندما يتم ترتيب إجمالي عدد السكان بطريقة ما (على سبيل المثال، قوائم الناخبين حسب الترتيب الأبجدي، وأرقام الهواتف، وأرقام المنازل والشقق). ويتم اختيار الوحدات على فترات زمنية معينة، وهي تساوي القيمة العكسية لنسبة أخذ العينات. لذا، مع عينة 2%، يتم اختيار كل 50 وحدة = 1/0.02، مع عينة 5%، كل 1/0.05 = 20 وحدة من عموم السكان.يتم تحديد النقطة المرجعية بطرق مختلفة: بشكل عشوائي، من منتصف الفاصل الزمني، مع تغيير النقطة المرجعية. الشيء الرئيسي هو تجنب الخطأ المنهجي. على سبيل المثال، في عينة 5%، إذا كانت الوحدة الأولى هي الثالثة عشر، فإن الوحدات التالية هي 33، 53، 73، إلخ.
من حيث الدقة، فإن الاختيار الميكانيكي قريب من أخذ العينات العشوائية الفعلية. ولهذا السبب، لتحديد متوسط الخطأ في أخذ العينات الميكانيكية، يتم استخدام صيغ الاختيار العشوائي المناسبة.
في اختيار نموذجييتم تقسيم السكان الذين يتم استطلاعهم بشكل مبدئي إلى مجموعات متجانسة ومتشابهة. على سبيل المثال، عند مسح المؤسسات، هذه هي الصناعات أو القطاعات الفرعية؛ عند دراسة السكان، هذه هي المناطق أو الفئات الاجتماعية أو العمرية. بعد ذلك، يتم إجراء اختيار مستقل من كل مجموعة آليًا أو عشوائيًا تمامًا.
يؤدي أخذ العينات النموذجي إلى نتائج أكثر دقة من الطرق الأخرى. تضمن كتابة المجتمع العام تمثيل كل مجموعة نمطية في العينة، مما يلغي تأثير التباين بين المجموعات على متوسط خطأ أخذ العينات. لذلك، عند العثور على خطأ عينة نموذجية وفقًا لقاعدة إضافة التباينات ()، من المهم للغاية أن نأخذ في الاعتبار متوسط تباينات المجموعة فقط. ثم متوسط خطأ العينة: مع أخذ العينات المتكررة، مع أخذ العينات غير المتكررة
، أين 
- متوسط التباينات داخل المجموعة في العينة.اختيار المسلسل (أو العش).يستخدم عندما يتم تقسيم السكان إلى سلاسل أو مجموعات قبل بدء مسح العينة. تشمل هذه السلسلة تغليف المنتجات النهائية ومجموعات الطلاب والألوية. يتم اختيار السلاسل للفحص ميكانيكياً أو عشوائياً بحتاً، وضمن السلاسل يتم إجراء فحص مستمر للوحدات. ولهذا السبب، يعتمد متوسط خطأ أخذ العينات فقط على التباين بين المجموعات (بين السلاسل)، والذي يتم حسابه باستخدام الصيغة:
حيث r هو عدد السلاسل المحددة؛ – متوسط السلسلة i-th. يتم حساب متوسط خطأ أخذ العينات التسلسلية: مع أخذ العينات المتكررة، مع أخذ العينات غير المتكررة 
حيث R هو العدد الإجمالي للسلسلة. مجموعالاختيار هو مزيج من طرق الاختيار المدروسة.يعتمد متوسط خطأ أخذ العينات لأي طريقة أخذ عينات بشكل أساسي على الحجم المطلق للعينة، وبدرجة أقل، على النسبة المئوية للعينة. لنفترض أنه تم إجراء 225 ملاحظة في الحالة الأولى من عدد سكان يبلغ 4500 وحدة وفي الحالة الثانية من عدد سكان يبلغ 225000 وحدة. التباينات في كلتا الحالتين تساوي 25. ففي الحالة الأولى، مع اختيار 5%، سيكون خطأ المعاينة:
في الحالة الثانية، مع اختيار 0.1%، سيكون مساوياً لـ:
ومع ذلك، عندما تم تخفيض نسبة أخذ العينات بمقدار 50 مرة، زاد خطأ أخذ العينات قليلاً، لأن حجم العينة لم يتغير. لنفترض أن حجم العينة قد زاد إلى 625 ملاحظة. وفي هذه الحالة يكون خطأ أخذ العينات كما يلي: 
إن زيادة العينة بمقدار 2.8 مرة بنفس حجم السكان يقلل من حجم خطأ العينة بأكثر من 1.6 مرة.22. طرق وأساليب تكوين مجتمع العينة.
في الإحصاء، يتم استخدام طرق مختلفة لتشكيل مجتمعات العينة، والتي تحددها أهداف الدراسة وتعتمد على تفاصيل موضوع الدراسة.
الشرط الأساسي لإجراء مسح العينة هو منع حدوث الأخطاء المنهجية التي تنشأ نتيجة مخالفة مبدأ تكافؤ الفرص لكل وحدة من عموم السكان المراد تضمينهم في العينة. يتم تحقيق الوقاية من الأخطاء المنهجية نتيجة لاستخدام الأساليب العلمية لتشكيل مجتمع العينة.
هناك الطرق التالية لاختيار الوحدات من عامة السكان: 1) الاختيار الفردي - يتم اختيار الوحدات الفردية للعينة؛ 2) اختيار المجموعة - تتضمن العينة مجموعات متجانسة نوعيا أو سلسلة من الوحدات قيد الدراسة؛ 3) الاختيار المشترك هو مزيج من الاختيار الفردي والجماعي. يتم تحديد طرق الاختيار من خلال قواعد تشكيل عينة السكان.
يجب أن تكون العينة:
- عشوائية في الواقعيتمثل في حقيقة أن مجتمع العينة يتكون نتيجة الاختيار العشوائي (غير المقصود) للوحدات الفردية من عامة السكان. وفي هذه الحالة، عادة ما يتم تحديد عدد الوحدات المختارة في مجتمع العينة على أساس نسبة العينة المقبولة. نسبة العينة هي نسبة عدد الوحدات في مجتمع العينة n إلى عدد الوحدات في عموم السكان N، ᴛ.ᴇ.
- ميكانيكييتكون من حقيقة أن اختيار الوحدات في عينة السكان يتم من عامة السكان، مقسمة إلى فترات متساوية (مجموعات). وفي هذه الحالة، يكون حجم الفاصل الزمني في المجتمع يساوي مقلوب حصة العينة. لذلك، مع عينة 2%، يتم اختيار كل وحدة 50 (1:0.02)، مع عينة 5%، كل وحدة 20 (1:0.05)، إلخ. ومع ذلك، وفقًا لنسبة الاختيار المقبولة، يتم تقسيم عامة السكان ميكانيكيًا إلى مجموعات متساوية. ويتم اختيار وحدة واحدة فقط من كل مجموعة للعينة.
- عادي -حيث يتم تقسيم عامة السكان أولاً إلى مجموعات نموذجية متجانسة. بعد ذلك، من كل مجموعة نموذجية، يتم استخدام عينة عشوائية أو ميكانيكية بحتة لاختيار الوحدات بشكل فردي في مجتمع العينة. من السمات المهمة للعينة النموذجية أنها تعطي نتائج أكثر دقة مقارنة بالطرق الأخرى لاختيار الوحدات في مجتمع العينة؛
- مسلسل- حيث يتم تقسيم عامة السكان إلى مجموعات متساوية الحجم - سلسلة. يتم اختيار السلسلة في عينة السكان. ضمن السلسلة، يتم إجراء المراقبة المستمرة للوحدات المتضمنة في السلسلة؛
- مجموع- يجب أن يتم أخذ العينات على مرحلتين. في هذه الحالة، يتم تقسيم السكان أولا إلى مجموعات. بعد ذلك، يتم اختيار المجموعات، وضمن الأخيرة يتم اختيار الوحدات الفردية.
في الإحصاء، يتم تمييز الطرق التالية لاختيار الوحدات في عينة السكان:
- مرحلة واحدةأخذ العينات - تتم دراسة كل وحدة مختارة على الفور وفقا لمعيار معين (أخذ العينات العشوائية والتسلسلية المناسبة)؛
- متعدد المراحلأخذ العينات - يتم الاختيار من إجمالي عدد السكان للمجموعات الفردية، ويتم اختيار الوحدات الفردية من المجموعات (أخذ عينات نموذجية بطريقة ميكانيكية لاختيار الوحدات في مجتمع العينة).
بالإضافة إلى ذلك، هناك:
- إعادة الاختيار- حسب مخطط الكرة المرتجعة. في هذه الحالة، يتم إرجاع كل وحدة أو سلسلة مدرجة في العينة إلى عامة السكان، وبالتالي يكون لديها فرصة لإدراجها في العينة مرة أخرى؛
- اختيار غير متكرر- حسب مخطط الكرة غير المرتجعة. لديها نتائج أكثر دقة بنفس حجم العينة.
23. تحديد حجم العينة المهم للغاية (باستخدام جدول t الخاص بالطالب).
أحد المبادئ العلمية في نظرية أخذ العينات هو التأكد من اختيار عدد كاف من الوحدات. من الناحية النظرية، يتم عرض الأهمية القصوى لمراعاة هذا المبدأ في إثباتات نظريات الحد في نظرية الاحتمالات، والتي تجعل من الممكن تحديد حجم الوحدات التي ينبغي اختيارها من السكان بحيث تكون كافية وتضمن تمثيل العينة.
إن الانخفاض في خطأ أخذ العينات القياسي، وبالتالي زيادة دقة التقدير، يرتبط دائمًا بزيادة في حجم العينة، لذلك، في مرحلة تنظيم مراقبة العينة، من الضروري تحديد الحجم من مجتمع العينة لضمان الدقة المطلوبة لنتائج المراقبة. يتم حساب حجم العينة المهم للغاية باستخدام صيغ مشتقة من صيغ الحد الأقصى لأخطاء أخذ العينات (A)، التي تتوافق مع نوع معين وطريقة اختيار معينة. لذلك، بالنسبة لحجم العينة العشوائي المتكرر (n) لدينا:
جوهر هذه الصيغة هو أنه مع أخذ العينات العشوائية المتكررة لأرقام مهمة للغاية، يتناسب حجم العينة بشكل مباشر مع مربع معامل الثقة (ت2)وتباين الخاصية التباينية (?2) ويتناسب عكسياً مع مربع الحد الأقصى لخطأ المعاينة (?2). وعلى وجه الخصوص، مع زيادة الحد الأقصى للخطأ بعامل اثنين، ينبغي تقليل حجم العينة المطلوب بعامل أربعة. من بين المعلمات الثلاثة، تم تعيين اثنين (t و؟) من قبل الباحث. وفي الوقت نفسه، يعتمد الباحث على الهدف
ويجب أن تحل مشاكل المسح بالعينة السؤال: في أي مجموعة كمية من الأفضل تضمين هذه المعلمات لضمان الخيار الأمثل؟ في إحدى الحالات، قد يكون راضيًا عن موثوقية النتائج التي تم الحصول عليها (t) أكثر من رضاه عن مقياس الدقة (؟)، وفي حالة أخرى - والعكس صحيح. من الصعب حل المشكلة المتعلقة بقيمة الحد الأقصى لخطأ المعاينة، حيث لا يتوفر لدى الباحث هذا المؤشر في مرحلة تصميم ملاحظة العينة، لذلك من الناحية العملية، من المعتاد تحديد قيمة الحد الأقصى لخطأ المعاينة؛ ، عادةً في حدود 10% من متوسط المستوى المتوقع للسمة. يمكن الوصول إلى تحديد المتوسط المقدر بطرق مختلفة: استخدام بيانات من مسوحات مماثلة أجريت سابقًا، أو استخدام بيانات من إطار أخذ العينات وإجراء عينة تجريبية صغيرة.
إن أصعب شيء يمكن تحديده عند تصميم عينة الملاحظة هو المعلمة الثالثة في الصيغة (5.2) - تباين مجتمع العينة. وفي هذه الحالة، من المهم للغاية استخدام جميع المعلومات المتاحة للباحث، والتي تم الحصول عليها في المسوحات المماثلة والتجريبية السابقة.
تصبح مسألة تحديد حجم العينة المهم للغاية أكثر تعقيدًا إذا كان مسح العينة يتضمن دراسة العديد من خصائص وحدات المعاينة. في هذه الحالة، يكون متوسط مستويات كل من الخصائص وتنوعها، كقاعدة عامة، مختلفًا، وفي هذا الصدد، تحديد التباين في أي من الخصائص التي يجب تفضيلها لا يمكن تحقيقه إلا مع مراعاة الغرض والأهداف من المسح.
عند تصميم عينة الملاحظة، يتم افتراض قيمة محددة مسبقًا لخطأ العينة المسموح به وفقًا لأهداف دراسة معينة واحتمالية الاستنتاجات بناءً على نتائج الملاحظة.
بشكل عام، تسمح لنا صيغة الحد الأقصى للخطأ في متوسط العينة بتحديد:
‣‣‣ حجم الانحرافات المحتملة لمؤشرات عموم السكان عن مؤشرات عينة السكان؛
‣‣‣ حجم العينة المطلوب لضمان الدقة المطلوبة، بحيث لا تتجاوز حدود الخطأ المحتمل قيمة محددة معينة؛
‣‣‣ احتمال أن يكون للخطأ في العينة حد معين.
توزيع الطلابفي نظرية الاحتمالات، هي عائلة ذات معلمة واحدة من التوزيعات المستمرة تمامًا.
24. المتسلسلة الديناميكية (الفاصل الزمني، العزم)، المتسلسلة الديناميكية الختامية.
سلسلة ديناميات- هذه هي قيم المؤشرات الإحصائية التي يتم تقديمها بتسلسل زمني معين.
تحتوي كل سلسلة زمنية على عنصرين:
1) مؤشرات الفترات الزمنية(السنوات أو الأرباع أو الأشهر أو الأيام أو التواريخ)؛
2) المؤشرات التي تميز الكائن قيد الدراسةلفترات زمنية أو في التواريخ المقابلة، والتي تسمى مستويات السلسلة.
يتم التعبير عن مستويات السلسلة بالقيم المطلقة والمتوسطة أو النسبية. مع الأخذ في الاعتبار الاعتماد على طبيعة المؤشرات، يتم بناء سلسلة ديناميكية من القيم المطلقة والنسبية والمتوسطة. يتم إنشاء سلسلة ديناميكية من القيم النسبية والمتوسطة على أساس سلسلة مشتقة من القيم المطلقة. هناك سلسلة زمنية ولحظية من الديناميكيات.
سلسلة الفاصل الديناميكييحتوي على قيم المؤشرات لفترات زمنية معينة. وفي سلسلة فواصل زمنية يمكن جمع المستويات للحصول على حجم الظاهرة على مدى فترة أطول، أو ما يسمى بالمجاميع المتراكمة.
سلسلة اللحظات الديناميكيةيعكس قيم المؤشرات في وقت معين (التاريخ الزمني). وفي المتسلسلة العزومية قد يهتم الباحث فقط باختلاف الظواهر التي تعكس التغير في مستوى المتسلسلة بين تواريخ معينة، حيث أن مجموع المستويات هنا ليس له محتوى حقيقي. لا يتم احتساب المجاميع التراكمية هنا.
الشرط الأكثر أهمية لبناء السلاسل الزمنية بشكل صحيح هو مقارنة مستويات السلسلةتنتمي إلى فترات مختلفة. ويجب تقديم المستويات بكميات متجانسة، كما يجب أن يكون هناك اكتمال متساوي لتغطية الأجزاء المختلفة من الظاهرة.
من أجل تجنب تشويه الديناميكيات الحقيقية، يتم إجراء الحسابات الأولية في البحث الإحصائي (إغلاق سلسلة الديناميكيات)، التي تسبق التحليل الإحصائي للسلسلة الزمنية. تحت إغلاق سلسلة الديناميكياتمن المقبول عمومًا فهم المجموعة في سلسلة واحدة من سلسلتين أو أكثر، والتي يتم حساب مستوياتها باستخدام منهجية مختلفة أو لا تتوافق مع الحدود الإقليمية، وما إلى ذلك. قد يعني إغلاق سلسلة الديناميكيات أيضًا جلب المستويات المطلقة لسلسلة الديناميكيات إلى أساس مشترك، مما يحيد عدم إمكانية المقارنة بين مستويات سلسلة الديناميكيات.
25. مفهوم المقارنة بين سلاسل الديناميكيات والمعاملات والنمو ومعدلات النمو.
سلسلة ديناميات- هذه سلسلة من المؤشرات الإحصائية التي تميز تطور الظواهر الطبيعية والاجتماعية مع مرور الوقت. تحتوي المجموعات الإحصائية التي نشرتها لجنة الدولة للإحصاء في روسيا على عدد كبير من سلاسل الديناميكيات في شكل جدول. تتيح السلسلة الديناميكية تحديد أنماط تطور الظواهر قيد الدراسة.
تحتوي سلسلة الديناميكيات على نوعين من المؤشرات. مؤشرات الوقت(سنوات، أرباع، أشهر، إلخ) أو نقاط زمنية (في بداية العام، في بداية كل شهر، إلخ). مؤشرات مستوى الصف. يمكن التعبير عن مؤشرات مستويات سلسلة الديناميكيات بالقيم المطلقة (إنتاج المنتجات بالطن أو الروبل)، والقيم النسبية (حصة سكان الحضر بنسبة٪) والقيم المتوسطة (متوسط راتب العاملين في الصناعة حسب السنة ، إلخ.). في شكل جدول، تحتوي السلسلة الزمنية على عمودين أو صفين.
يتطلب البناء الصحيح للسلاسل الزمنية استيفاء عدد من المتطلبات:
- يجب أن تكون جميع مؤشرات عدد من الديناميكيات مدعومة بأدلة علمية وموثوقة؛
- يجب أن تكون مؤشرات سلسلة الديناميكيات قابلة للمقارنة مع مرور الوقت. يجب أن يتم حسابها لنفس الفترات الزمنية أو في نفس التواريخ؛
- ويجب أن تكون مؤشرات عدد من الديناميكيات قابلة للمقارنة في جميع أنحاء الإقليم؛
- يجب أن تكون مؤشرات سلسلة الديناميكيات قابلة للمقارنة في المحتوى. وتحسب وفق منهجية واحدة وبنفس الطريقة؛
- وينبغي أن تكون مؤشرات عدد من الديناميكيات قابلة للمقارنة عبر نطاق المزارع التي تؤخذ في الاعتبار. يجب إعطاء جميع مؤشرات سلسلة الديناميكيات في نفس وحدات القياس.
يمكن للمؤشرات الإحصائية أن تميز إما نتائج العملية قيد الدراسة على مدى فترة من الزمن، أو حالة الظاهرة قيد الدراسة في وقت معين، ᴛ.ᴇ. يمكن أن تكون المؤشرات فاصلة (دورية) ولحظية. وبناء على ذلك، في البداية تكون سلسلة الديناميكيات إما فاصلة أو لحظة. تأتي سلسلة ديناميكيات العزوم بدورها بفترات زمنية متساوية وغير متساوية.
يمكن تحويل سلسلة الديناميكيات الأصلية إلى سلسلة من القيم المتوسطة وسلسلة من القيم النسبية (السلسلة والأساسية). تسمى هذه السلاسل الزمنية بالسلاسل الزمنية المشتقة.
تختلف منهجية حساب المستوى المتوسط في السلسلة الديناميكية اعتمادًا على نوع السلسلة الديناميكية. باستخدام الأمثلة، سننظر في أنواع السلاسل الديناميكية والصيغ لحساب المستوى المتوسط.
الزيادات المطلقة (Δy) أظهر عدد الوحدات التي تغير فيها المستوى اللاحق للسلسلة مقارنة بالمستوى السابق (gr. 3. - الزيادات المطلقة للسلسلة) أو مقارنة بالمستوى الأولي (gr. 4. - الزيادات المطلقة الأساسية). يمكن كتابة صيغ الحساب على النحو التالي:
عندما تنخفض القيم المطلقة للسلسلة، سيكون هناك "نقصان" أو "نقصان"، على التوالي.
وتشير مؤشرات النمو المطلقة إلى ذلك، على سبيل المثال، في عام 1998. زاد إنتاج المنتج "أ" مقارنة بعام 1997. بمقدار 4 آلاف طن، مقارنة بعام 1994ᴦ. - بمقدار 34 ألف طن؛ لسنوات أخرى، انظر الجدول. 11.5 جرام.
نشر على المرجع.rf
3 و 4.معدل النمويوضح عدد المرات التي تغير فيها مستوى السلسلة مقارنة بالمستوى السابق (جرام 5 - معاملات السلسلة للنمو أو الانخفاض) أو مقارنة بالمستوى الأولي (جرام 6 - المعاملات الأساسية للنمو أو الانخفاض). يمكن كتابة صيغ الحساب على النحو التالي:
معدلات النموأظهر النسبة المئوية للمستوى التالي من السلسلة مقارنة بالمستوى السابق (جرام 7 - معدلات نمو السلسلة) أو مقارنة بالمستوى الأولي (جرام 8 - معدلات النمو الأساسية). يمكن كتابة صيغ الحساب على النحو التالي:
لذلك، على سبيل المثال، في عام 1997. حجم إنتاج المنتج "أ" مقارنة بعام 1996 ᴦ. بلغت 105.5% (
معدل النموأظهر النسبة المئوية التي ارتفع بها مستوى الفترة المشمولة بالتقرير مقارنة بالمستوى السابق (العمود 9 - معدلات نمو السلسلة) أو مقارنة بالمستوى الأولي (العمود 10 - معدلات النمو الأساسية). يمكن كتابة صيغ الحساب على النحو التالي:
T pr = T r - 100% أو T pr = النمو المطلق / مستوى الفترة السابقة * 100%
لذلك، على سبيل المثال، في عام 1996. مقارنة بعام 1995 ᴦ. تم إنتاج المنتج "أ" بنسبة 3.8% (103.8% - 100%) أو (8:210)×100%، مقارنة بعام 1994. - بنسبة 9% (109% – 100%).
إذا انخفضت المستويات المطلقة في السلسلة، فإن المعدل سيكون أقل من 100٪، وبالتالي سيكون هناك معدل النقصان (معدل الزيادة مع علامة الطرح).
القيمة المطلقة للزيادة 1%(غرام.
نشر على المرجع.rf
11) يوضح عدد الوحدات المطلوب إنتاجها في فترة معينة بحيث يرتفع مستوى الفترة السابقة بنسبة 1%. في مثالنا، في عام 1995 ᴦ. كان من الضروري إنتاج 2.0 ألف طن، وفي عام 1998 ᴦ. - 2.3 ألف طن ᴛ.ᴇ. أكبر بكثير.يمكن تحديد القيمة المطلقة للنمو بنسبة 1% بطريقتين:
§ مستوى الفترة السابقة مقسوما على 100؛
§ الزيادات المطلقة في السلسلة تقسم على معدلات نمو السلسلة المقابلة لها.
القيمة المطلقة للزيادة 1% =
في الديناميكيات، خاصة على مدى فترة طويلة، من المهم إجراء تحليل مشترك لمعدل النمو مع محتوى كل نسبة زيادة أو نقصان.
لاحظ أن المنهجية المدروسة لتحليل السلاسل الزمنية تنطبق على السلاسل الزمنية، التي يتم التعبير عن مستوياتها بالقيم المطلقة (ر، ألف روبل، عدد الموظفين، وما إلى ذلك)، وعلى السلاسل الزمنية، مستوياتها يتم التعبير عنها بمؤشرات نسبية (% من العيوب، % من محتوى الرماد في الفحم، وما إلى ذلك) أو القيم المتوسطة (متوسط العائد بالسنتيمتر/هكتار، متوسط الراتب، وما إلى ذلك).
إلى جانب المؤشرات التحليلية المدروسة، والتي يتم حسابها لكل عام مقارنة بالمستوى السابق أو الأولي، عند تحليل سلسلة الديناميكيات، من المهم للغاية حساب متوسط المؤشرات التحليلية للفترة: متوسط مستوى السلسلة، المتوسط السنوي المطلق الزيادة (النقصان) ومتوسط معدل النمو السنوي ومعدل النمو.
تمت مناقشة طرق حساب المستوى المتوسط لسلسلة من الديناميكيات أعلاه. في سلسلة ديناميكيات الفاصل التي ندرسها، يتم حساب المستوى المتوسط للسلسلة باستخدام صيغة المتوسط الحسابي البسيط:
متوسط حجم الإنتاج السنوي للمنتج للأعوام 1994-1998. بلغت 218.4 ألف طن.
ويتم حساب متوسط النمو المطلق السنوي أيضًا باستخدام صيغة المتوسط الحسابي
الانحراف المعياري - المفهوم والأنواع. تصنيف ومميزات فئة "متوسط انحراف مربع" 2017، 2018.
الدرس رقم 4
الموضوع: "الإحصاء الوصفي. مؤشرات تنوع السمات في المجموع "
المعايير الرئيسية لتنوع الخاصية في مجتمع إحصائي هي: الحد والسعة والانحراف المعياري ومعامل التذبذب ومعامل الاختلاف. تمت مناقشة في الدرس السابق أن القيم المتوسطة توفر فقط خاصية عامة للخاصية التي تتم دراستها بشكل إجمالي ولا تأخذ في الاعتبار قيم متغيراتها الفردية: القيم الدنيا والقصوى، فوق المتوسط، أدناه متوسط، الخ.
مثال. متوسط قيم تسلسلين رقميين مختلفين: -100؛ -20؛ 100؛ 20 و 0.1؛ -0.2; 0.1 متطابقان ومتساويان تمامًاعن.ومع ذلك، فإن النطاقات المتناثرة لبيانات التسلسل المتوسط النسبي مختلفة جدًا.
يتم تحديد المعايير المدرجة لتنوع الخاصية في المقام الأول مع مراعاة قيمتها في العناصر الفردية للمجتمع الإحصائي.
مؤشرات لقياس تباين السمة هي مطلقو نسبي. تشمل مؤشرات التباين المطلقة: مدى التباين، الحد، الانحراف المعياري، التشتت. يشير معامل التباين ومعامل التذبذب إلى المقاييس النسبية للتباين.
الحد (ليم) –هذا معيار يتم تحديده من خلال القيم المتطرفة للمتغير في سلسلة التباين. بمعنى آخر، يقتصر هذا المعيار على الحد الأدنى والحد الأقصى لقيم السمة:
السعة (صباحا)أو نطاق التباين -هذا هو الفرق بين الخيارات المتطرفة. يتم حساب هذا المعيار عن طريق طرح الحد الأدنى لقيمته من الحد الأقصى لقيمة السمة، مما يسمح لنا بتقدير درجة تشتت الخيار:
عيب الحد والسعة كمعايير للتباين هو أنها تعتمد بشكل كامل على القيم المتطرفة للخاصية في سلسلة التباين. في هذه الحالة، لا تؤخذ في الاعتبار التقلبات في قيم السمات داخل السلسلة.
يتم توفير الوصف الأكثر اكتمالا لتنوع السمات في مجتمع إحصائي بواسطة الانحراف المعياري(سيجما)، وهو مقياس عام لانحراف الخيار عن قيمته المتوسطة. غالبا ما يسمى الانحراف المعياري الانحراف المعياري.
يعتمد الانحراف المعياري على مقارنة كل خيار بالمتوسط الحسابي لمجموعة سكانية معينة. نظرًا لأنه في المجموع سيكون هناك دائمًا خيارات أقل وأكثر منه، سيتم إلغاء مجموع الانحرافات بعلامة "" من خلال مجموع الانحرافات بعلامة ""، أي. مجموع كل الانحرافات هو صفر. ومن أجل تجنب تأثير علامات الفروق، يتم أخذ الانحرافات عن الوسط الحسابي التربيعي، أي. . مجموع الانحرافات التربيعية لا يساوي الصفر. للحصول على معامل يمكنه قياس التباين، خذ متوسط مجموع المربعات - تسمى هذه القيمة الفروق:
في جوهرها، التشتت هو متوسط مربع انحرافات القيم الفردية للخاصية عن قيمتها المتوسطة. تشتت – مربع الانحراف المعياري .
التباين هو كمية الأبعاد (المسمى). لذا، إذا تم التعبير عن متغيرات سلسلة الأرقام بالأمتار، فإن التباين يعطي أمتارًا مربعة؛ إذا تم التعبير عن الخيارات بالكيلوجرام، فإن التباين يعطي مربع هذا القياس (كجم 2)، وما إلى ذلك.
الانحراف المعياري– الجذر التربيعي للتباين :
ثم عند حساب التشتت والانحراف المعياري في مقام الكسر بدلاً من ذلكيجب أن توضع.
يمكن تقسيم حساب الانحراف المعياري إلى ست مراحل يجب تنفيذها بتسلسل معين:
تطبيق الانحراف المعياري:
أ) للحكم على تباين سلسلة التباين والتقييم المقارن لنموذجية (تمثيلية) المتوسطات الحسابية. وهذا ضروري في التشخيص التفريقي عند تحديد استقرار الأعراض.
ب) لإعادة بناء سلسلة الاختلاف، أي. استعادة استجابة التردد على أساس قواعد سيجما الثلاثة. في الفاصل (م ± 3σ) 99.7% من جميع متغيرات السلسلة تقع في الفاصل الزمني (م ± 2σ) - 95.5% وفي المدى (م ± 1σ) - 68.3% متغير الصف(رسم بياني 1).
ج) لتحديد الخيارات "المنبثقة".
د) لتحديد معالم القاعدة وعلم الأمراض باستخدام تقديرات سيجما
ه) لحساب معامل الاختلاف
و) لحساب متوسط خطأ الوسط الحسابي.
لتوصيف أي مجموعة سكانية لديهانوع التوزيع الطبيعي يكفي معرفة معلمتين: الوسط الحسابي والانحراف المعياري.
الشكل 1. قاعدة ثلاثة سيجما
مثال.
في طب الأطفال، يتم استخدام الانحراف المعياري لتقييم النمو البدني للأطفال من خلال مقارنة بيانات طفل معين مع المؤشرات القياسية المقابلة. يتم أخذ المتوسط الحسابي للنمو البدني للأطفال الأصحاء كمعيار. تتم مقارنة المؤشرات بالمعايير باستخدام جداول خاصة يتم فيها تقديم المعايير جنبًا إلى جنب مع مقاييس سيجما المقابلة لها. من المعتقد أنه إذا كان مؤشر النمو الجسدي للطفل ضمن المعيار (المتوسط الحسابي) ±σ، فإن النمو الجسدي للطفل (وفقًا لهذا المؤشر) يتوافق مع القاعدة. إذا كان المؤشر ضمن المعيار ±2σ، فسيكون هناك انحراف طفيف عن المعيار. إذا تجاوز المؤشر هذه الحدود، فإن النمو البدني للطفل يختلف بشكل حاد عن القاعدة (علم الأمراض ممكن).
بالإضافة إلى مؤشرات التباين المعبر عنها بالقيم المطلقة، يستخدم البحث الإحصائي مؤشرات التباين المعبر عنها بالقيم النسبية. معامل التذبذب -هذه هي نسبة نطاق التباين إلى متوسط قيمة السمة. معامل الاختلاف -هذه هي نسبة الانحراف المعياري إلى متوسط قيمة الخاصية. عادة، يتم التعبير عن هذه القيم كنسب مئوية.
صيغ حساب مؤشرات التباين النسبي:
من الصيغ المذكورة أعلاه يتضح أنه كلما زاد المعامل الخامس كلما كان أقرب إلى الصفر، كلما كان التباين في قيم الخاصية أصغر. الاكثر الخامسكلما كانت العلامة أكثر تنوعًا.
في الممارسة الإحصائية، غالبا ما يستخدم معامل الاختلاف. يتم استخدامه ليس فقط للتقييم المقارن للتباين، ولكن أيضًا لتوصيف تجانس السكان. ويعتبر السكان متجانسين إذا كان معامل التباين لا يتجاوز 33% (للتوزيعات القريبة من الطبيعي). من الناحية الحسابية، فإن نسبة σ والوسط الحسابي تحيد تأثير القيمة المطلقة لهذه الخصائص، والنسبة المئوية تجعل معامل التباين قيمة بلا أبعاد (غير مسماة).
يتم تقدير القيمة الناتجة لمعامل التباين وفقًا للتدرجات التقريبية لدرجة تنوع السمة:
ضعيف - يصل إلى 10٪
متوسط - 10 - 20%
قوي - أكثر من 20٪
يُنصح باستخدام معامل الاختلاف في الحالات التي يكون فيها من الضروري مقارنة الخصائص المختلفة في الحجم والأبعاد.
يظهر بوضوح الفرق بين معامل التباين ومعايير الانتثار الأخرى مثال.
الجدول 1
تكوين العاملين في المؤسسات الصناعية
واستنادا إلى الخصائص الإحصائية الواردة في المثال، يمكننا استخلاص استنتاج حول التجانس النسبي للتركيبة العمرية والمستوى التعليمي لموظفي المؤسسة، نظرا لانخفاض الاستقرار المهني للمجموعة التي شملتها الدراسة. ومن السهل أن نرى أن محاولة الحكم على هذه الاتجاهات الاجتماعية من خلال الانحراف المعياري من شأنه أن يؤدي إلى نتيجة خاطئة، كما أن محاولة مقارنة الخصائص المحاسبية "الخبرة العملية" و"العمر" مع المؤشر المحاسبي "التعليم" ستكون عمومًا أمرًا خاطئًا. غير صحيحة بسبب عدم تجانس هذه الخصائص.
الوسيط والنسب المئوية
بالنسبة للتوزيعات الترتيبية (الرتبة)، حيث يكون معيار منتصف السلسلة هو الوسيط، لا يمكن أن يكون الانحراف المعياري والتشتت بمثابة خصائص لتشتت المتغير.
وينطبق الشيء نفسه على سلسلة التباين المفتوحة. ويرجع هذا الظرف إلى حقيقة أن الانحرافات التي يتم حساب التباين وσ منها يتم قياسها من الوسط الحسابي، الذي لا يتم حسابه في سلسلة التباين المفتوحة وفي سلسلة توزيعات الخصائص النوعية. لذلك، للحصول على وصف مضغوط للتوزيعات، يتم استخدام معلمة مبعثرة أخرى - الكمية(مرادف - "المئوي")، مناسب لوصف الخصائص النوعية والكمية في أي شكل من أشكال توزيعها. يمكن أيضًا استخدام هذه المعلمة لتحويل الخصائص الكمية إلى خصائص نوعية. في هذه الحالة، يتم تعيين هذه التصنيفات اعتمادًا على الترتيب الكمي الذي يتوافق معه خيار معين.
في ممارسة البحوث الطبية الحيوية، يتم استخدام الكميات التالية في أغلب الأحيان:
- الوسيط؛
، - الربعيات (الأرباع)، حيث - الربع الأدنى، – الربع الأعلى.
تقسم الكميات مساحة التغييرات المحتملة في سلسلة التباين إلى فترات زمنية معينة. الوسيط (الكمي) هو خيار يقع في منتصف سلسلة التباين ويقسم هذه السلسلة إلى نصفين إلى جزأين متساويين ( 0,5 و 0,5 ). يقسم الربع السلسلة إلى أربعة أجزاء: الجزء الأول (الربيع السفلي) هو خيار يفصل بين الخيارات التي لا تتجاوز قيمها العددية 25% من الحد الأقصى الممكن في سلسلة معينة؛ ما يصل إلى 50٪ من الحد الأقصى الممكن. يفصل الربع العلوي () الخيارات بما يصل إلى 75% من الحد الأقصى للقيم الممكنة.
في حالة التوزيع غير المتماثل المتغير بالنسبة للوسط الحسابي، يتم استخدام الوسيط والرباعيات لتوصيفه.وفي هذه الحالة يتم استخدام النموذج التالي لعرض القيمة المتوسطة - مه (;). على سبيل المثال، السمة المدروسة - "الفترة التي بدأ فيها الطفل المشي بشكل مستقل" - لها توزيع غير متماثل في مجموعة الدراسة. في الوقت نفسه، يتوافق الربع السفلي () مع بداية المشي - 9.5 شهرا، المتوسط - 11 شهرا، الربع العلوي () - 12 شهرا. وبناء على ذلك، سيتم عرض خاصية الاتجاه المتوسط للسمة المحددة على أنها 11 (9.5؛ 12) شهرًا.
تقييم الأهمية الإحصائية لنتائج الدراسة
تُفهم الأهمية الإحصائية للبيانات على أنها درجة توافقها مع الواقع المعروض، أي. البيانات ذات الأهمية الإحصائية هي تلك التي لا تشوه الواقع الموضوعي وتعكسه بشكل صحيح.
إن تقييم الأهمية الإحصائية لنتائج البحث يعني تحديد احتمالية نقل النتائج التي تم الحصول عليها من عينة السكان إلى جميع السكان. من الضروري تقييم الأهمية الإحصائية لفهم مقدار الظاهرة التي يمكن استخدامها للحكم على الظاهرة ككل وأنماطها.
يتكون تقييم الأهمية الإحصائية لنتائج البحث من:
1. أخطاء التمثيل (أخطاء القيم المتوسطة والنسبية) - م;
2. حدود الثقة للقيم المتوسطة أو النسبية؛
3. ثبات الفرق في القيم المتوسطة أو النسبية حسب المعيار ر.
الخطأ المعياري للوسط الحسابيأو خطأ في التمثيليميز تقلبات المتوسط. وتجدر الإشارة إلى أنه كلما زاد حجم العينة، قل انتشار القيم المتوسطة. يتم حساب الخطأ المعياري للمتوسط باستخدام الصيغة:
في الأدبيات العلمية الحديثة، يتم كتابة الوسط الحسابي مع الخطأ التمثيلي:
أو مع الانحراف المعياري:
على سبيل المثال، خذ بعين الاعتبار البيانات المتعلقة بـ 1500 عيادة في المدينة (عموم السكان). ويبلغ متوسط عدد المرضى الذين تخدمهم العيادة 18,150 شخصًا. الاختيار العشوائي لـ 10% من المواقع (150 عيادة) يعطي متوسط عدد المرضى يساوي 20,051 شخصًا. من الواضح أن خطأ أخذ العينات يرجع إلى حقيقة أنه لم يتم تضمين جميع العيادات البالغ عددها 1500 في العينة، وهو يساوي الفرق بين هذه المتوسطات - المتوسط العام ( مالجين) ومتوسط العينة ( مالمحدد). إذا قمنا بتكوين عينة أخرى بنفس الحجم من مجتمعنا، فستعطي قيمة خطأ مختلفة. يتم توزيع جميع متوسطات العينة هذه، مع عينات كبيرة بما فيه الكفاية، بشكل طبيعي حول المتوسط العام مع وجود عدد كبير بما فيه الكفاية من تكرارات العينة لنفس العدد من العناصر من عموم السكان. الخطأ المعياري للمتوسط م- هذا هو الانتشار الحتمي لمتوسطات العينة حول المتوسط العام.
في حالة تقديم نتائج البحث بكميات نسبية (على سبيل المثال، النسب المئوية) - يتم حسابها الخطأ المعياري للكسر:
حيث P هو المؤشر بنسبة %، وn هو عدد الملاحظات.
يتم عرض النتيجة كما (ف ± م)٪. على سبيل المثال،وكانت نسبة الشفاء بين المرضى (95.2±2.5)%.
في حالة تعدد عناصر السكان، ثم عند حساب الأخطاء المعيارية للوسط والكسر في مقام الكسر، بدلا منيجب أن توضع.
بالنسبة للتوزيع الطبيعي (توزيع متوسطات العينة طبيعي)، فإننا نعرف أي جزء من السكان يقع ضمن أي فترة زمنية حول المتوسط. بخاصة:
ومن الناحية العملية، تكمن المشكلة في أن خصائص عامة السكان غير معروفة لنا، ويتم إجراء العينة بدقة بغرض تقديرها. وهذا يعني أنه إذا قمنا بعمل عينات من نفس الحجم نمن عامة السكان، ففي 68.3% من الحالات، سيحتوي الفاصل الزمني على القيمة م(في 95.5% من الحالات سيكون على الفاصل الزمني وفي 99.7% من الحالات – على الفاصل الزمني).
نظرًا لأنه تم أخذ عينة واحدة فقط بالفعل، فقد تمت صياغة هذا البيان من حيث الاحتمال: مع احتمال 68.3%، يقع متوسط قيمة السمة في المجتمع في الفاصل الزمني، مع احتمال 95.5% - في الفاصل الزمني الخ
من الناحية العملية، يتم إنشاء فاصل زمني حول قيمة العينة بحيث، مع وجود احتمالية معينة (عالية بما فيه الكفاية)، احتمال الثقة –سوف "يغطي" القيمة الحقيقية لهذه المعلمة في عموم السكان. يسمى هذا الفاصل فاصل الثقة.
احتمال الثقةص – هذه هي درجة الثقة بأن فاصل الثقة سيحتوي بالفعل على القيمة الحقيقية (غير المعروفة) للمعلمة في المجتمع.
على سبيل المثال، إذا كان احتمال الثقة رهي 90%، وهذا يعني أن 90 عينة من أصل 100 ستعطي التقدير الصحيح للمعلمة في المجتمع. وبناء على ذلك، فإن احتمال الخطأ، أي. تقدير غير صحيح للمعدل العام للعينة يساوي بالنسبة المئوية: . في هذا المثال، هذا يعني أن 10 عينات من أصل 100 ستعطي تقديرًا غير صحيح.
من الواضح أن درجة الثقة (احتمالية الثقة) تعتمد على حجم الفاصل الزمني: كلما اتسع الفاصل الزمني، زادت الثقة في أن قيمة غير معروفة للسكان ستقع فيه. ومن الناحية العملية، يتم استخدام ضعف خطأ أخذ العينات على الأقل لإنشاء فاصل ثقة لتوفير ثقة بنسبة 95.5% على الأقل.
يتيح لنا تحديد حدود الثقة للمتوسطات والقيم النسبية العثور على القيمتين المتطرفتين - الحد الأدنى الممكن والحد الأقصى الممكن، والذي يمكن أن يحدث من خلاله المؤشر المدروس في جميع السكان. بناء على هذا، حدود الثقة (أو فاصل الثقة)- هذه هي حدود القيم المتوسطة أو النسبية، والتي بعدها بسبب التقلبات العشوائية هناك احتمال ضئيل.
يمكن إعادة كتابة فترة الثقة على النحو التالي: ، أين ر- معيار الثقة.
يتم تحديد حدود الثقة للوسط الحسابي في المجتمع بالصيغة:
م الجين = م يختار + ر م م
للقيمة النسبية:
ر الجين = ص يختار + ر م ر
أين م الجينو ر الجين- القيم المتوسطة والنسبية لعامة السكان؛ م يختارو ر يختار- قيم المتوسط والقيم النسبية التي تم الحصول عليها من مجتمع العينة؛ م مو م ص- أخطاء القيم المتوسطة والنسبية؛ ر- معيار الثقة (معيار الدقة الذي يتم تحديده عند التخطيط للدراسة ويمكن أن يساوي 2 أو 3)؛ ر م- هذا هو فاصل الثقة أو Δ - الحد الأقصى لخطأ المؤشر الذي تم الحصول عليه في دراسة عينة.
وتجدر الإشارة إلى أن قيمة المعيار ريرتبط إلى حد ما باحتمالية التنبؤ الخالي من الأخطاء (p)، معبرًا عنه بنسبة٪. ويتم اختياره من قبل الباحث نفسه، مسترشداً بضرورة الحصول على النتيجة بالدرجة المطلوبة من الدقة. وبالتالي فإن احتمالية التنبؤ الخالي من الأخطاء تبلغ 95.5%، وتكون قيمة المعيار رهو 2، بنسبة 99.7% - 3.
تعتبر التقديرات المعطاة لفاصل الثقة مقبولة فقط بالنسبة للمجموعات الإحصائية التي يزيد عدد مشاهداتها عن 30. ومع حجم السكان الأصغر (عينات صغيرة)، يتم استخدام جداول خاصة لتحديد معيار t. في هذه الجداول، تقع القيمة المطلوبة عند تقاطع الخط المقابل لحجم السكان (ن-1)، وعمود يتوافق مع مستوى احتمالية التنبؤ الخالي من الأخطاء (95.5%، 99.7%) الذي اختاره الباحث. في الأبحاث الطبية، عند وضع حدود الثقة لأي مؤشر، فإن احتمالية التنبؤ الخالي من الأخطاء تبلغ 95.5% أو أكثر. وهذا يعني أن قيمة المؤشر الذي تم الحصول عليه من مجتمع العينة يجب أن تكون موجودة في عموم السكان في 95.5% على الأقل من الحالات.
أسئلة حول موضوع الدرس:
أهمية مؤشرات تنوع السمات في مجتمع إحصائي.
الخصائص العامة لمؤشرات التباين المطلق.
الانحراف المعياري، الحساب، التطبيق.
التدابير النسبية للاختلاف.
الوسيط، النتيجة الربعية.
تقييم الأهمية الإحصائية لنتائج الدراسة.
الخطأ المعياري للوسط الحسابي، صيغة الحساب، مثال للاستخدام.
حساب النسبة وخطأها المعياري.
مفهوم احتمالية الثقة، مثال للاستخدام.
10. مفهوم فترة الثقة وتطبيقها.
اختبار المهام حول الموضوع مع الإجابات القياسية:
1. المؤشرات المطلقة للاختلاف تشير إلى
1) معامل الاختلاف
2) معامل التذبذب
4) متوسط
2. المؤشرات النسبية للتغير تتعلق
1) التشتت
4) معامل الاختلاف
3. المعيار الذي يتم تحديده من خلال القيم القصوى لخيار في سلسلة متغيرة
2) السعة
3) التشتت
4) معامل الاختلاف
4. الفرق بين الخيارات المتطرفة هو
2) السعة
3) الانحراف المعياري
4) معامل الاختلاف
5. متوسط مربع انحرافات القيم الفردية لخاصية ما عن قيمها المتوسطة هو
1) معامل التذبذب
2) متوسط
3) التشتت
6. نسبة مقياس التباين إلى متوسط قيمة الشخصية هي
1) معامل الاختلاف
2) الانحراف المعياري
4) معامل التذبذب
7. نسبة متوسط الانحراف المربع إلى متوسط قيمة إحدى الخصائص هي
1) التشتت
2) معامل الاختلاف
3) معامل التذبذب
4) السعة
8. الخيار الذي يقع في منتصف سلسلة التنويع ويقسمها إلى جزأين متساويين هو
1) متوسط
3) السعة
9. في الأبحاث الطبية، عند وضع حدود الثقة لأي مؤشر، يتم قبول احتمالية التنبؤ الخالي من الأخطاء
10. إذا كانت 90 عينة من أصل 100 تعطي التقدير الصحيح للمعلمة في المجتمع، فهذا يعني أن احتمال الثقة صمتساوي
11. إذا أعطت 10 عينات من 100 تقديرًا غير صحيح، فإن احتمال الخطأ يكون متساويًا
12. حدود القيم المتوسطة أو النسبية، التي يكون تجاوزها بسبب التذبذبات العشوائية احتمالًا صغيرًا - هذا هو
1) فاصل الثقة
2) السعة
4) معامل الاختلاف
13. تعتبر عينة صغيرة من السكان
1) ن أقل من أو يساوي 100
2) ن أقل من أو يساوي 30
3) ن أقل من أو يساوي 40
4) ن قريب من 0
14. لاحتمالية التنبؤ الخالي من الأخطاء، قيمة المعيار 95% ريكون
15. لاحتمالية التنبؤ الخالي من الأخطاء 99% قيمة المعيار ريكون
16. بالنسبة للتوزيعات القريبة من التوزيع الطبيعي، يعتبر السكان متجانسين إذا لم يتجاوز معامل التباين
17. الخيار، الخيارات المنفصلة، التي لا تتجاوز قيمها العددية 25% من الحد الأقصى الممكن في سلسلة معينة - هذا هو
2) الربع الأدنى
3) الربع الأعلى
4) الربع
18. البيانات التي لا تشوه وتعكس الواقع الموضوعي بشكل صحيح تسمى
1) مستحيل
2) ممكن على قدم المساواة
3) موثوقة
4) عشوائية
19. وفقا لقاعدة "ثلاثة سيجما"، مع التوزيع الطبيعي للخاصية داخل
سوف يتم تحديد موقعه1) خيار 68.3%
التوقع والتباين
دعونا نقيس متغير عشوائي نمرات، على سبيل المثال، نقيس سرعة الرياح عشر مرات ونريد إيجاد القيمة المتوسطة. كيف ترتبط القيمة المتوسطة بوظيفة التوزيع؟
سنقوم برمي النرد عدد كبير من المرات. عدد النقاط التي ستظهر على حجر النرد مع كل رمية هو متغير عشوائي ويمكن أن يأخذ أي قيمة طبيعية من 1 إلى 6. والمتوسط الحسابي للنقاط المسقطة المحسوبة لجميع رميات النرد هو أيضًا متغير عشوائي، ولكن بالنسبة للرميات الكبيرة نإنه يميل إلى رقم محدد للغاية - التوقع الرياضي م ×. في هذه الحالة م × = 3,5.
كيف حصلت على هذه القيمة؟ اتركه نالاختبارات، بمجرد أن تحصل على نقطة واحدة، وبمجرد أن تحصل على نقطتين، وهكذا. اذا متى ن→ ∞ عدد النتائج التي تم فيها رمي نقطة واحدة، وبالمثل، وبالتالي
الموديل 4.5. حجر النرد
لنفترض الآن أننا نعرف قانون توزيع المتغير العشوائي سأي أننا نعلم أن المتغير العشوائي سيمكن أن تأخذ القيم س 1 , س 2 , ..., س كمع الاحتمالات ص 1 , ص 2 , ..., ص ك.
القيمة المتوقعة م ×متغير عشوائي سيساوي:
إجابة. 2,8.
إن التوقع الرياضي ليس دائما تقديرا معقولا لبعض المتغيرات العشوائية. وبالتالي، لتقدير متوسط \u200b\u200bالراتب، فمن المعقول استخدام مفهوم الوسيط، أي قيمة يتزامن فيها عدد الأشخاص الذين يتلقون راتبًا أقل من المتوسط مع راتب أعلى.
الوسيطالمتغير العشوائي يسمى رقم س 1/2 هكذا ص (س < س 1/2) = 1/2.
وبعبارة أخرى، الاحتمال ص 1 المتغير العشوائي سسوف تكون أصغر س 1/2، والاحتمال ص 2 المتغير العشوائي سسيكون أعظم س 1/2 متطابقة وتساوي 1/2. لا يتم تحديد الوسيط بشكل فريد لجميع التوزيعات.
دعنا نعود إلى المتغير العشوائي س، والتي يمكن أن تأخذ القيم س 1 , س 2 , ..., س كمع الاحتمالات ص 1 , ص 2 , ..., ص ك.
التباينمتغير عشوائي ستسمى القيمة المتوسطة لمربع انحراف المتغير العشوائي عن توقعه الرياضي :
مثال 2
في ظل ظروف المثال السابق، احسب التباين والانحراف المعياري للمتغير العشوائي س.
إجابة. 0,16, 0,4.
الموديل 4.6. إطلاق النار على الهدف
مثال 3
أوجد التوزيع الاحتمالي لعدد النقاط التي تم الحصول عليها عند رمية النرد الأولى، والوسيط، والتوقع الرياضي، والتباين، والانحراف المعياري.
من المرجح أن تسقط أي حافة بنفس القدر، لذلك سيبدو التوزيع كما يلي:
الانحراف المعياري يمكن ملاحظة أن انحراف القيمة عن القيمة المتوسطة كبير جدًا.
خصائص التوقع الرياضي:
- التوقع الرياضي لمجموع المتغيرات العشوائية المستقلة يساوي مجموع توقعاتها الرياضية:
مثال 4
أوجد التوقع الرياضي لمجموع ومنتج النقاط الملقاة على حجري نرد.
في المثال 3 وجدنا ذلك لمكعب واحد م (س) = 3.5. لذلك، لمكعبين
خصائص التشتت:
- إن تباين مجموع المتغيرات العشوائية المستقلة يساوي مجموع التباينات:
د × + ذ = د × + دي.
دع ل نلفات على النرد المدحرجة ذنقاط. ثم
هذه النتيجة صحيحة ليس فقط بالنسبة لفات النرد. وفي كثير من الحالات يتم تحديد دقة قياس التوقع الرياضي تجريبيا. ويمكن ملاحظة ذلك مع زيادة عدد القياسات نيتناقص انتشار القيم حول المتوسط، أي الانحراف المعياري، بشكل متناسب
يرتبط تباين المتغير العشوائي بالتوقع الرياضي لمربع هذا المتغير العشوائي بالعلاقة التالية:
دعونا نجد التوقعات الرياضية لكلا الجانبين من هذه المساواة. أ-بريوري،
التوقع الرياضي للجانب الأيمن من المساواة وفقا لخاصية التوقعات الرياضية يساوي
الانحراف المعياري
الانحراف المعيارييساوي الجذر التربيعي للتباين:
عند تحديد الانحراف المعياري لعدد كبير بما فيه الكفاية من السكان قيد الدراسة (ن > 30)، يتم استخدام الصيغ التالية:معلومات ذات صله.