توسيع سلسلة تايلور لوظيفة الطاقة. متسلسلات القوى، تقاربها، توسيع الدوال إلى متسلسلات قوى

من بين السلاسل الوظيفية، تحتل سلسلة الطاقة المكان الأكثر أهمية.

سلسلة الطاقة هي سلسلة

والتي تكون مصطلحاتها عبارة عن دوال قوى مرتبة في زيادة قوى الأعداد الصحيحة غير السالبة س، أ ج 0 , ج 1 , ج 2 , جن - القيم الثابتة. أرقام ج 1 , ج 2 , جن - معاملات شروط السلسلة، ج 0- عضو حر. يتم تعريف شروط سلسلة القوى على خط الأعداد بأكمله.

دعونا نتعرف على هذا المفهوم مجالات التقارب لمتسلسلات القوى.هذه مجموعة من القيم المتغيرة س، حيث تتقارب المتسلسلة. تحتوي متسلسلات القوى على منطقة تقارب بسيطة إلى حد ما. للقيم المتغيرة الحقيقية سمنطقة التقارب تتكون إما من نقطة واحدة، أو تكون فاصل معين (فاصل التقارب)، أو تتطابق مع المحور بأكمله ثور .

عند استبدال القيم في سلسلة الطاقة س= 0 سينتج عنه سلسلة أرقام

ج 0 +0+0+...+0+... ,

الذي يتقارب.

لذلك متى س= 0 أي متسلسلة قوى تتقارب، وبالتالي، منطقة التقارب لهالا يمكن أن تكون المجموعة الفارغة. هيكل منطقة التقارب لجميع سلاسل الطاقة هو نفسه. ويمكن تأسيسها باستخدام النظرية التالية.

النظرية 1 (نظرية هابيل). إذا تقاربت متسلسلة القوى عند قيمة ما س = س 0، يختلف عن الصفر، ثم يتقارب، علاوة على ذلك، بشكل مطلق لجميع قيم | س| < |س 0 |

. يرجى ملاحظة: يتم أخذ كل من قيمة البداية "X هي صفر" وأي قيمة لـ "X" يتم مقارنتها بقيمة البداية على أنها modulo - دون مراعاة الإشارة. عاقبة. لوتتباعد سلسلة القوى س = سفي بعض القيمة س| > |س 1 | .

1، فإنه يتباعد لجميع قيم | سوكما اكتشفنا سابقًا، فإن أي متسلسلة قوى تتقارب عند القيمة س= 0. هناك متسلسلة قوى تتقارب فقط عندما = 0 وتتباعد عن القيم الأخرى X س = س. وباستثناء هذه الحالة من الاعتبار، فإننا نفترض أن متسلسلة القوى تتقارب عند قيمة معينة س 0 |, |س 0، يختلف عن الصفر. ثم، حسب نظرية هابيل، فإنها تتقارب عند جميع نقاط الفترة ]-|

0 |[ (فاصل زمني حدوده اليسرى واليمنى هي قيم x التي تتقارب فيها سلسلة القوى، مأخوذة بعلامة الطرح وعلامة الجمع، على التوالي)، متماثلة حول الأصل. س = سإذا كانت متسلسلة القوى تتباعد عند قيمة معينة س 1 |, |س 1 |] . ويترتب على ذلك أنه بالنسبة لأي سلسلة قوى هناك فترة متماثلة بالنسبة إلى الأصل، تسمى فترة التقارب، عند كل نقطة تتقارب فيها السلسلة، عند الحدود يمكن أن تتقارب، أو يمكن أن تتباعد، وليس بالضرورة في نفس الوقت، وخارج المقطع تتباعد السلسلة. رقم ريسمى نصف قطر تقارب متسلسلة القوى

في حالات خاصة فترة التقارب لسلسلة الطاقةيمكن أن تتدهور إلى نقطة ما (ثم تتقارب السلسلة فقط عندما س= 0 ويعتبر ذلك ر= 0) أو تمثل خط الأعداد بأكمله (ثم تتقارب المتسلسلة عند جميع نقاط خط الأعداد ويفترض ذلك).

وبالتالي، فإن تحديد منطقة التقارب لمتسلسلة القوى يعني تحديد منطقة تقاربها شعاع التقارب رودراسة تقارب المتسلسلة عند حدود فترة التقارب (عند ).

النظرية 2. إذا كانت جميع معاملات متسلسلة القوى، بدءًا من معامل معين، مختلفة عن الصفر، فإن نصف قطر تقاربها يساوي الحد عند نسبة القيم المطلقة لمعاملات الحدود المشتركة السلسلة التي تتبعه، أي.

مثال 1. أوجد منطقة تقارب متسلسلة القوى

حل. هنا

وباستخدام الصيغة (28)، نجد نصف قطر تقارب هذه المتسلسلة:

دعونا ندرس تقارب المتسلسلة عند نهايات فترة التقارب. يوضح المثال 13 أن هذه المتسلسلة تتقارب عند س= 1 ويتباعد عند س= -1. وبالتالي فإن منطقة التقارب هي نصف الفترة.

مثال 2. أوجد منطقة تقارب متسلسلة القوى

حل. معاملات السلسلة موجبة، و

دعونا نجد الحد لهذه النسبة، أي. نصف قطر تقارب متسلسلة القوى:

دعونا ندرس تقارب المتسلسلة عند طرفي الفترة. استبدال القيم س= -1/5 و س= 1/5 في هذا الصف يعطي:

وتتقارب أول هذه المتسلسلة (انظر المثال 5). ولكن بعد ذلك، وبموجب النظرية في قسم "التقارب المطلق"، تتقارب السلسلة الثانية أيضًا، ومنطقة تقاربها هي القطعة

مثال 3. أوجد منطقة التقارب لمتسلسلة القوى

حل. هنا

باستخدام الصيغة (28) نجد نصف قطر تقارب السلسلة:

دعونا ندرس تقارب المتسلسلة لقيم . استبدالهم في هذه السلسلة، نحصل على التوالي

تتباعد كلتا السلسلتين بسبب عدم استيفاء الشرط الضروري للتقارب (مصطلحاتهما المشتركة لا تميل إلى الصفر عند ). إذن، عند طرفي فترة التقارب، تتباعد هذه المتسلسلة، ومنطقة تقاربها هي الفترة.

مثال 5. أوجد منطقة التقارب لمتسلسلة القوى

حل. نجد العلاقة حيث و :

ووفقا للصيغة (28)، فإن نصف قطر تقارب هذه السلسلة

,

أي أن المتسلسلة تتقارب فقط عندما س= 0 ويتباعد عن القيم الأخرى = 0 وتتباعد عن القيم الأخرى.

توضح الأمثلة أنه في نهايات فترة التقارب تتصرف السلسلة بشكل مختلف. في المثال 1، عند أحد طرفي فترة التقارب، تتقارب المتسلسلة، وفي المثال 2، تتقارب عند كلا الطرفين؛ في المثال 3، تتباعد عند كلا الطرفين.

يتم الحصول على صيغة نصف قطر تقارب متسلسلة القوى بافتراض أن جميع معاملات حدود المتسلسلة، بدءًا من نقطة معينة، تختلف عن الصفر. ولذلك فإن استخدام الصيغة (28) لا يجوز إلا في هذه الحالات. إذا تم انتهاك هذا الشرط، فيجب البحث عن نصف قطر تقارب متسلسلة القوى باستخدام اختبار دالمبيرت، أو عن طريق استبدال المتغير، تحويل السلسلة إلى الشكل الذي يتم فيه استيفاء الشرط المحدد.

مثال 6. أوجد فترة تقارب متسلسلة القوى

حل. لا تحتوي هذه السلسلة على مصطلحات ذات درجات فردية = 0 وتتباعد عن القيم الأخرى. لذلك، نقوم بتحويل السلسلة، الإعداد . ثم نحصل على السلسلة

لإيجاد نصف قطر التقارب الذي يمكننا تطبيق الصيغة (28) عليه. بما أن ، a ، فإن نصف قطر تقارب هذه السلسلة

ومن المساواة نحصل على أن هذه المتسلسلة تتقارب على الفترة.

مجموع متسلسلة القوى تفاضل وتكامل متسلسلات القوى

دعونا لسلسلة السلطة

نصف قطر التقارب ر> 0، أي هذه المتسلسلة تتقارب في الفترة .

ثم كل قيمة = 0 وتتباعد عن القيم الأخرىمن فترة التقارب يتوافق مع مجموع معين من السلسلة. وبالتالي فإن مجموع متسلسلة القوى هو دالة لـ = 0 وتتباعد عن القيم الأخرىعلى فترة التقارب. تدل عليه و(س)، يمكننا أن نكتب المساواة

فهمها بمعنى مجموع المتسلسلة عند كل نقطة = 0 وتتباعد عن القيم الأخرىمن فترة التقارب تساوي قيمة الدالة و(س) عند هذه النقطة. وبنفس المعنى، سنقول إن متسلسلة القوى (29) تتقارب مع الدالة و(س) على فترة التقارب.

خارج فترة التقارب، المساواة (30) لا معنى لها.

مثال 7. أوجد مجموع متسلسلة القوى

حل. هذه سلسلة هندسية لها أ= 1، أ س= س. لذلك، مجموعها هو وظيفة . تتقارب المتسلسلة إذا، و هي فترة التقارب الخاصة بها. وبالتالي المساواة

صالحة فقط للقيم، على الرغم من أن الوظيفة محددة لجميع القيم = 0 وتتباعد عن القيم الأخرى، يستثني = 0 وتتباعد عن القيم الأخرى= 1.

يمكن إثبات أن مجموع متسلسلة القوى و(س) مستمرة وقابلة للتفاضل في أي فترة ضمن فترة التقارب، وخاصة عند أي نقطة في فترة التقارب من السلسلة.

دعونا نقدم نظريات حول التمايز والتكامل لكل حد لمتسلسلات القوى.

النظرية 1. يمكن تمييز سلسلة القوى (30) في فترة تقاربها بعدد غير محدود من المرات، وسلسلة القوى الناتجة لها نفس نصف قطر التقارب مثل السلسلة الأصلية، ومجموعها يساوي على التوالي.

النظرية 2. يمكن دمج سلسلة الطاقة (30) مصطلحًا تلو الآخر لعدد غير محدود من المرات في المدى من 0 إلى = 0 وتتباعد عن القيم الأخرى، إذا ، وسلسلة القوى الناتجة لها نفس نصف قطر التقارب مثل السلسلة الأصلية، ومجموعها متساوي في المقابل

توسيع الوظائف إلى سلسلة الطاقة

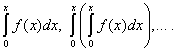
دع الوظيفة تعطى و(س)، والتي تحتاج إلى توسيعها إلى سلسلة الطاقة، أي. تمثل في النموذج (30):

المهمة هي تحديد المعاملات الصف (30). وللقيام بذلك، وبالتمييز بين المساواة (30) مصطلحًا بعد مصطلح، نجد باستمرار:

……………………………………………….. (31)

افتراض المساواة (30) و (31) = 0 وتتباعد عن القيم الأخرى= 0 نجد

استبدال التعبيرات الموجودة في المساواة (30) نحصل عليها

(32)

دعونا نجد توسعة متسلسلة ماكلورين لبعض الدوال الأولية.

مثال 8. قم بتوسيع الدالة في سلسلة ماكلورين

حل. تتطابق مشتقات هذه الوظيفة مع الوظيفة نفسها:

لذلك متى = 0 وتتباعد عن القيم الأخرى= 0 لدينا

باستبدال هذه القيم في الصيغة (32)، نحصل على التوسع المطلوب:

(33)

تتقارب هذه المتسلسلة على خط الأعداد بأكمله (نصف قطر التقارب).

في نظرية المتسلسلة الوظيفية، يحتل المكان المركزي القسم المخصص لتوسيع الدالة إلى سلسلة.

وهكذا يتم تعيين المهمة: لوظيفة معينة نحن بحاجة إلى العثور على مثل هذه السلسلة من القوى

والتي تقاربت في فترة معينة وكان مجموعها يساوي
, أولئك.

= ..

تسمى هذه المهمة مشكلة توسيع الدالة إلى سلسلة قوى.

شرط ضروري لتحلل وظيفة في سلسلة الطاقةهي قابلية تفاضلها لعدد لا حصر له من المرات - وهذا يتبع من خصائص سلسلة القوى المتقاربة. يتم استيفاء هذا الشرط، كقاعدة عامة، للوظائف الأولية في مجال تعريفها.

لذلك دعونا نفترض أن الوظيفة
لديه مشتقات من أي أمر. هل من الممكن توسيعها إلى سلسلة قوى، إذا كان الأمر كذلك، كيف يمكننا العثور على هذه السلسلة؟ الجزء الثاني من المشكلة أسهل في الحل، فلنبدأ به.

لنفترض أن الدالة
يمكن تمثيلها كمجموع متسلسلة قوى متقاربة في الفترة التي تحتوي على النقطة = 0 وتتباعد عن القيم الأخرى 0 :

= .. (*)

أين أ 0 ،أ 1 ،أ 2 ،...،أ ن ,... - معاملات غير معروفة (حتى الآن).

دعونا نضع القيمة على قدم المساواة (*). س = س 0 , ثم نحصل

.

دعونا نفرق بين مصطلحات سلسلة القوى (*) حسب المصطلح

= ..

والاعتقاد هنا س = س 0 , نحصل عليها

.

مع التمايز التالي نحصل على السلسلة

= ..

الاعتقاد س = س 0 , نحصل عليها
، أين
.

بعد ن-التمايز المتعدد الذي نحصل عليه

على افتراض المساواة الأخيرة س = س 0 , نحصل عليها
، أين

لذلك تم العثور على المعاملات

,
,
, …,
,….,

استبدال أي في السلسلة (*)، نحصل على

السلسلة الناتجة تسمى بجوار تايلورللوظيفة
.

وهكذا أثبتنا ذلك إذا كان من الممكن توسيع الدالة إلى سلسلة قوى في القوى (x - x 0 )، فإن هذا التوسع فريد والسلسلة الناتجة هي بالضرورة سلسلة تايلور.

لاحظ أنه يمكن الحصول على متسلسلة تايلور لأي دالة لها مشتقات من أي رتبة عند هذه النقطة س = س 0 . ولكن هذا لا يعني أنه يمكن وضع علامة المساواة بين الدالة والمتسلسلة الناتجة، أي. أن مجموع المتسلسلة يساوي الدالة الأصلية. أولاً، لا يمكن أن تكون هذه المساواة منطقية إلا في منطقة التقارب، وقد تتباعد سلسلة تايلور التي تم الحصول عليها للدالة، وثانيًا، إذا تقاربت سلسلة تايلور، فقد لا يتطابق مجموعها مع الوظيفة الأصلية.

3.2. الشروط الكافية لتحلل دالة في سلسلة تايلور

دعونا نقوم بصياغة بيان سيتم من خلاله حل المهمة.

إذا كانت الوظيفة
في بعض المناطق المجاورة للنقطة x 0 لديه مشتقات تصل إلى (ن+ 1) من النظام الشامل، ففي هذا الحي لديناصيغةتايلور

أينر ن (= 0 وتتباعد عن القيم الأخرى)- الحد المتبقي من صيغة تايلور – له الشكل (شكل لاغرانج)

أين نقطةξ تقع بين x وx 0 .

لاحظ أن هناك فرقًا بين متسلسلة تايلور وصيغة تايلور: صيغة تايلور عبارة عن مجموع محدود، أي. ع -رقم ثابت.

أذكر أن مجموع هذه السلسلة س(س) يمكن تعريفها على أنها نهاية التسلسل الوظيفي للمبالغ الجزئية س ن (س) في فترة ما X:

.

وفقًا لهذا، فإن توسيع دالة إلى سلسلة تايلور يعني العثور على سلسلة من هذا القبيل لأي منها = 0 وتتباعد عن القيم الأخرىX

دعونا نكتب صيغة تايلور في النموذج حيث

لاحظ أن
يحدد الخطأ الذي حصلنا عليه، واستبدال الوظيفة و(س) متعدد الحدود س ن (س).

لو
، الذي - التي
،أولئك. يتم توسيع الوظيفة إلى سلسلة تايلور. والعكس صحيح إذا
، الذي - التي
.

وهكذا أثبتنا معيار تحلل دالة في متسلسلة تايلور.

من أجل الوظيفةو(x) تتوسع إلى سلسلة تايلور، فمن الضروري والكافي أن يتم ذلك في هذه الفترة
، أينر ن (س) هو الحد المتبقي من سلسلة تايلور.

باستخدام المعيار المصاغ، يمكن الحصول عليه كافٍشروط تحلل دالة في سلسلة تايلور.

إذا كان فيبعض المناطق المجاورة للنقطة x 0 تقتصر القيم المطلقة لجميع مشتقات الدالة على نفس الرقم M≥ 0، أي.

، تo في هذا الحي تتوسع الدالة إلى سلسلة تايلور.

مما سبق يتبع خوارزميةتوسيع الوظيفةو(س) في سلسلة تايلورفي محيط نقطة ما = 0 وتتباعد عن القيم الأخرى 0 :

1. إيجاد مشتقات الدوال و(س):

و(x)، f’(x)، f”(x)، f’”(x)، f (ن) (x)،...

2. احسب قيمة الدالة وقيم مشتقاتها عند النقطة = 0 وتتباعد عن القيم الأخرى 0

و(س 0 ) ، و '(خ 0 )، و"(x 0 ) ، و '"(خ 0 ) ، ف (ن) (x 0 ),…

3. نكتب متسلسلة تايلور رسميًا ونجد منطقة التقارب لمتسلسلات القوى الناتجة.

4. نتحقق من استيفاء الشروط الكافية، أي. نحن نؤسس لذلك = 0 وتتباعد عن القيم الأخرىمن منطقة التقارب، المدة المتبقية ر ن (س) يميل إلى الصفر كما
أو
.

يسمى توسيع الوظائف إلى سلسلة تايلور باستخدام هذه الخوارزمية توسيع الدالة إلى سلسلة تايلور حسب التعريفأو التحلل المباشر.

كيفية إدراج الصيغ الرياضية على موقع على شبكة الانترنت؟

إذا كنت بحاجة إلى إضافة واحدة أو اثنتين من الصيغ الرياضية إلى صفحة ويب، فإن أسهل طريقة للقيام بذلك هي كما هو موضح في المقالة: يتم إدراج الصيغ الرياضية بسهولة على الموقع في شكل صور يتم إنشاؤها تلقائيًا بواسطة Wolfram Alpha . بالإضافة إلى البساطة، ستساعد هذه الطريقة العالمية في تحسين ظهور الموقع في محركات البحث. لقد كان يعمل لفترة طويلة (وأعتقد أنه سيعمل إلى الأبد)، لكنه عفا عليه الزمن بالفعل من الناحية الأخلاقية.

إذا كنت تستخدم الصيغ الرياضية بانتظام على موقعك، فإنني أوصيك باستخدام MathJax - وهي مكتبة JavaScript خاصة تعرض الرموز الرياضية في متصفحات الويب باستخدام علامات MathML أو LaTeX أو ASCIMathML.

هناك طريقتان لبدء استخدام MathJax: (1) باستخدام رمز بسيط، يمكنك توصيل البرنامج النصي MathJax بسرعة بموقعك على الويب، والذي سيتم تحميله تلقائيًا من خادم بعيد في الوقت المناسب (قائمة الخوادم)؛ (2) قم بتنزيل البرنامج النصي MathJax من خادم بعيد إلى الخادم الخاص بك وقم بتوصيله بجميع صفحات موقعك. الطريقة الثانية - الأكثر تعقيدًا وتستغرق وقتًا طويلاً - ستعمل على تسريع تحميل صفحات موقعك، وإذا أصبح خادم MathJax الأصلي غير متاح مؤقتًا لسبب ما، فلن يؤثر ذلك على موقعك بأي شكل من الأشكال. وعلى الرغم من هذه المزايا، إلا أنني اخترت الطريقة الأولى لأنها أبسط وأسرع ولا تتطلب مهارات فنية. اتبع مثالي، وفي 5 دقائق فقط ستتمكن من استخدام جميع ميزات MathJax على موقعك.

يمكنك توصيل البرنامج النصي لمكتبة MathJax من خادم بعيد باستخدام خيارين للتعليمات البرمجية مأخوذة من موقع MathJax الرئيسي أو من صفحة الوثائق:

يجب نسخ أحد خيارات التعليمات البرمجية هذه ولصقها في التعليمات البرمجية الخاصة بصفحة الويب الخاصة بك، ويفضل أن يكون ذلك بين العلامات و/أو بعد العلامة مباشرة. وفقًا للخيار الأول، يتم تحميل MathJax بشكل أسرع ويبطئ الصفحة بشكل أقل. لكن الخيار الثاني يقوم تلقائيًا بمراقبة وتحميل أحدث إصدارات MathJax. إذا قمت بإدراج الرمز الأول، فسوف تحتاج إلى تحديثه بشكل دوري. إذا قمت بإدخال الكود الثاني، فسيتم تحميل الصفحات بشكل أبطأ، لكنك لن تحتاج إلى مراقبة تحديثات MathJax باستمرار.

أسهل طريقة للاتصال بـ MathJax هي في Blogger أو WordPress: في لوحة تحكم الموقع، أضف أداة مصممة لإدراج كود JavaScript لجهة خارجية، وانسخ الإصدار الأول أو الثاني من كود التنزيل الموضح أعلاه، ثم ضع الأداة في مكان أقرب إلى بداية القالب (بالمناسبة، هذا ليس ضروريًا على الإطلاق، حيث يتم تحميل البرنامج النصي MathJax بشكل غير متزامن). هذا كل شيء. تعرف الآن على بناء الجملة الترميزي لـ MathML، وLaTeX، وASCIIMathML، وستكون جاهزًا لإدراج الصيغ الرياضية في صفحات الويب الخاصة بموقعك.

يتم إنشاء أي فراكتل وفقًا لقاعدة معينة، والتي يتم تطبيقها باستمرار لعدد غير محدود من المرات. كل مرة من هذا القبيل تسمى التكرار.

الخوارزمية التكرارية لبناء إسفنجة Menger بسيطة للغاية: يتم تقسيم المكعب الأصلي ذو الجانب 1 بواسطة مستويات موازية لوجهه إلى 27 مكعبًا متساويًا. تتم إزالة مكعب مركزي واحد و 6 مكعبات مجاورة له على طول الوجوه. والنتيجة هي مجموعة تتكون من المكعبات العشرين الأصغر المتبقية. وبفعل الشيء نفسه مع كل مكعب من هذه المكعبات، نحصل على مجموعة مكونة من 400 مكعب أصغر. مواصلة هذه العملية إلى ما لا نهاية، نحصل على اسفنجة Menger.

إذا كانت الدالة f(x) تحتوي على مشتقات لجميع الطلبات في فترة معينة تحتوي على النقطة a، فيمكن تطبيق صيغة تايلور عليها:
,
أين ص ن- ما يسمى بالحد المتبقي أو بقية السلسلة، ويمكن تقديره باستخدام صيغة لاغرانج:
حيث يقع الرقم x بين x و a.

و(خ)=

عند النقطة x 0 = عدد عناصر الصف 3 4 5 6 7

استخدم توسيع الدوال الأولية e x , cos(x), sin(x), ln(1+x), (1+x) m

قواعد لإدخال الوظائف:

إذا كان لبعض القيمة = 0 وتتباعد عن القيم الأخرى ص ن→0 في ن→∞، ثم في النهاية تصبح صيغة تايلور متقاربة لهذه القيمة سلسلة تايلور:
,
وبالتالي، يمكن توسيع الدالة f(x) إلى سلسلة تايلور عند النقطة x قيد النظر إذا:
1) لديها مشتقات من جميع الطلبات؛
2) تتقارب السلسلة المبنية عند هذه النقطة.

عندما تكون a = 0 نحصل على متسلسلة تسمى متسلسلة ماكلورين:
,
توسيع أبسط الدوال (الابتدائية) في سلسلة ماكلورين:
الدوال الأسية
، ص=∞
الدوال المثلثية
، ص=∞
، ص=∞
، (-π/2< x < π/2), R=π/2
الدالة actgx لا تتوسع في قوى x، لأن ctg0=∞
الدوال الزائدية


الدوال اللوغاريتمية
, -1