التكامل مع جيب التمام في المقام. دمج الدوال المثلثية

من الناحية العملية، غالبًا ما يكون من الضروري حساب تكاملات الدوال المتعالية التي تحتوي على دوال مثلثية. كجزء من هذه المادة، سنصف الأنواع الرئيسية من الدوال التكاملية ونوضح الطرق التي يمكن استخدامها لتكاملها.

تكامل الجيب وجيب التمام والظل وظل التمام

لنبدأ بطرق تكامل الدوال المثلثية الأساسية - sin، cos، t g، c t g. باستخدام جدول المشتقات العكسية، نكتب على الفور أن ∫ sin x d x = - cos x + C، و ∫ cos x d x = sin x + C.

لحساب التكاملات غير المحددة للدالتين t g وc t g، يمكنك استخدام العلامة التفاضلية:

∫ t g x d x = ∫ sin x cos x d x = d (cos x) = - sin x d x = = - ∫ d (cos x) cos x = - ln cos x + C ∫ c t g x d x = ∫ cos x sin x d x = d (sin x) = cos x d x = = ∫ d (sin x) sin x = ln sin x + C

كيف حصلنا على الصيغ ∫ d x sin x = ln 1 - cos x sin x + C و ∫ d x cos x = ln 1 + sin x cos x + C، المأخوذة من جدول المشتقات العكسية؟ ولنشرح حالة واحدة فقط، لأن الحالة الثانية ستتضح بالقياس.

وباستخدام طريقة الاستبدال نكتب:

∫ د x الخطيئة x = الخطيئة x = t ⇒ x = أ r c الخطيئة y ⇒ د x = د t 1 - t 2 = د t t 1 - t 2

نحن هنا بحاجة إلى دمج الوظيفة غير المنطقية. نستخدم نفس طريقة الاستبدال:

∫ د t t 1 - t 2 = 1 - t 2 = z 2 ⇒ t = 1 - z 2 ⇒ d t = - z d z 1 - z 2 = = ∫ - z d z z 1 - z 2 1 - z 2 = ∫ d z z 2 - 1 = ∫ d z (z - 1) (z +) = = 1 2 ∫ d z z - 1 - 1 2 ∫ d z z + 1 = 1 2 ln z - 1 - 1 2 z + 1 + C = = 1 2 ln z - 1 z + 1 + C = ln z - 1 z + 1 + C

الآن نجري التعويض العكسي z = 1 - t 2 و t = sin x:

∫ d x sin x = ∫ d t t 1 - t 2 = ln z - 1 z + 1 + C = = ln 1 - t 2 - 1 1 - t 2 + 1 + C = ln 1 - sin 2 x - 1 1 - sin 2 x + 1 + C = = ln cos x - 1 cos x + 1 + C = ln (cos x - 1) 2 sin 2 x + C = = ln cos x - 1 sin x + C

سنقوم بشكل منفصل بتحليل حالات التكاملات التي تحتوي على قوى الدوال المثلثية، مثل ∫ sin n x d x, ∫ cos n x d x, ∫ d x sin n x, ∫ d x cos n x.

يمكنك أن تقرأ عن كيفية حسابها بشكل صحيح في المقالة الخاصة بالتكامل باستخدام صيغ التكرار. إذا كنت تعرف كيفية اشتقاق هذه الصيغ، فيمكنك بسهولة حساب التكاملات مثل ∫ sin n x · cos m x d x مع m وn الطبيعي.

إذا كان لدينا مجموعة من الدوال المثلثية مع كثيرات الحدود أو الدوال الأسية، فيجب دمجها بالأجزاء. نوصي بقراءة مقال مخصص لطرق إيجاد التكاملات ∫ P n (x) · sin (a x) d x , ∫ P n (x) · cos (a x) d x , ∫ e a · x · sin (a x) d x , ∫ e a · س · كوس (أ س) د س .

أصعب المسائل هي تلك التي يشتمل فيها التكامل على دوال مثلثية ذات وسائط مختلفة. للقيام بذلك، تحتاج إلى استخدام صيغ علم المثلثات الأساسية، لذا يُنصح بحفظها أو الاحتفاظ بمذكرة عنها في متناول اليد.

مثال 1

أوجد مجموعة المشتقات العكسية للدالة y = sin (4 x) + 2 cos 2 (2 x) sin x · cos (3 x) + 2 cos 2 x 2 - 1 · sin (3 x) .

حل

لنستخدم صيغ تقليل الدرجة ونكتب cos 2 x 2 = 1 + cos x 2، وcos 2 2 x = 1 + cos 4 x 2. وسائل،

y = sin (4 x) + 2 cos 2 (2 x) sin x cos (3 x) + 2 cos 2 x 2 - 1 sin (3 x) = sin (4 x) + 2 1 + cos 4 x 2 sin x cos (3 x) + 2 1 + cos x 2 - 1 sin (3 x) = = cos (4 x) + cos (4 x) + 1 sin x cos (3 x) + cos x sin (3 x)

في المقام لدينا صيغة جيب المجموع. ثم يمكنك كتابتها مثل هذا:

y = sin (4 x) + cos (4 x) + 1 sin x cos (3 x) + cos x sin (3 x) = sin (4 x) + cos (4 x) + 1 sin (4 x ) = = 1 + جتا (4 س) جا (4 س)

لقد حصلنا على مجموع 3 تكاملات.

∫ sin (4 x) + cos (4 x) + 1 sin x · cos (3 x) + cos x · sin (3 x) d x = = ∫ d x + cos (4 x) d x sin (4 x) + ∫ d x sin (4 x) = = x + 1 4 ln ∫ d (sin (4 x)) sin (4 x) + 1 4 ln cos (4 x) - 1 sin (4 x) = = 1 4 ln sin ( 4 x) + 1 4 ln cos (4 x) - 1 sin (4 x) + C = x + 1 4 ln cos 4 x - 1 + C

في بعض الحالات، يمكن اختزال الدوال المثلثية في إطار التكامل إلى تعبيرات كسرية باستخدام طريقة الاستبدال القياسية. أولاً، لنأخذ الصيغ التي تعبر عن sin وcos وt g من خلال ظل نصف الوسيطة:

sin x = 2 t g x 2 1 + t g 2 x 2 , sin x = 1 - t g 2 x 2 1 + t g 2 x 2 , t g x = 2 t g x 2 1 - t g 2 x 2

سنحتاج أيضًا إلى التعبير عن التفاضل dx بدلالة ظل نصف الزاوية:

بما أن d t g x 2 = t g x 2 "d x = d x 2 cos 2 x 2، إذن

د x = 2 cos 2 x 2 d t g x 2 = 2 d t g x 2 1 cos 2 x 2 = 2 d t g x 2 cos 2 x 2 + sin 2 x 2 cos 2 x 2 = 2 d t g x 2 1 + t g 2 x 2

وبالتالي، sin x = 2 z 1 + z 2، cos x 1 - z 2 1 + z 2، t g x 2 z 1 - z 2، d x = 2 d z 1 + z 2 at z = t g x 2.

مثال 2

أوجد التكامل غير المحدد ∫ d x 2 sin x + cos x + 2 .

حل

نحن نستخدم طريقة الاستبدال المثلثية القياسية.

2 sin x + cos x + 2 = 2 2 z 1 + z 2 + 1 - z 2 1 + z 2 = z 2 + 4 z + 3 1 + z 2 ⇒ d x 2 sin x + cos x + 2 = 2 d z 1 + ض 2 ض 2 + 4 ض + 3 1 + ض 2 = 2 د ض ض 2 + 4 ض + 3

نحصل على ∫ d x 2 sin x + cos x + 2 = 2 d z z 2 + 4 z + 3 .

يمكننا الآن توسيع التكامل إلى كسور بسيطة والحصول على مجموع تكاملين:

∫ d x 2 sin x + cos x + 2 = 2 ∫ 2 d z z 2 + 4 z + 3 = 2 ∫ 1 2 1 z + 1 - 1 z + 3 d z = = ∫ d z z + 1 - ∫ C z + 3 = ln ض + 1 - ln z + 3 + C = ln z + 1 z + 3 + C

∫ d x 2 sin x + cos x + 2 = ln z + 1 z + 3 + C = ln t g x 2 + 1 t g x 2 + 3 + C

الإجابة: ∫ d x 2 sin x + cos x + 2 = ln t g x 2 + 1 t g x 2 + 3 + C

من المهم ملاحظة أن تلك الصيغ التي تعبر عن الدوال من خلال ظل وسيطة نصفية ليست متطابقات؛ لذلك، التعبير الناتج ln t g x 2 + 1 t g x 2 + 3 + C هو مجموعة المشتقات العكسية للدالة y = 1 2 sin x + cos x + 2 فقط في مجال التعريف.

لحل أنواع أخرى من المشاكل، يمكنك استخدام طرق التكامل الأساسية.

إذا لاحظت وجود خطأ في النص، فيرجى تحديده والضغط على Ctrl+Enter

يتم النظر بالتفصيل في أمثلة حلول التكاملات بالأجزاء، التي يكون تكاملها هو حاصل ضرب كثير الحدود بواسطة أسي (e إلى قوة x) أو بواسطة جيب (sin x) أو جيب تمام (cos x).

محتوى

أنظر أيضا: طريقة التكامل بالأجزاء
جدول التكاملات غير المحددة
طرق حساب التكاملات غير المحددة
الوظائف الأولية الأساسية وخصائصها

صيغة التكامل بالأجزاء

عند حل الأمثلة في هذا القسم، يتم استخدام صيغة التكامل بالأجزاء:
;
.

أمثلة على التكاملات التي تحتوي على حاصل ضرب كثيرة الحدود وsin x أو cos x أو e x

فيما يلي أمثلة على هذه التكاملات:
, , .

لتكامل مثل هذه التكاملات، يُشار إلى كثير الحدود بالرمز u، والجزء المتبقي بالرمز v dx. بعد ذلك، قم بتطبيق صيغة التكامل بالأجزاء.

فيما يلي حل مفصل لهذه الأمثلة.

أمثلة على حل التكاملات

مثال مع الأس، e لقوة x

تحديد التكامل:
.

دعونا نقدم الأس تحت علامة التفاضل:
ه - س دكس = - ه - س د(-x) = - د(ه - س).

دعونا نتكامل بالأجزاء.

هنا
.
ونقوم أيضًا بدمج التكامل المتبقي بالأجزاء.
.
.
.
وأخيراً لدينا:
.

مثال على تعريف التكامل مع الجيب

حساب التكامل:
.

دعونا نقدم جيب تحت العلامة التفاضلية:

دعونا نتكامل بالأجزاء.

هنا u = x 2 , v = كوس(2س+3)، دو = ( × 2 )′ dx

ونقوم أيضًا بدمج التكامل المتبقي بالأجزاء. للقيام بذلك، أدخل جيب التمام تحت علامة التفاضل.

هنا ش = س، الخامس = الخطيئة(2س+3)دو = دكس

وأخيراً لدينا:

مثال على منتج كثير الحدود وجيب التمام

حساب التكامل:
.

دعونا نقدم جيب التمام تحت العلامة التفاضلية:

دعونا نتكامل بالأجزاء.

هنا ش = س 2 + 3 س + 5، الخامس = الخطيئة 2 ×، دو = ( × 2 + 3 × + 5 )′ dx

تكاملات الدوال المثلثية.
أمثلة على الحلول

في هذا الدرس سوف نلقي نظرة على تكاملات الدوال المثلثية، أي أن ملء التكاملات سيكون الجيب وجيب التمام والظل وظل التمام في مجموعات مختلفة. سيتم تحليل جميع الأمثلة بالتفصيل، ويمكن الوصول إليها ومفهومة حتى بالنسبة لإبريق الشاي.

لدراسة تكاملات الدوال المثلثية بنجاح، يجب أن يكون لديك فهم جيد لأبسط التكاملات، بالإضافة إلى إتقان بعض تقنيات التكامل. يمكنك التعرف على هذه المواد في المحاضرات تكامل غير محدد. أمثلة على الحلولو .

والآن نحتاج إلى: جدول التكاملات, جدول المشتقاتو دليل الصيغ المثلثية. جميع الوسائل التعليمية تجدونها على الصفحة الصيغ والجداول الرياضية. أوصي بطباعة كل شيء. أركز بشكل خاص على الصيغ المثلثية، ينبغي أن يكونوا أمام عينيك– وبدون ذلك، ستنخفض كفاءة العمل بشكل ملحوظ.

لكن أولاً، حول ماهية التكاملات الموجودة في هذه المقالة لا. لا توجد تكاملات النموذج، - جيب التمام، جيب التمام، مضروبًا في بعض كثيرات الحدود (في كثير من الأحيان شيء ذو ظل أو ظل التمام). يتم التكامل بالأجزاء، ولمعرفة الطريقة، قم بزيارة درس التكامل بالأجزاء. أمثلة على الحلول هنا أيضًا لا توجد تكاملات مع "الأقواس" - قوس الزاوية، قوس الجيب، وما إلى ذلك، وغالبًا ما يتم دمجها أيضًا بالأجزاء.

عند إيجاد تكاملات الدوال المثلثية، يتم استخدام عدد من الطرق:

(4) نستخدم الصيغة الجدولية الفرق الوحيد هو أنه بدلاً من "X" لدينا تعبير معقد.

مثال 2

مثال 3

أوجد التكامل غير المحدد.

كلاسيكي من هذا النوع لأولئك الذين يغرقون في المنافسة. كما لاحظت على الأرجح، لا يوجد تكامل بين الظل وظل التمام في جدول التكاملات، ولكن مع ذلك، يمكن العثور على مثل هذه التكاملات.

(1) نستخدم الصيغة المثلثية

(2) نضع الدالة تحت علامة التفاضل.

(3) نستخدم تكامل الجدول .

مثال 4

أوجد التكامل غير المحدد.

وهذا مثال لحل مستقل، الحل الكامل والإجابة موجودة في نهاية الدرس.

مثال 5

أوجد التكامل غير المحدد.

ستزداد درجاتنا تدريجياً =).
أولا الحل:

(1) نستخدم الصيغة

(2) نستخدم الهوية المثلثية الرئيسية ، ومنه يترتب على ذلك .

(3) قسمة البسط على المقام حدا حدا.

(4) نستخدم الخاصية الخطية للتكامل غير المحدد.

(5) نتكامل باستخدام الجدول.

مثال 6

أوجد التكامل غير المحدد.

وهذا مثال لحل مستقل، الحل الكامل والإجابة موجودة في نهاية الدرس.

هناك أيضًا تكاملات الظل وظل التمام، والتي تكون في قوى أعلى. تمت مناقشة تكامل المماس المكعب في الدرس كيفية حساب مساحة الشكل المسطح؟يمكن الحصول على تكاملات الظل (ظل التمام) للقوى الرابعة والخامسة على الصفحة التكاملات المعقدة.

تقليل درجة التكامل

تعمل هذه التقنية عندما تكون الدوال التكاملية محشوة بالجيب وجيب التمام حتىدرجات. لتقليل الدرجة، استخدم الصيغ المثلثية , و، وغالبًا ما تُستخدم الصيغة الأخيرة في الاتجاه المعاكس: .

مثال 7

أوجد التكامل غير المحدد.

حل:

من حيث المبدأ، لا جديد هنا سوى أننا طبقنا الصيغة (خفض درجة التكامل). يرجى ملاحظة أنني اختصرت الحل. كلما اكتسبت الخبرة، يمكن العثور على تكامل شفهيًا، وهذا يوفر الوقت وهو مقبول تمامًا عند الانتهاء من المهام. في هذه الحالة، من المستحسن عدم وصف القاعدة ، أولاً نأخذ تكامل 1 لفظيًا، ثم .

مثال 8

أوجد التكامل غير المحدد.

وهذا مثال لحل مستقل، الحل الكامل والإجابة موجودة في نهاية الدرس.

وهذه هي الزيادة الموعودة في الدرجة:

مثال 9

أوجد التكامل غير المحدد.

أولا الحل ثم التعليقات:

(1) قم بإعداد التكامل لتطبيق الصيغة .

(2) نحن نطبق الصيغة بالفعل.

(٣) نقوم بتربيع المقام وإخراج الثابت من إشارة التكامل. كان من الممكن القيام بذلك بطريقة مختلفة قليلاً، لكن في رأيي، كان الأمر أكثر ملاءمة.

(4) نستخدم الصيغة

(5) في الحد الثالث نقوم مرة أخرى بتقليل الدرجة، ولكن باستخدام الصيغة .

(6) نقدم مصطلحات مماثلة (هنا قسمت المصطلح على المصطلح وقام بالإضافة).

(7) في الواقع، نحن نأخذ التكامل، قاعدة الخطية وطريقة إدراج دالة تحت العلامة التفاضلية تتم شفويا.

(8) تمشيط الجواب.

! في التكامل غير المحدد، غالبًا ما يمكن كتابة الإجابة بعدة طرق

في المثال الذي تم النظر فيه للتو، كان من الممكن كتابة الإجابة النهائية بشكل مختلف - فتح الأقواس وحتى القيام بذلك قبل دمج التعبير، أي أن النهاية التالية للمثال مقبولة تمامًا:

من الممكن أن يكون هذا الخيار أكثر ملاءمة، لقد شرحته للتو بالطريقة التي اعتدت على حلها بنفسي). فيما يلي مثال نموذجي آخر لحل مستقل:

مثال 10

أوجد التكامل غير المحدد.

يمكن حل هذا المثال بطريقتين، وقد تنجح إجابتين مختلفتين تماما(بتعبير أدق، سوف تبدو مختلفة تماما، ولكن من وجهة نظر رياضية ستكون متكافئة). على الأرجح، لن ترى الطريقة الأكثر عقلانية وستعاني عند فتح الأقواس واستخدام الصيغ المثلثية الأخرى. يتم تقديم الحل الأكثر فعالية في نهاية الدرس.

ولتلخيص الفقرة نستنتج: أي تكامل النموذج وأين و- حتىالأرقام، يتم حلها عن طريق تقليل درجة التكامل.
من الناحية العملية، صادفت تكاملات ذات 8 و10 درجات، وكان علي أن أحل هذه الفوضى الرهيبة عن طريق خفض الدرجة عدة مرات، مما أدى إلى إجابات طويلة جدًا.

طريقة الاستبدال المتغيرة

كما ذكر في المقال طريقة التغيير المتغير في التكامل غير المحدد، الشرط الأساسي لاستخدام طريقة الاستبدال هو حقيقة وجود دالة معينة ومشتقتها في التكامل:
(الوظائف ليست بالضرورة في المنتج)

مثال 11

أوجد التكامل غير المحدد.

ننظر إلى جدول المشتقات ونلاحظ الصيغ، ، أي أنه في تكاملنا توجد دالة ومشتقتها. ولكننا نرى أنه أثناء التفاضل يتحول جيب التمام وجيب التمام إلى بعضهما البعض، والسؤال الذي يطرح نفسه: كيف يتم تغيير المتغير وماذا نعني بجيب التمام أو جيب التمام؟! يمكن حل السؤال عن طريق الوخز العلمي: إذا قمنا بالاستبدال بشكل غير صحيح، فلن يأتي أي شيء جيد.

إرشادات عامة: في حالات مماثلة، تحتاج إلى تعيين الدالة الموجودة في المقام.

نقاطع الحل ونقوم بالاستبدال

كل شيء على ما يرام في القاسم، كل شيء يعتمد فقط على، الآن يبقى معرفة ما سيتحول إليه.
للقيام بذلك، نجد التفاضل:

أو باختصار:
ومن المساواة الناتجة، وباستخدام قاعدة التناسب، نعبر عن التعبير الذي نحتاجه:

لذا:

الآن، يعتمد التكامل بأكمله على الحل ويمكننا الاستمرار فيه

مستعد. اسمحوا لي أن أذكرك أن الغرض من الاستبدال هو تبسيط التكامل؛ في هذه الحالة، كان كل شيء يتعلق بتكامل دالة الطاقة وفقًا للجدول.

وليس من قبيل الصدفة أنني وصفت هذا المثال بهذا التفصيل، وذلك بغرض التكرار وتعزيز مواد الدرس طريقة التغيير المتغير في التكامل غير المحدد.

والآن مثالان للحل الخاص بك:

مثال 12

أوجد التكامل غير المحدد.

مثال 13

أوجد التكامل غير المحدد.

الحلول والأجوبة كاملة في نهاية الدرس.

مثال 14

أوجد التكامل غير المحدد.

هنا مرة أخرى، في التكامل، هناك جيب وجيب التمام (دالة بمشتقة)، ولكن في المنتج تنشأ معضلة - ماذا نعني بجيب التمام أو جيب التمام؟

يمكنك محاولة إجراء الاستبدال باستخدام الوخز العلمي، وإذا لم ينجح شيء، فقم بتعيينه كوظيفة أخرى، ولكن هناك:

إرشادات عامة: تحتاج إلى تعيين الوظيفة التي، بالمعنى المجازي، في "وضع غير مريح".

نرى أنه في هذا المثال، "يعاني" جيب تمام الطالب من الدرجة، ويجلس جيب التمام بحرية، من تلقاء نفسه.

لذلك، دعونا نجعل بديلا:

إذا كان أي شخص لا يزال يواجه صعوبات في خوارزمية استبدال المتغير وإيجاد التفاضل، فيجب عليك العودة إلى الدرس طريقة التغيير المتغير في التكامل غير المحدد.

مثال 15

أوجد التكامل غير المحدد.

دعونا نحلل التكامل، ما الذي ينبغي الإشارة إليه؟
دعونا نتذكر إرشاداتنا:
1) الدالة على الأرجح في المقام؛
2) الوظيفة في "وضع غير مناسب".

بالمناسبة، هذه الإرشادات صالحة ليس فقط للدوال المثلثية.

يناسب الجيب كلا المعيارين (خاصة الثاني)، لذلك يقترح البديل نفسه. من حيث المبدأ، يمكن إجراء الاستبدال بالفعل، ولكن أولا سيكون من الجيد معرفة ما يجب القيام به؟ أولاً، نحن "نقرص" جيب تمام واحد:

نحن نحتفظ بفرقنا "المستقبلي".

ونعبر عنها من خلال جيب الجيب باستخدام الهوية المثلثية الأساسية:

والآن إليك الاستبدال:

القاعدة العامة: إذا كانت إحدى الدوال المثلثية (جيب الجيب أو جيب التمام) موجودة في التكامل غريبالدرجة، فأنت بحاجة إلى "إزالة" وظيفة واحدة من الدرجة الفردية، وتعيين وظيفة أخرى خلفها.نحن نتحدث فقط عن التكاملات حيث يوجد جيب التمام والجيب.

في المثال الذي تم النظر فيه، كان لدينا جيب تمام عند قوة فردية، لذلك قمنا بإزالة جيب تمام واحد من القوة، وقمنا بتعيينه كجيب.

مثال 16

أوجد التكامل غير المحدد.

الدرجات تقلع =).
هذا مثال عليك حله بنفسك. الحل الكامل والإجابة في نهاية الدرس.

الاستبدال المثلثي العالمي

الاستبدال المثلثي العالمي هو حالة شائعة لطريقة الاستبدال المتغير. يمكنك محاولة استخدامه عندما "لا تعرف ماذا تفعل". ولكن في الواقع هناك بعض المبادئ التوجيهية لتطبيقه. التكاملات النموذجية التي يلزم فيها تطبيق الاستبدال المثلثي الشامل هي التكاملات التالية: , , , إلخ.

مثال 17

أوجد التكامل غير المحدد.

يتم تنفيذ الاستبدال المثلثي العالمي في هذه الحالة على النحو التالي. لنستبدل : . أنا لا أستخدم الحرف، لكن الحرف، هذا ليس نوعًا من القاعدة، إنه فقط، مرة أخرى، أنا معتاد على حل الأمور بهذه الطريقة.

هنا هو أكثر ملاءمة للعثور على التفاضل، من المساواة، أعرب عن:
أقوم بإرفاق قوس ظلي لكلا الجزأين:

قوس الظل والظل يلغي بعضهما البعض:

هكذا:

من الناحية العملية، ليس من الضروري أن تصفها بمثل هذه التفاصيل، ولكن ببساطة استخدم النتيجة النهائية:

! يكون التعبير صالحًا فقط إذا كان لدينا ببساطة "X" تحت جيب التمام وجيب التمام، للتكامل (والتي سنتحدث عنها لاحقا) كل شيء سيكون مختلفا قليلا!

عند الاستبدال، تتحول الجيوب وجيب التمام إلى الكسور التالية:
، ، تعتمد هذه المساواة على الصيغ المثلثية المعروفة: ,

لذلك، يمكن أن يبدو التصميم النهائي كما يلي:

لنجري استبدالًا مثلثيًا عالميًا:

ستكون هناك أيضًا مشكلات يتعين عليك حلها بنفسك، ويمكنك رؤية الإجابات عليها.

يمكن تحويل التكامل من حاصل ضرب الدوال المثلثية إلى المجموع

دعونا نفكر في التكاملات التي يكون التكامل فيها هو حاصل ضرب جيب التمام وجيب التمام من الدرجة الأولى لـ x مضروبًا في عوامل مختلفة، أي تكاملات النموذج

استخدام الصيغ المثلثية المعروفة

(2)
(3)
(4)
يمكن تحويل كل منتج من تكاملات الشكل (31) إلى مجموع جبري وتكامله حسب الصيغ

(5)

(6)

مثال 1.يجد

حل. وفقا للصيغة (2) في

مثال 2.يجد تكامل الدالة المثلثية

حل. وفقا للصيغة (3) في

مثال 3.يجد تكامل الدالة المثلثية

حل. وفقا للصيغة (4) في نحصل على التحويل التالي للتكامل:

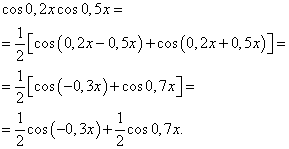
وبتطبيق الصيغة (6) نحصل على

تكامل حاصل ضرب قوى الجيب وجيب التمام لنفس الحجة

دعونا الآن نفكر في تكاملات الدوال التي هي نتاج قوى الجيب وجيب التمام لنفس الحجة، أي.

(7)

وفي حالات خاصة، أحد المؤشرات ( مأو ن) قد يكون صفراً.

عند دمج مثل هذه الوظائف، يتم استخدامه أنه يمكن التعبير عن القوة الزوجية لجيب التمام من خلال جيب التمام، ويكون تفاضل الجيب مساويًا لجيب التمام × دي إكس(أو حتى قوة الجيب يمكن التعبير عنها بدلالة جيب التمام، والتفاضل في جيب التمام يساوي - الخطيئة × دي إكس ) .

وينبغي التمييز بين حالتين: 1) واحد على الأقل من المؤشرات مو نغريب؛ 2) كلا المؤشرين متساويان.

لتكن الحالة الأولى هي المؤشر ن = 2ك+ 1 - غريب. ثم نظرا لذلك

يتم تقديم التكامل بطريقة يكون جزء منها دالة للجيب فقط، والآخر هو تفاضل الجيب. الآن باستخدام استبدال متغير ر= خطيئة سالحل يقلل من تكامل كثير الحدود فيما يتعلق ر. إلا إذا كانت الدرجة مأمر غريب، ثم يفعلون الشيء نفسه، ويعزلون عامل الخطيئة س، معبراً عن بقية التكامل بدلالة cos سوالاعتقاد ر=cos س. يمكن أيضًا استخدام هذه التقنية عندما دمج قوى حاصل الجيب وجيب التمام ، متى واحد على الأقل من المؤشرات غريب . بيت القصيد هو أن حاصل قسمة قوى الجيب وجيب التمام هو حالة خاصة لناتجهما : عندما تكون الدالة المثلثية في مقام التكامل فإن درجتها تكون سالبة. ولكن هناك أيضًا حالات لدوال مثلثية جزئية، عندما تكون قواها متساوية فقط. عنهم - في الفقرة التالية.

إذا كان كلا المؤشرين مو ن- حتى باستخدام الصيغ المثلثية

تقليل أسس الجيب وجيب التمام، وبعد ذلك يتم الحصول على تكامل من نفس النوع المذكور أعلاه. ولذلك ينبغي أن يستمر التكامل وفق نفس المخطط. إذا كان أحد الأسس الزوجية سالبًا، أي أنه يتم أخذ حاصل الضرب الزوجي لقوى الجيب وجيب التمام في الاعتبار، فإن هذا المخطط غير مناسب . ثم يتم استخدام تغيير المتغير اعتمادًا على كيفية تحويل التكامل. سيتم النظر في مثل هذه الحالة في الفقرة التالية.

مثال 4.يجد تكامل الدالة المثلثية

حل. الأس جيب التمام غريب. لذلك، دعونا نتخيل

ر= خطيئة س(ثم dt=cos س dx ). ثم نحصل

وبالعودة إلى المتغير القديم، نجد أخيرا

مثال 5.يجد تكامل الدالة المثلثية

حل. أس جيب التمام، كما في المثال السابق، غريب، ولكنه أكبر. دعنا نتخيل

وإجراء تغيير المتغير ر= خطيئة س(ثم dt=cos س dx ). ثم نحصل

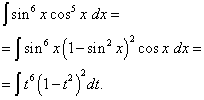
دعونا نفتح الأقواس

ونحصل

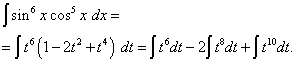
وبالعودة إلى المتغير القديم، حصلنا على الحل

مثال 6.يجد تكامل الدالة المثلثية

حل. أسس الجيب وجيب التمام متساوية. لذلك نقوم بتحويل الدالة التكاملية كما يلي:

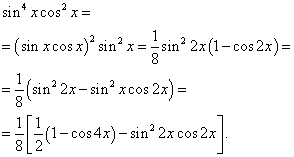
ثم نحصل

في التكامل الثاني نقوم بتغيير المتغير، الإعداد ر= الخطيئة2 س. ثم (1/2)dt= كوس2 س dx . لذلك،

أخيرا وصلنا

استخدام طريقة الاستبدال المتغير

طريقة الاستبدال المتغيرةعند تكامل الدوال المثلثية، يمكن استخدامه في الحالات التي يحتوي فيها التكامل على جيب التمام فقط أو جيب التمام فقط، وهو حاصل ضرب الجيب وجيب التمام، حيث يكون الجيب أو جيب التمام من الدرجة الأولى، الظل أو ظل التمام، وكذلك حاصل قسمة حتى قوى الجيب وجيب التمام لنفس الحجة. في هذه الحالة، من الممكن إجراء التباديل ليس فقط الخطيئة س = روالخطيئة س = ر، ولكن أيضًا تيراغرام س = رو CTG س = ر .

مثال 8.يجد تكامل الدالة المثلثية

حل. دعونا نغير المتغير: , ثم . يمكن دمج التكامل الناتج بسهولة باستخدام جدول التكاملات:

مثال 9.يجد تكامل الدالة المثلثية

حل. دعونا نحول الظل إلى نسبة الجيب وجيب التمام:

دعونا نغير المتغير: , ثم . التكامل الناتج هو تكامل الجدولمع علامة ناقص:

وبالعودة إلى المتغير الأصلي، نحصل أخيرا على:

مثال 10.يجد تكامل الدالة المثلثية

حل. دعونا نغير المتغير: , ثم .

دعونا نحول التكامل لتطبيق الهوية المثلثية :

نقوم بتغيير المتغير، دون أن ننسى وضع علامة الطرح أمام التكامل (انظر أعلاه، ما يساوي dt). بعد ذلك، نقوم بتحليل التكامل والتكامل باستخدام الجدول:

وبالعودة إلى المتغير الأصلي، نحصل أخيرا على:

أوجد تكامل الدالة المثلثية بنفسك، ثم انظر إلى الحل

الاستبدال المثلثي العالمي

الاستبدال المثلثي العالمي يمكن استخدامه في الحالات التي لا يندرج فيها التكامل ضمن الحالات التي تمت مناقشتها في الفقرات السابقة. في الأساس، عندما يكون جيب التمام أو جيب التمام (أو كليهما) في مقام الكسر. لقد ثبت أنه يمكن استبدال الجيب وجيب التمام بتعبير آخر يحتوي على ظل نصف الزاوية الأصلية كما يلي:

لكن لاحظ أن الاستبدال المثلثي الشامل غالبًا ما يستلزم تحويلات جبرية معقدة جدًا، لذلك من الأفضل استخدامه عندما لا تنجح أي طريقة أخرى. دعونا نلقي نظرة على الأمثلة التي يتم فيها استخدام الاستبدال تحت العلامة التفاضلية وطريقة المعاملات غير المحددة، إلى جانب الاستبدال المثلثي الشامل.

مثال 12.يجد تكامل الدالة المثلثية

حل. حل. دعونا نستفيد الاستبدال المثلثي العالمي. ثم
.

نضرب الكسور في البسط والمقام في ، ونخرج الاثنين ونضعهما أمام علامة التكامل. ثم

جدول المشتقات العكسية ("التكاملات"). جدول التكاملات. التكاملات الجدولية غير المحددة. (أبسط التكاملات والتكاملات مع المعلمة). صيغ التكامل بالأجزاء صيغة نيوتن-لايبنتز.

جدول المشتقات العكسية ("التكاملات"). التكاملات الجدولية غير المحددة. (أبسط التكاملات والتكاملات مع المعلمة).
جزء لا يتجزأ من وظيفة السلطة.	جزء لا يتجزأ من وظيفة السلطة.
تكامل يختزل إلى تكامل دالة القدرة إذا كانت x مدفوعة تحت العلامة التفاضلية.

	تكامل الأسي، حيث a هو رقم ثابت.
تكامل الدالة الأسية المعقدة.	تكامل الدالة الأسية.

تكامل يساوي اللوغاريتم الطبيعي.	التكامل: "اللوغاريتم الطويل".
	التكامل: "اللوغاريتم الطويل".
متكامل: "اللوغاريتم العالي".	التكامل، حيث يتم وضع x في البسط تحت العلامة التفاضلية (يمكن إضافة أو طرح الثابت الموجود تحت العلامة)، يشبه في النهاية تكاملًا يساوي اللوغاريتم الطبيعي.
متكامل: "اللوغاريتم العالي".

جيب التمام لا يتجزأ.	تكامل جيبي.
التكامل يساوي الظل.	التكامل يساوي ظل التمام.

التكامل يساوي كلاً من أركسين وأركوسين
تكامل يساوي كلاً من أركسين وأركوسين.	تكامل يساوي كلاً من الظل القوسي والظل القوسي.

التكامل يساوي قاطع التمام.	التكامل يساوي القاطع.
التكامل يساوي القوسي.	التكامل يساوي قوسي.
التكامل يساوي القوسي.	التكامل يساوي القوسي.

التكامل يساوي الجيب الزائدي.	التكامل يساوي جيب التمام الزائدي.

التكامل يساوي الجيب الزائدي، حيث sinhx هو الجيب الزائدي في النسخة الإنجليزية.	التكامل يساوي جيب التمام الزائدي، حيث sinhx هو جيب التمام الزائدي في النسخة الإنجليزية.
التكامل يساوي المماس الزائدي.	التكامل يساوي ظل التمام الزائدي.
التكامل يساوي القاطع الزائدي.	التكامل يساوي قاطع التمام الزائدي.

صيغ التكامل بالأجزاء قواعد التكامل.

صيغ التكامل بالأجزاء قواعد نيوتن-لايبنتز للتكامل.
دمج المنتج (الوظيفة) بواسطة ثابت:
دمج مجموع الوظائف:
التكاملات غير المحددة:
صيغة التكامل بالأجزاء التكاملات المحددة:
صيغة نيوتن-لايبنتز التكاملات المحددة:	حيث F(a),F(b) هي قيم المشتقات العكسية عند النقطتين b وa على التوالي.

جدول المشتقات. المشتقات الجدولية. مشتق من المنتج. مشتق من الحاصل. مشتق من وظيفة معقدة.

إذا كان x متغيرا مستقلا فإن:

جدول المشتقات. المشتقات الجدولية."مشتقات الجدول" - نعم، لسوء الحظ، هذه هي بالضبط الطريقة التي يتم البحث عنها على الإنترنت
	مشتق من وظيفة السلطة

	مشتق من الأس
مشتقة من وظيفة الأسية المعقدة	مشتق من الدالة الأسية

مشتق من دالة لوغاريتمية	مشتق من اللوغاريتم الطبيعي
	مشتق من اللوغاريتم الطبيعي للدالة

مشتق من الجيب	مشتق من جيب التمام
مشتق من قاطع التمام	مشتق من القاطع
مشتق من أركسين	مشتق من قوس جيب التمام
مشتق من أركسين	مشتق من قوس جيب التمام
مشتق الظل	مشتق من ظل التمام
مشتق من قوس الظل	مشتق من ظل التمام القوسي
مشتق من قوس الظل	مشتق من ظل التمام القوسي
مشتق من القاطع القوسي	مشتق من قوسي
مشتق من القاطع القوسي	مشتق من قوسي

مشتق من الجيب الزائدي مشتق من الجيب الزائدي في النسخة الإنجليزية	مشتق من جيب التمام الزائدي مشتق من جيب التمام الزائدي في النسخة الإنجليزية
مشتق من الظل الزائدي	مشتق من ظل التمام الزائدي
مشتق من القاطع الزائدي	مشتق من قاطع التمام الزائدي

قواعد التمايز. مشتق من المنتج. مشتق من الحاصل. مشتق من وظيفة معقدة.
مشتق المنتج (الدالة) بواسطة ثابت:
مشتق من المجموع (الوظائف):
مشتق من المنتج (الوظائف):
مشتق حاصل القسمة (الوظائف):
مشتق من وظيفة معقدة:

خصائص اللوغاريتمات. الصيغ الأساسية للوغاريتمات. العشري (LG) واللوغاريتمات الطبيعية (LN).

الهوية اللوغاريتمية الأساسية
دعونا نوضح كيف يمكن جعل أي دالة بالصيغة a b أسية. بما أن الدالة بالصيغة e x تسمى الأسية، إذن
يمكن تمثيل أي دالة على الصورة a b كقوة للعدد عشرة

اللوغاريتم الطبيعي ln (اللوغاريتم للأساس e = 2.718281828459045...) ln(e)=1; قانون الجنسية (1) = 0

سلسلة تايلور. توسيع سلسلة تايلور للدالة.

وتبين أن الأغلبية واجهت عمليايمكن تمثيل الوظائف الرياضية بأي دقة في محيط نقطة معينة في شكل سلسلة قوى تحتوي على قوى متغير بترتيب متزايد. على سبيل المثال، بالقرب من النقطة x=1:

عند استخدام سلسلة تسمى صفوف تايلور،يمكن التعبير عن الدوال المختلطة التي تحتوي، على سبيل المثال، على دوال جبرية ومثلثية وأسية كدوال جبرية بحتة. باستخدام المتسلسلة، يمكنك في كثير من الأحيان إجراء التمايز والتكامل بسرعة.

متسلسلة تايلور في جوار النقطة أ لها الشكل:

1) ، حيث f(x) هي دالة لها مشتقات من جميع الطلبات عند x=a. R n - يتم تحديد الحد المتبقي في سلسلة تايلور بواسطة التعبير

يتم تحديد معامل k (عند x k) للسلسلة بواسطة الصيغة

3) هناك حالة خاصة من سلسلة تايلور هي سلسلة ماكلورين (= ماكلارين). (يحدث التمدد حول النقطة a=0)

عند = 0

يتم تحديد أعضاء السلسلة بواسطة الصيغة

شروط استخدام سلسلة تايلور.

1. لكي يتم توسيع الدالة f(x) إلى سلسلة تايلور على الفاصل الزمني (-R;R)، فمن الضروري والكافي أن يكون الحد المتبقي في صيغة Taylor (Maclaurin (=McLaren)) لهذا تميل الدالة إلى الصفر كـ k →∞ في الفاصل الزمني المحدد (-R;R).

2. من الضروري أن تكون هناك مشتقات لدالة معينة عند النقطة التي سنقوم ببناء متسلسلة تايلور بالقرب منها.

خصائص سلسلة تايلور

إذا كانت f دالة تحليلية، فإن متسلسلة تايلور الخاصة بها عند أي نقطة a في مجال تعريف f تتقارب مع f في بعض المناطق المجاورة لـ a.

هناك دوال قابلة للاشتقاق بشكل لا نهائي وتتقارب متسلسلة تايلور، ولكنها في نفس الوقت تختلف عن الدالة الموجودة في أي حي من أ. على سبيل المثال:

تُستخدم متسلسلة تايلور في التقريب (التقريب هو أسلوب علمي يتكون من استبدال بعض الكائنات بأخرى، بمعنى أو بآخر قريب من الكائنات الأصلية، ولكن بشكل أبسط) للدالة بواسطة كثيرات الحدود. على وجه الخصوص، الخطية ((من الخطية - الخطية)، إحدى طرق التمثيل التقريبي للأنظمة غير الخطية المغلقة، حيث يتم استبدال دراسة النظام غير الخطي بتحليل النظام الخطي، بمعنى ما يعادل النظام الأصلي .) تحدث المعادلات عن طريق التوسع في سلسلة تايلور وقطع جميع الحدود فوق الدرجة الأولى.

وبالتالي، يمكن تمثيل أي دالة تقريبًا على أنها متعددة الحدود بدقة معينة.

أمثلة على بعض التوسعات الشائعة لدوال القدرة في متسلسلة ماكلورين (=ماكلارين، تايلور بالقرب من النقطة 0) وتايلور بالقرب من النقطة 1. الحدود الأولى لتوسيعات الدوال الرئيسية في متسلسلة تايلور وماكلارين.

أمثلة على بعض التوسعات الشائعة لدوال القدرة في متسلسلة ماكلورين (=ماكلارين، تايلور بالقرب من النقطة 0)