В классической ньютоновской механике размеры тел и промежутки времени между событиями рассматриваются как абсолютные величины. Это означает, что можно говорить о длине тел, не указывая, покоится это тело или движется.Т.е. линейные масштабы (длина отрезков) и промежутки времени остаются неизменными при переходе от 1-й системы отсчета к другой, т.е. не зависят от выбора системы отсчета.Эти представления отражают Ньютоновскую концепцию абсолютности пространства и времени.
2.Кинематика
Это раздел механики, в кот. изучают способы описания движения тел, не интересуясь порождающими это движение причинами.
3.Траектория
Это линия в пространстве, вдоль которой движется частица(геометрическое место концов радиус-вектора частицы)
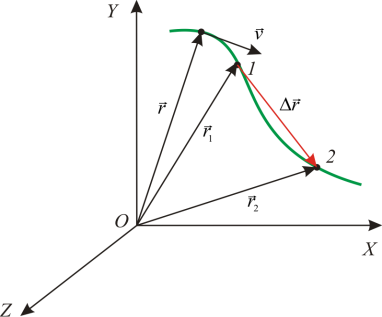
4.Перемещение
Dr = r 2 – r 1 за промежуток времени Dt называется вектор, проведенный из начального в конечное положение частицы (из точки 1 в точку 2 ).
5.Вектор средней скорости < v >.
Вектор средней скорости < v > – это вектор, равный отношению перемещения частицы ко времени Dt , за которое оно было совершено:
Вектор средней скорости < v > совпадает по направлению с вектором перемещения D r .
6.Мгновенной скоростью v частицы (или просто скоростью ) называется вектор, равный производной радиуса-вектора r по времени:
Мгновенная скорость v направлена по касательной к траектории в сторону движения частицы.СИ:м/с
7. Ускорением называется вектор, равный производной по времени скорости v частицы:
8. Закон движения
называется зависимость от времени координат частицы:
Между векторным и координатным способами описания движения существует простая связь. Любой вектор можно задать его проекциями на оси координат. Например, радиус-вектор частицы:
где i , j , k – орты координатных осей.
9. Скорость при координатном способе описания движения
Скорость v , как и любой вектор, может быть представлена через проекции на оси ДСК:
Т.е.,
скорость
v
частицы можно представить в следующем
виде:
Видно, что компоненты скорости,выраженные через функции x (t ), y (t ), z (t ), равны
10.Ускорение при координатном способе задания движения Ускорение a , как и любой вектор, может быть представлен через проекции на оси ДСК:
Т.е., скорость v частицы можно представить в следующем виде
11.
Путь
s
(или Ds
)
равен измеренному вдоль траектории
расстоянию, пройденному частицей в
процессе движения (длина траектории).
Путь является величиной скалярной,
неотрицательной и неубывающей.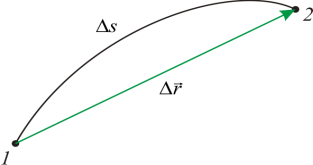
12. Полное ускорение частицы
a можно представить в виде суммы двух перпендикулярных друг другу составляющих:
Модуль
полного ускорения:
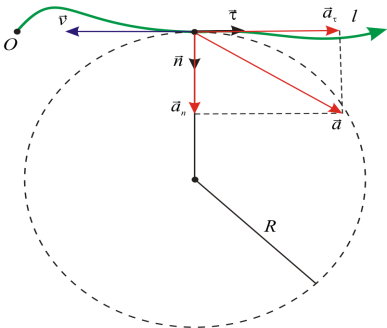
13.Тангенциальное(касательное) ускорение
Вектор a t направлен по касательной к траектории движения частицы; при этом a t v , если движение ускоренное; a t ¯v , если движение замедленное. Тангенциальное ускорение частицы характеризует изменение скорости частицы по модулю (если a t = 0, движение является равномерным).
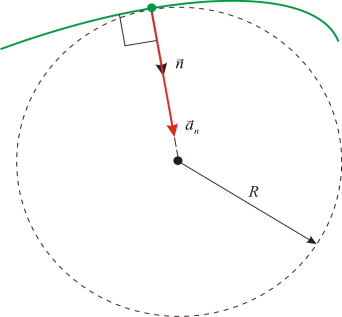
14. нормальное (центростремительное)
ускорение
Вектор a n всегда перпендикулярен касательной к тракетории движения, т.е. a n ^v и a n ^a t .
Нормальное ускорение характеризует изменение скорости по направлению (для прямолинейного движения, когда R = ¥, a n = 0)
15. Абсолютно твердое тело
в механике называют тело, при движении которого расстояния между любыми двумя его точками остаются неизменными. Таким образом, твердое тело не деформируется под действием внешних сил.
16. Число степеней свободы тела – это количество независимых переменных (величин), которые необходимо задать, чтобы определить положение тела в пространстве. Пример. Число степеней свободы материальной точки равно 3 (три независимые переменные (координаты) x , y , z ).
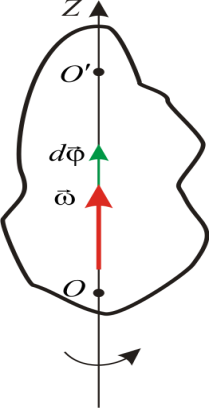
17.Угловая скорость тела
Пусть тело, вращаясь вокруг оси Z , совершило за малый промежуток времени dt элементарный поворот d j .Угловой скоростью тела называется вектор
Вектор w
совпадает по направлению с вектором
d
j
,
т.е. направлен вдоль оси вращения тела
так, что образует правый винт с
направлением вращения.Проекция вектора
w
на ось Z
и его модуль:
Единица измерения
w
– радиан в
секунду
(рад/с
)
Словосочетание линейная скорость используют тогда, когда рассматривая криволинейное движение тела, и хотят подчеркнуть разницу между скоростью $v\ $и уголовной скоростью $\omega $. Чаще всего слово линейная опускают и говорят просто скорость.
Вектор средней скорости
Определение
Отношение перемещения ($\Delta \overline{r}$) к промежутку времени в течение которого это перемещение произошло, называют средней скоростью ($\left\langle \overline{v}\right\rangle $) движения:
\[\left\langle \overline{v}\right\rangle =\frac{\Delta \overline{r}}{\Delta t}\left(1\right),\]
где $\Delta \overline{r}$ - изменение радиус-вектора материальной точки за время $\Delta t$ (рис.1).
Вектор средней скорости $\left\langle \overline{v}\right\rangle $ имеет такое же направление как вектор $\Delta \overline{r}$, так как $\Delta t>0$. Длина отрезка, изображающего вектор средней скорости (рис.1) не связана с длиной вектора $\Delta \overline{r}$.
Средняя скорость характеризует быстроту перемещения точки. Данная характеристика относится к определенному промежутку времени.
Если тело движется по кривой, то путь ($\Delta s$) больше модуля перемещения ($\Delta r$) за один и тот же промежуток времени, так как длина дуги всегда меньше длины стягивающей ее хорды (рис.1). Путь и перемещение совпадают при прямолинейном движении в одном направлении. Величина средней скорости прохождения пути определена как:
\[\left\langle v\right\rangle {\rm =}\frac{\Delta s}{\Delta t}\left(2\right).\]
Средняя скорость характеризует быстроту перемещения материальной точки за конечный промежуток времени
Мгновенная скорость
Определение
Уменьшая промежуток времени, в который рассматривается движение частицы ($\Delta t\to 0$), мы получаем характеристику движения точки в данный момент времени. Величина равная:
\[\overline{v}={\mathop{\lim }_{\Delta t\to 0} \left\langle \overline{v}\right\rangle =\ }{\mathop{\lim }_{\Delta t\to 0} \frac{\Delta \overline{r}}{\Delta t}=\frac{d\overline{r}}{dt}\left(3\right),\ }\]
называется мгновенной скоростью или просто скоростью.
При вычислении скорости по формуле (3) очевидно, что уменьшение промежутка времени $\Delta t$ ведет к тому, что в конце концов очередные получаемые величины средней скорости будут мало отличаться друг от друга. Поэтому при нахождении мгновенной скорости останавливаются на конечном значении $\Delta t,\ $но малом, для того чтобы была возможность получить необходимую точность величины скорости.
Предельный переход (3) имеет геометрический смысл. Вектор $\Delta \overline{r}$ направлен вдоль хорды, соединяющей две точки траектории, сближение этих точек ведет к тому, что этот вектор принимает положение касательной к траектории движения в данной точке. Получается, что вектор скорости направлен по касательной к траектории движения. При прямолинейном движении вектор скорости направлен по прямой.
Скорость прохождения пути определена аналогично:
Если траектория движения материальной точки - плавная кривая, то чем короче дуга, тем ближе она по длине к длине хорды. В предельном переходе при$\ \Delta t\to 0$ можно считать, что $\Delta s\to \Delta r$. Следовательно,
Сложение скоростей
Скорость является векторной величиной. Если материальная точка принимает участие в нескольких движениях, то его скорость находят как векторную сумму скоростей каждого из движений:
\[\overline{v}=\sum\limits_i{{\overline{v}}_i\left(6\right).}\]
В некоторых случаях удобно представлять сложное движение как наложение нескольких простых движений. Тогда равенство (6)можно рассматривать, как правило разложения вектора скорости на составляющие.
Скорость и ускорение движения
При неравномерном движении материальная точка обладает ускорением ($\overline{a}$). Ускорение является первой производной от скорости по времени:
\[\overline{a}=\frac{d\overline{v}}{dt}\left(7\right).\]
Из выражения (7) следует, что зная ускорение точки, скорость находят как:
\[\overline{v}=\int\limits^{t_2}_{t_1}{\overline{a}dt}\left(8\right).\]
Угловая и линейная скорости
При движении по окружности вместе со скоростью движения по траектории ($v$- линейная скорость) вводят угловую скорость ($\omega $), которая характеризует быстроту изменения угла поворота $\varphi $:
\[\omega =\frac{d\varphi }{dt}\left(9\right).\]
Связь между линейной и угловой скоростями задана выражением:
Примеры задач с решением
Пример 1
Задание. Изменение радиус-вектора, определяющего положение материальной точки, задано уравнением: $\overline{r\ }\left(t\right)=t^4\overline{i}+3t^2\overline{j},$ где $\overline{i}$ и $\overline{j}$ - единичные векторы осей X и Y (рис.2). Какова величина мгновенной скорости точки в момент времени $t=1$c?
Решение. Скорость частицы определим как:
\[\overline{v}={\frac{d\overline{r}}{dt} \left(1.1\right).\ }\]
Подставляем в формулу (1.1) уравнение для радиус-вектора $\overline{r\ }\left(t\right)=t^4\overline{i}+3t^2\overline{j},$ получаем:
\[\overline{v}=\frac{d}{dt}\left(t^4\overline{i}+3t^2\overline{j}\right)=4t^3\overline{i}+6t\overline{j}\ \left(1.2\right).\]
Из уравнения (1.2) мы видим, что:
\[\left\{ \begin{array}{c} v_x=4t^3 \\ v_y=6t \end{array} \right.\left(1.3\right).\]
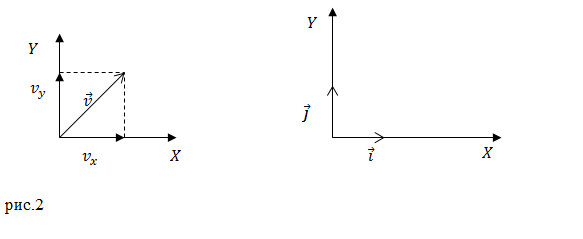
Следуя теореме Пифагора, модуль скорости найдем как:
Вычислим скорость, подставив в полученную формулу время $t=1$c:
Ответ. $v$=7,2 $\frac{м}{с}$
Пример 2
Задание. Материальная точка движется прямолинейно. Ускорение этой точки увеличивается в соответствии с графиком (рис.3). Какой будет скорость движения точки в момент времени $t_1?$
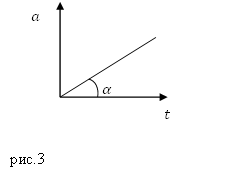
Решение. На графике рис.3 ускорение изображено прямой, выходящей из начала координат, на основе рис.3 аналитическое выражение для ускорения запишем как:
где $k=tg\ \alpha $.
Скорость точки найдем как:
Ответ. $v=\frac{tg\ \alpha \cdot t^2_1}{2}$
Уменьшая неограниченно промежуток времени t, за который произошло перемещение м. т. в пространстве в пределе, когда t 0, получим мгновенную скорость, т. е.
Вектор мгновенной скорости равен пределу отношения приращения радиус-вектора м. т. к тому промежутку времени, за которое это приращение произошло, когда t 0 или равен первой производной радиус-вектора по времени.
Вектор мгновенной скорости в данный момент времени направлен по касательной к траектории в данной точке (рис. 9).
Действительно,
при t
0, когда точка М 2
приближается к М 1 ,
хорда (секущая)
,
сближается с длиной отрезка дугиs
и в пределе s
=
,
а секущая переходит в касательную. Это
наглядно подтверждается опытами.
Например, искры при заточке инструмента
всегда направлены по касательной к
точильному кругу. Поскольку, скорость
– величина векторная, то модуль ее
.
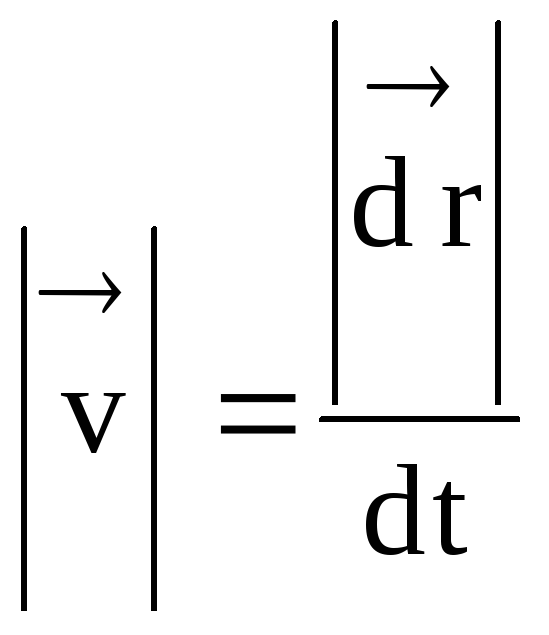В
некоторых типах ускорителей (например,
циклотронах и др.) частицы многократно
движутся по замкнутой траектории без
остановки. Следовательно, в любой точке
траектории модуль вектора мгновенной
скорости должен отличаться от нуля. Это
заключение подтверждается не только
уравнением (15), но и согласуется с понятием
средней скалярной скорости (формула
11). Если в уравнении (11) перейти к пределу
при t
0, то придется рассматривать такие малые
участки пути на траектории s,
которые не отличаются от модуля
элементарного вектора перемещения
.
Тогда на основании уравнения (11) можно
получить значение мгновенной скалярной
скорости
совпадающее
с модулем вектора мгновенной скорости
,
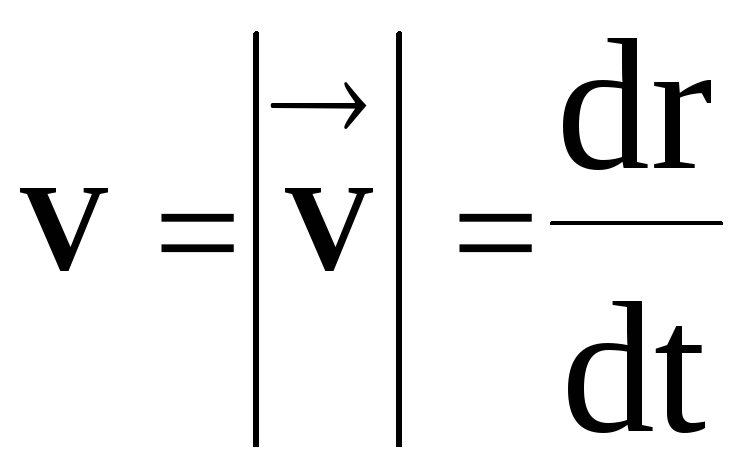так как r = s при t 0.
Одно уравнение вектора мгновенной скорости (15) можно заменить эквивалентной системой трех скалярных уравнений, проекций вектора скорости на оси координат
v x = dx/dt, v y = dy/dt, v z = dz/dt. (16)
Вектор мгновенной скорости связан с его проекциями на оси координат выражением
,
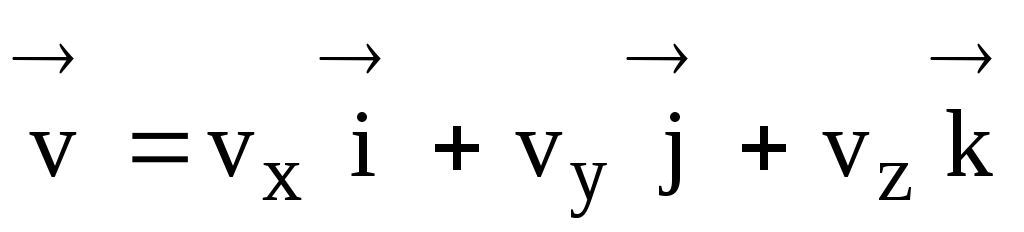(17)
где
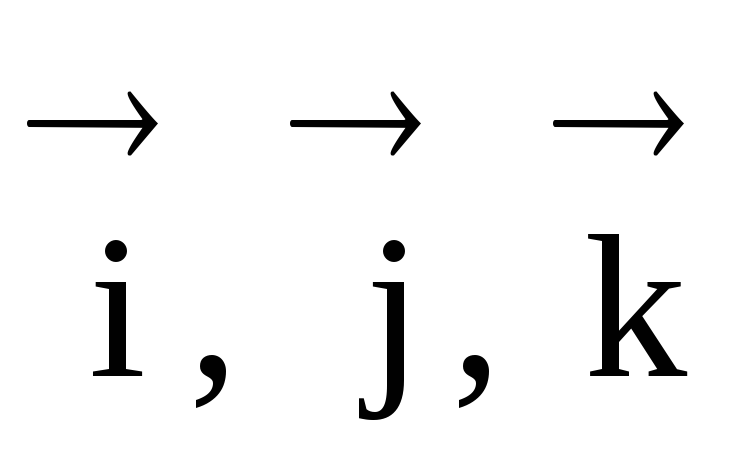– единичные векторы, направленные вдоль
осей Х, У,Z
соответственно.
По модулю
.
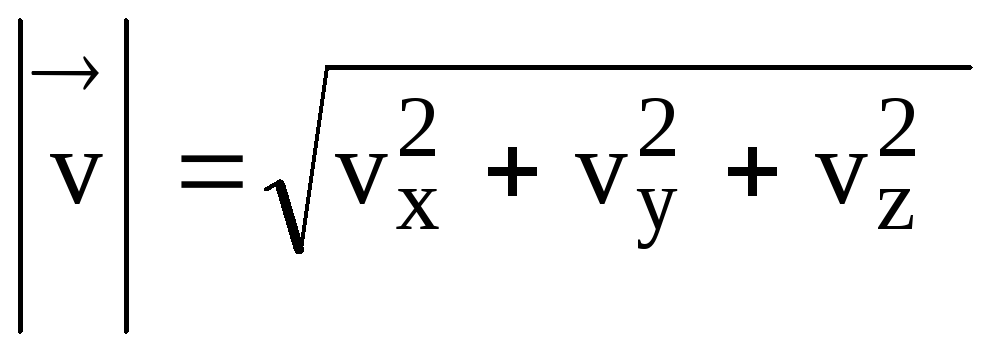(18)
Таким образом, вектор скорости характеризует быстроту изменения перемещения в пространстве по величине и направлению с течением времени. Скорость – функция времени.
1.12. Среднее ускорение
При движении тел скорость в общем случае может изменяться как по величине, так и по направлению.
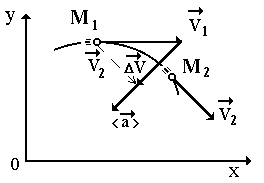
Пусть
м. т. в некоторый момент времени t 1
находится в пункте М 1
и движется со скоростью
,
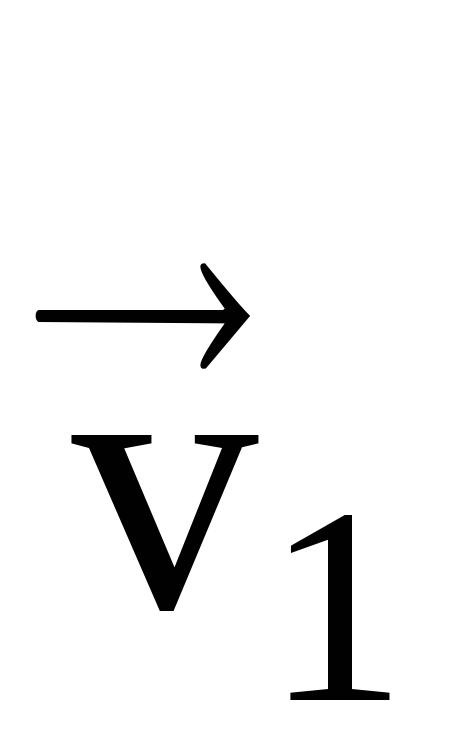а в момент времени t 2
– в пункте М 2
– со скоростью
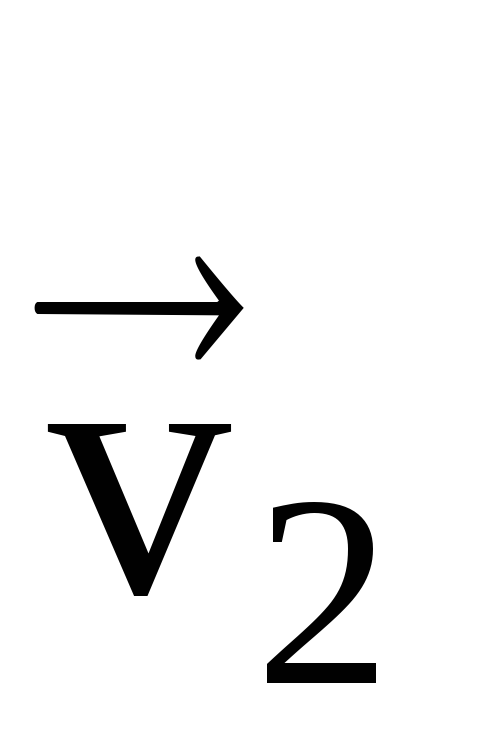(рис. 10).
Перенесем
вектор
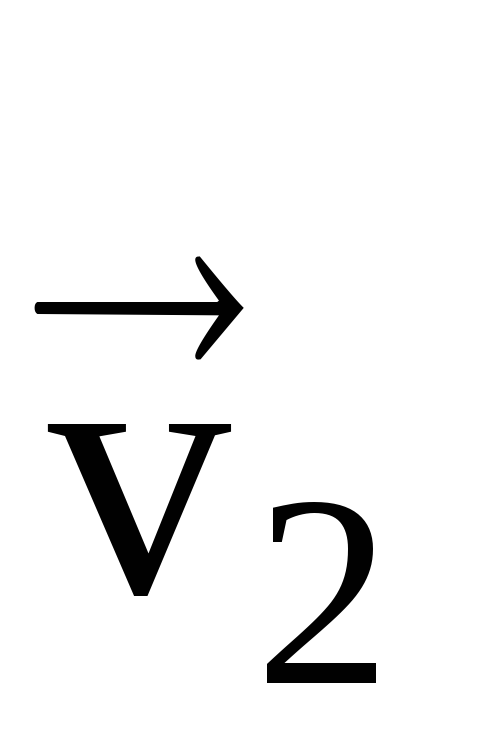параллельно самому себе в точку М 1
так, чтобы совпали начала векторов
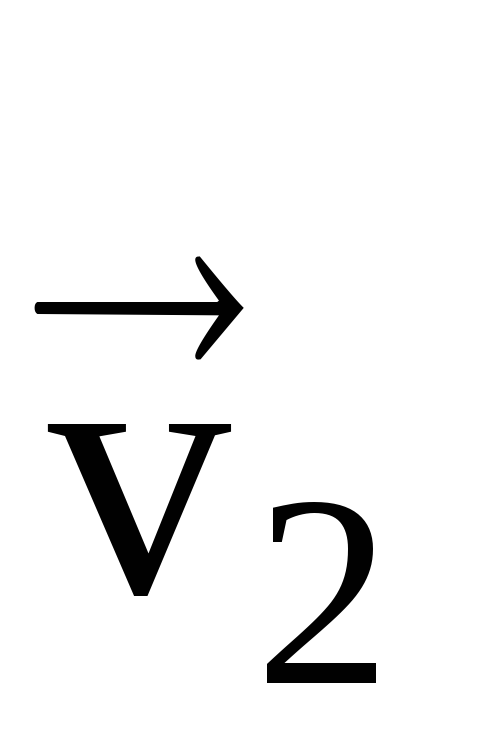и.
Тогда
разность векторов
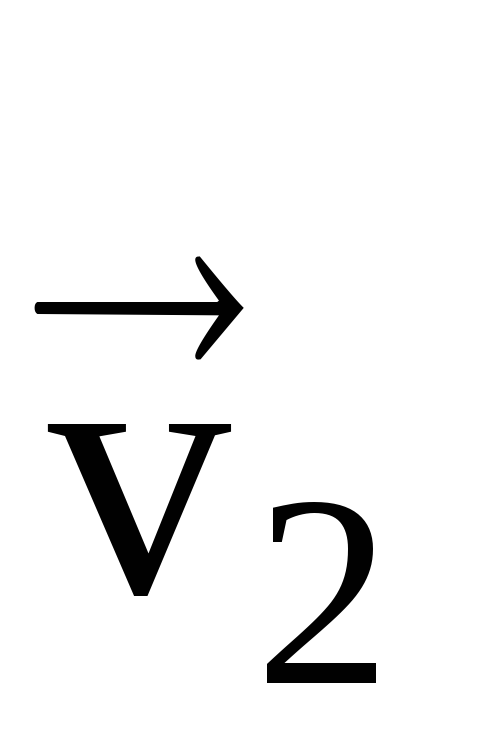иесть вектор изменения (приращения)
скорости за промежуток времениt
= t 2
– t 1 ,
т. е.
.
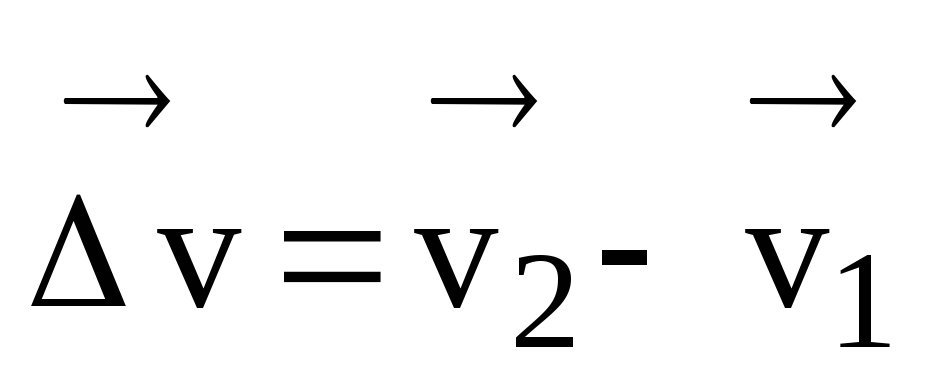(19)
Вектор среднего ускорения равен отношению вектора изменения скорости к промежутку времени, за которое это изменение произошло.
Следовательно,
.
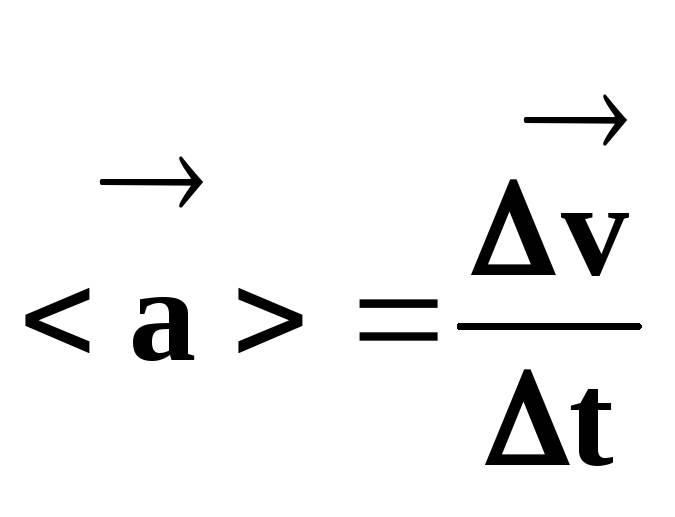(20)
Вектор среднего ускорения совпадает с направлением вектора изменения скорости и, направлен внутрь кривизны траектории.
Одному векторному уравнению (1.20) соответствует система из трех скалярных уравнений для проекций вектора среднего ускорения на оси координат
Модуль вектора среднего ускорения
.
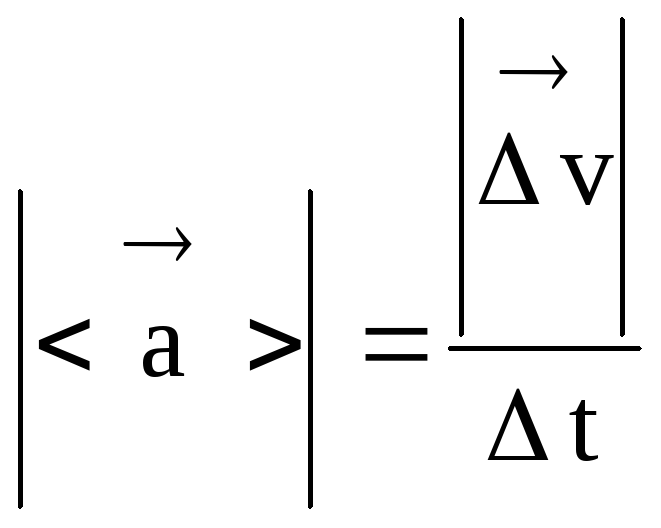(22)
За единицу измерения ускорения в СИ принят метр на секунду в квадрате.
Если величина скорости (или модуль вектора скорости) не меняется, движение равномерное, при изменении модуля скорости – неравномерное.
Равномерным называют движение, при котором за любые равные промежутки времени тело проходит одинаковые пути . В этом случае величина скорости остаётся неизменной (по направлению скорость может изменяться, если движение криволинейное).
Прямолинейным называют движение, при котором траектория является прямой линией . В этом случае направление скорости остаётся неизменным, (величина скорости может изменяться, если движение не равномерное).
Равномерным прямолинейным называют движение, которое является и равномерным и прямолинейным. В этом случае неизменными остаются и величина и направление.
В общем случае при движении тела изменяются и величина и направление вектора скорости. Для того, чтобы охарактеризовать насколько быстро происходят эти изменения, используют специальную величину – ускорение.
Ускорение – это величина, равная отношению изменения скорости движения тела к длительности промежутка времени, за которое это изменение скорости произошло . Среднее ускорение на основе этого определения равно, м/с²:
Мгновенным ускорением называется физическая величина, равная пределу, к которому стремится среднее ускорение за промежуток ∆t → 0, м/с²:
Поскольку вдоль траектории скорость может изменяться как по величине так и по направлению, вектор ускорения имеет две составляющие.
Составляющая вектора ускорения а, направленная вдоль касательной к траектории в данной точке, называется тангенциальным ускорением, которое характеризует изменение вектора скорости по величине.
Составляющая вектора ускорения а, направленная по нормали к касательной в данной точке траектории, называется нормальным ускорением. Оно характеризует изменение вектора скорости по направлению в случае криволинейного движения. Естественно, что когда тело движется по траектории, являющейся прямой линией, нормальное ускорение равно нулю.
Прямолинейное движение называется равнопеременным, если за любые промежутки времени скорость тела изменяется на одну и ту же величину. В этом случае отношение
∆V/ ∆t одинаково для любых интервалов времени. Поэтому величина и направление ускорения остаются неизменными: а = const.
Для прямолинейного движения вектор ускорения направлен по линии движения. Если направление ускорения совпадает с направлением вектора скорости, то величина скорости будет возрастать. В этом случае движение называют равноускоренным. Если направление ускорения противоположно направлению вектора скорости, то величина скорости будет уменьшаться. В этом случае движение называют равнозамедленным. В природе существует естественное равноускоренное движение – это свободное падение.
Свободным падением – называется падение тела, если на него действует единственная сила – сила тяжести . Опыты, проведённые Галилеем, показали, что при свободном падении все тела движутся с одинаковым ускорением свободного падения и обозначаются буквой ĝ. Вблизи поверхности Земли ĝ = 9,8 м/с². Ускорение свободного падения обусловлено притяжением со стороны Земли и направлено вертикально вниз. Строго говоря, такое движение возможно лишь в вакууме. Падение ввоздухе можно считать приблизительно свободным.
Траектория движения свободно падающего тела зависит от направления вектора начальной скорости. Если тело брошено вертикально вниз, то траектория – вертикальный отрезок, а движение называется равнопеременным. Если тело брошено вертикально вверх, то траектория состоит из двух вертикальных отрезков. Сначала тело поднимается, двигаясь равнозамедленно. В точке наивысшего подъёма скорость становится равной нулю, после чего тело опускается, двигаясь равноускоренно.
Если вектор начальной скорости направлен под углом к горизонту, то движение происходит по параболе. Так двигаются брошенный мяч, диск, спортсмен, прыгающий в длину, летящая пуля и др.