Сечения геометрических фигур имеют различные формы. У параллелепипеда сечение всегда представляет собой прямоугольник или квадрат. Оно имеет ряд параметров, которые могут быть найдены аналитическим способом.
Инструкция
Через параллелепипед можно провести четыре сечения, которые представляют собой квадраты или прямоугольники. Всего он имеет два диагональных и два поперечных сечения. Как правило, они имеют разные размеры. Исключением является куб, у которого они одинаковы.
Перед тем как строить сечение параллелепипеда, составьте представление о том, что представляет собой эта фигура. Существует два вида параллелепипедов - обычный и прямоугольный. У обычного параллелепипеда грани располагаются под некоторым углом к основанию, а у прямоугольного они перпендикулярны ему. Все грани прямоугольного параллелепипеда представляют собой прямоугольники или квадраты. Из этого следует,что куб - это частный случай прямоугольного параллелепипеда.
У любого сечения параллелепипеда есть определенные характеристики. Основными из них являются площадь, периметр, длины диагоналей. Если из условия задачи известны стороны сечения или какие-либо иные его параметры, этого достаточно, чтобы найти его периметр или площадь. По сторонам определяются также диагонали сечений. Первый из этих параметров - площадь диагонального сечения.
Для того чтобы найти площадь диагонального сечения, нужно знать высоту и стороны основания параллелепипеда. Если даны длина и ширина основания параллелепипеда, то диагональ найдите по теореме Пифагора:
d=?a^2+b^2.
Найдя диагональ и зная высоту параллелепипеда, вычислите площадь сечения параллелепипеда:
S=d*h.
Периметр диагонального сечения тоже можно вычислять по двум величинам - диагонали основания и высоте параллелепипеда. В этом случае вначале найдите две диагонали (верхнего и нижнего оснований) по теореме Пифагора, а затем сложите с удвоенным значением высоты.
Если провести плоскость, параллельную ребрам параллелепипеда, можно получить сечение-прямоугольник, сторонами которого являются одна из сторон основания параллелепипеда и высота. Площадь этого сечения найдите следующим образом:
S=a*h.
Периметр этого сечения найдите аналогичным образом по следующей формуле:
p=2*(a+h).
Последний случай возникает, когда сечение проходит параллельно двум основаниям параллелепипеда. Тогда его площадь и периметр равны значению площади и периметра оснований, т.е.:
S=a*b - площадь сечения;
Портфолио учителя математики НОУ СОШ «ЛАДА» Лисуновой Г.В.
Тема: « Построение сечений тетраэдра и параллелепипеда».
Предмет : геометрия Класс: 10 Используемые педагогические технологии: технология проектного обучения, информационные технологии. Тема урока : Построение сечений тетраэдра и параллелепипеда Тип урока : урок закрепления и развития знаний. Формы работы на уроке : фронтальная, индивидуальная Список используемых источников и программно-педагогических средств:Л.С. Атанасян. Геометрия. 10-11 классы,- М: Просвещение, 2006г.
В. Н. Литвиненко. Задачи на развитие пространственных представлений. Книга для учителя. - М.: Просвещение, 1991.
Г. Прокопенко. Методы решения задач на построение сечений многогранников. 10 класс. ЧПГУ, г. Челябинск. Еженедельная учебно-методическая газета "Математика" 31/2001.
А. Мордкович. Семинар девятый. Тема: Построение сечений многогранников (позиционные задачи). Еженедельное приложение к газете "Первое сентября". Математика. 3/94.
Мультимедийный интерактивный курс "Открытая математика. Стереометрия." Физикон
«Живая геометрия»
Проверить знание теоретического материала о многогранниках (тетраэдр, параллелепипед).
Продолжить формирование умения анализировать чертеж, выделять главные элементы при работе с моделью многогранника, намечать ход решения задачи, предвидеть конечный результат.
Отработать навыки решения задач на построение сечений многогранников.
Развивать графическую культуру и математическую речь.
Формировать навыки использования компьютерных технологий на уроках геометрии.
Развивающие:Развивать познавательный интерес учащихся.
Формировать и развивать у учащихся пространственное воображение.
Воспитательные:Воспитывать самостоятельность, аккуратность, трудолюбие.
Воспитывать умения работать индивидуально над задачей.
Воспитывать волю и настойчивость для достижения конечных результатов.
Техническое обеспечение:
Компьютер с установленными программами «Живая геометрия», Power Point, мультимедиапроектор.
Раздаточный материал:Бланки-карточки с заданиями для практической работы, бланки-карточки с ответами для взаимопроверки, опоры – памятки, презентация по теме «Аксиомы стереометрии, следствия из них», презентация ученика «Построение сечений параллелепипеда», цветные карандаши.
Структура урока.
| Приветствие. Организационный момент. | ||
| Постановка цели и задачи урока. | ||
| Повторение изученного материала с использованием презентации. | ||
| Актуализация опорных знаний. | ||
| Практическая работа на построение сечений. | ||
| Взаимопроверка. | ||
| Домашнее задание | ||
| Рефлексия. | ||
1)Приветствие. Организационный момент.
2) Постановка цели и задачи урока.
Задачи на построение сечений в многогранниках занимают заметное место в курсе стереометрии. Их роль обусловлена тем, что решение этого вида задач способствует усвоению аксиом стереометрии, следствий из них, развитию пространственных представлений и конструктивных навыков. Умение решать задачи на построение сечений являет-ся основой изучения почти всех тем курса стереометрии. При решении многих стереометрических задач используют сечения многогранников плоскостью. На предыдущих уроках мы с вами познакомились с аксиомами стереометрии, следствиями из аксиом и с теоремами о параллельности прямых и плоскостей в пространстве. Мы рассмотрели алгоритмы построения несложных сечений куба, тетраэдра и параллелепипеда. Эти сечения, как правило, задавались точками, расположенными на ребрах или гранях многогранника. Сегодня на уроке мы с вами повторим геометрические утверждения, позволяющие сформулировать правила построения сечений. А также научимся применять эти знания при решении задачи на построение сечения тетраэдра и параллелепипеда плоскостью, проходящей через три данные точки, такие, что никакие три из этих точек не лежат в одной грани.
3) Повторение изученного материала с использованием презентации.
Давайте повторим некоторые вопросы теории.
- Что такое секущая плоскость? Как можно задать секущую плоскость? Что такое сечение тетраэдра (параллелепипеда)? Какие многоугольники мы получали при построении сечений тетраэдра? А какие многоугольники мы можем получить при построении сечений параллелепипеда? Давайте повторим аксиомы стереометрии, следствия из них и способы задания плоскости (презентация 1, слайды 1-10)
4) Актуализация опорных знаний.
Презентация ученика «Построение сечений параллелепипеда».
Теперь давайте вспомним алгоритм построения сечения тетраэдра на примере двух задач (презентация 1, слайды 11-12). (построение комментируется пошагово учителем). - Пащенко Алексей с помощью своей презентации напомнит нам об алгоритмах построения сечений параллелепипеда (презентация 2, слайды 1-5) (ученик демонстрирует слайды, комментируя последовательность построения) - А сейчас с помощью программы «Живая геометрия» мы «оживим» пространство на примере сечения куба. Программа позволяет вращать многогранник, что позволит вам увидеть сечение со всех сторон.
5) Практическая работа на построение сечений с последующей взаимопроверкой.
Ученики получают бланки-карточки для практической работы (приложение 1) Малая наполняемость класса (5 человек), достаточно большое количество посадочных мест, а также последующая взаимопроверка позволяет выполнение работы одного варианта. На бланках также расположено несколько различных примеров построения сечений. У каждого ученика на парте опора-памятка (приложение 2). Практическая работа состоит из 12 заданий разного уровня сложности. 5-7 правильно выполненных заданий – оценка «3», 8-10 заданий - оценка «4», 11-12 заданий - оценка «5»
6) Взаимопроверка.
Ученики меняются листами с практической работой, получают для проверки бланки с ответами (приложение 3) . Проверяют работы друг друга, отмечая правильно построенные сечения.
7) Домашнее задание.
В качестве домашнего задания я попрошу вас решить задачи, аналогичные задачам в практической работе, но на построение сечений тетраэдра. Каждому предлагается выполнить по 4 задания (приложение 4) Задания имеют три уровня сложности.
8) Рефлексия.
Итак, подведем итог, чему мы научились сегодня на уроке? - Какие теоретические положения нам часто приходилось использовать? - Какие ошибки были допущены при решении задач? Как вы их устранили? - Кому приходилось возвращаться к задаче несколько раз? - Где в практической деятельности вам пригодится сегодняшний урок? На этапе рефлексии деятельности учащиеся анализируют, где и почему были допущены ошибки, каким способом они были исправлены, повторяют алгоритмы, вызвавшие затруднения, оценивают свою деятельность на уроке.
9) Итог урока.
В завершение урока учащиеся с помощью учителя фиксируют степень соответствия поставленной цели и результатов деятельности. Выставляются оценки.










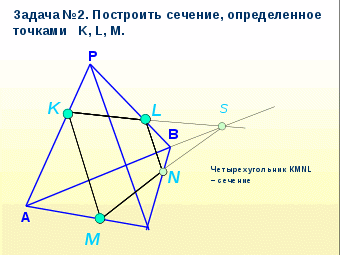





Практическая работа по построению сечений параллелепипеда. Приложение 1
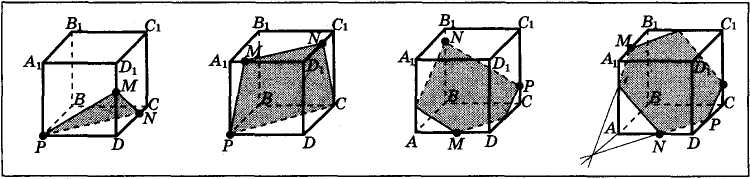



Приложение 2
Опора-памятка
- Аксиома
1
. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и причем только одна. Аксиома
2
. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. Аксиома
3
. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
- Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. Через две пересекающиеся прямые проходит плоскость, и притом только одна.




Приложение 3
Ответы к практической работе.
|
|
|
|
|
|
|
|
Вот такая вот задача по геометрии про прямоугольный параллелепипед и плоскость:
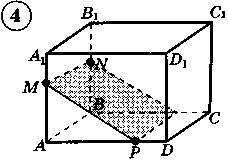
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра AA1 = 6, AB = 6, AD = 3 корня из 13. Найдите площадь сечения параллелепипеда плоскостью AMK, где точки М и К делят ребра BB1 и CC1 в отношении 1:2, считая от прямой ВС .
Для её решения этой задачи нужно просто представить то, что нам дано по условию и понять, что нужно найти. Рекомендую условие разбивать на части и каждую часть рассматривать отдельно. Сейчас я покажу, как это делается.
Читаем с самого начала: "В прямоугольном параллелепипеде..." - всё, достаточно. И так, у нас есть прямоугольный параллелепипед - трехмерная геометрическая фигура, которую лучше всего нарисовать на листочке бумаги. Вот как выглядит прямоугольный параллелепипед на рисунке. В жизни это обычная коробка для обуви.
"...известны ребра AA1 = 6, AB = 6, AD = 3 корня из 13." Вот теперь мы можем прямо на рисунке подписать длину этих ребер. Смотрим на буквы, я выделил эти три ребра синим цветом.
Фактически нам даны размеры параллелепипеда. И хотя на рисунке длина ребер не совсем соответствует условию, ничего страшного. На алгебру решения это нисколько не влияет. Мы не используем рисунок для графического решения задачи. Он нам нужен только для того, чтобы понять ход решения. Одинаковые задачи для параллелепипедов самых разных размеров будут иметь одинаковый ход решения. В конце только числа разные будут получаться.
Ничего не понятно. Откуда взялись точки М и К? После этих слов в условии задачи ещё что-то написано. По этому пропускаем этот фрагмент и читаем дальше.
"...где точки М и К делят ребра BB1 и CC1 в отношении 1:2..." Ага, вот и точки появились. Ребра на рисунке мы можем найти, но как их разделить "... в отношении 1:2..." ? Всё очень просто. Вспоминаем детский сад. "Разделите отрезок на три равные части и возьмите одну часть" - это очень простая задача, с которой справится даже ребенок. А мы уже взрослые. Как узнать, на сколько частей нужно делить? Выражение "Разделить в отношении 1:2" равнозначно выражению "Разделить на 3 части" . Ведь 1+2=3. Длина всех вертикальных ребер равна 6 см. Одна часть будет равна 6/3=2 см. Нам нужно взять одну часть. Но какую? Нижнюю, верхнюю или среднюю? Читаем дальше условие задачи: "...считая от прямой ВС" . Почему ребро ВС вдруг превратилось в прямую? Математики, как заправские карточные шулеры, очень любят подменять одни понятия другими, превращая простую задачу в настоящий ребус. Вот из-за таких ребусов многие ненавидят математику. Прямая ВС совпадает с ребром ВС и находится они на нижнем основании прямоугольного параллелепипеда, на донышке коробки. По этому мы берем нижнюю треть вертикальных граней. Обозначаем нужные точки на рисунке.
Всё условие задачи мы разобрали до конца и теперь самое время вернуться к пропущенному фрагменту: "Найдите площадь сечения параллелепипеда плоскостью AMK..." . Через точки М и К можно провести целое море плоскостей. Все они будут вращаться на отрезке МК, как шашлык на шампуре.
Нас же интересует только та плоскость, которая проходит через точку А. Такая плоскость всего одна. Поскольку отрезок МК параллелен ребру ВС, а тот в свою очередь параллелен ребру АD, значит наша плоскость проходит через это ребро. В сечении у нас получается прямоугольник АDМК, расположенный под углом к основанию.
Нам нужно найти площадь этого прямоугольника (на рисунке он закрашен голубеньким). Одна сторона у нас есть, нужно найти длину другой стороны. Если посмотреть на зелененький треугольник, то вторая сторона прямоугольника окажется гипотенузой прямоугольного треугольника АВМ. По теореме дедушки Пифагора мы без труда найдем длину этой гипотенузы. Как видите, детская задачка на два действия.
Вот только меня терзают смутные сомнения, что кто-то где-то запутался. Если для точек М и К брать не одну часть от ребер ВВ1 и СС1, а две части, тогда длина гипотенузы получается равной двум корням из тринадцати. При вычислении площади сечения число тринадцать вылезает из-под корня и площадь получается равной 78 сантиметров в квадрате. Явно кто-то ошибся. Либо математики при составлении своего ребуса, либо я не правильно расшифровал изящную словесность этого ребуса. Вот видите к чему могут приводить бездарные попытки казаться умнее, чем ты есть на самом деле. Это относится как ко мне, так и к математикам. Кстати, если бы в условии было указано соотношение 2:1, то и я бы правильно решил эту задачу и получил ответ без квадратного корня.
Для секущей плоскости А1МК решение получается очень даже красивое. Та же теорема Пифагора для зеленого треугольничка, та же площадь прямоугольника.
P.S. Рисовать картинки можно на бумаге. Я картинки рисую на компьютере для того, чтобы и вам их показывать. Вы тоже можете так делать. Берете заготовку прямоугольного параллелепипеда и разрисовываете её под условия своей задачи. Тогда находить решение вам будет гораздо проще. Если у вас есть ноутбук и он перегревается от вашего чрезмерного усердия, тогда охлаждающая подставка поможет вам избавиться от проблем. Работает такая подставка от самого ноутбука и подключается к нему через USB разъем. Никаких розеток с собою носить не нужно. Очень удобно и практично.