Кинематический анализ механизмов. Цели и задачи кинематического анализа
Кинематический анализ механизма – исследование его основных параметров с целью изучения законов изменения и на основе этого выбор из ряда известных наилучшего механизма. По сравнению с синтезом анализ механизма широко используется в практике.
Кинематический анализ механизма выполняется либо для заданного момента времени, либо для заданного положения входного звена; иногда для анализируемого положения механизма задают взаимное расположение каких-либо его звеньев.
Цели:
1. Определение кинематических характеристик звеньев: перемещение; скорость; ускорение; траектория движения; функция положения при известных законах движения входных (ведущих) звеньев.
2. Оценка кинематических условий работы рабочего (выходного) звена.
3. Определение необходимых численных данных для проведения силового, динамического, энергетического и других расчётов механизма.
Исходные данные:
1. Кинематическая схема механизма.
2. Размеры и иные геометрические параметры звеньев (но только такие, которые не изменяются при движении механизма).
3. Законы движения входных звеньев (или параметры движения, например, угловая скорость и угловое ускорение входного звена в выбранном для анализа положении механизма).
Для механизмов, подчиняющихся классификации Л. В. Ассура, порядок кинематического анализа определяется формулой строения: вначале находят параметры движения начальных механизмов и затем – структурных групп в порядке следования их в формуле строения. Здесь следует руководствоваться простым правилом: кинематика любогоэлемента формулы строения может быть изучена только после того, как она изучена для всех предшествующих в этой формуле элементов.
Задачи:
О положениях звеньев механизма. Определение траекторий движения точек;
О скоростях звеньев или отдельных точек механизма;
Об ускорениях звеньев или отдельных точек механизма.
Методы:
Графический (или метод графиков и диаграмм);
Графоаналитический (или метод планов скоростей и ускорений);
Аналитический;
Экспериментальный.
Графический метод кинематического анализа
Преимущество этого метода заключается в наглядности и простоте. Он хорош для кинематического анализа звеньев, совершающих возвратно-поступательное движение. Недостаток метода – невысокая точность, которая зависит от точности графических построений.
Задача о положениях решается построением нескольких совмещённых планов механизма в выбранном масштабе длин при различных последовательных положениях ведущего звена.
Решаются построением графиков (диаграмм) перемещений, скоростей и ускорений исследуемой точки.
Последовательность кинематического анализа:
1. Сначала строят несколько (чаще всего 12 и более) совмёщенных планов механизма в произвольно выбранном масштабе длин.
2. Затем строят график пути (перемещения) исследуемой точки или звена, для чего используют совмещённые планы механизма и последовательные положения на них исследуемой точки или звена.
3. Графическим дифференцированием графика перемещений строят график скорости исследуемой точки.
4. Графическим дифференцированием графика скоростей строят график ускорений.
Графическое дифференцирование можно производить методом хорд и методом касательных. С целью повышения точности удобно использовать оба метода одновременно.
Пример 1.
Даны кривошипно-ползунный механизм, длины звеньев которого – кривошипа и шатуна – L OA и L AB соответственно, и угловая скорость кривошипа .
Определить скорости и ускорения ползуна при различных положениях кривошипа.
Решение.
Выбираем масштабы длин , м/мм, где AO – длина отрезка, мм, изображающая кривошип длиной L ОА на строящемся плане механизма; эта длина выбирается произвольно с учётом того, что совмещённые планы механизма должны разместиться на отведённом месте чертежа, а сам масштаб длин был бы удобен для дальнейших расчётов.
Вычисляем длину отрезка , мм, изображающего шатун на плане механизма. При построении совмещенных планов механизма используют метод засечек (рис. 3.1).
Для построения графиков скоростей и ускорений (рис. 3.1) выбираются полюсные расстояния h u и h a , где h u – полюсное расстояние при построении графика скоростей, которое выбирается произвольной длины; рекомендуется его величину выбирать в пределах h u =30…40 мм; h a – полюсное расстояние при построении графика ускорений; его рекомендуется принимать в пределах h a =30…40 мм.
Масштабы времени, скорости и ускорения вычисляют по формулам, вывод которых приводится ниже.
Масштаб времени можно вычислить по формуле
где Т – период одного оборота кривошипа, с; L X – длина отрезка между точками 1 и 1 на графике (диаграмме) перемещений, мм.
Так как период Т можно вычислить по формулам
где – угловая скорость кривошипа, 1/с; n 1 – частота вращения кривошипа, об/мин, то масштаб времени
![]() ,
с/мм.
,
с/мм.
Масштаб скорости можно вывести из условия, что скорость исследуемой точки является производной перемещения S по времени:
![]() .
.
Здесь предполагается, что масштаб перемещений и масштаб времени являются постоянными величинами.
Так
как
,
то
![]() ,
отсюдаЗадача
о положениях
решается графическим методом, то есть
построением нескольких совмещённых
планов механизма в выбранном масштабе
длин.
,
отсюдаЗадача
о положениях
решается графическим методом, то есть
построением нескольких совмещённых
планов механизма в выбранном масштабе
длин.
Задачи о скоростях и ускорениях решаются построением планов скоростей и ускорений звеньев механизма при определённых (заданных) положениях ведущего звена на основе заранее составленных векторных уравнений скоростей и ускорений звеньев механизма.
Преимущество этого метода по сравнению с графическим в том, что он менее трудоёмок, так как позволяет определять скорости и ускорения (их величину и направление) на одном плане скоростей или плане ускорений для множества точек механизма.
Недостатком метода является то, что требуется построить планы скоростей и ускорений для нескольких положений механизма (если необходимо определять скорость и ускорение при различных положениях механизма и его звеньев).
Следует помнить, что в основе построения планов скоростей и ускорений лежат законы плоскопараллельного движения. Согласно этим законам:
1. План скоростей (а также план ускорений) получается в результате графического решения векторных уравнений для определения скоростей (ускорений) точек в плоскопараллельном движении;
2. Векторы абсолютных скоростей точек (при рассмотрении их движения относительно неподвижного звена) изображаются исходящими из полюса плана, а направление совпадает с касательными к траектории движения. Векторы относительных скоростей точек (при их движении относительно подвижных точек) изображаются отрезками, соединяющими концы соответствующих векторов абсолютных скоростей;
3. Длина векторов относительных скоростей пропорциональна длине тех участков звеньев, которые являются радиусами вращения точек в их относительном движении. Это положение, известное под названием теоремы подобия, облегчает определение скоростей многих точек, лежащих на звеньях плоскопараллельного и вращательного движения.
Является планом скоростей треугольника .
План скоростей жёсткого звена – геометрическое место точек концов векторов абсолютных скоростей любых точек звена, если они построены из одной общей точки , называемой полюсом плана скоростей.
План скоростей всегда строится в масштабе. В дисциплине «Теория машин и механизмов» масштаб имеет размерность, поэтому его принято называть масштабным коэффициентом: , .
План скоростей подобен самому звену, и повёрнут на девяносто градусов в сторону мгновенного вращения.
Если план скоростей жёсткого звена подобен своему звену, то план скоростей механизма не подобен самому механизму, так как в отличие от жёсткого звена механизм есть изменяемая подвижная система.
План скоростей механизма – совокупность планов скоростей отдельных звеньев, построенных из одной общей точки , называемой полюсом плана скоростей.
Кинематический анализ механизмов
Введение
5. Кинематические диаграммы
Литература
Введение
Тема контрольной работы "Кинематический анализ механизмов" по дисциплине "Теория механизмов и машин".
Цель работы: формирование знаний кинематического анализа механизмов.
Задачи выполнения работы: ознакомление с методами кинематического анализа механизмов.
Основные вопросы темы:
1. Основные задачи и методы кинематического анализа;
2. Построение положений звеньев механизма;
3. Функция положения механизма;
4. Основные уравнения для определения скоростей и ускорений;
5. Кинематические диаграммы.
1. Основные задачи и методы кинематического анализа
Основной задачей кинематики механизмов является изучение движения звеньев механизмов вне зависимости от сил, действующих на эти звенья.
При кинематическом исследовании механизмов рассматриваются следующие основные вопросы:
1) построение планов скоростей;
2) построение траектории любой точки механизма;
3) определение скоростей и ускорений любой точки механизма, определение угловых скоростей и ускорений любого звена механизма, определение радиуса кривизны в любой точке траектории и др.
Кинематическое исследование можно вести как с применением графических методов, так и аналитическим путем. Графические методы исследования, давая достаточную для инженерной практики точность, обычно оказываются проще и нагляднее аналитических. Однако, когда ведется систематическое углубленное исследование какого-либо определенного типа механизма, более удобным оказывается аналитический метод.
При графических построениях на чертеже приходится изображать не только длины звеньев, но и скорости и ускорения отдельных точек, а также и другие величины. В этих условиях удобно использовать масштабный коэффициент, которым называют отношение действительной величины к изображению:
Масштабный коэффициент;
Масштабный коэффициент;
Масштабный коэффициент
2. Построение положений звеньев механизма
Взаимное расположение звеньев движущегося механизма все время меняется, но в каждый данный момент времени расположение звеньев является вполне определенным. Графическое изображение взаимного расположения звеньев, соответствующее выбранному моменту времени, называется планом механизма. Ряд последовательных планов механизма, построенных для моментов времени, следующих друг за другом, называется планом положений и позволяет наглядно проследить за движением механизма.
Построение плана положений механизма начинают с изображения того звена, положение которого задано для данного момента времени.
Кривошипно-ползунный механизм

Из центра О - оси вращения кривошипа ОА радиусами и на оси X - Xдвижения ползуна отмечаем В 0 - правое В 6 - левое крайние ползуна В. Прямые ОА 0 В 0 и ОА 6 В 6 - положения механизма, соответствующие крайним положениям В 0 и В 6 ползуна. Траекторию пальца А кривошипа от точки А 0 делим на 12 равных частей и из полученных точек А 1 , А 2 , А 3 … А 11 радиусами АВ==… отмечаем положения В 1 , В 2 , В 3 …В 11 ползуна на линии В 0 В 6 . Соединив точки А 1 , А 2 , А 3 … А 11 с центром О и соответствующими точками В 1 , В 2 , В 3 …В 11 , получим планы механизма. Кривая, последовательно соединяющая центры S 0 , S 1 , S 2 …S 11 шатуна в различных его положениях, будет шатунной кривой.
3. Функция положения механизма
Функцией положения механизма называется зависимость координаты выходного звена от обобщенных координат механизма.
Перемещения, скорости и ускорения звеньев и точек механизма является функциями перемещений, скоростей и ускорений звеньев механизма, принятых за ведущие. Число ведущих звеньев механизма должно быть равно числу степеней подвижности механизма или, что то же самое, числу обобщенных координат механизма.
Рассмотрим, в какой форме могут быть заданы законы ведущих звеньев. Эти законы называют функциями перемещений, скоростей и ускорений.
Функция перемещений может быть задана в аналитической форме в виде соответствующей функции, связывающей перемещение ведущего звена со временем (рис.2).


Если ведущее звено входит во вращательную пару со стойкой, то задается функция φ=φ (t), где: φ - угол поворота ведущего звена относительно неподвижной системы координат ХОY, связанной со стойкой, а t - время.
Если ведущее звено входит в поступательную пару, то задается функция s=s (t), где s - перемещение произвольно выбранной точки А ведущего звена относительно неподвижной системы координат, связанной со стойкой, а t - время.
Функции φ=φ (t) и s=s (t) могут быть также заданы графически в виде кривых, где по осям ординат отложены углы поворота φ или перемещения sв некоторых выбранных масштабах и , а по осям абсцисс время tв выбранном масштабе (рис.3).
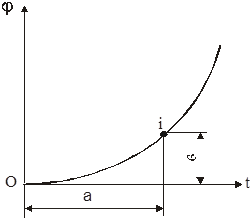
φ 0 = 0; φ i - φ 0 = · в;
Соответственно время t i , за которое ведущее звено повернулось на угол φ i равно:
t i - t 0 = ·a ;
Если закон движения ведущего звена задан в виде функций скоростей ω=ω (t) или v=v (t), то переход от функций скоростей к функциям перемещений может быть осуществлен путем вычисления интегралов:
кинематический анализ механизм ускорение
 и
и  ;
;
где: φ 0 , s 0 , t 0 - угол, перемещение и время, соответствующие начальному положению ведущего звена.
Если закон движения ведущего звена задан в виде функций ускорений ε=ε (t) и ω=ω (t), то переход к функциям скоростей осуществляется путем вычисления интегралов:
 и
и 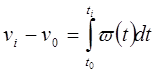
где: ω 0 , v 0 , t 0 - угловая скорость, линейная скорость и время, соответствующие начальному положению ведущего звена.
4. Основные уравнения для определения скоростей и ускорений
Связь между скоростями и ускорениями общих точек звеньев кинематической пары зависит от пары.
Рассмотрим два случая составления векторных уравнений скоростей и ускорений:
а) две точки принадлежат одному звену и удалены друг от друга на расстояние l ( рис.4).

Из теоретической механики известно, что скорость любой точки абсолютно твердого тела можно представить как геометрическую сумму скоростей переносного и относительного движений.
Переносным движением для рассматриваемого звена будем считать поступательное движение со скоростью точки А, а относительным - вращательное движение звена вокруг точки А. Векторное уравнение для скорости точки В:
![]() ;
;
При вращении звена вокруг точки А точка В движется по окружности ββ , описанной из точки А. Поэтому скорость V BA направлена по касательной к дуге ββ , т.е. перпендикулярна линии АВ.
Величина скорости V BA =ω·АВ или V BA =ω·.
По направлению V BA можно найти направление ω и наоборот.
Т.к. переносное движение выбрано поступательным, то ускорение точки В можно составить из 2-х ускорений: ускорения точки А и ускорения точки В при вращении звена вокруг точки А.
![]()
При движении точки В по окружности ββ ускорение W BA складывается из 2-х ускорений: нормального , направленного к центру вращения, и тангенциального , направленного по касательной к дуге ββ , т.е. перпендикулярно линии АВ. Векторное уравнение для ускорения точки В:
![]() ;
;
Величины ускорений и определяем по формулам:
=·ω 2
= ;
;
где: ε - угловое ускорение;
б) две точки принадлежат двум звеньям, образующим поступательную пару и в данный момент времени совпадают (рис.5).

Точка А принадлежит звену 1, точка В - звену 2. В данный момент времени точки А и В совпадают (точка В лежит над точкой А). Звенья 1 и 2 образуют поступательную пару с направляющей Н 12 .
Скорость точки В складывается из 2-х скоростей - переносной и относительной. Переносным движением здесь является движение звена 1, поэтому скорость точки А - V A будет переносной. Относительная скорость точки В равна скорости движения звена 2 относительно звена 1. При движении звена 2 относительно звена 1 точка В движется по прямой линии ββ , параллельной направляющей Н 12 . Поэтому относительная скорость V ВА параллельна Н 12 .
Ускорение точки В, когда переносное движение не является поступательным, складывается из 3-х ускорений: переносного, т.е. ускорения точки А, относительного и поворотного, или Кориолисова. В относительном движении точка В движется по линии ββ , поэтому в этом движении точка В имеет только тангенциальное ускорение, направленное по этой линии, т.е. параллельно направляющей Н 12 . Обозначим это ускорение через . Поворотное (Кориолисово) ускорение обозначим через .
Векторные уравнения для скорости и ускорения точки В будут иметь вид:

Так как звенья 1 и 2 образуют поступательную пару, то они не имеют относительного вращения. Поэтому эти звенья обладают одинаковыми угловыми скоростями и угловыми ускорениями, т.е.: ω 2 =ω 1 и ε 2 =ε 1 , где ω 1 - угловая скорость переносного движения (вращения звена 1).
Вектор направлен в ту сторону, в которую окажется направленным вектор , если повернуть его на 90 0 в направлении угловой скорости ω 1 . Величина его определяется по формуле:
Определим скорость и ускорение ползуна кривошипно-ползунного механизма.
Дан план механизма, размеры ℓ ОА, ℓ АВ, ω 2 , ε 2 .
Найдем скорость и ускорение звена 4 (точки В) и угловые скорость и ускорение звена 3 (шатуна).

Зная ω 2 , находим V А =ℓ ОА ·ω 2 . Скорость V А изобразим на плане скоростей в виде отрезка "Pа ", перпендикулярного ОА (рис.7). Поршень (звено 4) движется поступательно, поэтому все его точки имеют ту же скорость и то же ускорение, что и точка В.

Рис.7 Рис.8
Однако точка В принадлежит не только звену 4, но и звену 3. Точно также точка А есть общая точка для звеньев 2 и 3. Таким образом, на звене 3 имеются две точки А и В, удаленные друг от друга на расстояние ℓ АВ. Поэтому скорость точки В:
![]() где: ║
где: ║![]() ;
;
В соответствии с этим уравнением строим план скоростей. Проводим через точку а линию, перпендикулярную к АВ, а через точку Р - линию перпендикулярную Н 41 . В точке пересечения ставим в . Отрезок Рв изображает скорость точки В, а отрезок ав - скорость точки В относительно А (V ВА). Угловую скорость звена 3 находим по формуле:
Перенеся вектор в точку В, находим направление ω 3 (против часовой стрелки).
Ускорение точки А:
Отложив от полюса (рис.8) ускорение и в виде отрезков и , находим полное ускорение точки А (отрезок ).
Ускорение точки В:
![]()
где: ; ║ и АВ;
Ускорение направлено от точки В к точке А. Отложив от точки а ′ ( на плане ускорений) отрезок а ′ в ′′ , соответствующий , проводим через точку в ′′ линию, перпендикулярную АВ. Через полюс Р ′ проводим линию, параллельную Н 41 . Эти линии пересекаются в точке в ′ , отрезок Р ′ в ′ представляет искомое ускорение точки В (W B), а отрезок в ′′ в ′ - ускорение . Из сопоставления направлений W B и V B заключаем, что звено 4 в данный момент движется замедленно.
Угловое ускорение звена 3 находим по формуле: .
Перенос вектора в точку В показывает, что ε 3, как и ω 3 , направлено против часовой стрелки.
В уравнениях вектор, известный по величине и направлению подчеркиваем двумя линиями, а вектор, известный только по направлению - одной линией.
5. Кинематические диаграммы
Кинематическая диаграмма представляет собой графическое изображение одного из кинематических параметров (перемещений, скорости и ускорения) точки либо звена исследуемого механизма в функции времени, угла поворота или перемещения ведущего звена этого механизма, т.е. в функции обобщенной координаты. Кинематические диаграммы дают полную кинематическую характеристику механизма.
Построим кинематические диаграммы кривошипно-ползунного механизма.
Для перемещений S B , скоростей V B и ускорений W В точки В, как перемещающейся прямолинейно, удобно строить кинематические диаграммы в виде зависимостей этих величин от времени tили обобщенной координаты φ 2 , т.е. строить графическое изображение зависимостей:
S B =S B (t), V B =V B (t), W B =W B (t) или:
S B =S B (φ 2), V B =V B (φ 2), W B =W B (φ 2)
если угол φ 2 поворота звена 2 выбран в качестве обобщенной координаты.
Если исследованию подлежат угловые перемещения φ 3 , угловые скорости ω 3 и угловые ускорения ε 3 шатуна 3, то можно построить графическое изображение зависимостей:
φ 3 =φ 3 (t), ω 3 =ω 3 (t), ε 3 =ε 3 (t)
φ 3 =φ 3 (φ 2), ω 3 =ω 3 (φ 2), ε 3 =ε 3 (φ 2)
Кривошип ОА вращается с постоянной угловой скоростью ω 2 .
5.1 Построение диаграммы перемещений
1) Вычерчиваем схему механизма в масштабе μ е в нескольких, например, двенадцати положениях, соответствующих последовательным поворотам кривошипа ОА на 30 0 (рис.9). За начальное положение кривошипа принимаем ОА 0 , при котором ползун В занимает крайнее правое положение В 0 ;
2) строим оси координат S B
-t (рис.10а) и на оси абсцисс откладываем отрезок ℓ в мм, изображающий время одного полного оборота кривошипа в масштабе: ![]() ; где: рад/мм, ;
; где: рад/мм, ;
Отрезок ℓ делим на 12 равных частей и в соответствующих точках 1, 2, 3… по оси ординат откладываем расстояния S B 1 , S B 2 … пройденные точкой В от ее крайнего правого положения В 0 .
До крайнего левого положения В 6 расстояния возрастают, а начиная с положения В 6 , они будут уменьшаться; когда кривошип придет в начальное положение А 0 , ордината кривой (S B -t) будет равна нулю.
3) соединяем последовательно плавной линией полученные точки 0, 1 ΄ , 2 ΄ , 3 ΄ , …. Полученная кривая будет диаграммой расстояний точки В.
Если же по оси абсцисс откладывать углы поворота кривошипа φ, то данная кривая представит функциональную зависимость:
Диаграммы скоростей и ускорений могут быть построены с использованием планов скоростей и ускорений и методов графического дифференцирования:
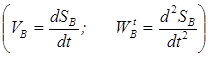 .
.
Метод графического дифференцирования:
1) под диаграммой (S B -t) строим оси координат O 1 V B , O 1 t (рис.2.10б) и на продолжении оси O 1 tвлево откладываем отрезок O 1 Р=Н 1 мм (произвольно, чтобы дифференциальная кривая разместилась на отведенном для нее месте чертежа);
2) из точки "Р" проводим лучи Р 1 , Р 2 , Р 3 … параллельно хордам кривой (S B -t) на участках 01΄; 1΄2΄; 2΄3΄….
Эти лучи отсекут на оси O 1 В отрезки 0 1 1; 0 1 2; 0 1 3…, пропорциональные средней скорости V c на соответствующем участке диаграммы;
3) отложим эти отрезки на средних ординатах соответствующих участков;
4) соединим ряд полученных точек I, II, III…плавной кривой; эта кривая будет диаграммой скорости (V 0 -t).
Имея диаграмму скоростей, аналогично строим диаграмму ускорений.
При построении диаграмм (V 0 -t) и (W B -t) данным методом нельзя получить те участки этих диаграмм, которые соответствуют половине крайних участков оси абсцисс. Чтобы закончить построение диаграмм, нужно дополнительно построить средние значения V В и для одного-двух участков следующего цикла.
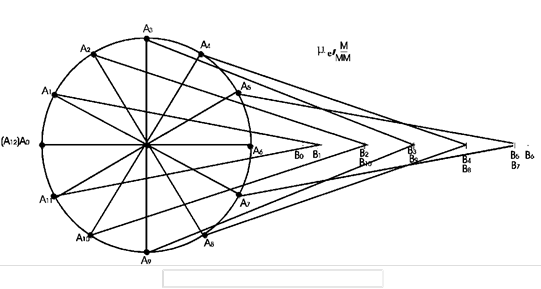
Рис.9 План положений скоростей

Рис.10 Кинематические диаграммы
Масштаб диаграмм остается таким же, как и раньше.
Масштабы по осям ординат определяются по формулам:
для диаграммы скоростей:  ;
;
для диаграммы ускорений:  ,
,
Метод построения диаграмм - прост и нагляден, но имеет следующие недостатки:
1) неточность, особенно при дифференцировании кривых с большой кривизной;
2) невозможность полностью исследовать криволинейное движение, т.к. дифференцированием кривой скоростей получаем диаграммы изменения только тангенциальных ускорений;
3) диаграммы дают лишь численные значения векторов, направление которых можно установить лишь после некоторых дополнительных построений.
Метод планов скоростей и ускорений не имеет упомянутых недостатков, поэтому его широко применяют при исследовании различных механизмов.
Литература
1. Артоболевский И.И. Теория механизмов и машин. М, 1975, с.103-182.
2. Кореняко А.С. и др. Курсовое проектирование по теории механизмов и машин. Киев, 1970, с.82-102.
3. Примеры кинематического анализа
3.1. Правила образования геометрически неизменяемых систем
Любую геометрически неизменяемую часть системы назовем диском .
п равило 1: узел присоединяется к диску двумя связями, не лежащими на одной прямой (рис. 3.1).
Правило 2: диск соединяется с другим диском тремя связями, не пересекающимися в одной точке и не параллельными друг другу (рис. 3.2).
Точка пересечения двух связей может рассматриваться как шарнир – действительный или фиктивный. Поэтому правило 2 можно трактовать как соединение двух дисков с помощью шарнира и одной связи, не проходящей через шарнир. Например, два диска, показанные на рис. 3.3, соединены действительным шарниром А и связью 3. Можно также считать, что диски соединены фиктивным шарниром В и связью 1.
Рис.3.1. Присоединение узла к диску

Рис.3.2. Соединение двух дисков тремя связями
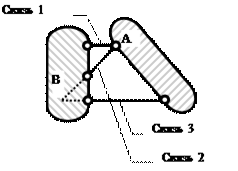
Рис.3.3. Соединение двух дисков шарниром и стержнем:
А – действительный шарнир; В – фиктивный шарнир
Правило 3: три диска соединяются друг с другом тремя шарнирами, не лежащими на одной прямой (рис. 3.4). Шарниры могут быть действительными или фиктивными.

Рис.3.4. Соединение трех дисков тремя шарнирами
Если какое-то из указанных правил нарушается, система оказывается геометрически изменяемой или мгновенно изменяемой.
Если система образована с использованием перечисленных правил, она будет обязательно геометрически неизменяемой.
Если при кинематическом анализе в геометрически неизменяемой системе обнаруживается n избыточных связей, то система оказывается n раз статически неопределимой. При отсутствии избыточных связей системаявляется статически определимой.
Системы, образование которых подчиняется указанным правилам, называются системами простого образования. Есть системы, порядок образования которых не может быть установлен с помощью упомянутых вышеправил. Для кинематического анализа таких систем применяют иные методы, например метод замены связей, которые в настоящем пособии не рассматриваются.
3.2. Степень свободы системы
Степенью свободы системы W называется число независимых параметров, определяющих положение системы в пространстве.
Обозначим:
Д – число дисков, из которых образована система;
Ш – число простых шарниров, соединяющих диски между собой;
С – число связей, соединяющих диски между собой;
С О – число опорных связей, соединяющих диски с землей.
Простым шарниром называется шарнир, соединяющий два диска, такой шарнир эквивалентен двум связям. Если шарнир соединяет d дисков, то он называется кратным шарниром и его кратность К =d–1 показывает, скольким простым шарнирам он эквивалентен (рис. 3.5).

Рис.3.5. Простой (а ) и кратные (б, в ) шарниры
Для произвольной плоской системы
W = 3Д – 2Ш – С – С О,(1)
причем диски не должны содержать избыточные связи.
Для ферм с шарнирными узлами степень свободы можно определить по более простой формуле
W = 2У – С – С О, (2)
где У – число узлов фермы; С – число стержней фермы; С О – число опорных связей.
Если W >
Если W
Если W < 0, то система геометрически неизменяемая и статически неопределимая.
Важно знать, что условия геометрической неизменяемости W = 0 и W <0 являются необходимыми, но недостаточными. Для окончательного вывода о виде системы следует анализировать порядок образования системы (см. примеры ниже).
Пример 1. Кинематический анализ балки (рис. 3.6, а ).
Балка собирается в такой последовательности:
1-й этап. К земле, как к диску, присоединяется Диск 1 (стержень АВС) с помощью трех связей (правило 2, рис. 3.6, б ).

Рис.3.6. Последовательность сборки балки
2-й этап. К образовавшейся системе «Земля + Диск 1», как к единому диску, присоединяется Диск 2 (стержень CDE ) с помощью шарнира С и опорной связи в точке D (вариант правила 2, рис. 3.6, в ).
3-й этап. К образовавшейся системе «Земля + Диск 1 + Диск 2», как к единому диску, присоединяется Диск 3 (стержень EF ) с помощью шарнира E и опорной связи в точке F (вариант правила 2, рис. 3.6, г ). Этим и заканчивается сборка балки.
Поскольку образование балки (рис. 3.6, а ) подчиняется установленным правилам и дополнительных (избыточных) связей не обнаружено, то заданная система является геометрически неизменяемой и статически определимой (ГН СО ).
Пример 2. Кинематический анализ фермы (рис. 3.7, а ).
Ферма собирается в такой последовательности:
1-й этап. Три стержня (1-2, 2-4, 1-4), как три диска, соединяются тремя шарнирами (1, 2, 4) согласно правилу 3.
2-й этап. К образовавшемуся Диску 1 (1-2-4) присоединяется узел 3 с помощью стержней 1-3 и 4-3 согласно правилу 1.
3-й этап. К образовавшемуся Диску 2 (1-2-4-3) присоединяется узел 6 с помощью стержней 4-6и 3-6 согласно правилу 1.
4-й этап. К образовавшемуся Диску 3 присоединяется узел 5 с помощью стержней 3-5и 6-5 согласно правилу 1.
5-й этап. Полученная ферма присоединяется к земле тремя опорными связями согласно правилу 2.

Рис.3.7. Последовательность сборки фермы: а - ферма; б - этапы сборки
Поскольку образование фермы (рис. 3.7, а ) подчиняется установленным правилам и дополнительных (избыточных) стержней не выявлено, то заданная система – геометрически неизменяемая и статически определимая (ГН СО ).
Ферма может быть собрана и в иной последовательности, но в любом случае вывод будет тем же.
Пример 3. Кинематический анализ рамы (рис. 3.8, а ).
Рама собирается в такой последовательности:
1-й этап. К земле прикрепляется стержень АВ(Диск 1 на рис. 3.8, б) с помощью жесткого защемления, которое эквивалентно трем связям (правило 2).

Рис.3.8. Последовательность сборки рамы
2-й этап. К образовавшейся системе «Земля + Диск 1» присоединяется диск 2 (стержень BCD) с помощью шарнира B и двух связей в точке С (рис. 3.8, в ).
По правилу 2 достаточно в точке С иметь одну связь, поэтому вторая связь является избыточной.
3-й этап. К получившейсясистеме «Земля + Диск 1+ Диск 2» присоединяется диск 3 (стержень DE на рис. 2.8, г ) с помощью шарнира D и опорного стержня в точке Е (правило 2).
Поскольку образование рамы (рис. 3.8, а ) подчиняется установленным правилам и выявлена одна избыточная связь, то заданная система – геометрически неизменяемая и один раз статически неопределимая (ГН СН).
Пример 4. Кинематический анализ фермы (рис. 3.9, а ).
Ферма собирается в такой последовательности.
1-й этап. Из трех стержней (1-2, 2-4, 1-4) образуется диск – треугольник 1-2-4 (правило 3), к которому прикрепляется узел 3 (правило 1) стержнями 1-3 и 4-3. Полученный диск 1-2-4-3 соединяется с землей тремя опорными связями (правило 2), образуя Диск 1 (рис. 3.9, б ).
2-й этап. Три стержня (5-6, 6-7, 5-7) образуют по правилу 3 Диск 2 (рис. 3.9, в ).
3-й этап. Диск 2 соединяется с Диском 1 тремя связями (4-6, 3-5, 7-8), но так как все эти связи пересекаются в одной точке 7, то правило 2 нарушается. Возможен взаимный поворот Диска 1 и Диска 2 относительно узла 7 на бесконечно малый угол.
![]()
Рис.3.9. Последовательность сборки фермы
Ввиду нарушения правила 2 заданная система является мгновенно изменяемой и не может служить расчетной схемой сооружения.
Пример 5. Найти степень свободы балки (см. рис. 3.6, а ).
Балка состоит из трех дисков (стержней) AC , CE , EF , соединенных между собой двумя простыми шарнирами С и Е и прикрепленных к земле пятью опорными связями. Поэтому Д = 3, Ш = 2, С = 0, С О = 5 и по формуле (1) получаем W = 3 · 3 – 2·2 – 0 – 5 = 9 – 9 = 0, что является необходимым признаком геометрически неизменяемой и статически определимой системы. Этот вывод подтверждается в примере 1.
Пример 6. Найти степень свободы фермы (см. рис. 3.7, а ).
Будем использовать формулу (1) и считать каждый стержень фермы диском, т. е. Д = 9. Шарниры 2 и 5 соединяют по два стержня фермы, поэтому они простые. Шарниры 1 и 6 соединяют по три стержня фермы, поэтому они двухкратные . Шарниры 3 и 4 – трехкратные. Общее число простых шарниров Ш = 2·1 + 2·2 + 2·3 =12. Опорных связей – три.
Получаем W = 3·9 – 2·12 – 3 = 27 – 27 = 0.
С = 9, У = 6, С О = 3.
Получаем W = 2·6 – 9 – 3 = 12 – 12 =0.
Этот пример демонстрирует преимущество формулы (2) перед формулой (1). Признак ГН СО системы подтверждается в примере 2.
Пример 7. Найти степень свободы рамы (см. рис. 3.8, а ).
Рама состоит из трех дисков AB , BCD и DE , соединенных между собой двумя простыми шарнирами B и D . К земле рама прикрепляется шестью опорными связями (три в жесткой заделке А , две в опоре С, одна в опоре Е). ПоэтомуД = 3, Ш = 2, С = 0, С О = 6 и по формуле (1) получаем
W = 3·3 – 2·2 – 0 – 6 = –1, что является необходимым признаком ГН СН системы. Этот вывод подтверждается в примере 3.
Пример 8. Найти степень свободы фермы (см. рис. 3.9, а ).
При использовании формулы (2) имеем С = 10, У = 7, С О = 4.
Получаем W = 2·7 – 10 – 4 = 14 – 14 =0, что указывает на ГН СО систему. Однако анализ образования фермы (см. пример 4) приводит к выводу о мгновенной изменяемости системы. Этот пример демонстрирует недостаточность вычисления степени свободы системы по формуле для окончательного вывода о виде системы.
Пример 9. Кинематический анализ системы (рис. 3.10, а ).
Система состоит из трех дисков Д1 , Д2 и Д3, которые соединяются между собой пятью связями 1…5. Диски Д1 и Д3 прикреплены к земле шарнирно-неподвижными опорами А и В, каждая из которых эквивалентна двум опорным связям. ПоэтомуД = 3, Ш = 0, С = 5, С О = 4 и по формуле (1) получаем
W = 3·3 – 2·0 – 5 – 4 = 9 – 9 = 0.
Система собирается в такой последовательности:
1-й этап. Диски Д2 и Д3 соединяются связями 3, 4, 5 по правилу 2 и образуют новый диск Д (рис. 3.10, б );
2-й этап. Три диска (Д1, Д и земля) по правилу 3 соединяются тремя шарнирами: действительными А , В и фиктивным С, не лежащими на одной прямой.
Следовательно, система – ГН СО .
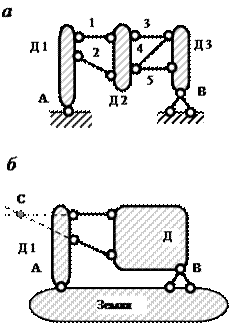
Рис.3.10. Схемы к примеру 9
Пример 10. Кинематический анализ системы (рис. 3.11).
Для вычисления степени свободы системы по формуле (1) рассмотрим два варианта. В первом варианте считаем, что система состоит из пяти дисков – ломаных стержней ABC , ADC и прямых стержней BE , CE , DE .
Тогда шарниры A , B , D – простые, а шарниры С и Е – двухкратные .
При Д = 5, Ш = 7, С = 0, С О = 3получаем
W = 3·5 – 2·7 – 0 – 3 = 15 – 17 = –2.

Рис.3.11. Схема к примеру 10
Во втором варианте считаем, что система состоит из трех дисков – ABC , ADC и EC , которые соединяются простым шарниром А , двухкратным шарниром С и двумя связями BE и DE .
При Д = 3, Ш = 3, С = 2, С О =3получаем
W = 3·3 – 2·3 – 2 – 3 = 9 – 11 = –2.
Замечание: нельзя считать систему состоящей только из двух дисков (ломаных стержней ABC и ADC ), так как в этом случае стержни BE , CE , DE не соединяют диски между собой.
Система собирается в следующей последовательности:
1-й этап.Диски ABC и ADC соединяются в один диск двумя шарнирами А и С, т. е. четырьмя связями, одна их которых будет избыточной (правило 2).
2-й этап.К полученному диску присоединяется узел Е тремя связями, одна их которых будет избыточной (правило 1).
3-й этап.Собранный диск с дв умя избыточными связями прикрепляется к земле тремя опорными связями (правило 3).
Следовательно, заданная система – ГН СН (два раза).
Пример 11. Произвести кинематический анализ системы (рис.3.12).
Определяем степень свободы системы по формуле П.Л.Чебышева :
W = 3Д – 2Ш – С 0 ,
где Д – число дисков, Ш – число простых шарниров, С 0 – количество стержней.

Рис.3.12. Схема к примеру 11
Отбрасывая все шарниры и опорные стержни, находим, что система состоит из пяти дисков (Д =5). Отбрасывая опорные стержни, определяем число шарниров, приведенных к простым (Ш =6: по два в точках В и С , по одному – в точках А и Д ). Число опорных стержней - С 0 =3.
Отсюда W = 3 ∙ 5 – 2 ∙ 6 – 3 = 0, то есть система может быть геометрически неизменяемой и статически неопределимой. Чтобы убедиться, что это так, выполним анализ структуры системы. Так как диски АВ , ВС и АС связаны тремя шарнирами А , В и С , не лежащими на одной прямой, то они образуют диск, к которому жестко присоединен диск ВД с помощью шарнира В и стержня СД , ось которого не проходит через центр шарнира. Эта неизменяемая фигура жестко присоединена к земле с помощью трех стержней, не пересекающихся в одной точке. Таким образом, система (рис.1.14) геометрически неизменяема и не является мгновенно изменяемой.
Пример 12. Выполнить кинематический анализ системы (рис.3.13).

Рис.3.13. Схема к примеру 12
Так как система является шарнирно-стержневой, то для определения ее степени свободы используем формулу (2):
W = 2У – С – С 0 ,
где У – число узлов фермы; С – число внутренних стержней; С 0 – число опорных стержней.
Здесь У =6, С =8, С 0 =3, следовательно, W = 2∙6 – 8 – 3 = 1.
Таким образом, система имеет одну степень свободы, и не может использоваться как строительная конструкция.
Пример 13. Исследовать ферму (рис.3.14).

Рис.3.14. Схема к примеру 13
По формуле (2) определяем степень свободы фермы: W = 2 ∙ 7 – 11 – 3 = 0, следовательно, система может быть геометрически изменяемой и статически определимой.
Проанализируем систему. Она состоит из трех дисков – треугольники АВС , CFG и стержень DЕ , связанных между собой стержнями ВЕ , АD , ЕG , DF , которые можно заменить фиктивными шарнирами О 1 , О 2 и шарниром С . Следовательно, можно сделать вывод: все стержни соединены между собой жестко и прикрепляются к земле так же жестко с помощью трех стержней, не пересекающихся в одной точке.
Для проверки системы на мгновенную изменяемость применим способ нулевой нагрузки – определим опорные реакции и усилия во всех стержнях при условии, что внешней нагрузки нет. Из условий равновесия всей системы (Σ М А = 0; Σ М В = 0; Σ У =0) находим, что опорные реакции равны нулю. Вырезая узел Е и проектируя все силы на вертикаль, находим, что усилие в вертикальном стержне N DЕ = 0. Затем, записывая уравнения проекций двух сил, сходящихся в узле D (третья сила - N DЕ = 0), на направления нормалей к этим стержням, находим, что усилия в стержнях DА и DF также равны нулю. Наконец, рассматривая равновесие узлов A, F, B, G , находим, что усилия во всех стержнях системы при отсутствии нагрузки равны нулю, следовательно, система неизменяемая.
Пример 14. Выполнить кинематический анализ системы (рис.3.15,а ).

Рис.3.15. Схема к примеру 14
По формуле (2) определяем степень свободы: W = 2 ∙ 9 – 11 – 7 = 0, то есть система обладает необходимым минимумом связей, чтобы быть геометрически неизменяемой. Для проверки того, является ли система действительно неизменяемой, используем метод замены стержней. Выберем заменяющую систему (рис.3.15,б ). Здесь отброшен стержень ВD , а его действие заменено силами Х 1 , и добавлен заменяющий стержень DG . Выбранная заменяющая система неизменяема: стержни АВ, ВС и земля жестко соединены тремя шарнирами, не лежащими на одной прямой. А нижняя часть системы неизменяема, поскольку состоит из треугольника (например, GHI ), к которому жестко прикреплены все остальные узлы с помощью диад, и все это прикреплено к земле тремя опорными стержнями.
Теперь определим усилие в заменяющем стержне от сил Х 1 = 1. Вырезая последовательно узлы E, I, G и рассматривая их равновесие, получим, что усилие в заменяющем стержне равно нулю, следовательно, исходная система - мгновенно изменяемая.
Пример 15. Произвести анализ образования системы, показанной на рис.3.16.

Рис.3.16. Схема к примеру 15
Вначале определяем степень свободы системы. Поскольку система является шарнирно-стержневой -воспользуемся формулой (2) W = 2У – С – С 0 . Число узлов системы У =6, число стержней системы С =8, число опорных стержней С 0 =3, следовательно, W = 2 ∙ 6 – 8 – 3 = 12 - 1 = +1.Система имеет одну степень свободы и не может быть использована в качестве строительной конструкции.
Пример 16. Произвести анализ образования системы, показанной на рис.3.17, а .

Рис.3.17. Схема к примеру 16
1. Пользуясь формулой (2) W = 2У – С – С 0 для шарнирно-стержневых систем определяем число степеней свободы. Поскольку, число узлов системы У =6, число стержней системы С =9, число опорных стержней С 0 =3, следовательно, W = 2 ∙ 6 – 9 – 3 = 0, следовательно, система имеет необходимое количество связей, чтобы быть неизменяемой и статически определимой.
2. Проводим анализ структуры системы. Рассмотрим треугольник 123, который в соответствии с третьим признаком является неизменяемой системой. Считая его жестким диском (заштрихован на рис. 3.17, б ), присоединим к нему двумя стержнями (3-4 и 2-4) узел 4. Этистержни не лежат на одной прямой, следовательно, на основании первого принципа узел 4 неподвижно прикреплен к диску 123. Полученная система также является жестким диском (заштрихован на рис.3.17, в ). Прикрепив к нему двумя стержнями (4-5 и 2-5) узел 5 снова получим жесткий диск, заштрихованный на рис.3.17, г ). К этому диску присоединим двумя стержнями (3-6 и 5-6) не лежащими на одной прямой последний узел 6.
Поскольку система образована в соответствии с принципами образования структурно неизменяемых систем, она неизменяема и не является мгновенно изменяемой. К земле система прикреплена так же жестко, с помощью трех опорных стержней, не пересекающихсяв одной точке.
Пример 17. к примеру 17
1. Пользуясь формулой W = 2У – С – С 0 для шарнирно-стержневых систем определяем число степеней свободы. Поскольку, число узлов системы У =9, число стержней системы С =15, число опорных стержней С 0 =3, следовательно, W = 2 ∙9 – 15 – 3 = 0, следовательно, система имеет необходимое количество связей, чтобы бытьгеометрически неизменяемой.
2. Проводим анализ структуры системы. Вначале найдем заведомо неизменяемые части системы – два диска, образованные треугольниками (заштрихованы на рис. 3.18, б ). Они соединены тремя стержнями. Однако эти стержни пересекаются в одной точке (т. k на рис. 3.18, б ). Следовательно, система мгновенно изменяемая.
Пример 18 . Проанализировать систему,изображенную на рис. 3.19.
Система состоит из четырех дисков (A С, С E , EF и FH ) т.е. Д= 4. Число шарниров Ш = 3 (все шарниры простые). Число опорных стержней С 0 =2+1 ∙ 4=6. Степень свободы системы по формуле W = 3Д – 2Ш – С 0 = 3 ∙ 4-2 ∙ 3-6=0.
Рис.3.19. Схема к примеру 18
Необходимое условие неизменяемости системы удовлетворено. Производим анализ структуры. Диск АС присоединен к земле тремя опорными стержнями, не пересекающимися в одной точке. Такое прикрепление обеспечивает неподвижность диска АС . К нему шарниром С и к земле опорным стержнем в точке D прикреплен диск СЕ. При этом ось стержня D не проходит через шарнир С. К полученной неизменяемой системе стержнем EF и двумя опорными стержнями в точках G и H присоединендиск FH . Эти три стержня не пересекаются в одной точке.
Таким образом, рассматриваемая система неизменяема и не является мгновенно изменяемой. По формуле W = 3Д – 2Ш – С 0 = 3 ∙2 -2 ∙1 -4=0.
Следовательно, система имеет необходимое количество связей, чтобынеизменяемой . Проанализируем ее структуру.
Вместе с землей система состоит из трех дисков, соединенных между собой шарниром Ш 1–2 и четырьмя стержнями, эквивалентными условным шарнирам Ш 1–3 и Ш 2–3 .
Так кактри шарнира, соединяющие три диска, лежат на одной прямой, система мгновенно изменяема.
Пример 20. Выполнить кинематический анализ шарнирно-стержневых систем (рис.3.21, а, б ).
а)
 б)
б)

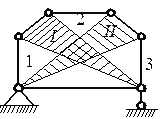
Рис.3.21. Схема к примеру 20
а) неприкрепленная ферма, где С = 9, У = 6, 9 = 2 ∙ 6 – 3, является геометрически неизменяемой, поскольку внутренний – I и внешний – II диски соединены тремя стержнями.
б) прикрепленная ферма, где С = 9, У = 6, С 0 = 3, 9 + 3 = 2 ∙ 6, является геометрически неизменяемой, так как диски I и II соединены тремя стержнями.
Пример 21. Выполнить кинематический анализ стержневых систем (рис.3.22, а, б , в ).
а) неприкрепленная шарнирно-стержневая система, где С = 11, У = 7, 11 = 2 ∙ 7 – 3, является геометрически неизменяемой. Образована способом трехшарнирной арки, то есть тремя дисками I, II, III, соединенными одним реальным (1, 2) и двумя фиктивными (2, 3; 1, 3) шарнирами, не лежащими на одной прямой.
б) прикрепленная шарнирно-стержневая система, где С = 6, У = 5, С 0 = 4, 6 + 4 = 2 ∙ 5, является мгновенно геометрически изменяемой. Поскольку три шарнира (1, 3; 1, 2; 2, 3), соединяющие три диска I, II, III лежат на одной прямой.
в) прикрепленная комбинированная система, где D = 2, Ш = 1, С 0 = 4, W = 3 ∙ 2 - 2 ∙ 1 – 4 = 0, является мгновенно геометрически изменяемой, так как один реальный (1, 2) и два фиктивных шарнира (1, 3; 2, 3), соединяющие три диска I, II, III, лежат на одной прямой.
а) б)
б) в)
в)
Рис.3.22. Схема к примеру 21
3.3. Степень изменяемости системы
Системы не связанные с землей
Для системы, не связанной с землей, вместо степени свободы W вводится характеристика степень изменяемости V , которую вычисляют по формулам:
V = 3Д – 2Ш – С – 3 ,(3)
V = 2У – С – 3 ,(4)
где смысл обозначений такой же, как в формулах (1) и (2).
Если V > 0, то система геометрически изменяемая.
Если V = 0, то система геометрически неизменяемая и статически определимая.
Если V < 0, то система геометрически неизменяемая и статически неопределимая.
Условия геометрической неизменяемости V =0 и V <0 являются необходимыми, но недостаточными. Для окончательного вывода о виде системы необходимо анализировать порядок образования системы (см.примеры ниже).
Пример 22. Кинематический анализ системы (рис. 3.23).
C читаем, что система состоит из двух ломаных стержней ABC , CDE и четырех прямых стержней AB , BC, CD, D E.
Шарниры A и Е – простые, шарниры B и D – двухкратные , шарнир С – трехкратный.
При Д = 6, Ш = 9, С = 0получаем
V = 3·6 – 2·9 – 0 – 3 = 18 – 21 = –3.

Рис.3.23. Схема кпримеру 22
Анализируем порядок образования системы. На ломаный стержень АВС накладываются две связи АВ и ВС, которые получаются избыточными. Аналогично, избыточными являются связи CD и DE для ломаного стержня CDE . Два диска АВС и CDE соединяются только шарниром С и для использования правила 2 не достает одной связи.
Следовательно, система геометрически изменяемая, хотя и содержит три избыточные связи в отдельных своих частях. Систему можно сделать геометрически неизменяемой, если изменить расположение некоторых связей, например, заменить стержень BC на стержень BD .
Пример 23. Кинематический анализ системы (рис. 3.24).
Рама имеет два замкнутых контура, а формула (3) не допускает наличия замкнутых контуров. Поэтому разделим раму четырьмя сечениями на три части (диска), соединенныхмежду собой тремя связями в каждом из проведенных сечений.
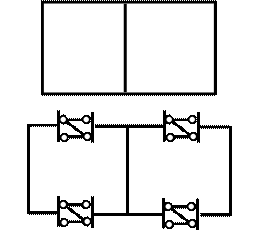
Рис.3.24. Схема к примеру 23
Тогда получаем Д = 3, Ш = 0,
С = 3∙4 =12и степень изменяемости
V = 3∙3 –0 – 12 – 3 = –6.
Анализируем порядок образования системы. К среднему диску прикрепляется левый диск с помощью шести связей, три из которых являются избыточными. Затем к образованному диску присоединяется правый диск с помощью шести связей, три из которых также избыточные.
Следовательно, анализируемая система геометрически неизменяемая и содержит шесть избыточных связей.
Введение
Цель курсового проекта по ТММ – формирование системного подхода к исследованию и проектированию механизмов, формирование навыков создания расчетных моделей механизмов и выполнения конкретных расчетов.
В данном курсовом проекте выполнен структурный, кинематический, кинетостатический расчет кривошипно-ползунного механизма рабочей машины и определены параметры противовесов, обеспечивающих его статическое уравновешивание.
В ходе кинематического анализа определены крайние положения механизма и построена его разметка для 12 положений; методом планов выполнен расчет скоростей и ускорений звеньев и точек звеньев; построены кинематические диаграммы перемещения, скорости и ускорения ползуна.
В ходе кинетостатического расчета методом планов определены реакции в кинематических парах и уравновешивающий момент. Кроме того, выполнен расчет уравновешивающего момента (уравновешивающей силы) методом рычага Н.Е. Жуковского.
С целью уменьшения переменного силового воздействия на стойку произведено статическое уравновешивание механизма. Методом замещающих масс определены параметры противовесов.
Структурный анализ механизма
Основная задача структурного анализа – определение подвижности механизма и его строения.
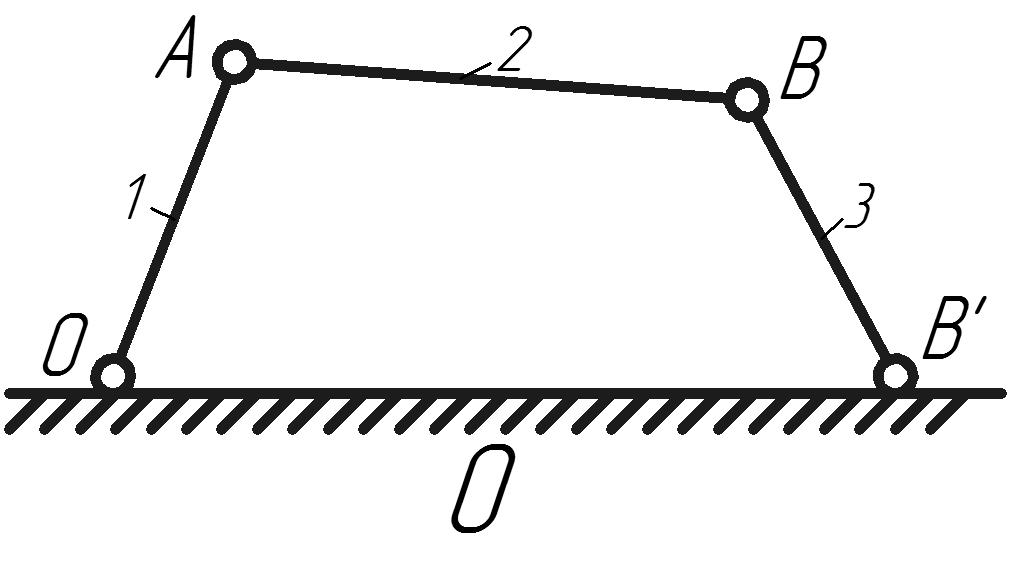
Исследуемый кривошипно-ползунный механизм (рис.1) состоит из 4-х звеньев: 0 – стойка; 1 – кривошип; 2 – шатун; 3 – ползун. Звенья образуют 4
кинематические пары пятого класса.
Рис. 1. Кинематическая схема механизма.
Подвижность механизмов определяется по формуле П.Л. Чебышева :
W = 3n – 2р 5 – р 4 ,
где n – количество подвижных звеньев, р 5 – количество кинематических пар пятого класса, р 4 – количество пар четвертого класса.
W = 3·3 – 2·4 – 0 = 1,
На рис. 2 приведена структурная схема механизма. Механизм состоит из исходного механизма и структурной группы II класса 2 порядка.
Формула строения механизма:
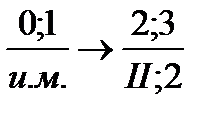 .
.
Исследуемый механизм является механизмом второго класса.
Формула строения механизма определяет порядок его кинематического и силового расчетов.
Кинематический анализ механизма
Цель кинематического анализа – изучение движения звеньев механизма.
Для ее достижения необходимо определить кинематические характеристики звеньев и точек звеньев. Задачи кинематики будем решать двумя методами – методом планов и методом диаграмм.
2.1.Кинематический анализ методом планов
Разметка механизма
Для определения скоростей и ускорений методом планов необходимо построить разметку механизма (рис. 3).
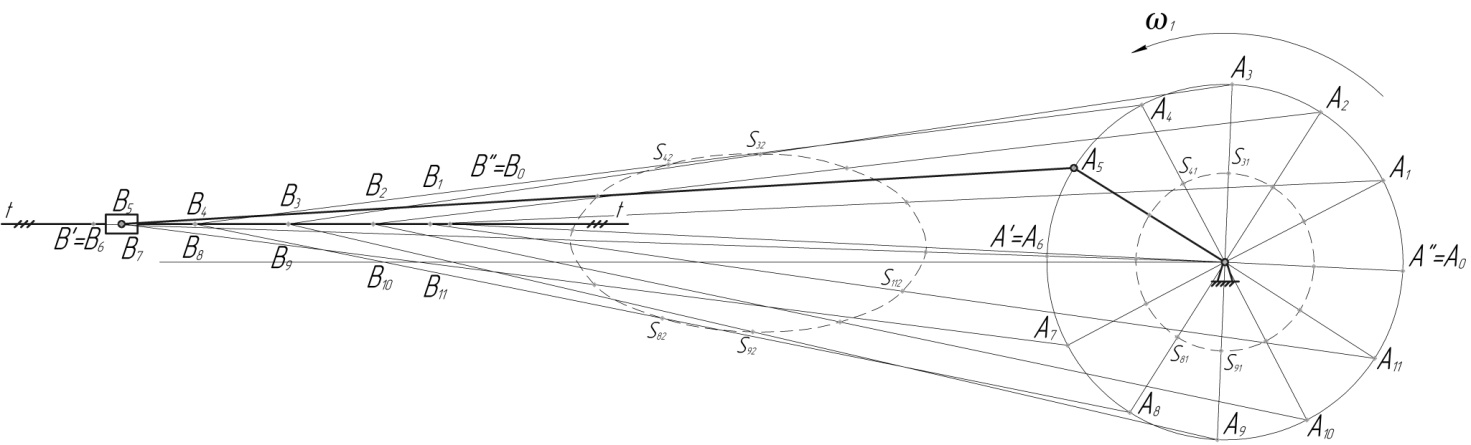
Рис. 3. План положений механизма
Разметка – ряд последовательных положений механизма, охватывающих цикл его движения. Разметка выполняется методом засечек в масштабе

В ходе разметки определяются крайние положения механизма. В этих положениях ползун меняет направление движения, т.е. V В = 0, а кривошип и шатун вытягиваются в одну прямую или складываются. Чтобы получить крайние положения механизма, надо на траектории движения ползуна из точки О сделать засечки раствором циркуля ОА + АВ и АВ – ОА. Получим точки B" и B" соответственно.
Отрезок B"B" в масштабе изображен ход Н ползуна. Соединим точки О и B". Прямую ОB" продолжим до пересечения с траекторией движения точки А (с окружностью). Получим точку А". В этом положении кривошип изображается прямой ОА", а шатун – прямой А"B".
Для определения второго крайнего положения механизма соединим точку B" с точкой О. Обозначим точку пересечения прямой ОB" с траекторией движения точки А кривошипа, как А". Отрезки ОА" и А"В" изображают кривошип и шатун во втором крайнем положении.
В положении ОА" кривошипа начинается рабочий ход механизма, а в положении ОА" рабочий ход заканчивается. В связи с этим, положения точек А" и В" примем за нулевые (точка А" совпадет с точкой А 0 , а точка В" – с точкой В 0). Соответственно точка А" совпадает с точкой А 6 , а точка В" – с точкой В 6 . Для построения промежуточных положений механизма разделим каждый из углов, образованных кривошипом и крайних его положениях, на шесть равных частей. Получим 10 промежуточных положений кривошипа. Нумерация положений производится в направлении вращения кривошипа.
Для каждого из этих положений методом засечек определяются соответствующие положения точек В шатуна и ползуна.
В каждом положении механизма и соответствии и исходными данными определяются положения центров масс S 1 кривошипа и S 2 и строятся траектории их движения.
Расчет скоростей
По известному значению ω 1 угловой скорости кривошипа определяется скорость точки А :
Вектор скорости направлен перпендикулярно кривошипу в рассматриваемом его положении в сторону вращения.
Шатун совершает плоскопараллельное движение. Скорости его точек А и В связанны зависимостью:
 , (1)
, (1)
где - переносная скорость точки В; - относительная скорость точки В;
Абсолютная скорость точки В.
Шатун в относительном движении вращается вокруг мгновенно неподвижной точки А. В связи с этим, вектор направлен перпендикулярно шатуну в рассматриваемом положении механизма, а - вдоль направляющей t-t ползуна.
Уравнение (1) имеет два неизвестных и может быть решено. Графическое решение этого уравнения называется планом скоростей.
Для построения планов скоростей надо выбрать масштабный коэффициент .
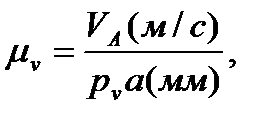
где - длина отрезка, которым скорость изображается на плане скоростей.
0,952/95,2 = 0,01 м/с.
Графическое решение уравнения (1) для четвертого положения механизма приведено на рис. 4.
Скорости V S 1 и V S 2 центров масс звеньев определяются по свойству подобия плана скоростей.

Рис.4. План скоростей

Из этой точки следует  .
.
Отрезок откладываем на плане скоростей (рис. 4) от полюса на прямой , получаем точку s 1 . Отрезок изображает в масштабе скорость центра масс кривошипа.
Для определения скорости центра масс шатуна составим пропорцию

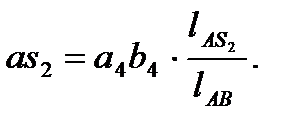
Отрезок откладываем на плане скоростей (рис. 4) от точки а 4 на прямой , получаем точку s 2 . Соединим ее с полюсом плана скоростей. Отрезок изображает скорость точки s 2 .
Расчет модулей скоростей в рассматриваемом (четвертом) положении механизма:
Расчет скоростей выполнен для 12 положений механизма, результаты представлены в табл. 1.
Таблица 1
| Скорость № п/п | V A | V S1 | V B | V S2 | V AB | ω 2 |
| м/с | 1/c | |||||
| 0,952 | 0,476 | 0,476 | 0,952 | 3,173 | ||
| 0,399 | 0,594 | 0,846 | 2,82 | |||
| 0,952 | 0,476 | 0,743 | 0,814 | 0,515 | 1,717 | |
| 0,946 | 0,949 | 0,039 | 0,13 | |||
| 0,898 | 0,898 | 0,488 | 1,494 | |||
| 0,552 | 0,665 | 0,809 | 2,696 | |||
| 0,476 | 0,952 | 3,173 | ||||
| 0,554 | 0,653 | 0,848 | 2,827 | |||
| 0,908 | 0,893 | 0,518 | 1,727 | |||
| 0,961 | 0,956 | 0,041 | 0,137 | |||
| 0,753 | 0,829 | 0,448 | 1,493 | |||
| 0,401 | 0,608 | 0,809 | 2,697 |
Расчет ускорений
Введение
1. Основные задачи и методы кинематического анализа
2. Построение положений звеньев механизма
3. Функция положения механизма
4. Основные уравнения для определения скоростей и ускорений
5. Кинематические диаграммы
5.1 Построение диаграммы перемещений
Литература
Введение
Тема контрольной работы "Кинематический анализ механизмов" по дисциплине "Теория механизмов и машин".
Цель работы: формирование знаний кинематического анализа механизмов.
Задачи выполнения работы: ознакомление с методами кинематического анализа механизмов.
Основные вопросы темы:
1. Основные задачи и методы кинематического анализа;
2. Построение положений звеньев механизма;
3. Функция положения механизма;
4. Основные уравнения для определения скоростей и ускорений;
5. Кинематические диаграммы.
1. Основные задачи и методы кинематического анализа
Основной задачей кинематики механизмов является изучение движения звеньев механизмов вне зависимости от сил, действующих на эти звенья.
При кинематическом исследовании механизмов рассматриваются следующие основные вопросы:
построение планов скоростей;
построение траектории любой точки механизма;
3) определение скоростей и ускорений любой точки механизма, определение угловых скоростей и ускорений любого звена механизма, определение радиуса кривизны в любой точке траектории и др.
Кинематическое исследование можно вести как с применением графических методов, так и аналитическим путем. Графические методы исследования, давая достаточную для инженерной практики точность, обычно оказываются проще и нагляднее аналитических. Однако, когда ведется систематическое углубленное исследование какого-либо определенного типа механизма, более удобным оказывается аналитический метод.
При графических построениях на чертеже приходится изображать не только длины звеньев, но и скорости и ускорения отдельных точек, а также и другие величины. В этих условиях удобно использовать масштабный коэффициент, которым называют отношение действительной величины к изображению:
Масштабный коэффициент;
Масштабный коэффициент;
Масштабный коэффициент
2. Построение положений звеньев механизма
Взаимное расположение звеньев движущегося механизма все время меняется, но в каждый данный момент времени расположение звеньев является вполне определенным. Графическое изображение взаимного расположения звеньев, соответствующее выбранному моменту времени, называется планом механизма. Ряд последовательных планов механизма, построенных для моментов времени, следующих друг за другом, называется планом положений и позволяет наглядно проследить за движением механизма.
Построение плана положений механизма начинают с изображения того звена, положение которого задано для данного момента времени.
Кривошипно-ползунный механизм

Из центра О - оси вращения кривошипа ОА радиусами и на оси X - X движения ползуна отмечаем В0 - правое В6 - левое крайние ползуна В. Прямые ОА0В0 и ОА6В6 - положения механизма, соответствующие крайним положениям В0 и В6 ползуна. Траекторию пальца А кривошипа от точки А0 делим на 12 равных частей и из полученных точек А1, А2, А3 … А11 радиусами АВ==… отмечаем положения В1, В2, В3 …В11 ползуна на линии В0В6. Соединив точки А1, А2, А3 … А11 с центром О и соответствующими точками В1, В2, В3 …В11, получим планы механизма. Кривая, последовательно соединяющая центры S0, S1, S2 …S11 шатуна в различных его положениях, будет шатунной кривой.
3. Функция положения механизма
Функцией положения механизма называется зависимость координаты выходного звена от обобщенных координат механизма.
Перемещения, скорости и ускорения звеньев и точек механизма является функциями перемещений, скоростей и ускорений звеньев механизма, принятых за ведущие. Число ведущих звеньев механизма должно быть равно числу степеней подвижности механизма или, что то же самое, числу обобщенных координат механизма.
Рассмотрим, в какой форме могут быть заданы законы ведущих звеньев. Эти законы называют функциями перемещений, скоростей и ускорений.
Функция перемещений может быть задана в аналитической форме в виде соответствующей функции, связывающей перемещение ведущего звена со временем (рис.2).


Если ведущее звено входит во вращательную пару со стойкой, то задается функция φ=φ (t), где: φ - угол поворота ведущего звена относительно неподвижной системы координат ХОY, связанной со стойкой, а t - время.
Если ведущее звено входит в поступательную пару, то задается функция s=s (t), где s - перемещение произвольно выбранной точки А ведущего звена относительно неподвижной системы координат, связанной со стойкой, а t - время.
Функции φ=φ (t) и s=s (t) могут быть также заданы графически в виде кривых, где по осям ординат отложены углы поворота φ или перемещения s в некоторых выбранных масштабах и , а по осям абсцисс время t в выбранном масштабе (рис.3).

φ0 = 0; φi - φ0 = · в;
Соответственно время ti, за которое ведущее звено повернулось на угол φi равно:
Если закон движения ведущего звена задан в виде функций скоростей ω=ω (t) или v=v (t), то переход от функций скоростей к функциям перемещений может быть осуществлен путем вычисления интегралов:
кинематический анализ механизм ускорение
 и
и
 ;
;
где: φ0, s0, t0 - угол, перемещение и время, соответствующие начальному положению ведущего звена.
Если закон движения ведущего звена задан в виде функций ускорений ε=ε (t) и ω=ω (t), то переход к функциям скоростей осуществляется путем вычисления интегралов:
 и
и
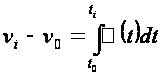
где: ω0, v0, t0 - угловая скорость, линейная скорость и время, соответствующие начальному положению ведущего звена.
4. Основные уравнения для определения скоростей и ускорений
Связь между скоростями и ускорениями общих точек звеньев кинематической пары зависит от пары.
Рассмотрим два случая составления векторных уравнений скоростей и ускорений:
а) две точки принадлежат одному звену и удалены друг от друга на расстояние l (рис.4).

Рис.4
Из теоретической механики известно, что скорость любой точки абсолютно твердого тела можно представить как геометрическую сумму скоростей переносного и относительного движений.
Переносным движением для рассматриваемого звена будем считать поступательное движение со скоростью точки А, а относительным - вращательное движение звена вокруг точки А. Векторное уравнение для скорости точки В:
![]() ;
;
При вращении звена вокруг точки А точка В движется по окружности ββ, описанной из точки А. Поэтому скорость VBA направлена по касательной к дуге ββ, т.е. перпендикулярна линии АВ.
Величина скорости VBA=ω·АВ или VBA=ω·.
По направлению V BA можно найти направление ω и наоборот.
Т.к. переносное движение выбрано поступательным, то ускорение точки В можно составить из 2-х ускорений: ускорения точки А и ускорения точки В при вращении звена вокруг точки А.
![]()
При движении точки В по окружности ββ ускорение WBA складывается из 2-х ускорений: нормального , направленного к центру вращения, и тангенциального , направленного по касательной к дуге ββ, т.е. перпендикулярно линии АВ. Векторное уравнение для ускорения точки В:
![]() ;
;
Величины ускорений и определяем по формулам:
=·ω2=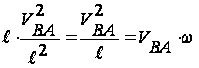 ;
;
где: ε - угловое ускорение;
б) две точки принадлежат двум звеньям, образующим поступательную пару и в данный момент времени совпадают (рис.5).
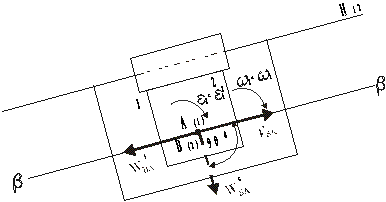
Точка А принадлежит звену 1, точка В - звену 2. В данный момент времени точки А и В совпадают (точка В лежит над точкой А). Звенья 1 и 2 образуют поступательную пару с направляющей Н12.
Скорость точки В складывается из 2-х скоростей - переносной и относительной. Переносным движением здесь является движение звена 1, поэтому скорость точки А - VA будет переносной. Относительная скорость точки В равна скорости движения звена 2 относительно звена 1. При движении звена 2 относительно звена 1 точка В движется по прямой линии ββ, параллельной направляющей Н12. Поэтому относительная скорость VВА параллельна Н12.
Ускорение точки В, когда переносное движение не является поступательным, складывается из 3-х ускорений: переносного, т.е. ускорения точки А, относительного и поворотного, или Кориолисова. В относительном движении точка В движется по линии ββ, поэтому в этом движении точка В имеет только тангенциальное ускорение, направленное по этой линии, т.е. параллельно направляющей Н12. Обозначим это ускорение через . Поворотное (Кориолисово) ускорение обозначим через .
Векторные уравнения для скорости и ускорения точки В будут иметь вид:

Так как звенья 1 и 2 образуют поступательную пару, то они не имеют относительного вращения. Поэтому эти звенья обладают одинаковыми угловыми скоростями и угловыми ускорениями, т.е.: ω2=ω1 и ε2=ε1, где ω1 - угловая скорость переносного движения (вращения звена 1).
Вектор направлен в ту сторону, в которую окажется направленным вектор , если повернуть его на 900 в направлении угловой скорости ω1. Величина его определяется по формуле:
Определим скорость и ускорение ползуна кривошипно-ползунного механизма.
Дан план механизма, размеры ℓОА, ℓАВ, ω2, ε2.
Найдем скорость и ускорение звена 4 (точки В) и угловые скорость и ускорение звена 3 (шатуна).

Зная ω2, находим VА=ℓОА·ω2. Скорость V А изобразим на плане скоростей в виде отрезка "Pа", перпендикулярного ОА (рис.7). Поршень (звено 4) движется поступательно, поэтому все его точки имеют ту же скорость и то же ускорение, что и точка В.

Рис.7 Рис.8
Однако точка В принадлежит не только звену 4, но и звену 3. Точно также точка А есть общая точка для звеньев 2 и 3. Таким образом, на звене 3 имеются две точки А и В, удаленные друг от друга на расстояние ℓАВ. Поэтому скорость точки В:
![]() где:
║
где:
║![]() ;
;
В соответствии с этим уравнением строим план скоростей. Проводим через точку а линию, перпендикулярную к АВ, а через точку Р - линию перпендикулярную Н41. В точке пересечения ставим в. Отрезок Рв изображает скорость точки В, а отрезок ав - скорость точки В относительно А (VВА). Угловую скорость звена 3 находим по формуле:
Перенеся вектор в точку В, находим направление ω3 (против часовой стрелки).
Ускорение точки А:
![]()
Отложив от полюса (рис.8) ускорение и в виде отрезков и , находим полное ускорение точки А (отрезок ).. Из сопоставления направлений WB и VB заключаем, что звено 4 в данный момент движется замедленно.
Угловое ускорение звена 3 находим по формуле: .
Перенос вектора в точку В показывает, что ε3, как и ω3, направлено против часовой стрелки.
В уравнениях вектор, известный по величине и направлению подчеркиваем двумя линиями, а вектор, известный только по направлению - одной линией.
5. Кинематические диаграммы
Кинематическая диаграмма представляет собой графическое изображение одного из кинематических параметров (перемещений, скорости и ускорения) точки либо звена исследуемого механизма в функции времени, угла поворота или перемещения ведущего звена этого механизма, т.е. в функции обобщенной координаты. Кинематические диаграммы дают полную кинематическую характеристику механизма.
Построим кинематические диаграммы кривошипно-ползунного механизма.
Для перемещений SB, скоростей VB и ускорений WВ точки В, как перемещающейся прямолинейно, удобно строить кинематические диаграммы в виде зависимостей этих величин от времени t или обобщенной координаты φ2, т.е. строить графическое изображение зависимостей:
SB=SB (t), VB=VB (t), WB=WB (t) или:
SB=SB (φ2), VB=VB (φ2), WB=WB (φ2)
если угол φ2 поворота звена 2 выбран в качестве обобщенной координаты.
Если исследованию подлежат угловые перемещения φ3, угловые скорости ω3 и угловые ускорения ε3 шатуна 3, то можно построить графическое изображение зависимостей:
φ3=φ3 (t), ω3=ω3 (t), ε3=ε3 (t)
φ3=φ3 (φ2), ω3=ω3 (φ2), ε3=ε3 (φ2)
Кривошип ОА вращается с постоянной угловой скоростью ω2.
5.1 Построение диаграммы перемещений
1) Вычерчиваем схему механизма в масштабе μе в нескольких, например, двенадцати положениях, соответствующих последовательным поворотам кривошипа ОА на 300 (рис.9). За начальное положение кривошипа принимаем ОА0, при котором ползун В занимает крайнее правое положение В0;
2) строим оси
координат SB-t
(рис.10а) и на оси
абсцисс откладываем
отрезок ℓ в мм,
изображающий
время одного
полного оборота
кривошипа в
масштабе:
![]() ;
где:
рад/мм,
;
;
где:
рад/мм,
;
Отрезок ℓ делим на 12 равных частей и в соответствующих точках 1, 2, 3… по оси ординат откладываем расстояния SB1, SB2… пройденные точкой В от ее крайнего правого положения В0.
До крайнего левого положения В6 расстояния возрастают, а начиная с положения В6, они будут уменьшаться; когда кривошип придет в начальное положение А0, ордината кривой (SB-t) будет равна нулю.
3) соединяем последовательно плавной линией полученные точки 0, 1΄, 2΄, 3΄, …. Полученная кривая будет диаграммой расстояний точки В.
Если же по оси абсцисс откладывать углы поворота кривошипа φ, то данная кривая представит функциональную зависимость:
Диаграммы скоростей и ускорений могут быть построены с использованием планов скоростей и ускорений и методов графического дифференцирования:
 .
.
Метод графического дифференцирования:
1) под диаграммой (SB-t) строим оси координат O1VB, O1t (рис.2.10б) и на продолжении оси O1t влево откладываем отрезок O1Р=Н1 мм (произвольно, чтобы дифференциальная кривая разместилась на отведенном для нее месте чертежа);
2) из точки "Р" проводим лучи Р1, Р2, Р3… параллельно хордам кривой (SB-t) на участках 01΄; 1΄2΄; 2΄3΄….
Эти лучи отсекут на оси O1В отрезки 011; 012; 013…, пропорциональные средней скорости Vc на соответствующем участке диаграммы;
3) отложим эти отрезки на средних ординатах соответствующих участков;
4) соединим ряд полученных точек I, II, III…плавной кривой; эта кривая будет диаграммой скорости (V0-t).
Имея диаграмму скоростей, аналогично строим диаграмму ускорений.
При построении диаграмм (V0-t) и (WB-t) данным методом нельзя получить те участки этих диаграмм, которые соответствуют половине крайних участков оси абсцисс. Чтобы закончить построение диаграмм, нужно дополнительно построить средние значения VВ и для одного-двух участков следующего цикла.

Рис.9 План положений скоростей

Рис.10 Кинематические диаграммы
Масштаб диаграмм остается таким же, как и раньше.
Масштабы по осям ординат определяются по формулам:
для диаграммы
скоростей:
 ;
;
для диаграммы
ускорений:
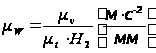 ,
,
Метод построения диаграмм - прост и нагляден, но имеет следующие недостатки:
1) неточность, особенно при дифференцировании кривых с большой кривизной;
2) невозможность полностью исследовать криволинейное движение, т.к. дифференцированием кривой скоростей получаем диаграммы изменения только тангенциальных ускорений;
3) диаграммы дают лишь численные значения векторов, направление которых можно установить лишь после некоторых дополнительных построений.
Метод планов скоростей и ускорений не имеет упомянутых недостатков, поэтому его широко применяют при исследовании различных механизмов.
Структурное и кинематическое исследование рычажного механизма. Построение кинематической схемы, планов скоростей и ускорений. Силовой расчет рычажного механизма. Определение сил, действующих на звенья механизма. Замена сил инерции и моментов сил.
Особенности расчета принципа работы инерционного конвейера: построение планов скоростей, ускорений, силовой анализ механизма станка. Изучение принципа зацепления зубчатых колес, а также способа их изготовления. Геометрический синтез зубчатой передачи.
Принципы работы, механизм и назначение насоса с качающейся кулисой. Структурный анализ и силовой расчет рычажного механизма. Особенности выполнения геометрического расчета зубчатой передачи. Синтез кулачкового механизма, порядок построения его профиля.
Структурный анализ, построение положений механизма и планов скоростей для рабочего и холостого хода, верхнего и нижнего крайних положений. Построение планов ускорений, кинетостатический расчет механизма. Определение сил инерции и сил тяжести звеньев.
Кинематический анализ плоского рычажного механизма. Определение нагрузок, действующих на звенья механизма. Силовой расчёт ведущего звена методом Жуковского. Синтез кулачкового механизма. Способы нахождения минимального начального радиуса кулачка.
Задачи и методы динамического синтеза и анализа машинного агрегата. Описание определения кинематических характеристик рычажного механизма. Определение работы сил сопротивления, истинной угловой скорости звена приведения, момента инерции маховика.
Динамический анализ рычажного механизма по коэффициенту неравномерности движения. Силовое исследование рычажного механизма. Проектирование зубчатой передачи и планетарного редуктора. Проектирование и расчет кулачкового механизма и его составляющих.
Кинематический и силовой анализ рычажного механизма поперечно-строгального станка. Методика определения уравновешивающей силы методом рычага Жуковского. Особенности проектирования планетарного редуктора. Анализ комбинированного зубчатого механизма станка.
Структурное и кинематическое исследование механизма: описание схемы; построение планов скоростей. Определение реакций в кинематических парах; силовой расчет ведущего звена методом Н.Е. Жуковского. Синтез зубчатого зацепления и кулачкового механизма.
Структурный анализ кривошипно-ползунного механизма, выявление его структурного состава. Синтез кинематической схемы. Кинематический анализ плоского механизма. Определение сил, действующих на звенья механизма. Кинетостатический метод силового анализа.
Кинематическая схема механизма кривошипно-балансирного механизма. Начальное положение ведущего звена. Кинематические диаграммы, планы скоростей и ускорений. Определение уравновешивающего момента на ведущем кривошипе, проверка методом рычага Жуковского.
Устройство, принцип работы и назначение долбежного станка. Кинематический анализ и выбор электродвигателя. Определение точки приложения и направление уравновешивающей силы. Построение диаграммы изменения кинетической энергии и истинной скорости.
Кинематическая схема шарнирного механизма. Определение длины кулисы и масштабного коэффициента длины. Построение плана положения механизма для заданного положения кривошипа методом засечек. Построение плана скоростей. Расчет углового ускорения кулисы.
Характеристика основных задач динамики механизмов. Движущие силы как основные силы, определяющие характер движения механизмов. Силы полезного сопротивления и инерции. Осуществление кинетостатического расчета механизмов. Применение теоремы Н. Жуковского.
Структурный, динамический и кинетостатический анализ плоского рычажного механизма. Определение угловых скоростей его звеньев; внешних сил и моментов инерции, действующих на каждое звено и кинематическую пару. Проектный расчет механизма на прочность.
