С дробями ученики знакомятся еще в 5 классе. Раньше людей, которые умели производить действия с дробями, считали очень умными. Первой дробью была 1/2, то есть половина, дальше появились 1/3 и т.д. Несколько веков примеры считались слишком сложными. Сейчас же разработаны подробные правила по преобразованию дробей, сложению, умножению и другим действиям. Достаточно немного разобраться в материале, и решение будет даваться легко.
Обыкновенная дробь, которую называют простой дробью, записывается как деление двух чисел: m и n.
M - это делимое, то есть числитель дроби, а делитель n называют знаменателем.
Выделяют правильные дроби (m < n) а также неправильные (m > n).
Правильная дробь меньше единицы (к примеру 5/6 — это значит, что от единицы взято 5 частей; 2/8 — от единицы взято 2 части). Неправильная дробь равна или больше 1 (8/7 — единицей будет 7/7 и плюсом взята еще одна часть).
Так, единица, это когда числитель и знаменатель совпали (3/3, 12/12, 100/100 и другие).
Действия с обыкновенными дробями 6 класс
С простыми дробями можно производить следующие действия:
- Расширять дробь. Если умножить верхнюю и нижнюю часть дроби на какое-либо одинаковое число (только не на ноль), то значение дроби не поменяется (3/5 = 6/10 (просто умножили на 2).
- Сокращение дробей — схоже расширению, но тут делят на какое-либо число.
- Сравнивать. Если у двух дробей числители одинаковыми, то большей окажется дробь с меньшим знаменателем. Если одинаковые знаменатели, то больше будет дробь с наибольшим числителем.
- Выполнять сложение и вычитание. При одинаковых знаменателях это сделать просто (суммируем верхние части, а нижняя не меняется). При разных придется найти общий знаменатель и дополнительные множители.
- Умножить и разделить дроби.
Примеры действий с дробями рассмотрим ниже.
Сокращенные дроби 6 класс
Сократить — значит поделить верхнюю и нижнюю часть дроби на какое-либо одинаковое число.
На рисунке представлены просты примеры сокращения. В первом варианте можно сразу догадаться, что числитель и знаменатель делятся на 2.
На заметку! Если число четное, то оно по-любому делится на 2. Четные числа — это 2, 4, 6…328 (заканчивается на четное) и т. д.
Во втором случае при делении 6 на 18 сразу видно, что числа делятся на 2. Разделив, получаем 3/9. Эта дробь делится еще на 3. Тогда в ответе получается 1/3. Если перемножить оба делителя: 2 на 3, то выйдет 6. Получается, что дробь была разделена на шестерку. Такое постепенное деление называется последовательным сокращением дроби на общие делители.
Кто-то сразу поделит на 6, кому-то понадобится деление частями. Главное, чтобы в конце осталась дробь, которую уже никак не сократить.
Отметим, что если число состоит из цифр, при сложении которых получится число, делящееся на 3, то и первоначальное также можно сократить на 3. Пример: число 341. Складываем цифры: 3 + 4 + 1 = 8 (8 на 3 не делится, значит, число 341 нельзя сократить на 3 без остатка). Другой пример: 264. Складываем: 2 + 6 + 4 = 12 (делится на 3). Получаем: 264: 3 = 88. Это упростит сокращение больших чисел.
Помимо метода последовательного сокращения дроби на общие делители есть и другие способы.
НОД — это самый большой делитель для числа. Найдя НОД для знаменателя и числителя, можно сразу сократить дробь на нужное число. Поиск осуществляется путем постепенного деления каждого числа. Далее смотрят, какие делители совпадают, если их несколько (как на картинке ниже), то нужно перемножить.
Смешанные дроби 6 класс
Все неправильные дроби можно превратить в смешанные, выделив в них целую часть. Целое число пишется слева.
Часто приходится из неправильной дроби делать смешанное число. Процесс преобразования на примере ниже: 22/4 = 22 делим на 4, получаем 5 целых (5 * 4 = 20). 22 — 20 = 2. Получаем 5 целых и 2/4 (знаменатель не меняется). Поскольку дробь можно сократить, то делим верхнюю и нижнюю часть на 2.
Смешанное число легко превратить в неправильную дробь (это необходимо при делении и умножении дробей). Для этого: целое число умножим на нижнюю часть дроби и прибавим к этому числитель. Готово. Знаменатель не меняется.
Вычисления с дробями 6 класс
Смешанные числа можно складывать. Если знаменатели одинаковые, то сделать это просто: складываем целые части и числители, знаменатель остается на месте.
При сложении чисел с разными знаменателями процесс сложнее. Сначала приводим числа к одному самому маленькому знаменателю (НОЗ).
В примере ниже для чисел 9 и 6 знаменателем будет 18. После этого нужны дополнительные множители. Чтобы их найти, следует 18 разделить на 9, так находится дополнительное число — 2. Его умножаем на числитель 4 получилась дробь 8/18). То же самое делают и со второй дробью. Преобразованные дроби уже складываем (целые числа и числители отдельно, знаменатель не меняем). В примере ответ пришлось преобразовать в правильную дробь (изначально числитель оказался больше знаменателя).
Обратите внимание, что при разности дробей алгоритм действий такой же.
При умножении дробей важно поместить обе под одну черту. Если число смешанное, то превращаем его в простую дробь. Далее умножаем верхнюю и нижнюю части и записываем ответ. Если видно, что дроби можно сократить, то сокращаем сразу.
В указанном примере сокращать ничего не пришлось, просто записали ответ и выделили целую часть.
В этом примере пришлось сократить числа под одной чертой. Хотя сокращать можно и готовый ответ.
При делении алгоритм почти такой же. Сначала превращаем смешанную дробь в неправильную, затем записываем числа под одной чертой, заменив деление умножением. Не забываем верхнюю и нижнюю часть второй дроби поменять местами (это правило деления дробей).
При необходимости сокращаем числа (в примере ниже сократили на пятерку и двойку). Неправильную дробь преобразуем, выделив целую часть.
Основные задачи на дроби 6 класс
На видео показано еще несколько задач. Для наглядности использованы графические изображения решений, которые помогут наглядно представить дроби.
Примеры умножения дроби 6 класс с пояснениями
Перемножающиеся дроби записываются под одной линией. После этого их сокращают путем деления на одни и те же числа (например, 15 в знаменателе и 5 в числителе можно разделить на пятерку).
Сравнение дробей 6 класс
Чтобы сравнить дроби, нужно запомнить два простых правила.
Правило 1. Если знаменатели разные
Правило 2. Когда знаменатели одинаковые
Например, сравним дроби 7/12 и 2/3.
- Смотрим на знаменатели, они не совпадают. Значит нужно найти общий.
- Для дробей общим знаменателем будет 12.
- Делим 12 сначала на нижнюю часть первой дроби: 12: 12 = 1 (это доп. множитель для 1-й дроби).
- Теперь 12 делим на 3, получаем 4 — доп. множитель 2-й дроби.
- Умножаем полученные цифры на числители, чтобы преобразовать дроби: 1 х 7 = 7 (первая дробь: 7/12); 4 х 2 = 8 (вторая дробь: 8/12).
- Теперь можем сравнивать: 7/12 и 8/12. Получилось: 7/12 < 8/12.
Чтобы представлять дроби лучше, можно для наглядности использовать рисунки, где предмет делится на части (к примеру, торт). Если требуется сравнить 4/7 и 2/3, то в первом случае торт делят на 7 частей и выбирают 4 из них. Во втором — делят на 3 части и берут 2. Невооруженным взглядом будет понятно, что 2/3 будет больше 4/7.
Примеры с дробями 6 класс для тренировки
В качестве тренировки можно выполнить следующие задания.
- Сравнить дроби
- выполнить умножение
Совет: если сложно найти наименьший общий знаменатель у дробей (особенно, если значения их небольшие), то можно перемножить знаменатель первой и второй дроби. Пример: 2/8 и 5/9. Найти их знаменатель просто: 8 умножаем на 9, получится 72.
Решение уравнений с дробями 6 класс
В решении уравнений требуется вспомнить действия с дробями: умножение, деление, вычитание и сложение. Если неизвестен один из множителей, то произведение (итог) делится на известный множитель, то есть дроби перемножаются (вторая переворачивается).
Если неизвестно делимое, то знаменатель умножается на делитель, а для поиска делителя нужно делимое разделить на частное.
Представим простые примеры решения уравнений:
Здесь требуется лишь произвести разность дробей, не приводя к общему знаменателю.
Ответ получился в виде неправильной дроби. Ее можно преобразовать в 1 целую и 3/5.
Во втором способе числитель и знаменатель умножили на 4, чтобы сократить нижнюю часть, а не переворачивать знаменатель.
Данная статья рассматривает действия над дробями. Будут сформированы и обоснованы правила сложения, вычитания, умножения, деления или возведения в степень дробей вида A B , где A и B могут быть числами, числовыми выражениями или выражениями с переменными. В заключении будут рассмотрены примеры решения с подробным описанием.
Yandex.RTB R-A-339285-1
Правила выполнения действий с числовыми дробями общего вида
Числовые дроби общего вида имеют числитель и знаменатель, в которых имеются натуральные числа или числовые выражения. Если рассмотреть такие дроби, как 3 5 , 2 , 8 4 , 1 + 2 · 3 4 · (5 - 2) , 3 4 + 7 8 2 , 3 - 0 , 8 , 1 2 · 2 , π 1 - 2 3 + π , 2 0 , 5 ln 3 , то видно, что числитель и знаменатель может иметь не только числа, но и выражения различного плана.
Определение 1
Существуют правила, по которым идет выполнение действий с обыкновенными дробями. Оно подходит и для дробей общего вида:
- При вычитании дробей с одинаковыми знаменателями складываются только числители, а знаменатель остается прежним, а именно: a d ± c d = a ± c d , значения a , c и d ≠ 0 являются некоторыми числами или числовыми выражениями.
- При сложении или вычитании дроби при разных знаменателях, необходимо произвести приведение к общему, после чего произвести сложение или вычитание полученных дробей с одинаковыми показателями. Буквенно это выглядит таком образом a b ± c d = a · p ± c · r s , где значения a , b ≠ 0 , c , d ≠ 0 , p ≠ 0 , r ≠ 0 , s ≠ 0 являются действительными числами, а b · p = d · r = s . Когда p = d и r = b , тогда a b ± c d = a · d ± c · d b · d .
- При умножении дробей выполняется действие с числителями, после чего со знаменателями, тогда получим a b · c d = a · c b · d , где a , b ≠ 0 , c , d ≠ 0 выступают в роли действительных чисел.
- При делении дроби на дробь первую умножаем на вторую обратную, то есть производим замену местами числителя и знаменателя: a b: c d = a b · d c .
Обоснование правил
Определение 2Существуют следующие математические моменты, на которые следует опираться при вычислении:
- дробная черта означает знак деления;
- деление на число рассматривается как умножение на его обратное значение;
- применение свойства действий с действительными числами;
- применение основного свойства дроби и числовых неравенств.
С их помощью можно производить преобразования вида:
a d ± c d = a · d - 1 ± c · d - 1 = a ± c · d - 1 = a ± c d ; a b ± c d = a · p b · p ± c · r d · r = a · p s ± c · e s = a · p ± c · r s ; a b · c d = a · d b · d · b · c b · d = a · d · a · d - 1 · b · c · b · d - 1 = = a · d · b · c · b · d - 1 · b · d - 1 = a · d · b · c b · d · b · d - 1 = = (a · c) · (b · d) - 1 = a · c b · d
Примеры
В предыдущем пункте было сказано про действия с дробями. Именно после этого дробь нуждается в упрощении. Подробно эта тема была рассмотрена в пункте о преобразовании дробей.
Для начала рассмотрим пример сложения и вычитания дробей с одинаковым знаменателем.
Пример 1
Даны дроби 8 2 , 7 и 1 2 , 7 , то по правилу необходимо числитель сложить, а знаменатель переписать.
Решение
Тогда получаем дробь вида 8 + 1 2 , 7 . После выполнения сложения получаем дробь вида 8 + 1 2 , 7 = 9 2 , 7 = 90 27 = 3 1 3 . Значит, 8 2 , 7 + 1 2 , 7 = 8 + 1 2 , 7 = 9 2 , 7 = 90 27 = 3 1 3 .
Ответ: 8 2 , 7 + 1 2 , 7 = 3 1 3
Имеется другой способ решения. Для начала производится переход к виду обыкновенной дроби, после чего выполняем упрощение. Это выглядит таким образом:
8 2 , 7 + 1 2 , 7 = 80 27 + 10 27 = 90 27 = 3 1 3
Пример 2
Произведем вычитание из 1 - 2 3 · log 2 3 · log 2 5 + 1 дроби вида 2 3 3 · log 2 3 · log 2 5 + 1 .
Так как даны равные знаменатели, значит, что мы выполняем вычисление дроби при одинаковом знаменателе. Получим, что
1 - 2 3 · log 2 3 · log 2 5 + 1 - 2 3 3 · log 2 3 · log 2 5 + 1 = 1 - 2 - 2 3 3 · log 2 3 · log 2 5 + 1
Имеются примеры вычисления дробей с разными знаменателями. Важный пункт – это приведение к общему знаменателю. Без этого мы не сможем выполнять дальнейшие действия с дробями.
Процесс отдаленно напоминает приведение к общему знаменателю. То есть производится поиск наименьшего общего делителя в знаменателе, после чего добавляются недостающие множители к дробям.
Если складываемые дроби не имеют общих множителей, тогда им может стать их произведение.
Пример 3
Рассмотрим на примере сложения дробей 2 3 5 + 1 и 1 2 .
Решение
В данном случае общим знаменателем выступает произведение знаменателей. Тогда получаем, что 2 · 3 5 + 1 . Тогда при выставлении дополнительных множителей имеем, что к первой дроби он равен 2 , а ко второй 3 5 + 1 . После перемножения дроби приводятся к виду 4 2 · 3 5 + 1 . Общее приведение 1 2 будет иметь вид 3 5 + 1 2 · 3 5 + 1 . Полученные дробные выражения складываем и получаем, что
2 3 5 + 1 + 1 2 = 2 · 2 2 · 3 5 + 1 + 1 · 3 5 + 1 2 · 3 5 + 1 = = 4 2 · 3 5 + 1 + 3 5 + 1 2 · 3 5 + 1 = 4 + 3 5 + 1 2 · 3 5 + 1 = 5 + 3 5 2 · 3 5 + 1
Ответ: 2 3 5 + 1 + 1 2 = 5 + 3 5 2 · 3 5 + 1
Когда имеем дело с дробями общего вида, тогда о наименьшем общем знаменателе обычно дело не идет. В качестве знаменателя нерентабельно принимать произведение числителей. Для начала необходимо проверить, имеется ли число, которое меньше по значению, чем их произведение.
Пример 4
Рассмотрим на примере 1 6 · 2 1 5 и 1 4 · 2 3 5 , когда их произведение будет равно 6 · 2 1 5 · 4 · 2 3 5 = 24 · 2 4 5 . Тогда в качестве общего знаменателя берем 12 · 2 3 5 .
Рассмотрим примеры умножений дробей общего вида.
Пример 5
Для этого необходимо произвести умножение 2 + 1 6 и 2 · 5 3 · 2 + 1 .
Решение
Следую правилу, необходимо переписать и в виде знаменателя написать произведение числителей. Получаем, что 2 + 1 6 · 2 · 5 3 · 2 + 1 2 + 1 · 2 · 5 6 · 3 · 2 + 1 . Когда дробь будет умножена, можно производить сокращения для ее упрощения. Тогда 5 · 3 3 2 + 1: 10 9 3 = 5 · 3 3 2 + 1 · 9 3 10 .
Используя правило перехода от деления к умножению на обратную дробь, получим дробь, обратную данной. Для этого числитель и знаменатель меняются местами. Рассмотрим на примере:
5 · 3 3 2 + 1: 10 9 3 = 5 · 3 3 2 + 1 · 9 3 10
После чего должны выполнить умножение и упростить полученную дробь. Если необходимо, то избавиться от иррациональности в знаменателе. Получаем, что
5 · 3 3 2 + 1: 10 9 3 = 5 · 3 3 · 9 3 10 · 2 + 1 = 5 · 2 10 · 2 + 1 = 3 2 · 2 + 1 = = 3 · 2 - 1 2 · 2 + 1 · 2 - 1 = 3 · 2 - 1 2 · 2 2 - 1 2 = 3 · 2 - 1 2
Ответ: 5 · 3 3 2 + 1: 10 9 3 = 3 · 2 - 1 2
Данный пункт применим, когда число или числовое выражение может быть представлено в виде дроби, имеющую знаменатель, равный 1 , тогда и действие с такой дробью рассматривается отдельным пунктом. Например, выражение 1 6 · 7 4 - 1 · 3 видно, что корень из 3 может быть заменен другим 3 1 выражением. Тогда эта запись будет выглядеть как умножение двух дробей вида 1 6 · 7 4 - 1 · 3 = 1 6 · 7 4 - 1 · 3 1 .
Выполнение действие с дробями, содержащими переменные
Правила, рассмотренные в первой статье, применимы для действий с дробями, содержащими переменные. Рассмотрим правило вычитания, когда знаменатели одинаковые.
Необходимо доказать, что A , C и D (D не равное нулю) могут быть любыми выражениями, причем равенство A D ± C D = A ± C D равноценно с его областью допустимых значений.
Необходимо взять набор переменных ОДЗ. Тогда А, С, D должны принимать соответственные значения a 0 , c 0 и d 0 . Подстановка вида A D ± C D приводит разность вида a 0 d 0 ± c 0 d 0 , где по правилу сложения получаем формулу вида a 0 ± c 0 d 0 . Если подставить выражение A ± C D , тогда получаем ту же дробь вида a 0 ± c 0 d 0 . Отсюда делаем вывод, что выбранное значение, удовлетворяющее ОДЗ, A ± C D и A D ± C D считаются равными.
При любом значении переменных данные выражения будут равны, то есть их называют тождественно равными. Значит это выражение считается доказываемым равенством вида A D ± C D = A ± C D .
Примеры сложения и вычитания дробей с переменными
Когда имеются одинаковые знаменатели, необходимо только складывать или вычитать числители. Такая дробь может быть упрощена. Иногда приходится работать с дробями, которые являются тождественно равными, но при первом взгляде это незаметно, так как необходимо выполнять некоторые преобразования. Например, x 2 3 · x 1 3 + 1 и x 1 3 + 1 2 или 1 2 · sin 2 α и sin a · cos a . Чаще всего требуется упрощение исходного выражения для того, чтобы увидеть одинаковые знаменатели.
Пример 6
Вычислить: 1) x 2 + 1 x + x - 2 - 5 - x x + x - 2 , 2) l g 2 x + 4 x · (l g x + 2) + 4 · l g x x · (l g x + 2) , x - 1 x - 1 + x x + 1 .
Решение
- Чтобы произвести вычисление, необходимо вычесть дроби, которым имеют одинаковые знаменатели. Тогда получаем, что x 2 + 1 x + x - 2 - 5 - x x + x - 2 = x 2 + 1 - 5 - x x + x - 2 . После чего можно выполнять раскрытие скобок с приведением подобных слагаемых. Получаем, что x 2 + 1 - 5 - x x + x - 2 = x 2 + 1 - 5 + x x + x - 2 = x 2 + x - 4 x + x - 2
- Так как знаменатели одинаковые, то остается только сложить числители, оставив знаменатель: l g 2 x + 4 x · (l g x + 2) + 4 · l g x x · (l g x + 2) = l g 2 x + 4 + 4 x · (l g x + 2)
Сложение было выполнено. Видно, что можно произвести сокращение дроби. Ее числитель может быть свернут по формуле квадрата суммы, тогда получим (l g x + 2) 2 из формул сокращенного умножения. Тогда получаем, что
l g 2 x + 4 + 2 · l g x x · (l g x + 2) = (l g x + 2) 2 x · (l g x + 2) = l g x + 2 x - Заданные дроби вида x - 1 x - 1 + x x + 1 с разными знаменателями. После преобразования можно перейти к сложению.
Рассмотрим двоякий способ решения.
Первый способ заключается в том, что знаменатель первой дроби подвергается разложению на множители при помощи квадратов, причем с ее последующим сокращением. Получим дробь вида
x - 1 x - 1 = x - 1 (x - 1) · x + 1 = 1 x + 1
Значит, x - 1 x - 1 + x x + 1 = 1 x + 1 + x x + 1 = 1 + x x + 1 .
В таком случае необходимо избавляться от иррациональности в знаменателе.
1 + x x + 1 = 1 + x · x - 1 x + 1 · x - 1 = x - 1 + x · x - x x - 1
Второй способ заключается в умножении числителя и знаменателя второй дроби на выражение x - 1 . Таким образом, мы избавляемся от иррациональности и переходим к сложению дроби при наличии одинакового знаменателя. Тогда
x - 1 x - 1 + x x + 1 = x - 1 x - 1 + x · x - 1 x + 1 · x - 1 = = x - 1 x - 1 + x · x - x x - 1 = x - 1 + x · x - x x - 1
Ответ: 1) x 2 + 1 x + x - 2 - 5 - x x + x - 2 = x 2 + x - 4 x + x - 2 , 2) l g 2 x + 4 x · (l g x + 2) + 4 · l g x x · (l g x + 2) = l g x + 2 x , 3) x - 1 x - 1 + x x + 1 = x - 1 + x · x - x x - 1 .
В последнем примере получили, что приведение к общему знаменателю неизбежно. Для этого необходимо упрощать дроби. Для сложения или вычитая всегда необходимо искать общий знаменатель, который выглядит как произведение знаменателей с добавлением дополниетльных множителей к числителям.
Пример 7
Вычислить значения дробей: 1) x 3 + 1 x 7 + 2 · 2 , 2) x + 1 x · ln 2 (x + 1) · (2 x - 4) - sin x x 5 · ln (x + 1) · (2 x - 4) , 3) 1 cos 2 x - x + 1 cos 2 x + 2 · cos x · x + x
Решение
- Никаких сложных вычислений знаменатель не требует, поэтому нужно выбрать их произведение вида 3 · x 7 + 2 · 2 , тогда к первой дроби x 7 + 2 · 2 выбирают как дополнительный множитель, а 3 ко второй. При перемножении получаем дробь вида x 3 + 1 x 7 + 2 · 2 = x · x 7 + 2 · 2 3 · x 7 + 2 · 2 + 3 · 1 3 · x 7 + 2 · 2 = = x · x 7 + 2 · 2 + 3 3 · x 7 + 2 · 2 = x · x 7 + 2 · 2 · x + 3 3 · x 7 + 2 · 2
- Видно, что знаменатели представлены в виде произведения, что означает ненужность дополнительных преобразований. Общим знаменателем будет считаться произведение вида x 5 · ln 2 x + 1 · 2 x - 4 . Отсюда x 4
является дополнительным множителем к первой дроби, а ln (x + 1)
ко второй. После чего производим вычитание и получаем, что:
x + 1 x · ln 2 (x + 1) · 2 x - 4 - sin x x 5 · ln (x + 1) · 2 x - 4 = = x + 1 · x 4 x 5 · ln 2 (x + 1) · 2 x - 4 - sin x · ln x + 1 x 5 · ln 2 (x + 1) · (2 x - 4) = = x + 1 · x 4 - sin x · ln (x + 1) x 5 · ln 2 (x + 1) · (2 x - 4) = x · x 4 + x 4 - sin x · ln (x + 1) x 5 · ln 2 (x + 1) · (2 x - 4) - Данный пример имеет смысл при работе со знаменателями дробями. Необходимо применить формулы разности квадратов и квадрат суммы, так как именно они дадут возможность перейти к выражению вида 1 cos x - x · cos x + x + 1 (cos x + x) 2 . Видно, что дроби приводятся к общему знаменателю. Получаем, что cos x - x · cos x + x 2 .
После чего получаем, что
1 cos 2 x - x + 1 cos 2 x + 2 · cos x · x + x = = 1 cos x - x · cos x + x + 1 cos x + x 2 = = cos x + x cos x - x · cos x + x 2 + cos x - x cos x - x · cos x + x 2 = = cos x + x + cos x - x cos x - x · cos x + x 2 = 2 · cos x cos x - x · cos x + x 2
Ответ:
1) x 3 + 1 x 7 + 2 · 2 = x · x 7 + 2 · 2 · x + 3 3 · x 7 + 2 · 2 , 2) x + 1 x · ln 2 (x + 1) · 2 x - 4 - sin x x 5 · ln (x + 1) · 2 x - 4 = = x · x 4 + x 4 - sin x · ln (x + 1) x 5 · ln 2 (x + 1) · (2 x - 4) , 3) 1 cos 2 x - x + 1 cos 2 x + 2 · cos x · x + x = 2 · cos x cos x - x · cos x + x 2 .
Примеры умножения дробей с переменными
При умножении дробей числитель умножается на числитель, а знаменатель на знаменатель. Тогда можно применять свойство сокращения.
Пример 8
Произвести умножение дробей x + 2 · x x 2 · ln x 2 · ln x + 1 и 3 · x 2 1 3 · x + 1 - 2 sin 2 · x - x .
Решение
Необходимо выполнить умножение. Получаем, что
x + 2 · x x 2 · ln x 2 · ln x + 1 · 3 · x 2 1 3 · x + 1 - 2 sin (2 · x - x) = = x - 2 · x · 3 · x 2 1 3 · x + 1 - 2 x 2 · ln x 2 · ln x + 1 · sin (2 · x - x)
Число 3 переносится на первое место для удобства подсчетов, причем можно произвести сокращение дроби на x 2 , тогда получим выражение вида
3 · x - 2 · x · x 1 3 · x + 1 - 2 ln x 2 · ln x + 1 · sin (2 · x - x)
Ответ: x + 2 · x x 2 · ln x 2 · ln x + 1 · 3 · x 2 1 3 · x + 1 - 2 sin (2 · x - x) = 3 · x - 2 · x · x 1 3 · x + 1 - 2 ln x 2 · ln x + 1 · sin (2 · x - x) .
Деление
Деление у дробей аналогично умножению, так как первую дробь умножают на вторую обратную. Если взять к примеру дробь x + 2 · x x 2 · ln x 2 · ln x + 1 и разделить на 3 · x 2 1 3 · x + 1 - 2 sin 2 · x - x , тогда это можно записать таким образом, как
x + 2 · x x 2 · ln x 2 · ln x + 1: 3 · x 2 1 3 · x + 1 - 2 sin (2 · x - x) , после чего заменить произведением вида x + 2 · x x 2 · ln x 2 · ln x + 1 · 3 · x 2 1 3 · x + 1 - 2 sin (2 · x - x)
Возведение в степень
Перейдем к рассмотрению действия с дробями общего вида с возведением в степень. Если имеется степень с натуральным показателем, тогда действие рассматривают как умножение одинаковых дробей. Но рекомендовано использовать общий подход, базирующийся на свойствах степеней. Любые выражения А и С, где С тождественно не равняется нулю, а любое действительное r на ОДЗ для выражения вида A C r справедливо равенство A C r = A r C r . Результат – дробь, возведенная в степень. Для примера рассмотрим:
x 0 , 7 - π · ln 3 x - 2 - 5 x + 1 2 , 5 = = x 0 , 7 - π · ln 3 x - 2 - 5 2 , 5 x + 1 2 , 5
Порядок выполнения действий с дробями
Действия над дробями выполняются по определенным правилам. На практике замечаем, что выражение может содержать несколько дробей или дробных выражений. Тогда необходимо все действия выполнять в строгом порядке: возводить в степень, умножать, делить, после чего складывать и вычитать. При наличии скобок первое действие выполняется именно в них.
Пример 9
Вычислить 1 - x cos x - 1 c o s x · 1 + 1 x .
Решение
Так как имеем одинаковый знаменатель, то 1 - x cos x и 1 c o s x , но производить вычитания по правилу нельзя, сначала выполняются действия в скобках, после чего умножение, а потом сложение. Тогда при вычислении получаем, что
1 + 1 x = 1 1 + 1 x = x x + 1 x = x + 1 x
При подстановке выражения в исходное получаем, что 1 - x cos x - 1 cos x · x + 1 x . При умножении дробей имеем: 1 cos x · x + 1 x = x + 1 cos x · x . Произведя все подстановки, получим 1 - x cos x - x + 1 cos x · x . Теперь необходимо работать с дробями, которые имеют разные знаменатели. Получим:
x · 1 - x cos x · x - x + 1 cos x · x = x · 1 - x - 1 + x cos x · x = = x - x - x - 1 cos x · x = - x + 1 cos x · x
Ответ: 1 - x cos x - 1 c o s x · 1 + 1 x = - x + 1 cos x · x .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Теперь, когда мы научились складывать и умножать отдельные дроби, можно рассматривать более сложные конструкции. Например, что, если в одной задаче встречается и сложение, и вычитание, и умножение дробей?
В первую очередь, надо перевести все дроби в неправильные. Затем последовательно выполняем требуемые действия - в том же порядке, как и для обычных чисел. А именно:
- Сначала выполняется возведение в степень - избавьтесь от всех выражений, содержащих показатели;
- Затем - деление и умножение;
- Последним шагом выполняется сложение и вычитание.
Разумеется, если в выражении присутствуют скобки, порядок действий изменяется - все, что стоит внутри скобок, надо считать в первую очередь. И помните о неправильных дробях: выделять целую часть надо лишь тогда, когда все остальные действия уже выполнены.
Переведем все дроби из первого выражения в неправильные, а затем выполним действия:
Теперь найдем значение второго выражения. Тут дробей с целой частью нет, но есть скобки, поэтому сначала выполняем сложение, и лишь затем - деление. Заметим, что 14 = 7 · 2 . Тогда:
Наконец, считаем третий пример. Здесь есть скобки и степень - их лучше считать отдельно. Учитывая, что 9 = 3 · 3 , имеем:
Обратите внимание на последний пример. Чтобы возвести дробь в степень, надо отдельно возвести в эту степень числитель, и отдельно - знаменатель.
Можно решать по-другому. Если вспомнить определение степени, задача сведется к обычному умножению дробей:
Многоэтажные дроби
До сих пор мы рассматривали лишь «чистые» дроби, когда числитель и знаменатель представляют собой обыкновенные числа. Это вполне соответствует определению числовой дроби, данному в самом первом уроке.
Но что, если в числителе или знаменателе разместить более сложный объект? Например, другую числовую дробь? Такие конструкции возникают довольно часто, особенно при работе с длинными выражениями. Вот пара примеров:
Правило работы с многоэтажными дробями всего одно: от них надо немедленно избавляться. Удалить «лишние» этажи довольно просто, если вспомнить, что дробная черта означает стандартную операцию деления. Поэтому любую дробь можно переписать следующим образом:
Пользуясь этим фактом и соблюдая порядок действий, мы легко сведем любую многоэтажную дробь к обычной. Взгляните на примеры:
Задача. Переведите многоэтажные дроби в обычные:
В каждом случае перепишем основную дробь, заменив разделительную черту знаком деления. Также вспомним, что любое целое число представимо в виде дроби со знаменателем 1. Т.е. 12 = 12/1; 3 = 3/1. Получаем:
В последнем примере перед окончательным умножением дроби были сокращены.
Специфика работы с многоэтажными дробями
В многоэтажных дробях есть одна тонкость, которую всегда надо помнить, иначе можно получить неверный ответ, даже если все вычисления были правильными. Взгляните:
- В числителе стоит отдельное число 7, а в знаменателе - дробь 12/5;
- В числителе стоит дробь 7/12, а в знаменателе - отдельное число 5.
Итак, для одной записи получили две совершенно разных интерпретации. Если подсчитать, ответы тоже будут разными:
Чтобы запись всегда читалась однозначно, используйте простое правило: разделяющая черта основной дроби должна быть длиннее, чем черта вложенной. Желательно - в несколько раз.
Если следовать этому правилу, то приведенные выше дроби надо записать так:
Да, возможно, это некрасиво и занимает слишком много места. Зато вы будете считать правильно. Напоследок - пара примеров, где действительно возникают многоэтажные дроби:
Задача. Найдите значения выражений:
Итак, работаем с первым примером. Переведем все дроби в неправильные, а затем выполним операции сложения и деления:
Аналогично поступим со вторым примером. Переведем все дроби в неправильные и выполним требуемые операции. Чтобы не утомлять читателя, я опущу некоторые очевидные выкладки. Имеем:
Благодаря тому, что в числителе и знаменателе основных дробей стоят суммы, правило записи многоэтажных дробей соблюдается автоматически. Кроме того, в последнем примере мы намеренно оставили число 46/1 в форме дроби, чтобы выполнить деление.
Также отмечу, что в обоих примерах дробная черта фактически заменяет скобки: первым делом мы находили сумму, и лишь затем - частное.
Кто-то скажет, что переход к неправильным дробям во втором примере был явно избыточным. Возможно, так оно и есть. Но этим мы страхуем себя от ошибок, ведь в следующий раз пример может оказаться намного сложнее. Выбирайте сами, что важнее: скорость или надежность.
Калькулятор дробей предназначен для быстрого расчета операций с дробями, поможет легко дроби сложить, умножить, поделить или вычесть.
Современные школьники начинают изучение дробей уже в 5 классе, с каждым годом упражнения с ними усложняются. Математические термины и величины, которые мы узнаем в школе, редко могут пригодиться нам во взрослой жизни. Однако дроби, в отличие от логарифмов и степеней, встречаются в повседневности достаточно часто (измерение расстояния, взвешивание товара и т.д.). Наш калькулятор предназначен для быстрого проведения операций с дробями.
Для начала определим, что такое дроби и какие они бывают. Дробями называют отношение одного числа к другому, это число, состоящее из целого количества долей единицы.
Разновидности дробей:
- Обыкновенные
- Десятичные
- Смешанные
Пример обыкновенных дробей:
Верхнее значение является числителем, нижнее знаменателем. Черточка показывает нам, что верхнее число делится на нижнее. Вместо подобного формата написания, когда черточка находится горизонтально, можно писать по-другому. Можно ставить наклонную линию, например:
1/2, 3/7, 19/5, 32/8, 10/100, 4/1
Десятичные дроби являются самой популярной разновидностью дробей. Они состоят из целой части и дробной, отделенные запятой.
Пример десятичных дробей:
0,2, или 6,71 или 0,125
Состоят из целого числа и дробной части. Чтобы узнать значение этой дроби, нужно сложить целое число и дробь.
Пример смешанных дробей:
Калькулятор дробей на нашем сайте способен быстро в онлайн-режиме выполнить любые математические операции с дробями:
- Сложение
- Вычитание
- Умножение
- Деление
Для осуществления расчета нужно ввести цифры в поля и выбрать действие. У дробей нужно заполнить числитель и знаменатель, целое число может не писаться (если дробь обыкновенная). Не забудьте нажать на кнопку «равно».
Удобно, что калькулятор сразу предоставляет процесс решения примера с дробями, а не только готовый ответ. Именно благодаря развернутому решению вы можете использовать данный материал при решении школьных задач и для лучшего освоения пройденного материала.
Вам нужно осуществить расчет примера:
После введения показателей в поля формы получаем:
Чтобы сделать самостоятельный расчет, введите данные в форму.
Калькулятор дробей
Введите две дроби:| + - * : | |||||||
Сопутствующие разделы.
Дроби — это обычные числа, их тоже можно складывать и вычитать. Но из-за того, что в них присутствует знаменатель, здесь требуются более сложные правила, нежели для целых чисел.
Рассмотрим самый простой случай, когда есть две дроби с одинаковыми знаменателями. Тогда:
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений.
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.
Внутри каждого выражения знаменатели дробей равны. По определению сложения и вычитания дробей получаем:
Как видите, ничего сложного: просто складываем или вычитаем числители — и все.
Но даже в таких простых действиях люди умудряются допускать ошибки. Чаще всего забывают, что знаменатель не меняется. Например, при сложении их тоже начинают складывать, а это в корне неправильно.
Избавиться от вредной привычки складывать знаменатели достаточно просто. Попробуйте сделать то же самое при вычитании. В результате в знаменателе получится ноль, и дробь (внезапно!) потеряет смысл.
Поэтому запомните раз и навсегда: при сложении и вычитании знаменатель не меняется!
Также многие допускают ошибки при сложении нескольких отрицательных дробей. Возникает путаница со знаками: где ставить минус, а где — плюс.
Эта проблема тоже решается очень просто. Достаточно вспомнить, что минус перед знаком дроби всегда можно перенести в числитель — и наоборот. Ну и конечно, не забывайте два простых правила:
- Плюс на минус дает минус;
- Минус на минус дает плюс.
Разберем все это на конкретных примерах:
Задача. Найдите значение выражения:
В первом случае все просто, а во втором внесем минусы в числители дробей:
Что делать, если знаменатели разные
Напрямую складывать дроби с разными знаменателями нельзя. По крайней мере, мне такой способ неизвестен. Однако исходные дроби всегда можно переписать так, чтобы знаменатели стали одинаковыми.
Существует много способов преобразования дробей. Три из них рассмотрены в уроке «Приведение дробей к общему знаменателю », поэтому здесь мы не будем на них останавливаться. Лучше посмотрим на примеры:
Задача. Найдите значение выражения:
В первом случае приведем дроби к общему знаменателю методом «крест-накрест». Во втором будем искать НОК. Заметим, что 6 = 2 · 3; 9 = 3 · 3. Последние множители в этих разложениях равны, а первые взаимно просты. Следовательно, НОК(6; 9) = 2 · 3 · 3 = 18.
Что делать, если у дроби есть целая часть
Могу вас обрадовать: разные знаменатели у дробей — это еще не самое большое зло. Гораздо больше ошибок возникает тогда, когда в дробях-слагаемых выделена целая часть.
Безусловно, для таких дробей существуют собственные алгоритмы сложения и вычитания, но они довольно сложны и требуют долгого изучения. Лучше используйте простую схему, приведенную ниже:
- Перевести все дроби, содержащие целую часть, в неправильные. Получим нормальные слагаемые (пусть даже с разными знаменателями), которые считаются по правилам, рассмотренным выше;
- Собственно, вычислить сумму или разность полученных дробей. В результате мы практически найдем ответ;
- Если это все, что требовалось в задаче, выполняем обратное преобразование, т.е. избавляемся от неправильной дроби, выделяя в ней целую часть.
Правила перехода к неправильным дробям и выделения целой части подробно описаны в уроке «Что такое числовая дробь ». Если не помните — обязательно повторите. Примеры:
Задача. Найдите значение выражения:
Здесь все просто. Знаменатели внутри каждого выражения равны, поэтому остается перевести все дроби в неправильные и сосчитать. Имеем:
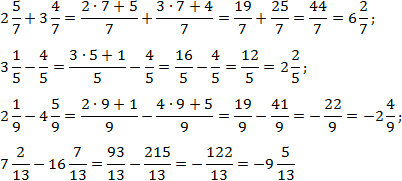
Чтобы упростить выкладки, я пропустил некоторые очевидные шаги в последних примерах.
Небольшое замечание к двум последним примерам, где вычитаются дроби с выделенной целой частью. Минус перед второй дробью означает, что вычитается именно вся дробь, а не только ее целая часть.
Перечитайте это предложение еще раз, взгляните на примеры — и задумайтесь. Именно здесь начинающие допускают огромное количество ошибок. Такие задачи обожают давать на контрольных работах. Вы также неоднократно встретитесь с ними в тестах к этому уроку, которые будут опубликованы в ближайшее время.
Резюме: общая схема вычислений
В заключение приведу общий алгоритм, который поможет найти сумму или разность двух и более дробей:
- Если в одной или нескольких дробях выделена целая часть, переведите эти дроби в неправильные;
- Приведите все дроби к общему знаменателю любым удобным для вас способом (если, конечно, этого не сделали составители задач);
- Сложите или вычтите полученные числа по правилам сложения и вычитания дробей с одинаковыми знаменателями;
- Если возможно, сократите полученный результат. Если дробь оказалась неправильной, выделите целую часть.
Помните, что выделять целую часть лучше в самом конце задачи, непосредственно перед записью ответа.