Деление и числителя и знаменателя дроби на их общий делитель , отличный от единицы, называют сокращением дроби .

Чтобы сократить обыкновенную дробь, нужно разделить ее числитель и знаменатель на одно и то же натуральное число.

Это число является наибольшим общим делителем числителя и знаменателя данной дроби.

Возможны следующие формы записи решения примеров на сокращение обыкновенных дробей.

Учащийся вправе выбрать любую форму записи.

Примеры. Упростить дроби.

Сократим дробь на 3 (делим числитель на 3;

делим знаменатель на 3).

Сокращаем дробь на 7.

Выполняем указанные действия в числителе и знаменателе дроби.

Полученную дробь сокращаем на 5.

Сократим данную дробь 4) на 5·7³ — наибольший общий делитель (НОД) числителя и знаменателя, который состоит из общих множителей числителя и знаменателя, взятых в степени с наименьшим показателем.

Разложим числитель и знаменатель этой дроби на простые множители.

Получаем: 756=2²·3³·7 и 1176=2³·3·7² .

Определяем НОД (наибольший общий делитель) числителя и знаменателя дроби 5) .

Это произведение общих множителей, взятых с наименьшими показателями.

НОД(756; 1176)=2²·3·7 .

Делим числитель и знаменатель данной дроби на их НОД, т. е. на 2²·3·7 получаем несократимую дробь 9/14 .

А можно было записать разложения числителя и знаменателя в виде произведения простых множителей, не применяя понятие степени, а затем произвести сокращение дроби, зачеркивая одинаковые множители в числителе и знаменателе. Когда одинаковых множителей не останется — перемножаем оставшиеся множители отдельно в числителе и отдельно в знаменателе и выписываем получившуюся дробь 9/14 .

И, наконец, можно было сокращать данную дробь 5) постепенно, применяя признаки деления чисел и к числителю и к знаменателю дроби. Рассуждаем так: числа 756 и 1176 оканчиваются четной цифрой, значит, оба делятся на 2 . Сокращаем дробь на 2 . Числитель и знаменатель новой дроби — числа 378 и 588 также делятся на 2 . Сокращаем дробь на 2 . Замечаем, что число 294 — четное, а 189 — нечетное, и сокращение на 2 уже невозможно. Проверим признак делимости чисел 189 и 294 на 3 .

(1+8+9)=18 делится на 3 и (2+9+4)=15 делится на 3, следовательно, и сами числа 189 и 294 делятся на 3 . Сокращаем дробь на 3 . Далее, 63 делится на 3, а 98 — нет. Перебираем другие простые множители. Оба числа делятся на 7 . Сокращаем дробь на 7 и получаем несократимую дробь 9/14 .

Дроби

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно "не очень..."
И для тех, кто "очень даже...")

Дроби в старших классах не сильно досаждают. До поры до времени. Пока не столкнётесь со степенями с рациональными показателями да логарифмами. А вот там…. Давишь, давишь калькулятор, а он все полное табло каких-то циферок кажет. Приходится головой думать, как в третьем классе.

Давайте уже разберёмся с дробями, наконец! Ну сколько можно в них путаться!? Тем более, это всё просто и логично. Итак, какие бывают дроби?

Виды дробей. Преобразования.

Дроби бывают трёх видов.

1. Обыкновенные дроби , например:

Иногда вместо горизонтальной чёрточки ставят наклонную черту: 1/2, 3/4, 19/5, ну, и так далее. Здесь мы часто будем таким написанием пользоваться. Верхнее число называется числителем , нижнее - знаменателем. Если вы постоянно путаете эти названия (бывает...), скажите себе с выражением фразу: "Ззззз апомни! Ззззз наменатель - вниззззз у!" Глядишь, всё и ззззапомнится.)

Чёрточка, что горизонтальная, что наклонная, означает деление верхнего числа (числителя) на нижнее (знаменатель). И всё! Вместо чёрточки вполне можно поставить знак деления - две точки.

Когда деление возможно нацело, это надо делать. Так, вместо дроби "32/8" гораздо приятнее написать число "4". Т.е. 32 просто поделить на 8.

32/8 = 32: 8 = 4

Я уж и не говорю про дробь "4/1". Которая тоже просто "4". А если уж не делится нацело, так и оставляем, в виде дроби. Иногда приходится обратную операцию проделывать. Делать из целого числа дробь. Но об этом далее.

2. Десятичные дроби , например:

Именно в таком виде нужно будет записывать ответы на задания "В".

3. Смешанные числа , например:

Смешанные числа практически не используются в старших классах. Для того, чтобы с ними работать, их всяко надо переводить в обыкновенные дроби. Но это точно надо уметь делать! А то попадётся такое число в задачке и зависните... На пустом месте. Но мы-то вспомним эту процедуру! Чуть ниже.

Наиболее универсальны обыкновенные дроби . С них и начнём. Кстати, если в дроби стоят всякие логарифмы, синусы и прочие буковки, это ничего не меняет. В том смысле что все действия с дробными выражениями ничем не отличаются от действий с обыкновенными дробями !

Основное свойство дроби.

Итак, поехали! Для начала я вас удивлю. Всё многообразие преобразований дробей обеспечивается одним-единственным свойством! Оно так и называется, основное свойство дроби . Запоминайте: если числитель и знаменатель дроби умножить (разделить) на одно и то же число, дробь не изменится. Т.е:

Понятно, что писать можно дальше, до посинения. Синусы и логарифмы пусть вас не смущают, с ними дальше разберёмся. Главное понять, что все эти разнообразные выражения есть одна и та же дробь . 2/3.

А оно нам надо, все эти превращения? Ещё как! Сейчас сами увидите. Для начала употребим основное свойство дроби для сокращения дробей . Казалось бы, вещь элементарная. Делим числитель и знаменатель на одно и то же число и все дела! Ошибиться невозможно! Но... человек - существо творческое. Ошибиться везде может! Особенно, если приходится сокращать не дробь типа 5/10, а дробное выражение со всякими буковками.

Как правильно и быстро сокращать дроби, не делая лишней работы, можно прочитать в особом Разделе 555 .

Нормальный ученик не заморачивается делением числителя и знаменателя на одно и то же число (или выражение)! Он просто зачеркивает всё одинаковое сверху и снизу! Здесь-то и таится типичная ошибка, ляп, если хотите.

Например, надо упростить выражение:

Тут и думать нечего, зачеркиваем букву "а" сверху и двойку снизу! Получаем:

Все правильно. Но реально вы поделили весь числитель и весь знаменатель на "а". Если вы привыкли просто зачеркивать, то, впопыхах, можете зачеркнуть "а" в выражении

и получить снова

Что будет категорически неверно. Потому что здесь весь числитель на "а" уже не делится ! Эту дробь сократить нельзя. Кстати, такое сокращение – это, гм… серьезный вызов преподавателю. Такого не прощают! Запомнили? При сокращении делить надо весь числитель и весь знаменатель!

Сокращение дробей сильно облегчает жизнь. Получится где-нибудь у вас дробь, к примеру 375/1000. И как теперь с ней дальше работать? Без калькулятора? Умножать, скажем, складывать, в квадрат возводить!? А если не полениться, да аккуратненько сократить на пять, да ещё на пять, да ещё... пока сокращается, короче. Получим 3/8! Куда приятнее, правда?

Основное свойство дроби позволяет переводить обыкновенные дроби в десятичные и наоборот без калькулятора ! Это важно на ЕГЭ, верно?

Как переводить дроби из одного вида в другой.

С десятичными дробями всё просто. Как слышится, так и пишется! Скажем, 0,25. Это ноль целых, двадцать пять сотых. Так и пишем: 25/100. Сокращаем (делим числитель и знаменатель на 25), получаем обычную дробь: 1/4. Всё. Бывает, и не сокращается ничего. Типа 0,3. Это три десятых, т.е. 3/10.

А если целых - не ноль? Ничего страшного. Записываем всю дробь без всяких запятых в числитель, а в знаменатель - то, что слышится. Например: 3,17. Это три целых, семнадцать сотых. Пишем в числитель 317, а в знаменатель 100. Получаем 317/100. Ничего не сокращается, значит всё. Это ответ. Элементарно, Ватсон! Из всего сказанного полезный вывод: любую десятичную дробь можно превратить в обыкновенную .

А вот обратное преобразование, обыкновенной в десятичную, некоторые без калькулятора не могут сделать. А надо! Как вы ответ записывать будете на ЕГЭ!? Внимательно читаем и осваиваем этот процесс.

Десятичная дробь чем характерна? У неё в знаменателе всегда стоит 10, или 100, или 1000, или 10000 и так далее. Если ваша обычная дробь имеет такой знаменатель, проблем нет. Например, 4/10 = 0,4. Или 7/100 = 0,07. Или 12/10 = 1,2. А если в ответе на задание раздела "В" получилось 1/2? Что в ответ писать будем? Там десятичные требуются...

Вспоминаем основное свойство дроби ! Математика благосклонно позволяет умножать числитель и знаменатель на одно и то же число. На любое, между прочим! Кроме нуля, разумеется. Вот и применим это свойство себе на пользу! На что можно умножить знаменатель, т.е. 2 чтобы он стал 10, или 100, или 1000 (поменьше лучше, конечно...)? На 5, очевидно. Смело умножаем знаменатель (это нам надо) на 5. Но, тогда и числитель надо умножить тоже на 5. Это уже математика требует! Получим 1/2 = 1х5/2х5 = 5/10 = 0,5. Вот и всё.

Однако, знаменатели всякие попадаются. Попадётся, например дробь 3/16. Попробуй, сообрази тут, на что 16 умножить, чтоб 100 получилось, или 1000... Не получается? Тогда можно просто разделить 3 на 16. За отсутствием калькулятора делить придётся уголком, на бумажке, как в младших классах учили. Получим 0,1875.

А бывают и совсем скверные знаменатели. Например, дробь 1/3 ну никак не превратишь в хорошую десятичную. И на калькуляторе, и на бумажке, мы получим 0,3333333... Это значит, что 1/3 в точную десятичную дробь не переводится . Так же, как и 1/7, 5/6 и так далее. Много их, непереводимых. Отсюда ещё один полезный вывод. Не каждая обыкновенная дробь переводится в десятичную !

Кстати, это полезная информация для самопроверки. В разделе "В" в ответ надо десятичную дробь записывать. А у вас получилось, например, 4/3. Эта дробь не переводится в десятичную. Это означает, что где-то вы ошиблись по дороге! Вернитесь, проверьте решение.

Итак, с обыкновенными и десятичными дробями разобрались. Осталось разобраться со смешанными числами. Для работы с ними их всяко нужно перевести в обыкновенные дроби. Как это сделать? Можно поймать шестиклассника и спросить у него. Но не всегда шестиклассник окажется под руками... Придётся самим. Это несложно. Надо знаменатель дробной части умножить на целую часть и прибавить числитель дробной части. Это будет числитель обычной дроби. А знаменатель? Знаменатель останется тем же самым. Звучит сложно, но на деле всё элементарно. Смотрим пример.

Пусть в задачке вы с ужасом увидели число:

Спокойно, без паники соображаем. Целая часть - это 1. Единица. Дробная часть - 3/7. Стало быть, знаменатель дробной части - 7. Этот знаменатель и будет знаменателем обыкновенной дроби. Считаем числитель. 7 умножаем на 1 (целая часть) и прибавляем 3 (числитель дробной части). Получим 10. Это будет числитель обыкновенной дроби. Вот и всё. Еще проще это выглядит в математической записи:

Ясненько? Тогда закрепите успех! Переведите в обыкновенные дроби. У вас должно получится 10/7, 7/2, 23/10 и 21/4.

Обратная операция - перевод неправильной дроби в смешанное число - в старших классах редко требуется. Ну если уж... И если Вы - не в старших классах - можете заглянуть в особый Раздел 555 . Там же, кстати, и про неправильные дроби узнаете.

Ну вот, практически и всё. Вы вспомнили виды дробей и поняли, как переводить их из одного вида в другой. Остаётся вопрос: зачем это делать? Где и когда применять эти глубокие познания?

Отвечаю. Любой пример сам подсказывает необходимые действия. Если в примере смешались в кучу обыкновенные дроби, десятичные, да ещё и смешанные числа, переводим всё в обыкновенные дроби. Это всегда можно сделать . Ну а если написано, что-нибудь типа 0,8 + 0,3, то так и считаем, безо всякого перевода. Зачем нам лишняя работа? Мы выбираем тот путь решения, который удобен нам !

Если в задании сплошь десятичные дроби, но гм... злые какие-то, перейдите к обыкновенным, попробуйте! Глядишь, всё и наладится. Например, придется в квадрат возводить число 0,125. Не так-то просто, если от калькулятора не отвыкли! Мало того, что числа перемножать столбиком надо, так ещё думай, куда запятую вставить! В уме точно не получится! А если перейти к обыкновенной дроби?

0,125 = 125/1000. Сокращаем на 5 (это для начала). Получаем 25/200. Ещё раз на 5. Получаем 5/40. О, ещё сокращается! Снова на 5! Получаем 1/8. Легко возводим в квадрат (в уме!) и получаем 1/64. Всё!

Подведём итоги этого урока.

1. Дроби бывают трёх видов. Обыкновенные, десятичные и смешанные числа.

2. Десятичные дроби и смешанные числа всегда можно перевести в обыкновенные дроби. Обратный перевод не всегда возможен.

3. Выбор вида дробей для работы с заданием зависит от этого самого задания. При наличии разных видов дробей в одном задании, самое надёжное - перейти к обыкновенным дробям.

Теперь можно потренироваться. Для начала переведите эти десятичные дроби в обыкновенные:

3,8; 0,75; 0,15; 1,4; 0,725; 0,012

Должны получиться вот такие ответы (в беспорядке!):

На этом и завершим. В этом уроке мы освежили в памяти ключевые моменты по дробям. Бывает, правда, что освежать особо нечего...) Если уж кто совсем крепко забыл, или ещё не освоил... Тем можно пройти в особый Раздел 555 . Там все основы подробненько расписаны. Многие вдруг всё понимать начинают. И решают дроби с лёту).

Если Вам нравится этот сайт...

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся - с интересом!)

можно познакомиться с функциями и производными.

Данная статья продолжает тему преобразования алгебраических дробей: рассмотрим такое действие как сокращение алгебраических дробей. Дадим определение самому термину, сформулируем правило сокращения и разберем практические примеры.

Yandex.RTB R-A-339285-1

Смысл сокращения алгебраической дроби

В материалах об обыкновенной дроби мы рассматривали ее сокращение. Мы определили сокращение обыкновенной дроби как деление ее числителя и знаменателя на общий множитель.

Сокращение алгебраической дроби представляет собой аналогичное действие.

Определение 1

Сокращение алгебраической дроби – это деление ее числителя и знаменателя на общий множитель. При этом, в отличие от сокращения обыкновенной дроби (общим знаменателем может быть только число), общим множителем числителя и знаменателя алгебраической дроби может служить многочлен, в частности, одночлен или число.

К примеру, алгебраическая дробь 3 · x 2 + 6 · x · y 6 · x 3 · y + 12 · x 2 · y 2 может быть сокращена на число 3 , в итоге получим: x 2 + 2 · x · y 6 · x 3 · y + 12 · x 2 · y 2 . Эту же дробь мы можем сократить на переменную х, и это даст нам выражение 3 · x + 6 · y 6 · x 2 · y + 12 · x · y 2 . Также заданную дробь возможно сократить на одночлен 3 · x или любой из многочленов x + 2 · y , 3 · x + 6 · y , x 2 + 2 · x · y или 3 · x 2 + 6 · x · y .

Конечной целью сокращения алгебраической дроби является дробь более простого вида, в лучшем случае – несократимая дробь.

Все ли алгебраические дроби подлежат сокращению?

Опять же из материалов об обыкновенных дробях мы знаем, что существуют сократимые и несократимые дроби. Несократимые – это дроби, не имеющие общих множителей числителя и знаменателя, отличных от 1 .

С алгебраическими дробями все так же: они могут иметь общие множители числителя и знаменателя, могут и не иметь. Наличие общих множителей позволяет упростить исходную дробь посредством сокращения. Когда общих множителей нет, оптимизировать заданную дробь способом сокращения невозможно.

В общих случаях по заданному виду дроби довольно сложно понять, подлежит ли она сокращению. Конечно, в некоторых случаях наличие общего множителя числителя и знаменателя очевидно. Например, в алгебраической дроби 3 · x 2 3 · y совершенно понятно, что общим множителем является число 3 .

В дроби - x · y 5 · x · y · z 3 также мы сразу понимаем, что сократить ее возможно на х, или y , или на х · y . И все же гораздо чаще встречаются примеры алгебраических дробей, когда общий множитель числителя и знаменателя не так просто увидеть, а еще чаще – он попросту отсутствует.

Например, дробь x 3 - 1 x 2 - 1 мы можем сократить на х - 1 , при этом указанный общий множитель в записи отсутствует. А вот дробь x 3 - x 2 + x - 1 x 3 + x 2 + 4 · x + 4 подвергнуть действию сокращения невозможно, поскольку числитель и знаменатель не имеют общего множителя.

Таким образом, вопрос выяснения сократимости алгебраической дроби не так прост, и зачастую проще работать с дробью заданного вида, чем пытаться выяснить, сократима ли она. При этом имеют место такие преобразования, которые в частных случаях позволяют определить общий множитель числителя и знаменателя или сделать вывод о несократимости дроби. Разберем детально этот вопрос в следующем пункте статьи.

Правило сокращения алгебраических дробей

Правило сокращения алгебраических дробей состоит из двух последовательных действий:

• нахождение общих множителей числителя и знаменателя;
• в случае нахождения таковых осуществление непосредственно действия сокращения дроби.

Самым удобным методом отыскания общих знаменателей является разложение на множители многочленов, имеющихся в числителе и знаменателе заданной алгебраической дроби. Это позволяет сразу наглядно увидеть наличие или отсутствие общих множителей.

Само действие сокращения алгебраической дроби базируется на основном свойстве алгебраической дроби, выражаемой равенством undefined , где a , b , c – некие многочлены, причем b и c – ненулевые. Первым шагом дробь приводится к виду a · c b · c , в котором мы сразу замечаем общий множитель c . Вторым шагом – выполняем сокращение, т.е. переход к дроби вида a b .

Характерные примеры

Несмотря на некоторую очевидность, уточним про частный случай, когда числитель и знаменатель алгебраической дроби равны. Подобные дроби тождественно равны 1 на всей ОДЗ переменных этой дроби:

5 5 = 1 ; - 2 3 - 2 3 = 1 ; x x = 1 ; - 3 , 2 · x 3 - 3 , 2 · x 3 = 1 ; 1 2 · x - x 2 · y 1 2 · x - x 2 · y ;

Поскольку обыкновенные дроби являются частным случаем алгебраических дробей, напомним, как осуществляется их сокращение. Натуральные числа, записанные в числителе и знаменателе, раскладываются на простые множители, затем общие множители сокращаются (если таковые имеются).

К примеру, 24 1260 = 2 · 2 · 2 · 3 2 · 2 · 3 · 3 · 5 · 7 = 2 3 · 5 · 7 = 2 105

Произведение простых одинаковых множителей возможно записать как степени, и в процессе сокращения дроби использовать свойство деления степеней с одинаковыми основаниями. Тогда вышеуказанное решение было бы таким:

24 1260 = 2 3 · 3 2 2 · 3 2 · 5 · 7 = 2 3 - 2 3 2 - 1 · 5 · 7 = 2 105

(числитель и знаменатель разделены на общий множитель 2 2 · 3 ). Или для наглядности, опираясь на свойства умножения и деления, решению дадим такой вид:

24 1260 = 2 3 · 3 2 2 · 3 2 · 5 · 7 = 2 3 2 2 · 3 3 2 · 1 5 · 7 = 2 1 · 1 3 · 1 35 = 2 105

По аналогии осуществляется сокращение алгебраических дробей, у которых в числителе и знаменателе имеются одночлены с целыми коэффициентами.

Пример 1

Задана алгебраическая дробь - 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z . Необходимо произвести ее сокращение.

Решение

Возможно записать числитель и знаменатель заданной дроби как произведение простых множителей и переменных, после чего осуществить сокращение:

27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = - 3 · 3 · 3 · a · a · a · a · a · b · b · c · z 2 · 3 · a · a · b · b · c · c · c · c · c · c · c · z = = - 3 · 3 · a · a · a 2 · c · c · c · c · c · c = - 9 · a 3 2 · c 6

Однако, более рациональным способом будет запись решения в виде выражения со степенями:

27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = - 3 3 · a 5 · b 2 · c · z 2 · 3 · a 2 · b 2 · c 7 · z = - 3 3 2 · 3 · a 5 a 2 · b 2 b 2 · c c 7 · z z = = - 3 3 - 1 2 · a 5 - 2 1 · 1 · 1 c 7 - 1 · 1 = · - 3 2 · a 3 2 · c 6 = · - 9 · a 3 2 · c 6 .

Ответ: - 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = - 9 · a 3 2 · c 6

Когда в числителе и знаменателе алгебраической дроби имеются дробные числовые коэффициенты, возможно два пути дальнейших действий: или отдельно осуществить деление этих дробных коэффициентов, или предварительно избавиться от дробных коэффициентов, умножив числитель и знаменатель на некое натуральное число. Последнее преобразование проводится в силу основного свойства алгебраической дроби (про него можно почитать в статье «Приведение алгебраической дроби к новому знаменателю»).

Пример 2

Задана дробь 2 5 · x 0 , 3 · x 3 . Необходимо выполнить ее сокращение.

Решение

Возможно сократить дробь таким образом:

2 5 · x 0 , 3 · x 3 = 2 5 3 10 · x x 3 = 4 3 · 1 x 2 = 4 3 · x 2

Попробуем решить задачу иначе, предварительно избавившись от дробных коэффициентов – умножим числитель и знаменатель на наименьшее общее кратное знаменателей этих коэффициентов, т.е. на НОК (5 , 10) = 10 . Тогда получим:

2 5 · x 0 , 3 · x 3 = 10 · 2 5 · x 10 · 0 , 3 · x 3 = 4 · x 3 · x 3 = 4 3 · x 2 .

Ответ: 2 5 · x 0 , 3 · x 3 = 4 3 · x 2

Когда мы сокращаем алгебраические дроби общего вида, в которых числители и знаменатели могут быть как одночленами, так и многочленами, возможна проблема, когда общий множитель не всегда сразу виден. Или более того, он попросту не существует. Тогда для определения общего множителя или фиксации факта о его отсутствии числитель и знаменатель алгебраической дроби раскладывают на множители.

Пример 3

Задана рациональная дробь 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 - 49 · b 3 . Необходимо ее сократить.

Решение

Разложим на множители многочлены в числителе и знаменателе. Осуществим вынесение за скобки:

2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 - 49 · b 3 = 2 · b 2 · (a 2 + 14 · a + 49) b 3 · (a 2 - 49)

Мы видим, что выражение в скобках возможно преобразовать с использованием формул сокращенного умножения:

2 · b 2 · (a 2 + 14 · a + 49) b 3 · (a 2 - 49) = 2 · b 2 · (a + 7) 2 b 3 · (a - 7) · (a + 7)

Хорошо заметно, что возможно сократить дробь на общий множитель b 2 · (a + 7) . Произведем сокращение:

2 · b 2 · (a + 7) 2 b 3 · (a - 7) · (a + 7) = 2 · (a + 7) b · (a - 7) = 2 · a + 14 a · b - 7 · b

Краткое решение без пояснений запишем как цепочку равенств:

2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 - 49 · b 3 = 2 · b 2 · (a 2 + 14 a + 49) b 3 · (a 2 - 49) = = 2 · b 2 · (a + 7) 2 b 3 · (a - 7) · (a + 7) = 2 · (a + 7) b · (a - 7) = 2 · a + 14 a · b - 7 · b

Ответ: 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 - 49 · b 3 = 2 · a + 14 a · b - 7 · b .

Случается, что общие множители скрыты числовыми коэффициентами. Тогда при сокращении дробей оптимально числовые множители при старших степенях числителя и знаменателя вынести за скобки.

Пример 4

Дана алгебраическая дробь 1 5 · x - 2 7 · x 3 · y 5 · x 2 · y - 3 1 2 . Необходимо осуществить ее сокращение, если это возможно.

Решение

На первый взгляд у числителя и знаменателя не существует общего знаменателя. Однако, попробуем преобразовать заданную дробь. Вынесем за скобки множитель х в числителе:

1 5 · x - 2 7 · x 3 · y 5 · x 2 · y - 3 1 2 = x · 1 5 - 2 7 · x 2 · y 5 · x 2 · y - 3 1 2

Теперь видна некая схожесть выражения в скобках и выражения в знаменателе за счет x 2 · y . Вынесем за скобку числовые коэффициенты при старших степенях этих многочленов:

x · 1 5 - 2 7 · x 2 · y 5 · x 2 · y - 3 1 2 = x · - 2 7 · - 7 2 · 1 5 + x 2 · y 5 · x 2 · y - 1 5 · 3 1 2 = = - 2 7 · x · - 7 10 + x 2 · y 5 · x 2 · y - 7 10

Теперь становится виден общий множитель, осуществляем сокращение:

2 7 · x · - 7 10 + x 2 · y 5 · x 2 · y - 7 10 = - 2 7 · x 5 = - 2 35 · x

Ответ: 1 5 · x - 2 7 · x 3 · y 5 · x 2 · y - 3 1 2 = - 2 35 · x .

Сделаем акцент на том, что навык сокращения рациональных дробей зависит от умения раскладывать многочлены на множители.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Дети в школе учат правила сокращения дробей в 6 классе. В этой статье мы сначала расскажем вам о том, что же означает это действие, затем разъясним, как сократимую дробь перевести в несократимую. Следующим пунктом будут правила сокращения дробей, а затем уже постепенно подберемся к примерам.

Что значит "сократить дробь "?

Итак, все мы знаем, что обычные дроби делятся на две группы: сократимые и несократимые. Уже по названиям можно понять, что те, что сократимые - сокращаются, а те, которые несократимые - не сокращаются.

• Сократить дробь - это значит разделить ее знаменатель и числитель на их (отличный от единицы) положительный делитель. В результате, конечно, выходит новая дробь с меньшим знаменателем и числителем. Полученная дробь будет равна исходной дроби.

Стоит отметить, что в книгах по математике с заданием "сократите дробь " это значит, что нужно исходную дробь привести именно к этому несократимому виду. Если говорить простыми словами, то деление знаменателя и числителя на их наибольший общий делитель и есть сокращение.

Как сократить дробь. Правила сокращения дробей (6 класс)

Итак, здесь всего два правила.

1. Первое правило сокращения дробей: сначала нужно будет найти наибольший общий делитель знаменателя и числителя вашей дроби.
2. Второе правило: делить знаменатель и числитель на наибольший общий делитель, в конечном итоге получить несократимую дробь.

Как сократить неправильную дробь?

Правила сокращения дробей идентичны правилам сокращения неправильных дробей.

Для того чтобы сократить неправильную дробь, для начала нужно будет расписать на простые множители знаменатель и числитель, а уже потом общие множители сокращать.

Сокращение смешанных дробей

Правила сокращения дробей также распространяется на сокращение смешанных дробей. Есть лишь небольшая разница: целую часть мы можем не трогать, а дробную сократить или смешанную дробь перевести в неправильную, затем сократить и опять перевести в правильную дробь.

Сократить смешанные дроби можно двумя способами.

Первый: расписать дробную часть на простые множители и целую часть тогда не трогать.

Второй способ: перевести сначала в неправильную дробь, расписать на обычные множители, потом сократить дробь. Уже полученную неправильную дробь перевести в правильную.

Примеры можно увидеть на фото выше.

Мы очень надеемся, что смогли помочь вам и вашим детям. Ведь на уроках они очень часто бывают невнимательными, поэтому приходится заниматься интенсивнее на дому самостоятельно.

С помощью дробей одну и ту же часть целого предмета можно записать разными способами.

На рисунке закрашена половина круга

Таким образом, все эти дроби равны.

Для удобства дополнительный множитель записывают на наклонной черте справа над дробью.

Вернёмся ещё раз к нашим дробям и запишем их в другом порядке.

Дробь, равную данной, можно получить, если числитель и знаменатель дроби одновременно разделить на одно и то же число, не равное нулю.

Такое преобразование дроби называют сокращением дроби .

Сокращение дроби обычно записывают следующим образом.

Числитель и знаменатель зачёркиваются чёрточками, и рядом с ними записываются результаты деления (частные) числителя и знаменателя на одно и то же число.

Число, на которое делили числитель и знаменатель, держим в уме.

В нашем примере мы сокращали (то есть делили и числитель, и знаменатель) дробь на двойку, которую держали в уме.

Сокращение дроби можно проводить последовательно.

Основное свойство дроби

Сформулируем основное свойство дроби.

Если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю, то получится дробь, равная данной.

Запишем это свойство в виде буквенных выражений.

, где « a », « b » и « k » - натуральные числа.

Сокращение дробей, правило и примеры сокращения дробей.

В этой статье мы подробно разберем, как проводится сокращение дробей . Сначала обговорим, что называют сокращением дроби. После этого поговорим о приведении сократимой дроби к несократимому виду. Дальше получим правило сокращения дробей и, наконец, рассмотрим примеры применения этого правила.

Навигация по странице.

Что значит сократить дробь?

Мы знаем, что обыкновенные дроби подразделяются на сократимые и несократимые дроби. По названиям можно догадаться, что сократимые дроби можно сократить, а несократимые – нельзя.

Что же значит сократить дробь? Сократить дробь – это значит разделить ее числитель и знаменатель на их положительный и отличный от единицы общий делитель. Понятно, что в результате сокращения дроби получается новая дробь с меньшим числителем и знаменателем, причем, в силу основного свойства дроби, полученная дробь равна исходной.

Для примера, проведем сокращение обыкновенной дроби 8/24 , разделив ее числитель и знаменатель на 2 . Иными словами, сократим дробь 8/24 на 2 . Так как 8:2=4 и 24:2=12 , то в результате такого сокращения получается дробь 4/12 , которая равна исходной дроби 8/24 (смотрите равные и неравные дроби). В итоге имеем .

Приведение обыкновенных дробей к несократимому виду

Обычно конечной целью сокращения дроби является получение несократимой дроби, которая равна исходной сократимой дроби. Эта цель может быть достигнута, если провести сокращение исходной сократимой дроби на наибольший общий делитель ее числителя и знаменателя. В результате такого сокращения всегда получается несократимая дробь. Действительно, дробь является несократимой, так как из свойств НОД известно, что и — взаимно простые числа. Здесь же скажем, что наибольший общий делитель числителя и знаменателя дроби является наибольшим числом, на которое можно сократить эту дробь.

Итак, приведение обыкновенной дроби к несократимому виду заключается в делении числителя и знаменателя исходной сократимой дроби на их НОД.

Разберем пример, для чего вернемся к дроби 8/24 и сократим ее на наибольший общий делитель чисел 8 и 24 , который равен 8 . Так как 8:8=1 и 24:8=3 , то мы приходим к несократимой дроби 1/3 . Итак, .

Заметим, что под фразой «сократите дробь» часто подразумевают приведение исходной дроби именно к несократимому виду. Другими словами, сокращением дроби очень часто называют деление числителя и знаменателя на их наибольший общий делитель (а не на любой их общий делитель).

Как сократить дробь? Правило и примеры сокращения дробей

Осталось лишь разобрать правило сокращения дробей, которое и объясняет, как сократить данную дробь.

Правило сокращения дробей состоит из двух шагов:

• во-первых, находится НОД числителя и знаменателя дроби;
• во-вторых, проводится деление числителя и знаменателя дроби на их НОД, что дает несократимую дробь, равную исходной.

Разберем пример сокращения дроби по озвученному правилу.

www.cleverstudents.ru

Сокращение дробей. Что значит сократить дробь?

Сокращение дробей нужно для того, чтобы привести дробь к более простому виду, например, в ответе полученном в результате решения выражения.

Сокращение дробей, определение и формула.

Что такое сокращение дробей? Что значит сократить дробь?

Определение:
Сокращение дробей – это разделение у дроби числитель и знаменатель на одно и то же положительное число не равное нулю и единице. В итоге сокращения получается дробь с меньшим числителем и знаменателем, равная предыдущей дроби согласно основному свойству рациональных чисел.

Формула сокращения дробей основного свойства рациональных чисел.

Рассмотрим пример:
Сократите дробь \(\frac \)

Решение:
Мы можем разложить дробь на простые множители и сократить общие множители.

Ответ: после сокращения получили дробь \(\frac \). По основному свойству рациональных чисел первоначальная и получившееся дробь равны.

Как сокращать дроби? Сокращение дроби до несократимого вида.

Чтобы нам получить в результате несократимую дробь, нужно найти наибольший общий делитель (НОД) для числителя и знаменателя дроби.

Есть несколько способов найти НОД мы воспользуемся в примере разложением чисел на простые множители.

Получите несократимую дробь \(\frac \).

Решение:
Найдем НОД(48, 136). Распишем числа 48 и 136 на простые множители.
48=2⋅2⋅2⋅2⋅3
136=2⋅2⋅2⋅17
НОД(48, 136)= 2⋅2⋅2=6

Правило сокращения дроби до несократимого вида.

1. Нужно найти наибольший общий делитель для числители и знаменателя.
2. Нужно поделить числитель и знаменатель на наибольший общий делитель в результате деления получить несократимую дробь.

Пример:
Сократите дробь \(\frac \).

Решение:
Найдем НОД(152, 168). Распишем числа 152 и 168 на простые множители.
152=2⋅2⋅2⋅19
168=2⋅2⋅2⋅3⋅7
НОД(152, 168)= 2⋅2⋅2=6

Ответ: \(\frac \) несократимая дробь.

Сокращение неправильной дроби.

Как сократить неправильную дробь?
Правила сокращения дробей для правильных и неправильных дробей одинаковы.

Рассмотрим пример:
Сократите неправильную дробь \(\frac \).

Решение:
Распишем на простые множители числитель и знаменатель. А потом общие множители сократим.

Сокращение смешанных дробей.

Смешанные дроби по тем же правилам что и обыкновенные дроби. Разница лишь в том, что мы можем целую часть не трогать, а дробную часть сократить или смешанную дробь перевести в неправильную дробь, сократить и перевести обратно в правильную дробь.

Рассмотрим пример:
Сократите смешанную дробь \(2\frac \).

Решение:
Решим двумя способами:
Первый способ:
Распишем дробную часть на простые множители, а целую часть не будем трогать.

Второй способ:
Переведем сначала в неправильную дробь, а потом распишем на простые множители и сократим. Полученную неправильную дробь переведем в правильную.

Вопросы по теме:
Можно ли сокращать дроби при сложении или вычитании?
Ответ: нет, нужно сначала сложить или вычесть дроби по правилам, а только потом сокращать. Рассмотрим пример:

Решение:
Часто допускают ошибку сокращая одинаковые числа в числителе и знаменателе в нашем случаем число 20, но их сокращать нельзя пока не выполните сложение и вычитание.

На какие числа можно сокращать дробь?
Ответ: можно сокращать дробь на наибольший общий делитель или обычный делитель числителя и знаменателя. Например, дробь \(\frac \).

Распишем на простые множители числа 100 и 150.
100=2⋅2⋅5⋅5
150=2⋅5⋅5⋅3
Наибольшим общим делителем будет число НОД(100, 150)= 2⋅5⋅5=50

Получили несократимую дробь \(\frac \).

Но необязательно всегда делить на НОД не всегда нужна несократимая дробь, можно сократить дробь на простой делитель числителя и знаменателя. Например, у числа 100 и 150 общий делитель 2. Сократим дробь \(\frac \) на 2.

Получили сократимую дробь \(\frac \).

Какие дроби можно сокращать?
Ответ: сокращать можно дроби у которых числитель и знаменатель имеют общий делитель. Например, дробь \(\frac \). У числа 4 и 8 есть число, на которое они оба делятся это число 2. Поэтому такую дробь можно сократить на число 2.

Пример:
Сравните две дроби \(\frac \) и \(\frac \).

Эти две дроби равны. Рассмотрим подробно дробь \(\frac \):

Две дроби равны тогда и только тогда, когда одна из них получена путем сокращения другой дроби на общий множитель числителя и знаменателя.

Пример:
Сократите если возможно следующие дроби: а) \(\frac \) б) \(\frac \) в) \(\frac \) г) \(\frac \)

Действия с обыкновенными дробями

Расширение дроби. Сокращение дроби. Сравнение дробей.

Приведение к общему знаменателю. Сложение и вычитание дробей.

Умножение дробей. Деление дробей.

Расширение дроби. Значение дроби не меняется, если умножить её числитель и знаменатель на одно и то же число, отличное от нуля расширением дроби . Например,



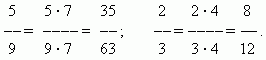
Сокращение дроби. Значение дроби не меняется, если разделить её числитель и знаменатель на одно и то же число, отличное от нуля . Это преобразование называется сокращением дроби . Например,



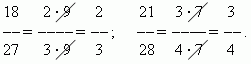
Сравнение дробей. Из двух дробей с одинаковыми числителями та больше, знаменатель которой меньше:



Из двух дробей с одинаковыми знаменателями та больше, числитель которой больше:



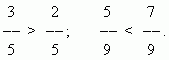
Для сравнения дробей, у которых числители и знаменатели различны, необходимо расширить их, чтобы привести к общему знаменателю.

П р и м е р. Сравнить две дроби:

Расширим первую дробь на знаменатель второй, а вторую — на знаменатель первой:

Использованное здесь преобразование называется приведением дробей к общему знаменателю .

Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то для того, чтобы сложить дроби, надо сложить их числители, а для того, чтобы вычесть дроби, надо вычесть их числители (в том же порядке). Полученная сумма или разность будет числителем результата; знаменатель останется тем же. Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю. При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел мы рекомендуем сначала преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется, к виду смешанного числа.



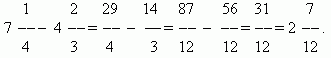
Умножение дробей. Умножить некоторое число на дробь означает умножить его на числитель и разделить произведение на знаменатель. Следовательно, мы имеем общее правило умножения дробей: для перемножения дробей необходимо перемножить отдельно их числители и знаменатели и разделить первое произведение на второе .

П р и м е р.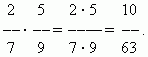

Деление дробей. Для того, чтобы разделить некоторое число на дробь, необходимо умножить это число на обратную дробь . Это правило вытекает из определения деления (см. раздел «Арифметические операции»).

П р и м е р.

Умножение и деление дробей

В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей»). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.

Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.

Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе - знаменателем.

Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.

Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.

В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь - ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.



Умножение дробей с целой частью и отрицательных дробей

Если в дробях присутствует целая часть, их надо перевести в неправильные - и только затем умножать по схемам, изложенным выше.

Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:

1. Плюс на минус дает минус;
2. Минус на минус дает плюс.

До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:

3. Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить - тот, которому не нашлось пары;
4. Если минусов не осталось, операция выполнена - можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.

Задача. Найдите значение выражения:

Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:



Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).

Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.

Сокращение дробей «на лету»

Умножение - весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей - это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:



По определению имеем:



Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.

Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.

Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:

Так делать нельзя!

Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.

Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:

Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.