МАЛАЯ АКАДЕМИЯ НАУК ШКОЛЬНИКОВ КРЫМА
«ИСКАТЕЛЬ»
Секция «Математическое моделирование»
Полуправильные
многогранники и многоугольники
Работу выполнил
____________________
Учащийся ____ класса
________________
Научный руководитель
ВВЕДЕНИЕ……………………………………………………………………………3
І. ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ…………………………………….4
I.1. Виды полуправильных многогранников…………………………………….. ..4
II. ПОЛУПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ……………………… ……........9
…………………………….9
……….……9
…………..17
……………...26
II.5. Построение полуправильных многоугольников……………………………28
ЗАКЛЮЧЕНИЕ……………………………………………………………………..30
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ…………………………….….31
Приложения………………………………………………………………..…….….32
Введение
Правильные многогранники и правильные многоугольники хорошо изучены и описаны. Существует пять видов правильных многогранников и бесконечное число правильных многоугольников, известны их свойства, формулы объемов и площадей. Менее популярны полуправильные многогранники, и совсем мало информации о полуправильных многоугольниках. При этом всем известный футбольный мяч в своем классическом виде, а также некоторые кристаллы имеют форму полуправильных многогранников, а полуправильные многоугольники присутствуют в паркетах. Не являясь идеальными телами и фигурами, тем не менее, полуправильные многогранники и многоугольники обладают рядом интересных свойств, не все из которых доказаны. Присущая этим телам и фигурам двойственность повышает интерес к их изучению, делает его логически завершенным и полным.
Объект исследования: полуправильные многогранники и многоугольники.
Цель исследования: изучить свойства полуправильных многогранников и многоугольников.
Задачи исследования: 1) изучить литературу по данному вопросу; 2) систематизировать информацию о полуправильных многогранниках и полуправильных многоугольниках; 3) сформулировать и доказать дополнительные свойства полуправильных многоугольников.
I. ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ
I.1. Виды полуправильных многогранников
Если в определении правильного многогранника допустить, чтобы гранями многогранника могли быть различные правильные многоугольники, то получим многогранники, которые называются полуправильными (равноугольно полуправильными). Полуправильным многогранником называется выпуклый многогранник, гранями которого являются правильные многоугольники (возможно, и с разным числом сторон) и все многогранные углы равны.
Как и в случае правильных многогранников, вместо второго условия (равенства многогранных углов) в определении полуправильного многогранника можно было бы сформулировать более слабое условие, а именно: в каждой вершине многогранника сходится одинаковое число ребер.
К полуправильным многогранникам относятся правильные n -угольные призмы, все ребра которых равны. Например, правильная пятиугольная призма на рисунке 1 имеет своими гранями два правильных пятиугольника - основания призмы, и пять квадратов, образующих боковую поверхность призмы. К полуправильным многогранникам относятся и так называемые антипризмы. На рисунке 2 изображена пятиугольная антипризма, полученная из пятиугольной призмы поворотом одного из оснований относительно другого на угол 36 . Каждая вершина верхнего и нижнего оснований соединена с двумя ближайшими вершинами другого основания.

Кроме этих двух бесконечных серий полуправильных многогранников имеется еще 13 полуправильных многогранников, которые впервые открыл и описал Архимед - это тела Архимеда. Самые простые из них получаются из правильных многогранников операцией "усечения", состоящей в отсечении плоскостями углов многогранника. Если срезать углы тетраэдра плоскостями, каждая из которых отсекает третью часть его ребер, выходящих из одной вершины, то получим усеченный тетраэдр , имеющий восемь граней (рис. 3). Из них четыре - правильные шестиугольники и четыре - правильные треугольники. В каждой вершине этого многогранника сходятся три ребра. Если указанным образом срезать вершины октаэдра и икосаэдра, то получим соответственно усеченный октаэдр (рис. 4) и усеченный икосаэдр (рис. 5). Известно, что поверхность футбольного мяча изготавливают в форме поверхности усеченного икосаэдра. Из куба и додекаэдра также можно получить усеченный куб (рис. 6) и усеченный додекаэдр (рис. 7).

Для того, чтобы получить еще один полуправильный многогранник, проведем в кубе отсекающие плоскости через середины ребер, выходящих из одной вершины. В результате получим полуправильный многогранник, который называется кубооктаэдром (рис. 8). Его гранями являются шесть квадратов, как у куба, и восемь правильных треугольников, как у октаэдра. Отсюда и его название - кубооктаэдр. Аналогично, если в додекаэдре отсекающие плоскости провести через середины ребер, выходящих из одной вершины, то получим многогранник, который называется икосододекаэдром (рис. 9). У него двадцать граней - правильные треугольники и двенадцать граней - правильные пятиугольники, т.е. все грани икосаэдра и додекаэдра.

Заметим, что повторное применение операции усечения к полученным полуправильным многогранникам уже не дает полуправильных многогранников. Дело в том, что многогранные углы данных многогранников не являются правильными. Поэтому многоугольники, получающиеся в сечении этих углов, также не будут правильными. Например, если операцию усечения применить к кубооктаэдру, то в сечениях многогранных углов получим прямоугольники, но не квадраты. Тем не менее, существует полуправильный многогранник (рис. 10), похожий на усеченный кубооктаэдр, гранями которого являются правильные восьмиугольники, шестиугольники и квадраты. Этот многогранник называется усеченным кубооктаэдром , хотя он не получается из кубооктаэдра операцией усечения. Аналогично, если операцию усечения применить к икосододекаэдру, то в сечениях многогранных углов получим прямоугольники, но не квадраты. Тем не менее, существует полуправильный многогранник (рис. 11), похожий на усеченный икосододекаэдр, гранями которого являются правильные десятиугольники, шестиугольники и квадраты. Этот многогранник называется усеченным икосододекаэдром , хотя он не получается из икосододекаэдра операцией усечения.
Рассмотрены 9 из 13 описанных Архимедом полуправильных многогранников. Четыре оставшихся - многогранники более сложного типа. На рисунке 12 изображен ромбокубооктаэдр . Его поверхность состоит из граней куба и октаэдра, к которым добавлены еще 12 квадратов. На рисунке 13 изображен ромбоикосододекаэдр , поверхность которого состоит из граней икосаэдра, додекаэдра и еще 30 квадратов. На рисунках 14, а, б представлены соответственно так называемые плосконосый (иногда называют курносый ) куб и плосконосый (курносый ) додекаэдр , поверхности которых состоят из граней куба или додекаэдра, окруженных правильными треугольниками.
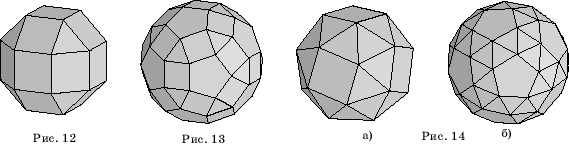
Как видим, каждая поверхность этих многогранников состоит из двух или трех типов граней: квадраты, треугольники, пятиугольники и треугольники, квадраты, пятиугольники и треугольники. Модели этих многогранников будут особенно привлекательны, если при их изготовлении грани каждого типа раскрасить в свой особый цвет.
Полуправильные многогранники называют также равноугольно полуправильными многогранниками, из-за того, что все их многогранные углы равны. Рассмотрим многогранники, двойственные к полуправильным многогранникам. Их центры граней являются вершинами полуправильных многогранников. Они образуют класс так называемых равногранно полуправильных многогранников. У этих многогранников равны все грани, которые, однако, не являются правильными многоугольниками, и равны все двугранные углы. На рисунках 15, а-в показаны многогранники, двойственные к усеченному тетраэдру, усеченному кубу и усеченному октаэдру.

На рисунках 15, г-н показаны многогранники, двойственные к остальным полуправильным многогранникам.

Рис. 15
Многогранник на рисунке 15, е называется ромбододекаэдром. Его гранями являются 12 ромбов. Форму этого многогранника имеет кристалл граната .
II. ПОЛУПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ
II.1. Определение полуправильных многоугольников
По определению выпуклый многоугольник называется правильным, если он равноугольный и равносторонний. Однако существует интересный класс фигур, не обладающих этими двумя свойствами одновременно. Мы будем называть полуправильными следующие многоугольники:
а) равноугольные, у которых стороны равны через одну;
б) равносторонние, у которых углы равны через один.
Примером полуправильного многоугольника первого рода является прямоугольник, а второго - ромб. Из описания полуправильных многоугольников видно, что у каждого из них четное число вершин; обозначим
его через 2 n .
II.2. Свойства полуправильных равноугольных многоугольников
1. Противоположные стороны равноугольного многоугольника параллельны.
Действительно, выполняя обход многоугольника, замечаем, что каждая сторона повернута относительно предыдущей на внешний угол, то есть на (рис. 2.1). Следовательно, сторона А n +1 A n +2 повернута относительно стороны A 1 A 2 на сумму n внешних углов, то есть на 180º.
2. Если соединить вершины полуправильного равноугольного многоугольника через одну (все нечетные или все четные вершины), то получится правильный многоугольник (рис. 2.1).
Доказательство: треугольники А 1 А 2 А 3 , А 3 А 4 А 5 , A 5 A 6 A 7 , … равны по первому признаку, значит, А 1 А 3 = А 3 А 5 =… . С другой стороны, из равенства треугольников следует равенство их соответственных углов. Обозначим внутренний угол полуправильного 2 n -угольника через α 2 n
α 2 n -(β+γ)= α 2 n -(180º- α 2 n )= 2α 2 n
n -угольника.

Рис. 2.1

Рис.2.2
3. Около полуправильного равноугольного многоугольника можно описать окружность.
Опишем окружность около правильного n -угольника А 1 А 3 А 5 … (рис. 2.2). Внутренний угол равноугольного 2 n -угольника равен 180º (1- ). Легко подсчитать, что дуга А 1 А 2 А 3 вдвое меньше градусной величины дуги А 3 А 5 А 1 , значит, точка А 2 лежит на построенной окружности. Это относится и к другим вершинам: А 4 , A 6 , … .
4. Если число вершин полуправильного равноугольного многоугольника кратно 4, то большие диагонали пересекаются в одной точке и делятся ею пополам.
 Для доказательства используем свойство 2: эти диагонали являются также диагоналями правильного многоугольника с четным числом сторон, поэтому они пересекаются в одной точке - центре описанной около многоугольника окружности - и делятся этой точкой пополам.
Если же число вершин полуправильного равноугольного многоугольника не кратно 4, то нетрудно построить пример (рис. 2.3), когда большие диагонали пересекаются в нескольких точках.
Для доказательства используем свойство 2: эти диагонали являются также диагоналями правильного многоугольника с четным числом сторон, поэтому они пересекаются в одной точке - центре описанной около многоугольника окружности - и делятся этой точкой пополам.
Если же число вершин полуправильного равноугольного многоугольника не кратно 4, то нетрудно построить пример (рис. 2.3), когда большие диагонали пересекаются в нескольких точках.
5. Центр окружности, описанной около полуправильного равноугольного 4 n -угольника, является его центром симметрии.
Из свойства 4 следует, что при центральной симметрии относительно центра окружности вершины
Рис 2.3 многоугольника переходят в вершины;
следовательно, стороны тоже переходят в стороны.
6. Прямая, проходящая через середины двух параллельных сторон полуправильного равноугольного многоугольника, является его осью симметрии.
По свойству параллельных хорд окружности эта прямая проходит через центр описанной окружности. Из равенства соответствующих хорд по обе стороны от прямой следует симметричность соответств ующих вершин многоугольника относительно проведенной прямой (рис. 2.4).

Рис.2.4
7. Пусть полуправильный равноугольный многоугольник имеет 2 n вершин, тогда центр описанной около него окружности является его центром симметрии порядка n .
Это 2 и 3.
8. Сумма расстояний от внутренней точки до сторон (или их продолжений) полуправильного равноугольного многоугольника постоянна.
Как известно, таким свойством обладает правильный многоугольник. Если соединить внутреннюю точку правильного многоугольника с вершинами, то сумма площадей полученных треугольников равна площади многоугольника. Обозначив сторону многоугольника через a , а расстояния до сторон через х 0 , x 1 , х 2 , х 3 , … получим
 … ,
… , 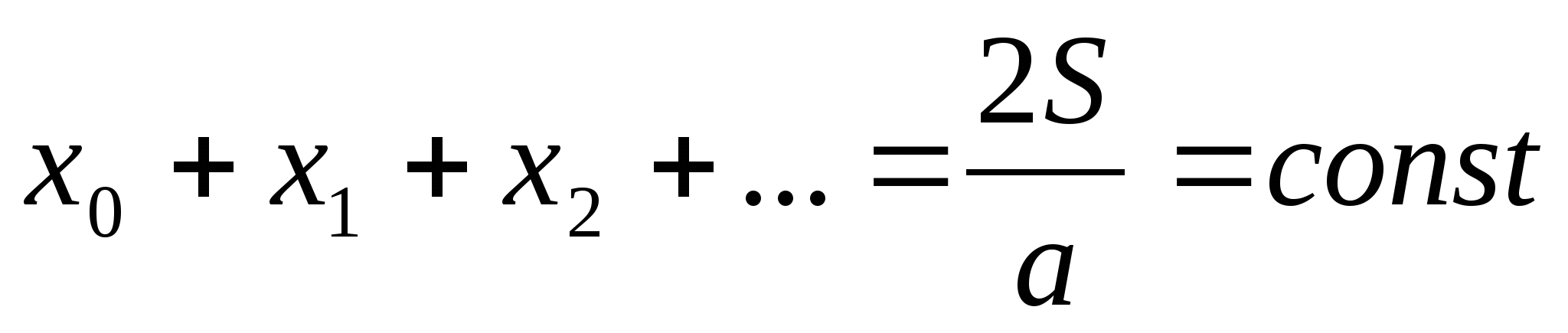
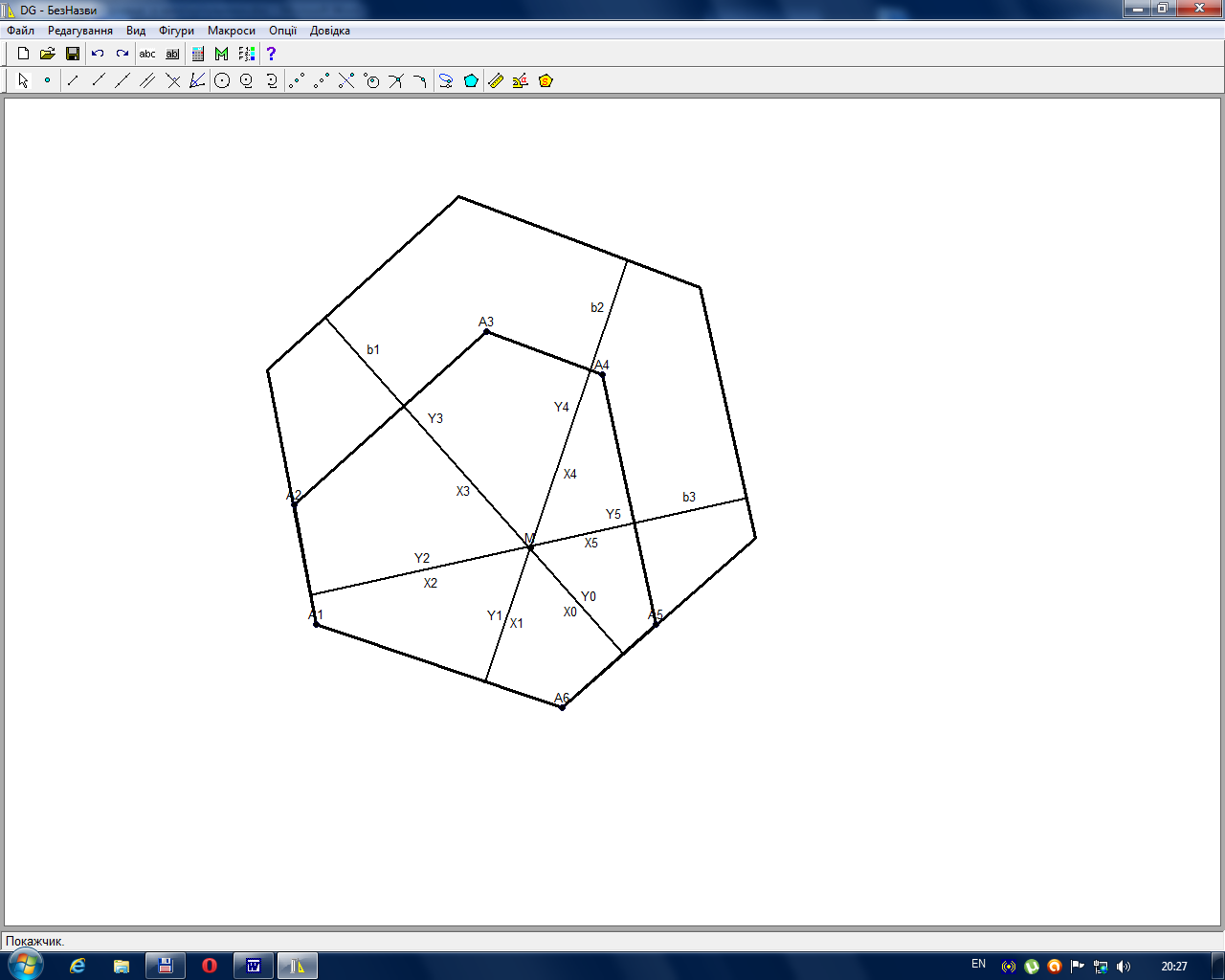
Рис. 2.5
Пусть в данном многоугольнике сторона А 1 А 6 больше стороны А 1 А 2 . Построим на А 1 А 6 правильный 2 n -угольник (рис. 2.5). Тогда все стороны исходного многоугольника (кроме трех) соответственно параллельны сторонам правильного многоугольника, а три (А 1 А 6 и смежные с ней) лежат на сторонах правильного многоугольника. Следовательно, расстояния от внутренней точки М до сторон правильного многоугольника таковы:
г де b 1 , b 2 , b 3 постоянны, а искомая сумма:

Рис.2.6
9. Если последовательно соединить середины сторон полуправильного равноугольного многоугольника, то получится полуправильный равносторонний многоугольник.
Действительно, по свойству 2 все малые диагонали полуправильного равноугольного многоугольника равны между собой. Стороны полученного многоугольника (рис. 2.6) вдвое меньше этих диагоналей, так как являются средними линиями треугольников А 1 А 2 А 3 , А 2 А 3 А 4 , A 3 A 4 A 5 , … Используя свойство 7, можно установить, что углы этого многоугольника равны через один.
10. Точки пересечения малых диагоналей полуправильного равноугольного многоугольника образуют полуправильный равносторонний многоугольник.
Это свойство следует из свойств 6 и 7. При отражении относительно прямой l (рис. 2.4) исходный многоугольник переходит в себя, следовательно, треугольник А 3 С 3 С 2 совмещается с треугольником А 4 С 3 С 4 , откуда С 2 С 3 =С 3 С 4 ; аналогичные равенства справедливы и для остальных сторон. Равенство углов через один у многоугольника С 1 С 2 С 3 С 4 … легко выводится из свойства 7 или из
теоремы о том, что угол между двумя хордами равен полусумме соответствующих дуг.
11. Сумма квадратов расстояний от любой точки описанной окружности до вершин полуправильного равноугольного 2 n -угольника равна 4 nR 2 .
Докажем свойство 11 для четных n . При этом достаточно заметить, что А 1 А n +1 , A 2 A n +2 , A 3 A n +3 , … - диаметры описанной окружности; потому для любой точки М этой окружности .
В общем случае: пусть М – точка описанной окружности, О – центр окружности (рис. 2.7), тогда

Рис.2.7
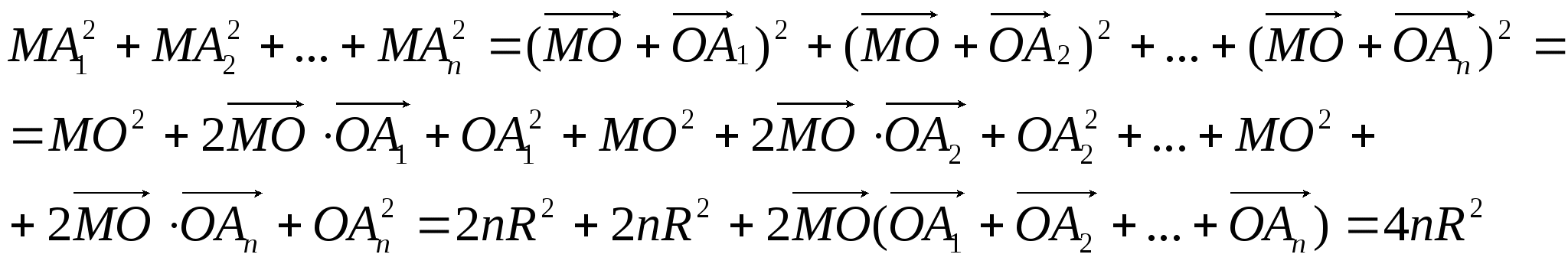
так как 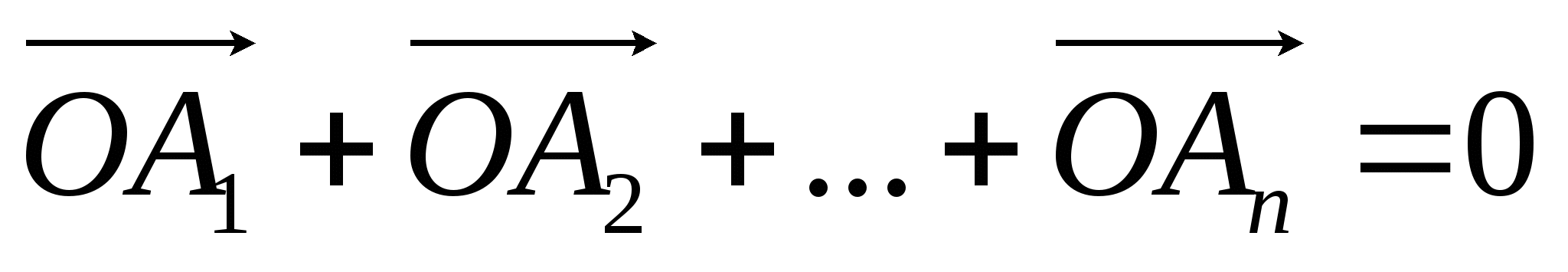
12. Площадь полуправильного равноугольного 2 n -угольника со сторонами А 1 А 2 = a , A 2 A 3 = b равна
(См. рис.2.1) Эта площадь равна сумме площадей правильного n -угольника и n треугольников, равных ∆ A 1 A 2 A 3 . Мы уже нашли, что А 1 А 2 А 3 =180º -
(при доказательстве свойства 1); теперь
![]()
Площадь правильного n - угольника А 1 А 3 А 5 …А 2 n -1 равна

По теореме косинусов для треугольника A 1 A 2 A 3

и окончательно
Например, площадь полуправильного равноугольного шестиугольника равна
 , а восьмиугольника -
, а восьмиугольника -  .
.
13. Радиус окружности, описанной около полуправильного равноугольного
2
n
-угольника со сторонами
a
и
b
и углом
α
равен 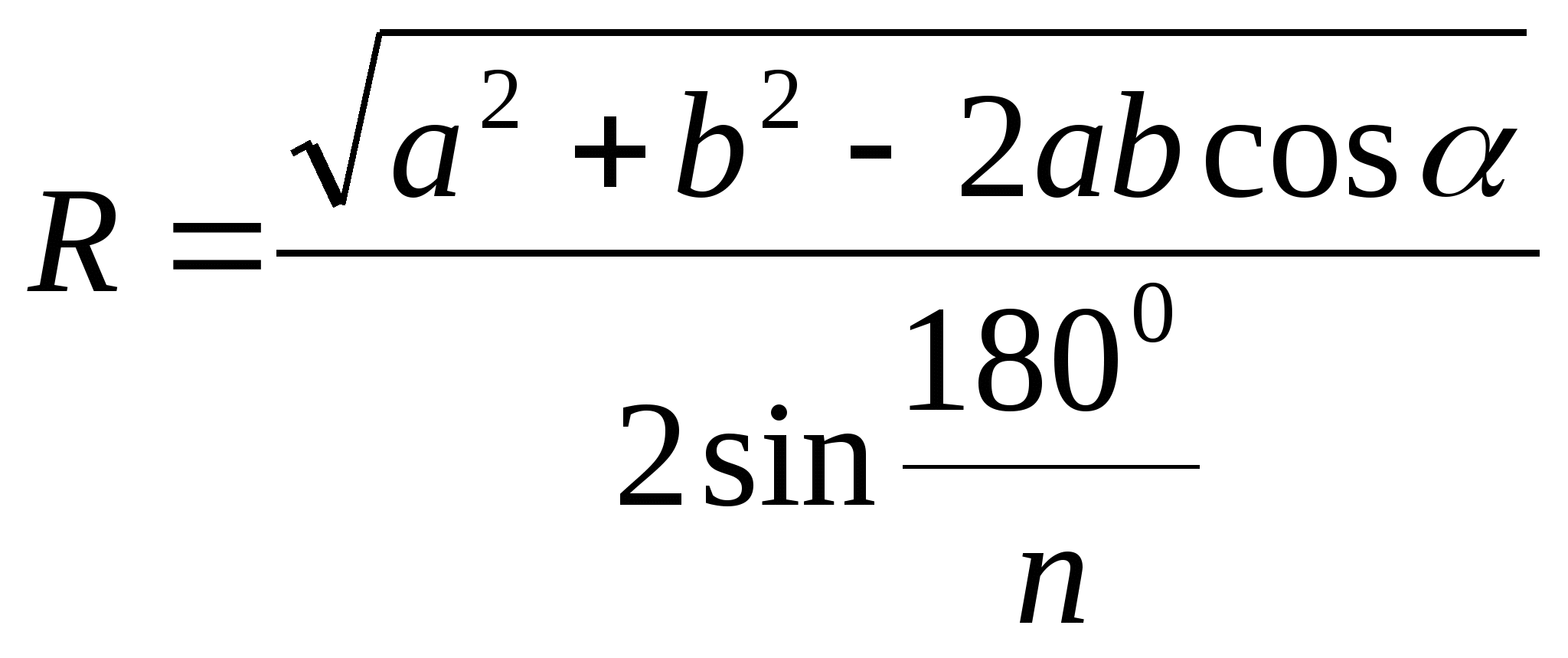
Для доказательства воспользуемся тем, что окружность, описанная около полуправильного равноугольного многоугольника, является также описанной около правильного многоугольника, образованного соединением вершин данного многоугольника через одну (свойство 2) (рис.2.2). Выразим по теореме косинусов сторону правильного многоугольника:
Воспользуемся формулой радиуса окружности, описанной около правильного
n -угольника
 , тогда
, тогда
II.3. Свойства полуправильных равносторонних многоугольников
1. Если число вершин полуправильного равностороннего многоугольника кратно 4, то его противоположные стороны параллельны .
Выполняя обход многоугольника, замечаем, что каждая сторона повернута относительно предыдущей на внешний угол (рис.2.8). Внутренние углы многоугольника по определению равны через один, значит, и внешние углы равны через один. Пусть внешние углы равны α и β , всего внешних углов 4 n , тогда 2 nα + 2 nβ = 360º. Следовательно, поротивоположные стороны полуправильного равностороннего многоугольника повернуты относительно друг друга на сумму nα + nβ = 180º.

Рис.2.8
2. Если соединить вершины полуправильного равностороннего многоугольника через одну, то получится правильный многоугольник (рис.2.9) .
Доказательство: равнобедренные ∆ А 1 А 2 А 3 = ∆ А 3 А 4 А 5 = ∆ A 5 A 6 A 7 =... () , значит, А 1 А 3 = А 3 А 5 =… . С другой стороны, из равенства треугольников следует равенство их соответственных углов. Пусть углы при основаниях равнобедренных треугольников равны γ. Обозначим внутренние углы полуправильного 2 n -угольника через α 2 n и β 2 n . Находим внутренние углы получившегося многоугольника: они равны
α 2 n -(γ + γ)= α 2 n -(180º- β 2 n )= α 2 n + β 2 n -180º=2·180º· (1-)-180º=180º· (1-),
как и должно быть у правильного n -угольника.
 Рис.2.9
Рис.2.9
3. Большие диагонали полуправильного равностороннего многоугольника пересекаются в одной точке и делятся ею пополам .
Большие диагонали полуправильного равностороннего многоугольника являются также диагоналями правильного многоугольника, образованного соединением вершин через одну. Диагонали правильного многоугольника пересекаются в одной точке, следовательно, и диагонали полуправильного равностороннего многоугольника пересекаются в одной точке и делятся ею пополам (рис.2.10).
4. В полуправильный равносторонний многоугольник можно вписать окружность .
Центр вписанной окружности равноудален от сторон многоугольника, то есть является точкой пересечения биссектрис. Значит, для доказательства этого свойства достаточно показать, что биссектрисы многоугольника пересекаются в одной точке. Большие диагонали полуправильного равностороннего многоугольника являются также диагоналями правильного многоугольника, образованного соединением вершин через одну. Диагонали правильного многоугольника пересекаются в одной точке и являются биссектрисами его углов, из этого следует, что эти диагонали также будут являтся биссектрисами углов полуправильного равностороннего многоугольника.
 Рис. 2.10.
Рис. 2.10.
5. Центр окружности, вписанной в полуправильный равносторонний 4 n -угольник, является его центром симметрии.
Из свойства 3 следует, что при центральной симметрии относительно центра окружности вершины многоугольника переходят в вершины; следовательно, стороны тоже переходят в стороны.
6. Большие диагонали полуправильного равностороннего многоугольника являются его осями симметрии .
Большая диагональ является осью симметрии правильного многоугольника; треугольники, дополняющие правильный многоугольник до полуправильного, равны (рис. 2.10). Значит, полуправильный многоугольник является симметричной фигурой.
7. Пусть полуправильный равносторонний многоугольник имеет 2 n вершин, тогда центр вписанной в него окружности является его центром симметрии порядка n
.
Это
означает, что при повороте вокруг центра окружности на угол, кратный
 , многоугольник совмещается сам с собой. Это следует из свойств
2, 4 и 5.
, многоугольник совмещается сам с собой. Это следует из свойств
2, 4 и 5.
8. Сумма расстояний от внутренней точки до сторон полуправильного равностороннего многоугольника постоянна (рис. 2.11) .
 Рис.2.11
Рис.2.11
Если соединить внутреннюю точку полуправильного равностороннего многоугольника с вершинами, то сумма площадей полученных треугольников равна площади многоугольника. Обозначив сторону многоугольника через a , а расстояния до сторон через х 0 , x 1 , х 2 , х 3 , … получим:
 …,
…, 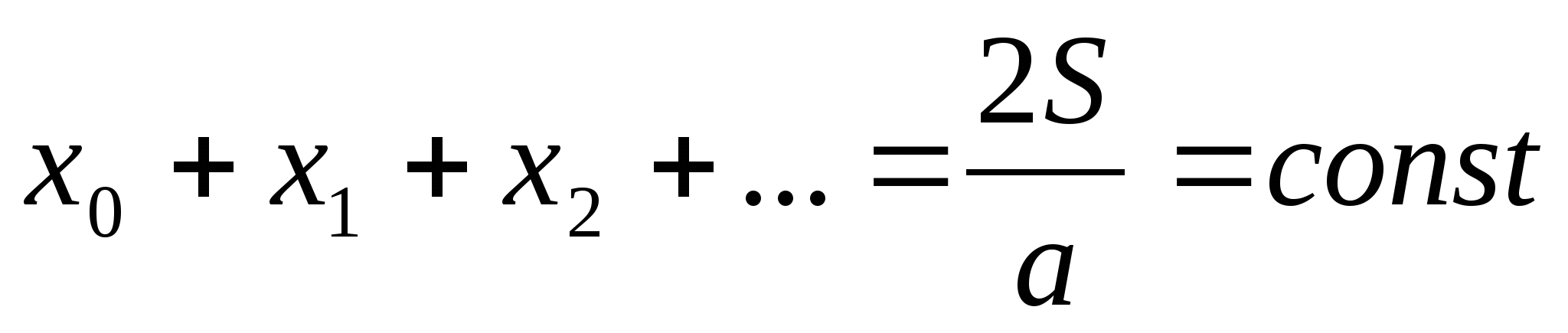
9. Если последовательно соединить середины сторон полуправильного равностороннего многоугольника, то получится полуправильный равноугольный многоугольник (рис.2.12) .

Рис.2.12
Рассмотрим полуправильный равносторонний многоугольник А 1 А 2 А 3 А 4 А 5 … с серединами сторон М 1 , М 2 , М 3 , М 4 , М 5 … . Соединим последовательно середины сторон. Отсеченные треугольники являются равнобедренными и равными через один по двум сторонам и углу между ними. Из равенства треугольников следует, что стороны образованного многоугольника равны через одну. Пусть углы при основаниях равнобедренных треугольников с четными вершинами равны α , а с нечетными – β. Тогда М 1 М 2 М 3 = 180º - (α + β) = М 2 М 3 М 4 = … . Значит, данный многоугольник является полуправильным равноугольным.
10. Точки пересечения малых диагоналей полуправильного равностороннего многоугольника являются вершинами полуправильного равноугольного многоугольника .
А 1 А 2 А 3 А 4 А 5 … , в котором проведены малые диагонали А 1 А 3 , А 2 А 4 , и т. д., пересекающиеся в точках В 1 , В 2 , В 3 и т. д. (рис.2.13). Образовались несколько серий равных треугольников:
∆А 1 А 2 А 3 = ∆ А 3 А 4 А 5 = ∆ A 5 A 6 A 7 =... (по двум сторонам и углу между ними );
∆А 2 А 3 А 4 = ∆ А 4 А 5 А 6 = ∆ A 6 A 7 A 8 =... (по двум сторонам и углу между ними );
из этого следует, что ∆ А 1 В 1 А 2 = ∆ А 3 В 2 А 2 = ∆ A 3 В 3 A 4 =... (по стороне и двум прилежащим углам );
далее ∆ В 1 А 2 В 2 = ∆ В 3 А 4 В 4 = ∆В 5 A 6 В 6 =... (по двум сторонам и углу между ними ), и, следовательно, В 1 В 2 = В 3 В 4 = В 5 В 6 =...;
также ∆ В 2 А 3 В 3 = ∆ В 4 А 5 В 5 = ∆В 6 A 7 В 7 =... (по двум сторонам и углу между ними ), и, следовательно, В 2 В 3 = В 4 В 5 = В 6 В 7 =... .
Углы образованного многоугольника являются вертикальными соответствующим углам в равных треугольниках, т. е. равны. П олучаем, что у образованного многоугольника углы равны, и стороны равны через одну, значит он является полуправильным равноугольным многоугольником.
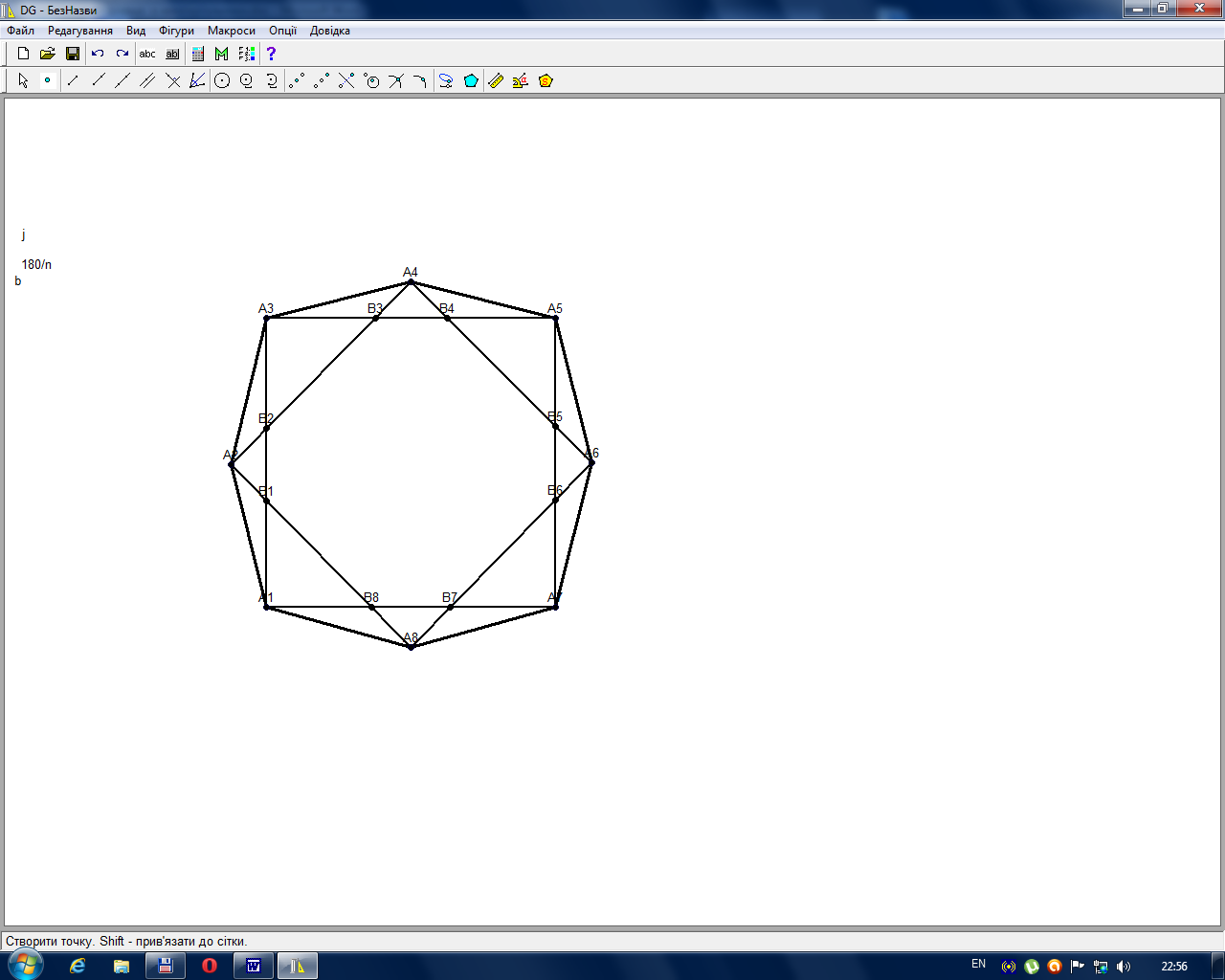 Рис. 2.13
Рис. 2.13
11. Сумма квадратов расстояний от любой точки вписанной окружности до точек касания полуправильного равностороннего 4 n - угольника равна 4 nr 2 .
Рассмотрим полуправильный равносторонний многоугольник А 1 А 2 А 3 А 4 А 5 … , в который вписана окружность с центром L 1 , Точки касания обозначим N 1 , N 2 , N 3 и т. д. (рис.2.14).
Заметим, что N 1 N n +1 , N 2 N n +2 , N 3 N n +3 , … - диаметры вписанной окружности; потому для любой точки М этой окружности:
.

Рис. 2.14
12. Площадь полуправильного равностороннего 2 n -угольника со стороной а и одним из углов β равна
.
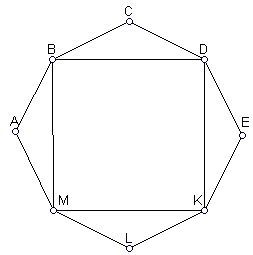
Рис. 2.15
Эта площадь равна сумме площадей правильного n -угольника и n треугольников, равных ∆ MAB , которые являются равнобедренными (рис.2.15):
![]()
Площадь правильного многоугольника, который образовался при соединении вершин полуправильного многогоугольника через одну, равна
По теореме косинусов для треугольника ∆ MAB :
и окончательно
13. Радиус окружности, вписанной в полуправильный равносторонний
2n-угольник со стороной а и углами α и β, равен
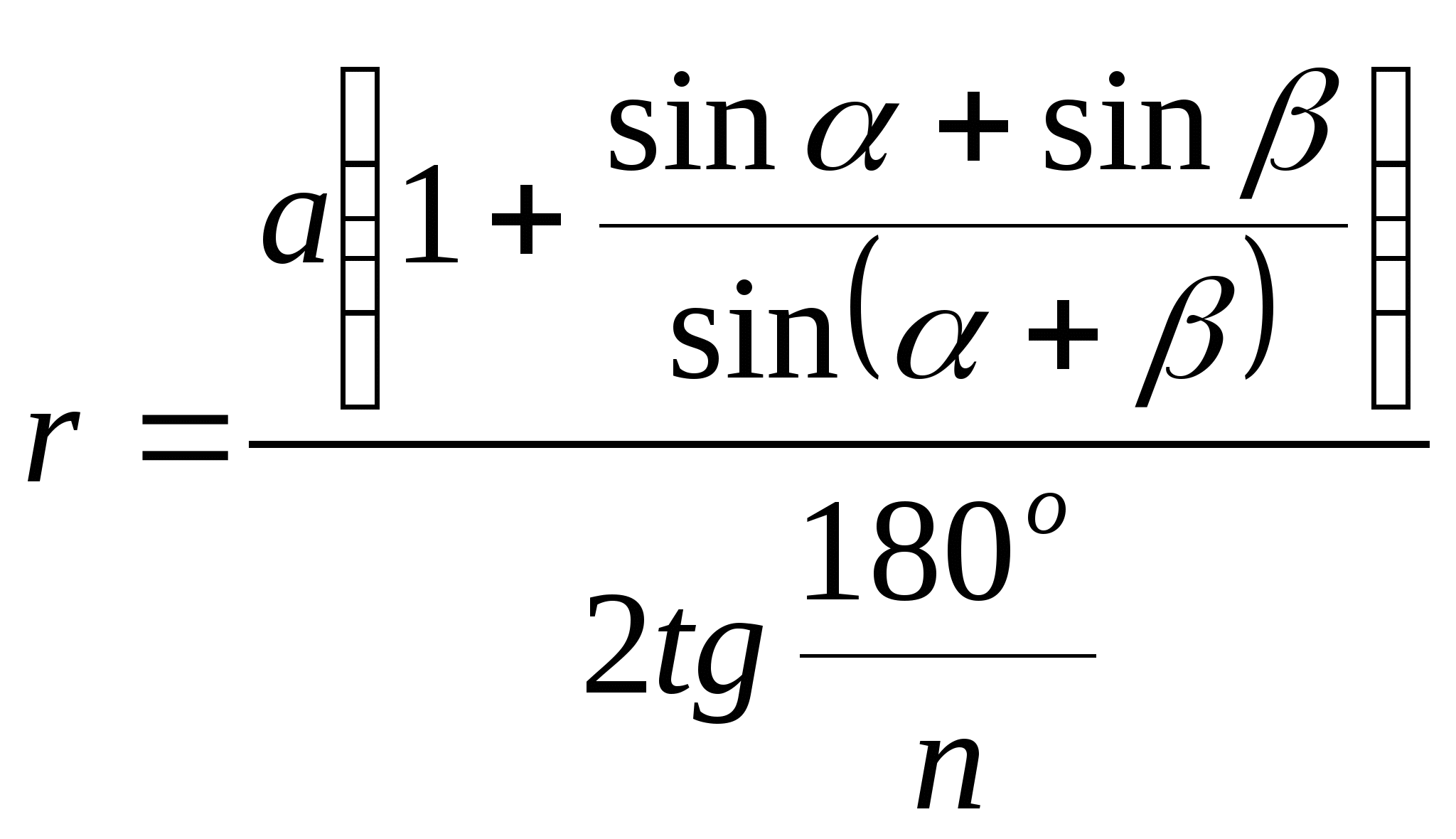

Рис.2.16
Доказательство: достроим полуправильный 2n-угольник до правильного n-угольника (рис.2.16). Рассмотрим треугольник A 2 A 3 В 2 . Один из углов этого треугольника, смежный с углом α , равен (180 º - α ), второй, смежный с углом β , равен (180 º - β ), третий угол - (α + β - 180º). По теореме синусов выразим стороны треугольника:
A
2
В
2
= 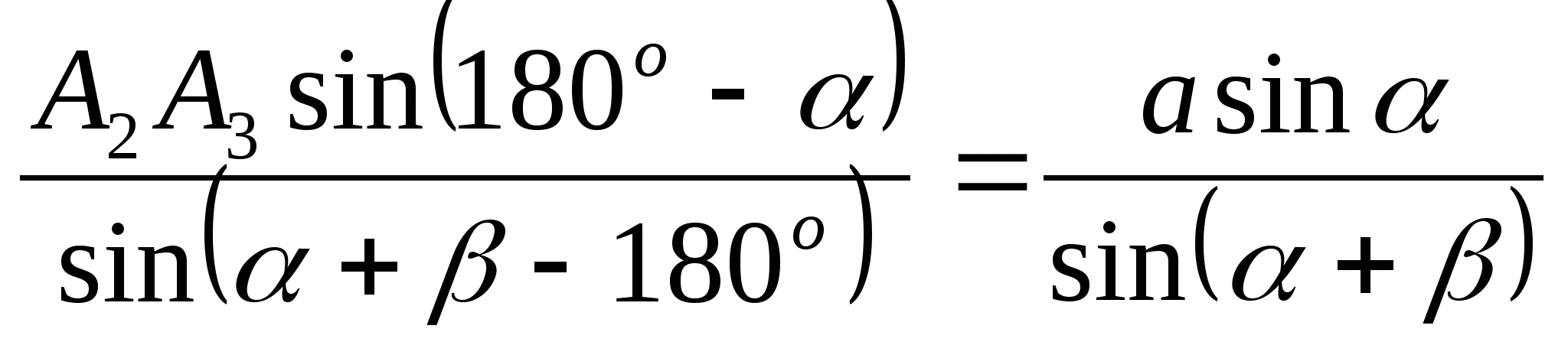 ,
A
3
В
2
=
,
A
3
В
2
= 
Сторона образованного правильного многоугольника равна сумме трех частей:
В
1
В
2
=
В
1
A
1
+
А
1
A
2
+
A
2
В
2
=
В
2
A
3
+
А
1
A
2
+
A
2
В
2
=
Подставляя полученное выражение для стороны в формулу для вычисления радиуса окружности, вписанной в правильный многоугольник, имеем:
 ,
,
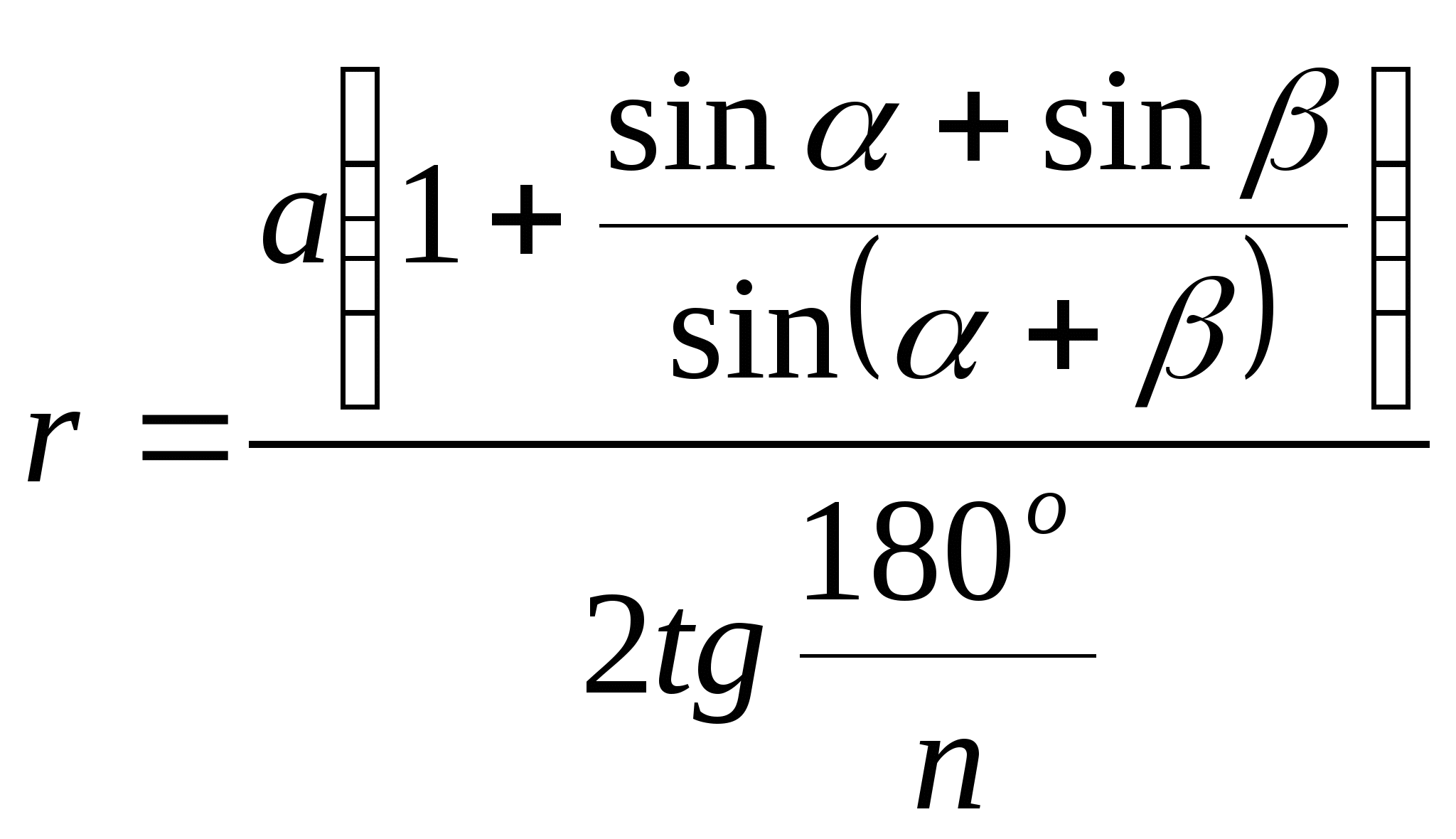
II.4. Полуправильные многоугольники на правильных паркетах
Известно, что если правильный многоугольник можно расположить на целочисленной решетке так, чтобы вершины многоугольника лежали в узлах решетки, то это квадрат. Интереснее дело обстоит с полуправильными (равноугольными и равносторонними) многоугольниками. Во второй половине двадцатого века Д. Боллом было показано, что равноугольный многоугольник с вершинами в целых точках обязан быть четырехугольником или восьмиугольником. Что касается равносторонних многоугольников на решетке  , то можно предъявить такие многоугольники с любым заданным четным числом сторон.
, то можно предъявить такие многоугольники с любым заданным четным числом сторон.
Множество узлов целочисленной решетки на плоскости можно рассматривать так же, как множество узлов квадратного паркета. Этот паркет является одним из одиннадцати правильных паркетов, то есть замощений плоскости правильными многоугольниками без пробелов и наложений, при которых любые два многоугольника либо не пересекаются, либо пересекаются по вершине или ребру и для которых все узлы замощения эквивалентны.
Если равноугольный многоугольник лежит на каком-либо из паркетов, то количество его сторон может быть равным 3, 4, 6, 8, 12, 16 или 24. Равносторонний же многоугольник с любым заданным числом сторон можно предъявить для каждого из паркетов, кроме квадратного и усеченного квадратного, для которых дополнительно необходимо потребовать выполнения условия четности числа сторон.
Паркетом называется любое покрытие плоскости правильными многоугольниками без пробелов и наложений, при котором любые два многоугольника имеют либо общую сторону, либо общую вершину, либо не пересекаются вовсе. Правильные многоугольники, составляющие паркет, мы будем называть базисными плитками паркета, а их вершины - узлами паркета.
Для каждого узла определим его тип как порядок, в котором базисные плитки паркета встречаются при обходе данного узла против часовой стрелки. Так, например, в квадратном паркете в каждом узле сходятся четыре квадрата, что означает, что тип узла этого паркета есть 4, 4, 4, 4 или (4)4.
Будем говорить, что паркет правильный, если его можно наложить самого на себя так, чтобы любая заданная вершина совместилась с другой произвольной заданной вершиной. Очевидно, что все вершины правильного паркета имеют одинаковый тип. Он называется типом правильного паркета.
Существует ровно 11 различных типов правильных паркетов. Три из них составлены из базисных плиток одного типа: (4)4; (6)3 и (3)6. Еще шесть включают в себя по два типа разных базисных плиток: 4, 8, 8; 3, 12, 12; 3, 6, 3, 6; (4) 3, 6; (3)3, (2)4; (2)3, 4, 3, 4. Наконец, последние два правильных паркета состоят из базисных плиток трех различных типов: 3, 4, 6, 4 и 4, 6, 12.
Будем говорить, что многоугольник F лежит на паркете T, если каждая вершина многоугольника F является узлом паркета T.
Какие полуправильные многоугольники могут быть расположены на каждом из правильных паркетов?
На паркетах (4)4 и 4, 8, 8 равносторонний многоугольник может лежать тогда и только тогда, когда количество его сторон четно. На каждом из остальных паркетов можно расположить равносторонний многоугольник с произвольным числом сторон.
На каждом из паркетов можно расположить равноугольный n-угольник тогда и только тогда, когда n принимает одно из значений, указанных в нижеследующей таблице:
(6)3(3)6
3, 6, 3, 6
3, 12, 12
(2)3, 4, 3, 4
3, 4, 6, 4
Число n
4, 8
4, 8, 16
3, 4, 6, 8
3, 4, 6, 12
3, 4, 6, 8, 12, 24

II.5. Построение полуправильных многоугольников
Способы построения полуправильных равноугольных многоугольников :
а) Строим правильный n -угольник А 1 А 3 А 5 … А 2 n -1 , описываем около него окружность. Затем находим (с помощью циркуля) на окружности точки А 2 , А 4 , А 6 , …, А 2 n , удаленные на одно и то же расстояние от соответствующих вершин n -угольника: А 1 А 2 = А 3 А 4 =… (рис.2.17)
б) Строим треугольник А 1 А 2 А 3 по двум произвольным сторонам и известному углу между ними, описываем около этого треугольника окружность. Затем с помощью циркуля последовательно находим остальные вершины.
в) Строим правильный многоугольник и отсекаем от него равные равнобедренные треугольники с вершинами в вершинах многоугольника (рис. 2.18).
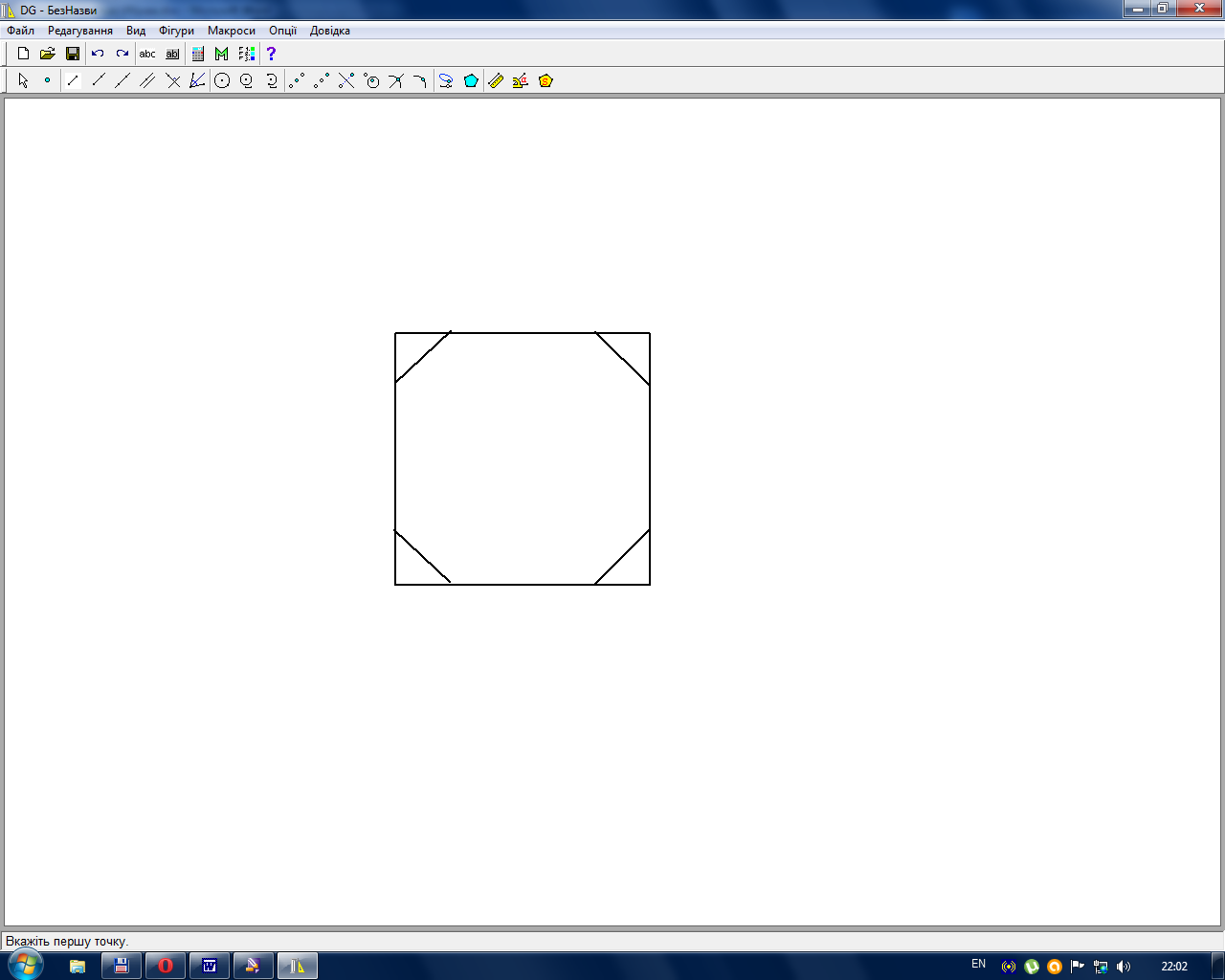
Рис. 2.17 Рис. 2.18
Способ построения полуправильного равностороннего многоугольника:
строим правильный многоугольник и на его сторонах как на основаниях строим равные равнобедренные треугольники (рис. 2.19)
Рис. 2.19
Заключение
В процессе поиска и сбора информации по теме работы было выявлено, что полуправильные многогранники – тела Архимеда – изучены и описаны достаточно полно. Полуправильные многоугольники, а именно, равноугольные со сторонами, равными через одну, и равносторонние с углами, равными через один, недостаточно описаны, информация о них найдена лишь в некоторых небольших статьях. В работе сформулированы и доказаны известные и дополнительные свойства полуправильных многоугольников, выведены формул радиусов вписанных и описанных окружностей.
Между равноугольными и равносторонними многоугольниками существует взаимосвязь, которую видно уже на примере ромба и прямоугольника. Так, если соединить середины сторон ромба, то получим прямоугольник, и наоборот. Около прямоугольника можно описать окружность, а в ромб – вписать. И тот, и другой имеют оси симметрии, центр симметрии и т. д. В работе эти и другие свойства обобщаются на случай произвольного n . Двойственность равноугольных и равносторонних полуправильных многоугольников видна в их свойствах: если последовательно соединить середины сторон полуправильного равностороннего многоугольника, то получится полуправильный равноугольный многоугольник и наоборот; точки пересечения малых диагоналей полуправильного равностороннего многоугольника являются вершинами полуправильного равноугольного многоугольника и наоборот и т. д.
Двойственны и полуправильные многогранники (равноугольные и равногранные). Двойственность повышает интерес к изучению полуправильных тел и фигур, делает его логически завершенным и полным.
Список использованной литературы
1. Лоповок Л. Полуправильные многоугольники //Квант. - 1971г. - №3 - стр. 25-29
2. Нурлигареев Х. Полуправильные многоугольники на правильных паркетах//
Ярославский педагогический вестник. - 2011. - №3. - Том III (Естественные науки)
3. Вавилов В.В., Устинов А.В. Многоугольники на решетках. - М.: МЦНМО, 2006.
Приложения
1.Формулы площадей поверхностей и объемов полуправильных многогранников
Название полуправильного многогранника
Формула площади поверхности ,
S
Формула объема ,
V
Кубооктаэдр
![]()
Икосододекаэдр
![]()
![]()
Усеченный
тетраэдр
![]()
У сечённый
куб
![]()
Усечённый
октаэдр
![]()
Усечённый
додекаэдр
![]()
![]()
Усечённый
икосаэдр
![]()

Ромбокубо
октаэдр
![]()
![]()
Ромбоусечён
ный кубоктаэдр
![]()
Ромбоикосо
додекаэдр

![]()
Ромбоусечён
ный икосододекаэдр
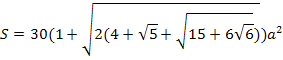
![]()
Курносый
куб
![]()
![]()
Курносый
додекаэдр
![]()
![]()
2. Число граней, вершин и ребер полуправильных многогранников
8
треугольников
6
квадратов
12
24
Икосододекаэдр
20
треугольников
12
пятиугольников
30
60
Усечённый тетраэдр
4
треугольника
4
шестиугольника
12
18
Усечённый октаэдр
6
квадратов
8
шестиугольников
24
36
Усечённый куб
8
треугольников
6
восьмиугольников
24
36
Усечённый икосаэдр
12
пятиугольников
20
шестиугольников
60
90
Усечённый додекаэдр
20
треугольников
12
десятиугольников
60
90
Ромбокубоктаэдр
8
треугольников
18
квадратов
24
48
Ромбоикосододекаэдр
12
квадратов
8
шестиугольников
6
восьмиугольников
48
72
Ромбоусечённый икосододекаэдр
30
квадратов
20
шестиугольников
12
десятиугольников
120
180
Усечённый икосаэдр
12
пятиугольников
20
шестиугольников
60
90
Курносый куб
32
треугольника
6
квадратов
24
60
Курносый додекаэдр
80
треугольников
12
пятиугольников
60
150
3. Образцы паркета с использованием в орнаменте полуправильных многоугольников


Ромбы

Прямоугольники и квадраты
![]()

Полуправильные восьмиугольники и квадраты
Мозаика Пенроуза
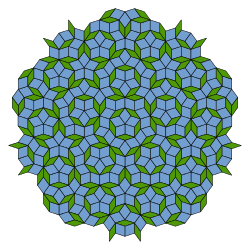

Мозаика Пенроуза , плитки Пенроуза - непериодическое разбиение плоскости, апериодические регулярные структуры, замощение двух типов - с углами 72° и 108° («толстые ромбы») и 36° и 144° («тонкие ромбы»), такими (подчиняются пропорции « »), что любые два соседних (то есть имеющих общую сторону) ромба не образуют вместе параллелограмм.
Геометрические тела
Введение
В стереометрии изучаются фигуры в пространстве, которые называются геометрическими телами .
Представление о геометрических телах дают окружающие нас предметы. В отличие от реальных предметов геометрические тела являются воображаемыми объектами. Наглядно геометрическое тело надо представлять себе как часть пространства, занятую материей (глина, дерево, металл, ...) и ограниченную поверхностью.
Все геометрические тела делятся на многогранники и круглые тела .
Многогранники
Многогранник – это геометрическое тело, поверхность которого состоит из конечного числа плоских многоугольников.
Гранями многогранника, называются многоугольники, составляющие его поверхность.
Ребрами многогранника, называются стороны граней многогранника.
Вершинами многогранника, называются вершины граней многогранника.
Многогранники делятся на выпуклые и невыпуклые .
Многогранник называется выпуклым , если он весь лежит по одну сторону от любой его грани.
Задание . Укажите грани , ребра и вершины куба изображенного на рисунке.
Выпуклые многогранники делятся на призмы и пирамиды .
Призма
Призма
– это многогранник, у которого две грани равные и параллельные
n
-угольники, а остальные n
граней – параллелограммы.
Два n -угольника называются основаниями призмы , параллелограммы – боковыми гранями . Стороны боковых граней и оснований называются ребрами призмы , концы ребер называются вершинами призмы . Боковыми ребрами называются ребра, не принадлежащие основаниям.
Многоугольники А 1 А 2 …А n и B 1 B 2 …B n – основания призмы.
Параллелограммы А 1 А 2 B 2 B 1 , … − боковые грани.
Свойства призмы:
· Основания призмы равны и параллельны.
· Боковые ребра призмы равны и параллельны.
Диагональю призмы называется отрезок, соединяющий две вершины, не принадлежащие одной грани.
Высотой призмы называется перпендикуляр, опущенный из точки верхнего основания на плоскость нижнего основания.
Призма называется 3-угольной,4-угольной, …, n
-угольной, если ее основания
3-угольники,4-угольники, …, n
-угольники.
Прямой призмой называется призма, у которой боковые ребра перпендикулярны основаниям. Боковые грани прямой призмы являются прямоугольниками.
Наклонной призмой называется призма, не являющаяся прямой. Боковые грани наклонной призмы являются параллелограммами.
Правильной призмой называется прямая призма, у которой в основаниях лежат правильные многоугольники.
Площадью полной поверхности призмы называется сумма площадей всех ее граней.
Площадью боковой поверхности призмы называется сумма площадей ее боковых граней.
S полн = S бок + 2·S осн
Изображение призмы
Изображение призмы строится следующим образом. Сначала строится одно из оснований. Это будет некоторый плоский многоугольник. Затем из вершин этого многоугольника проводятся боковые ребра призмы в виде параллельных отрезков равной длины. Концы этих отрезков соединяются, и получается другое основание призмы. Невидимые ребра проводятся штриховыми линиями.
Обозначают :
Задача
1. В прямой треугольной призме основание прямоугольный треугольник с катетами 8 см и 6 см. Боковое ребро призмы равно 12 см. Найдите площадь полной поверхности призмы.
Параллелепипед .Куб
Параллелепипед - это четырехугольная призма, основания которой являются параллелограммами. Параллелепипед имеет шесть граней, каждая из которых является параллелограммом. Отрезки, соединяющие вершины параллелепипеда, не принадлежащие одной грани, называются диагоналями параллелепипеда.
Свойства параллелепипеда:
· Противолежащие грани параллелепипеда попарно равны и параллельны.
· Все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
Прямоугольный параллелепипед – этопрямой параллелепипед, основаниями которого являются прямоугольники . Все грани прямоугольного параллелепипеда - прямоугольники.
Куб – это прямоугольный параллелепипед, у которого все ребра равны.
Длины трех ребер прямоугольного параллелепипеда, выходящих из одной вершины, называются линейными размерами или измерениями прямоугольного параллелепипеда.
Задачи :
1. У параллелепипеда три грани имеют площади 1 м 2 , 2 м 2 и 3 м 2 . Чему равна полная поверхность параллелепипеда.
2. Найдите поверхность прямоугольного параллелепипеда по трем его измерениям: 10 см, 22 см, 16 см.
Пирамида
Пирамида - это многогранник, у которого одна грань является многоугольником, а остальные грани - треугольники, имеющие одну общую вершину.
Многоугольник называется основанием , а треугольники - боковыми гранями . Общая вершина боковых граней называется вершиной пирамиды. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Различают треугольные , четырехугольные , пятиугольные и т. д. пирамиды в зависимости от вида многоугольника, лежащего в ее основании.
Изображение пирамиды
Изображение пирамиды строится следующим образом. Сначала строится основание. Это будет некоторый плоский многоугольник. Затем отмечается вершина пирамиды, которая соединяется боковыми ребрами с вершинами основания.
SABCD
- четырехугольная пирамида;
ABCD
- основание пирамиды;
ASAB
; ASBC
; ASDC
; ASDA
- боковые грани пирамиды;
S
- вершина пирамиды;
SA
; SB
; SC
; SD
- боковые ребра;
SO
- высота пирамиды
Площадью полной поверхности пирамиды является сумма площадей всех граней пирамиды, площадью боковой поверхности - сумма площадей боковых граней.
S полн = S бок + S осн
Правильная пирамида - это пирамида, у которой в основании лежит правильный многоугольник, а высота, опущенная из вершины пирамиды на плоскость основания, является отрезком, соединяющим вершину пирамиды с центром основания.
Свойства правильной пирамиды:
· Все боковые ребра правильной пирамиды равны между собой.
· Все боковые грани являются равными между собой равнобедренными треугольниками.
Задачи :
1. Основание пирамиды – прямоугольник со сторонами 6 см и 8 см. Каждое боковое ребро пирамиды равно 13 см. Вычислите высоту пирамиды.
2. Высота правильной четырехугольной пирамиды равна 7 см, а сторона основания 8 см. Найдите боковое ребро.
Усеченная пирамида
Усеченная пирамида - это пирамида, которая получается следующим способом: берется произвольная пирамида, и через точку бокового ребра проводится плоскость, параллельная основанию пирамиды. Данная плоскость разделила пирамиду на две фигуры: пирамиду подобную исходной и многогранник. Полученный многогранник называется усеченной пирамидой . Основаниями усеченной пирамиды служат подобные многоугольники.
ABCDA 1 B 1 C 1 D 1 – усеченная пирамида
Если усеченная пирамида получается из правильной пирамиды, то она называется правильной усеченной пирамидой . Боковые грани правильной усеченной пирамиды являются равными равнобедренными трапециями. Высота боковой грани называется апофемой правильной усеченной пирамиды. Перпендикуляр, опущенный из точки верхнего основания на нижнее, называется высотой усеченной пирамиды.
Площадь полной поверхности усеченной пирамиды равна сумме площадей оснований и боковых граней.
S полн = S бок + S осн 1 + S осн 2
Правильные многогранники
Правильный многогранник – это выпуклый многогранник, у которого все грани – одинаковые правильные многоугольники.
Существует пять типов правильных многогранников.
©2015-2017 сайт
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
РЕФЕРАТ
по геометрии
Тема:
«Многогранники».
Выполнила:
ученица 11-«б» класса
МОУ СОШ №3
Алябьева Юлия.
Проверила:
преподаватель математики
Сергеева Любовь Алексеевна.
г. Железноводск
План
I. Введение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
II. Теоретическая часть
Двугранный угол. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Трехгранный и многогранный углы. . . . . . . . . . . . . . . . 4
Многогранник. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Призма. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Изображение призмы и построение ее сечений. . . . . 7
Прямая призма. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
Параллелепипед. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
Центральная симметрия параллелепипеда. . . . . . . . 10
Прямоугольный параллелепипед. . . . . . . . . . . . . . . . . . 11
11. Пирамида. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
12. Построение пирамиды и ее плоских сечений. . . . . . 13
13. Усеченная пирамида. . . . . . . . . . . . . . . . . . . . . . . . . . . 15
14. Правильная пирамида. . . . . . . . . . . . . . . . . . . . . . . . . 15
15. Правильные многогранники. . . . . . . . . . . . . . . . . . . . 16
III. Практическая часть. . . . . . . . . . . . . . . . . . . . . . . . . . . 17
IV. Заключение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .19
V. Литература. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
I. Введение
Есть в школьной геометрии особые темы, которые ждешь с нетерпением, предвкушая встречу с невероятно красивым материалом. К таким темам можно отнести "Многогранники". Здесь не только открывается удивительный мир геометрических тел, обладающих неповторимыми свойствами, но и интересные научные гипотезы. И тогда урок геометрии становится своеобразным исследованием неожиданных сторон привычного школьного предмета.
Ни одни геометрические тела не обладают таким совершенством и красотой, как многогранники. "Многогранников вызывающе мало, - написал когда-то Л. Кэролл, - но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук".
II. Теоретическая часть.
1. Двугранный угол
Д вугранным углом
называется фигура, образованная двумя "полуплоскостями с общей ограничивающей их прямой (рис. 1). Полуплоскости называются гранями,
а ограничивающая их прямая - ребром
двугранного угла.
вугранным углом
называется фигура, образованная двумя "полуплоскостями с общей ограничивающей их прямой (рис. 1). Полуплоскости называются гранями,
а ограничивающая их прямая - ребром
двугранного угла.
Плоскость, перпендикулярная ребру двугранного угла, пересекает его грани по двум полупрямым. Угол, образованный этими полупрямыми, называется линейным. углом двугранного угла.
За меру двугранного угла принимается мера соответствующего ему линейного угла. Все линейные углы двугранного угла совмещаются параллельным переносом, а значит, равны. Поэтому мера двугранного угла не зависит от выбора линейного угла.
2. Трехгранный и многогранный углы
Рассмотрим три луча а, Ь, с, исходящие из одной точки и не лежащие в одной плоскости. Трехгранным углом (abc) называется фигура, составленная "из трех плоских углов (аЬ), (Ьс) и (ас) (рис. 2). Эти углы называются гранями трехгранного угла, а их стороны - ребрами, общая вершина плоских углов называется вершиной трехгранного угла. Двугранные углы, образованные гранями трехгранного угла, называются двугранными углами трехгранного угла.

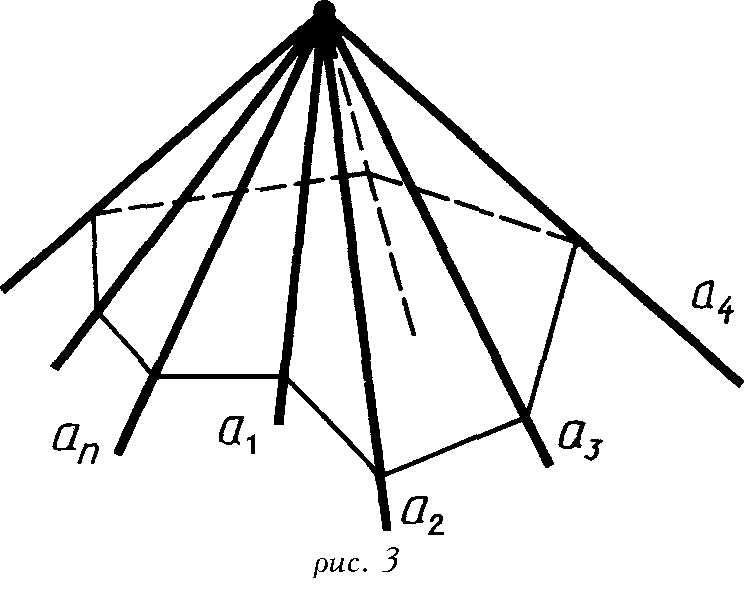
Аналогично определяется понятие многогранного угла (рис. 3).
3. Многогранник
В стереометрии изучаются фигуры в пространстве, называемые телами. Наглядно (геометрическое) тело надо представлять себе как часть пространства, занятую физическим телом и ограниченную поверхностью.
стереометрии изучаются фигуры в пространстве, называемые телами. Наглядно (геометрическое) тело надо представлять себе как часть пространства, занятую физическим телом и ограниченную поверхностью.
Многогранник - это такое тело, поверхность которого состоит из конечного числа плоских многоугольников (рис. 4). Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого плоского многоугольника на его поверхности. Общая часть такой плоскости и поверхности выпуклого многогранника называется гранью. Грани выпуклого многогранника являются плоскими выпуклыми многоугольниками. Стороны граней называются ребрами многогранника, а вершины - вершинами многогранника.
П оясним сказанное на примере знакомого вам куба (рис. 5). Куб есть выпуклый многогранник. Его поверхность состоит из шести квадратов: ABCD, BEFC, .... Они являются его гранями. Ребрами куба являются стороны этих квадратов: АВ, ВС, BE,... . Вершинами куба являются вершины квадратов: А, В, С, D, Е, .... У куба шесть граней, двенадцать ребер и восемь вершин.
оясним сказанное на примере знакомого вам куба (рис. 5). Куб есть выпуклый многогранник. Его поверхность состоит из шести квадратов: ABCD, BEFC, .... Они являются его гранями. Ребрами куба являются стороны этих квадратов: АВ, ВС, BE,... . Вершинами куба являются вершины квадратов: А, В, С, D, Е, .... У куба шесть граней, двенадцать ребер и восемь вершин.
Простейшим многогранникам - призмам и пирамидам, которые будут основным объектом нашего изучения,- мы дадим такие определения, которые, по существу, не используют понятие тела. Они будут определены как геометрические фигуры с указанием всех принадлежащих им точек пространства. Понятие геометрического тела и его поверхности в общем случае будет дано позже.
4. Призма
Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников (рис. 6). Многоугольники называются основаниями призмы, а отрезки, соединяющие соответствующие вершины,- боковыми ребрами призмы.
Так как параллельный перенос есть движение, то основания призмы равны.
Т ак как при параллельном переносе плоскость переходит в параллельную плоскость (или в себя), то у призмы основания лежат в параллельных плоскостях.
ак как при параллельном переносе плоскость переходит в параллельную плоскость (или в себя), то у призмы основания лежат в параллельных плоскостях.
Так как при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние, то у призмы боковые ребра параллельны и равны.
Поверхность призмы состоит из оснований и боковой поверхности. Боковая поверхность состоит из параллелограммов. У каждого из этих параллелограммов две стороны являются соответствующими сторонами оснований, а две другие - соседними боковыми ребрами.
Высотой призмы называется расстояние между плоскостями её оснований. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы.
Призма называется n-угольной, если ее основания - n-угольники.
В дальнейшем мы будем рассматривать только призмы, у которых основания - выпуклые многоугольники. Такие призмы являются выпуклыми многогранниками.
На рисунке 6 изображена пятиугольная призма. У нее основаниями являются пятиугольники А 1 А 2 ...А 5 , А 1 ’ А" 2 ...А" 5 . XX" - отрезок, соединяющий соответствующие точки оснований. Боковые ребра призмы-отрезки А 1 А" 2 , А 1 А" 2 , ..., А 5 А" 5 . Боковые грани призмы - параллелограммы А 1 А 2 А" 2 А 1 , А 2 А 3 А ’ 3 А" 2 , ... .
5. Изображение призмы и построение ее сечений
В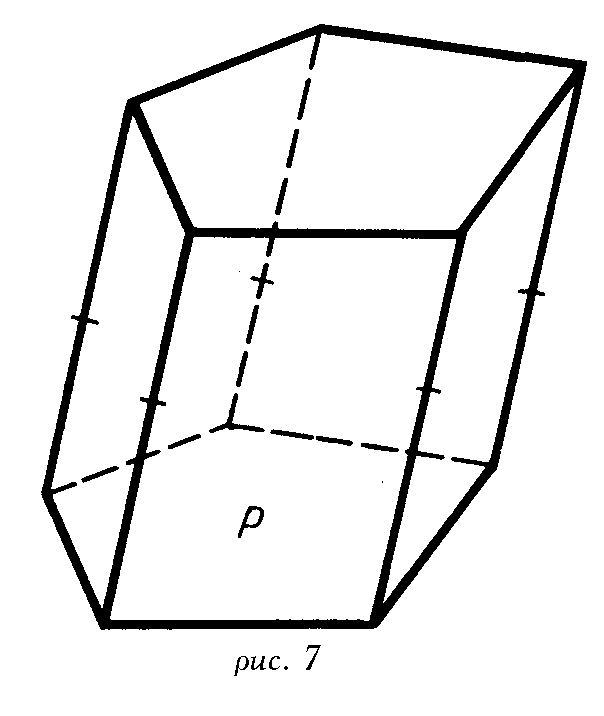 соответствии с правилами параллельного проектирования изображение призмы строится следующим образом. Сначала строится одно из оснований Р
(рис. 7). Это будет некоторый плоский многоугольник. Затем из вершин многоугольника Р
проводятся боковые ребра призмы в виде параллельных отрезков равной длины. Концы этих отрезков соединяются, и получается другое основание призмы. Невидимые ребра проводятся штриховыми линиями.
соответствии с правилами параллельного проектирования изображение призмы строится следующим образом. Сначала строится одно из оснований Р
(рис. 7). Это будет некоторый плоский многоугольник. Затем из вершин многоугольника Р
проводятся боковые ребра призмы в виде параллельных отрезков равной длины. Концы этих отрезков соединяются, и получается другое основание призмы. Невидимые ребра проводятся штриховыми линиями.
С ечения призмы плоскостями, параллельными боковым ребрам, являются параллелограммами. В частности, параллелограммами являются диагональные сечения. Это сечения плоскостями, проходящими через два боковых ребра, не принадлежащих одной грани (рис. 8).
ечения призмы плоскостями, параллельными боковым ребрам, являются параллелограммами. В частности, параллелограммами являются диагональные сечения. Это сечения плоскостями, проходящими через два боковых ребра, не принадлежащих одной грани (рис. 8).
На практике, в частности, при решении задач часто приходится строить сечение призмы плоскостью, проходящей через заданную прямую g на плоскости одного из оснований призмы. Такая прямая называется следом секущей плоскости на плоскости основания. Для построения сечения призмы достаточно построить отрезки пересечения секущей плоскости с гранями призмы. Покажем, как строится такое сечение, если известна какая-нибудь точка А на поверхности призмы, принадлежащая сечению (рис. 9).
Если данная точка А принадлежит другому основанию призмы, то его пересечение с секущей плоскостью представляет собой отрезок ВС, параллельный следу g и содержащий данную точку А (рис. 9, а).
Если данная точка А принадлежит боковой грани, то пересечение этой грани с секущей плоскостью строится, как показано на рисунке 9,б. Именно: сначала строится точка D, в которой плоскость грани пересекает заданный след g. Затем проводится прямая через точки А и D. Отрезок ВС прямой AD на рассматриваемой грани и есть пересечение этой грани с секущей плоскостью. Если грань, содержащая точку А, параллельна следу g, то секущая плоскость пересекает эту грань по отрезку ВС, проходящему через точку А и параллельному прямой g.

Концы отрезка ВС принадлежат и соседним граням. Поэтому описанным способом можно построить пересечение этих граней с нашей секущей плоскостью. И т. д.
На рисунке 10 показано построение сечения четырехугольной призмы плоскостью, проходящей через прямую а в плоскости нижнего основания призмы и точку А на одном из боковых ребер.

6. Прямая призма
Призма называется прямой, если ее боковые ребра перпендикулярны основаниям. В противном случае призма называется наклонной.
У прямой призмы боковые грани являются прямоугольниками. При изображении прямой призмы на рисунке боковые ребра обычно проводят вертикально (рис. 11).
П рямая призма называется правильной, если ее основания являются правильными многоугольниками.
рямая призма называется правильной, если ее основания являются правильными многоугольниками.
Боковой поверхностью призмы (точнее, площадью боковой поверхности) называется сумма площадей боковых граней. Полная поверхность призмы равна сумме боковой поверхности и площадей оснований.
Теорема 19.1. Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы, т. е. .на длину бокового ребра.
Доказательство. Боковые грани прямой призмы - прямоугольники. Основания этих прямоугольников являются сторонами многоугольника, лежащего в основании призмы, а высоты равны длине боковых ребер. Отсюда следует, что боковая поверхность призмы равна
S=a 1 l+a 1 l+...+a n l=pl,
где a 1 ,..., a n - длины ребер основания, р - периметр основания призмы, а 1 - длина боковых ребер. Теорема доказана.
7. Параллелепипед
Если основание призмы есть параллелограмм, то она называется параллелепипедом. У параллелепипеда все грани - параллелограммы.
Н а рисунке 12, а изображен наклонный параллелепипед, а на рисунке 12, б - прямой параллелепипед.
а рисунке 12, а изображен наклонный параллелепипед, а на рисунке 12, б - прямой параллелепипед.
Грани параллелепипеда, не имеющие общих вершин, называются противолежащими.
Т е о р е м а 19.2. У параллелепипеда противолежащие грани параллельны, и равны.
Доказательство. Рассмотрим какие-нибудь две противолежащие грани параллелепипеда, например А1А2А"2А"1 и A3A4A"4A"3. (рис. 13). Так как все грани параллелепипеда - параллелограммы, то прямая A1A2 параллельна прямой А4А3, а прямая А1А"1 параллельна прямой А4А4". Отсюда следует, что плоскости рассматриваемых граней параллельны.
Из того, что грани параллелепипеда - параллелограммы, следует, что отрезки А1А4, А1"А4", A"2A"3 и A2A3 - параллельны и равны. Отсюда заключаем, что грань А1А2А"2А"1 совмещается параллельным переносом вдоль ребра А1А4. с гранью А3А4А"4А"3. Значит, эти грани равны.
Аналогично доказывается параллельность и равенство любых других противолежащих граней параллелепипеда. Теорема доказана.

8. Центральная симметрия параллелепипеда
Теорема 19.3. Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
Доказательство. Рассмотрим какие-нибудь две диагонали параллелепипеда, например А 1 А" 3 и A 4 A" 2 (рис. 14). Так как четырехугольники А 1 А 2 А 3 А 4 и A 2 A" 2 A" 3 A 3 - параллелограммы с общей стороной A 2 A 3 , то их стороны А 1 А 4 и A" 2 A" 3 параллельны друг другу, а значит, лежат в одной плоскости. Эта плоскость пересекает плоскости противолежащих граней параллелепипеда по параллельным прямым A 1 A" 2 и A 4 A" 3 . Следовательно, четырехугольник A 4 A 1 A" 2 A" 3 - параллелограмм. Диагонали параллелепипеда A 1 A" 3 и A 4 A" 2 являются диагоналями этого параллелограмма. Поэтому они пересекаются и точкой пересечения О делятся пополам.
Аналогично доказывается, что диагонали A1A"3 и A2A"4, а также диагонали A1A"3 и A3A"1 пересекаются и точкой пересечения делятся пополам. Отсюда заключаем, что все четыре диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам. Теорема доказана.
И з теоремы 19.3 следует, что точка пересечения диагоналей параллелепипеда является его центром симметрий.
з теоремы 19.3 следует, что точка пересечения диагоналей параллелепипеда является его центром симметрий.
9. Прямоугольный параллелепипед
 Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани - прямоугольники.
Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани - прямоугольники.
Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
Длины непараллельных ребер прямоугольного параллелепипеда называются его линейными размерами (измерениями). У прямоугольного параллелепипеда три измерения.
Теорема 19.4. В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений.
Доказательство. Рассмотрим прямоугольный параллелепипед ABCDA"B"C"D" (рис. 15). Из прямоугольного треугольника AC"C по теореме Пифагора получаем:
AC" 2 = AC 2 + CC" 2 .
Из прямоугольного треугольника АСВ по теореме Пифагора получаем
АС 2 = АВ 2 + ВС 2 .
Отсюда AC" 2 =CC" 2 +AB 2 + BC 2 .
Ребра АВ, ВС и СС" не параллельны, а, следовательно, их длины являются линейными размерами параллелепипеда. Теорема доказана.
10. Симметрия прямоугольного параллелепипеда
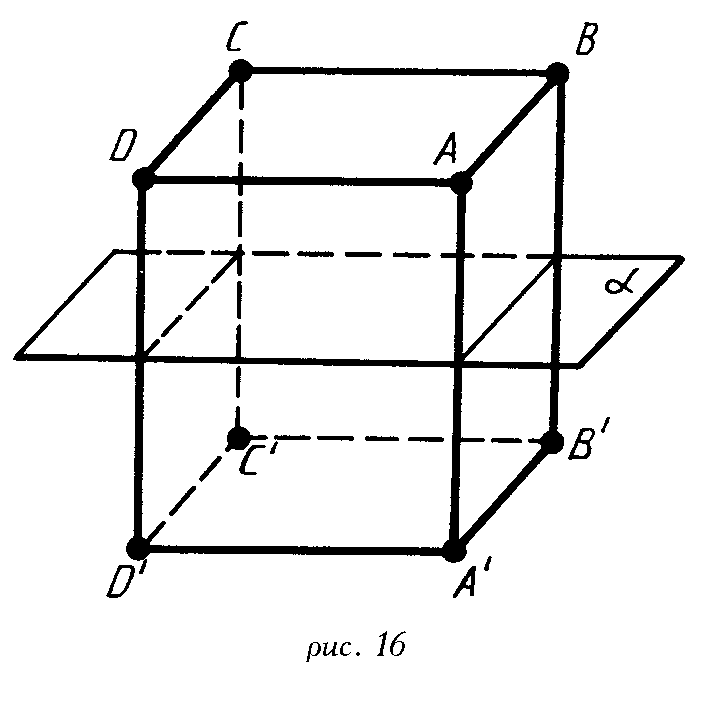
У прямоугольного параллелепипеда, как у всякого параллелепипеда, есть центр симметрии - точка пересечения его диагоналей. У него есть также три плоскости симметрий, проходящие через центр симметрии параллельно граням. На рисунке 16 показана одна из таких плоскостей. Она проходит через середины четырех параллельных ребер параллелепипеда. Концы ребер являются симметричными точками.
Если у параллелепипеда все линейные размеры разные, то у него нет других плоскостей симметрии, кроме названных.
Если же у параллелепипеда два линейных размера равны, то у него есть еще две плоскости симметрии. Это плоскости диагональных сечений, показанные на рисунке 17.
Если у параллелепипеда все линейные размеры равны, т. е. он является кубом, то у него плоскость любого диагонального сечения является плоскостью симметрии. Таким образом, у куба девять плоскостей симметрии.

11. Пирамида
П ирамидой
называется многогранник, который состоит из плоского многоугольника - основания пирамиды,
точки, не лежащей в плоскости основания,- вершины пирамиды
и всех отрезков, соединяющих вершину пирамиды с точками основания (рис. 18).
ирамидой
называется многогранник, который состоит из плоского многоугольника - основания пирамиды,
точки, не лежащей в плоскости основания,- вершины пирамиды
и всех отрезков, соединяющих вершину пирамиды с точками основания (рис. 18).
Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами.
Поверхность пирамиды состоит из основания и боковых граней. Каждая боковая грань - треугольник. Одной из его вершин является вершина пирамиды, а противолежащей стороной – сторона основания пирамиды.
Высотой пирамиды, называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Пирамида называется n-угольной, если ее основанием является n-угольник. Треугольная пирамида называется также тетраэдром.
У пирамиды, изображенной на рисунке 18, основание - многоугольник А 1 А 2 …A n , вершина пирамиды – S, боковые ребра - SА 1 , S А 2 , …, S А n , боковые грани – SА 1 А 2 , SА 2 А 3 , ... .
В дальнейшем мы будем рассматривать только пирамиды с выпуклым многоугольником в основании. Такие пирамиды являются выпуклыми многогранниками.
12. Построение пирамиды и ее плоских сечений
В соответствии с правилами параллельного проектирования изображение пирамиды строится следующим образом. Сначала строится основание. Это будет некоторый плоский многоугольник. Затем отмечается вершина пирамиды, которая соединяется боковыми ребрами с вершинами основания. На рисунке 18 показано изображение пятиугольной пирамиды.
Сечения пирамиды плоскостями, проходящими через ее вершину, представляют собой треугольники (рис. 19). В частности, треугольниками являются диагональные сечения. Это сечения плоскостями, проходящими через два несоседних боковых ребра пирамиды (рис. 20).
Сечение пирамиды плоскостью с заданным следом g на плоскости основания строится так же, как и сечение призмы.
Для построения сечения пирамиды плоскостью достаточно построить пересечения ее боковых граней с секущей плоскостью.
Если на грани, не параллельной следу g, известна какая-нибудь точка А, принадлежащая сечению, то сначала строится пересечение следа g секущей плоскости с плоскостью этой грани - точка D на рисунке 21. Точка D соединяется с точкой А прямой. Тогда отрезок этой прямой, принадлежащий грани, есть пересечение этой грани с секущей плоскостью. Если точка А лежит на грани, параллельной следу g, то секущая плоскость пересекает эту грань по отрезку, параллельному прямой g. Переходя к соседней боковой грани, строят ее пересечение с секущей плоскостью и т. д. В итоге получается требуемое сечение пирамиды.


На рисунке 22 построено сечение четырехугольной пирамиды плоскостью, проходящей через сторону основания и точку А на одном из ее боковых ребер.


13. Усеченная пирамида
T е о р е м а 19.5. Плоскость, пересекающая пирамиду и параллельная ее основанию, отсекает подобную пирамиду.
Доказательство. Пусть S - вершина пирамиды, А - вершина основания и А"- точка пересечения секущей плоскости с боковым ребром SA (рис. 23). Подвергнем пирамиду преобразованию гомотетии относительно вершины S с коэффициентом гомотетии
При этой гомотетии плоскость основания переходит в параллельную плоскость, проходящую через точку А", т. е. в секущую плоскость, а следовательно, вся пирамида - в отсекаемую этой плоскостью часть. Так как гомотетия есть преобразование подобия, то отсекаемая часть пирамиды является пирамидой, подобной данной. Теорема доказана.


По теореме 19.5 плоскость, параллельная плоскости основания пирамиды и пересекающая ее боковые ребра, отсекает от нее подобную пирамиду. Другая часть представляет собой многогранник, который называется усеченной пирамидой (рис. 24). Грани усеченной пирамиды, лежащие в параллельных плоскостях, называются основаниями; остальные грани называются боковыми гранями. Основания усеченной пирамиды представляют собой подобные (более того, гомотетичные) многоугольники, боковые грани - трапеции.
14. Правильная пирамида
Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника. Осью правильной пирамиды называется прямая, содержащая ее высоту. Очевидно, у правильной пирамиды боковые ребра равны; следовательно, боковые грани - равные равнобедренные треугольники.
Высота боковой грани правильной пирамиды, проведенная из её вершины, называется апофемой. Боковой поверхностью пирамиды называется сумма площадей ее боковых граней.
Т е о р е м а 19.6. Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.
Доказательство. Если сторона основания а, число сторон п, то боковая поверхность пирамиды равна:
(а1/2)ап=а1п/2= р1/2"
где I - апофема, a p - периметр основания пирамиды. Теорема доказана.
Усеченная пирамида, которая получается из правильной пирамиды, также называется правильной. Боковые грани правильной усеченной пирамиды - равные равнобокие трапеции; их высоты называются апофемами.
15. Правильные многогранники
Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер.)
Существует пять типов правильных выпуклых многогранников (рис.25): правильный тетраэдр (1), куб (2), октаэдр (3), додекаэдр (4); икосаэдр (5).
У правильного тетраэдра грани - правильные треугольники; в каждой вершине сходится по три ребра. Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны.
У куба все грани - квадраты; в каждой вершине сходится по три ребра. Куб представляет собой прямоугольный параллелепипед с равными ребрами.
У октаэдра грани - правильные треугольники, но в отличие от тетраэдра в каждой его вершине сходится по четыре ребра.
У додекаэдра грани - правильные пятиугольники. В каждой вершине сходится по три ребра.
У икосаэдра грани - правильные треугольники, но в отличие от тетраэдра и октаэдра в каждой вершине сходится по пять ребер.
икосаэдра грани - правильные треугольники, но в отличие от тетраэдра и октаэдра в каждой вершине сходится по пять ребер.
III. Практическая часть.
Задача 1.
Из точек А и В, лежащих в гранях двугранного угла, опущены перпендикуляры АА\ и ВВ\ на ребро угла. Найдите длину отрезка АВ, если АА 1 =а, ВВ 1 =b, А 1 В 1 =с и двугранный угол равен а (рис. 26).
Р ешение.
Проведем прямые A 1 C||BB 1 и ВС||А 1 В 1 . Четырехугольник А 1 В 1 ВС - параллелограмм, значит АА 1 ==ВВ 1 =b. Прямая А 1 В 1 перпендикулярна плоскости треугольника АA 1 C, так как она перпендикулярна двум прямым в этой плоскости АА 1 и СА 1 . Следовательно, параллельная ей прямая ВС тоже перпендикулярна этой плоскости. Значит, треугольник АВС - прямоугольный с прямым углом С. По теореме косинусов
ешение.
Проведем прямые A 1 C||BB 1 и ВС||А 1 В 1 . Четырехугольник А 1 В 1 ВС - параллелограмм, значит АА 1 ==ВВ 1 =b. Прямая А 1 В 1 перпендикулярна плоскости треугольника АA 1 C, так как она перпендикулярна двум прямым в этой плоскости АА 1 и СА 1 . Следовательно, параллельная ей прямая ВС тоже перпендикулярна этой плоскости. Значит, треугольник АВС - прямоугольный с прямым углом С. По теореме косинусов
AC 2 =AA 1 2 +A 1 C 2 -2AA 1 A 1 C cos =a 2 +b 2 -2abcos .
По теореме Пифагора
АВ =AC 2 + ВС 2 = a 2 + b 2 - 2ab cos + с 2 .
Задача 2.
У трехгранного угла (abc) двугранный угол при ребре с прямой, двугранный угол при ребре b равен , а плоский угол (bс) равен (,
Р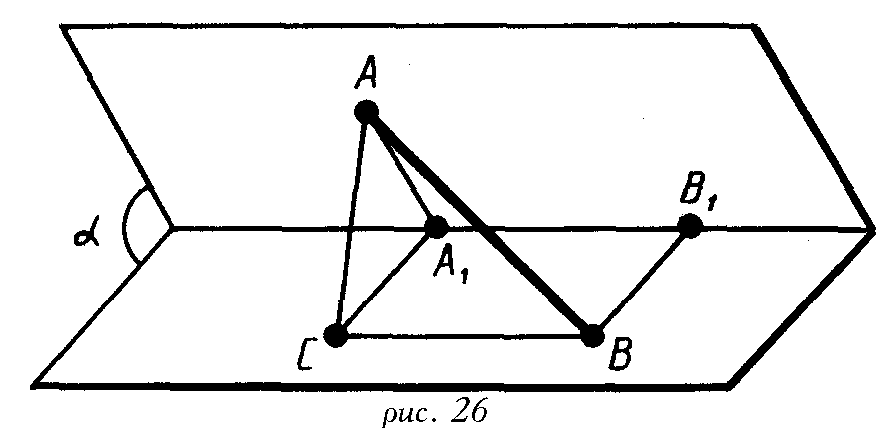 ешение.
Опустим из произвольной точки А ребра а перпендикуляр АВ на ребро b и перпендикуляр АС на ребро с (рис. 27). По теореме о трех перпендикулярах СВ - перпендикуляр к ребру b.
ешение.
Опустим из произвольной точки А ребра а перпендикуляр АВ на ребро b и перпендикуляр АС на ребро с (рис. 27). По теореме о трех перпендикулярах СВ - перпендикуляр к ребру b.
Из прямоугольных треугольников ОАВ, ОСВ, АОС и АВС получаем:
tg =AB/OB=(BC/ cos )/(BC/tg )= tg / cos
tg =AC/OC=BC tg / (BC/sin )= tg sin
Задача 3 .
В наклонной призме проведено сечение, перпендикулярное боковым ребрам и пересекающее все боковые ребра. Найдите боковую поверхность призмы, если п ериметр сечения равен р, а боковые ребра равны l.
ериметр сечения равен р, а боковые ребра равны l.
Решение.
Плоскость проведенного сечения разбивает призму на две части (рис. 28). Подвергнем одну из них параллельному переносу, совмещающему основания призмы. При этом получим прямую призму, у которой основанием служит сечение исходной призмы, а боковые ребра равны l. Эта призма имеет ту же боковую поверхность, что и исходная. Таким образом, боковая поверхность исходной призмы равна рl.
Задача 4.
Боковое ребро пирамиды разделено на четыре равные части и через точки деления проведены плоскости, параллельные основанию. Площадь основания равна 400 см2. Найдите площади сечений.
Решение. Сечения подобны основанию пирамиды с коэффициентами подобия ¼, 2/4, и ¾. Площади подобных фигур относятся как квадраты линейных размеров. Поэтому отношения площадей сечений к площади основания пирамиды есть (¼) 2 , (2/4) 2 , и (¾) 2 . Следовательно, площади сечений равны
400 (¼) 2 =25 (см 2),
400 (2/4) 2 =100 (см 2),
400 (¾) 2 =225 (см 2).
Задача 5.
Докажите, что боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.
Решение. Боковые грани усеченной пирамиды - трапеции с одним и тем же верхним основанием а, нижним b и высотой (апофемой) l. Поэтому площадь одной грани равна ½ (а + b)l. Площадь всех граней, т. е. боковая поверхность, равна ½ (аn + bn)l, где n - число вершин у основания пирамиды, an и bn - периметры оснований пирамиды.
IV. Заключение
Благодаря этой работе я обобщила и систематизировала знания, полученные за курс обучения в 11 классе, ознакомилась с правилами выполнения творческой работы, получила новые знания и применила их на практике.
Хочу отметить 3 наиболее понравившиеся мне книги:. А.В. Погорелов «Геометрия», Г. Якушева «Математика - справочник школьника», Л.Ф. Пичурин «За страницами учебника геометрии». Эти книги помогли мне больше, чем другие.
Мне бы хотелось чаще использовать свои новые полученные знания на практике.
V. Литература
1. А.В. Погорелов «Геометрия». – М.: Просвещение, 1992
2. Г. Якушева «Математика - справочник школьника». М.: Слово, 1995
3. Л.Д. Кудрявцев «Курс математического анализа» т.1, Москва 1981
4. Л.Ф. Пичурин «За страницами учебника геометрии». – М.: Просвещение, 1990
5. И.Н. Башмаков «Геометрия».
