Розмноження простих дробів з різними знаменниками приклади. Множення та поділ дробів

Минулого разу ми навчилися складати та віднімати дроби (див. урок «Складання та віднімання дробів»). Найбільш складним моментом у тих діях було приведення дробів до спільного знаменника.

Тепер настав час розібратися з множенням та поділом. Хороша новина полягає в тому, що ці операції виконуються навіть простіше, ніж додавання та віднімання. Спочатку розглянемо найпростіший випадок, коли є два позитивні дроби без виділеної цілої частини.

Щоб помножити два дроби, треба окремо помножити їх чисельники та знаменники. Перше число буде чисельником нового дробу, а друге – знаменником.

Щоб розділити два дроби, треба перший дріб помножити на «перевернутий» другий.

Позначення:

З визначення випливає, що розподіл дробів зводиться до множення. Щоб «перевернути» дріб, досить поміняти місцями чисельник та знаменник. Тому весь урок ми розглядатимемо переважно множення.

В результаті множення може виникнути (і найчастіше дійсно виникає) скоротитий дріб - його, зрозуміло, треба скоротити. Якщо після всіх скорочень дріб виявився неправильним, у ньому слід виділити цілу частину. Але чого точно не буде при множенні, так це приведення до спільного знаменника: жодних методів «хрест-навхрест», найбільших множників та найменших спільних кратних.

За визначенням маємо:

Розмноження дробів з цілою частиною та негативних дробів

Якщо в дробах є ціла частина, їх треба перевести в неправильні - і тільки потім множити за схемами, викладеними вище.

Якщо в чисельнику дробу, у знаменнику або перед ним стоїть мінус, його можна винести за межі множення або взагалі прибрати за такими правилами:

Плюс мінус дає мінус;
Мінус на мінус дає плюс.

Досі ці правила зустрічалися тільки при складанні та відніманні негативних дробів, коли потрібно було позбутися цілої частини. Для твору їх можна узагальнити, щоб спалювати відразу кілька мінусів:

Викреслюємо мінуси парами доти, доки вони повністю не зникнуть. У крайньому випадку, один мінус може вижити – той, якому не знайшлося пари;
Якщо мінусів не залишилося, операція виконана – можна приступати до множення. Якщо ж останній мінус не закреслено, оскільки йому не знайшлося пари, виносимо його за межі множення. Вийде негативний дріб.

Завдання. Знайдіть значення виразу:

Усі дроби переводимо в неправильні, а потім виносимо мінуси за межі множення. Те, що залишилося, множимо за звичайними правилами. Отримуємо:

Ще раз нагадаю, що мінус, який стоїть перед дробом із виділеною цілою частиною, відноситься саме до всього дробу, а не лише до його цілої частини (це стосується двох останніх прикладів).

Також зверніть увагу на негативні числа: при множенні вони полягають у дужках. Це зроблено для того, щоб відокремити мінуси від знаків множення і зробити весь запис більш обережним.

Скорочення дробів «на льоту»

Множення - дуже трудомістка операція. Числа тут виходять досить великі, і щоб спростити завдання, можна спробувати скоротити ще до множення. Адже по суті чисельники і знаменники дробів - це звичайні множники, і, отже, їх можна скорочувати, використовуючи основну властивість дробу. Погляньте на приклади:

Завдання. Знайдіть значення виразу:

За визначенням маємо:

У всіх прикладах червоним кольором відзначені числа, які зазнали скорочення, і те, що від них залишилося.

Зверніть увагу: у першому випадку множники скоротилися повністю. На їхньому місці залишилися одиниці, які, власне кажучи, можна не писати. У другому прикладі повного скорочення досягти не вдалося, але сумарний обсяг обчислень все одно зменшився.

Однак у жодному разі не використовуйте цей прийом при складанні та відніманні дробів! Так, іноді там трапляються схожі числа, які так і хочеться скоротити. Ось, подивіться:

Так робити не можна!

Помилка виникає через те, що при додаванні в чисельнику дробу з'являється сума, а не добуток чисел. Отже, застосовувати основну властивість дробу не можна, оскільки в цій властивості йдеться саме про множення чисел.

Інших підстав для скорочення дробів просто не існує, тому правильне вирішення попереднього завдання виглядає так:

Правильне рішення:

Як бачите, правильна відповідь виявилася не такою гарною. Загалом будьте уважні.

Ще одна дія, яку можна виконувати зі звичайними дробами, – множення. Ми спробуємо роз'яснити його основні правила при вирішенні завдань, покажемо, як множиться звичайний дріб на натуральне число і як правильно виконати множення трьох звичайних дробів і більше.

Запишемо спочатку основне правило:

Визначення 1

Якщо ми помножимо один звичайний дріб, то чисельник дробу, отриманого в результаті, дорівнюватиме добутку чисельників вихідних дробів, а знаменник – добутку їх знаменників. У літерному вигляді для двох дробів a / b і c / d це можна виразити як a b · c d = a · c b · d.

Подивимося з прикладу, як правильно застосувати це правило. Припустимо, у нас є квадрат, сторона якого дорівнює одній числовій одиниці. Тоді площа фігури становитиме 1 кв. одиницю. Якщо розділити квадрат на рівні прямокутники зі сторонами, рівними 14 і 18 числової одиниці, у нас вийде, що він тепер складається з 32 прямокутників (бо 8 · 4 = 32). Відповідно, площа кожного їх дорівнюватиме 1 32 від площі всієї фігури, тобто. 1 32 кв. одиниці.

У нас вийшов зафарбований фрагмент зі сторонами, рівними 5 8 числової одиниці та 3 4 числової одиниці. Відповідно, для обчислення його площі треба помножити перший дріб на другий. Вона дорівнюватиме 5 8 · 3 4 кв. одиниць. Але ми можемо просто підрахувати, скільки прямокутників входить у фрагмент: їх 15, отже, загальна площа становить 1532 квадратних одиниць.

Оскільки 5 · 3 = 15 і 8 · 4 = 32 ми можемо записати таку рівність:

5 8 · 3 4 = 5 · 3 8 · 4 = 15 32

Воно є підтвердженням сформульованого нами правила множення звичайних дробів, яке виражається як a b · c d = a · c b · d. Воно діє однаково як правильних, так неправильних дробів; за його допомогою можна помножити дроби і з різними, і з однаковими знаменниками.

Розберемо розв'язання кількох завдань на множення звичайних дробів.

Приклад 1

Помножте 7 11 на 9 8 .

Рішення

Для початку підрахуємо добуток чисельників зазначених дробів, помноживши 7 на 9 . У нас вийшло 63 . Потім обчислимо добуток знаменників та отримаємо: 11 · 8 = 88 . Складемо їх двох чисел відповідь: 63 88 .

Усі рішення можна записати так:

7 11 · 9 8 = 7 · 9 11 · 8 = 63 88

Відповідь: 7 11 · 9 8 = 63 88 .

Якщо у відповіді у нас вийшов скоротитий дріб, потрібно довести обчислення до кінця і виконати його скорочення. Якщо ж у нас вийшов неправильний дріб, з нього треба виділити цілу частину.

Приклад 2

Обчисліть добуток дробів 4 15 та 55 6 .

Рішення

Згідно з вивченим вище правилом, нам треба помножити чисельник на чисельник, а знаменник на знаменник. Запис рішення виглядатиме так:

4 15 · 55 6 = 4 · 55 15 · 6 = 220 90

Ми отримали скоротитий дріб, тобто. таку, яка має ознаку ділимості на 10 .

Виконаємо скорочення дробу: 220 90 НОД (220 , 90) = 10 , 220 90 = 220: 10 90: 10 = 22 9 . У результаті у нас вийшов неправильний дріб, з якого ми виділимо цілу частину та отримаємо змішане число: 22 9 = 2 4 9 .

Відповідь: 4 15 · 55 6 = 2 4 9 .

Для зручності обчислення ми можемо скоротити і вихідні дроби перед виконанням дії множення, для чого нам треба привести дріб до виду a · c b · d. Розкладемо значення змінних на прості множники і однакові їх скоротимо.

Пояснимо, як це виглядає, використовуючи дані конкретного завдання.

Приклад 3

Обчисліть добуток 4 15 · 55 6 .

Рішення

Запишемо обчислення, з правила множення. У нас вийде:

4 15 · 55 6 = 4 · 55 15 · 6

Оскільки як 4 = 2 · 2, 55 = 5 · 11, 15 = 3 · 5 і 6 = 2 · 3, значить, 4 · 55 15 · 6 = 2 · 2 · 5 · 11 3 · 5 · 2 · 3 .

2 · 11 3 · 3 = 22 9 = 2 4 9

Відповідь: 4 15 · 55 6 = 2 4 9 .

Числовий вираз, в якому має місце множення звичайних дробів, має переміщувальну властивість, тобто при необхідності ми можемо змінити порядок проходження множників:

a b · c d = c d · a b = a · c b · d

Як перемножити звичайний дріб з натуральним числом

Запишемо одразу основне правило, а потім спробуємо пояснити його на практиці.

Визначення 2

Щоб помножити звичайний дріб на натуральне число, потрібно помножити чисельник цього дробу цього числа. При цьому знаменник підсумкового дробу дорівнюватиме знаменнику вихідного звичайного дробу. Примноження деякого дробу a b на натуральне число n можна записати у вигляді формули a b · n = a · n b .

Зрозуміти цю формулу легко, якщо згадати, що будь-яке натуральне число може бути представлене у вигляді звичайного дробу зі знаменником, рівним одиниці, тобто:

a b · n = a b · n 1 = a · n b · 1 = a · n b

Пояснимо нашу думку конкретними прикладами.

Приклад 4

Обчисліть добуток 2 27 на 5 .

Рішення

В результаті множення чисельника вихідного дробу на другий множник отримаємо 10 . У силу правила, зазначеного вище, ми отримаємо в результаті 10 27 . Усі рішення наведено у цьому записі:

2 27 · 5 = 2 · 5 27 = 10 27

Відповідь: 2 27 · 5 = 10 27

Коли ми перемножуємо натуральне число зі звичайним дробом, то часто доводиться скорочувати результат або подавати його як змішане число.

Приклад 5

Умова: обчисліть добуток 8 на 5 12 .

Рішення

За правилом вище ми множимо натуральне число на чисельник. Через війну отримуємо, що 5 12 · 8 = 5 · 8 12 = 40 12 . Підсумковий дріб має ознаки подільності на 2, тому нам потрібно виконати її скорочення:

НОК (40, 12) = 4, отже, 40 12 = 40: 4 12: 4 = 10 3

Тепер нам залишилося лише виділити цілу частину та записати готову відповідь: 10 3 = 3 1 3 .

У цьому записі можна бачити все рішення повністю: 5 12 · 8 = 5 · 8 12 = 40 12 = 10 3 = 3 1 3 .

Також ми могли скоротити дріб за допомогою розкладання чисельника і знаменника на прості множники, і результат вийшов би таким самим.

Відповідь: 5 12 · 8 = 3 1 3 .

Числове вираз, у якому натуральне число множиться на дріб, також має властивість переміщення, тобто порядок розташування множників не впливає на результат:

a b · n = n · a b = a · n b

Як виконати множення трьох і більше звичайних дробів

Ми можемо поширити дію множення звичайних дробів самі властивості, які притаманні множення натуральних чисел. Це випливає з визначення даних понять.

Завдяки знанню поєднаного і переміщувального властивості можна перемножувати три прості дроби і більше. Допустимо переставляти множники місцями для більшої зручності або розставляти дужки так, як буде легше рахувати.

Покажемо з прикладу, як це робиться.

Приклад 6

Помножте чотири звичайні дроби 1 20 , 12 5 , 3 7 та 5 8 .

Рішення: для початку зробимо запис твору. У нас вийде 1 20 · 12 5 · 3 7 · 5 8 . Нам треба перемножити між собою всі чисельники та всі знаменники: 1 20 · 12 5 · 3 7 · 5 8 = 1 · 12 · 3 · 5 20 · 5 · 7 · 8 .

Перед початком множення ми можемо трохи полегшити собі завдання і розкласти деякі числа на прості множники для подальшого скорочення. Це буде простіше, ніж скорочувати вже готовий дріб, що вийшов у результаті.

1 · 12 · 3 · 5 20 · 5 · 7 · 8 = 1 · (2 · 2 · 3) · 3 · 5 2 · 2 · 5 · 5 · 7 (2 · 2 · 2) = 3 · 3 5 · 7 · 2 · 2 · 2 = 9280

Відповідь: 1 · 12 · 3 · 5 20 · 5 · 7 · 8 = 9 280 .

Приклад 7

Перемножте 5 чисел 7 8 · 12 · 8 · 5 36 · 10 .

Рішення

Для зручності ми можемо згрупувати дріб 7 8 з числом 8 , а число 12 з дробом 5 36 , оскільки нам будуть очевидні майбутні скорочення. У результаті в нас вийде:
7 8 · 12 · 8 · 5 36 · 10 = 7 8 · 8 · 12 · 5 36 · 10 = 7 · 8 8 · 12 · 5 36 · 10 = 7 1 · 2 · 2 · 3 · 5 2 · 2 · 3 · 3 · 10 = = 7 · 5 3 · 10 = 7 · 5 · 10 3 = 350 3 = 116 2 3

Відповідь: 7 8 · 12 · 8 · 5 36 · 10 = 116 2 3 .

Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter

Розмноження звичайних дробів

Розглянемо приклад.

Нехай на тарілці лежить частина яблука $\frac(1)(3)$. Потрібно знайти $\frac(1)(2)$ частина від неї. Необхідна частина є результатом множення дробів $ frac (1) (3) $ і $ frac (1) (2) $. Результат множення двох звичайних дробів - це звичайний дріб.

Розмноження двох звичайних дробів

Правило множення звичайних дробів:

Результатом множення дробу на дріб є дріб, чисельник якого дорівнює добутку чисельників дробів, що множаться, а знаменник дорівнює добутку знаменників:

Приклад 1

Виконати множення звичайних дробів $\frac(3)(7)$ і $\frac(5)(11)$.

Рішення.

Скористаємося правилом множення звичайних дробів:

\[\frac(3)(7)\cdot \frac(5)(11)=\frac(3\cdot 5)(7\cdot 11)=\frac(15)(77)\]

Відповідь:$\frac(15)(77)$

Якщо в результаті множення дробів виходить скоротитий або неправильний дріб, то потрібно його спростити.

Приклад 2

Виконати множення дробів $frac(3)(8)$ і $frac(1)(9)$.

Рішення.

Використовуємо правило множення звичайних дробів:

\[\frac(3)(8)\cdot \frac(1)(9)=\frac(3\cdot 1)(8\cdot 9)=\frac(3)(72)\]

В результаті отримали скоротитий дріб (за ознакою поділу на $3$. Чисельник і знаменник дробу розділимо на $3$, отримаємо:

\[\frac(3)(72)=\frac(3:3)(72:3)=\frac(1)(24)\]

Коротке рішення:

\[\frac(3)(8)\cdot \frac(1)(9)=\frac(3\cdot 1)(8\cdot 9)=\frac(3)(72)=\frac(1) (24) \]

Відповідь:$\frac(1)(24).$

При множенні дробів скорочувати чисельники та знаменники можна до знаходження їх твору. При цьому чисельник і знаменник дробу розкладається на прості множники, після чого скорочуються множники, що повторюються, і знаходиться результат.

Приклад 3

Обчислити добуток дробів $ frac (6) (75) $ і $ frac (15) (24) $.

Рішення.

Скористаємося формулою множення звичайних дробів:

\[\frac(6)(75)\cdot \frac(15)(24)=\frac(6\cdot 15)(75\cdot 24)\]

Очевидно, що в чисельнику і знаменнику є числа, які можна попарно скоротити на числа $2$, $3$ і $5$. Розкладемо чисельник і знаменник на прості множники і зробимо скорочення:

\[\frac(6\cdot 15)(75\cdot 24)=\frac(2\cdot 3\cdot 3\cdot 5)(3\cdot 5\cdot 5\cdot 2\cdot 2\cdot 2\cdot 3)=\frac(1)(5\cdot 2\cdot 2)=\frac(1)(20)\]

Відповідь:$\frac(1)(20).$

При множенні дробів можна застосовувати переміщувальний закон:

Розмноження звичайного дробу на натуральне число

Правило множення звичайного дробу на натуральне число:

Результатом множення дробу на натуральне число є дріб, у якого чисельник дорівнює добутку чисельника дробу, що множиться на натуральне число, а знаменник дорівнює знаменнику дробу, що множиться:

де $ \ frac (a) (b) $ - звичайний дріб, $ n $ - натуральне число.

Приклад 4

Виконати множення дробу $\frac(3)(17)$ на $4$.

Рішення.

Скористаємося правилом множення звичайного дробу на натуральне число:

\[\frac(3)(17)\cdot 4=\frac(3\cdot 4)(17)=\frac(12)(17)\]

Відповідь:$\frac(12)(17).$

Не слід забувати про перевірку результату множення на скоротність дробу або на неправильний дріб.

Приклад 5

Помножити дріб $\frac(7)(15)$ на число $3$.

Рішення.

Скористаємося формулою множення дробу на натуральне число:

\[\frac(7)(15)\cdot 3=\frac(7\cdot 3)(15)=\frac(21)(15)\]

За ознакою розподілу на число $3$) можна визначити, що отриманий дріб можна скоротити:

\[\frac(21)(15)=\frac(21:3)(15:3)=\frac(7)(5)\]

В результаті отримали неправильний дріб. Виділимо цілу частину:

\[\frac(7)(5)=1\frac(2)(5)\]

Коротке рішення:

\[\frac(7)(15)\cdot 3=\frac(7\cdot 3)(15)=\frac(21)(15)=\frac(7)(5)=1\frac(2) (5)\]

Скоротити дроби також можна було заміною чисел у чисельнику та знаменнику на їх розкладання на прості множники. У такому разі рішення можна було записати так:

\[\frac(7)(15)\cdot 3=\frac(7\cdot 3)(15)=\frac(7\cdot 3)(3\cdot 5)=\frac(7)(5)= 1\frac(2)(5)\]

Відповідь:$1\frac(2)(5).$

При множенні дробу на натуральне число можна використовувати закон:

Розподіл звичайних дробів

Операція поділу є зворотною до множення і результатом її є дріб, на який потрібно помножити відомий дріб, щоб отримати відомий добуток двох дробів.

Поділ двох звичайних дробів

Правило поділу звичайних дробів:Очевидно, що чисельник і знаменник отриманого дробу можна розкласти на прості множники і скоротити:

\[\frac(8\cdot 35)(15\cdot 12)=\frac(2\cdot 2\cdot 2\cdot 5\cdot 7)(3\cdot 5\cdot 2\cdot 2\cdot 3)= \frac(2\cdot 7)(3\cdot 3)=\frac(14)(9)\]

В результаті отримали неправильний дріб, з якого виділимо цілу частину:

\[\frac(14)(9)=1\frac(5)(9)\]

Відповідь:$1\frac(5)(9).$

§ 87. Додавання дробів.

Додавання дробів має багато подібності зі складанням цілих чисел. Додавання дробів є дія, що полягає в тому, що декілька даних чисел (доданків) з'єднуються в одне число (суму), що містить у собі всі одиниці та частки одиниць доданків.

Ми послідовно розглянемо три випадки:

1. Додавання дробів з однаковими знаменниками.
2. Додавання дробів з різними знаменниками.
3. Додавання змішаних чисел.

1. Додавання дробів з однаковими знаменниками.

Розглянемо приклад: 1/5 + 2/5.

Візьмемо відрізок АВ (рис. 17), приймемо його за одиницю і розділимо на 5 рівних частин, тоді частина АС цього відрізка дорівнюватиме 1 / 5 відрізка АВ, а частина того ж відрізка CD дорівнюватиме 2 / 5 АВ.

З креслення видно, що й узяти відрізок AD, він дорівнюватиме 3 / 5 АВ; Проте відрізок AD таки є сума відрізків АС і CD. Отже, можна записати:

1 / 5 + 2 / 5 = 3 / 5

Розглядаючи дані доданку та отриману суму, бачимо, що чисельник суми вийшов від складання чисельників доданків, а знаменник залишився без зміни.

Звідси отримуємо таке правило: щоб скласти дроби з однаковими знаменниками, треба скласти їх чисельники та залишити той самий знаменник.

Розглянемо приклад:

2. Додавання дробів з різними знаменниками.

Складемо дроби: 3/4 + 3/8 Попередньо їх потрібно привести до найменшого спільного знаменника:

Проміжне ланка 6/8 + 3/8 можна було б і не писати; ми написали його тут для більшої ясності.

Таким чином, щоб скласти дроби з різними знаменниками, потрібно заздалегідь привести їх до найменшого спільного знаменника, скласти їх чисельники та підписати спільний знаменник.

Розглянемо приклад (додаткові множники писатимемо над відповідними дробами):

3. Додавання змішаних чисел.

Складемо числа: 2 3/8 + 3 5/6 .

Наведемо спочатку дрібні частини наших чисел до спільного знаменника і знову їх перепишемо:

Тепер складемо послідовно цілі та дробові частини:

§ 88. Віднімання дробів.

Віднімання дробів визначається так само, як і віднімання цілих чисел. Це є дію, з допомогою якого з цієї сумі двох доданків і одному їх перебуває інше доданок. Розглянемо послідовно три випадки:

1. Віднімання дробів з однаковими знаменниками.
2. Віднімання дробів із різними знаменниками.
3. Віднімання змішаних чисел.

1. Віднімання дробів з однаковими знаменниками.

Розглянемо приклад:

13 / 15 - 4 / 15

Візьмемо відрізок АВ (рис. 18), приймемо його за одиницю та розділимо на 15 рівних частин; тоді частина АС цього відрізка буде 1/15 від АВ, а частина AD того ж відрізка буде відповідати 13/15 AB. Відкладемо ще відрізок ED, що дорівнює 4/15 АВ.

Нам потрібно відняти з 13/15 дріб 4/15. На кресленні це означає, що від відрізка AD потрібно відібрати відрізок ED. В результаті залишиться відрізок AЕ, який становить 9/15 відрізка АВ. Отже, ми можемо написати:

Зроблений нами приклад показує, що чисельник різниці вийшов від віднімання чисельників, а знаменник залишився той самий.

Отже, щоб зробити віднімання дробів з однаковими знаменниками, потрібно відняти чисельник віднімається з чисельника зменшуваного і залишити колишній знаменник.

2. Віднімання дробів із різними знаменниками.

приклад. 3/4 - 5/8

Попередньо приведемо ці дроби до найменшого спільного знаменника:

Проміжна ланка 6/8 - 5/8 написана тут для більшої ясності, але її можна надалі пропускати.

Таким чином, щоб відняти дріб з дробу, потрібно попередньо привести їх до найменшого спільного знаменника, потім від чисельника зменшуваного відняти чисельник віднімається і під їх різницею підписати спільний знаменник.

Розглянемо приклад:

3. Віднімання змішаних чисел.

приклад. 10 3/4-7 2/3.

Наведемо дробові частини зменшуваного і віднімається до найменшого спільного знаменника:

Ми відняли ціле з цілого та дріб із дробу. Але бувають випадки, коли дробова частина віднімається більше дробової частини зменшуваного. У разі потрібно взяти одну одиницю з цілої частини зменшуваного, роздробити їх у ті частки, у яких виражена дробова частина, і додати до дробової частини зменшуваного. А потім віднімання виконуватиметься так само, як і в попередньому прикладі:

§ 89. Множення дробів.

При вивченні множення дробів ми розглядатимемо такі питання:

1. Розмноження дробу на ціле число.
2. Знаходження дробу цього числа.
3. Множення цілого числа на дріб.
4. Розмноження дробу на дріб.
5. Збільшення змішаних чисел.
6. Поняття про відсоток.
7. Знаходження відсотків цього числа. Розглянемо їх послідовно.

1. Розмноження дробу на ціле число.

Множення дробу на ціле число має той самий сенс, що й множення цілого числа на ціле. Помножити дріб (множинне) на ціле число (множник) - означає скласти суму однакових доданків, в якій кожен доданок дорівнює множині, а число доданків дорівнює множнику.

Значить, якщо потрібно 1/9 помножити на 7, то це можна виконати так:

Ми легко отримали результат, оскільки дія звелася до додавання дробів з однаковими знаменниками. Отже,

Розгляд цієї дії показує, що множення дробу на ціле число рівносильне збільшенню цього дробу в стільки разів, скільки одиниць міститься в цілому. Оскільки збільшення дробу досягається або шляхом збільшення її чисельника

або шляхом зменшення її знаменника ,то ми можемо або помножити чисельник ціле, або розділити нею знаменник, якщо таке розподіл можливо.

Звідси отримуємо правило:

Щоб помножити дріб на ціле число, потрібно помножити на це ціле число чисельник і залишити той самий знаменник або, якщо можливо, розділити на це число знаменник, залишивши без змін чисельник.

При множенні можливі скорочення, наприклад:

2. Знаходження дробу цього числа.Існує безліч завдань, при вирішенні яких доводиться знаходити або обчислювати частину даного числа. Відмінність цих завдань від інших полягає в тому, що в них дається кількість яких-небудь предметів або одиниць виміру і потрібно знайти частину цього числа, яка тут же вказується певним дробом. Для полегшення розуміння ми спочатку наведемо приклади таких завдань, а потім познайомимо із способом їх вирішення.

Завдання 1.У мене було 60 руб.; 1/3 цих грошей я витратив на купівлю книг. Скільки коштували книжки?

Завдання 2.Поїзд має пройти відстань між містами А та В, що дорівнює 300 км. Він уже пройшов 2/3 цієї відстані. Скільки це кілометрів?

Завдання 3.У селі 400 будинків, з них 3/4 цегляних, решта дерев'яних. Скільки всього цегляних будинків?

Ось деякі з тих численних завдань на знаходження частини від цієї кількості, з якими нам доводиться зустрічатися. Їх зазвичай називають завданнями знаходження дробу даного числа.

Розв'язання задачі 1.З 60 руб. я витратив на книги 1/3; Отже, для знаходження вартості книг потрібно число 60 розділити на 3:

Розв'язання задачі 2.Сенс завдання полягає в тому, що потрібно знайти 2/3 від 300 км. Обчислимо спочатку 1/3 від 300; це досягається за допомогою розподілу 300 км на 3:

300: 3 = 100 (це 1/3 від 300).

Для знаходження двох третин від 300 потрібно отримане приватне збільшити вдвічі, тобто помножити на 2:

100 х 2 = 200 (це 2/3 від 300).

Розв'язання задачі 3.Тут потрібно визначити кількість цегляних будинків, які становлять 3/4 від 400. Знайдемо спочатку 1/4 від 400,

400: 4 = 100 (це 1/4 від 400).

Для обчислення трьох чвертей від 400 отримане приватне потрібно збільшити втричі, тобто помножити на 3:

100 х 3 = 300 (це 3/4 від 400).

З вирішення цих завдань ми можемо вивести таке правило:

Щоб знайти величину дробу від даного числа, потрібно розділити це число на знаменник дробу та отримане приватне помножити на його чисельник.

3. Множення цілого числа на дріб.

Раніше (§ 26) було встановлено, що множення цілих чисел потрібно розуміти як додавання однакових доданків (5 x 4 = 5+5 +5+5 = 20). У цьому параграфі (пункт 1) було встановлено, що помножити дріб на ціле число - це означає знайти суму однакових доданків, що дорівнює цьому дробу.

В обох випадках множення полягало у знаходженні суми однакових доданків.

Тепер ми переходимо до множення цілого числа на дріб. Тут ми зустрінемося з таким, наприклад, множенням: 9 2/3 . Цілком очевидно, що колишнє визначення множення не підходить до цієї нагоди. Це видно з того, що ми не можемо таке множення замінити додаванням рівних між собою чисел.

Через це нам доведеться дати нове визначення множення, тобто, іншими словами, відповісти на питання, що слід розуміти під множенням на дріб, як треба розуміти цю дію.

Сенс множення цілого числа на дріб з'ясовується з наступного визначення: помножити ціле число (множинне) на дріб (множник) - значить знайти цей дріб множимого.

Саме, помножити 9 на 2/3 – значить знайти 2/3 від дев'яти одиниць. У попередньому пункті вирішувалися такі завдання; тому легко збагнути, що в нас в результаті вийде 6.

Але тепер виникає цікаве та важливе питання: чому такі на перший погляд різні дії, як знаходження суми рівних чисел і знаходження дробу числа, в арифметиці називаються одним і тим же словом «множення»?

Відбувається це тому, що колишня дія (повторення числа доданків кілька разів) та нова дія (знаходження дробу числа) дають відповідь на однорідні питання. Отже, ми виходимо з тих міркувань, що однорідні питання чи завдання вирішуються однією й тією ж дією.

Щоб це зрозуміти, розглянемо таке завдання: «1 м сукна коштує 50 руб. Скільки буде коштувати 4 м такого сукна?

Це завдання вирішується множенням числа рублів (50) на число метрів (4), тобто 50 х 4 = 200 (руб.).

Візьмемо таке саме завдання, але в ній кількість сукна буде виражена дробовим числом: «1 м сукна коштує 50 руб. Скільки буде коштувати 3/4 м такого сукна?

Це завдання теж потрібно вирішувати множенням числа рублів (50) на число метрів (3/4).

Можна ще кілька разів, не змінюючи сенсу завдання, змінити у ній числа, наприклад взяти 9 / 10 м або 2 3 / 10 м тощо.

Так як ці завдання мають один і той же зміст і відрізняються тільки числами, то ми називаємо дії, які застосовуються при їх вирішенні, одним і тим самим словом - множення.

Як виконується множення цілого числа на дріб?

Візьмемо числа, що зустрілися в останній задачі:

Відповідно до визначення ми повинні знайти 3/4 від 50. Знайдемо спочатку 1/4 від 50, а потім 3/4.

1/4 числа 50 становить 50/4;

3/4 числа 50 становлять.

Отже.

Розглянемо ще один приклад: 12 5/8 = ?

1/8 числа 12 складає 12/8,

5/8 числа 12 становлять.

Отже,

Звідси отримуємо правило:

Щоб помножити ціле число на дріб, треба помножити ціле число на чисельник дробу і цей твір зробити чисельником, а знаменником підписати знаменник даного дробу.

Запишемо це правило за допомогою букв:

Щоб це правило стало зрозумілим, слід пам'ятати, що дріб можна розглядати як приватне. Тому знайдене правило корисно порівняти з правилом множення числа на приватне, викладене в § 38

Необхідно пам'ятати, що перш ніж виконувати множення, слід робити (якщо можливо) скорочення, наприклад:

4. Розмноження дробу на дріб.Множення дробу на дріб має той самий сенс, що і множення цілого числа на дріб, тобто при множенні дробу на дріб потрібно від першого дробу (множини) знайти дріб, що стоїть у множнику.

Саме, помножити 3/4 на 1/2 (половину) – це означає знайти половину від 3/4.

Як виконується множення дробу на дріб?

Візьмемо приклад: 3/4 помножити на 5/7. Це означає, що потрібно знайти 5/7 від 3/4. Знайдемо спочатку 1/7 від 3/4, а потім 5/7

1/7 числа 3/4 висловиться так:

5/7 числа 3/4 виразиться так:

Таким чином,

Ще приклад: 5/8 помножити на 4/9.

1/9 числа 5/8 складає,

4/9 числа 5/8 становлять.

Таким чином,

З розгляду цих прикладів можна вивести таке правило:

Щоб помножити дріб на дріб, потрібно помножити чисельник на чисельник, а знаменник – на знаменник і перший твір зробити чисельником, а другий – знаменником твору.

Це правило у загальному вигляді можна записати так:

При множенні необхідно робити (якщо можливо) скорочення. Розглянемо приклади:

5. Збільшення змішаних чисел.Оскільки змішані числа можуть бути замінені неправильними дробами, то цією обставиною зазвичай користуються при множенні змішаних чисел. Це означає, що у випадках, коли множимое, чи множник, чи обидва сомножителя виражені змішаними числами, їх замінюють неправильними дробами. Перемножимо, наприклад, змішані числа: 2 1/2 та 3 1/5 . Звернімо кожне з них у неправильний дріб і потім перемножуватимемо отримані дроби за правилом множення дробу на дріб:

Правило.Щоб перемножити змішані числа, потрібно попередньо звернути їх у неправильні дроби і потім перемножити за правилом множення дробу на дріб.

Примітка.Якщо один із співмножників - ціле число, то множення може бути виконане на підставі розподільчого закону так:

6. Поняття про відсоток.При вирішенні завдань та при виконанні різних практичних розрахунків ми користуємось різноманітними дробами. Але треба мати на увазі, що багато величин допускають не будь-які, а природні для них підрозділи. Наприклад, можна взяти одну соту (1/100) рубля, це буде копійка, дві сотих – це 2 коп., три сотих – 3 коп. Можна взяти 1/10 рубля, це буде "10 коп., або гривеньник. Можна взяти чверть рубля, тобто 25 коп., половину рубля, тобто 50 коп. (полтинник). Але практично не беруть, наприклад 2 / 7 рубля тому, що рубль на сьомі частки не ділиться.

Одиниця виміру ваги, тобто кілограм, допускає насамперед десяткові підрозділи, наприклад 1/10 кг, або 100 г. А такі частки кілограма, як 1/6, 1/11, 1/13 невживані.

Загалом наші (метричні) заходи є десятковими та допускають десяткові підрозділи.

Однак треба зауважити, що вкрай корисно та зручно у найрізноманітніших випадках користуватися однаковим (одноманітним) способом підрозділу величин. Багаторічний досвід показав, що таким поділом, що добре виправдав себе, є «сотенний» поділ. Розглянемо кілька прикладів, що стосуються найрізноманітніших галузей людської практики.

1. Ціна на книги знизилася на 12/100 колишньої ціни.

приклад. Колишня ціна книги 10 руб. Вона знизилася на 1 карбованець. 20 коп.

2. Ощадні каси виплачують протягом року вкладникам 2/100 суми, яка покладена на заощадження.

приклад. У касу належить 500 крб., дохід із цієї суми протягом року становить 10 крб.

3. Число випускників однієї школи становило 5/100 від загальної кількості учнів.

П р і м е р. У школі навчалося всього 1200 учнів, з них закінчили школу 60 осіб.

Сота частина числа називається відсотком.

Слово «відсоток» запозичене з латинської мови та її корінь «цент» означає сто. Разом із прийменником (pro centum) це слово означає «за сотню». Сенс такого висловлювання випливає з тієї обставини, що спочатку у Стародавньому Римі відсотками називалися гроші, які платив боржник позикодавцю «за сотню». Слово «цент» чується у таких усім знайомих словах: центнер (сто кілограмів), центиметр (говориться сантиметр).

Наприклад, замість того, щоб говорити, що завод за місяць, що минув, дав шлюбу 1/100 від усієї виробленої ним продукції, ми говоритимемо так: завод за минулий місяць дав один відсоток шлюбу. Замість того, щоб говорити: завод виробив продукції на 4/100 більше встановленого плану, ми говоритимемо: завод перевиконав план на 4 відсотки.

Викладені вище приклади можна висловити інакше:

1. Ціна на книги знизилася на 12 відсотків колишньої ціни.

2. Ощадні каси виплачують вкладникам протягом року 2 відсотки із суми, покладеної заощадження.

3. Кількість випускників однієї школи становила 5 відсотків числа всіх учнів школи.

Для скорочення листа прийнято замість слова відсоток писати значок %.

Однак слід пам'ятати, що у обчисленнях значок % зазвичай не пишеться, він може бути записаний в умові завдання та в остаточному результаті. При виконанні обчислень потрібно писати дріб зі знаменником 100 замість цілого числа з цим значком.

Потрібно вміти замінювати ціле число із зазначеним значком дробом із знаменником 100:

Назад, потрібно звикнути замість дробу зі знаменником 100 писати ціле число із зазначеним значком:

7. Знаходження відсотків цього числа.

Завдання 1.Школа здобула 200 куб. м дров, причому березові дрова становили 30%. Скільки було березових дров?

Сенс цього завдання полягає в тому, що березові дрова становили лише частину тих дров, які були доставлені до школи, і ця частина виражається дробом 30/100. Отже, маємо завдання знаходження дробу від числа. Для її вирішення ми повинні 200 помножити на 30/100 (завдання на знаходження дробу числа вирішуються множенням числа на дріб.).

Отже, 30% від 200 дорівнюють 60.

Дроб 30 / 100 , що зустрічалася у цій задачі, допускає скорочення на 10. Можна було б від початку виконати це скорочення; розв'язання завдання від цього не змінилося б.

Завдання 2.У таборі було 300 дітей різного віку. Діти 11 років становили 21%, діти 12 років становили 61% та, нарешті, 13-річних дітей було 18%. Скільки було дітей кожного віку у таборі?

У цьому вся завдання потрібно виконати три обчислення, т. е. послідовно знайти число дітей 11 років, потім 12 років і, нарешті, 13 років.

Отже, тут потрібно буде тричі знайти дріб від числа. Зробимо це:

1) Скільки було дітей 11-річного віку?

2) Скільки було дітей 12-річного віку?

3) Скільки було дітей 13-річного віку?

Після розв'язання задачі корисно скласти знайдені числа; сума їх повинна становити 300:

63 + 183 + 54 = 300

Слід також звернути увагу, що сума відсотків, даних за умови завдання, становить 100:

21% + 61% + 18% = 100%

Це свідчить про те, що загальна кількість дітей, які перебували у таборі, було прийнято за 100%.

3 а да ч а 3.Робітник отримав протягом місяця 1 200 крб. З них 65% він витратив на харчування, 6% - на квартиру та опалення, 4% - на газ, електрику та радіо, 10% - на культурні потреби та 15% - зберіг. Скільки грошей витрачено на потреби, що вказані в задачі?

Для вирішення цього завдання потрібно 5 разів знайти дріб від числа 1200. Зробимо це.

1) Скільки грошей витрачено на харчування? У задачі сказано, що ця витрата становить 65% від усього заробітку, тобто 65/100 від числа 1200. Зробимо обчислення:

2) Скільки грошей сплачено за квартиру з опаленням? Розмірковуючи подібно до попереднього, ми прийдемо до наступного обчислення:

3) Скільки грошей сплатили за газ, електрику та радіо?

4) Скільки грошей витрачено на культурні потреби?

5) Скільки грошей робітник зберіг?

Для перевірки корисно скласти числа, знайдені у цих 5 питаннях. Сума повинна становити 1 200 руб. Весь заробіток прийнято за 100%, що легко перевірити, склавши числа відсотків, дані за умови завдання.

Ми вирішили три завдання. Незважаючи на те, що в цих завданнях йшлося про різні речі (доставка дров для школи, кількість дітей різного віку, витрати робітника), вони вирішувалися одним і тим же способом. Це сталося тому, що у всіх завданнях потрібно було знайти кілька відсотків даних чисел.

§ 90. Розподіл дробів.

При вивченні поділу дробів ми розглядатимемо такі питання:

1. Розподіл цілого числа на ціле.
2. Розподіл дробу на ціле число
3. Розподіл цілого числа на дріб.
4. Розподіл дробу на дріб.
5. Розподіл змішаних чисел.
6. Знаходження числа з даного його дробу.
7. Знаходження числа за його відсотками.

Розглянемо їх послідовно.

1. Розподіл цілого числа на ціле.

Як було зазначено у відділі цілих чисел, розподілом називається дія, яка полягає в тому, що за даним твором двох співмножників (ділимому) та одному з цих співмножників (ділителю) знаходиться інший співмножник.

Розподіл цілого числа на ціле ми розглядали у відділі цілих чисел. Ми зустріли там два випадки поділу: поділ без залишку, або «націло» (150: 10 = 15), і поділ із залишком (100: 9 = 11 і 1 у залишку). Ми можемо, отже, сказати, що у області цілих чисел точне розподіл який завжди можливе, оскільки ділене який завжди є твором дільника ціле число. Після введення множення на дріб ми можемо всякий випадок поділу цілих чисел вважати за можливе (виключається тільки поділ на нуль).

Наприклад, розділити 7 на 12 - це означає знайти таке число, добуток якого на 12 було б 7. Таким числом є дріб 7/12 тому що 7/12 12 =7. Ще приклад: 14: 25 = 14/25, тому що 14/25 25 = 14.

Таким чином, щоб розділити ціле число на ціле, потрібно скласти дріб, чисельник якого дорівнює ділимому, а знаменник - дільнику.

2. Розподіл дробу на ціле число.

Розділити дріб 6/7 на 3. Відповідно до цього вище визначення розподілу ми маємо тут добуток (6/7) та один із співмножників (3); потрібно знайти такий другий співмножник, який від множення на 3 дав би цей твір 6/7. Очевидно, він має бути втричі меншим від цього твору. Отже, поставлене перед нами завдання полягало в тому, щоб дріб 6/7 зменшити у 3 рази.

Ми вже знаємо, що зменшення дробу можна виконати або шляхом зменшення його чисельника, або шляхом збільшення його знаменника. Тому можна написати:

В даному випадку чисельник 6 ділиться на 3 тому слід зменшити в 3 рази чисельник.

Візьмемо інший приклад: 5/8 розділити на 2. Тут чисельник 5 не ділиться націло на 2, отже, на це число доведеться помножити знаменник:

На підставі цього можна висловити правило: щоб розділити дріб на ціле число, потрібно розділити на це ціле число чисельник дробу(якщо це можливо), залишивши той же знаменник, або помножити на це число знаменник дробу, залишивши той самий чисельник.

3. Розподіл цілого числа на дріб.

Нехай потрібно розділити 5 на 1/2, тобто знайти таке число, яке після множення на 1/2 дасть твір 5. Очевидно, це число має бути більше 5, тому що 1/2 є правильний дріб, а при множенні числа на правильний дріб твір має бути меншим від множиного. Щоб це було зрозуміліше, запишемо наші дії так: 5: 1 / 2 = х , Отже, х 1 / 2 = 5.

Ми повинні знайти таке число х , яке, будучи помножено на 1/2, дало б 5. Так як помножити деяке число на 1/2 - це означає знайти 1/2 цього числа, то, отже, 1/2 невідомого числа х дорівнює 5, а все число х удвічі більше, тобто 52 = 10.

Таким чином, 5: 1/2 = 5 2 = 10

Перевіримо:

Розглянемо ще один приклад. Нехай потрібно розділити 6 на 2/3. Спробуємо спочатку знайти потрібний результат за допомогою креслення (рис. 19).

Рис.19

Зобразимо відрізок АВ, рівний 6 якимось одиницям, і розділимо кожну одиницю на 3 рівні частини. У кожній одиниці три третини (3/3) у всьому відрізку АВ у 6 разів більше,т. е. 18/3. З'єднаємо за допомогою маленьких дужок 18 отриманих відрізків по 2; вийде лише 9 відрізків. Значить дріб 2/3 міститься в б одиницях 9 разів, або, іншими словами, дріб 2/3 у 9 разів менший за 6 цілих одиниць. Отже,

Як отримати цей результат без креслення за допомогою одних лише обчислень? Будемо міркувати так: потрібно 6 розділити на 2/3, тобто потрібно відповісти на запитання, скільки разів 2/3 містяться у 6. Дізнаємося спочатку: скільки разів 1/3 міститься у 6? У цілій одиниці - 3 третини, а у 6 одиницях - у 6 разів більше, тобто 18 третин; для знаходження цього числа ми повинні 6 помножити на 3. Значить, 1 / 3 міститься в б одиницях 18 разів, а 2 / 3 містяться в б не 18 разів, а вдвічі менше разів, тобто 18: 2 = 9. Отже , при розподілі 6 на 2/3 ми виконали такі дії:

Звідси отримуємо правило розподілу цілого числа на дріб. Щоб розділити ціле число на дріб, треба це ціле число помножити на знаменник даного дробу і, зробивши цей добуток чисельником, розділити його на чисельник цього дробу.

Запишемо правило за допомогою букв:

Щоб це правило стало зрозумілим, слід пам'ятати, що дріб можна розглядати як приватне. Тому знайдене правило корисно порівняти з правилом розподілу числа на приватне, що було викладено у § 38. Зверніть увагу на те, що там була отримана така сама формула.

При розподілі можливі скорочення, наприклад:

4. Розподіл дробу на дріб.

Нехай потрібно розділити 3/4 на 3/8. Що позначатиме число, яке вийде в результаті розподілу? Воно даватиме відповідь на запитання, скільки разів дроб 3/8 міститься в дробі 3/4. Щоб розібратися у цьому питанні, зробимо креслення (рис. 20).

Візьмемо відрізок АВ, приймемо його за одиницю, розділимо на 4 рівні частини та відзначимо 3 такі частини. Відрізок АС дорівнюватиме 3/4 відрізка АВ. Розділимо тепер кожен із чотирьох початкових відрізків навпіл, тоді відрізок АВ розділиться на 8 рівних частин і кожна така частина дорівнюватиме 1/8 відрізка АВ. З'єднаємо дугами по 3 таких відрізки, тоді кожен з відрізків AD і DC дорівнюватиме 3/8 відрізка АВ. Креслення показує, що відрізок, рівний 3 / 8 міститься у відрізку, рівному 3 / 4 , рівно 2 рази; значить, результат поділу можна записати так:

3 / 4: 3 / 8 = 2

Розглянемо ще один приклад. Нехай потрібно розділити 15/16 на 3/32:

Ми можемо міркувати так: потрібно знайти таке число, яке після множення на 3/32 дасть твір, що дорівнює 15/16 . Запишемо обчислення так:

15 / 16: 3 / 32 = х

3 / 32 х = 15 / 16

3 / 32 невідомого числа х становлять 15 / 16

1/32 невідомого числа х складає ,

32 / 32 числа х складають.

Отже,

Таким чином, щоб розділити дріб на дріб, потрібно чисельник першого дробу помножити на знаменник другого, а знаменник першого дробу помножити на чисельник другий і перший добуток чисельником, а другий - знаменником.

Запишемо правило за допомогою букв:

При розподілі можливі скорочення, наприклад:

5. Розподіл змішаних чисел.

При розподілі змішаних чисел їх потрібно попередньо перетворювати на неправильні дроби, а потім робити розподіл отриманих дробів за правилами розподілу дробових чисел. Розглянемо приклад:

Обернемо змішані числа в неправильні дроби:

Тепер розділимо:

Таким чином, щоб розділити змішані числа, потрібно звернути їх до неправильних дробів і потім розділити за правилом поділу дробів.

6. Знаходження числа з даного його дробу.

Серед різних завдань на дроби іноді зустрічаються такі, в яких дається величина якогось дробу невідомого числа і потрібно знайти це число. Цього типу завдання будуть оберненими по відношенню до завдань на знаходження дробу даного числа; там давалося число і потрібно знайти деяку дріб від цього числа, тут дається дріб від числа і потрібно знайти саме це число. Ця думка стане ще зрозумілішою, якщо ми звернемося до вирішення такого типу завдань.

Завдання 1.У перший день шибки склали 50 вікон, що складає 1/3 всіх вікон збудованого будинку. Скільки всього вікон у цьому будинку?

Рішення.У задачі сказано, що засклені 50 вікон становлять 1/3 всіх вікон будинку, отже, всього вікон у 3 рази більше, тобто.

У будинку було 150 вікон.

Завдання 2.Магазин продав 1500 кг борошна, що становить 3/8 всього запасу борошна, що був у магазині. Яким був початковий запас борошна у магазині?

Рішення.З умови завдання видно, що продані 1500 кг борошна складають 3/8 всього запасу; значить, 1/8 цього запасу буде в 3 рази менше, тобто для її обчислення потрібно 1500 зменшити у 3 рази:

1500: 3 = 500 (це 1/8 запасу).

Очевидно, весь запас буде у 8 разів більшим. Отже,

500 8 = 4000 (кг).

Початковий запас борошна в магазині дорівнював 4 000 кг.

З розгляду цього завдання можна вивести таке правило.

Щоб знайти число за даною величиною його дробу, достатньо розділити цю величину на чисельник дробу і результат помножити на знаменник дробу.

Ми вирішили дві задачі на знаходження числа з даного дробу. Такі завдання, як це особливо добре видно з останньої, вирішуються двома діями: розподілом (коли знаходять одну частину) та множенням (коли знаходять все число).

Однак після того, як ми вивчили поділ дробів, зазначені вище завдання можна вирішувати однією дією, а саме: поділом на дріб.

Наприклад, остання задача може бути вирішена однією дією так:

Надалі завдання на перебування числа з його дробу ми вирішуватимемо однією дією - поділом.

7. Знаходження числа за його відсотками.

У цих завданнях потрібно буде знайти число, знаючи кілька відсотків цього числа.

Завдання 1.На початку поточного року я отримав у ощадній касі 60 руб. доходу із суми, покладеної мною на заощадження рік тому. Скільки грошей я поклав до ощадної каси? (Каси дають вкладникам 2% доходу на рік.)

Сенс завдання полягає в тому, що деяка сума грошей була покладена мною до ощадної каси і пролежала там рік. Через рік я отримав з неї 60 руб. доходу, що становить 2/100 тих грошей, які я поклав. Скільки грошей я поклав?

Отже, знаючи частину цих грошей, виражену двома способами (у рублях і дробом), ми повинні знайти всю поки що невідому суму. Це звичайне завдання на знаходження числа з даного його дробу. Вирішуються такі завдання розподілом:

Отже, в ощадну касу було покладено 3000 крб.

Завдання 2.Рибалки за два тижні виконали місячний план на 64%, заготовивши 512 т риби. Який мали план?

З умови завдання відомо, що рибалки виконали частину плану. Ця частина дорівнює 512 т, що становить 64% від плану. Скільки тонн риби потрібно заготовити за планом, нам невідомо. У знаходженні цього числа і полягатиме розв'язання задачі.

Такі завдання вирішуються поділом:

Отже, за планом потрібно заготовити 800 тонн риби.

Завдання 3.Потяг йшов із Риги до Москви. Коли він пройшов 276-й кілометр, один із пасажирів запитав кондуктора, який проходить, яку частину шляху вони вже проїхали. На це кондуктор відповів: «Проїхали вже 30% усього шляху». Яка відстань від Риги до Москви?

З умови завдання видно, що 30% шляху від Риги до Москви становлять 276 км. Нам потрібно знайти всю відстань між цими містами, тобто по цій частині знайти ціле:

§ 91. Взаємно обернені числа. Заміна поділу множенням.

Візьмемо дріб 2/3 і переставимо чисельник на місце знаменника, вийде 3/2. Ми отримали дріб, протилежний даній.

Щоб отримати дріб, зворотний даної, потрібно її чисельник поставити місце знаменника, а знаменник - місце чисельника. Цим способом ми можемо отримати дріб, зворотний до будь-якого дробу. Наприклад:

3/4, зворотна 4/3; 5/6, зворотна 6/5

Два дроби, що володіють тією властивістю, що чисельник першої є знаменником другої, а знаменник першої є чисельником другої, називаються взаємно оберненими.

Тепер подумаємо, який дріб буде зворотним для 1/2 . Очевидно, це буде 2 / 1, або просто 2. Знаходячи дріб, зворотний даної, ми отримали ціле число. І цей випадок непоодинокий; навпаки, для всіх дробів з чисельником 1 (одиниця) оберненими будуть цілі числа, наприклад:

1/3, зворотна 3; 1 / 5 , зворотна 5

Так як при відшуканні зворотних дробів ми зустрілися і з цілими числами, то надалі ми говоритимемо не про зворотні дроби, а про зворотні числа.

З'ясуємо, як написати число, обернене до цілого числа. Для дробів це вирішується просто: потрібно знаменник поставити на місце чисельника. Цим самим способом можна отримати зворотне число і для цілого числа, тому що у будь-якого цілого числа можна мати на увазі знаменник 1. Значить, число, зворотне 7, буде 1/7, тому що 7 = 7/1; для числа 10 зворотне буде 1/10, тому що 10 = 10/1

Цю думку можна висловити інакше: число, зворотне даному числу, виходить від розподілу одиниці на дане число. Таке твердження справедливе як цілих чисел, але й дробів. Справді, якщо потрібно написати число, обернене дробу 5/9, то ми можемо взяти 1 і розділити її на 5/9, тобто.

Тепер вкажемо одне властивістьвзаємно зворотних чисел, яке буде нам корисним: добуток взаємно зворотних чисел дорівнює одиниці.Справді:

Користуючись цією властивістю, ми можемо знаходити обернені числа наступним шляхом. Нехай потрібно знайти число, яке зворотне 8.

Позначимо його літерою х тоді 8 х = 1, звідси х = 1/8. Знайдемо ще число, зворотне 7 / 12 позначимо його буквою х , тоді 7 / 12 х = 1, звідси х = 1: 7 / 12 або х = 12 / 7 .

Ми ввели тут поняття про взаємно зворотні числа для того, щоб трохи доповнити відомості про поділ дробів.

Коли ми ділимо число 6 на 3/5, то ми виконуємо такі дії:

Зверніть особливу увагу на вираз і порівняйте його із заданим: .

Якщо взяти вираз окремо, без зв'язку з попереднім, то не можна вирішити питання, звідки воно виникло: від поділу 6 на 3/5 або від множення 6 на 5/3. В обох випадках виходить те саме. Тому ми можемо сказати, що розподіл одного числа інше можна замінити множенням поділеного на число, зворотне дільнику.

Приклади, що ми даємо нижче, цілком підтверджують цей висновок.

ОБІЙ ВЖЕ ЦІ ГРАБЛІ! 🙂

Множення та розподіл дробів.

Увага!
До цієї теми є додаткові
матеріали у розділі 555.
Для тих, хто сильно не дуже. »
І для тих, хто дуже навіть. »)

Ця операція набагато приємніша за складання-віднімання! Бо простіше. Нагадую: щоб помножити дріб на дріб, потрібно перемножити чисельники (це буде чисельник результату) та знаменники (це буде знаменник). Тобто:

Все дуже просто. І, будь ласка, не шукайте спільного знаменника! Не треба його тут…

Щоб розділити дріб на дріб, потрібно перевернути другу(це важливо!) дріб і їх перемножити, тобто:

Якщо трапилося множення чи поділ із цілими числами та дробами – нічого страшного. Як і при додаванні, робимо з цілого числа дріб з одиницею в знаменнику - і вперед! Наприклад:

У старших класах часто доводиться мати справу з триповерховими (або навіть чотириповерховими!) дробами. Наприклад:

Як цей дріб привести до пристойного вигляду? Так, дуже просто! Використовувати поділ через дві точки:

Але не забувайте про порядок розподілу! На відміну від множення, це дуже важливо! Звичайно, 4:2, або 2:4, ми не сплутаємо. А ось у триповерховому дробі легко помилитись. Зверніть увагу, наприклад:

У першому випадку (вираз зліва):

У другому (вираз праворуч):

Відчуваєте різницю? 4 та 1/9!

А чим визначається порядок розподілу? Або дужками, або (як тут) довжиною горизонтальних рис. Розвивайте окомір. А якщо немає ні дужок, ні рисок, типу:

то ділимо-множимо по порядку, зліва направо!

І ще дуже простий та важливий прийом. У діях зі ступенями він вам ох як знадобиться! Поділимо одиницю на будь-який дріб, наприклад, на 13/15:

Дріб перекинувся! І так завжди буває. При розподілі 1 на будь-який дріб, в результаті отримуємо той же дріб, тільки перевернутий.

Ось і всі події з дробами. Річ досить проста, але помилок дає більш ніж достатньо. Візьміть до уваги практичні поради, і їх (помилок) буде менше!

1. Найголовніше при роботі з дрібними виразами - акуратність і уважність! Це не загальні слова, не добрі побажання! Це сувора потреба! Усі обчислення на ЄДІ робіть як повноцінне завдання, зосереджено та чітко. Краще написати два зайві рядки в чернетці, ніж накосячіть при розрахунку в умі.

2. У прикладах із різними видами дробів — переходимо до звичайних дробів.

3. Усі дроби скорочуємо до упору.

4. Багатоповерхові дробові вирази зводимо до звичайних, використовуючи розподіл через дві точки (стежимо за порядком розподілу!).

Ось вам завдання, які потрібно обов'язково вирішувати. Відповіді наведено після всіх завдань. Використовуйте матеріали цієї теми та практичні поради. Накиньте, скільки прикладів ви змогли вирішити правильно. З першого разу! Без калькулятора! І зробіть правильні висновки.

Пам'ятайте - правильна відповідь, отриманий з другого (тим більше – третього) разу – не рахується!Таке суворе життя.

Отже, вирішуємо в режимі іспиту ! Це вже підготовка до ЄДІ, між іншим. Вирішуємо приклад, перевіряємо, вирішуємо наступний. Вирішили все — перевірили знову з першого до останнього. І тільки потімдивимося відповіді.

Шукаємо відповіді, які збігаються із вашими. Я спеціально їх безладно записав, подалі від спокуси, так би мовити. Ось вони, відповіді, через крапку з комою записані.

0; 17/22; 3/4; 2/5; 1; 25.

А тепер робимо висновки. Якщо все вийшло – радий за вас! Елементарні обчислення з дробами – не ваша проблема! Можна зайнятися серйознішими речами. Якщо ні.

Значить у вас одна з двох проблем. Або обидві відразу.) Нестача знань та (або) неуважність. Але. Це розв'язувані проблеми.

У Особливому розділі 555 «Дроби» розібрано всі ці (і не лише!) приклади. З докладними поясненнями, що, навіщо і як. Такий розбір чудово допомагає при нестачі знань та навичок!

Та й з другої проблеми там є дещо.) Цілком практична порада, як стати уважніше. Так Так! Порада, яка може застосувати кожен.

Крім знань та уважності для успіху потрібен певний автоматизм. Де його взяти? Чую важке зітхання ... Так, тільки в практиці, більше ніде.

Можете для тренування зайти на веб-сайт 321start.ru. Там у опції «Спробувати» є 10 прикладів для всіх бажаючих. З миттєвою перевіркою. Для зареєстрованих користувачів – 34 приклади від простих до суворих. Це лише з дробів.

Якщо вам подобається цей сайт.

До речі, у мене є ще кілька цікавих сайтів для Вас.)

Ось тут можна потренуватися у вирішенні прикладів та дізнатися свій рівень. Тестування з миттєвою перевіркою. Вчимося - з інтересом!)

А ось тут можна познайомитися з функціями та похідними.

Правило 1.

Щоб помножити дріб на натуральне число, треба його чисельник помножити на число, а знаменник залишити без зміни.

Правило 2

Щоб помножити дріб на дріб, треба:

1. знайти добуток чисельників та добуток знаменників цих дробів

2. перший твір записати чисельнику, а другий - знаменником.

Правило 3

Для того, щоб виконати множення змішаних чисел, треба записати їх у вигляді неправильних дробів, а потім скористатися правилом множення дробів.

Правило 4

Щоб розділити один дріб в інший, треба ділене помножити число, зворотне дільнику.

приклад 1.

Обчисліть

приклад 2.

Обчисліть

приклад 3.

Обчисліть

приклад 4.

Обчисліть

Математика. Інші матеріали

Зведення числа до раціонального ступеня. (

Зведення числа до натурального ступеня. (

Узагальнений метод інтервалів під час вирішення алгебраїчних нерівностей (Автор Колчанов А.В.)

Метод заміни множників під час вирішення алгебраїчних нерівностей (Автор Колчанов А.В.)

Ознаки ділимості (Лунгу Альона)

Перевір себе на тему 'Умноження і розподіл звичайних дробів'

Розмноження дробів

Розмноження звичайних дробів розглянемо у кількох можливих варіантах.

Розмноження звичайного дробу на дріб

Це найпростіший випадок, у якому потрібно скористатися наступними правилами множення дробів.

Щоб помножити дріб на дріб, Треба:

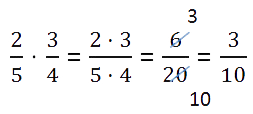
чисельник першого дробу помножити на чисельник другого дробу та його добуток записати до чисельника нового дробу;

знаменник першого дробу помножити на знаменник другого дробу та його добуток записати у знаменник нового дробу;

Перш ніж перемножувати чисельники та знаменники перевірте, чи не можна скоротити дроби. Скорочення дробів при розрахунках значно полегшить ваші обчислення.

Розмноження дробу на натуральне число

Щоб дріб помножити на натуральне числотреба чисельник дробу помножити цього числа, а знаменник дробу залишити без зміни.

Якщо в результаті множення вийшов неправильний дріб, не забудьте перетворити його на змішане число, тобто виділити цілу частину.

Розмноження змішаних чисел

Щоб перемножити змішані числа, треба спочатку перетворити їх на неправильні дроби і після цього помножити за правилом множення звичайних дробів.

Інший спосіб множення дробу на натуральне число

Іноді при розрахунках зручніше скористатися іншим способом множення звичайного дробу на число.

Щоб помножити дріб на натуральне число, потрібно знаменник дробу розділити на це число, а чисельник залишити тим самим.

Як бачимо з прикладу, цим варіантом правила зручніше користуватися, якщо знаменник дробу ділиться без залишку на натуральне число.

Розподіл дробу на число

Як розділити дріб на число найшвидше? Розберемо теорію, зробимо висновок і на прикладах подивимося, як поділ дробу на число можна виконувати за новим коротким правилом.

Зазвичай розподіл дробу на число виконують за правилом розподілу дробів. Перше число (дріб) множимо на число, зворотне другому. Оскільки друге число ціле, зворотне щодо нього число - дріб, чисельник якої дорівнює одиниці, а знаменник - даному числу. Схематично розподіл дробу на натуральне число виглядає так:

Звідси робимо висновок:

щоб розділити дріб на число, треба знаменник помножити на це число, а чисельник залишити тим самим. Правило можна сформулювати ще коротше:

при розподілі дробу на число йде в знаменник.

Виконати розподіл дробу на число:

Щоб розділити дріб на число, чисельник перепишемо без змін, а знаменник помножимо на це число. Скорочуємо 6 та 3 на 3.

При розподілі дробу на число чисельник переписуємо, а знаменник множимо цього числа. Скорочуємо 16 та 24 на 8.

При розподілі дробу на число йде в знаменник, тому чисельник залишаємо таким же, а знаменник множимо на дільник. Скорочуємо 21 та 35 на 7.

Множення та поділ дробів

Минулого разу ми навчилися складати і віднімати дроби (див. урок «Складання та віднімання дробів»). Найбільш складним моментом у тих діях було приведення дробів до спільного знаменника.

Щоб помножити два дроби, треба окремо помножити їх чисельники та знаменники. Перше число буде чисельником нового дробу, а друге – знаменником.

Щоб розділити два дроби, треба перший дріб помножити на «перевернутий» другий.

Завдання. Знайдіть значення виразу:

За визначенням маємо:

Розмноження дробів з цілою частиною та негативних дробів

Плюс мінус дає мінус;
Мінус на мінус дає плюс.

Викреслюємо мінуси парами доти, доки вони повністю не зникнуть. У крайньому випадку, один мінус може вижити – той, якому не знайшлося пари;
Якщо мінусів не залишилося, операція виконана – можна приступати до множення. Якщо ж останній мінус не закреслено, оскільки йому не знайшлося пари, виносимо його за межі множення. Вийде негативний дріб.

Скорочення дробів «на льоту»

У всіх прикладах червоним кольором відзначені числа, які зазнали скорочення, і те, що від них залишилося.

Так робити не можна!

Як бачите, правильна відповідь виявилася не такою гарною. Загалом будьте уважні.

Розподіл дробів.

Розподіл дробу на натуральне число.

Приклади поділу дробу на натуральне число

Розподіл натурального числа на дріб.

Приклади поділу натурального числа на дріб

Розподіл звичайних дробів.

Приклади поділу звичайних дробів

Розподіл змішаних чисел.

перетворити змішані дроби на неправильні;
помножити перший дріб на дріб, зворотний другий;
скоротити отриманий дріб;
якщо вийшов неправильний дріб перетворити неправильний дріб на змішану.

Приклади поділу змішаних чисел

1 1 2: 2 2 3 = 1 · 2 + 1 2: 2 · 3 + 2 3 = 3 2: 8 3 = 3 2 · 3 8 = 3 · 3 2 · 8 = 9 16

2 1 7: 3 5 = 2 · 7 + 1 7: 3 5 = 15 7: 3 5 = 15 7 · 5 3 = 15 · 5 7 · 3 = 5 · 5 7 = 25 7 = 7 · 3 + 4 7 = 3 4 7

Будь-які нецензурні коментарі будуть видалені, а їх автори занесені до чорного списку!

Ласкаво просимо в OnlineMSchool.
Мене звуть Довжик Михайло Вікторович. Я власник і автор цього сайту, мною написаний весь теоретичний матеріал, а також розроблені онлайн-вправи та калькулятори, якими Ви можете скористатися для вивчення математики.

Дроби. Множення та розподіл дробів.

Розмноження звичайного дробу на дріб.

Щоб перемножити звичайні дроби, необхідно помножити чисельник на чисельник (отримаємо чисельник твору) та знаменник на знаменник (отримаємо знаменник твору).

Формула множення дробів:

Перед тим, як приступити до множення чисельників та знаменників, необхідно перевірити можливість скорочення дробу. Якщо вдасться скоротити дріб, то вам легше далі робити розрахунки.

Зверніть увагу! Тут не потрібно шукати спільний знаменник!

Розподіл звичайного дробу на дріб.

Розподіл звичайного дробу на дріб відбувається так: перевертаєте другий дріб (тобто змінюєте чисельник і знаменник місцями) і після цього дроби перемножуються.

Формула поділу звичайних дробів:

Розмноження дробу на натуральне число.

Зверніть увагу!При множенні дробу на натуральне число чисельник дробу множиться на наше натуральне число, а знаменник дробу залишаємо тим самим. Якщо результатом твору виявився неправильний дріб, то обов'язково виділіть цілу частину, перетворивши неправильний дріб на змішаний.

Розподіл дробів за участю натурального числа.

Це не так страшно, як здається. Як і у випадку зі складанням, переводимо ціле число в дріб з одиницею в знаменнику. Наприклад:

Розмноження змішаних дробів.

Правила множення дробів (змішаних):

перетворюємо змішані дроби на неправильні;
перемножуємо чисельники та знаменники дробів;
скорочуємо дріб;
якщо отримали неправильний дріб, то перетворюємо неправильний дріб на змішану.

Зверніть увагу!Щоб помножити змішаний дріб на інший змішаний дріб, потрібно, спершу, привести їх до виду неправильних дробів, а далі помножити за правилом множення звичайних дробів.

Другий спосіб множення дробу на натуральне число.

Буває зручніше використовувати другий спосіб множення звичайного дробу на число.

Зверніть увагу!Для множення дробу на натуральне число необхідно знаменник дробу розділити це число, а чисельник залишити без зміни.

З наведеного вище прикладу зрозуміло, що цей варіант зручніше для використання, коли знаменник дробу ділиться без залишку на натуральне число.

Багатоповерхові дроби.

У старших класах найчастіше зустрічаються триповерхові (або більше) дроби. Приклад:

Щоб привести такий дріб до звичного вигляду, використовують поділ через 2 точки:

Зверніть увагу!У розподілі дробів дуже важливий порядок розподілу. Будьте уважні, тут легко заплутатися.

Зверніть увагу, наприклад:

При поділі одиниці на будь-який дріб, результатом буде той самий дріб, тільки перевернутий:

Практичні поради при множенні та розподілі дробів:

1. Найважливішим у роботі з дробовими виразами є акуратність та уважність. Усі обчислення робіть уважно та акуратно, зосереджено та чітко. Краще запишіть кілька зайвих рядків у чернетці, ніж заплутатися у розрахунках в умі.

2. У завданнях із різними видами дробів — переходьте до виду звичайних дробів.

3. Всі дроби скорочуємо доти, доки скорочувати вже буде неможливо.

4. Багатоповерхові дробові вирази наводимо на вигляд звичайних, користуючись розподілом через 2 точки.

Недо- і не до- Перероблена пісня "Весняне танго" (Приходить час - птахи з півдня прилітають) - муз. Валерій Міляєв Недочув, недозрозумів, недогнав, у сенсі тому, що я не здогадався, всі дієслова не роздільно написав, про приставку недоя не знав. Буває так, […]
Сторінка не знайдена У третьому читанні було прийнято пакет документів Уряду, які передбачають створення спеціальних адміністративних районів (САР). Внаслідок виходу з Євросоюзу, Великобританія не буде включена до Європейської зони ПДВ та […]
Об'єднаний слідчий комітет з'явиться вже восени Об'єднаний слідчий комітет з'явиться вже восени Наслідок усіх силових структур зберуть під одним дахом із четвертої спроби Вже восени 2014-го, за даними «Известий», президент Володимир Путін […]
Патент на алгоритм Як патент на алгоритм виглядає Як патент на алгоритм готується Підготовка технічних описів способів зберігання, обробки, передачі, сигналів та/або даних саме для цілей патентування особливих складнощів зазвичай не представляє, і […]
ЩО ВАЖЛИВО ЗНАТИ ПРО НОВИЙ ЗАКОНОПРОЕКТ ПРО ПЕНСІЇ 12 грудня 1993 року КОНСТИТУЦІЯ РОСІЙСЬКОЇ ФЕДЕРАЦІЇ (з урахуванням поправок, внесених Законами Російської Федерації про поправки до Конституції Російської Федерації від 30.12.2008 N 2, 2008 N . […]
Частинки про пенсію жінці прикольні для ювіляра чоловіки для ювіляра чоловіки - хором для ювіляра жінки - посвята у пенсіонери жінки жартівливі Будуть цікаві конкурси для пенсіонерів Ведучий: Дорогі друзі! Хвилинку уваги! Сенсація! Тільки […]