Tanım
Piramit bir çokgen \(A_1A_2...A_n\) ve \(n\) üçgenlerinden oluşan, ortak bir köşe noktası \(P\) (çokgenin düzleminde yer almayan) ve bunun karşısındaki kenarları olan ve şu şekilde çakışan bir çokyüzlüdür: çokgenin kenarları.
Tanım: \(PA_1A_2...A_n\) .
Örnek: beşgen piramit \(PA_1A_2A_3A_4A_5\) .
Üçgenler \(PA_1A_2, \PA_2A_3\), vb. denir yan yüzler piramitler, segmentler \(PA_1, PA_2\), vb. – yan kaburgalar, çokgen \(A_1A_2A_3A_4A_5\) – temel, nokta \(P\) – tepe.
Yükseklik piramitler, piramidin tepesinden taban düzlemine doğru inen dik bir çizgidir.
Tabanında üçgen bulunan piramite denir dörtyüzlü.
Piramit denir doğru tabanı düzgün bir çokgen ise ve aşağıdaki koşullardan biri karşılanıyorsa:
\((a)\) yanal piramidin kenarları eşit;
\((b)\) piramidin yüksekliği tabanın yakınında çevrelenen dairenin merkezinden geçer;
\((c)\) yan kaburgalar taban düzlemine aynı açıda eğimlidir.
\((D)\) yan yüzler taban düzlemine aynı açıda eğimlidir.
Düzenli tetrahedron tüm yüzleri eşit eşkenar üçgen olan üçgen bir piramittir.
Teorem
\((a), (b), (c), (d)\) koşulları eşdeğerdir.
Kanıt
Piramidin yüksekliğini \(PH\) bulalım. Piramidin tabanının düzlemi \(\alpha\) olsun.

1) \((a)\)'dan \((b)\)'nin çıktığını kanıtlayalım. \(PA_1=PA_2=PA_3=...=PA_n\) olsun.
Çünkü \(PH\perp \alpha\), o zaman \(PH\) bu düzlemde yer alan herhangi bir çizgiye diktir, bu da üçgenlerin dik açılı olduğu anlamına gelir. Bu, bu üçgenlerin ortak kenarı \(PH\) ve hipotenüsün \(PA_1=PA_2=PA_3=...=PA_n\) eşit olduğu anlamına gelir. Bu, \(A_1H=A_2H=...=A_nH\) anlamına gelir. Bu, \(A_1, A_2, ..., A_n\) noktalarının \(H\) noktasından aynı uzaklıkta olduğu anlamına gelir, dolayısıyla \(A_1H\) yarıçapıyla aynı daire üzerinde bulunurlar. Bu daire, tanımı gereği \(A_1A_2...A_n\) çokgeni etrafında çevrelenmiştir.
2) \((b)\)'nin \((c)\) anlamına geldiğini kanıtlayalım.
\(PA_1H, PA_2H, PA_3H,..., PA_nH\) Dikdörtgen ve iki ayak üzerinde eşit. Bu, açılarının da eşit olduğu anlamına gelir, dolayısıyla \(\angle PA_1H=\angle PA_2H=...=\angle PA_nH\).
3) \((c)\)'nin \((a)\) anlamına geldiğini kanıtlayalım.
İlk noktaya benzer şekilde üçgenler \(PA_1H, PA_2H, PA_3H,..., PA_nH\) dikdörtgen ve bacak boyunca ve keskin köşe. Bu, hipotenüslerinin de eşit olduğu anlamına gelir, yani \(PA_1=PA_2=PA_3=...=PA_n\) .
4) \((b)\)'nin \((d)\) anlamına geldiğini kanıtlayalım.
Çünkü düzgün bir çokgende, çevrelenmiş ve yazılı dairelerin merkezleri çakışır (genel olarak konuşursak, bu noktaya düzgün çokgenin merkezi denir), o zaman \(H\) yazılı dairenin merkezi olur. \(H\) noktasından tabanın kenarlarına dik çizgiler çizelim: \(HK_1, HK_2\), vb. Bunlar yazılı dairenin yarıçaplarıdır (tanım gereği). O zaman TTP'ye göre (\(PH\) düzleme diktir, \(HK_1, HK_2\), vb. kenarlara dik çıkıntılardır) eğimli \(PK_1, PK_2\), vb. \(A_1A_2, A_2A_3\), vb. kenarlara dik. sırasıyla. Yani tanım gereği \(\angle PK_1H, \angle PK_2H\) yan yüzler ile taban arasındaki açılara eşittir. Çünkü \(PK_1H, PK_2H, ...\) üçgenleri eşittir (iki tarafı dikdörtgen şeklinde), sonra açılar \(\angle PK_1H, \angle PK_2H, ...\) eşittir.
5) \((d)\) öğesinin \((b)\) anlamına geldiğini kanıtlayalım.
Dördüncü noktaya benzer şekilde, \(PK_1H, PK_2H, ...\) üçgenleri eşittir (bacak boyunca dikdörtgen ve dar açı olarak), yani \(HK_1=HK_2=...=HK_n\) doğru parçalarıdır. eşit. Bu, tanım gereği \(H\)'nin tabanda yazılı bir dairenin merkezi olduğu anlamına gelir. Ama çünkü en düzenli çokgenler yazılı ve çevrelenmiş dairelerin merkezleri çakışıyorsa \(H\) çevrelenmiş dairenin merkezidir. Chtd.
Sonuçlar
Düzenli bir piramidin yan yüzleri eşit ikizkenar üçgenlerdir.
Tanım
Düzgün bir piramidin tepe noktasından çizilen yan yüzünün yüksekliğine ne denir? özlü söz.
Düzenli bir piramidin tüm yan yüzlerinin özleri birbirine eşittir ve aynı zamanda kenarortay ve açıortaydır.
Önemli Notlar
1. Yükseklik doğru üçgen piramit tabanın (taban normal bir üçgendir) rakımlarının (veya açıortaylarının veya kenarortaylarının) kesişme noktasına düşer.
2. Yükseklik doğru dörtgen piramit tabanın köşegenlerinin kesişme noktasına düşer (taban bir karedir).
3. Yükseklik doğru altıgen piramit tabanın köşegenlerinin kesişme noktasına düşer (taban normal bir altıgendir).
4. Piramidin yüksekliği tabanda uzanan herhangi bir düz çizgiye diktir.
Tanım
Piramit denir dikdörtgen yan kenarlarından biri taban düzlemine dik ise.

Önemli Notlar
1. Dikdörtgen piramitte tabana dik olan kenar piramidin yüksekliğidir. Yani \(SR\) yüksekliktir.
2. Çünkü \(SR\) tabandan herhangi bir doğruya diktir, bu durumda \(\üçgen SRM, \üçgen SRP\) – dik üçgenler.
3. Üçgenler \(\üçgen SRN, \üçgen SRK\)- ayrıca dikdörtgen.
Yani bu kenarın oluşturduğu herhangi bir üçgen ve bu kenarın tabanda bulunan tepe noktasından çıkan köşegen dikdörtgen olacaktır.
\[(\Large(\text(Piramitin hacmi ve yüzey alanı))))\]
Teorem
Piramidin hacmi, taban alanı ile piramidin yüksekliğinin çarpımının üçte birine eşittir: \
Sonuçlar
\(a\) tabanın kenarı, \(h\) piramidin yüksekliği olsun.
1. Düzenli üçgen piramidin hacmi \(V_(\text(sağ üçgen.pir.))=\dfrac(\sqrt3)(12)a^2h\),
2. Düzenli bir dörtgen piramidin hacmi \(V_(\text(right.four.pir.))=\dfrac13a^2h\).
3. Düzgün altıgen piramidin hacmi \(V_(\text(right.six.pir.))=\dfrac(\sqrt3)(2)a^2h\).
4. Cilt düzenli tetrahedron eşittir \(V_(\text(right tetra.))=\dfrac(\sqrt3)(12)a^3\).
Teorem
Düzenli bir piramidin yan yüzeyinin alanı, tabanın çevresi ile apothemin yarı ürününe eşittir.
\[(\Large(\text(Frustum))))\]
Tanım
Rastgele bir piramit \(PA_1A_2A_3...A_n\) düşünün. Piramidin yan kenarında bulunan belirli bir noktadan piramidin tabanına paralel bir düzlem çizelim. Bu uçak piramidi iki çokyüzlüye bölecek, bunlardan biri piramit (\(PB_1B_2...B_n\)), diğeri ise piramit olarak adlandırılacak kesik piramit(\(A_1A_2...A_nB_1B_2...B_n\) ).
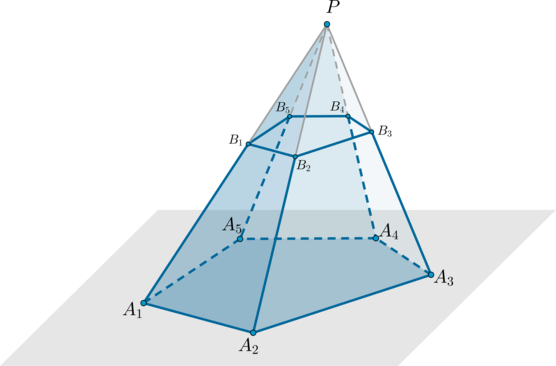
Kesik piramidin iki tabanı vardır - birbirine benzeyen çokgenler \(A_1A_2...A_n\) ve \(B_1B_2...B_n\).
Kesik bir piramidin yüksekliği, üst tabanın bir noktasından alt tabanın düzlemine çizilen diktir.
Önemli Notlar
1. Kesik bir piramidin tüm yan yüzleri yamuktur.
2. Düzenli bir kesik piramidin (yani normal bir piramidin kesitiyle elde edilen bir piramidin) tabanlarının merkezlerini birleştiren segment yüksekliktir.
Yan yüzlerin tabana dik olduğu piramitlerin hangi özelliklere sahip olduğunu düşünelim.
Eğer piramidin iki bitişik yan yüzü tabana diktir, O bu yüzlerin ortak yan kenarı piramidin yüksekliğidir. Sorun bunu söylüyorsa bir piramidin kenarı onun yüksekliğidir, O hakkında konuşuyoruzözellikle bu tip piramit hakkında.
Piramidin tabana dik yüzleri dik üçgenlerdir.
Piramidin tabanı üçgen ise
Böyle bir piramidin yan yüzeyi genel durum bunu tüm yan yüzlerin alanlarının toplamı olarak ararız.
Piramidin tabanı ortogonal projeksiyon yüz tabana dik değil (içinde bu durumda, SBC). Bu, dik izdüşüm alanı teoremine göre, tabanın alanının bu yüzün alanının çarpımına ve bununla taban düzlemi arasındaki açının kosinüsüne eşit olduğu anlamına gelir. .
Piramidin tabanı dik üçgen ise

Bu durumda piramidin tüm yüzleri dik üçgendir.
SA piramidin yüksekliği olduğundan SAB ve SAC üçgenleri dikdörtgendir. ABC Üçgeni Koşullara göre dikdörtgen.
SBC üçgeninin dik açılı olması, üç dik teoreminden kaynaklanmaktadır (AB, eğimli SB'nin taban düzlemi üzerindeki izdüşümüdür. AB, koşul gereği BC'ye dik olduğundan, SB, BC'ye diktir).
Bu durumda SBC'nin yan yüzü ile taban arasındaki açı ABS açısıdır.
Yan yüzey alanı dik üçgenlerin alanlarının toplamına eşittir:
Bu durumda olduğundan
![]()
Piramidin tabanı ikizkenar üçgen ise
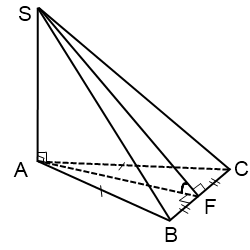
Bu durumda, yan yüz düzlemi BCS ile taban düzlemi arasındaki açı AFS açısıdır; burada AF yükseklik, ortanca ve açıortaydır. ikizkenar üçgen ABC.
Benzer şekilde, eğer piramidin tabanında yer alıyorsa eşkenar üçgen ABC.
Piramidin tabanı paralelkenar ise
 Bu durumda piramidin tabanı, tabana dik olmayan yan yüzlerin dik bir çıkıntısıdır.
Bu durumda piramidin tabanı, tabana dik olmayan yan yüzlerin dik bir çıkıntısıdır.
Tabanı iki üçgene bölersek
burada α ve β sırasıyla ADS ve CDS düzlemleri ile taban düzlemi arasındaki açılardır.

BF ve BK paralelkenarın yükseklikleriyse, BFS açısı CDS yan yüzünün taban düzlemine eğim açısıdır ve BKS açısı ADS tarafının eğim açısıdır.
(çizim B'nin geniş açı olduğu durum için yapılmıştır).
Piramidin tabanı ABCD eşkenar dörtgeni ise, BFS ve BKS açıları eşittir. Bu durumda ABS ve CBS üçgenlerinin yanı sıra ADS ve CDS üçgenleri de eşittir.
Piramidin tabanı dikdörtgen ise
 Bu durumda yan yüz düzlemi SAD ile taban düzlemi arasındaki açı SAB açısıdır,
Bu durumda yan yüz düzlemi SAD ile taban düzlemi arasındaki açı SAB açısıdır,
ve SCD yan yüzünün düzlemi ile taban düzlemi arasındaki açı SCB açısıdır
(üç dik teoremine göre).
Sırasıyla,
Buradan yan yüzey olarak bulunabilir
Burada piramidin tüm yan yüzleri dik üçgenlerdir(SAD ve SCD açıları üç dik teoremine göre dik açılardır). Bu nedenle yan yüzey doğrudan aranabilir:
Piramidin tabanı ABCD karesi ise sorun basitleştirilir: ABS ve BCS üçgenleri ile ADS ve CDS üçgenleri bu durumda eşittir.
15 Aralık 2012
“Kenarların tabana dik olduğu piramitler” hakkında incelemeler (12)
-
Rusça "dikdörtgen piramit" kelimesini Google'da ararsanız, materyaliniz ilk beşte yer alır. Bu sayfada sadece bir tane dikdörtgen piramit olduğunu görüyorum, sonuncusu ve tanımlamalar tamamen doğru değil. Google, Wikipedia ile birlikte garip bir tanım ortaya attı: dik bir kenar ve piramidin tabanındakiyle aynı. Bu arada, İngilizce Genel olarak dikdörtgen bir piramit, tabanında bir dikdörtgen bulunan bir piramittir ve yüksekliğin nerede olduğu hiç önemli değildir.
Metinde dikdörtgen piramit ile ilgili tek bir kelime yok. Çoğu zaman, tabana dik iki yan yüzün bulunduğu piramitlerle ilgili problemlerde, yan yüz düzlemi ile taban düzlemi arasındaki açıdan bahsediyoruz.
İÇİNDE bu malzeme tabandaki çokgene bağlı olarak bu açının nasıl belirleneceğini düşünün. Taban bir paralelkenar içeriyorsa (eşkenar dörtgen dahil), paralelkenarın yüksekliğini piramidin yüksekliğinin tabanından çizmeniz gerekir. zıt taraflar(veya bu kenarları içeren düz bir çizgi). Taban bir dikdörtgense (kare dahil), dikdörtgenin kenarları birbirine dik olduğundan yükseklik çizmeye gerek yoktur. Bu durumda taban ile yan kenar arasındaki açı belirlenir. doğrusal açı piramidin kenarlarının oluşturduğu; yan yüzler dik üçgenlerdir.
Tabanın dikdörtgen olmayan bir paralelkenar olduğu durumdan bu farkı vurgulamak için tabandaki dik açılar vurgulanmıştır.Çünkü "dikdörtgen piramidi" kaldırdınız, ancak arama motorlarının nasıl çalıştığını bilen ve anlayan teknisyenlerin argümanlarınız tarafından ikna edilmesi pek mümkün değil. Sadece matematik değil, BT öğrenin.
Sevgili Nataşok! Beni yalan söylemekle mi suçluyorsun? Çalışmalarımda “dikdörtgen piramit” tabirini kullanmadığımı söylemiştim.
Not: Ne yazık ki bir BT uzmanı değilim. Katılıyorum, her alanda okuryazarlığa ihtiyaç var: hem matematikte hem de Bilişim teknolojisi ve yazımda.
Şekil piramidin tabanında bir dikdörtgenin olduğu durumu göstermektedir. Paralel tasarımda açılar korunmadığından dikdörtgen paralelkenar olarak çizilir. Şekildeki ikinci dik açı, üç dikler teoremi ile bağlantılı olarak belirtilmiştir.
Öncelikle çizim değil, çizim. Çizimde çizim yaparsınız ama matematikte bunlar hâlâ çizimdir. İkinci olarak son çizime bakın. Üç dikle ilgili teorem yoktur. Tekrar ediyorum, son çizimdeki taban dikdörtgen değil. Onu nasıl tasvir ettiğiniz önemli değil. Notasyonları takip ediyorum. Ancak aşağıdaki üçüncü çizimin de benim için net olmadığını fark ettim. Paralelkenar çizimde işaretlenmemiştir. Sadece bir dörtgen! Görünümü bir paralelkenara benzer, ancak atamalar arzulanan çok şey bırakıyor.
1) Evet, geometride çizim yapıyoruz ama metnin illüstrasyonu çizimdir. Herhangi bir geometri ders kitabında “Çizim 1'de” değil, “Şekil 1'de” yazıyorlar.
2) Paralel tasarım sırasında açılar korunmadığından stereometride bir dikdörtgen paralelkenar olarak gösterilir. Ancak çizgilerin paralelliği korunur. Dörtgenin karşılıklı kenarları paralel çizgiler üzerinde uzanıyormuş gibi tasvir edilmiştir. Buradan bu dörtgenin bir paralelkenar olduğu sonucu çıkar.Dörtgenin karşılıklı kenarları paralel çizgiler üzerinde uzanıyormuş gibi tasvir edilmiştir. Bu çizgilerin paralel olduğuna dair herhangi bir belirti görmüyorum ve metinde paralel tasarıma işaret edilmiyordu. Yani benim için temel hala son çizimde keyfi dörtgen
Sevgili Nataşa! Resim mekansal figürler uçakta kurallara uygun olarak gerçekleştirilir paralel tasarım. Bu, çizimdeki paralel çizgilerin paralel çizgiler olarak gösterildiği ve paralel olmayan çizgilerin paralel olmadığı anlamına gelir.
Dikdörtgen piramidin tanımına katılmıyorum. Dikdörtgen piramit bir köşesinde üç dik açı bulunan bir piramittir. Cahil bir Vikipedi düzeyinde neden hatalı materyal yaydığınızı bana yazın.
Eğer piramidin tabanı bir dikdörtgen ise, neden resimde bunu belirtmek için iki zıt köşe işaretlenmiştir? Son çizimde bu taban bir eşkenar dörtgen ve başka bir dörtgen olabilir.
Yan kaburgalardan birinin tabana dik olduğu.
Bu durumda bu kenar piramidin yüksekliği olacaktır.
Piramidin özellikleri.
1. Tüm yan kenarlar aynı boyuta sahip olduğunda:
- piramidin tabanına yakın olanı tanımlamak kolaydır daire piramidin tepesi bu dairenin merkezine yansıtılacakken;
- yan kaburgalar aynı formdadır açılar ;
- Üstelik bunun tersi de doğrudur; yan kaburgalar taban düzlemi ile oluştuğunda eşit açılar veya piramidin tabanına yakın bir daire tanımlanabildiğinde ve piramidin tepesi bu dairenin merkezine yansıtıldığında, bu da piramidin tüm yan kenarlarının aynı boyutta olduğu anlamına gelir.
2. Yan yüzler taban düzlemine aynı değerde bir eğim açısına sahip olduğunda:
- piramidin tabanına yakın bir daire tanımlamak kolaydır ve piramidin tepesi bu dairenin merkezine yansıtılacaktır;
- yan yüzlerin yükseklikleri eşit uzunluk;
- yan yüzeyin alanı, tabanın çevresinin ve yan yüzün yüksekliğinin ½ çarpımına eşittir.
3. Piramit hakkında tarif edilebilir küre Piramidin tabanında, çevresinde bir dairenin tanımlanabileceği bir çokgen bulunması durumunda (gerekli ve yeterli koşul). Kürenin merkezi olacak nokta piramidin kenarlarının ortasından geçen düzlemlerin kendilerine dik kesişimleri. Bu teoremden, bir kürenin hem herhangi bir üçgenin hem de herhangi bir düzenli piramidin çevresinde tanımlanabileceği sonucuna varıyoruz;
4. İç açıortay düzlemleri bir piramidin içine bir küre yazılabilir. dihedral açılar piramitler 1. noktada kesişir (gerekli ve yeterli koşul). Bu nokta kürenin merkezi olacak.
5. Köşeleri çakıştığında koni piramidin içine yazılacak ve koninin tabanı piramidin tabanına yazılacaktır. Bu durumda, bir koniyi bir piramite yerleştirmek ancak piramidin özleri eşit boyutlara sahipse (gerekli ve yeterli bir koşul) mümkündür;
6. Koni köşeleri çakışırsa piramidin yakınında tanımlanacak ve koninin tabanı piramidin tabanının yakınında tanımlanacaktır. Bu durumda piramidin yakınındaki bir koniyi ancak piramidin tüm yan kenarlarının aynı olması durumunda tanımlamak mümkündür. aynı değerler(gerekli ve yeterli koşul). Bu konilerin ve piramitlerin yükseklikleri aynıdır.
7. Silindir Tabanlarından biri, tabana paralel bir düzlem tarafından piramidin kesitine yazılan bir daire ile çakışıyorsa ve ikinci taban piramidin tabanına aitse, piramitin içine yazılacaktır.
8. Piramidin tepesi tabanlarından birine ait olduğunda silindir piramidin yakınında, silindirin ikinci tabanı ise piramidin tabanına yakın olarak tanımlanacaktır. Bu durumda, piramidin yakınındaki bir silindiri ancak piramidin tabanı yazılı bir çokgen ise (gerekli ve yeterli koşul) tanımlamak mümkündür.
Dikdörtgen piramidin hacmini ve alanını belirlemek için formüller.
V- piramidin hacmi,
S- piramidin tabanının alanı,
H- piramidin yüksekliği,
Sb- piramidin yan yüzeyinin alanı,
A- apothem (ile karıştırılmamalıdır) α ) piramitler,
P- piramidin tabanının çevresi,
N- piramidin tabanının kenar sayısı,
B- uzunluk yan kaburga piramitler,
α - piramidin tepesindeki düz açı.
