จุดที่อยู่เหนือเวกเตอร์ความเร็วหมายถึงอะไร ความเร็วเชิงเส้น

ในกลศาสตร์นิวตันแบบดั้งเดิม ขนาดของวัตถุและช่วงเวลาระหว่างเหตุการณ์ถือเป็นค่าสัมบูรณ์ ซึ่งหมายความว่าเราสามารถพูดถึงความยาวของร่างกายได้โดยไม่ต้องระบุว่าร่างกายนี้พักหรือเคลื่อนไหวอยู่

สเกลเชิงเส้น (ความยาวของส่วน) และช่วงเวลายังคงไม่เปลี่ยนแปลงเมื่อย้ายจากระบบอ้างอิงที่ 1 ไปยังอีกระบบหนึ่ง เช่น ไม่ได้ขึ้นอยู่กับการเลือกระบบอ้างอิง แนวคิดเหล่านี้สะท้อนถึงแนวคิดของนิวตันเกี่ยวกับความสมบูรณ์ของอวกาศและเวลา

2.จลนศาสตร์

นี่คือหมวดกลศาสตร์นะแมว พวกเขาศึกษาวิธีการอธิบายการเคลื่อนไหวของร่างกายโดยไม่สนใจสาเหตุที่ทำให้เกิดการเคลื่อนไหวนี้.

3. วิถี

นี่คือเส้นในอวกาศที่อนุภาคเคลื่อนที่ (ตำแหน่งทางเรขาคณิตของปลายเวกเตอร์รัศมีของอนุภาค)

4.การขนย้าย ดี = ดี 2 – ดี 1 ร เป็นระยะเวลาหนึ่ง Dที 1 เป็นเวกเตอร์ที่ดึงจากตำแหน่งเริ่มต้นถึงตำแหน่งสุดท้ายของอนุภาค (จากจุด 2 ).

ตรงประเด็น< 5. เวกเตอร์ความเร็วเฉลี่ย>.

โวลต์< 5. เวกเตอร์ความเร็วเฉลี่ย> เวกเตอร์ความเร็วเฉลี่ย เป็นระยะเวลาหนึ่ง Dเป็นเวกเตอร์เท่ากับอัตราส่วนของการกระจัดของอนุภาคต่อเวลา D

โวลต์ < 5. เวกเตอร์ความเร็วเฉลี่ย> ซึ่งได้กระทำไว้ดังนี้ เกิดขึ้นพร้อมกันในทิศทางเดียวกับเวกเตอร์การกระจัดดี.

ดี5. เวกเตอร์ความเร็วเฉลี่ย 6.ความเร็วทันที อนุภาค (หรือเพียงแค่ความเร็ว ดี) เป็นเวกเตอร์เท่ากับอนุพันธ์ของเวกเตอร์รัศมี

ตามเวลา: 5. เวกเตอร์ความเร็วเฉลี่ยความเร็วทันที มุ่งตรงไปยังวิถีการเคลื่อนที่ในทิศทางการเคลื่อนที่ของอนุภาค

7. .SI:m/sการเร่งความเร็ว 5. เวกเตอร์ความเร็วเฉลี่ยเรียกว่าเวกเตอร์เท่ากับอนุพันธ์ของเวลาของความเร็ว

อนุภาค:

8. กฎการเคลื่อนที่

เรียกว่าการพึ่งพาเวลาของพิกัดอนุภาค:

มีการเชื่อมโยงอย่างง่ายระหว่างเวกเตอร์และวิธีพิกัดในการอธิบายการเคลื่อนไหว เวกเตอร์ใดๆ สามารถกำหนดได้โดยการฉายภาพบนแกนพิกัด ตัวอย่างเช่น เวกเตอร์รัศมีของอนุภาค: ที่ไหน, ฉัน, เจเค

9. – หน่วยเวกเตอร์ของแกนพิกัด

ความเร็วด้วยวิธีพิกัดอธิบายการเคลื่อนไหว 5. เวกเตอร์ความเร็วเฉลี่ยความเร็ว

เช่นเดียวกับเวกเตอร์อื่นๆ สามารถแสดงผ่านการฉายภาพบนแกน DSC: เหล่านั้น.,5. เวกเตอร์ความเร็วเฉลี่ยความเร็ว

อนุภาคสามารถแสดงได้ในรูปแบบต่อไปนี้: จะเห็นได้ว่าองค์ประกอบความเร็วแสดงออกผ่านฟังก์ชันต่างๆ(เป็นระยะเวลาหนึ่ง D), x(เป็นระยะเวลาหนึ่ง D), ย(เป็นระยะเวลาหนึ่ง D z

10.) เท่ากันความเร่งด้วยวิธีพิกัดระบุการเคลื่อนที่ การเร่งความเร็วก

เช่นเดียวกับเวกเตอร์อื่นๆ สามารถแสดงผ่านการฉายภาพบนแกน DSC: เหล่านั้น.,5. เวกเตอร์ความเร็วเฉลี่ยเช่นเดียวกับเวกเตอร์อื่นๆ สามารถแสดงผ่านการฉายภาพบนแกน DSC:

11.อนุภาคสามารถแสดงได้ในรูปแบบต่อไปนี้เส้นทางส เส้นทาง) เท่ากับระยะทางที่วัดได้ตามแนววิถีและเคลื่อนที่ของอนุภาคระหว่างการเคลื่อนที่ (ความยาววิถี)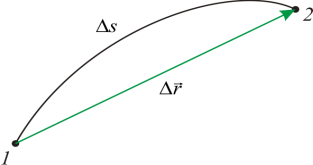

12. เส้นทางเป็นปริมาณสเกลาร์ ไม่เป็นลบ และไม่ลดลง

การเร่งความเร็วความเร่งรวมของอนุภาค

สามารถแสดงเป็นผลรวมขององค์ประกอบทั้งสองตั้งฉากกัน:

13.โมดูลเร่งความเร็วเต็ม:

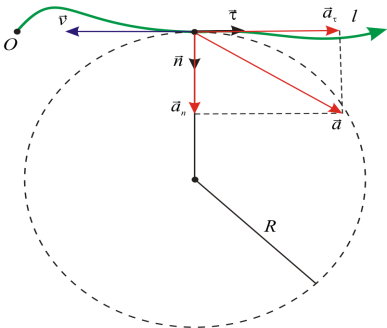
ความเร่งในวงสัมผัส (วงสัมผัส) การเร่งความเร็ว เป็นระยะเวลาหนึ่ง Dเวกเตอร์ การเร่งความเร็วมุ่งตรงไปยังวิถีโคจรของอนุภาค ในเวลาเดียวกัน 5. เวกเตอร์ความเร็วเฉลี่ยที การเร่งความเร็ว, ถ้าการเคลื่อนไหวถูกเร่ง; 5. เวกเตอร์ความเร็วเฉลี่ยตร การเร่งความเร็วหากการเคลื่อนไหวช้า ความเร่งในวงสัมผัสของอนุภาคจะแสดงลักษณะเฉพาะของการเปลี่ยนแปลงความเร็วของโมดูโลของอนุภาค (ถ้า

14.t = 0 การเคลื่อนที่สม่ำเสมอ)

ปกติ (ศูนย์กลาง)

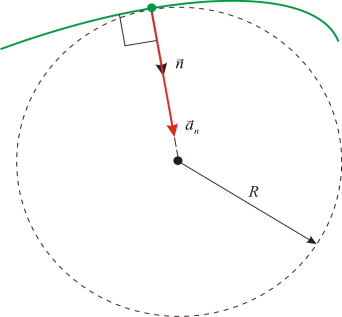
ความเร่งในวงสัมผัส (วงสัมผัส) การเร่งความเร็ว การเร่งความเร็ว n การเร่งความเร็ว การเร่งความเร็ว ^5. เวกเตอร์ความเร็วเฉลี่ยตั้งฉากกับเส้นสัมผัสกันกับวิถีการเคลื่อนที่เสมอเช่น การเร่งความเร็ว การเร่งความเร็ว ^การเร่งความเร็วและ

ที ความเร่งปกติจะแสดงลักษณะของการเปลี่ยนแปลงความเร็วในทิศทาง (สำหรับการเคลื่อนที่เชิงเส้น เมื่อใด = ¥, การเร่งความเร็ว การเร่งความเร็ว = 0)

15.ร

ร่างกายแข็งทื่ออย่างแน่นอน

16. ในกลศาสตร์ พวกมันเรียกว่าวัตถุ ในระหว่างการเคลื่อนที่ซึ่งระยะห่างระหว่างจุดสองจุดใดๆ ยังคงไม่เปลี่ยนแปลง ดังนั้นร่างกายที่มั่นคงจึงไม่เปลี่ยนรูปภายใต้อิทธิพลของแรงภายนอกจำนวนองศาอิสระของร่างกาย คือจำนวนตัวแปรอิสระ (ปริมาณ) ที่ต้องกำหนดเพื่อกำหนดตำแหน่งของร่างกายในอวกาศตัวอย่าง. จะเห็นได้ว่าองค์ประกอบความเร็วแสดงออกผ่านฟังก์ชันต่างๆ, x, ย).

17.จำนวนองศาความเป็นอิสระของจุดวัสดุคือ 3 (ตัวแปรอิสระ 3 ตัว (พิกัด)

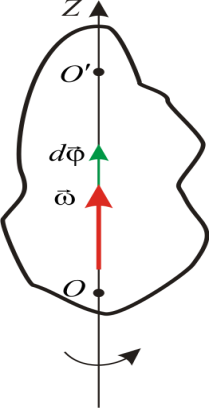
ความเร็วเชิงมุมของร่างกาย ให้ร่างกายหมุนรอบแกนซี สำเร็จได้ภายในระยะเวลาอันสั้น dt การเลี้ยวเบื้องต้นฉัน.งความเร็วเชิงมุมของร่างกาย

เรียกว่าเวกเตอร์ เวกเตอร์ว การเลี้ยวเบื้องต้นฉันเกิดขึ้นพร้อมกับเวกเตอร์ เวกเตอร์, เช่น. กำกับตามแนวแกนการหมุนของตัวเครื่องเพื่อให้เกิดสกรูด้านขวาพร้อมกับทิศทางการหมุนของเวกเตอร์ ให้ร่างกายหมุนรอบแกนต่อแกน

และโมดูลของมัน: เวกเตอร์ – หน่วยวัด (เรเดียนต่อวินาที)

ราด/เอส

วลี ความเร็วเชิงเส้น ใช้ในการพิจารณาการเคลื่อนที่โค้งของร่างกาย และต้องการเน้นความแตกต่างระหว่างความเร็ว $v\ $ และความเร็วทางอาญา $\omega $ ส่วนใหญ่แล้วคำว่าเชิงเส้นจะถูกละเว้นและพวกเขาก็บอกว่าความเร็ว

เวกเตอร์ความเร็วเฉลี่ย

คำนิยาม อัตราส่วนของการเคลื่อนไหว ($\Delta \overline(r)$) ต่อช่วงเวลาที่การเคลื่อนไหวนี้เกิดขึ้นเรียกว่าความเร็วเฉลี่ย

การเคลื่อนไหว ($\left\langle \overline(v)\right\rangle $):

\[\left\langle \overline(v)\right\rangle =\frac(\Delta \overline(r))(\Delta t)\left(1\right),\]

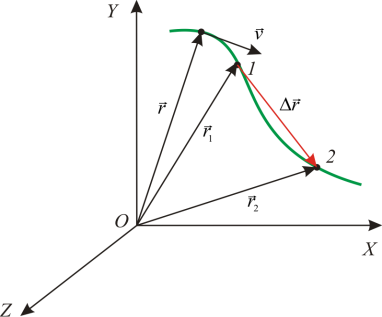
เวกเตอร์ความเร็วเฉลี่ย $\left\langle \overline(v)\right\rangle $ มีทิศทางเดียวกันกับเวกเตอร์ $\Delta \overline(r)$ เนื่องจาก $\Delta t>0$ ความยาวของเซ็กเมนต์ที่แสดงเวกเตอร์ความเร็วเฉลี่ย (รูปที่ 1) ไม่สัมพันธ์กับความยาวของเวกเตอร์ $\Delta \overline(r)$

ความเร็วเฉลี่ยแสดงถึงความเร็วที่จุดเคลื่อนที่ ลักษณะนี้หมายถึงช่วงระยะเวลาหนึ่ง

หากวัตถุเคลื่อนที่ไปตามเส้นโค้ง ดังนั้นเส้นทาง ($\Delta s$) จะมากกว่าโมดูลัสการกระจัด ($\Delta r$) ในช่วงเวลาเดียวกัน เนื่องจากความยาวของส่วนโค้งจะน้อยกว่าความยาวเสมอ ของคอร์ดที่หดตัว (รูปที่ 1) เส้นทางและการกระจัดเกิดขึ้นพร้อมกันเมื่อเคลื่อนที่เป็นเส้นตรงในทิศทางเดียว ความเร็วเฉลี่ยของเส้นทางถูกกำหนดเป็น:

\[\left\langle v\right\rangle (\rm =)\frac(\Delta s)(\Delta t)\left(2\right).\]

ความเร็วเฉลี่ยแสดงลักษณะความเร็วของการเคลื่อนที่ของจุดวัสดุในช่วงเวลาจำกัด

ความเร็วทันที

เวกเตอร์ความเร็วเฉลี่ย

ด้วยการลดระยะเวลาในการพิจารณาการเคลื่อนที่ของอนุภาค ($\Delta t\to 0$) เราจะได้คุณลักษณะของการเคลื่อนที่ของจุดในช่วงเวลาที่กำหนด ค่าจะเท่ากับ:

\[\overline(v)=(\mathop(\lim )_(\Delta t\to 0) \left\langle \overline(v)\right\rangle =\ )(\mathop(\lim )_(\ เดลต้า t\ถึง 0) \frac(\Delta \overline(r))(\Delta t)=\frac(d\overline(r))(dt)\left(3\right),\ )\]

เรียกว่า ความเร็วทันทีหรือเพียงแค่ความเร็ว

เมื่อคำนวณความเร็วโดยใช้สูตร (3) เห็นได้ชัดว่าการลดลงของช่วงเวลา $\Delta t$ นำไปสู่ความจริงที่ว่าในท้ายที่สุดค่าที่ได้รับถัดไปของความเร็วเฉลี่ยจะแตกต่างกันเล็กน้อยจากกัน ดังนั้น เมื่อค้นหาความเร็วชั่วขณะ พวกเขาหยุดที่ค่าสุดท้าย $\Delta t\ $แต่น้อย เพื่อให้สามารถได้รับความแม่นยำที่จำเป็นของค่าความเร็ว

การผ่านไปยังขีดจำกัด (3) มีความหมายทางเรขาคณิต เวกเตอร์ $\Delta \overline(r)$ ถูกกำหนดทิศทางไปตามคอร์ดที่เชื่อมต่อจุดสองจุดของวิถี; การบรรจบกันของจุดเหล่านี้นำไปสู่ความจริงที่ว่าเวกเตอร์นี้รับตำแหน่งของเส้นสัมผัสกับวิถีการเคลื่อนที่ ณ จุดที่กำหนด . ปรากฎว่าเวกเตอร์ความเร็วมีทิศทางสัมผัสกับวิถีการเคลื่อนที่ในแนวสัมผัส ในการเคลื่อนที่เป็นเส้นตรง เวกเตอร์ความเร็วจะมีทิศทางเป็นเส้นตรง

ความเร็วของการเดินทางถูกกำหนดในทำนองเดียวกัน:

ถ้าวิถีการเคลื่อนที่ของจุดวัสดุเป็นเส้นโค้งเรียบ ยิ่งส่วนโค้งสั้นเท่าไร ความยาวก็จะยิ่งใกล้กับความยาวของคอร์ดมากขึ้นเท่านั้น ในข้อความถึงขีดจำกัดที่ $\ \Delta t\to 0$ เราสามารถสรุปได้ว่า $\Delta s\to \Delta r$ เพราะฉะนั้น,

เพิ่มความเร็ว

ความเร็วเป็นปริมาณเวกเตอร์ หากจุดวัสดุมีส่วนร่วมในการเคลื่อนไหวหลายครั้ง ความเร็วของจุดนั้นจะถูกพบเป็นผลรวมเวกเตอร์ของความเร็วของการเคลื่อนไหวแต่ละครั้ง:

\[\overline(v)=\sum\limits_i((\overline(v))_i\left(6\right).)\]

ในบางกรณี เป็นการสะดวกที่จะคิดว่าการเคลื่อนไหวที่ซับซ้อนเป็นการซ้อนทับของการเคลื่อนไหวง่ายๆ หลายๆ อย่าง จากนั้นความเท่าเทียมกัน (6) ก็ถือได้ว่าเป็นกฎสำหรับการแยกเวกเตอร์ความเร็วออกเป็นส่วนประกอบต่างๆ

ความเร็วและความเร่งของการเคลื่อนไหว

เมื่อเคลื่อนที่ไม่สม่ำเสมอ จุดวัสดุมีความเร่ง ($\overline(a)$) ความเร่งเป็นอนุพันธ์อันดับหนึ่งของความเร็วเมื่อเทียบกับเวลา:

\[\overline(a)=\frac(d\overline(v))(dt)\left(7\right).\]

จากนิพจน์ (7) จะได้ว่าเมื่อทราบความเร่งของจุดใดจุดหนึ่ง จะได้ความเร็วดังนี้

\[\overline(v)=\int\limits^(t_2)_(t_1)(\overline(a)dt)\left(8\right).\]

ความเร็วเชิงมุมและเชิงเส้น

เมื่อเคลื่อนที่เป็นวงกลมพร้อมกับความเร็วของการเคลื่อนที่ไปตามวิถี ($v$ - ความเร็วเชิงเส้น) จะมีการแนะนำความเร็วเชิงมุม ($\omega $) ซึ่งแสดงลักษณะความเร็วของการเปลี่ยนแปลงในมุมการหมุน $\varphi $:

\[\omega =\frac(d\varphi )(dt)\left(9\right).\]

ความสัมพันธ์ระหว่างความเร็วเชิงเส้นและเชิงมุมได้รับจากนิพจน์:

ตัวอย่างปัญหาพร้อมวิธีแก้ไข

ตัวอย่างที่ 1

ออกกำลังกาย.การเปลี่ยนแปลงเวกเตอร์รัศมีที่กำหนดตำแหน่งของจุดวัสดุจะได้รับจากสมการ: $\overline(r\ )\left(t\right)=t^4\overline(i)+3t^2\overline( j),$ โดยที่ $\ overline(i)$ และ $\overline(j)$ เป็นเวกเตอร์หน่วยของแกน X และ Y (รูปที่ 2) ความเร็วชั่วขณะของจุด ณ เวลา $t=1$c เป็นเท่าใด

สารละลาย.ลองกำหนดความเร็วของอนุภาคดังนี้:

\[\overline(v)=(\frac(d\overline(r))(dt) \left(1.1\right).\ )\]

เราแทนลงในสูตร (1.1) สมการสำหรับเวกเตอร์รัศมี $\overline(r\ )\left(t\right)=t^4\overline(i)+3t^2\overline(j),$ เราได้:

\[\overline(v)=\frac(d)(dt)\left(t^4\overline(i)+3t^2\overline(j)\right)=4t^3\overline(i)+6t \overline(j)\ \left(1.2\right).\]

จากสมการ (1.2) เราจะเห็นว่า:

\[\left\( \begin(array)(c) v_x=4t^3 \\ v_y=6t \end(array) \right.\left(1.3\right).\]

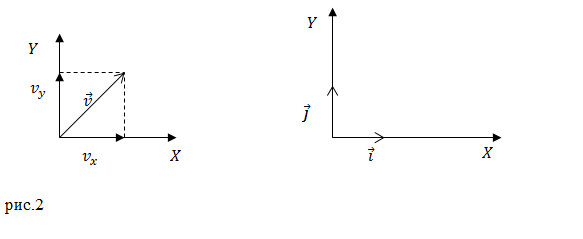
ตามทฤษฎีบทพีทาโกรัส เราจะพบว่าโมดูลความเร็วเป็น:

ลองคำนวณความเร็วโดยการแทนเวลา $t=1$c ลงในสูตรผลลัพธ์:

คำตอบ.$v$=7.2 $\frac(m)(s)$

ตัวอย่างที่ 2

ออกกำลังกาย.จุดวัสดุเคลื่อนที่เป็นเส้นตรง ความเร่งของจุดนี้จะเพิ่มขึ้นตามกราฟ (รูปที่ 3) ความเร็วของจุด ณ เวลา $t_1?$ จะเป็นเท่าใด

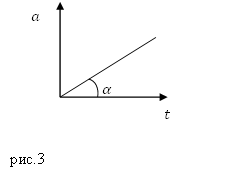
สารละลาย.ในกราฟในรูปที่ 3 ความเร่งจะแสดงเป็นเส้นตรงที่มาจากจุดกำเนิดของพิกัด ตามรูปที่ 3 เราเขียนนิพจน์เชิงวิเคราะห์สำหรับการเร่งความเร็วเป็น:

โดยที่ $k=tg\ \alpha $

เราหาความเร็วของจุดได้ดังนี้:

คำตอบ.$v=\frac(tg\ \alpha \cdot t^2_1)(2)$

การลดระยะเวลาอย่างไม่มีกำหนด t ในระหว่างที่ m.t. เคลื่อนที่ในอวกาศในขอบเขต เมื่อ t  0 เราได้ความเร็วทันที เช่น

เวกเตอร์ความเร็วชั่วขณะเท่ากับขีดจำกัดของอัตราส่วนการเพิ่มขึ้นของเวกเตอร์รัศมี m.t. ต่อช่วงเวลาที่การเพิ่มขึ้นนี้เกิดขึ้นเมื่อใด เป็นระยะเวลาหนึ่ง D 0 หรือเท่ากับอนุพันธ์อันดับหนึ่งของเวกเตอร์รัศมีเทียบกับเวลา

เวกเตอร์ความเร็วชั่วขณะ ณ เวลาที่กำหนดจะพุ่งไปในแนวสัมผัสกับวิถีที่จุดที่กำหนด (รูปที่ 9)

อันที่จริง ที่ t  0 เมื่อจุด M 2 เข้าใกล้ M 1 คอร์ด (เซแคนต์) 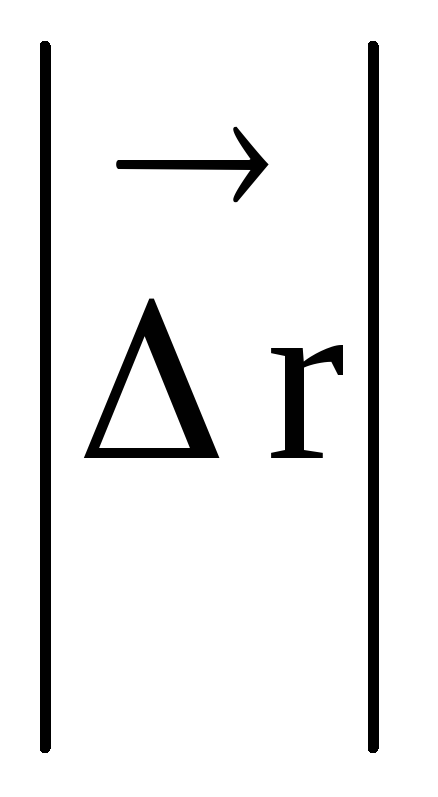เข้าใกล้ความยาวของส่วนโค้ง s และอยู่ในขีดจำกัด s = และเส้นตัดกลายเป็นแทนเจนต์ สิ่งนี้ได้รับการยืนยันอย่างชัดเจนจากการทดลอง ตัวอย่างเช่น ประกายไฟเมื่อลับคมเครื่องมือจะพุ่งตรงไปที่ล้อเจียรในแนวสัมผัสเสมอ เนื่องจากความเร็วเป็นปริมาณเวกเตอร์ โมดูลัสของมัน

.

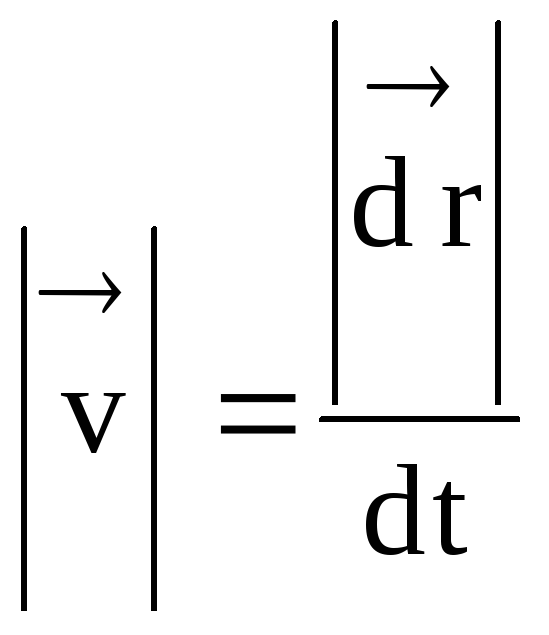ในเครื่องเร่งความเร็วบางประเภท (เช่น ไซโคลตรอน ฯลฯ) อนุภาคจะเคลื่อนที่ซ้ำๆ ในวิถีปิดโดยไม่หยุด ดังนั้น ณ จุดใดๆ ของวิถี ค่าสัมบูรณ์ของเวกเตอร์ความเร็วชั่วขณะจะต้องแตกต่างจากศูนย์ ข้อสรุปนี้ได้รับการยืนยันไม่เพียงแต่โดยสมการ (15) เท่านั้น แต่ยังสอดคล้องกับแนวคิดเรื่องความเร็วสเกลาร์เฉลี่ย (สูตร 11) หากในสมการ (11) เราไปถึงขีด จำกัด ที่ t  0 เราจะต้องพิจารณาส่วนเล็ก ๆ ของเส้นทางบนวิถีโคจร s ที่ไม่แตกต่างจากโมดูลของเวกเตอร์การกระจัดเบื้องต้น - จากนั้นตามสมการ (11) เราจะได้ค่าของความเร็วสเกลาร์ชั่วขณะ

สอดคล้องกับขนาดของเวกเตอร์ความเร็วชั่วขณะ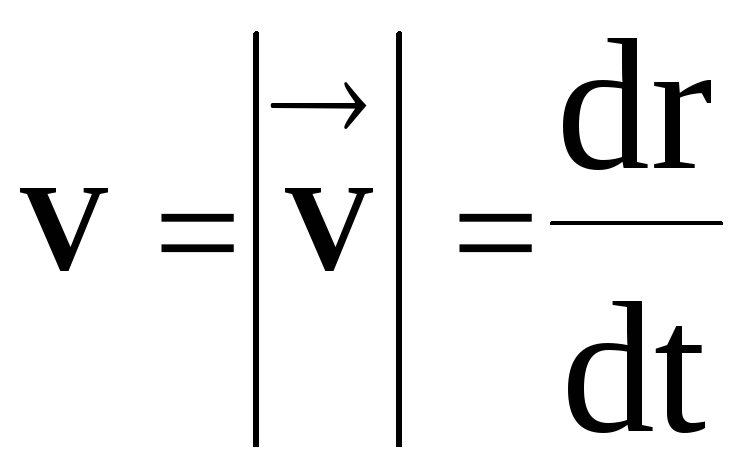

,

เนื่องจาก r = s ที่ t  0

สมการหนึ่งของเวกเตอร์ความเร็วชั่วขณะ (15) สามารถถูกแทนที่ด้วยระบบสมการของสมการสเกลาร์สามสมการ ซึ่งก็คือเส้นโครงของเวกเตอร์ความเร็วบนแกนพิกัด

v x = dx/dt, v y = dy/dt, v z = dz/dt (16)

เวกเตอร์ความเร็วชั่วขณะสัมพันธ์กับเส้นโครงบนแกนพิกัดโดยนิพจน์

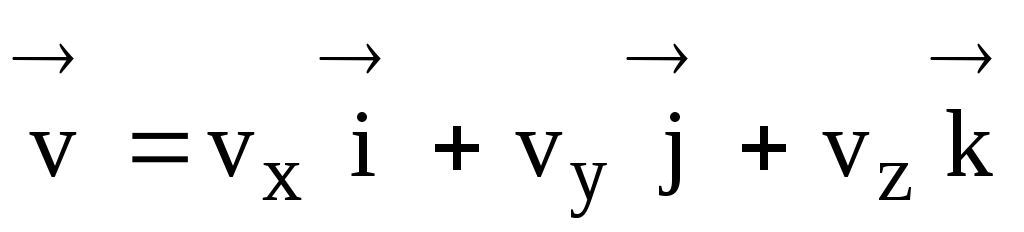, (17)

ที่ไหน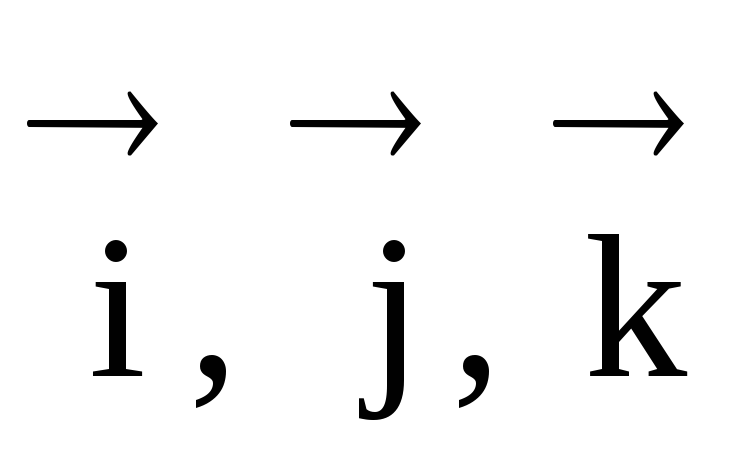

– เวกเตอร์หน่วยกำกับตามแกน X, Y, Z ตามลำดับ

โมดูโล่

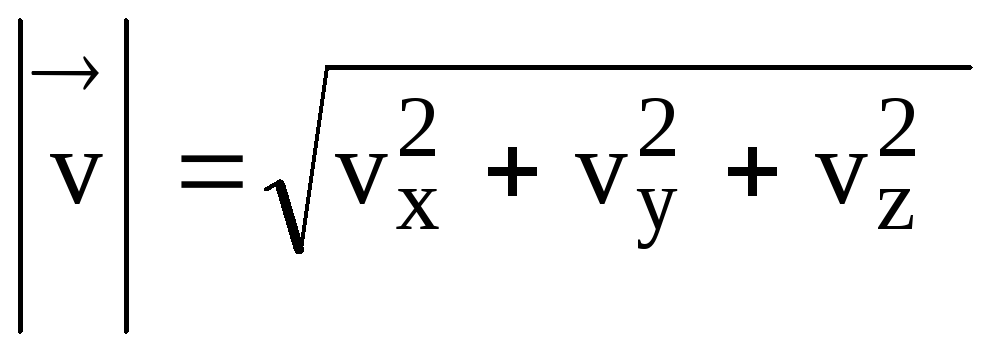. (18)

ดังนั้นเวกเตอร์ความเร็วจึงแสดงลักษณะของความเร็วของการเปลี่ยนแปลงการเคลื่อนที่ในอวกาศทั้งขนาดและทิศทางในช่วงเวลาหนึ่ง ความเร็วเป็นหน้าที่ของเวลา

1.12. อัตราเร่งเฉลี่ย

เมื่อวัตถุเคลื่อนที่ ความเร็วในกรณีทั่วไปสามารถเปลี่ยนแปลงได้ทั้งขนาดและทิศทาง

ตัวอย่างของการเคลื่อนไหวดังกล่าว ได้แก่ การเคลื่อนที่ของระบบสุริยะรอบใจกลางกาแล็กซีของเรา หรือการเคลื่อนที่ของรถไฟขณะเบรก เป็นต้น การเคลื่อนที่สม่ำเสมอของมวลในวงกลมเป็นตัวอย่างเมื่อความเร็วของมันเปลี่ยนทิศทางโดยคงค่าคงที่ใน ขนาด. หากเครื่องจักรเคลื่อนที่ไปตามวิถีที่แน่นอนโดยเปลี่ยนขนาดและทิศทางของความเร็ว ดังนั้นเพื่อระบุลักษณะการเคลื่อนที่ของมัน มันไม่เพียงพอที่จะทราบการกระจัดและความเร็วอีกต่อไป คุณต้องทราบอัตราการเปลี่ยนแปลงของความเร็วด้วย เช่น ปกติ (ศูนย์กลาง).

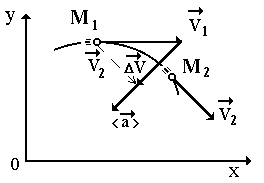
ปล่อยให้ m.t. ในช่วงเวลาหนึ่ง t 1 อยู่ที่จุด M 1 และเคลื่อนที่ด้วยความเร็ว 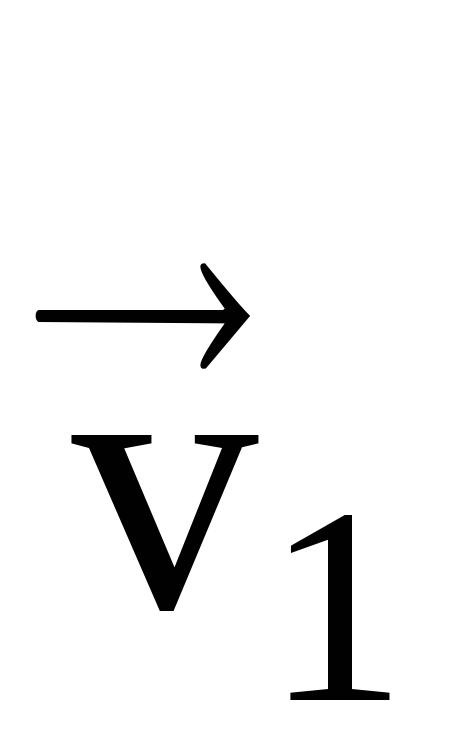และในเวลา เสื้อ 2 - ที่จุด M 2 - ด้วยความเร็ว 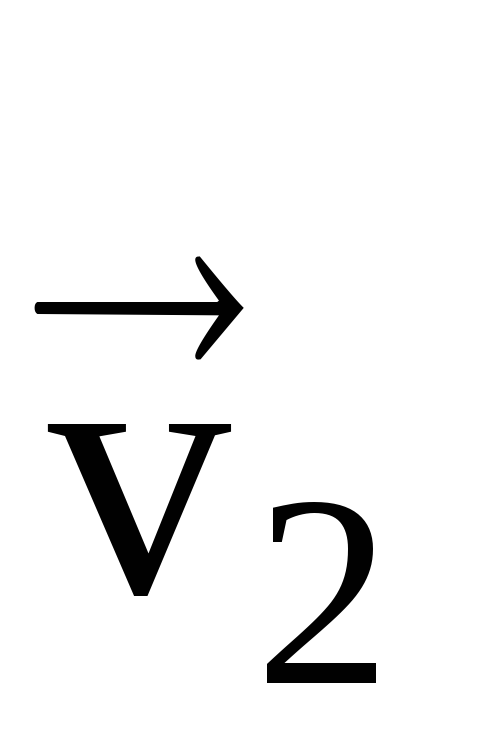(รูปที่ 10)

ลองย้ายเวกเตอร์กัน 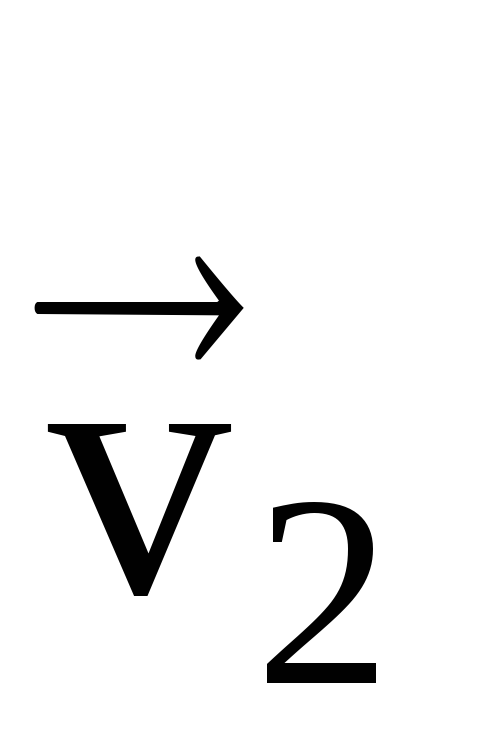ขนานกับตัวมันเองที่จุด M 1 เพื่อให้ต้นกำเนิดของเวกเตอร์ตรงกัน 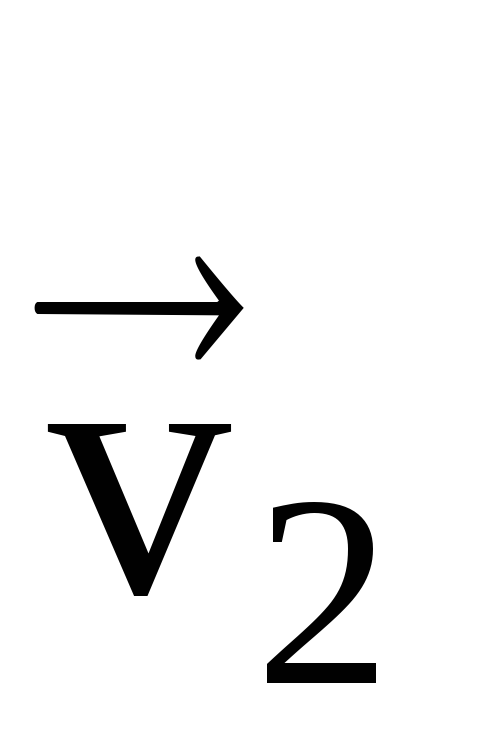และ .

แล้วผลต่างเวกเตอร์ 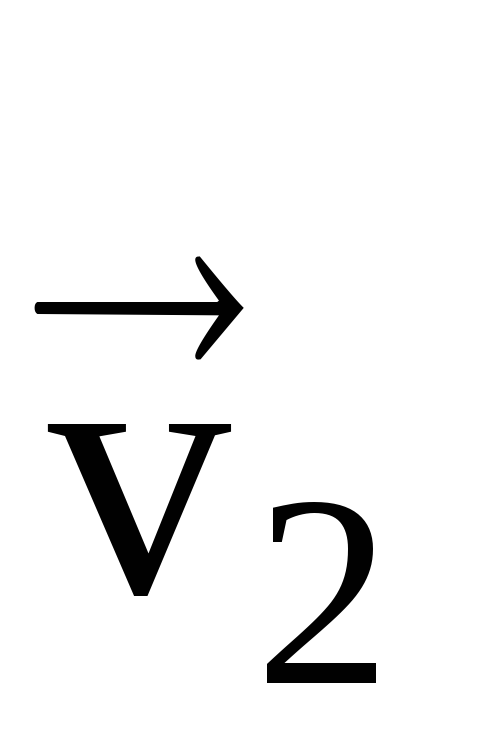และ คือเวกเตอร์ของการเปลี่ยนแปลง (เพิ่มขึ้น) ของความเร็วในช่วงเวลา t = t 2 – t 1 เช่น

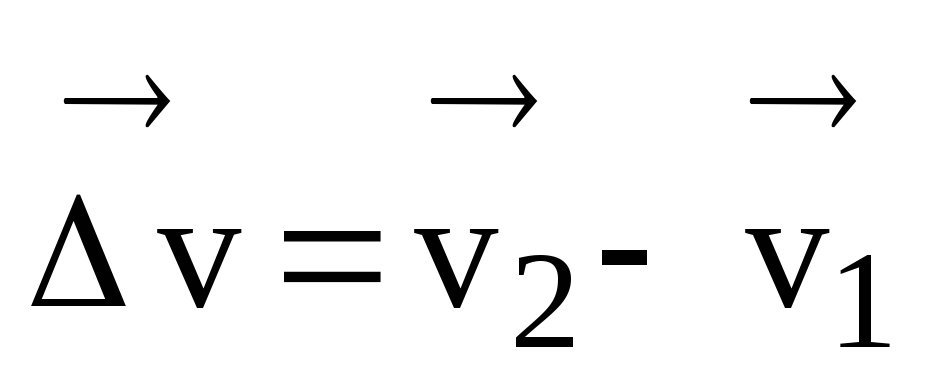. (19)

เวกเตอร์ความเร่งเฉลี่ยเท่ากับอัตราส่วนของเวกเตอร์การเปลี่ยนแปลงความเร็วต่อช่วงเวลาที่การเปลี่ยนแปลงนี้เกิดขึ้น

เพราะฉะนั้น,

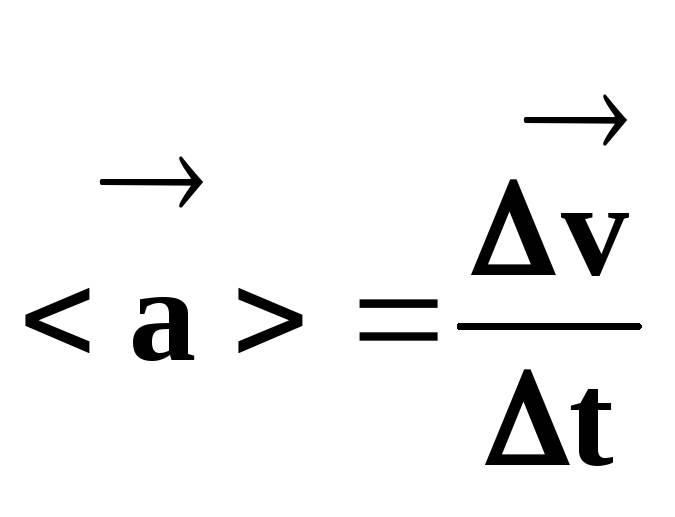. (20)

เวกเตอร์ความเร่งเฉลี่ยเกิดขึ้นพร้อมกับทิศทางของเวกเตอร์การเปลี่ยนแปลงความเร็วและมีทิศทางอยู่ภายในส่วนโค้งของวิถี

สมการเวกเตอร์หนึ่งสมการ (1.20) สอดคล้องกับระบบสมการสเกลาร์สามสมการสำหรับการฉายเวกเตอร์ความเร่งเฉลี่ยลงบนแกนพิกัด

โมดูลเวกเตอร์ความเร่งเฉลี่ย

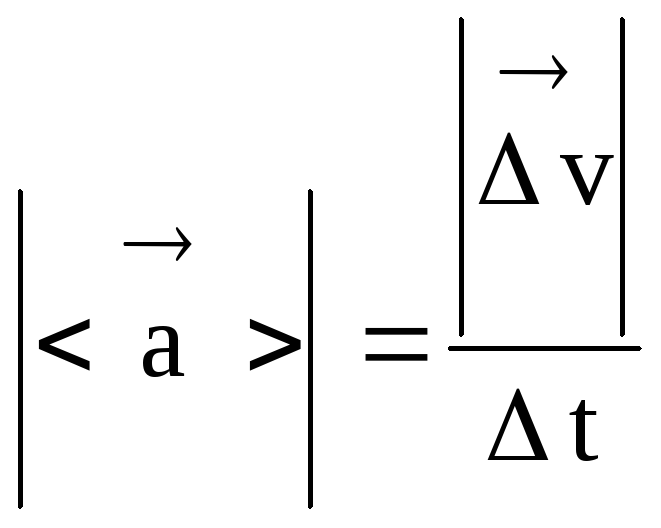. (22)

หน่วย SI ของความเร่งคือ เมตรต่อวินาทียกกำลังสอง

ถ้าขนาดของความเร็ว (หรือขนาดของเวกเตอร์ความเร็ว) ไม่เปลี่ยนแปลง การเคลื่อนที่จะสม่ำเสมอ เมื่อขนาดของความเร็วเปลี่ยนแปลง การเคลื่อนที่ก็จะไม่สม่ำเสมอ

เครื่องแบบเรียกว่า การเคลื่อนไหวที่ร่างกายเดินทางในเส้นทางเดียวกันในช่วงเวลาที่เท่ากัน- ในกรณีนี้ ขนาดของความเร็วยังคงไม่เปลี่ยนแปลง (ในทิศทาง ความเร็วสามารถเปลี่ยนแปลงได้หากการเคลื่อนที่เป็นแบบโค้ง)

ตรงไปตรงมาเรียกว่า การเคลื่อนไหวที่มีวิถีเป็นเส้นตรง- ในกรณีนี้ ทิศทางของความเร็วยังคงไม่เปลี่ยนแปลง (ขนาดของความเร็วสามารถเปลี่ยนแปลงได้หากการเคลื่อนที่ไม่สม่ำเสมอ)

เครื่องแบบตรงเรียกว่าการเคลื่อนไหวที่มีทั้งความสม่ำเสมอและเป็นเส้นตรง ในกรณีนี้ ทั้งขนาดและทิศทางยังคงไม่เปลี่ยนแปลง

ในกรณีทั่วไป เมื่อวัตถุเคลื่อนที่ ทั้งขนาดและทิศทางของเวกเตอร์ความเร็วจะเปลี่ยนไป เพื่อระบุว่าการเปลี่ยนแปลงเหล่านี้เกิดขึ้นเร็วเพียงใด จะใช้ปริมาณพิเศษ - ความเร่ง

การเร่งความเร็ว – นี่เป็นปริมาณเท่ากับอัตราส่วนของการเปลี่ยนแปลงความเร็วการเคลื่อนที่ของร่างกายต่อระยะเวลาของช่วงเวลาที่การเปลี่ยนแปลงความเร็วนี้เกิดขึ้น- ความเร่งเฉลี่ยตามคำจำกัดความนี้คือ m/s²:

การเร่งความเร็วทันทีเรียกว่า ปริมาณทางกายภาพเท่ากับขีดจำกัดที่ความเร่งเฉลี่ยมีแนวโน้มที่จะเกิดขึ้นในช่วงเวลาหนึ่ง∆t → 0, ม./วินาที²:

เนื่องจากความเร็วสามารถเปลี่ยนแปลงได้ทั้งขนาดและทิศทางตามแนววิถี เวกเตอร์ความเร่งจึงมีองค์ประกอบสองส่วน

ส่วนประกอบของเวกเตอร์ความเร่ง a ซึ่งพุ่งไปตามเส้นแทนเจนต์ไปยังวิถี ณ จุดที่กำหนด เรียกว่า ความเร่งในวงสัมผัส ซึ่งแสดงลักษณะการเปลี่ยนแปลงของเวกเตอร์ความเร็วในขนาด

องค์ประกอบของเวกเตอร์ความเร่ง a ซึ่งพุ่งไปตามเส้นปกติถึงแทนเจนต์ ณ จุดที่กำหนดบนวิถี เรียกว่า ความเร่งปกติ เป็นการแสดงลักษณะการเปลี่ยนแปลงทิศทางของเวกเตอร์ความเร็วในกรณีของการเคลื่อนที่แบบโค้ง โดยธรรมชาติแล้ว เมื่อวัตถุเคลื่อนที่ไปตามวิถีที่เป็นเส้นตรง ความเร่งปกติจะเป็นศูนย์

การเคลื่อนที่เป็นเส้นตรงเรียกว่าตัวแปรสม่ำเสมอหากความเร็วของร่างกายเปลี่ยนแปลงไปตามปริมาณที่เท่ากันในช่วงเวลาใดๆ ก็ตาม ในกรณีนี้คือความสัมพันธ์

∆V/ ∆t จะเหมือนกันทุกช่วงเวลา ดังนั้น ขนาดและทิศทางของความเร่งยังคงไม่เปลี่ยนแปลง: a = const

สำหรับการเคลื่อนที่เป็นเส้นตรง เวกเตอร์ความเร่งจะพุ่งไปตามแนวการเคลื่อนที่ ถ้าทิศทางความเร่งตรงกับทิศทางของเวกเตอร์ความเร็ว ขนาดของความเร็วก็จะเพิ่มขึ้น ในกรณีนี้ การเคลื่อนไหวเรียกว่าการเร่งความเร็วสม่ำเสมอ ถ้าทิศทางความเร่งอยู่ตรงข้ามกับทิศทางของเวกเตอร์ความเร็ว ขนาดของความเร็วก็จะลดลง ในกรณีนี้ การเคลื่อนไหวเรียกว่าช้าสม่ำเสมอ ในธรรมชาติมีการเคลื่อนไหวที่มีความเร่งสม่ำเสมอตามธรรมชาติ - นี่คือการตกอย่างอิสระ

ตกฟรี- เรียกว่า การตกของร่างกายหากแรงเดียวที่กระทำต่อวัตถุนั้นคือแรงโน้มถ่วง- การทดลองของกาลิเลโอแสดงให้เห็นว่าในระหว่างการตกอย่างอิสระ วัตถุทั้งหมดเคลื่อนที่ด้วยความเร่งแรงโน้มถ่วงเท่ากัน และมีตัวอักษร ĝ เขียนแทนด้วย ใกล้พื้นผิวโลก ĝ = 9.8 เมตร/วินาที² ความเร่งของการตกอย่างอิสระเกิดจากแรงโน้มถ่วงจากโลกและมุ่งลงสู่แนวตั้งในแนวตั้ง พูดอย่างเคร่งครัด การเคลื่อนไหวดังกล่าวเกิดขึ้นได้ในสุญญากาศเท่านั้น การตกลงไปในอากาศถือว่าฟรีโดยประมาณ

วิถีการเคลื่อนที่ของวัตถุที่ตกลงอย่างอิสระขึ้นอยู่กับทิศทางของเวกเตอร์ความเร็วเริ่มต้น หากวัตถุถูกโยนลงในแนวตั้ง วิถีโคจรจะเป็นส่วนแนวตั้ง และการเคลื่อนไหวจะเรียกว่าตัวแปรสม่ำเสมอ หากวัตถุถูกเหวี่ยงขึ้นในแนวตั้ง วิถีโคจรจะประกอบด้วยส่วนแนวตั้งสองส่วน ประการแรก ร่างกายจะลุกขึ้นและเคลื่อนไหวช้าๆ เท่าๆ กัน เมื่อถึงจุดสูงสุด ความเร็วจะกลายเป็นศูนย์ หลังจากนั้นร่างกายจะเคลื่อนตัวลงมาและเคลื่อนที่ด้วยความเร่งสม่ำเสมอ

ถ้าเวกเตอร์ความเร็วเริ่มต้นตั้งตรงทำมุมกับขอบฟ้า การเคลื่อนที่จะเกิดขึ้นตามแนวพาราโบลา นี่คือลักษณะการเคลื่อนที่ของลูกบอลที่ถูกโยน, จาน, นักกีฬาที่กระโดดไกล, กระสุนบิน ฯลฯ