ทฤษฎีบท- ให้ฟังก์ชัน x=φ(เสื้อ)อย่างต่อเนื่อง ณ จุดหนึ่ง กและฟังก์ชัน y=ฉ(x)อย่างต่อเนื่อง ณ จุดหนึ่ง ข=φ(ก)- แล้วฟังก์ชันเชิงซ้อน y=ฉ[φ(เสื้อ)]=F(เสื้อ)อย่างต่อเนื่อง ณ จุดหนึ่ง ก.

อนุญาต x=φ(เสื้อ)และ y=ฉ(x)- ฟังก์ชันพื้นฐานที่ง่ายที่สุด มีหลายค่า (เอ็กซ์)ฟังก์ชั่น x=φ(เสื้อ)คือขอบเขตของฟังก์ชัน y=ฉ(x)- ดังที่เราทราบ ฟังก์ชันพื้นฐานมีความต่อเนื่องในทุกจุดของโดเมนที่กำหนด ดังนั้นตามทฤษฎีบทที่แล้ว ฟังก์ชันเชิงซ้อน y=ฉ(φ(t))นั่นคือการทับซ้อนของฟังก์ชันพื้นฐานสองตัวจะต่อเนื่องกัน ตัวอย่างเช่น ฟังก์ชันมีความต่อเนื่อง ณ จุดใดๆ x ≠ 0เป็นฟังก์ชันเชิงซ้อนของฟังก์ชันพื้นฐาน 2 ฟังก์ชัน x=เสื้อ -1และ y=บาป x- ยังทำหน้าที่ y=ln บาป xอย่างต่อเนื่อง ณ จุดใดช่วงหนึ่ง (2kπ,(2k+1)π), k ∈ Z (บาป x>0).

คำนิยาม.ให้นิยามฟังก์ชัน y = f(x) ที่จุด x0 และบริเวณใกล้เคียงบางส่วน ฟังก์ชัน y = f(x) ถูกเรียก ต่อเนื่องที่จุด x0, ถ้า:

1. มีอยู่
2. ขีดจำกัดนี้เท่ากับค่าของฟังก์ชันที่จุด x0:

เมื่อกำหนดขีดจำกัด มีการเน้นย้ำว่า f(x) อาจไม่ได้ถูกกำหนดไว้ที่จุด x0 และหากมีการกำหนด ณ จุดนี้ ค่าของ f(x0) จะไม่มีส่วนร่วมในการกำหนดขีดจำกัดแต่อย่างใด เมื่อพิจารณาความต่อเนื่อง สิ่งสำคัญคือต้องมี f(x0) อยู่ และค่านี้จะต้องเท่ากับ lim f(x)

คำนิยาม.ให้นิยามฟังก์ชัน y = f(x) ที่จุด x0 และบริเวณใกล้เคียงบางส่วน ฟังก์ชัน f(x) เรียกว่าต่อเนื่องที่จุด x0 ถ้าทุก ε>0 มีเลขบวก δ โดยที่สำหรับ x ทั้งหมดในพื้นที่ใกล้เคียงของจุด x0 (เช่น |x-x0|
ที่นี่พิจารณาว่าค่าของขีด จำกัด จะต้องเท่ากับ f(x0) ดังนั้นเมื่อเปรียบเทียบกับคำจำกัดความของขีด จำกัด เงื่อนไขของการเจาะของ δ-พื้นที่ใกล้เคียง 0 จะถูกลบออก
ให้เราให้คำจำกัดความอีกคำหนึ่ง (เทียบเท่ากับคำก่อนหน้า) ในแง่ของการเพิ่มขึ้น สมมติว่า Δх = x - x0; เราจะเรียกค่านี้ว่าการเพิ่มขึ้นของอาร์กิวเมนต์ ตั้งแต่ x->x0 จากนั้น Δx->0 เช่น Δx - b.m (ไม่สิ้นสุด) ปริมาณ ให้เราแสดงว่า Δу = f(x)-f(x0) เราจะเรียกค่านี้ว่าการเพิ่มขึ้นของฟังก์ชันเนื่องจาก |Δу| ควรเป็น (สำหรับขนาดเล็กเพียงพอ | Δх|) น้อยกว่าตัวเลขที่ต้องการ ε>0 ดังนั้น Δу- ก็คือ bm เช่นกัน คุณค่าดังนั้น

คำนิยาม.ให้นิยามฟังก์ชัน y = f(x) ที่จุด x0 และบริเวณใกล้เคียงบางส่วน ฟังก์ชัน f(x) ถูกเรียก ต่อเนื่องที่จุด x0ถ้าการเพิ่มขึ้นเล็กน้อยในอาร์กิวเมนต์สอดคล้องกับการเพิ่มขึ้นเล็กน้อยในฟังก์ชัน

คำนิยาม.ฟังก์ชัน f(x) ซึ่งไม่ต่อเนื่องที่จุด x0 เรียกว่าไม่ต่อเนื่องณ จุดนี้

คำนิยาม.ฟังก์ชัน f(x) เรียกว่าต่อเนื่องบนเซต X ถ้าฟังก์ชัน f(x) มีความต่อเนื่องที่ทุกจุดของเซตนี้

ทฤษฎีบทเรื่องความต่อเนื่องของผลบวก ผลหาร

ทฤษฎีบทเรื่องการผ่านไปยังลิมิตภายใต้เครื่องหมายของฟังก์ชันต่อเนื่อง

ทฤษฎีบทเรื่องความต่อเนื่องของการซ้อนของฟังก์ชันต่อเนื่อง

ปล่อยให้ฟังก์ชัน f(x) ถูกกำหนดในช่วงเวลาหนึ่งและเป็นโมโนโทนิกในช่วงเวลานี้ จากนั้น f(x) จะมีได้เฉพาะจุดที่ไม่ต่อเนื่องของประเภทแรกบนเซกเมนต์นี้

ทฤษฎีบทค่ากลางหากฟังก์ชัน f(x) ต่อเนื่องกันบนเซกเมนต์และที่จุดสองจุด a และ b (a น้อยกว่า b) รับค่าที่ไม่เท่ากัน A = f(a) ≠ B = f(b) ดังนั้นสำหรับตัวเลข C ใด ๆ ซึ่งอยู่ระหว่าง A และ B จะมีจุด c ∈ ซึ่งค่าของฟังก์ชันเท่ากับ C: f(c) = C

ทฤษฎีบทเรื่องขอบเขตของฟังก์ชันต่อเนื่องในช่วงเวลาหนึ่งถ้าฟังก์ชัน f(x) ต่อเนื่องกันในช่วงเวลาหนึ่ง ฟังก์ชันนั้นจะถูกผูกไว้กับช่วงเวลานี้

ทฤษฎีบทว่าด้วยการเข้าถึงค่าต่ำสุดและค่าสูงสุดถ้าฟังก์ชัน f(x) ต่อเนื่องกันในช่วงเวลาหนึ่ง ฟังก์ชันจะไปถึงขอบเขตล่างและบนของช่วงเวลานี้

ทฤษฎีบทเรื่องความต่อเนื่องของฟังก์ชันผกผันปล่อยให้ฟังก์ชัน y=f(x) ต่อเนื่องและเพิ่ม (ลดลง) อย่างเคร่งครัดในช่วงเวลา [a,b] จากนั้นบนเซ็กเมนต์จะมีฟังก์ชันผกผัน x = g(y) และยังเพิ่ม (ลดลง) ซ้ำซากและต่อเนื่อง

ความต่อเนื่องของฟังก์ชัน จุดแตกหัก

วัวเดินแกว่งไปแกว่งมาถอนหายใจ:
- โอ้กระดานกำลังจะหมดแล้วตอนนี้ฉันจะล้มลง!

ในบทนี้ เราจะตรวจสอบแนวคิดเรื่องความต่อเนื่องของฟังก์ชัน การจำแนกจุดความไม่ต่อเนื่อง และปัญหาในทางปฏิบัติทั่วไป การศึกษาความต่อเนื่องของฟังก์ชัน- จากชื่อหัวข้อ หลายคนคาดเดาได้อย่างสังหรณ์ใจว่าจะมีการพูดคุยเรื่องอะไรและคิดว่าเนื้อหาค่อนข้างเรียบง่าย นี่เป็นเรื่องจริง แต่เป็นงานง่ายๆ ที่มักถูกลงโทษเนื่องจากการละเลยและเป็นแนวทางแก้ไขปัญหาอย่างผิวเผิน ดังนั้นฉันขอแนะนำให้คุณศึกษาบทความอย่างระมัดระวังและทำความเข้าใจรายละเอียดปลีกย่อยและเทคนิคทั้งหมด

คุณต้องรู้และสามารถทำอะไรได้บ้าง?ไม่มาก. หากต้องการเรียนรู้บทเรียนให้ดีคุณต้องเข้าใจว่ามันคืออะไร ขีดจำกัดของฟังก์ชัน- สำหรับผู้อ่านที่มีการเตรียมตัวน้อยก็สามารถเข้าใจบทความได้ ขีดจำกัดของฟังก์ชัน ตัวอย่างการแก้ปัญหาและดูความหมายทางเรขาคณิตของขีดจำกัดในคู่มือ กราฟและคุณสมบัติของฟังก์ชันเบื้องต้น- ขอแนะนำให้ทำความคุ้นเคยด้วย การแปลงทางเรขาคณิตของกราฟเนื่องจากการปฏิบัติในกรณีส่วนใหญ่เกี่ยวข้องกับการสร้างภาพวาด โอกาสเป็นแง่ดีสำหรับทุกคนและแม้แต่กาต้มน้ำเต็มก็สามารถรับมือกับงานได้ด้วยตัวเองในชั่วโมงหรือสองชั่วโมงข้างหน้า!

ความต่อเนื่องของฟังก์ชัน เบรกพอยต์และการจำแนกประเภท

แนวคิดเรื่องความต่อเนื่องของฟังก์ชัน

ลองพิจารณาฟังก์ชันบางอย่างที่ต่อเนื่องกันบนเส้นจำนวนทั้งหมด:

หรือพูดให้กระชับยิ่งขึ้น ฟังก์ชันของเราเปิดต่อเนื่อง (เซตของจำนวนจริง)

เกณฑ์ "ฟิลิสเตีย" ของความต่อเนื่องคืออะไร? แน่นอนว่ากราฟของฟังก์ชันต่อเนื่องสามารถวาดได้โดยไม่ต้องยกดินสอออกจากกระดาษ

ในกรณีนี้ ควรแยกแยะแนวคิดง่ายๆ สองแนวคิดอย่างชัดเจน: โดเมนของฟังก์ชันและ ความต่อเนื่องของฟังก์ชัน- โดยทั่วไปแล้ว มันไม่เหมือนกัน- ตัวอย่างเช่น:

ฟังก์ชันนี้ถูกกำหนดไว้บนเส้นจำนวนทั้งหมด นั่นคือ สำหรับ ทุกคนความหมายของ "x" มีความหมายของ "y" ในตัวเอง โดยเฉพาะถ้า แล้ว . โปรดทราบว่าอีกจุดหนึ่งจะถูกคั่นด้วยเครื่องหมายวรรคตอน เนื่องจากตามคำจำกัดความของฟังก์ชัน ค่าของอาร์กิวเมนต์จะต้องสอดคล้องกัน สิ่งเดียวเท่านั้นค่าฟังก์ชัน ดังนั้น, ขอบเขตของคำจำกัดความฟังก์ชั่นของเรา: .

อย่างไรก็ตาม ฟังก์ชั่นนี้ไม่ได้เปิดต่อเนื่อง !เห็นได้ชัดว่าถึงจุดที่เธอกำลังทุกข์อยู่ ช่องว่าง- คำนี้ค่อนข้างเข้าใจง่ายและมองเห็นได้ แน่นอนว่าดินสอจะต้องถูกฉีกออกจากกระดาษอยู่แล้ว อีกไม่นานเราจะดูการจำแนกประเภทของเบรกพอยต์

ความต่อเนื่องของฟังก์ชัน ณ จุดหนึ่งและตามช่วงเวลา

ในปัญหาทางคณิตศาสตร์บางข้อ เราสามารถพูดถึงความต่อเนื่องของฟังก์ชัน ณ จุดหนึ่ง ความต่อเนื่องของฟังก์ชันในช่วงเวลาหนึ่ง ครึ่งช่วง หรือความต่อเนื่องของฟังก์ชันบนเซ็กเมนต์ นั่นคือ ไม่มี "ความต่อเนื่องเพียงอย่างเดียว"– ฟังก์ชั่นสามารถต่อเนื่องได้ที่ไหนสักแห่ง และ "องค์ประกอบพื้นฐาน" พื้นฐานของทุกสิ่งทุกอย่างก็คือ ความต่อเนื่องของฟังก์ชัน ตรงจุด .

ทฤษฎีการวิเคราะห์ทางคณิตศาสตร์ให้คำจำกัดความของความต่อเนื่องของฟังก์ชันที่จุดหนึ่งโดยใช้ย่านใกล้เคียง "เดลต้า" และ "เอปไซลอน" แต่ในทางปฏิบัติ มีคำจำกัดความที่แตกต่างกันในการใช้งาน ซึ่งเราจะให้ความสนใจเป็นพิเศษ

ก่อนอื่นมาจำกันก่อน ข้อจำกัดด้านเดียวที่เข้ามาในชีวิตเราในบทเรียนแรก เกี่ยวกับกราฟฟังก์ชัน- พิจารณาสถานการณ์ในชีวิตประจำวัน:

ถ้าเราเข้าใกล้แกนจนถึงจุด ซ้าย(ลูกศรสีแดง) จากนั้นค่าที่สอดคล้องกันของ "เกม" จะไปตามแกนไปยังจุด (ลูกศรสีแดงเข้ม) ในทางคณิตศาสตร์ข้อเท็จจริงนี้ได้รับการแก้ไขโดยใช้ ขีดจำกัดด้านซ้าย:

ให้ความสนใจกับข้อความ (อ่านว่า “x มีแนวโน้มไปทางซ้าย”) สัญลักษณ์ "สารเติมแต่ง" "ลบศูนย์" โดยพื้นฐานแล้วหมายความว่าเรากำลังเข้าใกล้ตัวเลขจากด้านซ้าย

ในทำนองเดียวกัน หากเข้าใกล้จุด “กะ” ขวา(ลูกศรสีน้ำเงิน) จากนั้น “เกม” จะมาตามค่าเดียวกันแต่ตามลูกศรสีเขียวและ ขีดจำกัดทางขวามือจะถูกจัดรูปแบบดังนี้:

“สารเติมแต่ง” เป็นสัญลักษณ์ของ และข้อความอ่านว่า: “x มีแนวโน้มไปทางขวา”

หากขีดจำกัดด้านเดียวมีจำกัดและเท่ากัน(เช่นในกรณีของเรา): แล้วเราจะบอกว่ามีขีดจำกัดทั่วไป ง่ายๆ ข้อจำกัดทั่วไปคือ “ปกติ” ของเรา ขีดจำกัดของฟังก์ชันเท่ากับจำนวนจำกัด

โปรดทราบว่าหากไม่ได้กำหนดฟังก์ชันไว้ที่ (ชี้จุดสีดำบนกิ่งกราฟ) การคำนวณข้างต้นจะยังคงใช้ได้ ดังที่ได้กล่าวไปแล้วหลายครั้งโดยเฉพาะในบทความ เกี่ยวกับฟังก์ชันอันไม่สิ้นสุดสำนวนหมายความว่า "x" ปิดอย่างไม่มีที่สิ้นสุดเข้าใกล้จุดในขณะที่ ไม่สำคัญไม่ว่าฟังก์ชันจะถูกกำหนดไว้ที่จุดที่กำหนดหรือไม่ก็ตาม ตัวอย่างที่ดีจะพบได้ในย่อหน้าถัดไป เมื่อมีการวิเคราะห์ฟังก์ชัน

คำนิยาม: ฟังก์ชันจะต่อเนื่องที่จุดหนึ่งถ้าขีดจำกัดของฟังก์ชันที่จุดที่กำหนดเท่ากับค่าของฟังก์ชันที่จุดนั้น:

คำจำกัดความมีรายละเอียดตามข้อกำหนดต่อไปนี้:

1) ต้องกำหนดฟังก์ชันที่จุด นั่นคือ ต้องมีค่าอยู่

2) จะต้องมีขีดจำกัดทั่วไปของฟังก์ชัน ตามที่ระบุไว้ข้างต้น สิ่งนี้แสดงถึงความมีอยู่และความเท่าเทียมกันของขีดจำกัดด้านเดียว: .

3) ขีดจำกัดของฟังก์ชัน ณ จุดที่กำหนดจะต้องเท่ากับค่าของฟังก์ชัน ณ จุดนี้: .

หากฝ่าฝืน อย่างน้อยหนึ่งรายการจากเงื่อนไขทั้งสามนี้ ฟังก์ชันจะสูญเสียคุณสมบัติของความต่อเนื่องที่จุดนั้น

ความต่อเนื่องของฟังก์ชันในช่วงเวลาหนึ่งได้รับการกำหนดสูตรอย่างชาญฉลาดและเรียบง่ายมาก: ฟังก์ชันจะต่อเนื่องในช่วงเวลาถ้าฟังก์ชันต่อเนื่องที่ทุกจุดของช่วงเวลาที่กำหนด

โดยเฉพาะอย่างยิ่ง ฟังก์ชันจำนวนมากมีความต่อเนื่องในช่วงเวลาไม่สิ้นสุด กล่าวคือ บนเซตของจำนวนจริง นี่คือฟังก์ชันเชิงเส้น พหุนาม เลขชี้กำลัง ไซน์ โคไซน์ ฯลฯ และโดยทั่วไปแล้ว ฟังก์ชั่นเบื้องต้นอย่างต่อเนื่องบนมัน ขอบเขตของคำจำกัดความตัวอย่างเช่น ฟังก์ชันลอการิทึมจะต่อเนื่องในช่วงเวลา หวังว่าตอนนี้คุณคงพอมีความคิดที่ดีแล้วว่ากราฟของฟังก์ชันพื้นฐานจะเป็นอย่างไร ข้อมูลรายละเอียดเพิ่มเติมเกี่ยวกับความต่อเนื่องของพวกเขาสามารถรับได้จากชายผู้ใจดีชื่อ Fichtenholtz

ด้วยความต่อเนื่องของฟังก์ชันในส่วนและช่วงครึ่งเวลาทุกอย่างก็ไม่ใช่เรื่องยาก แต่เป็นการเหมาะสมกว่าที่จะพูดคุยเกี่ยวกับเรื่องนี้ในชั้นเรียน เกี่ยวกับการค้นหาค่าต่ำสุดและสูงสุดของฟังก์ชันบนเซ็กเมนต์แต่สำหรับตอนนี้เราไม่ต้องกังวลกับมันแล้ว

การจำแนกประเภทของจุดพัก

ชีวิตอันน่าทึ่งของฟังก์ชั่นนั้นเต็มไปด้วยประเด็นพิเศษทุกประเภท และจุดพักเป็นเพียงหนึ่งในหน้าชีวประวัติของพวกเขา

บันทึก : เผื่อไว้ผมจะอยู่ที่จุดเบื้องต้น จุดแตกหักอยู่เสมอ จุดเดียว– ไม่มี “จุดพักหลายจุดติดต่อกัน” กล่าวคือ ไม่มีสิ่งที่เรียกว่า “ช่วงพัก”

ประเด็นเหล่านี้กลับแบ่งออกเป็นสองกลุ่มใหญ่: การแตกร้าวประเภทแรกและ การแตกร้าวของประเภทที่สอง- ช่องว่างแต่ละประเภทมีคุณสมบัติเฉพาะของตัวเอง ซึ่งเราจะพิจารณาในตอนนี้:

จุดไม่ต่อเนื่องของชนิดแรก

หากสภาพความต่อเนื่องถูกละเมิด ณ จุดใดจุดหนึ่ง และขีดจำกัดด้านเดียว มีจำกัด แล้วมันถูกเรียกว่า จุดไม่ต่อเนื่องของชนิดแรก.

เริ่มจากกรณีที่มองโลกในแง่ดีที่สุดกันก่อน ตามแนวคิดดั้งเดิมของบทเรียน ฉันอยากจะบอกทฤษฎี "ในแง่ทั่วไป" แต่เพื่อที่จะแสดงให้เห็นถึงความเป็นจริงของเนื้อหา ฉันจึงตัดสินใจเลือกตัวเลือกที่มีอักขระเฉพาะ

มันน่าเศร้า เหมือนภาพคู่บ่าวสาวที่มีฉากหลังเป็นเปลวไฟนิรันดร์ แต่ภาพต่อไปนี้เป็นที่ยอมรับโดยทั่วไป ให้เราพรรณนากราฟของฟังก์ชันในรูปวาด:


ฟังก์ชันนี้จะต่อเนื่องบนเส้นจำนวนทั้งหมด ยกเว้นจุด ที่จริง ตัวส่วนไม่สามารถเท่ากับศูนย์ได้. อย่างไรก็ตามตามความหมายของขีดจำกัดเราทำได้ ปิดอย่างไม่มีที่สิ้นสุดเข้าใกล้ "ศูนย์" ทั้งจากด้านซ้ายและด้านขวานั่นคือมีขอบเขตด้านเดียวและเห็นได้ชัดว่าเกิดขึ้นพร้อมกัน:
(เงื่อนไขที่ 2 ของความต่อเนื่องเป็นที่พอใจ)

แต่ฟังก์ชันไม่ได้ถูกกำหนดไว้ที่จุด ดังนั้น เงื่อนไขหมายเลข 1 ของความต่อเนื่องจึงถูกละเมิด และฟังก์ชันจะประสบกับความไม่ต่อเนื่อง ณ จุดนี้

ตัวแบ่งประเภทนี้ (กับที่มีอยู่ ขีดจำกัดทั่วไป) ถูกเรียก ช่องว่างที่ซ่อมแซมได้- ทำไมต้องถอด? เพราะฟังก์ชั่นสามารถ กำหนดใหม่ที่จุดแตกหัก:

มันดูแปลกไหม? อาจจะ. แต่สัญกรณ์ฟังก์ชันดังกล่าวไม่ได้ขัดแย้งอะไรเลย! ตอนนี้ช่องว่างปิดลงแล้ว และทุกคนก็มีความสุข:


เรามาตรวจสอบอย่างเป็นทางการกัน:

2) – มีข้อจำกัดทั่วไป
3)

ดังนั้น เงื่อนไขทั้งสามจึงเป็นที่พอใจ และฟังก์ชันจะต่อเนื่องที่จุดหนึ่งโดยนิยามของความต่อเนื่องของฟังก์ชันที่จุดหนึ่ง

อย่างไรก็ตาม ผู้เกลียดชัง Matan สามารถกำหนดฟังก์ชันในลักษณะที่ไม่ดีได้ เป็นต้น :


ที่น่าสนใจคือตรงตามเงื่อนไขความต่อเนื่องสองข้อแรกที่นี่:
1) – ฟังก์ชั่นถูกกำหนด ณ จุดที่กำหนด;
2) – มีข้อจำกัดทั่วไป

แต่ขอบเขตที่สามยังไม่ผ่าน: นั่นคือขีดจำกัดของฟังก์ชัน ณ จุดนั้น ไม่เท่ากันค่าของฟังก์ชันที่กำหนด ณ จุดที่กำหนด

ดังนั้นเมื่อถึงจุดหนึ่งฟังก์ชันจะเกิดความไม่ต่อเนื่อง

ประการที่สองเรียกว่ากรณีที่น่าเศร้ากว่า การแตกร้าวประเภทแรก ด้วยการกระโดด- และความโศกเศร้าก็เกิดขึ้นจากขอบเขตด้านเดียวนั่นเอง มีขอบเขตและแตกต่าง- ตัวอย่างแสดงไว้ในภาพวาดที่สองของบทเรียน ช่องว่างดังกล่าวมักเกิดขึ้นใน ฟังก์ชันที่กำหนดเป็นชิ้นๆซึ่งได้รับการกล่าวถึงแล้วในบทความ เกี่ยวกับการแปลงกราฟ.

พิจารณาฟังก์ชันทีละชิ้น และเราจะวาดรูปให้เสร็จ จะสร้างกราฟได้อย่างไร? ง่ายมาก ในช่วงครึ่งเวลาเราวาดส่วนของพาราโบลา (สีเขียว) ในช่วงเวลา - ส่วนของเส้นตรง (สีแดง) และในช่วงครึ่ง - เส้นตรง (สีน้ำเงิน)

นอกจากนี้ เนื่องจากความไม่เท่าเทียมกัน ค่าจึงถูกกำหนดสำหรับฟังก์ชันกำลังสอง (จุดสีเขียว) และเนื่องจากความไม่เท่าเทียมกัน ค่าจึงถูกกำหนดสำหรับฟังก์ชันเชิงเส้น (จุดสีน้ำเงิน):

ในกรณีที่ยากที่สุด คุณควรหันไปสร้างกราฟแต่ละส่วนแบบจุดต่อจุด (ดูข้อแรก บทเรียนเกี่ยวกับกราฟของฟังก์ชัน).

ตอนนี้เราจะสนใจเฉพาะประเด็นนี้เท่านั้น มาตรวจสอบความต่อเนื่องกัน:

2) มาคำนวณขีดจำกัดด้านเดียวกัน

ทางด้านซ้ายเรามีส่วนของเส้นสีแดง ดังนั้นขีดจำกัดด้านซ้ายคือ:

ทางด้านขวาคือเส้นตรงสีน้ำเงิน และขีดจำกัดทางขวา:

เป็นผลให้เราได้รับ จำนวนจำกัดและพวกเขา ไม่เท่ากัน- เนื่องจากข้อจำกัดด้านเดียว มีขอบเขตและแตกต่าง: แล้วฟังก์ชันของเราก็จะทนได้ ความไม่ต่อเนื่องของประเภทแรกด้วยการกระโดด.

เป็นเหตุผลที่ไม่สามารถกำจัดช่องว่างได้ - ฟังก์ชั่นนี้ไม่สามารถกำหนดเพิ่มเติมได้และ "ติดกาวเข้าด้วยกัน" ดังในตัวอย่างก่อนหน้านี้

จุดไม่ต่อเนื่องของประเภทที่สอง

โดยปกติแล้ว กรณีอื่นๆ ของการแตกร้าวจะถูกจำแนกออกเป็นหมวดหมู่นี้อย่างชาญฉลาด ฉันจะไม่แสดงรายการทุกอย่าง เพราะในทางปฏิบัติ 99% ของปัญหาที่คุณจะพบ ช่องว่างที่ไม่มีที่สิ้นสุด– เมื่อถนัดซ้ายหรือถนัดขวา และบ่อยกว่านั้น ขีดจำกัดทั้งสองนั้นไม่มีที่สิ้นสุด

และแน่นอนว่าภาพที่เห็นได้ชัดที่สุดคือไฮเปอร์โบลาที่จุดศูนย์ ขีดจำกัดด้านเดียวทั้งสองนี้ไม่มีที่สิ้นสุด: ดังนั้น ฟังก์ชันจึงเกิดความไม่ต่อเนื่องของชนิดที่สอง ณ จุดนั้น

ฉันพยายามเติมเนื้อหาที่หลากหลายให้มากที่สุดในบทความของฉัน ดังนั้นเรามาดูกราฟของฟังก์ชันที่ยังไม่เคยเห็นมาก่อน:

ตามรูปแบบมาตรฐาน:

1) ฟังก์ชันไม่ได้ถูกกำหนด ณ จุดนี้เนื่องจากตัวส่วนไปที่ศูนย์

แน่นอน เราสามารถสรุปได้ทันทีว่าฟังก์ชันประสบกับความไม่ต่อเนื่องที่จุด แต่จะเป็นการดีที่จะจำแนกลักษณะของความไม่ต่อเนื่อง ซึ่งมักจำเป็นตามเงื่อนไข เมื่อต้องการทำสิ่งนี้:

ฉันขอเตือนคุณว่าโดยการบันทึกเราหมายถึง จำนวนลบที่น้อยที่สุดและภายใต้รายการ - จำนวนบวกที่น้อยที่สุด.

ขีดจำกัดด้านเดียวไม่มีที่สิ้นสุด ซึ่งหมายความว่าฟังก์ชันจะประสบกับความไม่ต่อเนื่องของประเภทที่ 2 ที่จุด แกน y คือ เส้นกำกับแนวตั้งสำหรับกราฟ

ไม่ใช่เรื่องแปลกที่ขีดจำกัดด้านเดียวจะมีอยู่ทั้งสองแบบ แต่มีเพียงอันเดียวเท่านั้นที่ไม่มีที่สิ้นสุด เช่น:

นี่คือกราฟของฟังก์ชัน

เราตรวจสอบจุดเพื่อความต่อเนื่อง:

1) ฟังก์ชั่นไม่ได้ถูกกำหนดไว้ ณ จุดนี้

2) มาคำนวณขีดจำกัดด้านเดียวกัน:

เราจะพูดถึงวิธีการคำนวณขีดจำกัดด้านเดียวดังกล่าวในสองตัวอย่างสุดท้ายของการบรรยายแม้ว่าผู้อ่านหลายคนจะได้เห็นและเดาทุกอย่างแล้วก็ตาม

ขีดจำกัดทางซ้ายมีขอบเขตจำกัดและเท่ากับศูนย์ (เรา “ไม่ได้ไปที่จุดนั้นเอง”) แต่ขีดจำกัดทางขวามือนั้นไม่มีที่สิ้นสุด และกิ่งก้านสีส้มของกราฟเข้าใกล้อย่างไม่สิ้นสุด เส้นกำกับแนวตั้งกำหนดโดยสมการ (เส้นประสีดำ)

ดังนั้นฟังก์ชันจึงทนทุกข์ทรมาน ความไม่ต่อเนื่องประเภทที่สองณ จุด

สำหรับความไม่ต่อเนื่องของประเภทที่ 1 สามารถกำหนดฟังก์ชันได้ที่จุดความไม่ต่อเนื่องนั้นเอง ตัวอย่างเช่น สำหรับฟังก์ชันทีละชิ้น คุณสามารถใส่จุดตัวหนาสีดำที่จุดเริ่มต้นของพิกัดได้ตามต้องการ ทางด้านขวามือเป็นกิ่งก้านของไฮเปอร์โบลา และขีดจำกัดทางขวามือนั้นไม่มีที่สิ้นสุด ฉันคิดว่าเกือบทุกคนมีความคิดว่ากราฟนี้มีลักษณะอย่างไร

สิ่งที่ทุกคนรอคอย:

จะตรวจสอบฟังก์ชันเพื่อความต่อเนื่องได้อย่างไร?

การศึกษาฟังก์ชันเพื่อความต่อเนื่อง ณ จุดหนึ่งจะดำเนินการตามแผนงานประจำที่กำหนดไว้แล้ว ซึ่งประกอบด้วยการตรวจสอบเงื่อนไขความต่อเนื่องสามประการ:

ตัวอย่างที่ 1

สำรวจฟังก์ชั่น

สารละลาย:

1) จุดเดียวภายในขอบเขตคือตำแหน่งที่ไม่ได้กำหนดฟังก์ชัน

2) มาคำนวณขีดจำกัดด้านเดียวกัน: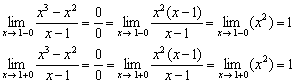

ขีดจำกัดด้านเดียวมีจำกัดและเท่ากัน

ดังนั้น ณ จุดที่ฟังก์ชันประสบปัญหาความไม่ต่อเนื่องแบบถอดได้

กราฟของฟังก์ชันนี้มีลักษณะอย่างไร

ฉันอยากจะทำให้มันง่ายขึ้น และดูเหมือนว่าจะได้พาราโบลาธรรมดามา แต่ฟังก์ชันดั้งเดิมไม่ได้ถูกกำหนดไว้ที่ point ดังนั้นจึงจำเป็นต้องมีส่วนคำสั่งต่อไปนี้:

มาวาดรูปกันเถอะ:

คำตอบ: ฟังก์ชันจะต่อเนื่องบนเส้นจำนวนทั้งหมด ยกเว้นจุดที่เกิดการไม่ต่อเนื่องแบบถอดได้

ฟังก์ชั่นสามารถกำหนดเพิ่มเติมได้ในทางที่ดีหรือไม่ดีนัก แต่ตามเงื่อนไขนี้ไม่จำเป็น

คุณบอกว่านี่เป็นตัวอย่างที่ลึกซึ้งใช่ไหม? ไม่เลย. สิ่งนี้เกิดขึ้นหลายสิบครั้งในทางปฏิบัติ งานเกือบทั้งหมดของไซต์มาจากงานอิสระและการทดสอบจริง

กำจัดโมดูลที่เราชื่นชอบ:

ตัวอย่างที่ 2

สำรวจฟังก์ชั่น เพื่อความต่อเนื่อง กำหนดลักษณะของความไม่ต่อเนื่องของฟังก์ชัน หากมี ดำเนินการวาดภาพ

สารละลาย: ด้วยเหตุผลบางประการ นักเรียนจึงกลัวและไม่ชอบฟังก์ชันที่มีโมดูล แม้ว่าจะไม่มีอะไรซับซ้อนก็ตาม เราได้สัมผัสเรื่องดังกล่าวแล้วเล็กน้อยในบทเรียน การแปลงเรขาคณิตของกราฟ- เนื่องจากโมดูลไม่เป็นค่าลบ จึงมีการขยายดังนี้: โดยที่ "อัลฟ่า" คือสำนวนบางอย่าง ในกรณีนี้ และฟังก์ชันของเราควรจะเขียนเป็นชิ้นๆ: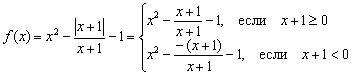

แต่เศษส่วนของทั้งสองชิ้นจะต้องลดลง การลดลงตามตัวอย่างก่อนหน้านี้จะไม่เกิดขึ้นโดยไม่มีผลกระทบ ฟังก์ชันดั้งเดิมไม่ได้ถูกกำหนดไว้ที่จุดเนื่องจากตัวส่วนไปที่ศูนย์ ดังนั้น ระบบควรระบุเงื่อนไขเพิ่มเติม และทำให้อสมการแรกเข้มงวด:

ตอนนี้เกี่ยวกับเทคนิคการตัดสินใจที่มีประโยชน์มาก: ก่อนที่จะจบงานในแบบร่าง จะเป็นประโยชน์ถ้าต้องเขียนแบบ (ไม่ว่าเงื่อนไขจะกำหนดหรือไม่ก็ตาม) สิ่งนี้จะช่วยให้มองเห็นจุดต่อเนื่องและจุดไม่ต่อเนื่องได้ทันที และประการที่สอง จะปกป้องคุณจากข้อผิดพลาด 100% เมื่อค้นหาขีดจำกัดด้านเดียว

มาวาดรูปกันเถอะ ตามการคำนวณของเรา ทางด้านซ้ายของจุดจำเป็นต้องวาดส่วนของพาราโบลา (สีน้ำเงิน) และทางด้านขวา - ชิ้นส่วนของพาราโบลา (สีแดง) ในขณะที่ไม่ได้กำหนดฟังก์ชันไว้ที่ ชี้ตัวเอง:

หากมีข้อสงสัย ให้นำค่า x สองสามค่ามาเสียบเข้ากับฟังก์ชัน (จำไว้ว่าโมดูลทำลายเครื่องหมายลบที่เป็นไปได้) และตรวจสอบกราฟ

ให้เราตรวจสอบฟังก์ชันเพื่อความต่อเนื่องในเชิงวิเคราะห์:

1) ฟังก์ชันไม่ได้ถูกกำหนดไว้ที่จุด ดังนั้นเราจึงบอกได้ทันทีว่ามันไม่ต่อเนื่องกันที่จุดนั้น

2) มากำหนดลักษณะของความไม่ต่อเนื่องกัน โดยคำนวณขีดจำกัดด้านเดียว:

ขีดจำกัดด้านเดียวมีจำกัดและแตกต่างกัน ซึ่งหมายความว่าฟังก์ชันจะทนทุกข์ทรมานจากความไม่ต่อเนื่องของประเภทที่ 1 ด้วยการกระโดดไปที่จุด โปรดทราบอีกครั้งว่าเมื่อค้นหาขีดจำกัด ไม่สำคัญว่าฟังก์ชันที่จุดพักจะถูกกำหนดหรือไม่

ตอนนี้สิ่งที่เหลืออยู่คือการถ่ายโอนภาพวาดจากแบบร่าง (มันถูกสร้างขึ้นราวกับได้รับความช่วยเหลือจากการวิจัย ;-)) และทำงานให้เสร็จสิ้น:

คำตอบ: ฟังก์ชันจะต่อเนื่องกันบนเส้นจำนวนทั้งหมด ยกเว้นจุดที่ฟังก์ชันดังกล่าวเกิดความไม่ต่อเนื่องแบบแรกด้วยการกระโดด

บางครั้งจำเป็นต้องมีข้อบ่งชี้เพิ่มเติมเกี่ยวกับการไม่ต่อเนื่องของการกระโดด คำนวณง่ายๆ - จากขีด จำกัด ด้านขวาคุณต้องลบขีด จำกัด ด้านซ้าย: นั่นคือที่จุดพักฟังก์ชันของเรากระโดดลงมา 2 หน่วย (ตามที่เครื่องหมายลบบอกเรา)

ตัวอย่างที่ 3

สำรวจฟังก์ชั่น เพื่อความต่อเนื่อง กำหนดลักษณะของความไม่ต่อเนื่องของฟังก์ชัน หากมี วาดรูป.

นี่เป็นตัวอย่างให้คุณแก้ด้วยตัวเอง ซึ่งเป็นตัวอย่างวิธีแก้ปัญหาในตอนท้ายของบทเรียน

เรามาดูงานที่ได้รับความนิยมและแพร่หลายที่สุดกันดีกว่าเมื่อฟังก์ชันประกอบด้วยสามส่วน:

ตัวอย่างที่ 4

ตรวจสอบฟังก์ชันเพื่อความต่อเนื่องและวาดกราฟของฟังก์ชัน .

สารละลาย: เห็นได้ชัดว่าทั้งสามส่วนของฟังก์ชันมีความต่อเนื่องในช่วงเวลาที่สอดคล้องกัน ดังนั้นจึงยังคงต้องตรวจสอบ "ทางแยก" เพียงสองจุดระหว่างส่วนต่างๆ ก่อนอื่นเรามาร่างแบบร่างกันก่อนฉันแสดงความคิดเห็นเกี่ยวกับเทคนิคการก่อสร้างโดยละเอียดเพียงพอในส่วนแรกของบทความ สิ่งเดียวคือเราต้องปฏิบัติตามจุดเอกพจน์ของเราอย่างระมัดระวัง: เนื่องจากความไม่เท่าเทียมกัน ค่าจึงเป็นของเส้นตรง (จุดสีเขียว) และเนื่องจากความไม่เท่าเทียมกัน ค่าจึงเป็นของพาราโบลา (จุดสีแดง):


โดยหลักการแล้วทุกอย่างชัดเจน =) สิ่งที่เหลืออยู่คือการตัดสินใจอย่างเป็นทางการ สำหรับแต่ละจุด "ร่วม" เราจะตรวจสอบเงื่อนไขความต่อเนื่อง 3 ประการตามมาตรฐาน:

ฉัน)เราตรวจสอบจุดเพื่อความต่อเนื่อง

1)

ขีดจำกัดด้านเดียวมีจำกัดและแตกต่างกัน ซึ่งหมายความว่าฟังก์ชันจะทนทุกข์ทรมานจากความไม่ต่อเนื่องของประเภทที่ 1 ด้วยการกระโดดไปที่จุด

ให้เราคำนวณการกระโดดไม่ต่อเนื่องเนื่องจากความแตกต่างระหว่างขีดจำกัดด้านขวาและด้านซ้าย:
นั่นคือกราฟกระตุกขึ้นหนึ่งหน่วย

ครั้งที่สอง)เราตรวจสอบจุดเพื่อความต่อเนื่อง

1) – ฟังก์ชั่นถูกกำหนด ณ จุดที่กำหนด

2) ค้นหาขีดจำกัดด้านเดียว:

– ขีดจำกัดด้านเดียวมีจำกัดและเท่ากัน ซึ่งหมายความว่ามีขีดจำกัดทั่วไป

3) – ขีดจำกัดของฟังก์ชัน ณ จุดหนึ่งเท่ากับค่าของฟังก์ชันนี้ที่จุดที่กำหนด

ในขั้นตอนสุดท้าย เราถ่ายโอนภาพวาดไปยังเวอร์ชันสุดท้าย หลังจากนั้นเราใส่คอร์ดสุดท้าย:

คำตอบ: ฟังก์ชันจะต่อเนื่องกันบนเส้นจำนวนทั้งหมด ยกเว้นจุดที่ฟังก์ชันดังกล่าวเกิดความไม่ต่อเนื่องแบบแรกด้วยการกระโดด

ตัวอย่างที่ 5

ตรวจสอบฟังก์ชันเพื่อความต่อเนื่องและสร้างกราฟ .

นี่คือตัวอย่างสำหรับวิธีแก้ปัญหาแบบอิสระ วิธีแก้ปัญหาสั้นๆ และตัวอย่างปัญหาโดยประมาณในตอนท้ายของบทเรียน

คุณอาจรู้สึกว่า ณ จุดหนึ่งฟังก์ชันจะต้องต่อเนื่อง และอีกจุดหนึ่งจะต้องมีความไม่ต่อเนื่อง ในทางปฏิบัติสิ่งนี้ไม่ได้เป็นเช่นนั้นเสมอไป พยายามอย่าละเลยตัวอย่างที่เหลือ - จะมีคุณสมบัติที่น่าสนใจและสำคัญหลายประการ:

ตัวอย่างที่ 6

กำหนดให้มีฟังก์ชัน - ตรวจสอบฟังก์ชันเพื่อความต่อเนื่องที่จุดต่างๆ สร้างกราฟ

สารละลาย: และดำเนินการวาดแบบร่างทันทีอีกครั้ง:

ลักษณะเฉพาะของกราฟนี้คือฟังก์ชันชิ้นเดียวได้มาจากสมการของแกนแอบซิสซา ที่นี่บริเวณนี้วาดด้วยสีเขียว แต่ในสมุดบันทึกมักจะเน้นด้วยดินสอธรรมดาด้วยตัวหนา และแน่นอนว่า อย่าลืมแกะของเราด้วย: ค่าเป็นของกิ่งแทนเจนต์ (จุดสีแดง) และค่าเป็นของเส้นตรง

ทุกอย่างชัดเจนจากการวาดภาพ - ฟังก์ชั่นต่อเนื่องตลอดเส้นจำนวนทั้งหมด สิ่งที่เหลืออยู่คือทำให้โซลูชันเป็นระเบียบซึ่งนำไปสู่ระบบอัตโนมัติเต็มรูปแบบอย่างแท้จริงหลังจาก 3-4 ตัวอย่างที่คล้ายกัน:

ฉัน)เราตรวจสอบจุดเพื่อความต่อเนื่อง

1) – ฟังก์ชั่นถูกกำหนดไว้ที่จุดที่กำหนด

2) มาคำนวณขีดจำกัดด้านเดียวกัน:

ซึ่งหมายความว่ามีขีดจำกัดทั่วไป

ในกรณีนี้ ฉันขอเตือนคุณถึงข้อเท็จจริงเล็กน้อย: ขีดจำกัดของค่าคงที่เท่ากับค่าคงที่นั้นเอง ในกรณีนี้ ขีดจำกัดของศูนย์จะเท่ากับศูนย์เอง (ขีดจำกัดทางซ้าย)

3) – ขีดจำกัดของฟังก์ชัน ณ จุดหนึ่งเท่ากับค่าของฟังก์ชันนี้ที่จุดที่กำหนด

ดังนั้นฟังก์ชันจะมีความต่อเนื่องที่จุดหนึ่งโดยนิยามของความต่อเนื่องของฟังก์ชันที่จุดหนึ่ง

ครั้งที่สอง)เราตรวจสอบจุดเพื่อความต่อเนื่อง

1) – ฟังก์ชั่นถูกกำหนดไว้ที่จุดที่กำหนด

2) ค้นหาขีดจำกัดด้านเดียว:

และตรงนี้ – ขีดจำกัดของหนึ่งเท่ากับหน่วยของมันเอง

– มีข้อจำกัดทั่วไป

3) – ขีดจำกัดของฟังก์ชัน ณ จุดหนึ่งเท่ากับค่าของฟังก์ชันนี้ที่จุดที่กำหนด

ดังนั้นฟังก์ชันจะมีความต่อเนื่องที่จุดหนึ่งโดยนิยามของความต่อเนื่องของฟังก์ชันที่จุดหนึ่ง

ตามปกติหลังจากการวิจัย เราจะโอนภาพวาดของเราไปยังเวอร์ชันสุดท้าย

คำตอบ: ฟังก์ชันมีความต่อเนื่องที่จุดต่างๆ

โปรดทราบว่าในสภาวะที่เราไม่ได้ถามอะไรเกี่ยวกับการศึกษาฟังก์ชันทั้งหมดเพื่อความต่อเนื่องและถือเป็นรูปแบบทางคณิตศาสตร์ที่ดีในการกำหนด แม่นยำและชัดเจนคำตอบสำหรับคำถามที่ถูกโพสต์ อย่างไรก็ตาม หากเงื่อนไขไม่ต้องการให้คุณสร้างกราฟ คุณก็มีสิทธิที่จะไม่สร้างกราฟนั้น (แม้ว่าครูจะบังคับให้คุณทำเช่นนี้ในภายหลังก็ตาม)

"ลิ้นบิด" ทางคณิตศาสตร์ขนาดเล็กสำหรับการแก้ปัญหาด้วยตัวเอง:

ตัวอย่างที่ 7

กำหนดให้มีฟังก์ชัน - ตรวจสอบฟังก์ชันเพื่อความต่อเนื่องที่จุดต่างๆ จำแนกเบรกพอยต์ ถ้ามี ดำเนินการวาดภาพ

พยายาม "ออกเสียง" "คำ" ทั้งหมดให้ถูกต้อง =) และวาดกราฟได้แม่นยำยิ่งขึ้นแม่นยำจะไม่ฟุ่มเฟือยทุกที่ ;-)

ดังที่คุณจำได้ ฉันแนะนำให้วาดรูปเป็นแบบร่างทันที แต่ในบางครั้งคุณจะพบตัวอย่างที่คุณไม่สามารถทราบได้ทันทีว่ากราฟมีลักษณะอย่างไร ดังนั้นในบางกรณี การหาขีดจำกัดด้านเดียวก่อนจึงเป็นประโยชน์ จากนั้นจึงแสดงภาพกิ่งก้านตามการศึกษา ในสองตัวอย่างสุดท้าย เราจะเรียนรู้เทคนิคในการคำนวณขีดจำกัดด้านเดียวด้วย:

ตัวอย่างที่ 8

ตรวจสอบฟังก์ชันเพื่อความต่อเนื่องและสร้างกราฟแผนผัง

สารละลาย: จุดเสียนั้นชัดเจน: (ลดตัวส่วนของเลขชี้กำลังให้เป็นศูนย์) และ (ลดตัวส่วนของเศษส่วนทั้งหมดให้เหลือศูนย์) ยังไม่ชัดเจนว่ากราฟของฟังก์ชันนี้มีลักษณะอย่างไร ซึ่งหมายความว่าควรศึกษาข้อมูลก่อนจะดีกว่า

คำนิยาม
ฟังก์ชัน ฉ (เอ็กซ์)เรียกว่า ต่อเนื่องที่จุด x 0 ย่านใกล้เคียงของจุดนี้ และถ้าลิมิตเป็น x มีแนวโน้มเป็น x 0 เท่ากับค่าฟังก์ชันที่ x 0 :
.

เราสามารถให้ได้โดยใช้คำจำกัดความของ Cauchy และ Heine ของขีดจำกัดของฟังก์ชัน ขยายคำจำกัดความของความต่อเนื่องของฟังก์ชัน ณ จุดหนึ่ง .

เราสามารถกำหนดแนวคิดเรื่องความต่อเนื่องได้ใน ในแง่ของการเพิ่มขึ้น- เพื่อทำเช่นนี้ เราแนะนำตัวแปรใหม่ ซึ่งเรียกว่าการเพิ่มขึ้นของตัวแปร x ณ จุดนั้น
.
จากนั้นฟังก์ชันจะต่อเนื่องที่จุดถ้า
.
ขอแนะนำฟังก์ชันใหม่: พวกเขาโทรหาเธอเพิ่มฟังก์ชัน
.

ณ จุด
ฟังก์ชัน ฉ (เอ็กซ์)เรียกว่า จากนั้นฟังก์ชันจะต่อเนื่องที่จุดถ้า 0 หากถูกกำหนดไว้ที่บริเวณใกล้เคียงด้านขวา (ด้านซ้าย) ของจุดนี้ และหากกำหนดขอบเขตด้านขวา (ซ้าย) ที่จุด x 0 เท่ากับค่าฟังก์ชันที่ x 0 :
.

ทฤษฎีบทเรื่องขอบเขตของฟังก์ชันต่อเนื่อง
ปล่อยให้ฟังก์ชัน f (เอ็กซ์)มีความต่อเนื่องที่จุด x 0 - แล้วก็มีย่าน U (x0)ซึ่งฟังก์ชันมีจำกัด

ทฤษฎีบทการรักษาสัญลักษณ์ของฟังก์ชันต่อเนื่อง
ให้ฟังก์ชันต่อเนื่อง ณ จุดนั้น
.
และปล่อยให้มันมีค่าบวก (ลบ) ณ จุดนี้:
จากนั้นจะมีย่านใกล้เคียงของจุดที่ฟังก์ชันมีค่าบวก (ลบ):

ที่ .
คุณสมบัติทางคณิตศาสตร์ของฟังก์ชันต่อเนื่อง
ให้ฟังก์ชันและต่อเนื่องกันตรงจุด
แล้วทำหน้าที่และต่อเนื่องกันที่จุดนั้น

ถ้า แล้วฟังก์ชันจะต่อเนื่องกันที่จุดนั้น
คุณสมบัติความต่อเนื่องซ้าย-ขวา

ฟังก์ชันจะต่อเนื่องที่จุดหนึ่งก็ต่อเมื่อฟังก์ชันต่อเนื่องทางขวาและซ้ายเท่านั้น

ความต่อเนื่องของฟังก์ชันที่ซับซ้อน

การพิสูจน์คุณสมบัติแสดงไว้ในหน้า “คุณสมบัติของฟังก์ชันต่อเนื่อง ณ จุดหนึ่ง”
ทฤษฎีบทความต่อเนื่องของฟังก์ชันเชิงซ้อน
ให้ฟังก์ชันต่อเนื่อง ณ จุดนั้น

และปล่อยให้ฟังก์ชันต่อเนื่องตรงจุดนั้น

จากนั้นฟังก์ชันเชิงซ้อนจะต่อเนื่องกันที่จุดนั้น
ขีดจำกัดของฟังก์ชันที่ซับซ้อน
.
ทฤษฎีบทเกี่ยวกับขีดจำกัดของฟังก์ชันต่อเนื่องของฟังก์ชัน 0 ให้มีขีดจำกัดของฟังก์ชันที่ และจะเท่ากับ:
นี่คือจุด T
อาจมีขอบเขตจำกัดหรือห่างไกลได้ไม่จำกัด: .
.

และปล่อยให้ฟังก์ชันต่อเนื่องตรงจุดนั้น
ฟังก์ชันที่ซับซ้อนจะมีขีดจำกัด และจะเท่ากับ:
ทฤษฎีบทเกี่ยวกับขีดจำกัดของฟังก์ชันเชิงซ้อน
ปล่อยให้ฟังก์ชันมีขีดจำกัดและแมปย่านใกล้เคียงที่เจาะทะลุของจุดหนึ่งไปยังย่านใกล้เคียงที่เจาะทะลุของจุดหนึ่ง
.

ปล่อยให้ฟังก์ชันถูกกำหนดในย่านนี้และมีขีดจำกัด

นี่คือจุดสุดท้ายหรือจุดที่อยู่ห่างไกลอย่างไม่สิ้นสุด: .
บริเวณใกล้เคียงและขีดจำกัดที่สอดคล้องกันสามารถเป็นได้ทั้งแบบสองด้านหรือด้านเดียว ฟังก์ชันที่ซับซ้อนจะมีขีดจำกัดและมีค่าเท่ากับ:จุดพัก
การกำหนดจุดแตกหัก
ให้ฟังก์ชันถูกกำหนดไว้ในพื้นที่ใกล้เคียงที่ถูกเจาะทะลุของจุด

ประเด็นนี้เรียกว่า
จุดพักฟังก์ชัน จุดไม่ต่อเนื่องของชนิดแรกหากตรงตามเงื่อนไขข้อใดข้อหนึ่งต่อไปนี้:
.

1) ไม่ได้กำหนดไว้ใน ;
2) ถูกกำหนดไว้ที่ แต่ไม่ได้อยู่ที่จุดนี้การกำหนดจุดไม่ต่อเนื่องของชนิดที่ 1
.

ประเด็นนี้เรียกว่า
จุดพักฟังก์ชัน , ถ้า เป็นจุดพักและมีขีดจำกัดด้านเดียวด้านซ้ายและขวา:คำจำกัดความของการข้ามฟังก์ชัน
,
ฟังก์ชันกระโดด Δ

ดังนั้นจุดของความไม่ต่อเนื่องแบบถอดได้คือจุดของความไม่ต่อเนื่องของชนิดที่ 1 ซึ่งการกระโดดของฟังก์ชันมีค่าเท่ากับศูนย์

การกำหนดจุดไม่ต่อเนื่องของชนิดที่ 2
จุดพักฟังก์ชัน จุดไม่ต่อเนื่องของประเภทที่สองถ้าไม่ใช่จุดไม่ต่อเนื่องของชนิดที่ 1

นั่นคือ หากไม่มีขีดจำกัดด้านเดียวอย่างน้อยหนึ่งขีดจำกัด หรืออย่างน้อยหนึ่งขีดจำกัดด้านเดียวที่จุดหนึ่งจะเท่ากับอนันต์

คุณสมบัติของฟังก์ชันต่อเนื่องในช่วงเวลาหนึ่ง
คำจำกัดความของฟังก์ชันต่อเนื่องในช่วงเวลาหนึ่ง

ฟังก์ชันจะเรียกว่าต่อเนื่องในช่วงเวลา (at) ถ้าฟังก์ชันต่อเนื่องที่ทุกจุดของช่วงเปิด (at) และที่จุด a และ b ตามลำดับ
ทฤษฎีบทแรกของไวเออร์ชตราสเกี่ยวกับขอบเขตของฟังก์ชันต่อเนื่องในช่วงเวลาหนึ่ง

ถ้าฟังก์ชันต่อเนื่องในช่วงเวลาหนึ่ง ฟังก์ชันนั้นจะถูกผูกไว้กับช่วงเวลานี้
การกำหนดความสำเร็จสูงสุด (ขั้นต่ำ)
ฟังก์ชันจะถึงค่าสูงสุด (ขั้นต่ำ) ในชุดหากมีข้อโต้แย้ง

สำหรับทุกคน
การกำหนดความสามารถในการเข้าถึงของใบหน้าส่วนบน (ล่าง)
.

ฟังก์ชันจะไปถึงขอบเขตบน (ล่าง) ของชุดหากมีข้อโต้แย้ง
ทฤษฎีบทที่สองของไวเออร์ชตราสเกี่ยวกับค่าสูงสุดและต่ำสุดของฟังก์ชันต่อเนื่อง

ฟังก์ชันที่ต่อเนื่องบนเซ็กเมนต์ถึงขอบเขตบนและล่างของมัน หรือซึ่งเหมือนกัน คือไปถึงจุดสูงสุดและต่ำสุดบนเซ็กเมนต์
ทฤษฎีบทค่ากลางโบลซาโน-คอชี
.

ปล่อยให้ฟังก์ชันต่อเนื่องบนเซ็กเมนต์
และให้ C เป็นตัวเลขใดก็ได้ที่อยู่ระหว่างค่าของฟังก์ชันที่ส่วนท้ายของเซ็กเมนต์: และ .
.

แล้วมีจุดที่
ข้อพิสูจน์ 1
จากนั้นจะมีย่านใกล้เคียงของจุดที่ฟังก์ชันมีค่าบวก (ลบ):

ปล่อยให้ฟังก์ชันต่อเนื่องบนเซ็กเมนต์

และปล่อยให้ค่าฟังก์ชันที่ส่วนท้ายของเซกเมนต์มีเครื่องหมายต่างกัน: หรือ .
จากนั้นจะมีจุดที่ค่าของฟังก์ชันเท่ากับศูนย์:
ฟังก์ชันจะถึงค่าสูงสุด (ขั้นต่ำ) ในชุดหากมีข้อโต้แย้ง
ข้อพิสูจน์ 2 ปล่อยให้ฟังก์ชันต่อเนื่องบนเซ็กเมนต์และปล่อยให้มันเป็นไป
.

จากนั้นฟังก์ชันจะใช้ตามช่วงเวลาของค่าทั้งหมดจากและเฉพาะค่าเหล่านี้:
;
ฟังก์ชันผกผัน
ฟังก์ชันจะถึงค่าสูงสุด (ขั้นต่ำ) ในชุดหากมีข้อโต้แย้ง

นิยามของฟังก์ชันผกผัน
ปล่อยให้ฟังก์ชันมีโดเมนคำจำกัดความ X และชุดของค่า Y

และปล่อยให้มีทรัพย์สิน:
กราฟของฟังก์ชันตรงและฟังก์ชันผกผันมีความสมมาตรเมื่อเทียบกับเส้นตรง

ทฤษฎีบทเกี่ยวกับการดำรงอยู่และความต่อเนื่องของฟังก์ชันผกผันในช่วงเวลาหนึ่ง
ปล่อยให้ฟังก์ชันมีความต่อเนื่องและเพิ่มขึ้น (ลดลง) ในส่วนของเซ็กเมนต์อย่างเคร่งครัด

จากนั้นฟังก์ชันผกผันจะถูกกำหนดและต่อเนื่องบนเซ็กเมนต์ ซึ่งจะเพิ่ม (ลดลง) อย่างเคร่งครัด

สำหรับฟังก์ชั่นที่เพิ่มขึ้น
สำหรับการลดลง - .

ทฤษฎีบทเกี่ยวกับการดำรงอยู่และความต่อเนื่องของฟังก์ชันผกผันในช่วงเวลาหนึ่ง
ปล่อยให้ฟังก์ชันมีความต่อเนื่องและเพิ่มขึ้น (ลดลง) อย่างเคร่งครัดในช่วงเปิดหรือช่วงอนันต์

จากนั้นฟังก์ชันผกผันจะถูกกำหนดและต่อเนื่องในช่วงเวลาซึ่งจะเพิ่มขึ้น (ลดลง) อย่างเคร่งครัด

สำหรับฟังก์ชั่นที่เพิ่มขึ้น

สำหรับการลดลง: .

ในทำนองเดียวกัน เราสามารถกำหนดทฤษฎีบทเกี่ยวกับการมีอยู่และความต่อเนื่องของฟังก์ชันผกผันในช่วงครึ่งเวลาได้

คุณสมบัติและความต่อเนื่องของฟังก์ชันเบื้องต้น ฟังก์ชันเบื้องต้นและการผกผันของฟังก์ชันจะต่อเนื่องกันในขอบเขตของคำจำกัดความ ด้านล่างนี้เราจะนำเสนอสูตรของทฤษฎีบทที่เกี่ยวข้องและมีลิงก์ไปยังข้อพิสูจน์ฟังก์ชันเลขชี้กำลัง > 0 ฟังก์ชันเลขชี้กำลังฉ
,
(x) = ขวาน
.

โดยมีฐาน ก
คือขีดจำกัดของลำดับ
โดยที่ลำดับของจำนวนตรรกยะโดยพลการพุ่งไปที่ x:ทฤษฎีบท. คุณสมบัติของฟังก์ชันเลขชี้กำลัง
ฟังก์ชันเลขชี้กำลังมีคุณสมบัติดังต่อไปนี้:(ป.0) 1 กำหนดไว้ สำหรับ สำหรับทั้งหมด ;
(หน้า 1)สำหรับ ≠
มีหลายความหมาย ;
(ป.2) ;
เพิ่มขึ้นอย่างเคร่งครัดที่ , ลดลงอย่างเคร่งครัดที่ , คงที่ที่ ; ;
(ป.3) ;
(หน้า 3*) ;
(ป.4) ;
(หน้า 5)(หน้า 6)
(หน้า 7)(หน้า 8)
จากนั้นจะมีย่านใกล้เคียงของจุดที่ฟังก์ชันมีค่าบวก (ลบ):

ต่อเนื่องสำหรับทุกคน

(หน้า 9) ที่ ;ลอการิทึมฟังก์ชันลอการิทึมหรือลอการิทึม y

= บันทึก a x
โดยมีฐาน ก คือค่าผกผันของฟังก์ชันเลขชี้กำลังที่มีฐาน aทฤษฎีบท. คุณสมบัติของลอการิทึม
ฟังก์ชันลอการิทึมที่มีฐาน a, y =เข้าสู่ระบบ x
มีคุณสมบัติดังต่อไปนี้:กำหนดไว้ สำหรับ สำหรับทั้งหมด ;
(ฏ.1)กำหนดและต่อเนื่อง สำหรับ และ สำหรับค่าบวกของอาร์กิวเมนต์
(ฏ.2)(หน้า 8)
(หน้า 8)
(ฏ.3) ;
เพิ่มขึ้นอย่างเคร่งครัดเมื่อ ลดลงอย่างเคร่งครัดเมื่อ ;(หน้า 8)
(ฏ.4)(หน้า 8)
(ฏ.5)(หน้า 8)
(ฏ.6)จากนั้นจะมีย่านใกล้เคียงของจุดที่ฟังก์ชันมีค่าบวก (ลบ):

(ฏ.7)

(ฏ.8)
.
(ฏ.9)

เลขชี้กำลังและลอการิทึมธรรมชาติ
ในคำจำกัดความของฟังก์ชันเลขชี้กำลังและลอการิทึม ค่าคงที่จะปรากฏขึ้น ซึ่งเรียกว่าฐานของกำลังหรือฐานของลอการิทึม ในการวิเคราะห์ทางคณิตศาสตร์ ในกรณีส่วนใหญ่ การคำนวณจะง่ายกว่าหากใช้ตัวเลข e เป็นฐาน:
"ลอการิทึมธรรมชาติ ฟังก์ชัน ln x"

ฟังก์ชั่นพลังงาน

ฟังก์ชันยกกำลังพร้อมเลขชี้กำลัง pคือฟังก์ชัน f (x) = xpซึ่งค่าที่จุด x เท่ากับค่าของฟังก์ชันเลขชี้กำลังที่มีฐาน x ที่จุด p
นอกจากนี้ฉ (0) = 0 พิ = 0สำหรับพี > 0 .

ที่นี่เราจะพิจารณาคุณสมบัติของฟังก์ชันกำลัง y = x p สำหรับค่าที่ไม่เป็นลบของอาร์กิวเมนต์
สำหรับเหตุผล สำหรับค่า m คี่ ฟังก์ชันกำลังก็ถูกกำหนดไว้สำหรับค่าลบ x เช่นกัน

ในกรณีนี้สามารถรับคุณสมบัติของมันได้โดยใช้เลขคู่หรือคี่
กรณีเหล่านี้จะกล่าวถึงโดยละเอียดและแสดงไว้ในหน้า “ฟังก์ชันกำลัง คุณสมบัติและกราฟ”
ทฤษฎีบท. คุณสมบัติของฟังก์ชันกำลัง (x ≥ 0)ฟังก์ชันยกกำลัง y = x p โดยมีเลขชี้กำลัง p มีคุณสมบัติดังต่อไปนี้:
(ค.1)
กำหนดและต่อเนื่องบนชุด

ที่ ,

ที่ ".
ฟังก์ชันตรีโกณมิติ ทฤษฎีบทเรื่องความต่อเนื่องของฟังก์ชันตรีโกณมิติฟังก์ชันตรีโกณมิติ: ไซน์ ( บาป x), โคไซน์ ( เพราะ x) แทนเจนต์ ( ทีจีเอ็กซ์

) และโคแทนเจนต์ (
ซีทีจี x ทฤษฎีบทเรื่องความต่อเนื่องของฟังก์ชันตรีโกณมิติผกผันฟังก์ชันตรีโกณมิติผกผัน: อาร์คไซน์ ( อาร์คซิน x), ส่วนโค้งโคไซน์ ( อาร์คคอส x), อาร์กแทนเจนต์ ( อาร์คแทน เอ็กซ์) และส่วนโค้งแทนเจนต์ (

อาร์คซีจี x
) มีความต่อเนื่องในขอบเขตคำจำกัดความ
วรรณกรรมที่ใช้:
โอ.ไอ. เบซอฟ. บรรยายเรื่องการวิเคราะห์ทางคณิตศาสตร์ ตอนที่ 1 มอสโก 2547