ฟังก์ชัน Ex tre moma วิธีค้นหาจุดปลายสุดของฟังก์ชัน

ผ่านความไม่เท่าเทียมกันเหล่านี้ไปจนถึงขีดจำกัดที่ Δ x→ 0 และคำนึงถึงอนุพันธ์ด้วย ฉ "(x 0) มีอยู่ ดังนั้นขีดจำกัดทางด้านซ้ายจึงไม่ขึ้นอยู่กับว่า Δ เป็นอย่างไร x→ 0 เราได้: ที่ Δ x → 0 – 0 ฉ" (x 0) ≥ 0 a ที่Δ x → 0 + 0 ฉ" (x 0) ≤ 0 เนื่องจาก ฉ" (x 0) กำหนดตัวเลข ดังนั้นอสมการทั้งสองนี้จะเข้ากันได้ก็ต่อเมื่อ ฉ" (x 0) = 0.

ทฤษฎีบทที่ได้รับการพิสูจน์แล้วระบุว่าคะแนนสูงสุดและต่ำสุดสามารถพบได้เฉพาะในค่าของการโต้แย้งที่อนุพันธ์กลายเป็นศูนย์เท่านั้น

เราพิจารณากรณีที่ฟังก์ชันมีอนุพันธ์ที่ทุกจุดของเซกเมนต์หนึ่งๆ กรณีที่ไม่มีอนุพันธ์จะเป็นอย่างไร? ลองดูตัวอย่าง

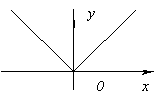
ย =|x |.

ฟังก์ชันไม่มีอนุพันธ์ ณ จุดนั้น x=0 ( ณ จุดนี้ กราฟของฟังก์ชันไม่มีค่าแทนเจนต์ที่กำหนดไว้) แต่ ณ จุดนี้ ฟังก์ชันมีค่าต่ำสุด เนื่องจาก ย(0)=0 และสำหรับทั้งหมด x ≠ 0ย > 0.

ดังนั้น จากตัวอย่างที่ให้มาและทฤษฎีบทที่จัดทำขึ้น เป็นที่ชัดเจนว่าฟังก์ชันสามารถมีจุดสุดขั้วได้ในสองกรณีเท่านั้น: 1) ณ จุดที่มีอนุพันธ์อยู่และเท่ากับศูนย์; 2) ณ จุดที่ไม่มีอนุพันธ์อยู่

อย่างไรก็ตามหากถึงจุดใดจุดหนึ่ง x 0 เรารู้สิ่งนั้น ฉ "(x 0 ) =0 จึงไม่สามารถสรุปได้ว่า ณ จุดนั้น x 0 ฟังก์ชันมีปลายสุด

ตัวอย่างเช่น.

แต่ช่วง x=0 ไม่ใช่จุดสุดขั้ว เนื่องจากทางด้านซ้ายของจุดนี้ ค่าฟังก์ชันจะอยู่ใต้แกน วัวและทางด้านขวาด้านบน

ค่าของอาร์กิวเมนต์จากโดเมนของฟังก์ชันที่อนุพันธ์ของฟังก์ชันหายไปหรือไม่มีอยู่เรียกว่า จุดวิกฤติ .

จากที่กล่าวมาทั้งหมด จุดปลายสุดของฟังก์ชันจะอยู่ในหมู่จุดวิกฤต อย่างไรก็ตาม ไม่ใช่ทุกจุดวิกฤติที่จะเป็นจุดปลายสุด ดังนั้น ในการค้นหาจุดปลายสุดของฟังก์ชัน คุณจะต้องค้นหาจุดวิกฤตทั้งหมดของฟังก์ชัน จากนั้นตรวจสอบแต่ละจุดแยกกันเพื่อหาค่าสูงสุดและค่าต่ำสุด ทฤษฎีบทต่อไปนี้มีจุดประสงค์นี้

ทฤษฎีบท 2 (เงื่อนไขที่เพียงพอสำหรับการมีอยู่ของจุดสุดขั้ว) ปล่อยให้ฟังก์ชันต่อเนื่องในช่วงเวลาหนึ่งซึ่งมีจุดวิกฤติ x 0 และสามารถหาอนุพันธ์ได้ในทุกจุดของช่วงเวลานี้ (ยกเว้น บางทีอาจจะเป็นจุดนั้นเอง) x 0) เมื่อย้ายจากซ้ายไปขวาผ่านจุดนี้ ถ้าอนุพันธ์เปลี่ยนเครื่องหมายจากบวกเป็นลบ แล้วไปที่จุดนั้น x = xฟังก์ชัน 0 มีจำนวนสูงสุด หากเมื่อผ่าน. x 0 จากซ้ายไปขวา อนุพันธ์เปลี่ยนเครื่องหมายจากลบเป็นบวก แล้วฟังก์ชันจะมีค่าต่ำสุด ณ จุดนี้

ดังนั้นหาก

ฉ "(x)>0 ณ x <x 0 และ ฉ "(x)< 0 ณ x>x 0 แล้ว x 0 – จุดสูงสุด;

การพิสูจน์- ให้เราสันนิษฐานไว้ก่อนว่าเมื่อผ่านไปแล้ว x 0 อนุพันธ์เปลี่ยนเครื่องหมายจากบวกเป็นลบ เช่น ต่อหน้าทุกคน x,ใกล้จุด x 0 ฉ "(x)> 0 สำหรับ x< x 0 , ฉ "(x)< 0 สำหรับ x>x 0 . ลองใช้ทฤษฎีบทของลากรองจ์กับความแตกต่างกัน ฉ(x) - ฉ(x 0 ) = ฉ "(ค)(x- x 0) ที่ไหน คอยู่ระหว่าง xและ x 0 .

อนุญาต x< x 0 . แล้ว ค< x 0 และ ฉ "(ค)> 0. นั่นเป็นเหตุผล ฉ "(ค)(x- x 0)< 0 และดังนั้น

ฉ(x) - ฉ(x 0 )< 0 เช่น ฉ(x)< f(x 0 ).

อนุญาต x > x 0 . แล้ว ค>x 0 และ ฉ "(ค)< 0. วิธี ฉ "(ค)(x- x 0)< 0. นั่นเป็นเหตุผล ฉ(x) - ฉ(x 0 ) <0,т.е.ฉ(x) < ฉ(x 0 ) .

ดังนั้นสำหรับทุกค่า xใกล้พอที่จะ x 0 ฉ(x) < ฉ(x 0 ) - และนี่หมายความว่า ณ จุดนั้น xฟังก์ชัน 0 มีจำนวนสูงสุด

ส่วนที่สองของทฤษฎีบทขั้นต่ำก็พิสูจน์ในลักษณะเดียวกัน

ให้เราอธิบายความหมายของทฤษฎีบทนี้ในรูป อนุญาต ฉ "(x 1 ) =0 และสำหรับใดๆ เอ็กซ์,ใกล้พอที่จะ x 1 ความไม่เท่าเทียมกันมีความพึงพอใจ

ฉ "(x)< 0 ณ x< x 1 , ฉ "(x)> 0 ณ x>x 1 .

จากนั้นไปทางซ้ายของจุด x 1 ฟังก์ชั่นจะเพิ่มขึ้นและลดลงทางด้านขวา ดังนั้น เมื่อใด x = x 1 ฟังก์ชันเปลี่ยนจากเพิ่มขึ้นไปสู่ลดลง นั่นคือมีค่าสูงสุด

ในทำนองเดียวกัน เราสามารถพิจารณาประเด็นต่างๆ ได้ x 2 และ x 3 .

ทั้งหมดข้างต้นสามารถแสดงเป็นแผนผังในภาพ:

กฎสำหรับการศึกษาฟังก์ชัน y=f(x) สำหรับส่วนปลายสุด

ค้นหาโดเมนของฟังก์ชัน ฉ(x)

ค้นหาอนุพันธ์อันดับหนึ่งของฟังก์ชัน ฉ "(x) .

กำหนดจุดวิกฤติสำหรับสิ่งนี้:

ค้นหารากที่แท้จริงของสมการ ฉ "(x) =0;

ค้นหาค่าทั้งหมด xซึ่งอนุพันธ์นั้น ฉ "(x)ไม่มีอยู่จริง

กำหนดเครื่องหมายของอนุพันธ์ทางซ้ายและขวาของจุดวิกฤต เนื่องจากเครื่องหมายของอนุพันธ์ยังคงที่ระหว่างจุดวิกฤตสองจุด จึงเพียงพอที่จะระบุเครื่องหมายของอนุพันธ์ที่จุดหนึ่งทางซ้ายและอีกจุดทางด้านขวาของจุดวิกฤติ

คำนวณค่าของฟังก์ชันที่จุดปลายสุด

ค่าสุดขีดของฟังก์ชันคืออะไร และเงื่อนไขที่จำเป็นสำหรับค่าสุดขีดคืออะไร?

ปลายสุดของฟังก์ชันคือค่าสูงสุดและต่ำสุดของฟังก์ชัน

เงื่อนไขที่จำเป็นสำหรับค่าสูงสุดและต่ำสุด (สุดขีด) ของฟังก์ชันมีดังต่อไปนี้: หากฟังก์ชัน f(x) มีจุดสุดขีดที่จุด x = a ดังนั้น ณ จุดนี้อนุพันธ์จะเป็นศูนย์ อนันต์ หรือไม่ก็ได้ มีอยู่.

เงื่อนไขนี้จำเป็นแต่ไม่เพียงพอ อนุพันธ์ที่จุด x = a สามารถไปถึงศูนย์ อนันต์ หรือไม่มีอยู่ได้หากไม่มีฟังก์ชันสุดขั้ว ณ จุดนี้

เงื่อนไขที่เพียงพอสำหรับส่วนปลายของฟังก์ชัน (สูงสุดหรือต่ำสุด) คืออะไร?

เงื่อนไขแรก:

หากอยู่ใกล้จุด x = a มากพอ อนุพันธ์ของ f?(x) เป็นบวกทางด้านซ้ายของ a และเป็นลบทางด้านขวาของ a แล้วที่จุด x = a ฟังก์ชัน f(x) จะมี สูงสุด

หากอยู่ใกล้จุด x = a มากพอ อนุพันธ์ของ f?(x) เป็นลบทางด้านซ้ายของ a และเป็นบวกทางด้านขวาของ a แล้วที่จุด x = a ฟังก์ชัน f(x) จะมี ขั้นต่ำโดยมีเงื่อนไขว่าฟังก์ชัน f(x) ในที่นี้เป็นฟังก์ชันต่อเนื่อง

คุณสามารถใช้เงื่อนไขที่สองที่เพียงพอสำหรับส่วนปลายสุดของฟังก์ชันแทนได้:

ให้ ณ จุด x = a อนุพันธ์อันดับหนึ่ง f?(x) หายไป; ถ้าอนุพันธ์อันดับสอง f??(a) เป็นลบ แสดงว่าฟังก์ชัน f(x) จะมีค่าสูงสุดที่จุด x = a หากเป็นบวก ก็จะมีค่าต่ำสุด

จุดวิกฤตของฟังก์ชันคืออะไร และจะค้นหาได้อย่างไร

นี่คือค่าของอาร์กิวเมนต์ของฟังก์ชันที่ฟังก์ชันมีจุดสิ้นสุด (เช่น สูงสุดหรือต่ำสุด) เพื่อค้นหาสิ่งที่คุณต้องการ หาอนุพันธ์ฟังก์ชัน f?(x) และเมื่อเท่ากับศูนย์ แก้สมการ f?(x) = 0 รากของสมการนี้รวมถึงจุดที่อนุพันธ์ของฟังก์ชันนี้ไม่มีอยู่เป็นจุดวิกฤตเช่นค่าของอาร์กิวเมนต์ที่สามารถมีจุดสุดยอดได้ พวกเขาสามารถระบุได้ง่ายโดยการดู กราฟอนุพันธ์: เราสนใจค่าของการโต้แย้งที่กราฟของฟังก์ชันตัดกับแกน Abscissa (แกน Ox) และค่าที่กราฟประสบความไม่ต่อเนื่อง

เช่น เรามาค้นหากัน ส่วนปลายของพาราโบลา.

ฟังก์ชัน y(x) = 3x2 + 2x - 50

อนุพันธ์ของฟังก์ชัน: y?(x) = 6x + 2

แก้สมการ: y?(x) = 0

6x + 2 = 0, 6x = -2, x = -2/6 = -1/3

ในกรณีนี้ จุดวิกฤตคือ x0=-1/3 มันขึ้นอยู่กับค่าอาร์กิวเมนต์นี้ที่ฟังก์ชันมี สุดขั้ว- ถึงเขา หาให้แทนที่ตัวเลขที่พบในนิพจน์สำหรับฟังก์ชันแทน "x":

y0 = 3*(-1/3)2 + 2*(-1/3) - 50 = 3*1/9 - 2/3 - 50 = 1/3 - 2/3 - 50 = -1/3 - 50 = -50.333.

วิธีกำหนดค่าสูงสุดและต่ำสุดของฟังก์ชัน เช่น ค่าที่ใหญ่ที่สุดและเล็กที่สุดคืออะไร?

หากเครื่องหมายของอนุพันธ์เมื่อผ่านจุดวิกฤติ x0 เปลี่ยนจาก "บวก" เป็น "ลบ" แล้ว x0 คือ จุดสูงสุด- ถ้าเครื่องหมายของอนุพันธ์เปลี่ยนจากลบเป็นบวก แล้ว x0 คือ จุดต่ำสุด- หากเครื่องหมายไม่เปลี่ยนแปลง เมื่อถึงจุด x0 จะไม่มีทั้งค่าสูงสุดและค่าต่ำสุด

สำหรับตัวอย่างที่พิจารณา:

เราใช้ค่าอาร์กิวเมนต์ตามอำเภอใจทางด้านซ้ายของจุดวิกฤติ: x = -1

ที่ x = -1 ค่าของอนุพันธ์จะเป็น y?(-1) = 6*(-1) + 2 = -6 + 2 = -4 (นั่นคือ เครื่องหมายคือ “ลบ”)

ตอนนี้เรารับค่าอาร์กิวเมนต์ตามอำเภอใจทางด้านขวาของจุดวิกฤติ: x = 1

ที่ x = 1 ค่าของอนุพันธ์จะเป็น y(1) = 6*1 + 2 = 6 + 2 = 8 (นั่นคือ เครื่องหมายคือ “บวก”)

อย่างที่คุณเห็น อนุพันธ์เปลี่ยนเครื่องหมายจากลบเป็นบวกเมื่อผ่านจุดวิกฤติ ซึ่งหมายความว่าที่ค่าวิกฤต x0 เรามีจุดต่ำสุด

ค่าที่ใหญ่ที่สุดและน้อยที่สุดของฟังก์ชัน ในช่วงเวลา(บนเซ็กเมนต์) จะถูกพบโดยใช้ขั้นตอนเดียวกัน โดยคำนึงถึงข้อเท็จจริงที่ว่าบางทีจุดวิกฤติไม่ใช่ทั้งหมดจะอยู่ภายในช่วงเวลาที่กำหนดเท่านั้น จุดวิกฤตเหล่านั้นที่อยู่นอกช่วงเวลาจะต้องถูกแยกออกจากการพิจารณา หากมีจุดวิกฤตเพียงจุดเดียวภายในช่วงเวลา จะมีค่าสูงสุดหรือต่ำสุด ในกรณีนี้ เพื่อกำหนดค่าที่ใหญ่ที่สุดและเล็กที่สุดของฟังก์ชัน เรายังคำนึงถึงค่าของฟังก์ชันที่ส่วนท้ายของช่วงเวลาด้วย

ตัวอย่างเช่น ลองหาค่าที่ใหญ่ที่สุดและน้อยที่สุดของฟังก์ชัน

y(x) = 3ซิน(x) - 0.5x

เป็นระยะ:

แล้วอนุพันธ์ของฟังก์ชันคือ

y?(x) = 3cos(x) - 0.5

เราแก้สมการ 3cos(x) - 0.5 = 0

คอส(x) = 0.5/3 = 0.16667

x = ±อาร์คคอส(0.16667) + 2πk

เราพบจุดวิกฤตในช่วงเวลา [-9; 9]:

x = ส่วนโค้ง (0.16667) - 2π*2 = -11.163 (ไม่รวมในช่วงเวลา)

x = -อาร์คคอส(0.16667) – 2π*1 = -7.687

x = ส่วนโค้ง (0.16667) - 2π*1 = -4.88

x = -อาร์คคอส(0.16667) + 2π*0 = -1.403

x = ส่วนโค้ง (0.16667) + 2π*0 = 1.403

x = -อาร์คคอส(0.16667) + 2π*1 = 4.88

x = ส่วนโค้ง (0.16667) + 2π*1 = 7.687

x = -arccos(0.16667) + 2π*2 = 11.163 (ไม่รวมในช่วงเวลา)

เราค้นหาค่าของฟังก์ชันตามค่าวิกฤตของอาร์กิวเมนต์:

y(-7.687) = 3cos(-7.687) - 0.5 = 0.885

y(-4.88) = 3cos(-4.88) - 0.5 = 5.398

y(-1.403) = 3cos(-1.403) - 0.5 = -2.256

y(1.403) = 3cos(1.403) - 0.5 = 2.256

y(4.88) = 3cos(4.88) - 0.5 = -5.398

y(7.687) = 3cos(7.687) - 0.5 = -0.885

จะเห็นได้ว่าในช่วง [-9; 9] ฟังก์ชันมีค่ามากที่สุดที่ x = -4.88:

x = -4.88, y = 5.398,

และเล็กที่สุด - ที่ x = 4.88:

x = 4.88, y = -5.398

ในช่วงเวลา [-6; -3] เรามีจุดวิกฤตเพียงจุดเดียว: x = -4.88 ค่าของฟังก์ชันที่ x = -4.88 เท่ากับ y = 5.398

ค้นหาค่าของฟังก์ชันที่ส่วนท้ายของช่วงเวลา:

y(-6) = 3cos(-6) - 0.5 = 3.838

y(-3) = 3cos(-3) - 0.5 = 1.077

ในช่วงเวลา [-6; -3] เรามีค่ามากที่สุดของฟังก์ชัน

y = 5.398 ที่ x = -4.88

ค่าน้อยที่สุด -

y = 1.077 ที่ x = -3

จะค้นหาจุดเปลี่ยนของกราฟฟังก์ชันและกำหนดด้านนูนและด้านเว้าได้อย่างไร

ในการค้นหาจุดเปลี่ยนเว้าทั้งหมดของเส้น y = f(x) คุณต้องค้นหาอนุพันธ์อันดับสอง จัดให้มันเป็นศูนย์ (แก้สมการ) และทดสอบค่าทั้งหมดของ x ซึ่งอนุพันธ์อันดับสองเป็นศูนย์ อนันต์หรือไม่มีอยู่จริง เมื่อส่งผ่านค่าใดค่าหนึ่งเหล่านี้ หากอนุพันธ์อันดับสองเปลี่ยนสัญญาณ กราฟของฟังก์ชันจะมีการเปลี่ยนแปลง ณ จุดนี้ ถ้าไม่เปลี่ยนก็ไม่มีโค้งงอ

รากของสมการ f? (x) = 0 รวมถึงจุดที่เป็นไปได้ของความไม่ต่อเนื่องของฟังก์ชันและอนุพันธ์อันดับสอง ให้แบ่งโดเมนของคำจำกัดความของฟังก์ชันออกเป็นช่วงจำนวนหนึ่ง ความนูนในแต่ละช่วงเวลาถูกกำหนดโดยเครื่องหมายของอนุพันธ์อันดับสอง หากอนุพันธ์อันดับสอง ณ จุดหนึ่งในช่วงเวลาที่กำลังศึกษาเป็นบวก เส้น y = f(x) จะเว้าขึ้น และหากเป็นลบ ก็จะเว้าลง

จะค้นหา extrema ของฟังก์ชันของตัวแปรสองตัวได้อย่างไร?

ในการค้นหาเอ็กซ์ตรีมของฟังก์ชัน f(x,y) ซึ่งหาอนุพันธ์ได้ในโดเมนของข้อกำหนดเฉพาะ คุณจะต้อง:

1) ค้นหาจุดวิกฤตและเพื่อสิ่งนี้ - แก้ระบบสมการ

ฉะ? (x,y) = 0, แล้ว? (x,y) = 0

2) สำหรับแต่ละจุดวิกฤต P0(a;b) ตรวจสอบว่าสัญญาณของความแตกต่างยังคงไม่เปลี่ยนแปลงหรือไม่

สำหรับทุกจุด (x;y) ใกล้กับ P0 เพียงพอ หากความแตกต่างยังคงเป็นบวก จากนั้นที่จุด P0 เรามีค่าต่ำสุด หากเป็นลบ เราก็จะมีค่าสูงสุด หากความแตกต่างไม่คงเครื่องหมายไว้ แสดงว่าไม่มีจุดสิ้นสุดที่จุด P0

ค่าสุดขีดของฟังก์ชันถูกกำหนดในทำนองเดียวกันสำหรับอาร์กิวเมนต์จำนวนมากขึ้น

วันโทรทัศน์โลกตรงกับเดือนพฤศจิกายนเมื่อใด
เมื่อวันที่ 17 ธันวาคม พ.ศ. 2539 สมัชชาใหญ่ได้ประกาศให้วันที่ 21 พฤศจิกายนเป็น "วันโทรทัศน์โลก" เพื่อรำลึกถึงวันที่มีการประชุม World Television Forum ครั้งแรกที่สหประชาชาติ รัฐถูกขอให้รำลึกถึงวันนี้ด้วยการแลกเปลี่ยนรายการโทรทัศน์ในประเด็นต่างๆ เช่น สันติภาพ และความมั่นคง

เชอร์รี่นกคืออะไร
Bird cherry เป็นเชอร์รี่สายพันธุ์หนึ่งในวงศ์ Rosaceae มีถิ่นกำเนิดในยุโรปเหนือและเอเชียเหนือ นี่เป็นไม้พุ่มที่ค่อนข้างสูงซึ่งสูงถึง 16 เมตร โดยปกติแล้วความสูงของนกเชอร์รี่จะอยู่ที่ประมาณ 9 เมตร โดดเด่นด้วยกลิ่นหอมของดอกไม้ เติบโตสูงจากระดับน้ำทะเลอย่างน้อย 800 เมตร ชอบดินโอ๊คที่เป็นกรด

ระยะการแบ่งเซลล์ (ระยะ M) มี 2 ระยะอะไรบ้าง?
วัฏจักรของเซลล์คือช่วงเวลาของการดำรงอยู่ของเซลล์นับจากช่วงเวลาที่เซลล์ก่อตัวโดยการแบ่งเซลล์แม่จนกระทั่งมีการแบ่งตัวหรือตายไปเอง ความยาวของวัฏจักรของเซลล์แตกต่างกันไปในแต่ละเซลล์ เซลล์ของสิ่งมีชีวิตที่เติบโตเต็มวัยอย่างรวดเร็ว เช่น เซลล์เม็ดเลือดหรือเซลล์ฐานของหนังกำพร้าและลำไส้เล็ก สามารถเข้าสู่วัฏจักรของเซลล์ได้

เหตุใดเบราว์เซอร์ Opera จึงไม่แสดงเมนูหลัก
เพื่อประหยัดพื้นที่หน้าจอในเบราว์เซอร์ Opera ตั้งแต่เวอร์ชัน 10.5 เป็นต้นไป เมนูหลักจะถูกปิดตามค่าเริ่มต้น นักพัฒนาได้ทำการตัดสินใจนี้โดยเกี่ยวข้องกับการแพร่หลายของเน็ตบุ๊กที่มีจอแสดงผลขนาดเล็กและจอภาพ LCD แบบไวด์ซึ่งมีความสูงของหน้าจอน้อยกว่าความกว้างอย่างมาก เข้าถึงฟังก์ชั่นทั้งหมดที่อยู่ในเมนูหลัก

เมือง Bratsk อยู่ที่ไหน?
Bratsk เป็นเมืองในรัสเซียในภูมิภาคอีร์คุตสค์ ที่ตั้งทางภูมิศาสตร์ของ Bratsk กำหนดการเปลี่ยนแปลงให้เป็น "ประตู" ของภาคเหนือ เมืองนี้ตั้งอยู่ในใจกลางของภูมิภาคไซบีเรียตะวันออกของรัสเซีย ในตอนกลางของสันเขาอังการา ริมฝั่งอ่างเก็บน้ำ Bratsk บนแม่น้ำอังการา ระยะทางไปยังศูนย์กลางภูมิภาค - เมืองอีร์คุตสค์:

ชาดกคืออะไร
ชาดก (จากภาษากรีก allegoria - ชาดก) เป็นหนึ่งในรูปแบบของชาดกการถ่ายทอดแนวคิดเชิงนามธรรมหรือการตัดสินอย่างมีเงื่อนไขผ่านภาพเฉพาะ ชาดกเป็นเรื่องธรรมดาที่สุดในทัศนศิลป์ (ผู้หญิงที่มีผ้าปิดตาและมีตาชั่งอยู่ในมือ - ความยุติธรรม, สมอ - ความหวัง ฯลฯ ) ในวรรณคดีมีภาพเชิงเปรียบเทียบมากมาย

วิธีดูแลเฮลิไครซัม
Helichrysum (Immortelle, Tsmin) ชื่อละติน: Helichrysum หมวดหมู่: พืชล้มลุก, พืชสวนหิน วงศ์: Asteraceae (Compositae) บ้านเกิด: Helichrysum เติบโตในเขตอบอุ่นของยุโรป เอเชีย แอฟริกา และออสเตรเลีย บ้านเกิดของ Tsmina ของ Milford อยู่ที่ชานเมืองเคปทาวน์ แบบฟอร์ม: ไม้ล้มลุก

ใครเป็นคนเขียนนวนิยายเรื่อง "ขาวกับดำ"
นวนิยายเรื่อง "White and Black" เป็นเรื่องเกี่ยวกับผู้เล่นหมากรุกและหมากรุก บุคคลสำคัญของนวนิยายเรื่องนี้คือนักเล่นหมากรุกผู้ยิ่งใหญ่ Alexander Alyokhin แชมป์โลก ผู้แต่งนวนิยายเรื่อง "White and Black" เป็นนักเล่นหมากรุกโซเวียตที่โดดเด่น ปรมาจารย์ระดับนานาชาติ นักเขียน สมาชิกสหภาพนักเขียน

ชื่อเต็มของหนังสือเล่มที่สองในไตรภาค Robinson Crusoe ของ Daniel Defoe คืออะไร
Daniel Defoe (ภาษาอังกฤษ Daniel Defoe; เกิดภายใต้ชื่อ Daniel Foe; แคลิฟอร์เนีย ค.ศ. 1660 - 1731) - นักเขียนและนักประชาสัมพันธ์ชาวอังกฤษ ซึ่งรู้จักกันในปัจจุบันส่วนใหญ่เป็นผู้เขียนนวนิยายเรื่อง "Robinson Crusoe" (ตามธรรมเนียมในการวิจารณ์วรรณกรรมทางวิทยาศาสตร์และการตีพิมพ์)

สโต๊ตกินอะไร?
สัตว์จำพวกแมร์มีน (Mustela erminea) เป็นสัตว์ขนที่มีค่าในตระกูลมัสเตลิด รูปร่าง. ตัวแทนของสกุลคุ้ยเขี่ยทั้งหมดเป็นสัตว์ที่มีรูปร่างที่ยืดหยุ่นและยาว สง่างามและว่องไวมาก แตกต่างจากมาร์เทนโดยมีสีขาวที่ปลายปากกระบอกปืน หูมีขนาดเล็กมน ความยาวลำตัวของแมวน้ำคือ 16-3

โรคอะไรที่ไม่รับเข้ากองทัพ?
หมวดหมู่ความเหมาะสมสำหรับการรับราชการทหาร (“A”, “B”, “C”, “D”, “D”) จะถูกกำหนดโดยคณะกรรมการการแพทย์ทหารในระหว่างการตรวจสุขภาพของทหารเกณฑ์ เอ - เหมาะสำหรับการรับราชการทหาร บีแอนด์บี

จากบทความนี้ ผู้อ่านจะได้เรียนรู้เกี่ยวกับคุณค่าการทำงานขั้นสูงสุด รวมถึงคุณสมบัติของการใช้งานในกิจกรรมภาคปฏิบัติ การศึกษาแนวคิดดังกล่าวมีความสำคัญอย่างยิ่งในการทำความเข้าใจรากฐานของคณิตศาสตร์ระดับสูง หัวข้อนี้เป็นหัวข้อพื้นฐานสำหรับการศึกษาเชิงลึกของหลักสูตร

สุดขั้วคืออะไร?

ในหลักสูตรของโรงเรียน มีการให้คำจำกัดความมากมายของแนวคิด "สุดขั้ว" บทความนี้มีวัตถุประสงค์เพื่อให้ความเข้าใจที่ลึกซึ้งและชัดเจนที่สุดเกี่ยวกับคำศัพท์สำหรับผู้ที่ไม่รู้ประเด็น ดังนั้นจึงเข้าใจได้ว่าช่วงการทำงานจะได้ค่าต่ำสุดหรือสูงสุดในชุดใดชุดหนึ่ง

สุดขีดคือทั้งค่าต่ำสุดของฟังก์ชันและค่าสูงสุดในเวลาเดียวกัน มีจุดต่ำสุดและจุดสูงสุดนั่นคือค่าสุดขีดของอาร์กิวเมนต์บนกราฟ ศาสตร์หลักที่ใช้แนวคิดนี้คือ:

• สถิติ;
• การควบคุมเครื่องจักร
• เศรษฐมิติ

จุดสุดโต่งมีบทบาทสำคัญในการกำหนดลำดับของฟังก์ชันที่กำหนด ระบบพิกัดในกราฟที่ดีที่สุดจะแสดงการเปลี่ยนแปลงในตำแหน่งสุดขั้วโดยขึ้นอยู่กับการเปลี่ยนแปลงฟังก์ชันการทำงาน

สุดขีดของฟังก์ชันอนุพันธ์

นอกจากนี้ยังมีปรากฏการณ์เช่น "อนุพันธ์" มีความจำเป็นต้องกำหนดจุดปลายสุด สิ่งสำคัญคืออย่าสับสนระหว่างคะแนนต่ำสุดหรือสูงสุดกับค่าสูงสุดและต่ำสุด สิ่งเหล่านี้เป็นแนวคิดที่แตกต่างกัน แม้ว่าอาจดูคล้ายกันก็ตาม

ค่าของฟังก์ชันเป็นปัจจัยหลักในการกำหนดวิธีหาจุดสูงสุด อนุพันธ์ไม่ได้ถูกสร้างขึ้นจากค่านิยม แต่มาจากตำแหน่งสุดขั้วในลำดับใดลำดับหนึ่งเท่านั้น

อนุพันธ์นั้นพิจารณาจากจุดสุดขั้วเหล่านี้ และไม่ใช่จากมูลค่าที่ใหญ่ที่สุดหรือน้อยที่สุด ในโรงเรียนของรัสเซีย เส้นแบ่งระหว่างแนวคิดทั้งสองนี้ไม่ได้วาดไว้อย่างชัดเจน ซึ่งส่งผลต่อความเข้าใจในหัวข้อนี้โดยทั่วไป

ตอนนี้ให้เราพิจารณาแนวคิดเช่น "ภาวะสุดโต่งเฉียบพลัน" วันนี้มีค่าต่ำสุดเฉียบพลันและค่าสูงสุดเฉียบพลัน คำจำกัดความได้รับตามการจำแนกจุดวิกฤตของฟังก์ชันของรัสเซีย แนวคิดเรื่องจุดสุดขั้วเป็นพื้นฐานในการค้นหาจุดวิกฤตบนกราฟ

เพื่อกำหนดแนวคิดดังกล่าว พวกเขาใช้ทฤษฎีบทของแฟร์มาต์ มันเป็นสิ่งสำคัญที่สุดในการศึกษาจุดสุดขั้วและให้ความคิดที่ชัดเจนเกี่ยวกับการมีอยู่ของมันในรูปแบบใดรูปแบบหนึ่ง เพื่อให้มั่นใจถึงความสุดขั้ว สิ่งสำคัญคือต้องสร้างเงื่อนไขบางประการสำหรับการลดลงหรือเพิ่มขึ้นบนกราฟ

หากต้องการตอบคำถาม “วิธีหาจุดสูงสุด” อย่างถูกต้อง คุณต้องปฏิบัติตามหลักเกณฑ์เหล่านี้:

1. การค้นหาโดเมนคำจำกัดความที่แน่นอนบนกราฟ
2. ค้นหาอนุพันธ์ของฟังก์ชันและจุดปลายสุด
3. แก้ความไม่เท่าเทียมกันมาตรฐานสำหรับโดเมนที่พบอาร์กิวเมนต์
4. สามารถพิสูจน์ได้ว่าฟังก์ชันใดที่จุดบนกราฟถูกกำหนดและต่อเนื่องกัน

ความสนใจ!การค้นหาจุดวิกฤตของฟังก์ชันจะเป็นไปได้ก็ต่อเมื่อมีอนุพันธ์ในลำดับที่สองเป็นอย่างน้อย ซึ่งมั่นใจได้จากสัดส่วนที่สูงของการมีอยู่ของจุดสุดขั้ว

เงื่อนไขที่จำเป็นสำหรับส่วนปลายของฟังก์ชัน

เพื่อให้สุดขั้วมีอยู่ สิ่งสำคัญคือต้องมีทั้งจุดต่ำสุดและสูงสุด หากปฏิบัติตามกฎนี้เพียงบางส่วนเท่านั้น เงื่อนไขของการมีอยู่ของสุดขั้วจะถูกละเมิด

แต่ละฟังก์ชันในตำแหน่งใดๆ จะต้องมีความแตกต่างกันเพื่อให้สามารถระบุความหมายใหม่ได้ สิ่งสำคัญคือต้องเข้าใจว่ากรณีที่จุดที่กลายเป็นศูนย์ไม่ใช่หลักการหลักในการค้นหาจุดที่หาอนุพันธ์ได้

ค่าสุดโต่งเฉียบพลันและฟังก์ชันขั้นต่ำเป็นส่วนสำคัญอย่างยิ่งในการแก้ปัญหาทางคณิตศาสตร์โดยใช้ค่าสุดขั้ว เพื่อให้เข้าใจส่วนประกอบนี้ได้ดีขึ้น สิ่งสำคัญคือต้องอ้างอิงค่าแบบตารางเพื่อระบุฟังก์ชันการทำงาน

พิจารณากราฟของฟังก์ชันต่อเนื่อง y=ฉ(x)แสดงในรูป

ค่าฟังก์ชัน ณ จุดหนึ่ง x 1 จะมากกว่าค่าฟังก์ชันที่จุดใกล้เคียงทั้งหมดทั้งด้านซ้ายและด้านขวาของ x 1. ในกรณีนี้เราบอกว่าฟังก์ชันมีตรงประเด็น xสูงสุด 1 ตรงจุด xเห็นได้ชัดว่าฟังก์ชั่น 3 มีจำนวนสูงสุดเช่นกัน ถ้าเราพิจารณาประเด็นแล้ว x 2 ดังนั้นค่าฟังก์ชันในนั้นจะน้อยกว่าค่าใกล้เคียงทั้งหมด ในกรณีนี้เราบอกว่าฟังก์ชันมีตรงประเด็น x 2 ขั้นต่ำ ในทำนองเดียวกันสำหรับประเด็น x 4 .

การทำงาน y=ฉ(x)ตรงจุด x 0 มี สูงสุดหากค่าของฟังก์ชัน ณ จุดนี้มากกว่าค่าของฟังก์ชัน ณ จุดทั้งหมดที่มีจุดนั้นอยู่ x 0 เช่น หากมีบริเวณใกล้จุดดังกล่าว x 0 ซึ่งเหมาะสำหรับทุกคน x≠x 0 , ที่อยู่ในละแวกนี้ก็มีความไม่เท่าเทียมกัน ฉ(x)<ฉ(x 0 ) .

การทำงาน y=ฉ(x)มี ขั้นต่ำตรงจุด x 0 , หากมีบริเวณใกล้จุดดังกล่าว x 0 , นั่นสำหรับทุกคน x≠x 0 อยู่ในละแวกนี้ ความไม่เท่าเทียมกันยังคงอยู่ ฉ(x)>ฉ(x 0.

จุดที่ฟังก์ชันถึงค่าสูงสุดและต่ำสุดเรียกว่าจุดสุดขีดและค่าของฟังก์ชันที่จุดเหล่านี้เรียกว่าจุดสุดขีดของฟังก์ชัน

ให้เราใส่ใจกับความจริงที่ว่าฟังก์ชันที่กำหนดไว้ในเซ็กเมนต์สามารถเข้าถึงค่าสูงสุดและต่ำสุดได้เฉพาะจุดที่อยู่ในเซ็กเมนต์ที่อยู่ระหว่างการพิจารณาเท่านั้น

โปรดทราบว่าหากฟังก์ชันมีค่าสูงสุดที่จุดหนึ่ง ไม่ได้หมายความว่า ณ จุดนั้นฟังก์ชันจะมีค่ามากที่สุดในขอบเขตคำจำกัดความทั้งหมด จากรูปที่กล่าวข้างต้น ฟังก์ชัน ณ จุดนั้น x 1 มีค่าสูงสุดแม้ว่าจะมีจุดที่ค่าฟังก์ชันมากกว่าจุดนั้นก็ตาม x 1 . โดยเฉพาะอย่างยิ่ง ฉ(x 1) < ฉ(x 4) เช่น ค่าต่ำสุดของฟังก์ชันมากกว่าค่าสูงสุด จากคำจำกัดความของค่าสูงสุด จะตามมาเพียงว่านี่คือค่าที่ใหญ่ที่สุดของฟังก์ชันที่จุดที่ใกล้กับจุดสูงสุดเพียงพอ

ทฤษฎีบท 1 (เงื่อนไขที่จำเป็นสำหรับการดำรงอยู่ของสุดขั้ว)ถ้าฟังก์ชันหาอนุพันธ์ได้ y=ฉ(x)มีตรงจุด x=x 0 สุดขั้ว แล้วอนุพันธ์ของมัน ณ จุดนี้จะกลายเป็นศูนย์

การพิสูจน์- ให้ตรงจุดอย่างแน่นอน xฟังก์ชัน 0 มีจำนวนสูงสุด จากนั้นสำหรับการเพิ่มทีละน้อยเพียงพอ Δ xเรามี ฉ(x 0 + Δ เอ็กซ์) 0 ) , เช่น. แต่แล้ว