W klasycznej mechanice Newtona rozmiary ciał i odstępy czasowe pomiędzy zdarzeniami traktowane są jako wartości bezwzględne. Oznacza to, że możemy mówić o długości ciał bez wskazania, czy to ciało jest w spoczynku, czy w ruchu. skale liniowe (długość odcinków) i odstępy czasowe pozostają niezmienione przy przechodzeniu z pierwszego układu odniesienia do drugiego, tj. nie zależą od wyboru układu odniesienia. Idee te odzwierciedlają koncepcję Newtona dotyczącą absolutności przestrzeni i czasu.
2.Kinematyka
To dział mechaniki, kat. Badają sposoby opisu ruchu ciał, nie interesując się przyczynami powodującymi ten ruch.
3. Trajektoria
Jest to linia w przestrzeni, wzdłuż której porusza się cząstka (geometryczne położenie końców wektora promienia cząstki)
4.Przeprowadzka
D R = R 2 – R 1 przez pewien czas D T jest wektorem narysowanym od początkowego do końcowego położenia cząstki (od punktu 1 Dokładnie 2 ).
5. Wektor średniej prędkości< w>.
Wektor średniej prędkości< w> jest wektorem równym stosunkowi przemieszczenia cząstki do czasu D T dla którego zostało popełnione:
Wektor średniej prędkości < w> pokrywa się w kierunku z wektorem przemieszczenia DR.
6. Natychmiastowa prędkośćw cząstki (lub po prostu prędkość) jest wektorem równym pochodnej wektora promienia R z czasem:
Chwilowa prędkość w skierowane stycznie do trajektorii w kierunku ruchu cząstek .SI:m/s
7. Przyśpieszenie nazywa się wektorem równym pochodnej prędkości po czasie w cząstki:
8. Prawo ruchu
nazywa się zależnością współrzędnych cząstki od czasu:
Istnieje proste powiązanie pomiędzy wektorową i współrzędną metodą opisu ruchu. Każdy wektor można zdefiniować poprzez jego rzuty na osie współrzędnych. Na przykład wektor promienia cząstki:
Gdzie I, J, k– wektory jednostkowe osi współrzędnych.
9. Prędkość metodą współrzędnych opisu ruchu
Prędkość w, jak każdy wektor, można przedstawić poprzez rzuty na oś DSC:
Te., prędkośćw cząstki można przedstawić w następującej postaci: 
Można zauważyć, że składowe prędkości wyrażone są poprzez funkcje X(T), y(T), z(T), są równe
10.Przyspieszenie metodą współrzędnych określenia ruchu Przyśpieszenie A, jak każdy wektor, można przedstawić poprzez rzuty na oś DSC:
Te., prędkośćw cząstki można przedstawić w następującej postaci
11.ŚcieżkaS(lub D S) jest równa odległości mierzonej wzdłuż trajektorii i przebytej przez cząstkę podczas jej ruchu (długość trajektorii). Ścieżka jest wielkością skalarną, nieujemną i niemalejącą.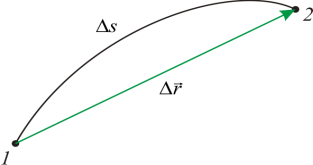 
12. Całkowite przyspieszenie cząstek
A można przedstawić jako sumę dwóch składowych prostopadłych do siebie:
Moduł pełnego przyspieszenia: 
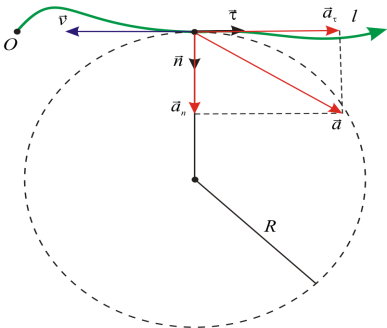
13.Przyspieszenie styczne (styczne).
Wektor A T skierowany stycznie do trajektorii cząstki; w której A T w, jeśli ruch jest przyspieszony; A T w, jeśli ruch jest powolny. Przyspieszenie styczne cząstki charakteryzuje zmianę prędkości cząstki modulo (jeśli A t = 0, ruch jest jednostajny).
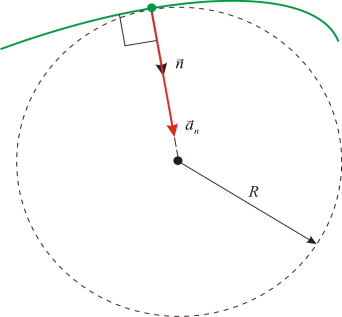
14.normalny (dośrodkowy)
przyśpieszenie
Wektor A N zawsze prostopadle do stycznej do trajektorii ruchu, tj. A N ^w I A N ^A T.
Przyspieszenie normalne charakteryzuje zmianę prędkości w kierunku (dla ruchu liniowego, kiedy R = ¥, A N = 0)
15.Absolutnie sztywny korpus
w mechanice nazywają je ciałem, podczas ruchu którego odległości pomiędzy dowolnymi dwoma jego punktami pozostają niezmienione. Dzięki temu ciało stałe nie odkształca się pod wpływem sił zewnętrznych.
16. Liczba stopni swobody ciała to liczba niezależnych zmiennych (ilości), które należy ustawić, aby określić położenie ciała w przestrzeni. Przykład. Liczba stopni swobody punktu materialnego wynosi 3 (trzy zmienne niezależne (współrzędne) X, y, z).
17.Prędkość kątowa ciała
Pozwól ciału obracać się wokół osi Z, zrealizowany w krótkim czasie dt elementarny zwrot DJ.Prędkość kątowa ciała zwany wektorem
Wektor w pokrywa się w kierunku z wektorem DJ, tj. skierowany wzdłuż osi obrotu korpusu tak, że tworzy prawą śrubę z kierunkiem obrotu wektora w na oś Z i jego moduł: 
Jednostka w
– radianów na sekundę
(rad/s)
Wyrażenie prędkość liniowa jest używane przy rozważaniu krzywoliniowego ruchu ciała i ma na celu podkreślenie różnicy pomiędzy prędkością $v\ $ a prędkością kryminalną $\omega $. Najczęściej pomija się słowo liniowy i mówi się po prostu prędkość.
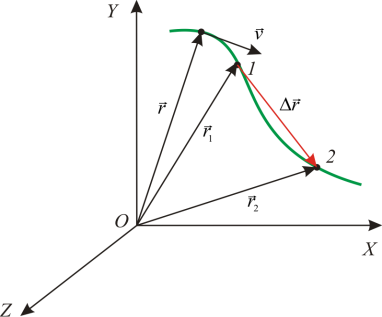
Wektor średniej prędkości
Definicja
Stosunek ruchu ($\Delta \overline(r)$) do okresu czasu, w którym ten ruch miał miejsce, nazywa się Średnia prędkość($\lewy\lange \overline(v)\prawy\rangle $) ruchy:
\[\left\langle \overline(v)\right\rangle =\frac(\Delta \overline(r))(\Delta t)\left(1\right),\]
gdzie $\Delta \overline(r)$ jest zmianą wektora promienia punktu materialnego w czasie $\Delta t$ (rys. 1).
Wektor średniej prędkości $\left\langle \overline(v)\right\rangle $ ma ten sam kierunek co wektor $\Delta \overline(r)$, ponieważ $\Delta t>0$. Długość odcinka obrazującego wektor prędkości średniej (rys. 1) nie jest powiązana z długością wektora $\Delta \overline(r)$.
Prędkość średnia charakteryzuje prędkość, z jaką porusza się punkt. Cecha ta odnosi się do określonego okresu czasu.
Jeśli ciało porusza się po krzywej, to droga ($\Delta s$) jest większa niż moduł przemieszczenia ($\Delta r$) w tym samym czasie, ponieważ długość łuku jest zawsze mniejsza od długości cięciwy ją zaciskającej (ryc. 1). Ścieżka i przemieszczenie pokrywają się podczas poruszania się po linii prostej w jednym kierunku. Średnią prędkość trasy definiuje się jako:
\[\left\langle v\right\rangle (\rm =)\frac(\Delta s)(\Delta t)\left(2\right).\]
Prędkość średnia charakteryzuje prędkość ruchu punktu materialnego w skończonym okresie czasu
Chwilowa prędkość
Definicja
Skracając okres czasu, w którym uwzględniany jest ruch cząstki ($\Delta t\do 0$), otrzymujemy charakterystykę ruchu punktu w danym momencie. Wartość jest równa:
\[\overline(v)=(\mathop(\lim )_(\Delta t\to 0) \left\langle \overline(v)\right\rangle =\ )(\mathop(\lim )_(\ Delta t\to 0) \frac(\Delta \overline(r))(\Delta t)=\frac(d\overline(r))(dt)\left(3\right),\ )\]
zwany chwilowa prędkość lub po prostu prędkość.
Przy obliczaniu prędkości za pomocą wzoru (3) jest oczywiste, że zmniejszenie przedziału czasu $\Delta t$ prowadzi do tego, że ostatecznie kolejne uzyskane wartości prędkości średniej będą się od siebie niewiele różnić. Dlatego przy znajdowaniu prędkości chwilowej zatrzymują się na wartości końcowej $\Delta t,\ $, ale małej, aby móc uzyskać niezbędną dokładność wartości prędkości.
Przejście do granicy (3) ma znaczenie geometryczne. Wektor $\Delta \overline(r)$ jest skierowany wzdłuż cięciwy łączącej dwa punkty trajektorii; zbieżność tych punktów powoduje, że wektor ten przyjmuje położenie stycznej do trajektorii ruchu w danym punkcie. . Okazuje się, że wektor prędkości jest skierowany stycznie do trajektorii ruchu. W ruchu prostoliniowym wektor prędkości jest skierowany po linii prostej.
Prędkość podróży określa się w podobny sposób:
Jeżeli trajektoria punktu materialnego jest gładką krzywą, to im krótszy łuk, tym jego długość jest bliższa długości cięciwy. W przejściu do granicy w $\ \Delta t\to 0$ możemy założyć, że $\Delta s\to \Delta r$. Stąd,
Dodawanie prędkości
Prędkość jest wielkością wektorową. Jeżeli punkt materialny bierze udział w kilku ruchach, wówczas jego prędkość oblicza się jako sumę wektorową prędkości każdego z ruchów:
\[\overline(v)=\suma\limits_i((\overline(v))_i\left(6\right).)\]
W niektórych przypadkach wygodnie jest myśleć o złożonym ruchu jako o superpozycji kilku prostych ruchów. Wówczas równość (6) można uznać za regułę rozkładu wektora prędkości na składowe.
Szybkość i przyspieszenie ruchu
Podczas nierównego ruchu punkt materialny ma przyspieszenie ($\overline(a)$). Przyspieszenie jest pierwszą pochodną prędkości po czasie:
\[\overline(a)=\frac(d\overline(v))(dt)\left(7\right).\]
Z wyrażenia (7) wynika, że znając przyspieszenie punktu, prędkość oblicza się jako:
\[\overline(v)=\int\limits^(t_2)_(t_1)(\overline(a)dt)\left(8\right).\]
Prędkości kątowe i liniowe
Podczas poruszania się po okręgu wraz z prędkością ruchu po trajektorii ($v$ - prędkość liniowa) wprowadzana jest prędkość kątowa ($\omega $), która charakteryzuje prędkość zmiany kąta obrotu $\varphi $:
\[\omega =\frac(d\varphi)(dt)\left(9\right).\]
Zależność pomiędzy prędkościami liniowymi i kątowymi wyraża się wzorem:
Przykłady problemów z rozwiązaniami
Przykład 1
Ćwiczenia. Zmiana wektora promienia wyznaczającego położenie punktu materialnego jest określona równaniem: $\overline(r\ )\left(t\right)=t^4\overline(i)+3t^2\overline( j),$ gdzie $\ overline(i)$ i $\overline(j)$ są wektorami jednostkowymi osi X i Y (ryc. 2). Jaka jest prędkość chwilowa punktu w chwili $t=1$c?
Rozwiązanie. Zdefiniujmy prędkość cząstki jako:
\[\overline(v)=(\frac(d\overline(r))(dt) \left(1.1\right).\ )\]
Podstawiamy do wzoru (1.1) równanie wektora promienia $\overline(r\ )\left(t\right)=t^4\overline(i)+3t^2\overline(j),$ otrzymujemy:
\[\overline(v)=\frac(d)(dt)\left(t^4\overline(i)+3t^2\overline(j)\right)=4t^3\overline(i)+6t \overline(j)\ \left(1.2\right).\]
Z równania (1.2) widzimy, że:
\[\left\( \begin(array)(c) v_x=4t^3 \\ v_y=6t \end(array) \right.\left(1.3\right).\]
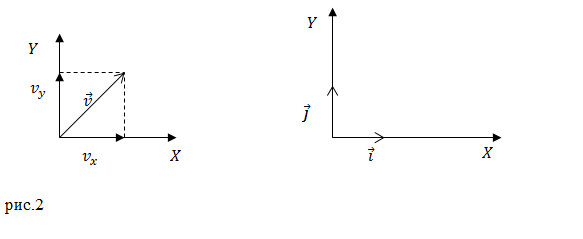
Zgodnie z twierdzeniem Pitagorasa moduł prędkości znajdujemy jako:
Obliczmy prędkość, podstawiając czas $t=1$c do otrzymanego wzoru:
Odpowiedź.$v$=7,2 $\frac(m)(s)$
Przykład 2
Ćwiczenia. Punkt materialny porusza się po linii prostej. Przyspieszenie tego punktu wzrasta zgodnie z wykresem (rys. 3). Jaka będzie prędkość punktu w chwili $t_1?$
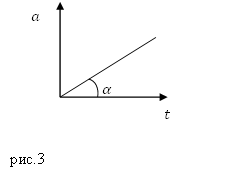
Rozwiązanie. Na wykresie na rys. 3 przyspieszenie przedstawiono jako linię prostą wychodzącą z początku współrzędnych, na podstawie rys. 3 zapisujemy wyrażenie analityczne na przyspieszenie jako:
gdzie $k=tg\ \alfa $.
Obliczamy prędkość punktu jako:
Odpowiedź.$v=\frac(tg\\alfa \cdot t^2_1)(2)$
Skracając w nieskończoność czas t, w którym m.t poruszał się w przestrzeni w granicy, gdy t 0, otrzymujemy prędkość chwilową, tj.
Wektor prędkości chwilowej jest równy granicy stosunku przyrostu wektora promienia m.t do okresu czasu, w którym ten przyrost nastąpił, kiedy T 0 lub równa pierwszej pochodnej wektora promienia po czasie.
Wektor prędkości chwilowej w danym czasie skierowany jest stycznie do trajektorii w danym punkcie (rys. 9).
Rzeczywiście, w t 0, gdy punkt M 2 zbliża się do M 1, cięciwa (sieczna) 
, zbliża się do długości odcinka łuku s i w granicy s = , a sieczna staje się styczną. Potwierdzają to wyraźnie eksperymenty. Na przykład iskry podczas ostrzenia narzędzia są zawsze kierowane stycznie do ściernicy. Ponieważ prędkość jest wielkością wektorową, jej moduł
.
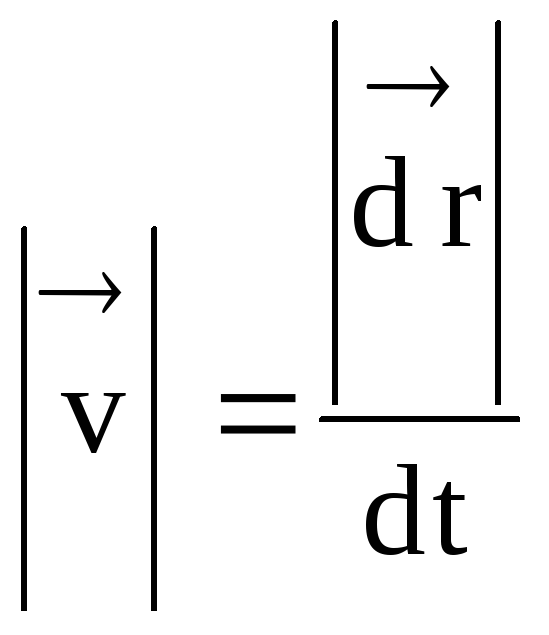W niektórych typach akceleratorów (na przykład cyklotronach itp.) cząstki poruszają się wielokrotnie po zamkniętej trajektorii, bez zatrzymywania się. W konsekwencji w dowolnym punkcie trajektorii wartość bezwzględna wektora prędkości chwilowej musi być różna od zera. Wniosek ten potwierdza nie tylko równanie (15), ale jest także zgodny z koncepcją średniej prędkości skalarnej (wzór 11). Jeśli w równaniu (11) dojdziemy do granicy przy t 0, to będziemy musieli uwzględnić takie małe odcinki toru na trajektorii s, które nie różnią się od modułu wektora przemieszczenia elementarnego . Następnie na podstawie równania (11) możemy otrzymać wartość chwilowej prędkości skalarnej 
pokrywa się z wielkością wektora prędkości chwilowej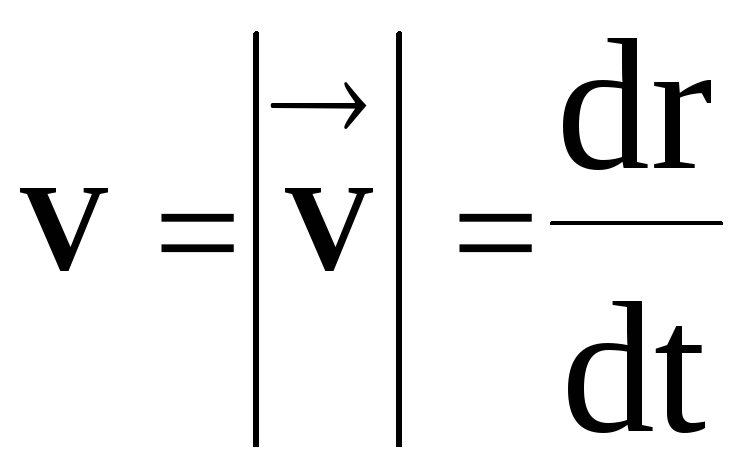 
,
ponieważ r = s przy t 0.
Jedno równanie wektora prędkości chwilowej (15) można zastąpić równoważnym układem trzech równań skalarnych, rzutami wektora prędkości na osie współrzędnych
v x = dx/dt, v y = dy/dt, v z = dz/dt. (16)
Wektor prędkości chwilowej jest powiązany z jego rzutami na osie współrzędnych za pomocą wyrażenia
,
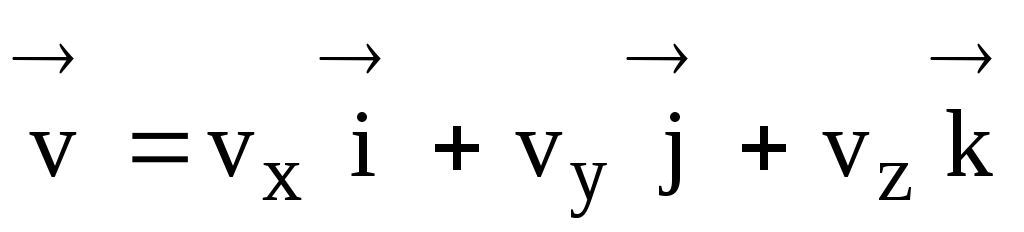(17)
Gdzie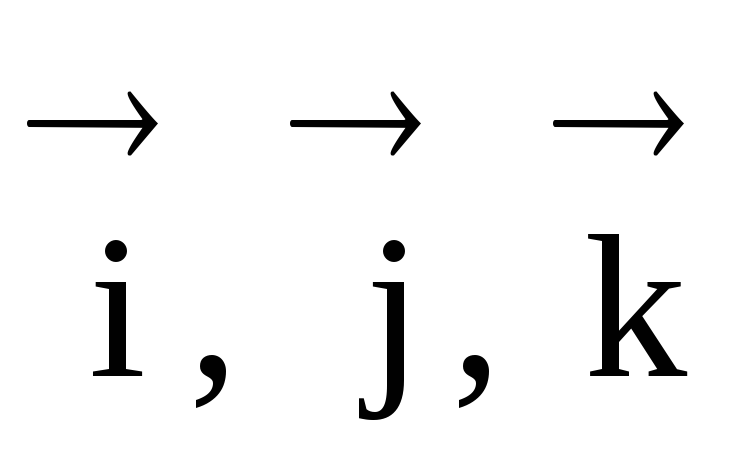 
– wektory jednostkowe skierowane odpowiednio wzdłuż osi X, Y, Z.
Modulo
.
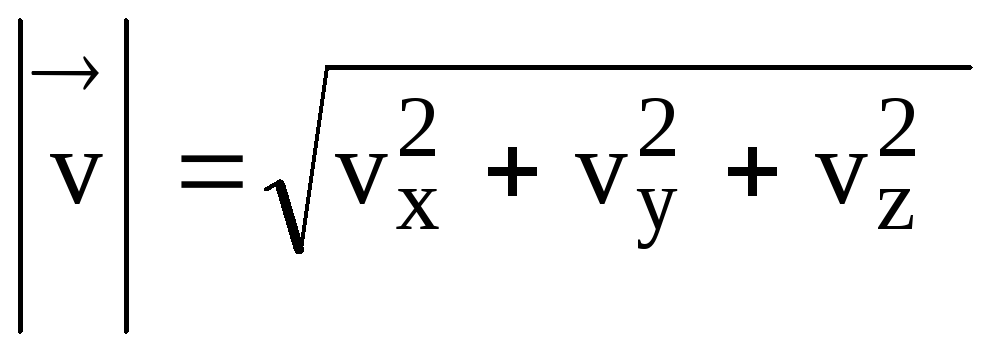(18)
Zatem wektor prędkości charakteryzuje prędkość zmiany ruchu w przestrzeni pod względem wielkości i kierunku w czasie. Prędkość jest funkcją czasu.
1.12. Średnie przyspieszenie
Kiedy ciała się poruszają, prędkość w ogólnym przypadku może zmieniać się zarówno pod względem wielkości, jak i kierunku.
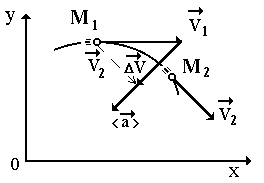
Niech m.t. w pewnym momencie t 1 znajdzie się w punkcie M 1 i porusza się z prędkością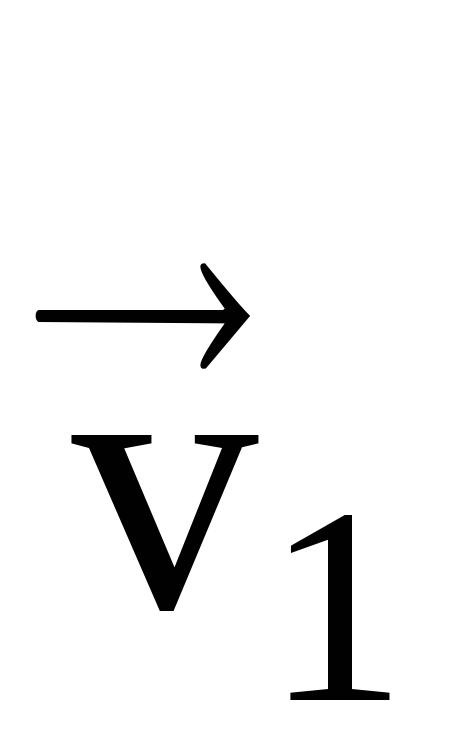 
i w czasie t 2 - w punkcie M 2 - z prędkością 
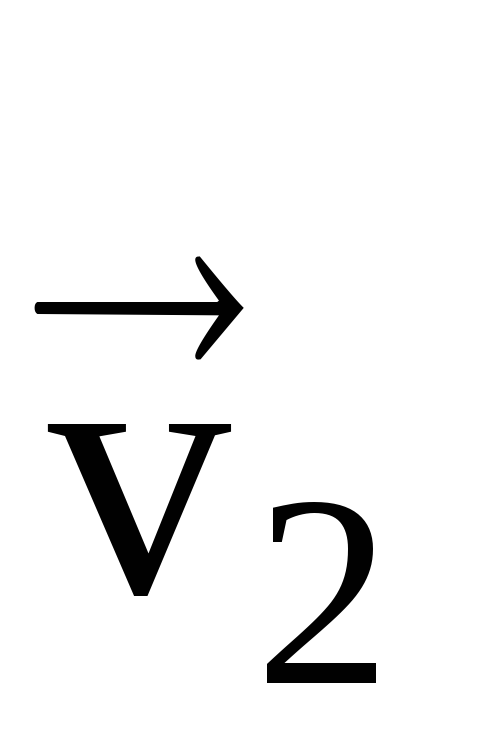(ryc. 10).
Przesuńmy wektor 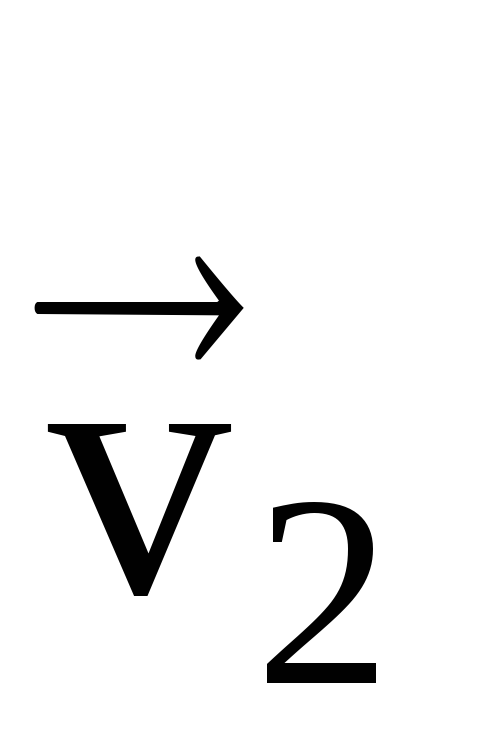równolegle do siebie w punkcie M 1, tak że początki wektorów pokrywają się 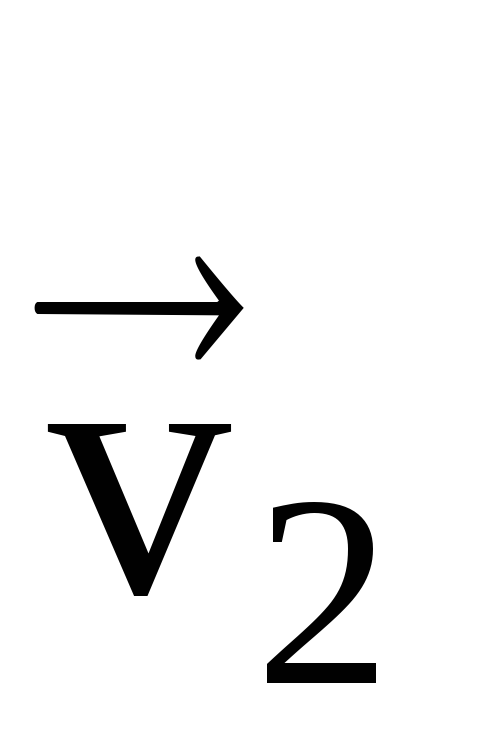I .
Potem różnica wektorów 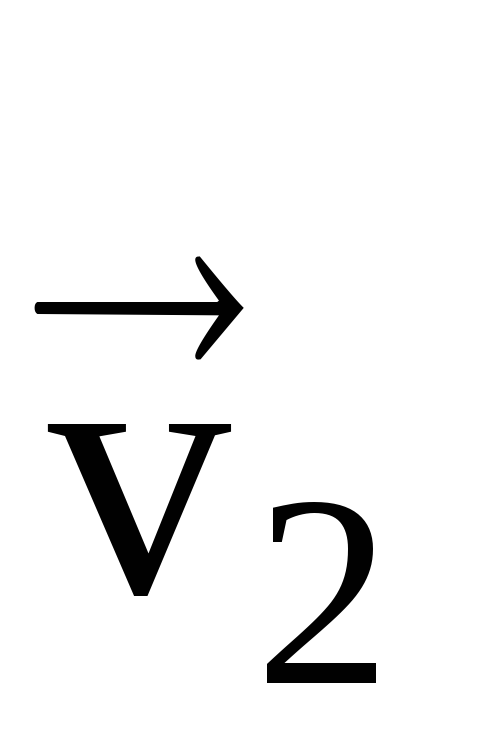I jest wektorem zmiany (przyrostu) prędkości w czasie t = t 2 – t 1, tj.
.
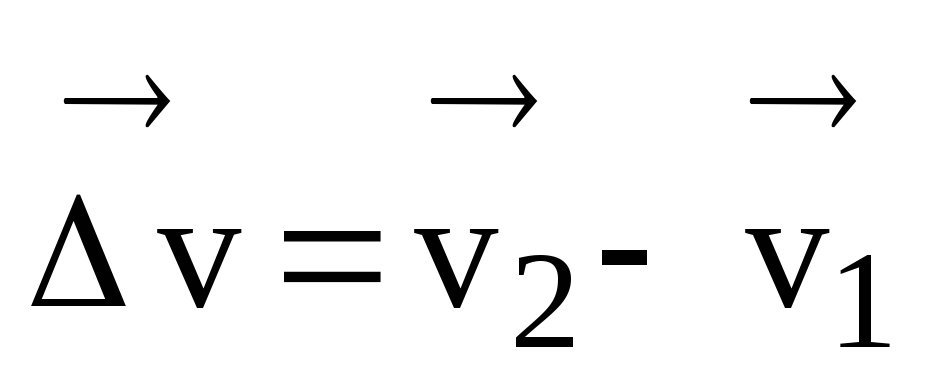(19)
Wektor średniego przyspieszenia jest równy stosunkowi wektora zmiany prędkości do okresu czasu, w którym ta zmiana nastąpiła.
Stąd,
.
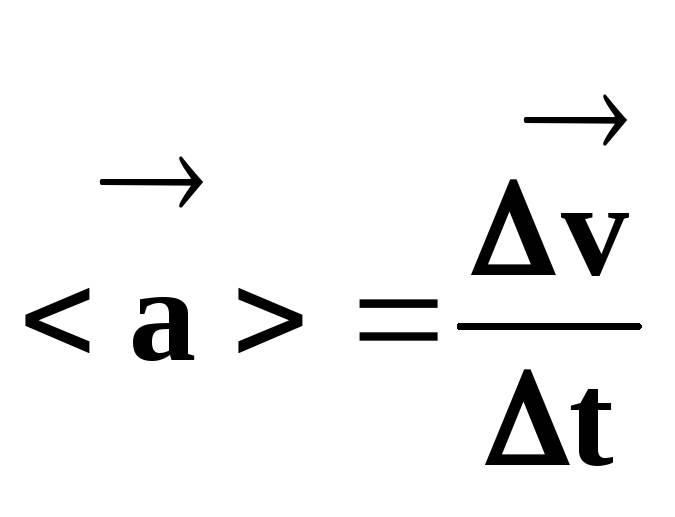(20)
Wektor średniego przyspieszenia pokrywa się z kierunkiem wektora zmiany prędkości i jest skierowany wewnątrz krzywizny trajektorii.
Jedno równanie wektora (1.20) odpowiada układowi trzech równań skalarnych dla rzutów wektora średniego przyspieszenia na osie współrzędnych
Moduł wektora średniego przyspieszenia
.
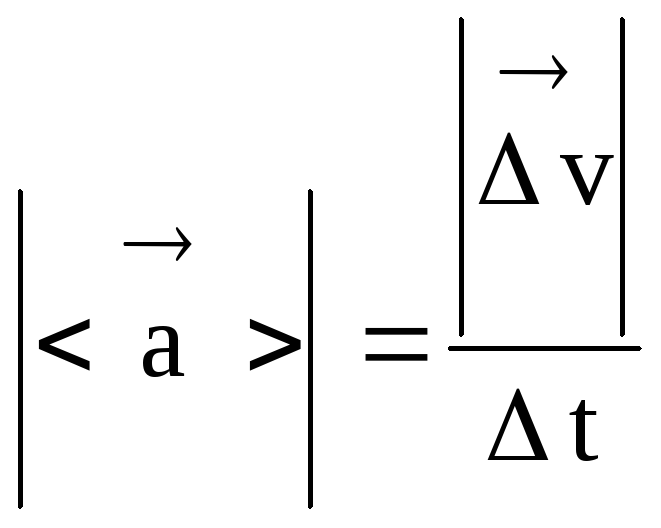(22)
Jednostką przyspieszenia w układzie SI jest metr na sekundę do kwadratu.
Jeśli wielkość prędkości (lub wielkość wektora prędkości) nie zmienia się, ruch jest jednostajny, gdy zmienia się wielkość prędkości, jest nierówny.
Mundur zwany ruch, podczas którego ciało porusza się po tych samych drogach w równych odstępach czasu. W tym przypadku wielkość prędkości pozostaje niezmieniona (w kierunku, w którym prędkość może się zmienić, jeśli ruch jest krzywoliniowy).
Prosty zwany ruch, którego trajektoria jest linią prostą. W takim przypadku kierunek prędkości pozostaje niezmieniony (wielkość prędkości może się zmienić, jeśli ruch nie jest równomierny).
Jednolite proste zwany ruchem, który jest zarówno jednostajny, jak i prostoliniowy. W tym przypadku zarówno wielkość, jak i kierunek pozostają niezmienione.
W ogólnym przypadku, gdy ciało się porusza, zmienia się zarówno wielkość, jak i kierunek wektora prędkości. Aby scharakteryzować, jak szybko zachodzą te zmiany, stosuje się specjalną wielkość - przyspieszenie.
Przyśpieszenie – jest to wielkość równa stosunkowi zmiany prędkości ciała do czasu trwania okresu, w którym nastąpiła ta zmiana prędkości. Średnie przyspieszenie oparte na tej definicji wynosi, m/s²:
Natychmiastowe przyspieszenie zwany wielkość fizyczna równa granicy, do której dąży średnie przyspieszenie w pewnym przedziale∆t → 0, m/s²:
Ponieważ prędkość może zmieniać się zarówno pod względem wielkości, jak i kierunku wzdłuż trajektorii, wektor przyspieszenia ma dwie składowe.
Składowa wektora przyspieszenia a, skierowana wzdłuż stycznej do trajektorii w danym punkcie, nazywana jest przyspieszeniem stycznym, które charakteryzuje zmianę wielkości wektora prędkości.
Składowa wektora przyspieszenia a, skierowana wzdłuż normalnej do stycznej w danym punkcie trajektorii, nazywana jest przyspieszeniem normalnym. Charakteryzuje zmianę kierunku wektora prędkości w przypadku ruchu krzywoliniowego. Naturalnie, gdy ciało porusza się po torze będącym linią prostą, normalne przyspieszenie wynosi zero.
Ruch prostoliniowy nazywamy ruchem jednostajnie zmiennym, jeśli w dowolnym czasie prędkość ciała zmienia się o tę samą wielkość. W tym wypadku relacja
∆V/ ∆t jest takie samo dla dowolnych przedziałów czasu. Dlatego wielkość i kierunek przyspieszenia pozostają niezmienione: a = const.
W przypadku ruchu prostoliniowego wektor przyspieszenia jest kierowany wzdłuż linii ruchu. Jeśli kierunek przyspieszenia pokrywa się z kierunkiem wektora prędkości, wówczas wielkość prędkości wzrośnie. W tym przypadku ruch nazywa się równomiernie przyspieszonym. Jeśli kierunek przyspieszenia jest przeciwny do kierunku wektora prędkości, wówczas wielkość prędkości będzie się zmniejszać. W tym przypadku ruch nazywa się równomiernie powolnym. W przyrodzie występuje naturalny ruch równomiernie przyspieszony - jest to spadek swobodny.
Swobodny spadek- zwany upadek ciała, jeśli jedyną siłą działającą na nie jest grawitacja. Eksperymenty przeprowadzone przez Galileusza wykazały, że podczas swobodnego spadania wszystkie ciała poruszają się z tym samym przyspieszeniem ziemskim i są oznaczone literą ĝ. W pobliżu powierzchni Ziemi ĝ = 9,8 m/s². Przyspieszenie swobodnego spadania spowodowane jest grawitacją Ziemi i jest skierowane pionowo w dół. Ściśle mówiąc, taki ruch jest możliwy tylko w próżni. Upadek w powietrzu można uznać za w przybliżeniu swobodny.
Trajektoria swobodnie spadającego ciała zależy od kierunku wektora prędkości początkowej. Jeśli ciało rzucono pionowo w dół, to jego trajektoria jest odcinkiem pionowym, a ruch nazywa się jednostajnie zmiennym. Jeżeli ciało zostanie wyrzucone pionowo w górę, to jego trajektoria składa się z dwóch pionowych odcinków. Najpierw ciało unosi się, poruszając się równie wolno. W momencie maksymalnego wznoszenia prędkość wynosi zero, po czym ciało opada, poruszając się ze stałym przyspieszeniem.
Jeżeli wektor prędkości początkowej jest skierowany pod kątem do horyzontu, wówczas ruch odbywa się po paraboli. W ten sposób porusza się rzucona piłka, dysk, sportowiec wykonujący skok w dal, lecąca kula itp.