Ułamkowa liczba zespolona. Liczby zespolone

FEDERALNA AGENCJA EDUKACJI

PAŃSTWOWA INSTYTUCJA EDUKACYJNA

WYŻSZE WYKSZTAŁCENIE ZAWODOWE

„PAŃSTWOWY UNIWERSYTET PEDAGOGICZNY WORONEŻA”

ZAKŁAD AGLEBRA I GEOMETRII

Liczby zespolone

(wybrane zadania)

PRACA KWALIFIKUJĄCA ABSOLWENTA

specjalność 050201.65 matematyka

(z dodatkową specjalnością 050202.65 informatyka)

Ukończył: student V roku

fizyczne i matematyczne

Wydział

Doradca naukowy:

WORONEŻ – 2008

1. Wstęp……………………………………………………...…………..…

2. Liczby zespolone (wybrane problemy)

2.1. Liczby zespolone w postaci algebraicznej….…...……….….

2.2. Interpretacja geometryczna liczb zespolonych………..…

2.3. Postać trygonometryczna liczb zespolonych

2.4. Zastosowanie teorii liczb zespolonych do rozwiązywania równań III i IV stopnia……………..…………………………………………………………

2.5. Liczby zespolone i parametry…………………………………..….

3. Zakończenie…………………………………………………………………………….

4. Lista referencji………………………….………………………......

1. Wstęp

W szkolnym programie nauczania matematyki wprowadza się teorię liczb na przykładach zbiorów liczb naturalnych, całkowitych, wymiernych, niewymiernych, tj. na zbiorze liczb rzeczywistych, których obrazy wypełniają całą oś liczbową. Ale już w ósmej klasie nie ma wystarczającej liczby liczb rzeczywistych, rozwiązujących równania kwadratowe z ujemnym dyskryminatorem. Dlatego konieczne było uzupełnienie zapasów liczb rzeczywistych za pomocą liczb zespolonych, dla których pierwiastek kwadratowy z liczby ujemnej ma sens.

Wybór tematu „Liczby zespolone” na temat mojej końcowej pracy kwalifikacyjnej jest taki, że pojęcie liczby zespolonej poszerza wiedzę uczniów o systemach liczbowych, o rozwiązywaniu szerokiej klasy problemów zarówno o treści algebraicznej, jak i geometrycznej, o rozwiązywaniu problemów algebraicznych równania dowolnego stopnia oraz o rozwiązywaniu problemów z parametrami.

Niniejsza praca bada rozwiązania 82 problemów.

Pierwsza część głównej sekcji „Liczby zespolone” zawiera rozwiązania problemów z liczbami zespolonymi w formie algebraicznej, definiuje operacje dodawania, odejmowania, mnożenia, dzielenia, operację sprzęgania liczb zespolonych w postaci algebraicznej, potęgę jednostki urojonej , moduł liczby zespolonej, a także określa regułę wyodrębniania pierwiastka kwadratowego z liczby zespolonej.

W drugiej części rozwiązano problemy interpretacji geometrycznej liczb zespolonych w postaci punktów lub wektorów płaszczyzny zespolonej.

W trzeciej części omówiono operacje na liczbach zespolonych w formie trygonometrycznej. Stosowane wzory to: Moivre i wyodrębnianie pierwiastka liczby zespolonej.

Część czwarta poświęcona jest rozwiązywaniu równań III i IV stopnia.

Przy rozwiązywaniu problemów z ostatniej części „Liczby zespolone i parametry” wykorzystuje się i konsoliduje informacje podane w poprzednich częściach. Szereg problemów zawartych w rozdziale poświęconych jest wyznaczaniu rodzin prostych w płaszczyźnie zespolonej określonych równaniami (nierównościami) z parametrem. W części ćwiczeń należy rozwiązać równania z parametrem (nad polem C). Istnieją zadania, w których zmienna zespolona spełnia jednocześnie kilka warunków. Szczególną cechą rozwiązywania problemów w tej sekcji jest redukcja wielu z nich do rozwiązania równań (nierówności, układów) drugiego stopnia, niewymiernych, trygonometrycznych z parametrem.

Cechą prezentacji materiału w każdej części jest wstępne wprowadzenie podstaw teoretycznych, a następnie ich praktyczne zastosowanie w rozwiązywaniu problemów.

Na końcu pracy znajduje się wykaz wykorzystanej literatury. Większość z nich przedstawia materiał teoretyczny w sposób wystarczająco szczegółowy i przystępny, omawia rozwiązania niektórych problemów i podaje praktyczne zadania do samodzielnego rozwiązania. Szczególną uwagę chciałbym zwrócić na takie źródła jak:

1. Gordienko N.A., Belyaeva E.S., Firstov V.E., Serebryakova I.V. Liczby zespolone i ich zastosowania: Podręcznik. . Materiał podręcznika przedstawiony jest w formie wykładów i ćwiczeń praktycznych.

2. Shklyarsky D.O., Chentsov N.N., Yaglom I.M. Wybrane problemy i twierdzenia matematyki elementarnej. Arytmetyka i algebra. Książka zawiera 320 zagadnień związanych z algebrą, arytmetyką i teorią liczb. Zadania te znacząco różnią się charakterem od standardowych zadań szkolnych.

2. Liczby zespolone (wybrane problemy)

2.1. Liczby zespolone w postaci algebraicznej

Rozwiązanie wielu problemów matematyki i fizyki sprowadza się do rozwiązywania równań algebraicznych, tj. równania postaci

,

gdzie a0, a1, …, an są liczbami rzeczywistymi. Dlatego badanie równań algebraicznych jest jednym z najważniejszych zagadnień matematyki. Na przykład równanie kwadratowe z ujemnym wyróżnikiem nie ma rzeczywistych pierwiastków. Najprostszym takim równaniem jest równanie

.

Aby to równanie miało rozwiązanie należy rozszerzyć zbiór liczb rzeczywistych dodając do niego pierwiastek równania

.

Oznaczmy ten pierwiastek przez

. Zatem z definicji lub

stąd,

. zwaną jednostką urojoną. Za jego pomocą i za pomocą pary liczb rzeczywistych kompilowane jest wyrażenie postaci.

Powstałe wyrażenie nazwano liczbami zespolonymi, ponieważ zawierało zarówno części rzeczywiste, jak i urojone.

Zatem liczby zespolone są wyrażeniami postaci

, i są liczbami rzeczywistymi oraz jest pewnym symbolem spełniającym warunek . Liczbę nazywa się częścią rzeczywistą liczby zespolonej, a liczba jest jej częścią urojoną. Do ich oznaczenia służą symbole .

Liczby zespolone w postaci

są liczbami rzeczywistymi i dlatego zbiór liczb zespolonych zawiera zbiór liczb rzeczywistych.

Liczby zespolone w postaci

nazywane są czysto urojonymi. Mówi się, że dwie liczby zespolone w postaci i są równe, jeśli ich części rzeczywiste i urojone są równe, tj. jeśli równości , .

Notacja algebraiczna liczb zespolonych pozwala na operacje na nich zgodnie ze zwykłymi zasadami algebry.

Suma dwóch liczb zespolonych

i nazywa się liczbą zespoloną w postaci .

Iloczyn dwóch liczb zespolonych

Aby rozwiązać problemy z liczbami zespolonymi, musisz zrozumieć podstawowe definicje. Głównym celem tego artykułu przeglądowego jest wyjaśnienie, czym są liczby zespolone i przedstawienie metod rozwiązywania podstawowych problemów z liczbami zespolonymi. Zatem liczba zespolona będzie nazywana liczbą postaci z = a + bi, Gdzie a, b- liczby rzeczywiste, które nazywane są odpowiednio częściami rzeczywistymi i urojonymi liczby zespolonej i oznaczają a = Re(z), b=Im(z).
I zwaną jednostką urojoną. ja 2 = -1. W szczególności każdą liczbę rzeczywistą można uznać za złożoną: a = a + 0i, gdzie a jest rzeczywiste. Jeśli a = 0 I b ≠ 0, wówczas liczbę nazywa się zwykle liczbą czysto urojoną.

Przedstawmy teraz operacje na liczbach zespolonych.
Rozważmy dwie liczby zespolone z 1 = za 1 + b 1 ja I z 2 = za 2 + b 2 ja.

Rozważmy z = a + bi.

Zbiór liczb zespolonych rozszerza zbiór liczb rzeczywistych, co z kolei rozszerza zbiór liczb wymiernych itp. Ten łańcuch inwestycji widać na rysunku: N – liczby naturalne, Z – liczby całkowite, Q – wymierne, R – rzeczywiste, C – zespolone.

Reprezentacja liczb zespolonych

Notacja algebraiczna.

Rozważ liczbę zespoloną z = a + bi, nazywa się tę formę zapisywania liczby zespolonej algebraiczny. Tę formę zapisu szczegółowo omówiliśmy już w poprzednim rozdziale. Poniższy rysunek wizualny jest używany dość często

Forma trygonometryczna.

Z rysunku widać, że liczba z = a + bi można napisać inaczej. To oczywiste a = rcos(φ), b = rsin(φ), r=|z|, stąd z = rcos(φ) + rsin(φ)i, φ ∈ (-π; π) nazywa się argumentem liczby zespolonej. Ta reprezentacja liczby zespolonej nazywa się postać trygonometryczna. Czasami bardzo wygodna jest forma zapisu trygonometrycznego. Na przykład wygodnie jest go użyć do podniesienia liczby zespolonej do potęgi całkowitej, a mianowicie jeśli z = rcos(φ) + rsin(φ)i, To z n = r n cos(nφ) + r n sin(nφ)i, ta formuła nazywa się Wzór Moivre’a.

Forma demonstracyjna.

Rozważmy z = rcos(φ) + rsin(φ)i- liczbę zespoloną w postaci trygonometrycznej, zapisz ją w innej formie z = r(cos(φ) + sin(φ)i) = re iφ, ostatnia równość wynika ze wzoru Eulera, uzyskaliśmy zatem nową formę zapisu liczby zespolonej: z = reiφ, który jest nazywany orientacyjny. Ta forma zapisu jest również bardzo wygodna w przypadku podnoszenia liczby zespolonej do potęgi: z n = r n mi inφ, Tutaj N niekoniecznie liczba całkowita, ale może być dowolną liczbą rzeczywistą. Ta forma notacji jest dość często używana do rozwiązywania problemów.

Podstawowe twierdzenie wyższej algebry

Wyobraźmy sobie, że mamy równanie kwadratowe x 2 + x + 1 = 0. Oczywiście dyskryminator tego równania jest ujemny i nie ma pierwiastków rzeczywistych, ale okazuje się, że równanie to ma dwa różne pierwiastki zespolone. Zatem podstawowe twierdzenie wyższej algebry stwierdza, że ​​każdy wielomian stopnia n ma co najmniej jeden pierwiastek zespolony. Wynika z tego, że każdy wielomian stopnia n ma dokładnie n pierwiastków zespolonych, biorąc pod uwagę ich krotność. Twierdzenie to jest bardzo ważnym wynikiem w matematyce i jest szeroko stosowane. Prostym następstwem tego twierdzenia jest to, że istnieje dokładnie n różnych pierwiastków stopnia n jedności.

Główne typy zadań

W tej sekcji omówione zostaną główne typy prostych problemów związanych z liczbami zespolonymi. Konwencjonalnie problemy dotyczące liczb zespolonych można podzielić na następujące kategorie.

• Wykonywanie prostych operacji arytmetycznych na liczbach zespolonych.
• Znajdowanie pierwiastków wielomianów w liczbach zespolonych.
• Podnoszenie liczb zespolonych do potęg.
• Wyodrębnianie pierwiastków z liczb zespolonych.
• Używanie liczb zespolonych do rozwiązywania innych problemów.

Przyjrzyjmy się teraz ogólnym metodom rozwiązywania tych problemów.

Najprostsze operacje arytmetyczne na liczbach zespolonych wykonuje się według zasad opisanych w pierwszej części, jednak jeśli liczby zespolone są przedstawione w postaci trygonometrycznej lub wykładniczej, to w tym przypadku można je przekształcić do postaci algebraicznej i wykonać operacje według znanych zasad.

Znalezienie pierwiastków wielomianów zwykle sprowadza się do znalezienia pierwiastków równania kwadratowego. Załóżmy, że mamy równanie kwadratowe, jeśli jego wyróżnik jest nieujemny, to jego pierwiastki będą rzeczywiste i można je znaleźć według dobrze znanego wzoru. Jeśli dyskryminator jest ujemny, tj. D = -1∙a 2, Gdzie A jest pewną liczbą, wówczas dyskryminator można przedstawić jako D = (ia) 2, stąd √D = i|a|, a następnie możesz skorzystać ze znanego już wzoru na pierwiastki równania kwadratowego.

Przykład. Wróćmy do równania kwadratowego wspomnianego powyżej x 2 + x + 1 = 0.
Dyskryminujący - re = 1 - 4 ∙ 1 = -3 = -1(√3) 2 = (i√3) 2.
Teraz możemy łatwo znaleźć korzenie:

Podnoszenie liczb zespolonych do potęgi można wykonać na kilka sposobów. Jeśli chcesz podnieść liczbę zespoloną w formie algebraicznej do małej potęgi (2 lub 3), możesz to zrobić przez bezpośrednie mnożenie, ale jeśli potęga jest większa (w problemach często jest znacznie większa), musisz to zrobić zapisz tę liczbę w postaci trygonometrycznej lub wykładniczej i skorzystaj ze znanych już metod.

Przykład. Rozważmy z = 1 + i i podnieś go do potęgi dziesiątej.
Zapiszmy z w postaci wykładniczej: z = √2 e iπ/4.
Następnie z 10 = (√2 e iπ/4) 10 = 32 e 10iπ/4.
Wróćmy do postaci algebraicznej: z 10 = -32i.

Wyodrębnianie pierwiastków z liczb zespolonych jest odwrotną operacją potęgowania i dlatego wykonuje się je w podobny sposób. Aby wyodrębnić pierwiastki, często używa się wykładniczej formy zapisu liczby.

Przykład. Znajdźmy wszystkie pierwiastki trzeciego stopnia jedności. Aby to zrobić, znajdziemy wszystkie pierwiastki równania z 3 = 1, będziemy szukać pierwiastków w formie wykładniczej.
Podstawmy do równania: r 3 e 3iφ = 1 lub r 3 e 3iφ = e 0 .
Stąd: r = 1, 3φ = 0 + 2πk, zatem φ = 2πk/3.
Różne pierwiastki otrzymuje się przy φ = 0, 2π/3, 4π/3.
Zatem 1, e i2π/3, e i4π/3 są pierwiastkami.
Lub w formie algebraicznej: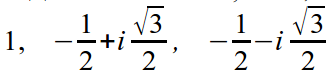

Ostatni rodzaj problemów obejmuje ogromną różnorodność problemów i nie ma ogólnych metod ich rozwiązywania. Podajmy prosty przykład takiego zadania:

Znajdź kwotę grzech(x) + grzech(2x) + grzech(2x) + … + grzech(nx).

Chociaż sformułowanie tego problemu nie obejmuje liczb zespolonych, można je łatwo rozwiązać za ich pomocą. Aby go rozwiązać, stosuje się następujące reprezentacje:


Jeśli teraz podstawimy tę reprezentację na sumę, wówczas problem sprowadza się do zsumowania zwykłego postępu geometrycznego.

Wniosek

Liczby zespolone są szeroko stosowane w matematyce; w tym artykule przeglądowym zbadano podstawowe operacje na liczbach zespolonych, opisano kilka rodzajów standardowych problemów i krótko opisano ogólne metody ich rozwiązywania; w celu bardziej szczegółowego zbadania możliwości liczb zespolonych zaleca się korzystaj z literatury specjalistycznej.

Literatura

Liczby zespolone są minimalnym rozszerzeniem znanego nam zbioru liczb rzeczywistych. Ich zasadnicza różnica polega na tym, że pojawia się element, który po podniesieniu do kwadratu daje -1, tj. ja lub .

Każda liczba zespolona składa się z dwóch części: prawdziwe i wyimaginowane:

Zatem jasne jest, że zbiór liczb rzeczywistych pokrywa się ze zbiorem liczb zespolonych z zerową częścią urojoną.

Najpopularniejszym modelem zbioru liczb zespolonych jest zwykła płaszczyzna. Pierwsza współrzędna każdego punktu będzie jego częścią rzeczywistą, a druga częścią urojoną. Wtedy rolą samych liczb zespolonych będą wektory mające początek w punkcie (0,0).

Operacje na liczbach zespolonych.

Tak naprawdę, jeśli weźmiemy pod uwagę model zbioru liczb zespolonych, intuicyjnie widać, że dodawanie (odejmowanie) i mnożenie dwóch liczb zespolonych wykonuje się w taki sam sposób, jak odpowiadające im operacje na wektorach. Co więcej, mamy na myśli iloczyn wektorowy wektorów, ponieważ wynikiem tej operacji jest ponownie wektor.

1.1 Dodatek.

(Jak widać, ta operacja odpowiada dokładnie)

1.2 Odejmowanie podobnie wytwarza się według następującej zasady:

2. Mnożenie.

3. Podział.

Zdefiniowane po prostu jako odwrotna operacja mnożenia.

Forma trygonometryczna.

Moduł liczby zespolonej z jest następującą wielkością:

,

oczywiście jest to znowu tylko moduł (długość) wektora (a, b).

Najczęściej moduł liczby zespolonej oznacza się jako ρ.

Okazało się, że

z = ρ(cosφ+isinφ).

Poniższe wynika bezpośrednio z trygonometrycznej formy zapisu liczby zespolonej: formuły :

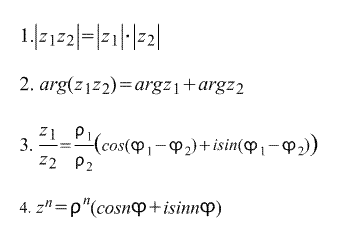
Ostatnia formuła nazywa się Wzór Moivre’a. Formuła wywodzi się bezpośrednio z niego n-ty pierwiastek liczby zespolonej:

zatem istnieje n n-tych pierwiastków liczby zespolonej z.

§ 1. Liczby zespolone: ​​definicje, interpretacja geometryczna, działania w postaciach algebraicznych, trygonometrycznych i wykładniczych

Definicja liczby zespolonej

Równości złożone

Geometryczna reprezentacja liczb zespolonych

Moduł i argument liczby zespolonej

Formy algebraiczne i trygonometryczne liczby zespolonej

Postać wykładnicza liczby zespolonej

Wzory Eulera

§ 2. Funkcje całe (wielomiany) i ich podstawowe własności. Rozwiązywanie równań algebraicznych na zbiorze liczb zespolonych

Definicja równania algebraicznego stopnia

Podstawowe własności wielomianów

Przykłady rozwiązywania równań algebraicznych na zbiorze liczb zespolonych

Pytania autotestowe

Słowniczek

§ 1. Liczby zespolone: ​​definicje, interpretacja geometryczna, działania na postaciach algebraicznych, trygonometrycznych i wykładniczych

Definicja liczby zespolonej ( Podaj definicję liczby zespolonej)

Liczba zespolona z jest wyrażeniem w postaci:

Liczba zespolona w postaci algebraicznej,(1)

Gdzie x, y Î;

- zespolona liczba sprzężona liczba z ;

- przeciwny numer liczba z ;

- zero zespolone ;

– tak oznacza się zbiór liczb zespolonych.

1)z = 1 + IÞ Odp z= 1, Im z = 1, = 1 – I, = –1 – I ;

2)z = –1 + IÞ Odp z= –1, Im z = , = –1 – I, = –1 –I ;

3)z = 5 + 0I= 5 Þ Re z= 5, Im z = 0, = 5 – 0I = 5, = –5 – 0I = –5

Þ jeśli jestem z= 0, zatem z = X- prawdziwy numer;

4)z = 0 + 3I = 3IÞ Odp z= 0, Im z = 3, = 0 – 3I = –3I , = –0 – 3I = – 3I

Þ jeśli Re z= 0, zatem z = j - liczba czysto urojona.

Równości złożone (Sformułuj znaczenie równości zespolonej)

1) ;

2) .

Jedna złożona równość jest równoważna systemowi dwóch równości rzeczywistych. Te rzeczywiste równości uzyskuje się z równości zespolonej poprzez oddzielenie części rzeczywistej i urojonej.

1) ;

2) .

Geometryczna reprezentacja liczb zespolonych ( Jaka jest reprezentacja geometryczna liczb zespolonych?)

Liczba zespolona z reprezentowany przez kropkę ( X , y) na płaszczyźnie zespolonej lub wektorze promienia tego punktu.

Podpisać z w drugim kwartale oznacza, że ​​kartezjański układ współrzędnych będzie używany jako płaszczyzna zespolona.

Moduł i argument liczby zespolonej ( Jaki jest moduł i argument liczby zespolonej?)

Moduł liczby zespolonej jest nieujemną liczbą rzeczywistą

.(2)

Z geometrycznego punktu widzenia moduł liczby zespolonej to długość wektora reprezentującego liczbę z lub promień biegunowy punktu ( X , y).

Narysuj następujące liczby na płaszczyźnie zespolonej i zapisz je w postaci trygonometrycznej.

1)z = 1 + I Þ

,

Þ

Þ ;

,

Þ

Þ ;

,

5),

to znaczy dla z = 0 tak będzie

, J nieokreślony.

Działania arytmetyczne na liczbach zespolonych (Podaj definicje i wymień główne właściwości działań arytmetycznych na liczbach zespolonych.)

Dodawanie (odejmowanie) liczb zespolonych

z 1 ± z 2 = (X 1 + j 1) ± ( X 2 + j 2) = (X 1 ± X 2) + I (y 1 ± y 2),(5)

to znaczy podczas dodawania (odejmowania) liczb zespolonych dodaje się (odejmuje) ich części rzeczywiste i urojone.

1)(1 + I) + (2 – 3I) = 1 + I + 2 –3I = 3 – 2I ;

2)(1 + 2I) – (2 – 5I) = 1 + 2I – 2 + 5I = –1 + 7I .

Podstawowe właściwości dodatku

1)z 1 + z 2 = z 2 + z 1;

2)z 1 + z 2 + z 3 = (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3);

3)z 1 – z 2 = z 1 + (– z 2);

4)z + (–z) = 0;

Mnożenie liczb zespolonych w formie algebraicznej

z 1∙z 2 = (X 1 + j 1)∙(X 2 + j 2) = X 1X 2 + X 1j 2 + j 1X 2 + I 2y 1y 2 = (6)

= (X 1X 2 – y 1y 2) + I (X 1y 2 + y 1X 2),

to znaczy mnożenie liczb zespolonych w formie algebraicznej odbywa się zgodnie z zasadą algebraicznego mnożenia dwumianu przez dwumian, a następnie zastępowanie i redukcja podobnych w kategoriach rzeczywistych i urojonych.

1)(1 + I)∙(2 – 3I) = 2 – 3I + 2I – 3I 2 = 2 – 3I + 2I + 3 = 5 – I ;

2)(1 + 4I)∙(1 – 4I) = 1 – 42 I 2 = 1 + 16 = 17;

3)(2 + I)2 = 22 + 4I + I 2 = 3 + 4I .

Mnożenie liczb zespolonych w formie trygonometrycznej

z 1∙z 2 = R 1 (kos J 1 + I grzech J 1)× R 2 (kos J 2 + I grzech J 2) =

= R 1R 2 (kos J 1co J 2 + I sałata J 1 grzech J 2 + I grzech J 1co J 2 + I 2 grzech J 1 grzech J 2) =

= R 1R 2((kos J 1co J 2 – grzech J 1 grzech J 2) + I(sałata J 1 grzech J 2 + grzech J 1co J 2))

Iloczyn liczb zespolonych w formie trygonometrycznej, to znaczy podczas mnożenia liczb zespolonych w formie trygonometrycznej, ich moduły są mnożone i ich argumenty są dodawane.

Podstawowe własności mnożenia

1)z 1× z 2 = z 2× z 1 - przemienność;

2)z 1× z 2× z 3 = (z 1× z 2)× z 3 = z 1×( z 2× z 3) - łączność;

3)z 1×( z 2 + z 3) = z 1× z 2 + z 1× z 3 - rozdzielność ze względu na dodawanie;

4)z×0 = 0; z×1 = z ;

Podział liczb zespolonych

Dzielenie jest odwrotnością mnożenia, tzw

Jeśli z × z 2 = z 1 i z 2 ¹ 0, wtedy .

Podczas dzielenia w formie algebraicznej licznik i mianownik ułamka są mnożone przez złożony koniugat mianownika:

Dzielenie liczb zespolonych w formie algebraicznej.(7)

Podczas dzielenia w formie trygonometrycznej moduły są dzielone, a argumenty odejmowane:

Dzielenie liczb zespolonych w formie trygonometrycznej.(8)

2)
.

Podnoszenie liczby zespolonej do potęgi naturalnej

Wygodniej jest wykonywać potęgowanie w formie trygonometrycznej:

Wzór Moivre’a, (9)

to znaczy, gdy liczbę zespoloną podnosi się do potęgi naturalnej, jej moduł podnosi się do tej potęgi, a argument jest mnożony przez wykładnik.

Oblicz (1 + I)10.

Notatki

1. Wykonując operacje mnożenia i podniesienia do potęgi naturalnej w formie trygonometrycznej, można uzyskać wartości kątów przekraczające jeden pełny obrót. Ale zawsze można je zredukować do kątów lub przez upuszczenie całkowitej liczby pełnych obrotów, korzystając z właściwości okresowości funkcji i .

2. Znaczenie nazywana wartością główną argumentu liczby zespolonej;

w tym przypadku wartości wszystkich możliwych kątów są oznaczone przez ;

to oczywiste, że ,.

Wyodrębnianie pierwiastka stopnia naturalnego z liczby zespolonej

Wzory Eulera(16)

dla którego funkcje trygonometryczne i zmienna rzeczywista wyrażane są poprzez funkcję wykładniczą (wykładnik) z wykładnikiem czysto urojonym.

§ 2. Funkcje całe (wielomiany) i ich podstawowe własności. Rozwiązywanie równań algebraicznych na zbiorze liczb zespolonych

Dwa wielomiany tego samego stopnia N są sobie jednakowo równe wtedy i tylko wtedy, gdy ich współczynniki pokrywają się dla tych samych potęg zmiennej X, to jest

Dowód

w Tożsamość (3) obowiązuje dla „xО (lub „xО)

Þ obowiązuje przez; podstawiając, otrzymujemy jakiś = miliard .

Anulujmy wzajemnie warunki w (3) jakiś I miliard i podziel obie części przez X :

Tożsamość ta dotyczy także „ X, w tym kiedy X = 0

Þ zakładając X= 0, otrzymujemy jakiś – 1 = miliard – 1.

Anulujmy wzajemnie warunki w (3") jakiś– 1 i A N– 1 i podziel obie strony przez X, w rezultacie otrzymujemy

Kontynuując analogicznie rozumowanie, otrzymujemy to jakiś – 2 = miliard –2, …, A 0 = B 0.

Udowodniono zatem, że identyczna równość wielomianów 2-x implikuje zbieżność ich współczynników w tych samych stopniach X .

Stwierdzenie odwrotne jest słusznie oczywiste, tj. jeżeli dwa wielomiany mają takie same współczynniki, to są to identyczne funkcje, zatem ich wartości pokrywają się dla wszystkich wartości argumentu, czyli są identycznie równe. Właściwość 1 została całkowicie udowodniona. w

Podczas dzielenia wielomianu Pn (X) przez różnicę ( X – X 0) reszta jest równa Pn (X 0), tj

Twierdzenie Bezouta(4)

Gdzie Qn – 1(X) - całkowita część dzielenia, jest wielomianem stopnia ( N – 1).

Dowód

w Zapiszmy wzór na dzielenie z resztą:

Pn (X) = (X – X 0)∙Qn – 1(X) + A ,

Gdzie Qn – 1(X) - wielomian stopnia ( N – 1),

A- reszta, która jest liczbą ze względu na dobrze znany algorytm dzielenia wielomianu przez dwumian „w kolumnie”.

Ta równość jest prawdziwa dla „ X, w tym kiedy X = X 0 Þ

Pn (X 0) = (X 0 – X 0)× Qn – 1(X 0) + A Þ

A = Pn (X 0) itp. w

Wniosek z twierdzenia Bezouta. O dzieleniu wielomianu przez dwumian bez reszty

Jeśli numer X 0 jest zerem wielomianu, wówczas wielomian ten dzieli się przez różnicę ( X – X 0) bez reszty, tj

Þ .(5)

1) , ponieważ P 3 ust. 1° 0

2) ponieważ P 4(–2)° 0

3) ponieważ P 2(–1/2) ° 0

Dzielenie wielomianów na dwumiany „w kolumnie”:

_

_

_

_

_

Każdy wielomian stopnia n ³ 1 ma co najmniej jedno zero, rzeczywiste lub zespolone

Dowód tego twierdzenia wykracza poza zakres naszego kursu. Dlatego przyjmujemy twierdzenie bez dowodu.

Popracujmy nad tym twierdzeniem i twierdzeniem Bezouta z wielomianem Pn (X).

Po N-wielokrotne zastosowanie tych twierdzeń to otrzymujemy

Gdzie A 0 to współczynnik przy X N V Pn (X).

Wniosek z podstawowego twierdzenia algebry. O rozkładzie wielomianu na czynniki liniowe

Dowolny wielomian stopnia na zbiorze liczb zespolonych można rozłożyć na N czynniki liniowe, tj

Rozwinięcie wielomianu na czynniki liniowe, (6)

gdzie x1, x2, ... xn są zerami wielomianu.

Co więcej, jeśli k numery z zestawu X 1, X 2, … xn pokrywają się ze sobą i z liczbą a, następnie w iloczynie (6) mnożnik ( X- A) k. Potem numer X= a nazywa się k-krotne zero wielomianu Pn ( X) . Jeśli k= 1, wówczas wywoływane jest zero proste zero wielomianu Pn ( X) .

1)P 4(X) = (X – 2)(X– 4)3 Þ X 1 = 2 - proste zero, X 2 = 4 - potrójne zero;

2)P 4(X) = (X – I)4 Þ X = I- krotność zerowa 4.

Właściwość 4 (o liczbie pierwiastków równania algebraicznego)

Każde równanie algebraiczne Pn(x) = 0 stopnia n ma dokładnie n pierwiastków ze zbioru liczb zespolonych, jeśli policzymy każdy pierwiastek tyle razy, ile wynosi jego krotność.

1)X 2 – 4X+ 5 = 0 - równanie algebraiczne drugiego stopnia

Þ X 1,2 = 2 ± = 2 ± I- dwa korzenie;

2)X 3 + 1 = 0 - równanie algebraiczne trzeciego stopnia

Þ X 1,2,3 = - trzy korzenie;

3)P 3(X) = X 3 + X 2 – X– 1 = 0 Þ X 1 = 1, ponieważ P 3(1) = 0.

Podziel wielomian P 3(X) NA ( X – 1):

X 3	+	X 2	–	X	–	1	X – 1
X 3	–	X 2	X 2 + 2X +1
2X 2	–	X
2X 2	–	2X
X	–	1
X	–	1
0

Oryginalne równanie

P 3(X) = X 3 + X 2 – X– 1 = 0 Û( X – 1)(X 2 + 2X+ 1) = 0 Û( X – 1)(X + 1)2 = 0

Þ X 1 = 1 - pierwiastek prosty, X 2 = –1 - podwójny pierwiastek.

1) – sparowane złożone korzenie sprzężone;

Każdy wielomian o rzeczywistych współczynnikach rozkłada się na iloczyn funkcji liniowych i kwadratowych o rzeczywistych współczynnikach.

Dowód

w Niech X 0 = A + bi- zero wielomianu Pn (X). Jeśli wszystkie współczynniki tego wielomianu są liczbami rzeczywistymi, to on również wynosi zero (według własności 5).

Obliczmy iloczyn dwumianów :

równanie wielomianu liczb zespolonych

Dostał ( X – A)2 + B 2 - trójmian kwadratowy z rzeczywistymi współczynnikami.

Zatem dowolna para dwumianów ze złożonymi pierwiastkami sprzężonymi we wzorze (6) prowadzi do trójmianu kwadratowego z rzeczywistymi współczynnikami. w

1)P 3(X) = X 3 + 1 = (X + 1)(X 2 – X + 1);

2)P 4(X) = X 4 – X 3 + 4X 2 – 4X = X (X –1)(X 2 + 4).

Przykłady rozwiązywania równań algebraicznych na zbiorze liczb zespolonych ( Podaj przykłady rozwiązywania równań algebraicznych na zbiorze liczb zespolonych)

1. Równania algebraiczne pierwszego stopnia:

, jest jedynym prostym pierwiastkiem.

2. Równania kwadratowe:

, – zawsze ma dwa pierwiastki (różne lub równe).

1) .

3. Dwumianowe równania stopnia:

, – zawsze ma inne korzenie.

,

Odpowiedź: , .

4. Rozwiąż równanie sześcienne.

Równanie trzeciego stopnia ma trzy pierwiastki (rzeczywiste lub złożone) i każdy pierwiastek należy policzyć tyle razy, ile wynosi jego wielokrotność. Ponieważ wszystkie współczynniki tego równania są liczbami rzeczywistymi, zespolone pierwiastki równania, jeśli takie istnieją, będą sprzężeniami zespolonymi parami.

Przez selekcję znajdujemy pierwszy pierwiastek równania, ponieważ .

Zgodnie z twierdzeniem Bezouta. Obliczamy ten podział „w kolumnie”:

_
_
_

Przedstawiając teraz wielomian jako iloczyn współczynnika liniowego i kwadratowego, otrzymujemy:

.

Inne pierwiastki znajdujemy jako pierwiastki równania kwadratowego:

Odpowiedź: , .

5. Skonstruuj równanie algebraiczne najmniejszego stopnia ze współczynnikami rzeczywistymi, jeśli wiadomo, że liczby X 1 = 3 i X 2 = 1 + I są jego korzenie i X 1 to podwójny pierwiastek, i X 2 - proste.

Liczba jest także pierwiastkiem równania, ponieważ współczynniki równania muszą być rzeczywiste.

W sumie wymagane równanie ma 4 pierwiastki: X 1, X 1,X 2, . Dlatego jego stopień wynosi 4. Wielomian czwartego stopnia tworzymy z zerami X

11. Co to jest zero zespolone?

13. Formułować znaczenie równości zespolonej.

15. Jaki jest moduł i argument liczby zespolonej?

17. Jaki jest argument liczby zespolonej?

18. Jaka jest nazwa lub znaczenie tej formuły?

19. Wyjaśnij znaczenie zapisu w tym wzorze:

27. Podaj definicje i wymień główne własności działań arytmetycznych na liczbach zespolonych.

28. Jaka jest nazwa lub znaczenie tej formuły?

29. Wyjaśnij znaczenie zapisu w tym wzorze:

31. Jaka jest nazwa lub znaczenie tej formuły?

32. Wyjaśnij znaczenie zapisu w tym wzorze:

34. Jaka jest nazwa lub znaczenie formuły?

35. Wyjaśnij znaczenie zapisu w tym wzorze:

61. Wymień główne właściwości wielomianów.

63. Podaj własność dzielenia wielomianu przez różnicę (x – x0).

65. Jaka jest nazwa lub znaczenie tej formuły?

66. Wyjaśnij znaczenie zapisu w tym wzorze:

67. ⌂ .

69. Podaj twierdzenie: podstawowe twierdzenie algebry.

70. Jaka jest nazwa lub znaczenie tej formuły?

71. Wyjaśnij znaczenie zapisu w tym wzorze:

75. Podaj własność liczby pierwiastków równania algebraicznego.

78. Podaj własność rozkładu wielomianu o współczynnikach rzeczywistych na czynniki liniowe i kwadratowe.

Słowniczek

K-krotne zero wielomianu to... (s. 18)

wielomian algebraiczny nazywa się... (s. 14)

równanie algebraiczne n-tego stopnia nazywa się... (s. 14)

postać algebraiczna liczby zespolonej nazywa się... (s. 5)

argumentem liczby zespolonej jest... (strona 4)

częścią rzeczywistą liczby zespolonej z jest... (strona 2)

złożona liczba sprzężona to... (strona 2)

Zero zespolone to... (strona 2)

liczba zespolona nazywa się... (strona 2)

pierwiastek stopnia n liczby zespolonej nazywa się... (s. 10)

pierwiastkiem równania jest... (s. 14)

współczynniki wielomianu wynoszą... (s. 14)

jednostką urojoną jest... (strona 2)

część urojona liczby zespolonej z to... (strona 2)

moduł liczby zespolonej nazywa się... (s. 4)

zero funkcji nazywa się... (s. 14)

postać wykładnicza liczby zespolonej nazywa się... (s. 11)

wielomian nazywa się... (s. 14)

proste zero wielomianu nazywa się... (s. 18)

przeciwna liczba to... (strona 2)

stopień wielomianu to... (s. 14)

postać trygonometryczna liczby zespolonej nazywa się... (s. 5)

Wzór Moivre’a to... (s. 9)

Wzory Eulera to... (strona 13)

cała funkcja nazywa się... (s. 14)

liczba czysto urojona to... (s. 2)

Przypomnijmy niezbędne informacje o liczbach zespolonych.

Liczba zespolona jest wyrazem formy A + bi, Gdzie A, B są liczbami rzeczywistymi i I- tak zwana wyimaginowana jednostka, czyli symbol, którego kwadrat jest równy –1 I 2 = –1. Numer A zwany prawdziwa część i numer B - część wyimaginowana Liczba zespolona z = A + bi. Jeśli B= 0, to zamiast tego A + 0I po prostu piszą A. Można zauważyć, że liczby rzeczywiste są szczególnym przypadkiem liczb zespolonych.

Działania arytmetyczne na liczbach zespolonych są takie same jak na liczbach rzeczywistych: można je dodawać, odejmować, mnożyć i dzielić. Dodawanie i odejmowanie odbywa się według reguły ( A + bi) ± ( C + di) = (A ± C) + (B ± D)I, a mnożenie jest zgodne z regułą ( A + bi) · ( C + di) = (AC – bd) + (ogłoszenie + pne)I(tutaj używa się tego I 2 = –1). Liczba = A – bi zwany złożony koniugat Do z = A + bi. Równość z · = A 2 + B 2 pozwala zrozumieć, jak podzielić jedną liczbę zespoloną przez inną (niezerową) liczbę zespoloną:

(Na przykład, .)

Liczby zespolone mają wygodną i wizualną reprezentację geometryczną: liczba z = A + bi można przedstawić za pomocą wektora ze współrzędnymi ( A; B) na płaszczyźnie kartezjańskiej (lub, co prawie to samo, punkt - koniec wektora o tych współrzędnych). W tym przypadku suma dwóch liczb zespolonych jest przedstawiana jako suma odpowiednich wektorów (co można znaleźć za pomocą reguły równoległoboku). Zgodnie z twierdzeniem Pitagorasa długość wektora ze współrzędnymi ( A; B) jest równe . Ta ilość nazywa się moduł Liczba zespolona z = A + bi i jest oznaczony przez | z|. Nazywa się kąt, jaki ten wektor tworzy z dodatnim kierunkiem osi x (liczonym w kierunku przeciwnym do ruchu wskazówek zegara). argument Liczba zespolona z i jest oznaczony przez Arg z. Argument nie jest jednoznacznie zdefiniowany, ale tylko do dodania wielokrotności 2 π radiany (lub 360°, jeśli liczyć w stopniach) - w końcu jasne jest, że obrót o taki kąt wokół początku układu współrzędnych nie zmieni wektora. Ale jeśli wektor długości R tworzy kąt φ z dodatnim kierunkiem osi x, wówczas jej współrzędne są równe ( R sałata φ ; R grzech φ ). Stąd się okazuje zapis trygonometryczny Liczba zespolona: z = |z| · (cos(Arg z) + I grzech (arg z)). Często wygodnie jest zapisywać liczby zespolone w tej formie, ponieważ znacznie upraszcza to obliczenia. Mnożenie liczb zespolonych w formie trygonometrycznej jest bardzo proste: z 1 · z 2 = |z 1 | · | z 2 | · (cos(Arg z 1 + argument z 2) + I grzech (arg z 1 + argument z 2)) (przy mnożeniu dwóch liczb zespolonych ich moduły są mnożone i dodawane są ich argumenty). Stąd podążaj Wzory Moivre’a: z n = |z|N· (bo( N· (Arg z)) + I grzech( N· (Arg z))). Korzystając z tych wzorów, łatwo jest nauczyć się wyodrębniać pierwiastki dowolnego stopnia z liczb zespolonych. n-ty pierwiastek z- to liczba zespolona w, Co w n = z. Jest oczywiste, że , I gdzie k może przyjmować dowolną wartość ze zbioru (0, 1, ..., N- 1). Oznacza to, że zawsze jest dokładnie N korzenie N stopień liczby zespolonej (na płaszczyźnie znajdują się one w wierzchołkach regularnej N-gon).