Kraften til universell tyngdekraft. Tyngdeloven

På begynnelsen av 1600-tallet ble verdens heliosentriske system anerkjent av de fleste vitenskapsmenn. På den tiden ble imidlertid ikke grunnene og lovene som planetene beveger seg etter forstått.

I. Kepler behandlet resultatene av mange av sine observasjoner og observasjonene til hans kollega T. Brahe, og formulerte lovene for planetarisk bevegelse rundt Solen. Det ble klart at for å forklare Keplers lover, er det nødvendig å bestemme hvilke krefter som virker på planetene. Men Kepler og hans samtidige klarte ikke å oppnå dette. Problemet ble løst av I. Newton.

Omtrent kan vi anta at planetene beveger seg jevnt i baner nær sirkler. Med denne typen bevegelse av et materialpunkt har det en sentripetalakselerasjon, som er rettet mot midten av banen (for en planet er sentripetalakselerasjonen rettet mot Solen). Av Newtons andre lov følger det at en viss kraft virker på planeten, som genererer normal akselerasjon. Det viser seg at solen virker på hver planet med en kraft rettet mot midten. I samsvar med Newtons tredje lov virker planeten på Solen med en kraft som er lik den forrige kraften, men i motsatt retning.

Tyngdeloven

Vi vet at månen roterer rundt jorden. Månen tiltrekker jorden, jorden tiltrekker seg månen. I. Newton foreslo at tyngdekraften som Jorden tiltrekker alle legemer nær overflaten med, og kraften som den tiltrekker Månen med, har samme opphav. Newton sammenlignet gravitasjonsakselerasjonen ($g=9,81\ \frac(m)(s^(2\ ))$ nær jordoverflaten) og sentripetalakselerasjonen ($a_n$) som månen har når den beveger seg langs sin bane. Newton fant ut at Månens normale akselerasjon er lik $a_n=2,72\cdot (10)^(-3)\frac(m)(s^2)$. Newton forklarte avviket i verdier med det faktum at tyngdekraften avtar med økende avstand mellom tiltrekkende kropper. Akselerasjonen forårsaket av tyngdekraften avtar i omvendt proporsjon med kvadratet på avstanden ($r$) mellom kroppene:

hvor $K=konst$.

Formulering av loven om universell gravitasjon

En analyse av Månens normale akselerasjon når den beveger seg nær Jorden tillot I. Newton å konkludere med at alle kropper i naturen tiltrekkes av visse krefter, som kalles gravitasjonskrefter.

La oss anta at vi har to legemer hvis masse er lik $m_1$ og $m_2$. De er plassert i en avstand $r$ fra hverandre. Disse kroppene samhandler med hverandre med krefter:

\[\ F_1=m_1a_1og\ F_2=m_2a_2\venstre(2\høyre)\]

I følge Newtons tredje lov har vi:

\[\venstre|F_1\høyre|=\venstre|F_2\høyre|\venstre(3\høyre).\]

Ved å ta hensyn til uttrykk (1), får vi:

Uttrykk (4) vil være tilfredsstilt hvis $K_1=\gamma m_2,$ og $K_2=\gamma m_1,$ hvor $\gamma $ =konst. Det vil si at vi fikk det:

Formel (5) er et matematisk uttrykk for loven om universell gravitasjon: Tyngdekraften mellom to materielle punkter er direkte proporsjonal med massene deres og omvendt proporsjonal med kvadratet på avstanden mellom dem.

For nøyaktig å beregne kraften til gjensidig tiltrekning, kan formel (5) bare brukes hvis kroppene er homogene kuler hvis masse er lik $m_(1\ ) og\ m_2$, og $r$ er avstanden mellom sentrene deres.

Gravitasjonskonstant

Koeffisienten $\gamma $ kalles gravitasjonskonstanten. I International System of Units (SI-systemet) er det lik $\gamma \approx 6.67\cdot (10)^(-11)\frac(m^3)(s^2\cdot kg).\ $ Den gravitasjonsmessige konstant er numerisk lik kraften av samspillet til materielle punkter som har en masse på ett kilo, plassert i en avstand på en meter. Gravitasjonskonstanten finnes eksperimentelt.

Et av de første eksperimentene for å måle tyngdekraften under laboratorieforhold ble utført av Cavendish. Slik ble gravitasjonskonstanten bestemt.

Eksempler på problemer med løsninger

Eksempel

Trening. Hva er essensen av Cavendishs eksperiment for å måle tyngdekraften?

Løsning. La oss lage en tegning.

For å gjennomføre forsøket brukte Cavendish en torsjonsbalanse (fig. 1). En lett stang ble hengt opp i en tynn kvartstråd. Et lite speil var stivt festet til tråden. En lysstråle traff speilet, reflekterte fra det og falt på vekten. Hvis stangen ble rotert, beveget strålen seg langs skalaen. Slik ble trådens vridningsvinkel notert. To blykuler, hver med en masse på $m$, ble festet til endene av stangen. To symmetrisk plasserte blykuler med masse $M$ ble brakt til disse kulene. Tråden ble vridd til det øyeblikket da den elastiske kraften til den deformerte tråden ikke balanserer kraften til gravitasjonsinteraksjonen mellom kulene. Samhandlingskraften ble målt ved vridningsvinkelen til tråden. Ved å vite massene til kulene og avstanden mellom sentrene deres, ble gravitasjonskonstanten beregnet.

Eksempel 2

Trening. To identiske homogene jernkuler berører hverandre (fig. 2). Radiusen til hver kule er $R=0,1$ m. Hva er gravitasjonskraften som virker mellom disse kulene?

Løsning. La oss lage en tegning.

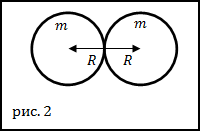
Grunnlaget for å løse problemet er loven om universell gravitasjon:

der $m_1=m_2=m$ er massene til hver av kulene, så skriver vi tyngdeloven på formen:

Avstanden mellom midten av kulene (fig. 2) er lik: $r=2R.$ Vi finner massene til kulene som:

Vi transformerer formel (2.2) som følger:

For å beregne tyngdekraften finner vi i oppslagsverk tettheten til jern ($\rho =7800\ \frac(kg)(m^3)$). Gravitasjonskonstanten er lik: $\gamma =6.67\cdot (10)^(-11)\frac(m^3)(s^2\cdot kg).$ La oss utføre beregningene:

Svar.$F=1,78\cdot (10)^(-6)$Н

La oss først definere Newtons lov om universell gravitasjon og de grunnleggende mengdene som brukes i den, og deretter vurdere hva som førte til oppdagelsen av denne loven, og om vi virkelig skylder utseendet til denne største oppdagelsen til eplet.

1. Mellom to materielle punkter er det krefter av gjensidig tiltrekning, direkte proporsjonale med produktet av massene til disse punktene og omvendt proporsjonal med kvadratet på avstanden mellom dem

F 12 = g (m 1 m 2 /R 2) R 12/R

Hvor F 12 - gravitasjonskraft som virker på et punkt med masse m 1, R 12 - radiusvektor tegnet fra dette punktet til et punkt med masse m 2, R = | R 12 | - avstand mellom punktene. Koeffisienten  kalles gravitasjonskonstant (tyngdekraftens konstant). Det er numerisk lik kraften til gjensidig tiltrekning mellom to materielle punkter som har identiske masser lik enhetsmasse og er plassert i en avstand fra hverandre lik lengdeenhet. Gravitasjonskonstanten bestemmes eksperimentelt. Dens numeriske verdi avhenger bare av valget av systemet med måleenheter:

g = 6,67*10 -11 N*m 2 /kg 2 = g = 6,67*10 -8 dyn*cm 2 /g 2

I følge Newtons tredje lov, kraft F 21 som virker på et materialpunkt med masse m 2 er numerisk lik kraften F 12, men rettet i motsatt retning:

F 12 = - F 21

2. Vekt legeme kalles kraften P som en kropp ubevegelig i forhold til jorden trykker på støtten på grunn av sin tiltrekning til jorden. Kroppsvekten er lik vektorkraftforskjellen F tyngdekraften til et legeme mot jorden og sentripetalkraften F c, som bestemmer kroppens deltakelse i jordens daglige rotasjon:

P = F - F C

F c = mw 2 Rcos j,

hvor m - kroppsmasse, w er vinkelhastigheten til jordens daglige rotasjon, R er jordens radius, og j er den geografiske breddegraden til observasjonsstedet EN.

Ved de geografiske polene (j = 90°) F C = 0 og kroppens vekt er lik kraften til dens tiltrekning til jorden. På grunn av det faktum at jordens radius og sentripetalkraft avhenger av geografisk breddegrad, er vekten av legemer maksimalt ved polene og minimum ved ekvator. Denne forskjellen overstiger imidlertid ikke 0,55 %. Derfor, i mange tekniske problemer, kan man neglisjere påvirkningen av jordens daglige rotasjon på vekten av en kropp og forskjellen i form fra sfærisk.

Tyngdepunkt av et legeme kalles anvendelsespunktet for de resulterende kreftene til vekten til alle partikler i denne kroppen. Tyngdepunktet til en kropp faller sammen med treghetssenteret.

3. Fritt fall er bevegelsen til et legeme under påvirkning av en enkelt kraft lik vekten. Akselerasjonen av fritt fall er den samme for alle kropper og, i likhet med vekten deres, avhenger av geografisk breddegrad og høyde over havet. Standard (normal) g-verdi, akseptert for barometriske beregninger og ved konstruksjon av systemer av enheter er lik 9,80665 m/s 2 .

Loven om universell gravitasjon ble oppdaget av engelskmannen I. Newton i 1666. Loven lyder slik: gravitasjonskraften mellom to materielle punkter er direkte proporsjonal med produktet av massene deres og omvendt proporsjonal med kvadratet på avstanden mellom dem.

Loven gjelder også for utvidede legemer med en sfærisk symmetrisk massefordeling, mens r er avstanden mellom legemenes symmetrisentre. For ikke-sfæriske legemer overholdes loven tilnærmet, og jo større avstand mellom legene (mellom deres massesentre) i forhold til kroppens størrelse, jo mer nøyaktig.

Alt dette vet vi godt, og det ser ut til at uten matematiske beregninger er det ikke noe mer som må legges til. Men det er ikke sant. I astronomi er det for eksempel svært viktig å spore opp visse fenomener og trekke visse konklusjoner og konsekvenser av denne loven.

I henhold til formelen F = G*m 1 *m 2 /r 2

der r er avstanden mellom legemer, og G er gravitasjonskonstanten, er tiltrekningskraften proporsjonal med massene og omvendt proporsjonal med kvadratet av avstanden. Men massen er proporsjonal med kuben av den lineære størrelsen på kroppen. Dette betyr at hvis størrelsen på legemer og avstandene mellom dem (mens tetthetene opprettholdes) økes proporsjonalt, for eksempel med 10 ganger, vil massene deres øke med 1000 ganger, og kvadratet på avstanden - bare med 100, så tiltrekningskraften vil øke med 10 ganger! Det vil si at når skalaen øker, vokser massen en størrelsesorden raskere enn kvadratet på avstanden! På grunn av den ubetydelige verdien av gravitasjonskonstanten, er tiltrekningskraften mellom individuelle objekter på jordoverflaten ekstremt liten sammenlignet med tiltrekningskraften til jorden selv, men allerede på en interplanetarisk skala (hundrevis av millioner kilometer) , kompenserer økningen i masse for G og tyngdekraften blir hovedkraften.

Når skalaen reduseres, vises den motsatte effekten, selv om dette allerede er fra biologien. Hvis du for eksempel reduserer en person til størrelsen på en maur, dvs. omtrent 100 ganger, så vil massen minke med 1 000 000 ganger. Og siden styrken til muskler er omtrent proporsjonal med deres tverrsnitt, dvs. kvadrat med lineær størrelse, så vil den avta bare 10 000 ganger, dvs. det vil være en 100x vinnerkraft! Det er ikke vanskelig å gjette at insekter faktisk lever under tyngdeforhold som er sterkt redusert sammenlignet med større dyr. Derfor gir spørsmålet om hvor mye vekt en maur kunne løfte hvis den var på størrelse med en elefant rett og slett ikke fornuftig. Kroppsstrukturen til insekter og generelt alle små dyr er optimal nettopp for lav tyngdekraft, og bena til en maur tåler rett og slett ikke vekten av kroppen, for ikke å nevne noen ekstra belastning. Tyngdekraften legger altså begrensninger på størrelsen på landdyr, og de største av dem (for eksempel dinosaurer) tilbrakte tilsynelatende en betydelig del av tiden sin i vann.

Flyevnen i dyreriket er også begrenset av kroppsmasse. Ikke bare muskelstyrke, men også vingenes areal vokser i forhold til kvadratet av de lineære dimensjonene, dvs. For en viss maksimal kroppsmasse blir flyreiser umulige. Denne kritiske massen er omtrent 15-20 kg, som tilsvarer vekten til de tyngste fuglene på jorden. Derfor er det svært tvilsomt at de gamle kjempeøglene virkelig kunne fly; mest sannsynlig tillot vingene dem bare å gli fra tre til tre.

Og bemerkningen er ikke helt på temaet. Det er en ganske utbredt oppfatning at vektløfting bremser veksten til idrettsutøvere, og det er grunnen til at det visstnok er så mange korte mennesker blant vektløftere. Faktisk forekommer kortvoksthet hos vektløftere, men kun i begrensede vektklasser, spesielt blant lettvektere. En bok om atletikk forklarer til og med at lavvokste vinner oftere fordi de må løfte vektstangen til en lavere høyde. Etter min mening er et slikt argument fullstendig lite overbevisende. Men følgende forklaring tilbys også. Hver type vev (muskler, bein, hud, fett osv.) som utgjør kroppen, utgjør en viss prosentandel av dens totale vekt. Og hvis vi antar at disse proporsjonene er de samme for to personer med forskjellig høyde, vil den kortere personen naturlig nok veie mindre. Men hvis han går opp i samme kroppsvekt som en høy person på grunn av muskler, vil dette bety at han har mer absolutt muskelmasse (siden han rett og slett har mindre ikke-muskelvev per definisjon). Og mer muskelmasse betyr mer muskeltverrsnitt, og derfor, under disse forholdene, med lik kroppsvekt, er en kort vektløfter faktisk sterkere enn en høy, så sistnevnte blir ganske enkelt eliminert.

Ris. 1 Tidevannskrefter.

La oss imidlertid gå tilbake til astronomi. Hvis vi vurderer effekten av gravitasjonskraften til et legeme O (la oss konvensjonelt representere det som et punkt) på et forlenget legeme med et senter Q (fig. 1), så kan vi legge merke til at forskjellige krefter virker på forskjellige deler av kroppen. kropp. Dermed vil det nærmeste punktet B tiltrekkes sterkere enn det lengste A (på grunn av forskjeller i avstander), derfor langs linjen QO som forbinder tyngdepunktene til begge legemer, vil kropp O ha en tendens til å strekke segmentet AB. Ved punktene C og D, fjernt fra linjen OQ, vil tiltrekningskraften virke i en vinkel til linjen QO, og denne kraften kan dekomponeres i to komponenter: en rettet parallelt med retningen QO, og den andre vinkelrett på den. - mot midten av kroppen Q. Det vil si at punkter som ikke ligger på OQ-aksen blir påvirket av en kraft som har en tendens til å komprimere kroppen i en retning vinkelrett på retningen til det tiltrekkende legemet O. Disse strekk- og kompresjonskreftene kalles tidevannskrefter. Deres handling på jorden fra månen og solen forårsaker (som du kanskje gjetter ut fra navnet) flo og fjære.

For å estimere høyden til en flodbølge på jorden, kan det gjøres beregninger som ligner på å estimere kompresjonen av jorden. For enkelhets skyld, la oss glemme jordens daglige rotasjon og anta at all dens ikke-sfærisitet er forårsaket av månens tiltrekning. Ved å sette likhetstegn mellom vekten av hvert elementært volum som befinner seg i en avstand r fra jordens senter med dens radius vinkelrett på retningen til månen og rettet mot månen, får vi:

m*g p (r) = m*gl (r) - G*m*Ml/b 2

der g p (r) er tyngdeakselerasjonen ved en radius vinkelrett på retningen til månen, g l (r) er akselerasjonen ved en radius rettet mot månen, M l er månens masse, b er avstanden til månen, lik differansen mellom halvhovedaksen a til bane månen og radiusvektoren r. Avhengigheten av tyngdeakselerasjonen ved begge radiene er den samme: g p (r) = g l (r) = GM/r 2, hvor M er massen innenfor radius r: M(r) = *4* *r 3 / 3, hvor  er tettheten til stoffet. Hvis vi legger alt dette inn i ligningen, reduserer det med m og G og integrerer det over hele jordens radius, får vi:

R p 2 = R l 2 - M l /2//*(1/a - 1/(a-Rl)). Hvis vi her erstatter verdiene til jordens radius, massen og månens halvhovedakse, får vi R l - R p ~ 7,3 m, som er mye større enn høyden til den virkelige flodbølgen , men det kan antas at i virkeligheten, på grunn av rotasjon, har ikke jordens faste skall tid til å endre form, og i virkeligheten dannes en flodbølge hovedsakelig av et vann- og luftskall, og den totale amplituden av vibrasjon av den faste skorpen ikke overstiger en meter.

For planeter begrenser tidevannskrefter minimumsavstanden som et tilstrekkelig stort legeme, for eksempel en satellitt, kan nærme seg dem. Dette ble demonstrert veldig effektivt under det nylige fallet til Shoemaker-Levy-kometen på Jupiter, da kometens kjerne ble revet i mange deler, og fallet forårsaket så mange reaksjoner i den vitenskapelige verden. Minimumsradiusen til en sirkulær bane der satellitten ikke blir ødelagt av tidevannskreftene til sentrallegemet kalles Roche-grense. Hvis massen til satellitten er mye mindre enn massen til planeten, så er avhengigheten av Roche-grensen a R på radiusen til planeten R, tetthetene til satellitten  s og planeten  p som følger:

a R = 2,46*( s / p) 1/3 *R (5)

Inne i en kule med radius R er gravitasjonskondensering av materie for å danne et enkelt legeme også umulig. Dette er sannsynligvis årsaken til dannelsen av ringer av gigantiske planeter.

La oss nå gå til historien og vurdere hendelsene i disse fjerne tider ved vitenskapens morgen. Loven om universell gravitasjon ble oppdaget av Isaac Newton i 1682. Tilbake i 1665 foreslo 23 år gamle I. Newton at kreftene som holder Månen i sin bane er av samme natur som kreftene som får et eple til å falle til jorden. I følge hans hypotese virker tiltrekningskrefter (gravitasjonskrefter) mellom alle universets kropper, rettet langs linjen som forbinder massesentrene. For en kropp i form av en homogen ball, sammenfaller massesenteret med midten av ballen. I de påfølgende årene prøvde Newton å finne en fysisk forklaring på lovene for planetarisk bevegelse oppdaget av astronomen Johannes Kepler på begynnelsen av 1600-tallet, og å gi et kvantitativt uttrykk for gravitasjonskrefter. Når han visste hvordan planetene beveger seg, ønsket Newton å finne ut hvilke krefter som virker på dem. Denne banen kalles det omvendte problemet med mekanikk. Hvis mekanikkens hovedoppgave er å bestemme koordinatene til et legeme med kjent masse og dets hastighet til enhver tid basert på kjente krefter som virker på kroppen og gitte startforhold (mekanikkens direkte problem), så når man løser det inverse problem er det nødvendig å bestemme kreftene som virker på kroppen hvis det er kjent hvordan den beveger seg. Løsningen på dette problemet førte Newton til oppdagelsen av loven om universell gravitasjon.

På bakgrunn av de imponerende suksessene til moderne fysikk er tyngdekraften fortsatt det mest mystiske naturfenomenet. Tyngdekraftens storhet ligger i det faktum at alt som eksisterer i verden er underlagt det, starter fra universet selv og slutter med dets bestanddeler. For første gang ble dette mest fullstendig realisert av den store engelske vitenskapsmannen Isaac Newton (1643...1727). I 1687 publiserte Newton sitt berømte verk "Mathematical Principles of Natural Philosophy", som avslørte for menneskeheten for første gang teoriene om planetarisk bevegelse og tyngdekraftsprinsippene. Newtons lov om universell gravitasjon, som ble den første vitenskapelige loven, gyldig i hele universet, sier: hver to partikler av materie tiltrekker hverandre hverandre, eller graviterer mot hverandre, med en kraft som er direkte proporsjonal med produktet av massene deres og omvendt proporsjonal med kvadratet på avstanden mellom dem:

(1)

Newtons samtidige innså ikke umiddelbart tyngdekraftens storhet. Christiaan Huygens, som Newton selv kalte en stor vitenskapsmann, skrev: «Newtons idé om gjensidig tiltrekning anser jeg som absurd, og jeg er overrasket over hvordan en mann som Newton kunne gjøre så vanskelige studier av beregninger som ikke har noe bedre som grunnlag enn dette. idé."

Ideen om at himmellegemer har egenskapen til å tiltrekke seg ble tidligere uttrykt før Newton av Nicholas av Cusa, Leonardo da Vinci, Copernicus og Kepler. “Tyngekraft er en gjensidig tilbøyelighet mellom beslektede kropper som streber etter å smelte sammen, forene sammen... Uansett hvor vi plasserer jorden, vil tunge kropper, på grunn av deres naturlige evne, alltid bevege seg mot det... Hvis det et eller annet sted i verden er var to steiner i nær avstand fra hverandre og utenfor handlingssfæren til enhver beslektet kropp, så ville disse steinene streve etter å forbinde seg med hverandre som to magneter..." - skrev Kepler i sin bok "New Astronomy". Keplers strålende uttalelser var bare begynnelsen på en lang reise som fortsatt måtte overvinnes. Av de mange forskerne var Newton bestemt til å gå gjennom denne vanskelige veien.

Den triumferende marsj for loven om universell gravitasjon ble innledet av en vanskelig periode med dannelsen. Robert Hooke (1635...1703) kom til ideen om universell gravitasjon noe tidligere enn Newton. Det var en lang strid mellom Hooke og Newton om prioritet i oppdagelsen av loven om universell gravitasjon. I motsetning til Hookes uttalelser utviklet Newton en matematisk gravitasjonsteori og beviste virkemåten til gravitasjonsloven ved å bruke numeriske metoder. Newton reflekterte synet på tyngdekraften til sine forgjengere i én formel (1), som er en matematisk modell av gravitasjonssamspillet mellom to materielle legemer.

Etter Isaac Newtons død (1727) ble loven om universell gravitasjon utsatt for nye tester. Den siste alvorlige innvendingen mot loven om universell gravitasjon anses å være publiseringen av den franske matematikeren og astronomen Alexis-Claude Clairaut i 1745. Noen detaljer om Månens bane han beregnet, krever etter hans mening korrigering av loven om universell gravitasjon.

A. Clairaut anså et av de viktigste problemene for å være teorien om Månens bevegelse basert på Newtons lov om universell gravitasjon, eller mer presist, studiet av den ulikheten «som fikk den mørkeste utviklingen fra Newton, nemlig bevegelsen av månens perigeum.» A. Clairauts opprinnelige uavhengige forskningsvei fører til den samme verdien som Newton selv oppnådde i sin tid, som avvek fra de observerte dataene med nesten to ganger. En annen forsker, Jean Leron d'Alembert (1717...1783), kom til de samme konklusjonene uavhengig. Han, i likhet med A. Clairaut, kom til den konklusjon at under påvirkning av Newtonsk tiltrekning, skulle perigeumet til Månens bane ha fullført én revolusjon på 18 år, og ikke på 9 år, slik det faktisk skjer.

Uavhengig av hverandre kom A. Clairaut og J. d'Alembert, engasjert i forskning innen Newtonsk mekanikk og gravitasjonsteorien, til den samme konklusjonen at Newtons teori ikke er i stand til å forklare bevegelsen til perigeumet til Måne og krever endringer. Newton selv foreslo denne veien.

En liten endring av A. Clairaut til formen til Newtons universelle gravitasjonslov ble presentert i følgende form:

Hvor M Og m– masser av to kropper;

R- avstanden mellom dem;

γ – gravitasjonskonstant;

α er en liten verdi valgt eksperimentelt.

J. d’Alemberts uttalelse indikerer også behovet for et tilleggsbegrep: «Månen blir tiltrukket av jorden av en annen, liten kraft, som ikke virker i henhold til loven om omvendt proporsjonalitet til kvadratene på avstandene.»

Den berømte franske naturforskeren Georges Buffon (1707...1783) motsatte seg konklusjonen til A. Clairaut og J. D'Alembert. Med sin autoritet reddet han Newtons formel fra korreksjon, og erklærte at de tilbød oss noe vilkårlig, i stedet for å gjengi sannheten.» Etter den første endringen kunne etterfølgende medlemmer etter hans mening oppstå uten hindring. "Enhver fysisk lov er en lov bare fordi dens uttrykk har unikhet og enkelhet," sa J. Buffon.

Den dag i dag antas det at Clairaut dobbeltsjekket resultatene og oppdaget en feil. Vi kan ikke være enig i dette synspunktet. Innenfor rammen av sin rent analytiske modell korrigerte han faktisk motsetningene i modellen sin, og lot ufullkommenhetene i Newtons lov om universell gravitasjon være urørt. Etter vår mening motarbeidet ikke A. Clairaut seg selv mot autoriteten til Newton selv eller hans tilhengere og la ut på en uavhengig forskningsvei. Han klargjorde ikke formelen for loven om universell gravitasjon og unngikk dermed de mulige opphetede diskusjonene som ventet ham i fremtiden. Som historien vil vise, ga denne strategien resultater. A. Clairaut vil vinne konkurransen annonsert i 1750 av St. Petersburg Academy, motta strålende kritikker fra sine samtidige, publisere boken «The Theory of the Motion of the Moon, Derived from the Single Principle of Attraction, inversely proporsjonal to the Squares of the Distances» i 1752 og vil bli valgt til et korresponderende medlem av St. Petersburg Academy of Sciences i 1754

Alle kreftene til A. Clairaut var konsentrert om gjennomføringen av hans eget forskningsprogram: «Etter mye refleksjon over Newtons teori og ikke oppnådd den grad av overbevisning som jeg forventet, bestemte jeg meg for ikke å låne noe annet fra ham og selvstendig søke etter definisjoner av bevegelsen til himmellegemer, med en enkelt antagelse om deres gjensidige tiltrekning." Denne tilnærmingen tillot ham å bygge en rent analytisk modell for gravitasjonsinteraksjon.

350 år har gått siden den gang. Loven om universell gravitasjon i sin opprinnelige form møtte vellykket det andre årtusenet. Tvilen til A. Clairaut og J. d'Alembert angående Newtons lov om universell gravitasjon, etter vår mening, har ikke blitt fjernet. Rekkefølgen av følgende resonnement fører oss til uventede resultater.

La oss vurdere den såkalte raffinerte loven om universell gravitasjon.

To materielle kropper M Og m tiltrekke hverandre med like stor kraft F. Gravitasjonsfelt av masse M forårsaker akselerasjon m :

g = γ · ( M / R 2).

Følgelig er massen m forårsaker akselerasjon M :

g = γ · ( m / R 2).

Relativ akselerasjon av to kropper M Og m g fra lik til forskjell g M – g m, og siden g M og g m er rettet i motsatte retninger, da g fra er lik summen av akselerasjoner g M og g m:

Følgelig er akselerasjonen under den relative bevegelsen til to tiltrekkende materielle legemer M Og m vi kan anta at kraften kommer fra et stasjonært senter og vi kan studere bevegelsen til bare ett legeme.

La oss forklare dette med følgende eksempel og i praksis sjekke om formel (3) er tilstrekkelig til den omgivende virkeligheten. På jordoverflaten, det vil si i en avstand på 6371,032 km fra sentrum, er akselerasjonen g Jorden = 9,81 m/s 2. Akselerasjon forårsaket av jordens tyngdekraft på avstand r= 384400 km til Månen bør reduseres med 384400 2 / 6371.032 2 = 3640.38 ganger. Månens akselerasjon forårsaket av jordens tyngdekraft er lik:

g Jord-Måne = 9,81 m/s2 / 3640,38 = 0,2695 cm/s2.

Følgelig, på overflaten av månen, på avstand r= 1738 km fra sentrum, akselerasjon g Månen = 1,62 m/s 2. Dette er akselerasjonen forårsaket av tiltrekningen av Månen på avstand r= 384400 km til Jorden skal reduseres med 384400 2 / 1738 2 = 48917,83 ganger.

Jordens akselerasjon forårsaket av månens tyngdekraft er:

g Måne-Jord = 1,62 m/s2 / 48917,83 = 0,0033 cm/s2.

Relativ akselerasjon av månen g fra vil være lik summen av akselerasjoner

g fra = g Jord-måne + g Måne-Jord = 0,2695 cm/s2 + 0,0033 cm/s2 = 0,2728 cm/s2.

Den oppnådde verdien av den relative akselerasjonen til månen g du kan sjekke det på følgende måte. Forutsatt at månen beveger seg i en sirkel, beregner vi dens faktiske akselerasjon ved å bruke formelen:

G fra = V 2 / r ,

Hvor V- hastigheten på månens bane;

r- avstand fra jorden til månen.

Hastigheten til månens bane V kan beregnes ved hjelp av formelen:

V= (2π r) / T ,

Hvor T- siderisk periode av månens revolusjon, T= 27,3 dager;

r- avstand fra jorden til månen ( r= 384400 km).

La oss beregne verdien V Og G fra:

V= (2 · 3,14 · 384400 km) / 2358720 sek = 1,02345 km/sek

G fra = (1,02345 km/sek) 2 / 384400 km = 0,2725 cm/sek 2 .

Beregninger viser det G fra = g fra og den relative feilen til disse to indikatorene er G fra - g fra = 0,2728 cm/sek 2 – 0,2725 cm/sek 2 = 0,0003 cm/sek 2 eller 0,12 %.

Numeriske beregninger g Basert på reelle data fra Jorden og Månen, bekrefter de at formel (3) er tilstrekkelig for omverdenen.

La oss nå vurdere bevegelsen til kroppen m relativt M. Kraftens størrelse F opptrer mellom m Og M lik masseproduktet m for relativ akselerasjon g fra:

(4)

Formel (4) kan representeres som en sum av to ledd:

(5)

Det første begrepet sammenfaller med formel (1) – loven om universell gravitasjon, og generelt ligner formel (5) formel (2), som en gang ble foreslått av A. Clairaut for å korrigere Newtons universelle lov.

Hvis m betydelig mindre enn M, dvs. m << M, da er verdien av det andre leddet i forhold til det første ubetydelig. Som kjent avviste J. Buffon på et tidspunkt formel (2) på grunn av at A. Clairaut la til det andre leddet vilkårlig, men i vårt tilfelle i formel (5) er første og andre ledd avledet fra verden rundt oss . Derfor har vi rett til å si at Newtons lov om universell gravitasjon er et spesielt tilfelle av formlene (4) og (5).

Det første leddet i formel (5) reiser ingen spørsmål. Dette er Newtons lov om universell gravitasjon. La oss gå videre til å analysere den andre perioden. Hvorfor er telleren for det andre leddet produktet m · m, men ikke M · M? Handling M allerede manifestert seg i den første termen, genererte det gravitasjonspotensialet (γ · M) / R 2 og det var der rollen hennes sluttet. Den andre termen avslører essensen av gravitasjonspotensialet til det andre legemet m og det er lik (γ · m) / R 2. Nå gjenstår det å beregne kraften i andre ledd, og for dette, i henhold til den tradisjonelle ordningen, er det nødvendig (γ · m) / R 2 ganger M, dvs. vi får (γ · m · M) / R 2 igjen Newtons universelle gravitasjonslov! Men dette motsier formel (4), som vi oppnådde analytisk fra beregninger av akselerasjoner mellom Jorden og Månen. Faktisk vil den reelle kraften være lik (γ · m · m) / R 2. Her kommer vi til det faktum at gravitasjonspotensialet generert av kroppen m forårsaker akselerert bevegelse av selve kroppen m til siden M. Og dette strider ikke mot Newtons tredje lov. Kropp m M og tilsvarende M beveger seg jevnt akselerert til siden m. Men siden m betydelig mindre enn M kraft uttrykt i formen (γ · m · m) / R 2 gjenspeiler objektivt kraften generert av massen m. Masse M kan beskrives som en sentral kropp som kroppen beveger seg rundt m. Kroppen som beveger seg i forhold til den sentrale kroppen vil være kriteriet for å velge den inn i andre ledd.

La oss nå formulere en ny, raffinert lov om universell gravitasjon:

hver to partikler av materie tiltrekker hverandre hverandre, eller graviterer mot hverandre, med en kraft som er direkte proporsjonal med produktet av summen av de to massene og massen av kroppen som beveger seg i forhold til den sentrale massen og omvendt proporsjonal med kvadratet på avstanden mellom dem (4).

Fra synspunkt av teori og metodikk for å studere tyngdeloven, avslører overgangen fra formel (1) til (4) mest fullstendig essensen av loven om universell gravitasjon. Fra formel (1) ser vi bare gravitasjonsvirkningen til ett legeme M eller m, samtidig gjenspeiler formel (4) den gjensidige gravitasjonsvirkningen til to legemer M Og m samtidig.

En liten endring av Newtons lov om universell gravitasjon fører til interessante konsekvenser. Hva følger av formel (4)? For å gjøre dette bør vi skynde oss til det berømte skjeve tårnet i Pisa før det faller og gjenta Galileos eksperiment. Resultatet blir følgende - i motsetning til hva mange tror, vil en tyngre kropp nå jorden raskere! Eksperimentet er ikke vanskelig å gjennomføre, bare trøbbel vil bli skapt av mengder av turister som ikke fantes på 1500-tallet.

Denne korreksjonen er enda mer uttalt når m = M. Styrkeverdi F beregnet ved formel (4) F= γ 2 M 2 / r 2 er dobbelt så stor som kraftverdien beregnet ved formel (1) F = γ · M 2 / r 2 .

Aristoteles hadde rett i å hevde at fallet i massen av gull eller bly, eller en hvilken som helst annen kropp, skjer jo raskere, jo større er dens størrelse! Leonardo da Vinci kom også til denne konklusjonen. Den store kunstneren og vitenskapsmannen kastet kropper med forskjellig vekt og kom til samme resultat: hastigheten på kroppens fall avhenger av kroppens vekt.

Av formel (4) følger det at tyngdekraften er ikke-additiv. La oss vurdere dette ved å bruke eksemplet med tyngdekraften til to kropper m 1 og m 2 i forhold til bakken. Kropp m 1 utøver en kraft på bakken F 1. og andre kropp m 2 handler deretter med kraft F 2. Legge til massene til to kropper m 1 og m 2 får vi den tredje kroppen m 3 hvor m 3 = m 1 + m 2. Den virker også på bakken med en kraft lik F 3. For vårt eksempel betyr brudd på tyngdekraftens additivitet:

F 1 + F 2 < F 3

Hvis vi holder oss til den tradisjonelle formelen (1), brytes ikke additiviteten og betingelsen for tyngdekraften er oppfylt:

F 1 + F 2 = F 3

Med fremkomsten av formel (4) viker likhet (7) for ulikhet (6), som en konsekvens av et nytt vitenskapelig faktum.

Den briljante fysikeren Einstein la eksepsjonell vekt på gravitasjonsegenskapen, etter Galileo og argumenterte for at alle legemer på et gitt punkt i rommet faller inn i gravitasjonsfeltet med samme akselerasjon. Denne uttalelsen i klassisk fysikk var en av fakta - på en måte til og med tilfeldig og spilte ikke noen stor rolle i det som utgjorde det ideologiske grunnlaget for Galileo-Newton-mekanikken. Imidlertid legger Einstein ekstremt viktig og mest generell betydning til denne egenskapen, tildeler den en plass blant de "grunnleggende tingene" i moderne fysikk og plasserer den ved siden av relativitetsprinsippet.

Einsteins interesse for tyngdekraften er ikke tilfeldig, for den er direkte relatert til prinsippet om ekvivalens. Som kjent betraktes masser i fysikk i to former: inert og gravitasjon. Fallet til alle legemer med samme akselerasjon er en tilstrekkelig betingelse for likheten mellom gravitasjons- og treghetsmasse. Denne likheten ble hevet av Einstein til rangering av et grunnleggende prinsipp i hans teori. Tilfeldighet – ekvivalensen til disse massene er innholdet i Einsteins ekvivalensprinsipp.

Denne antagelsen er feil fra vårt ståsted. Fra formlene (4) og (7) følger det at forskjellige legemer på et gitt punkt i rommet faller i gravitasjonsfeltet med forskjellige akselerasjoner og følgelig brytes ekvivalensprinsippet.

For å tydeliggjøre våre utsagn vil vi bruke tankeeksperimentene til Einstein selv. La oss plassere testlaboratoriet vårt i en heisvogn. La oss forestille oss, etter Einstein, «en enorm heis i et skyskrapertårn... Plutselig knekker tauet som støtter heisen og heisen faller fritt mot bakken. Eksperimentatoren i laboratoriet hans utfører følgende eksperiment: "tar frem et lommetørkle og klokken fra lommen og slipper dem fra hendene." En heis med et laboratorium, en eksperimentator, en klokke og et skjerf faller i forhold til skyskraperen.

La oss se hvordan både observatører, interne og eksterne, beskriver hva som skjer i heisen.

Den interne observatøren er en eksperimentator. Heisgulvet begynner sakte å forsvinne under føttene dine. Klokken med lommetørkleet beveger seg sakte oppover i forhold til eksperimentatoren. Lommetørkleet beveger seg raskere opp enn en klokke. Eksperimentatoren konkluderer: alle kropper beveger seg mot bakken med forskjellige akselerasjoner. Den raskeste akselerasjonen er ved heisen, deretter ved ham selv, etterfulgt av klokken, og lommetørkleet faller tregest. Konklusjon - systemet er ikke-treghetsfullt.

Ekstern observatør. Alle de fire kroppene: heisen, eksperimentatoren, klokken og lommetørkleet faller med forskjellige akselerasjoner mot bakken. Hans konklusjon er også sammenfallende med den interne observatørens mening - systemet er ikke-treg.

Einsteins interne og eksterne observatør argumenterer forskjellig: «En ekstern observatør legger merke til bevegelsen til heisen og alle legemer i den, og finner den i samsvar med Newtons gravitasjonslov. For ham er bevegelsen ikke ensartet, men akselerert, på grunn av jordens gravitasjonsfelt.

En generasjon fysikere født og oppvokst i en heis ville imidlertid tenke helt annerledes. Den ville være sikker på at den har en treghetsramme, og vil relatere alle naturlovene til heisen sin, og erklære med tillit at lovene har en spesielt enkel form i deres referanseramme. Det ville være naturlig for dem å betrakte heisen deres for å være i ro og koordinatsystemet deres som treghet.

Det er umulig å etablere en grunnleggende forskjell mellom den eksterne og den interne observatøren. Hver av dem kunne kreve retten til å henføre alle hendelser til sitt eget koordinatsystem. Begge beretningene om hendelser kan gjøres like konsistente. Fra dette eksemplet ser vi at en konsistent beskrivelse av fysiske fenomener i to forskjellige koordinatsystemer er mulig, selv om de ikke beveger seg rettlinjet og jevnt i forhold til hverandre. Men for en slik beskrivelse må vi ta hensyn til tyngdekraften, som skaper så å si en "bro" som lar oss bevege oss fra ett koordinatsystem til et annet. Gravitasjonsfeltet eksisterer for en ekstern observatør, men for en intern observatør eksisterer det ikke. Den akselererte bevegelsen til heisen i gravitasjonsfeltet eksisterer for en ekstern observatør, men for den interne observatøren er det hvile og fravær av et gravitasjonsfelt. Men «broen», dvs. gravitasjonsfeltet, som gjør beskrivelse i begge koordinatsystemene mulig, hviler på en svært viktig støtte: ekvivalensen av tunge og treghetsmasser. Uten denne veiledende ideen, som forble ubemerket i klassisk mekanikk, ville vårt nåværende resonnement fullstendig forsvinne." Men fra formel (4) følger det at prinsippet om ekvivalens av tunge og treghetsmasser er brutt, og derfor kollapser, trist nok, Einsteins "bro" som fører til det vakre slottet til den generelle relativitetsteorien.

Denne konklusjonen kan også bekreftes av følgende tankeeksperiment. Fra klassisk mekanikk følger det at et legeme opprettholder en hviletilstand eller ensartet rettlinjet bevegelse hvis den ikke påvirkes av ytre krefter.

Tenk på kroppen m, som er i ro. Denne kroppen er et eksempel på treghetsmasse per definisjon. Kropp m kan også betraktes som gravitasjonsmasse, dvs. en masse som har et gravitasjonsfelt og er i ro.

La oss nå se på kroppen M, som er i ro på avstand R fra m. La oss gjennomføre lignende resonnement og komme til samme konklusjon: kroppen M er en gravitasjons- og treghetsmasse. Så lenge vi vurderte hver kropp separat, oppsto det ingen motsetninger i resonnementet vårt.

Når man vurderer to kropper M Og m Samtidig vil det virkelige bildet endre seg. Kropp M Og m, som vi anså for å være i ro, er faktisk i akselerert bevegelse mot hverandre på grunn av deres gravitasjonsinteraksjon. De er, som før, gravitasjonsmasser, men er ikke lenger treghetsmasser, fordi beveger seg raskt.

For å løse motsigelsen som har oppstått, er det nødvendig å trekke følgende konklusjoner. For det første består det fysiske bildet av verden av mange gravitasjonsmasser som ikke kan være i ro og som regel beveger seg med jevn akselerasjon. For det andre er det ingen reelle treghetsmasser i naturen. Treghetsmasse i fysikk er en ideell modell - en abstraksjon.

Enhver masse er gravitasjonsmessig og er konstant i interaksjon med omverdenen. Bare gjennom et tankeeksperiment kan vi fjerne gravitasjonsfeltet fra en masse, og etter det kan det betraktes som en treghetsmasse som kan være i ro eller bevege seg jevnt og i en rett linje.

Fra disse posisjonene reduseres alle anstrengelser, både teoretiske og praktiske, for å underbygge ekvivalensprinsippet til et fåfengt forsøk på å etablere ekvivalensen til ekte gravitasjonsmasse og ideell treghetsmasse, som ikke eksisterer i naturen.

Som kjent, ved bruk av Cavendish-metoden, ble konstanten γ, som er inkludert i formel (1) i loven om universell gravitasjon, bestemt numerisk. I dag er denne konstanten kjent opp til det fjerde sifferet. V.D. Lyakhovets gir i sin artikkel "Problemer med metrologisk støtte for målinger av gravitasjonskonstanten" en tabell:

Tabell 1

Ifølge V.D. Lyakhovets, forblir gravitasjonskonstanten γ en av de minst nøyaktig målte fundamentale konstantene. Det følger av tabellen at selv om den relative feilen for individuelle målinger etter land er 10 –4, bestemmes selve gravitasjonsverdien med en feil på 10 –3. Oppgaven med å bestemme γ mer nøyaktig er fortsatt langt fra å være fjernet fra dagsorden. Denne situasjonen får oss til å tenke på mulige faktorer som påvirker den målte verdien av gravitasjonskonstanten. Etter mange forskeres mening er en av dem endring (4) til formel (1) - loven om universell gravitasjon.

Men virker loven om universell gravitasjon på submillimeter avstander?

For flere år siden dukket det opp en rekke teoretiske konstruksjoner i partikkelfysikken som spådde unormale gravitasjonseffekter ved avstander i størrelsesorden brøkdeler av en millimeter. Årsakene til slike anomalier kan være forskjellige: fra ytterligere romlige dimensjoner komprimert på en skala i størrelsesorden en millimeter, til dilatonginteraksjoner på samme skalaer i noen strengteorier. På en eller annen måte forutså alle disse teoriene uunngåelig avvik fra 1/r 2-loven om universell gravitasjon på submillimeterskalaen.

Til nå har loven om universell gravitasjon blitt bekreftet bare ved avstander i størrelsesorden 1 cm eller mer. Derfor, for å teste de uvanlige spådommene til teoriene, var det nødvendig med et nytt, miniatyreksperiment som ville teste 1/r 2-avhengigheten til gravitasjonskraften på submillimeteravstander. Et slikt eksperiment ble utført ved University of Washington i Seattle.

Kraften til gravitasjonsinteraksjon ble målt ved hjelp av en torsjonspendel: en metallring hengt opp på en tynn tråd over en tiltrekningsplate (en "attraktor"). Fordelingen av masser over overflaten av platen og langs ringen var ujevn på grunn av 10 symmetrisk plasserte hull, på grunn av hvilke rotasjonen av den nedre tiltrekningsplaten førte til utseendet av et dreiemoment som virket på torsjonspendelen, og derfor til dens avbøyning. Ved å studere avhengigheten av avbøyningsvinkelen av tid ved ulike gap mellom ringen og platen, kunne forsøksmenn således måle hvordan gravitasjonskraften endres med størrelsen på gapet, det vil si med avstanden mellom de tiltrekkende overflatene.

De eksperimentelle resultatene viste at med en spaltetykkelse på opptil 218 μm, blir den målte kraftavhengigheten av avstanden fullstendig reprodusert av loven om universell gravitasjon. Dermed er det ikke oppdaget nye gravitasjonseffekter på submillimeterskalaen. I tillegg ble det oppnådd alvorlige restriksjoner på parameterne som er tilstede i teoriene nevnt ovenfor.

Bibliografi

A. Einstein, A. Infeld. Evolusjon av fysikk. – M.: Nauka, 1965.

O.A. Bykovsky. Problemer med moderne fysikk. – Alma-Ata: Gym. 1995.

P.I. Bakulin, E.V. Kononovich, V.I. Fryser. Generelt astronomikurs. – M.: Nauka, 1966.

Yu.A. Ryabov. Bevegelse av himmellegemer. – M.: Nauka, 1988.

Tidsskrifter og spesielt "Science News"

Naturlig slacker!
Sitt, gjør ingenting,
studer fysikk hele dagen!

Konas tanker høyt

Hvor M Og m– partikkelmasser;
R- avstanden mellom dem;
γ – gravitasjonskonstant.

En liten endring av A. Clairaut til formen til Newtons universelle gravitasjonslov ble presentert i følgende form:

Hvor M Og m– masser av to kropper;
R- avstanden mellom dem;
γ – gravitasjonskonstant;
n – n> 2 (for eksempel n = 3, n = 4);
α er en liten verdi valgt eksperimentelt.

350 år har gått siden den gang. Loven om universell gravitasjon (1) i sin opprinnelige form feiret 2000-årsjubileet. Tvilen til A. Clairaut og J. d'Alembert angående Newtons lov om universell gravitasjon, etter vår mening, har ikke blitt fjernet. Rekkefølgen av følgende resonnement fører oss til uventede resultater.

To materielle kropper M Og m tiltrekke hverandre med like stor kraft F. Gravitasjonsfelt av masse M forårsaker akselerasjon m:
g = γ · ( M/ R 2).

Følgelig er massen m forårsaker akselerasjon M:
g = γ · ( m/ R 2).

Relativ akselerasjon av to kropper M Og m g fra lik til forskjell g M – g m, og siden g M og g m er rettet i motsatte retninger, da g fra er lik summen av akselerasjoner g M og g m:

g Jord-Måne = 9,81 m/s2 / 3640,38 = 0,2695 cm/s2.

Jordens akselerasjon forårsaket av månens tyngdekraft er:

g Måne-Jord = 1,62 m/s2 / 48917,83 = 0,0033 cm/s2.

Relativ akselerasjon av månen g fra vil være lik summen av akselerasjoner

g fra = g Jord-måne + g Måne-Jord = 0,2695 cm/s2 + 0,0033 cm/s2 = 0,2728 cm/s2.

G fra = V 2 / r ,

Hvor V- hastigheten på månens bane;
r- avstand fra jorden til månen.

Hastigheten til månens bane V kan beregnes ved hjelp av formelen:

V= (2π r) / T ,

Hvor T- siderisk periode av månens revolusjon, T= 27,3 dager;
r- avstand fra jorden til månen ( r= 384400 km).

La oss beregne verdien V Og G fra:

V= (2 · 3,14 · 384400 km) / 2358720 sek = 1,02345 km/sek

G fra = (1,02345 km/sek) 2 / 384400 km = 0,2725 cm/sek 2 .

Beregninger viser det G fra = g fra og den relative feilen til disse to indikatorene er G fra - g fra = 0,2728 cm/sek 2 – 0,2725 cm/sek 2 = 0,0003 cm/sek 2 eller 0,12 %.

Numeriske beregninger g Basert på reelle data fra Jorden og Månen, bekrefter de at formel (3) er tilstrekkelig for omverdenen.

La oss nå vurdere bevegelsen til kroppen m relativt M. Kraftens størrelse F opptrer mellom m Og M lik masseproduktet m for relativ akselerasjon g fra:

Hvis m betydelig mindre enn M, dvs. m M, da er verdien av det andre leddet i forhold til det første ubetydelig. Som kjent avviste J. Buffon på et tidspunkt formel (2) på grunn av at A. Clairaut la til det andre leddet vilkårlig, men i vårt tilfelle i formel (5) er første og andre ledd avledet fra verden rundt oss . Derfor har vi rett til å si at Newtons lov om universell gravitasjon er et spesielt tilfelle av formlene (4) og (5).

La oss nå formulere en ny, raffinert lov om universell gravitasjon:
hver to partikler av materie tiltrekker hverandre hverandre, eller graviterer mot hverandre, med en kraft som er direkte proporsjonal med produktet av summen av de to massene og massen av kroppen som beveger seg i forhold til den sentrale massen og omvendt proporsjonal med kvadratet på avstanden mellom dem(4).

Korreksjonen vår er enda mer uttalt når m = M. Styrkeverdi F beregnet ved formel (4) F= γ 2 M 2 / r 2 er dobbelt så stor som kraftverdien beregnet ved formel (1) F = γ · M 2 / r 2 .

Med fremkomsten av formel (4) viker likhet (7) for ulikhet (6), som en konsekvens av et nytt vitenskapelig faktum.

La oss se hvordan både observatører, interne og eksterne, beskriver hva som skjer i heisen.

Konklusjonen vår kan også bekreftes av følgende tankeeksperiment. Fra klassisk mekanikk følger det at et legeme opprettholder en hviletilstand eller ensartet rettlinjet bevegelse hvis den ikke påvirkes av ytre krefter.

Tabell 1

Ifølge V.D. Lyakhovets, forblir gravitasjonskonstanten γ en av de minst nøyaktig målte fundamentale konstantene. Det følger av tabellen at selv om den relative feilen for individuelle målinger etter land er 10 –4, bestemmes selve gravitasjonsverdien med en feil på 10 –3. Oppgaven med å bestemme γ mer nøyaktig er fortsatt langt fra å være fjernet fra dagsorden. Denne situasjonen får oss til å tenke på mulige faktorer som påvirker den målte verdien av gravitasjonskonstanten. Etter vår mening er en av dem endring (4) til formel (1) - loven om universell gravitasjon.

Som avslutning på vårt lille arbeid med stor tyngdekraft, understreker vi den avgjørende rollen til eksperimenter for å forstå tyngdekraften. Det er ganske vanskelig å sette opp et aktivt gravitasjonseksperiment, fordi... Gravitasjonsmassene i jordens laboratorium er for små. Derfor var det ingen tilfeldighet at vår oppmerksomhet var rettet mot Jorden og Månen, som naturlige laboratorier som kunne tjene som standard for alle forskere for å teste eventuelle hypoteser innen tyngdekraften.

Litteratur:

Yu.A. Ryabov. Bevegelse av himmellegemer. – M.: Nauka, 1988. – 238 s.
V.A. Bronshten. Hvordan beveger månen seg? – M.: Nauka, 1990. – 205 s.
P.I. Bakulin, E.V. Kononovich, V.I. Fryser. Generelt astronomikurs. – M.: Nauka, 1966. – 527 s.
A. Einstein, A. Infeld. Evolusjon av fysikk. – M.: Nauka, 1965. – 326 s.
O.A. Bykovsky. Problemer med moderne fysikk. – Alma-Ata: Gym. 1995. – 128 s.