Denne artikkelen handler om vinkelen mellom fly og hvordan du finner den. Først gis definisjonen av vinkelen mellom to plan og en grafisk illustrasjon. Etter dette analyseres prinsippet om å finne vinkelen mellom to kryssende plan ved hjelp av koordinatmetoden, og det oppnås en formel som lar deg beregne vinkelen mellom kryssende plan ved hjelp av de kjente koordinatene til normalvektorene til disse planene. Avslutningsvis er det vist detaljerte løsninger karakteristiske oppgaver.
Sidenavigering.
Vinkel mellom plan - definisjon.
La oss presentere argumenter som vil tillate oss å gradvis nærme oss bestemmelsen av vinkelen mellom to kryssende plan.
La oss få to kryssende plan og . Disse planene skjærer hverandre langs en rett linje, som vi betegner med bokstaven c. La oss konstruere et plan som går gjennom punktet M på linje c og vinkelrett på linje c. I dette tilfellet vil flyet krysse flyene og. La oss betegne den rette linjen som planene skjærer langs som a, og den rette linjen som planene skjærer langs som b. Det er klart at linjene a og b skjærer hverandre i punktet M.

Det er lett å vise at vinkelen mellom kryssende linjer a og b ikke er avhengig av plasseringen av punktet M på linjen c som flyet går gjennom.
La oss konstruere et plan vinkelrett på linjen c og forskjellig fra planet. Planet er krysset av plan og langs rette linjer, som vi betegner som henholdsvis a 1 og b 1.
Fra metoden for å konstruere plan følger det at linjene a og b er vinkelrette på linje c, og linjene a 1 og b 1 er vinkelrette på linje c. Siden linjene a og a 1 ligger i samme plan og er vinkelrett på linje c, så er de parallelle. På samme måte ligger linjene b og b 1 i samme plan og er vinkelrette på linje c, derfor er de parallelle. Så du kan gjøre parallell overføring plan til plan, der rett linje a 1 sammenfaller med rett linje a, og rett linje b med rett linje b 1. Derfor er vinkelen mellom to kryssende linjer a 1 og b 1 lik vinkel mellom kryssende linjer a og b.

Dette beviser at vinkelen mellom kryssende linjer a og b som ligger i kryssende plan og ikke er avhengig av valget av punkt M som planet passerer gjennom. Derfor er det logisk å ta denne vinkelen som vinkelen mellom to kryssende plan.
Nå kan du gi uttrykk for definisjonen av vinkelen mellom to kryssende plan og.
Definisjon.
Vinkelen mellom to plan som skjærer i en rett linje og- dette er vinkelen mellom to kryssende linjer a og b, langs hvilke planene og skjærer med planet vinkelrett på linjen c.

Definisjonen av vinkelen mellom to plan kan gis litt annerledes. Hvis på den rette linjen c som planene og skjærer, merker du et punkt M og tegner rette linjer a og b gjennom det, vinkelrett på den rette linjen c og ligger i henholdsvis planene, og da vinkelen mellom de rette linjene a og b er vinkelen mellom planene og. Vanligvis i praksis utføres nettopp slike konstruksjoner for å oppnå vinkelen mellom planene.
Siden vinkelen mellom kryssende linjer ikke overstiger , følger det av den oppgitte definisjonen at gradsmål vinkelen mellom to kryssende plan uttrykkes reelt tall fra intervallet. I dette tilfellet kalles kryssende plan vinkelrett, hvis vinkelen mellom dem er nitti grader. Vinkelen mellom parallelle plan er enten ikke bestemt i det hele tatt eller anses som lik null.
Finne vinkelen mellom to kryssende plan.
Vanligvis, når du finner en vinkel mellom to kryssende plan, må du først utføre ytterligere konstruksjoner for å se de kryssende rette linjene, vinkelen mellom disse er lik ønsket vinkel, og deretter relatere denne vinkelen til de originale dataene ved hjelp av likhetstester, likhet. tester, cosinussetningen eller definisjoner av sinus, cosinus og tangens til vinkelen. I løpet av geometri videregående skole lignende problemer oppstår.
Som et eksempel, la oss gi løsningen på problem C2 fra Unified State Examination i matematikk for 2012 (betingelsen ble med vilje endret, men dette påvirker ikke løsningsprinsippet). I den måtte du bare finne vinkelen mellom to kryssende plan.
Eksempel.
Løsning.
La oss først lage en tegning.

La oss utføre ytterligere konstruksjoner for å "se" vinkelen mellom flyene.
Først, la oss definere en rett linje langs hvilken planene ABC og BED 1 krysser hverandre. Punkt B er et av deres felles punkter. La oss finne den andre felles poeng disse flyene. Linjene DA og D 1 E ligger i samme plan ADD 1, og de er ikke parallelle, og krysser derfor hverandre. På den annen side ligger linje DA i planet ABC, og linje D 1 E - i planet BED 1, derfor vil skjæringspunktet mellom linjene DA og D 1 E være et felles punkt ABC-fly og SENG 1. Så la oss fortsette linjene DA og D 1 E til deres skjæringspunkt, og angir skjæringspunktet med bokstaven F. Da er BF den rette linjen som planene ABC og BED 1 skjærer langs.

Det gjenstår å konstruere to linjer som ligger i henholdsvis planene ABC og BED 1, som går gjennom ett punkt på linjen BF og vinkelrett på linjen BF - vinkelen mellom disse linjene vil per definisjon være lik den ønskede vinkelen mellom fly ABC og BED 1. La oss gjøre dette.
Prikk A er projeksjonen av punkt E på plan ABC. La oss tegne en rett linje som skjærer linje BF i rette vinkler ved punkt M. Da er den rette linjen AM projeksjonen av den rette linjen EM på planet ABC, og ved teoremet om tre perpendikulære.

Dermed er den nødvendige vinkelen mellom planene ABC og BED 1 lik .
Vi kan bestemme sinus, cosinus eller tangens til denne vinkelen (og derfor selve vinkelen) fra den rettvinklede trekanten AEM hvis vi vet lengdene på de to sidene. Fra betingelsen er det lett å finne lengden AE: siden punkt E deler side AA 1 i forholdet 4 til 3, tellende fra punkt A, og lengden på siden AA 1 er 7, så er AE = 4. La oss finne lengden AM.
For å gjøre dette, vurder rettvinklet trekant ABF med rett vinkel A, der AM er høyden. Etter betingelse AB = 2. Vi kan finne lengden på side-AF fra likheten mellom rettvinklede trekanter DD 1 F og AEF: 
Ved å bruke Pythagoras teorem finner vi fra trekant ABF. Vi finner lengden AM gjennom arealet av trekanten ABF: på den ene siden er arealet av trekanten ABF lik ![]() , på den andre siden
, på den andre siden ![]() , hvor
, hvor  .
.
Dermed har vi fra den høyre trekanten AEM  .
.
Da er den nødvendige vinkelen mellom planene ABC og BED 1 lik (merk at  ).
).
Svare:

I noen tilfeller, for å finne vinkelen mellom to kryssende plan, er det praktisk å sette Oxyz og bruke koordinatmetoden. La oss stoppe der.
La oss sette oppgaven: finne vinkelen mellom to kryssende plan og . La oss betegne ønsket vinkel som .
Vi vil anta at vi i et gitt rektangulært koordinatsystem Oxyz kjenner koordinatene til normalvektorene til kryssende plan og eller har mulighet til å finne dem. La ![]() er normalvektoren til planet, og
er normalvektoren til planet, og ![]() er normalvektoren til planet. Vi skal vise hvordan man finner vinkelen mellom kryssende plan og gjennom koordinatene til normalvektorene til disse planene.
er normalvektoren til planet. Vi skal vise hvordan man finner vinkelen mellom kryssende plan og gjennom koordinatene til normalvektorene til disse planene.
La oss betegne den rette linjen langs hvilken planene og krysser som c. Gjennom punkt M på linje c tegner vi et plan vinkelrett på linje c. Planet skjærer planene og langs linjene a og b, henholdsvis skjærer linjene a og b i punkt M. Per definisjon er vinkelen mellom kryssende plan og lik vinkelen mellom kryssende linjer a og b.
La oss plotte normalvektorene og -planene og fra punktet M i planet. I dette tilfellet ligger vektoren på en linje som er vinkelrett på linje a, og vektoren ligger på en linje som er vinkelrett på linje b. Således, i planet er vektoren normalvektoren til linjen a, er normalvektoren til linjen b.

I artikkelen om å finne vinkelen mellom kryssende linjer, mottok vi en formel som lar deg beregne cosinus til vinkelen mellom kryssende linjer ved å bruke koordinatene til normale vektorer. Dermed cosinus til vinkelen mellom linjene a og b, og følgelig, cosinus av vinkelen mellom kryssende plan og finnes av formelen hvor ![]() Og
Og ![]() er normalvektorene til planene og hhv. Da er det beregnet som
er normalvektorene til planene og hhv. Da er det beregnet som  .
.
La oss løse det forrige eksemplet ved å bruke koordinatmetoden.
Eksempel.
Dan kuboid ABCDA 1 B 1 C 1 D 1, der AB=2, AD=3, AA 1 =7 og punkt E deler side AA 1 i forholdet 4 til 3, tellende fra punkt A. Finn vinkelen mellom planene ABC og BED 1.
Løsning.
Siden sidene av et rektangulært parallellepiped ved ett toppunkt er parvis vinkelrett, er det praktisk å introdusere rektangulært system koordinater Oxyz slik: juster begynnelsen med toppunktet C, og rett koordinataksene Ox, Oy og Oz langs sidene CD, CB og CC 1, henholdsvis.

Vinkelen mellom ABC- og BED 1-planene kan finnes gjennom koordinatene til normalvektorene til disse planene ved å bruke formelen , hvor og er normalvektorene til henholdsvis ABC- og BED 1-planene. La oss bestemme koordinatene til normale vektorer.
Mål på vinkelen mellom planene er spiss vinkel, dannet av to rette linjer som ligger i disse planene og tegnet vinkelrett på skjæringslinjen deres.
Konstruksjonsalgoritme
- Fra et vilkårlig punkt K tegnes perpendikulære til hvert av de gitte planene.
- Ved å rotere rundt nivålinjen bestemmes vinkelen γ° med toppunktet i punktet K.
- Regn ut vinkelen mellom planene ϕ° = 180 – γ°, forutsatt at γ° > 90°. Hvis γ°< 90°, то ∠ϕ° = ∠γ°.
Figuren viser tilfellet når planene α og β er gitt ved spor. Alle nødvendige konstruksjoner ble utført i henhold til algoritmen og er beskrevet nedenfor.
Løsning
- På et vilkårlig sted på tegningen markerer vi punktet K. Fra det senker vi perpendikulære henholdsvis m og n til planene α og β. Retningen til projeksjonene m og n er som følger: m""⊥f 0α , m"⊥h 0α , n""⊥f 0β , n"⊥h 0β .
- Vi bestemmer den faktiske størrelsen ∠γ° mellom linjene m og n. For å gjøre dette, rundt frontal f roterer vi vinkelplanet med toppunkt K til en posisjon parallelt med frontal projeksjonsplan. Svingradius R for punkt K lik verdien hypotenusen til en rettvinklet trekant O""K""K 0, hvis side er K""K 0 = y K – y O.
- Ønsket vinkel er ϕ° = ∠γ°, siden ∠γ° er spiss.
Figuren under viser løsningen på et problem der det kreves å finne vinkelen γ° mellom planene α og β, gitt av henholdsvis parallelle og kryssende linjer.

Løsning
- Vi bestemmer retningen til projeksjonene til horisontalene h 1, h 2 og frontene f 1, f 2, som tilhører flyα og β, i rekkefølgen angitt av pilene. Fra et vilkårlig punkt K på torget. α og β utelater vi perpendikulære e og k. I dette tilfellet, e""⊥f"" 1 , e"⊥h" 1 og k""⊥f"" 2 , k"⊥h" 2 .
- Vi definerer ∠γ° mellom linjene e og k. For å gjøre dette, tegn en horisontal linje h 3 og rundt den roterer vi punktet K til posisjon K 1, hvor △CKD vil bli parallell med horisontalplanet og vil bli reflektert på det i naturlig størrelse - △C"K" 1 D ". Projeksjonen av rotasjonssenteret O" er plassert på tegnet til h" 3 vinkelrett på K"O". Radius R bestemmes fra den rette trekanten O"K"K 0, hvis side K"K 0 = Å O – Å K.
- Verdien av den ønskede verdien er ∠ϕ° = ∠γ°, siden vinkelen γ° er spiss.
Artikkelen snakker om å finne vinkelen mellom planene. Etter å ha gitt definisjonen vil vi gi en grafisk illustrasjon og vurdere en detaljert metode for å finne koordinater ved hjelp av metoden. Vi får en formel for kryssende plan, som inkluderer koordinatene til normale vektorer.
Yandex.RTB R-A-339285-1
Materialet vil bruke data og begreper som tidligere ble studert i artikler om planet og linjen i rommet. Først må vi gå videre til resonnement som lar oss ha en viss tilnærming til å bestemme vinkelen mellom to kryssende plan.
To kryssende plan γ 1 og γ 2 er gitt. Krysset deres vil ha betegnelsen c. Konstruksjonen av χ-planet er assosiert med skjæringspunktet mellom disse planene. Planet χ går gjennom punktet M som en rett linje c. Skjæringen mellom planene γ 1 og γ 2 vil bli laget ved hjelp av planet χ. Vi tar betegnelsen på linjen som skjærer γ 1 og χ som linje a, og linjen som skjærer γ 2 og χ som linje b. Vi finner at skjæringspunktet mellom linjene a og b gir punktet M.
Plasseringen av punktet M påvirker ikke vinkelen mellom kryssende linjer a og b, og punktet M ligger på linje c, som planet χ går gjennom.
Det er nødvendig å konstruere et plan χ 1 vinkelrett på linjen c og forskjellig fra planet χ. Skjæringspunktet mellom planene γ 1 og γ 2 ved hjelp av χ 1 vil ta betegnelsen av linjene a 1 og b 1.
Det kan sees at når du konstruerer χ og χ 1, er linjene a og b vinkelrette på linje c, deretter er a 1, b 1 plassert vinkelrett på linje c. Finne rette linjer a og a 1 i planet γ 1 med perpendikularitet til rett linje c, så kan de betraktes som parallelle. På samme måte indikerer plasseringen av b og b 1 i γ 2-planet med perpendikularitet til rett linje c deres parallellitet. Dette betyr at det er nødvendig å gjøre en parallell overføring av planet χ 1 til χ, hvor vi får to sammenfallende rette linjer a og a 1, b og b 1. Vi finner at vinkelen mellom skjærende linjer a og b 1 er lik vinkelen til skjærende linjer a og b.
La oss se på figuren nedenfor.

Denne påstanden bevises av det faktum at mellom de kryssende linjene a og b er det en vinkel som ikke er avhengig av plasseringen av punktet M, det vil si skjæringspunktet. Disse linjene er plassert i planene γ 1 og γ 2. Faktisk kan den resulterende vinkelen betraktes som vinkelen mellom to kryssende plan.
La oss gå videre til å bestemme vinkelen mellom de eksisterende kryssende planene γ 1 og γ 2.
Definisjon 1
Vinkelen mellom to kryssende plan γ 1 og γ 2 kalt vinkelen som dannes av skjæringspunktet mellom linjene a og b, der planene γ 1 og γ 2 skjærer planet χ vinkelrett på linje c.
Tenk på figuren nedenfor.
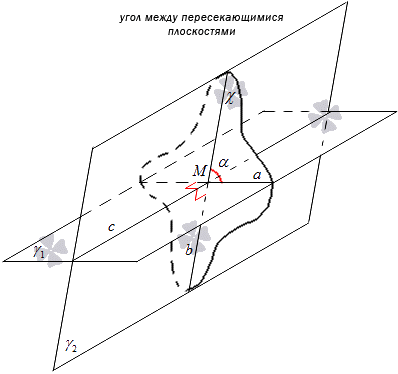
Avgjørelsen kan sendes i annen form. Når planene γ 1 og γ 2 skjærer hverandre, hvor c er linjen de skjærer seg på, markerer du et punkt M som trekker linjene a og b vinkelrett på linje c og ligger i planene γ 1 og γ 2, så vinkelen mellom linjene a og b vil være vinkelen mellom planene. I praksis er dette anvendelig for å konstruere vinkelen mellom planene.
Ved skjæring dannes det en vinkel som er mindre enn 90 grader i verdi, det vil si at gradmålet på vinkelen er gyldig på et intervall av denne typen (0, 90]. Samtidig kalles disse planene perpendikulære hvis en rett vinkel dannes i skjæringspunktet. Vinkelen mellom parallelle plan regnes som lik null.
Den vanlige måten å finne vinkelen mellom kryssende plan er å utføre tilleggskonstruksjoner. Dette bidrar til å bestemme det med nøyaktighet, og dette kan gjøres ved å bruke tegn på likhet eller likhet i en trekant, sinus og cosinus i en vinkel.
La oss vurdere å løse problemer ved å bruke et eksempel fra Unified State Exam problemer blokk C 2.
Eksempel 1
Gitt et rektangulært parallellepipedum A B C D A 1 B 1 C 1 D 1, hvor side A B = 2, A D = 3, A A 1 = 7, deler punkt E side A A 1 i forholdet 4:3. Finn vinkelen mellom planene A B C og B E D 1.
Løsning
For klarhet er det nødvendig å lage en tegning. Det skjønner vi

En visuell representasjon er nødvendig for å gjøre det mer praktisk å jobbe med vinkelen mellom planene.
Vi bestemmer den rette linjen langs hvilken skjæringspunktet mellom planene A B C og B E D 1 oppstår. Punkt B er et felles punkt. Et annet felles skjæringspunkt bør finnes. La oss vurdere de rette linjene D A og D 1 E, som er plassert i samme plan A D D 1. Deres plassering indikerer ikke parallellitet, det betyr at de har et felles skjæringspunkt.
Rett linje D A ligger imidlertid i planet A B C, og D 1 E i B E D 1. Fra dette får vi at de rette linjene D A Og D 1 E ha et felles skjæringspunkt, som er felles for planene A B C og B E D 1. Indikerer skjæringspunktet mellom linjer D A og D 1 E bokstaven F. Fra dette får vi at B F er den rette linjen langs hvilken planene A B C og B E D 1 skjærer.
La oss se på figuren nedenfor.

For å få svaret er det nødvendig å konstruere rette linjer plassert i planene A B C og B E D 1 som går gjennom et punkt som ligger på linje B F og vinkelrett på det. Da regnes den resulterende vinkelen mellom disse rette linjene som den ønskede vinkelen mellom planene A B C og B E D 1.
Av dette kan vi se at punktet A er projeksjonen av punktet E på planet A B C. Det er nødvendig å tegne en rett linje som skjærer linjen B F i rett vinkel i punktet M. Det kan ses at den rette linjen A M er projeksjonen av rett linje E M på planet A B C, basert på teoremet om disse perpendikulære A M ⊥ B F . Tenk på figuren nedenfor.

∠ A M E er den ønskede vinkelen dannet av planene A B C og B E D 1. Fra den resulterende trekanten A E M kan vi finne sinus, cosinus eller tangens til vinkelen, og deretter selve vinkelen, bare hvis de to sidene er kjent. Ved betingelse har vi at lengden A E finnes på denne måten: rett linje A A 1 deles på punktet E i forholdet 4:3, som betyr at den totale lengden på den rette linjen er 7 deler, da er A E = 4 deler. Vi finner A M.
Det er nødvendig å vurdere en rettvinklet trekant A B F. Vi har en rett vinkel A med høyden A M. Fra betingelsen A B = 2 kan vi finne lengden A F ved likheten mellom trekanter D D 1 F og A E F. Vi får at A E D D 1 = A F D F ⇔ A E D D 1 = A F D A + A F ⇒ 4 7 = A F 3 + A F ⇔ A F = 4
Det er nødvendig å finne lengden på siden B F i trekanten A B F ved å bruke Pythagoras teorem. Vi får at B F = A B 2 + A F 2 = 2 2 + 4 2 = 2 5 . Lengden på siden A M finnes gjennom arealet av trekanten A B F. Vi har at arealet kan være lik både S A B C = 1 2 · A B · A F og S A B C = 1 2 · B F · A M .
Vi får at A M = A B A F B F = 2 4 2 5 = 4 5 5
Da kan vi finne verdien av tangenten til vinkelen til trekanten A E M. Vi får:
t g ∠ A M E = A E A M = 4 4 5 5 = 5
Den ønskede vinkelen oppnådd ved skjæringen av planene A B C og B E D 1 er lik a r c t g 5, så får vi ved forenkling a r c t g 5 = a r c sin 30 6 = a r c cos 6 6.
Svare: a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .
Noen tilfeller av å finne vinkelen mellom kryssende linjer spesifiseres ved hjelp av koordinatplan O x y z og koordinatmetoden. La oss ta en nærmere titt.
Dersom det er gitt en oppgave hvor det er nødvendig å finne vinkelen mellom planene γ 1 og γ 2 som skjærer hverandre, betegner vi ønsket vinkel som α.
Da gitt system koordinater viser at vi har koordinatene til normalvektorene til de kryssende planene γ 1 og γ 2. Da betegner vi at n 1 → = n 1 x, n 1 y, n 1 z er normalvektoren til planet γ 1, og n 2 → = (n 2 x, n 2 y, n 2 z) - for plan γ 2. La oss vurdere detaljert funn vinkelen som ligger mellom disse planene langs koordinatene til vektorene.
Det er nødvendig å angi den rette linjen langs hvilken planene γ 1 og γ 2 krysser bokstaven c. På linjen c har vi et punkt M som vi tegner et plan χ vinkelrett på c. Planet χ langs linjene a og b skjærer planene γ 1 og γ 2 i punktet M. av definisjonen følger det at vinkelen mellom de skjærende planene γ 1 og γ 2 er lik vinkelen til de kryssende linjene a og b som hører til disse planene, henholdsvis.
I χ-planet plotter vi normalvektorer fra punktet M og betegner dem n 1 → og n 2 → . Vektor n 1 → er plassert på en linje vinkelrett på linje a, og vektor n 2 → er plassert på en linje vinkelrett på linje b. Herfra får vi det gitt flyχ har en normalvektor av linje a lik n 1 → og for linje b lik n 2 →. Tenk på figuren nedenfor.
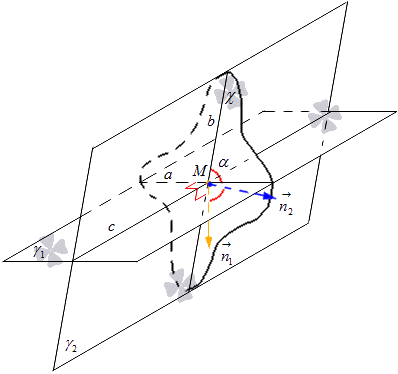
Herfra får vi en formel som vi kan beregne sinusen til vinkelen til kryssende linjer ved å bruke koordinatene til vektorer. Vi fant at cosinus til vinkelen mellom rette linjer a og b er den samme som cosinus mellom kryssende plan γ 1 og γ 2, som er utledet fra cos formlerα = cos n 1 → , n 2 → ^ = n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2, hvor vi har at n 1 → = (n 1 x, n 1 y, n 1 z) og n 2 → = (n 2 x, n 2 y, n 2 z) er koordinatene til vektorene til de representerte planene.
Vinkelen mellom kryssende linjer beregnes ved hjelp av formelen
α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2
Eksempel 2
I henhold til betingelsen er parallellepipedet A B C D A 1 B 1 C 1 D 1 gitt , der A B = 2, A D = 3, A A 1 = 7, og punkt E deler siden A A 1 4: 3. Finn vinkelen mellom planene A B C og B E D 1.
Løsning
Fra tilstanden er det klart at sidene er parvis vinkelrette. Dette betyr at det er nødvendig å innføre et koordinatsystem O x y z med toppunktet i punktet C og koordinataksene O x, O y, O z. Det er nødvendig å sette retningen til de riktige sidene. Tenk på figuren nedenfor.

Kryssende fly A B C Og B E D 1 danne en vinkel som kan finnes av formelen α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2, der n 1 → = (n 1 x, n 1 y, n 1 z) og n 2 → = (n 2 x, n 2 y, n 2 z ) er normale vektorer av disse flyene. Det er nødvendig å bestemme koordinatene. Av figuren ser vi det koordinataksen O x y faller sammen med planet A B C, dette betyr at koordinatene til normalvektoren k → er lik verdien n 1 → = k → = (0, 0, 1).
Normalvektoren til planet B E D 1 tas vektor produkt B E → og B D 1 → , hvor deres koordinater er funnet av koordinater ekstreme punkter B, E, D 1, som bestemmes ut fra forholdene til problemet.
Vi får at B (0, 3, 0), D 1 (2, 0, 7). Fordi A E E A 1 = 4 3, fra koordinatene til punktene A 2, 3, 0, A 1 2, 3, 7 finner vi E 2, 3, 4. Vi finner at B E → = (2 , 0 , 4) , B D 1 → = 2 , - 3 , 7 n 2 → = B E → × B D 1 = i → j → k → 2 0 4 2 - 3 7 = 12 · i → - 6 j → - 6 k → ⇔ n 2 → = (12 , - 6 , - 6)
Det er nødvendig å erstatte de funnet koordinatene i formelen for å beregne vinkelen gjennom buen cosinus. Vi får
α = a r c cos 0 12 + 0 (- 6) + 1 (- 6) 0 2 + 0 2 + 1 2 12 2 + (- 6) 2 + (- 6) 2 = a r c cos 6 6 6 = a r c cos 6 6
Koordinatmetoden gir et lignende resultat.
Svare: a r c cos 6 6 .
Den siste oppgaven vurderes med mål om å finne vinkelen mellom kryssende plan gitt de kjente ligningene til planene.
Eksempel 3
Regn ut sinus, cosinus til vinkelen og verdien av vinkelen dannet av to kryssende linjer, som er definert i koordinatsystemet O x y z og gitt av ligningene 2 x - 4 y + z + 1 = 0 og 3 y - z - 1 = 0.
Løsning
Når du studerer et emne generell ligning rett linje av formen A x + B y + C z + D = 0 viste at A, B, C er koeffisienter lik koordinatene til normalvektoren. Dette betyr at n 1 → = 2, - 4, 1 og n 2 → = 0, 3, - 1 er normalvektorer for de gitte linjene.
Det er nødvendig å erstatte koordinatene til de normale vektorene til planene i formelen for å beregne ønsket vinkel på kryssende plan. Da får vi det
α = a r c cos 2 0 + - 4 3 + 1 (- 1) 2 2 + - 4 2 + 1 2 = a r c cos 13 210
Herfra har vi at cosinus til vinkelen tar cos utsikt a = 13.210. Da er ikke vinkelen på kryssende linjer stump. Bytter inn trigonometrisk identitet, finner vi at verdien av sinusen til vinkelen er lik uttrykket. La oss regne ut og finne det
sin α = 1 - cos 2 α = 1 - 13 210 = 41 210
Svare: sin α = 41.210, cos α = 13.210, α = a r c cos 13.210 = a r c sin 41.210.
Hvis du oppdager en feil i teksten, merk den og trykk Ctrl+Enter
Jobbtype: 14
Tema: Vinkel mellom planene
Betingelse
Dana riktig prisme ABCDA_1B_1C_1D_1, M og N er midtpunktene til henholdsvis kantene AB og BC, punkt K er midtpunktet til MN.
EN) Bevis at linjene KD_1 og MN er vinkelrette.
b) Finn vinkelen mellom planene MND_1 og ABC if AB=8, AA_1=6\sqrt 2.
Vis løsningLøsning
EN) I \triangle DCN og \triangle MAD har vi: \angle C=\angle A=90^(\circ), CN=AM=\frac12AB, CD=DA.
Derfor \triangle DCN=\triangle MAD på to ben. Da MD=DN, \triangle DMN likebenet. Dette betyr at medianen DK også er høyden. Derfor DK \perp MN.
DD_1 \perp MND etter tilstand, D_1K - skrå, KD - projeksjon, DK \perp MN.
Derfor, ved teoremet om tre perpendikulære MN\perp D_1K.
b) Som det ble bevist i EN), DK \perp MN og MN \perp D_1K, men MN er skjæringslinjen mellom planene MND_1 og ABC, som betyr \vinkel DKD_1 - lineær vinkel dihedral vinkel mellom planene MND_1 og ABC.
I \triangle DAM i henhold til Pythagoras teorem DM= \sqrt (DA^2+AM^2)= \sqrt (64+16)= 4\sqrt 5, MN= \sqrt (MB^2+BN^2)= \sqrt (16+16)= 4\sqrt 2. Derfor, i \triangle DKM ved Pythagoras teorem DK= \sqrt (DM^2-KM^2)= \sqrt (80-8)= 6\sqrt 2. Så i \triangle DKD_1, tg\vinkel DKD_1=\frac(DD_1)(DK)=\frac(6\sqrt 2)(6\sqrt 2)=1.
Dette betyr \angle DKD_1=45^(\circ).
Svare
45^(\sirkel).
Jobbtype: 14
Tema: Vinkel mellom planene
Betingelse
Til høyre firkantet prisme ABCDA_1B_1C_1D_1 sider av basen er 4, side ribber er lik 6. Punkt M er midten av kant CC_1, punkt N er markert på kant BB_1, slik at BN:NB_1=1:2.
EN) I hvilket forhold deler AMN-planet kanten DD_1?
b) Finn vinkelen mellom planene ABC og AMN.
Vis løsningLøsning
EN) Planet AMN skjærer kanten DD_1 i punktet K, som er det fjerde toppunktet i seksjonen av et gitt prisme ved dette planet. Tverrsnittet er et parallellogram ANMK fordi de motsatte flatene til et gitt prisme er parallelle.
.png)
BN =\frac13BB_1=2. La oss tegne KL \parallell CD, så er trekanter ABN og KLM like, som betyr ML=BN=2, LC=MC-ML=3-2=1, KD=LC=1. Så KD_1=6-1=5.
b) Nå kan du finne forholdet KD:KD_1=1:5.
F er skjæringspunktet mellom rette linjer CD og KM. Planene ABC og AMN skjærer hverandre langs rett linje AF. Vinkel \angle KHD =\alpha er den lineære vinkelen til en dihedral vinkel (HD\perp AF, deretter ved teoremet invers til teoremet av tre perpendikulære, KH \perp AF), og er en spiss vinkel til en rettvinklet trekant KHD, ben KD=1. Trekanter FKD og FMC er like (KD \parallell MC), derfor FD:FC=KD:MC, løser andelen FD:(FD+4)=1:3, får vi FD=2. I en rettvinklet trekant AFD (\angle D=90^(\circ)) med ben 2 og 4, beregner vi hypotenusen AF=\sqrt (4^2+2^2)=2\sqrt 5, DH= AD\cdot FD:AF=
\frac(4\cdot 2)(2\sqrt 5)= \frac4(\sqrt 5). I en rettvinklet trekant KHD finner vi tg \alpha =\frac(KD)(DH)=\frac(\sqrt 5)4,
Svare
EN) 1:5;
b) dette betyr ønsket vinkel
\alpha =arctg\frac(\sqrt 5)4. arctg\frac(\sqrt 5)4. Kilde: «Matematikk. Forberedelse til Unified State Exam 2017.
Jobbtype: 14
Tema: Vinkel mellom planene
Betingelse
Profilnivå " Ed. F. F. Lysenko, S. Yu.
EN) Konstruer et utsnitt av pyramiden med et plan som går gjennom linjen NF parallelt med diagonalen MP, hvis punktet F er midten av kanten MK.
b) Finn vinkelen mellom snittplanet og KMP-planet.
Vis løsningLøsning
EN) La KO være høyden på pyramiden, F midtpunktet til MK ; FE \parallell MP (i PKM-planet) . Siden FE er midtlinje\triangle PKM, da FE=\frac(MP)2.

La oss konstruere en del av pyramiden med et plan som går gjennom NF og parallelt med MP, det vil si planet NFE. L er skjæringspunktet mellom EF og KO. Siden punktene L og N tilhører den ønskede seksjonen og ligger i KQN-planet, så er punktet T, oppnådd som skjæringspunktet mellom LN og KQ, også skjæringspunktet for ønsket seksjon og kanten KQ. NETF er den nødvendige delen.
b) Planene NFE og MPK skjærer hverandre langs rett linje FE. Dette betyr at vinkelen mellom disse planene er lik den lineære vinkelen til den dihedrale vinkelen OFEN , la oss konstruere den: LO\perpMP, MP\parallell FE, derfor, LO\perpFE;\triangle NFE - likebenet (NE=NF som de tilsvarende medianene like trekanter KPN og KMN ), NL er medianen (EL=LF, siden PO=OM, og \triangle KEF \sim \triangle KPM). Derfor er NL \perp FE og \angle NLO den ønskede.
PÅ=\frac12QN=\frac12MN\sqrt 2=3\sqrt 2.
\triangle KON - rektangulær.
Leg KO i henhold til Pythagoras teorem er lik KO=\sqrt (KN^2-ON^2).
OL= \frac12KO= \frac12\sqrt(KN^2-ON^2)= \frac12\sqrt (9\cdot 26-9\cdot 2)= \frac12\sqrt(9(26-2))= \frac32\sqrt (24)= \frac32\cdot 2\sqrt 6= 3\sqrt 6.
tg\angle NLO =\frac(ON)(OL)=\frac(3\sqrt 2)(3\sqrt 6)=\frac1(\sqrt 3),
\angle NLO=30^(\circ).
Svare
Kilde: «Matematikk. Forberedelse til Unified State Exam 2017. Profilnivå." Ed. F. F. Lysenko, S. Yu.
Jobbtype: 14
Tema: Vinkel mellom planene
Betingelse
Alle kantene på et vanlig trekantet prisme ABCA_(1)B_(1)C_(1) er lik 6. Et skjæreplan trekkes gjennom midtpunktene til kantene AC og BB_(1) og toppunktet A_(1).
EN) Bevis at kanten BC er delt med skjæreplanet i forholdet 2:1, regnet fra toppunktet C.
b) Finn vinkelen mellom skjæreplanet og grunnplanet.
Vis løsningLøsning
EN) La D og E være midtpunktene til henholdsvis kantene AC og BB_(1).

I planet AA_(1)C_(1) tegner vi en rett linje A_(1)D, som skjærer den rette linjen CC_(1) i punkt K, i planet BB_(1)C_(1) - en rett linje KE, som skjærer kanten BC i punkt F . Forbindelsespunktene A_(1) og E, liggende i planet AA_(1)B_(1), samt D og F, liggende i planet ABC, får vi seksjon A_(1)EFD.
\bigtriangleup AA_(1)D=\bigtriangleup CDK langs ben AD=DC og spiss vinkel.
\angle ADA_(1)=\angle CDK - som vertikale, følger det at AA_(1)=CK=6. \bigtriangleup CKF og \bigtriangleup BFE er like i to vinkler\angle FBE=\angle KCF=90^\circ,
\angle BFE=\angle CFK - som vertikale.\frac(CK)(BE)=\frac(6)(3)=2,
b) det vil si at likhetskoeffisienten er 2, som betyr at CF:FB=2:1. La oss gjennomføre AH \perp DF. Vinkelen mellom snittplanet og grunnplanet er lik vinkel AHA_(1).
Faktisk er segmentet AH \perp DF (DF er skjæringslinjen for disse planene) projeksjonen av segmentet A_(1)H på grunnplanet, derfor, i henhold til teoremet om tre perpendikulære, A_(1)H \perp DF.

\angle AHA_(1)=arctg\frac(AA_(1))(AH).
AA_(1)=6. La oss finne AH. \angle ADH =\angle FDC (samme som vertikal).
Ved cosinus-teoremet i \bigtriangleup DFC:
DF^2=FC^2+DC^2- 2FC \cdot DC \cdot \cos 60^\circ,
DF^2=4^2+3^2-2 \cdot 4 \cdot 3 \cdot \frac(1)(2)=13.
FC^2=DF^2+DC^2-
2DF\cdot DC\cdot\cos\angle FDC,
4^2=13+9-2\sqrt(13) \cdot 3 \cdot \cos \angle FDC,\cos \angle FDC=\frac(6)(2\sqrt(13) \cdot 3)=\frac(1)(\sqrt(13)).
Som følge av den grunnleggende trigonometriske identiteten \sin \angle FDC=\sqrt(1-\venstre (\frac(1)(\sqrt(13))\høyre)^2)=\frac(2\sqrt(3))(\sqrt(13)) .
Fra \bigtriangleup ADH finner vi AH : AH=AD \cdot \sin \vinkel ADH, (\vinkel FDC=\vinkel ADH). AH=3 \cdot \frac(2\sqrt(3))(\sqrt(13))=\frac(6\sqrt(13))(\sqrt(13)). \angle AHA_(1)=
Svare
arctg\frac(AA_(1))(AH)=
Kilde: «Matematikk. Forberedelse til Unified State Exam 2017. Profilnivå." Ed. F. F. Lysenko, S. Yu.
Jobbtype: 14
Tema: Vinkel mellom planene
Betingelse
arctg\frac(6 \cdot \sqrt(13))(6\sqrt(3))= arctg\frac(\sqrt(39))(3). arctg\frac(\sqrt(39))(3).
EN) Basen til et høyre prisme ABCDA_(1)B_(1)C_(1)D_(1) er en rombe med
b) stump vinkel
Vis løsningLøsning
EN) B lik 120^\circ. Alle kanter på dette prismet er lik 10. Punktene P og K er midtpunktene til henholdsvis kantene CC_(1) og CD. Bevis at linjene PK og PB_(1) er vinkelrette.

Finn vinkelen mellom planene PKB_(1) og C_(1)B_(1)B. Vi vil bruke koordinatmetoden. La oss finne prikkprodukt vektorene \vec(PK) og \vec(PB_(1)), og deretter cosinus til vinkelen mellom disse vektorene. La oss rette Oy-aksen langs CD, Oz-aksen langs CC_(1), og Ox-aksen \perp CD. C er opprinnelsen. Deretter C (0;0;0);
C_(1)(0;0;10); P(0;0;5);
K(0;5;0);
B(BC \cos 30^\circ; BC\sin 30^\circ; 0), det vil si B(5\sqrt(3); 5;0),
\cos \alpha =0, som betyr \vec(PK) \perp \vec(PB_(1)) og linjene PK og PB_(1) er vinkelrette.
b) Vinkelen mellom plan er lik vinkelen mellom vektorer som ikke er null vinkelrett på disse planene (eller, hvis vinkelen er stump, vinkelen ved siden av den). Slike vektorer kalles normaler til plan. La oss finne dem.
La \vec(n_(1))=\(x; y; z\) være vinkelrett på planet PKB_(1). La oss finne det ved å løse systemet
\begin(cases) \vec(n_(1)) \perp \vec(PK), \\ \vec(n_(1)) \perp \vec(PB_(1)). \end(saker)
\begin(cases) \vec(n_(1)) \cdot \vec(PK)=0, \\ \vec(n_(1)) \cdot \vec(PB_(1))=0; \end(saker)
\begin(cases) 0x+5y-5z=0, \\ 5\sqrt(3)x+5y+5z=0; \end(saker)
\begin(cases)y=z, \\ x=\frac(-y-z)(\sqrt(3)). \end(saker) La oss ta y=1; z=1; x=\frac(-2)(\sqrt(3)),
\vec(n_(1))=\venstre \( \frac(-2)(\sqrt(3)); 1;1 \høyre \). La \vec(n_(2))=\(x; y; z\) være vinkelrett på planet C_(1)B_(1)B.
La oss finne det ved å løse systemet
\begin(cases) \vec(n_(2)) \perp \vec(CC_(1)), \\ \vec(n_(2)) \perp \vec(CB). \end(saker)
\vec(CC_(1))=\(0;0;10\), \vec(CB)=\(5\sqrt(3); 5; 0\).
\begin(cases) \vec(n_(2)) \cdot \vec(CC_(1))=0, \\ \vec(n_(2)) \cdot \vec(CB)=0; \end(saker)
\begin(cases)y=z, \\ x=\frac(-y-z)(\sqrt(3)). \end(saker) \begin(cases) 0x+0y+10z=0, \\ 5\sqrt(3)x+5y+0z=0; \end(saker) \begin(cases)z=0, \\ y=-\sqrt(3)x. \end(saker)
x=1; y=-\sqrt(3); z=0, \vec(n_(2))=\(1; -\sqrt(3);0\). La oss finne cosinus til ønsket vinkel \beta (it
lik modul cosinus av vinkelen mellom \vec(n_(1)) og \vec(n_(2)) ). \cos \beta= \frac(|\vec(n_(1)) \cdot \vec(n_(2))|)(|\vec(n_(1))| \cdot |\vec(n_(2))|)= \frac(\venstre |-\dfrac(2)(\sqrt(3))\cdot 1+1 \cdot (-\sqrt(3))+1 \cdot 0 \right |)(\sqrt(\dfrac( 4)(3)+1+1) \cdot \sqrt(1+3+0))=
\frac(\dfrac(5)(\sqrt(3)))(2\sqrt(\dfrac(10)(3)))= \frac(\sqrt(10))(4).
Svare
\cos \beta =\frac(\sqrt(10))(4),
Kilde: «Matematikk. Forberedelse til Unified State Exam 2017. Profilnivå." Ed. F. F. Lysenko, S. Yu.
\beta=\arccos\frac(\sqrt(10))(4). \arccos\frac(\sqrt(10))(4) ABCD er en firkant og

sideflater
- like rektangler. Siden snittplanet går gjennom punktene M og D parallelt med diagonalen AC, så for å konstruere det i planet A_(1)AC gjennom punktet M tegner vi et segment MN parallelt med AC. Vi får AC \parallell (MDN) basert på parallelliteten til linjen og planet. Planet MDN skjærer de parallelle planene A_(1)AD og B_(1)BC, deretter etter egenskap
parallelle plan
, skjæringslinjene for flatene A_(1)ADD_(1) og B_(1)BCC_(1) med MDN-planet er parallelle.
b) La oss finne vinkelen mellom snittplanet og grunnplanet. La snittplanet skjære grunnplanet langs en rett linje p som går gjennom punkt D. AC \parallell MN, derfor AC \parallell p (hvis et plan passerer gjennom en linje parallelt med et annet plan og skjærer dette planet, så er skjæringslinjen til planene parallell med denne linjen). BD \perp AC som diagonalene til et kvadrat, som betyr BD \perp p.
BD er projeksjonen av ED på planet ABC, deretter ved teoremet om tre perpendikulære ED \perp p, derfor er \angle EDB den lineære vinkelen til den dihedrale vinkelen mellom seksjonsplanet og grunnplanet.
Angi typen firsidet DMEN. MD \parallel EN, lik ME \parallel DN, som betyr at DMEN er et parallellogram, og siden MD=DN (rettvinklet MAD og NCD er like på to ben: AD=DC som sidene av kvadratet, AM=CN som avstandene mellom parallelle linjer AC og MN), derfor er DMEN en rombe. Derfor er F midtpunktet til MN. Etter betingelse AM:MA_(1)=2:3, da
AM=\frac(2)(5)AA_(1)=\frac(2)(5) \cdot 5\sqrt(6)=2\sqrt(6). AMNC er et rektangel, F er midten av MN, O er midten av AC. betyr, FO\parallell MA, FO\perp AC,
FO=MA=2\sqrt(6). Å vite at diagonalen til et kvadrat er a\sqrt(2), hvor a er siden av firkanten, får vi BD=4\sqrt(2).
OD=\frac(1)(2)BD=\frac(1)(2) \cdot 4\sqrt(2)=2\sqrt(2). I en rettvinklet trekant FOD\enspace tg \angle FDO=\frac(FO)(OD)=\frac(2\sqrt(6))(2\sqrt(2))=\sqrt(3).
Derfor er \angle FDO=60^\circ.
\(\blacktriangleright\) Dihedral vinkel er en vinkel som dannes av to halvplan og en rett linje \(a\), som er deres felles grense. \(\blacktriangleright\) For å finne vinkelen mellom planene \(\xi\) og \(\pi\) , må du finne den lineære vinkelen (og krydret eller direkte
) dihedral vinkel dannet av planene \(\xi\) og \(\pi\): Trinn 1: la \(\xi\cap\pi=a\) (skjæringslinjen mellom flyene). I planet \(\xi\) noterer vi vilkårlig poeng
\(F\) og utfør \(FA\perp a\) ;
Trinn 2: utfør \(FG\perp \pi\) ;
Trinn 3: i henhold til TTP (\(FG\) – vinkelrett, \(FA\) – skrå, \(AG\) – projeksjon) har vi: \(AG\perp a\) ;
Trinn 4: Vinkelen \(\angle FAG\) kalles den lineære vinkelen til den dihedrale vinkelen som dannes av planene \(\xi\) og \(\pi\) .
Merk at trekanten \(AG\) er rettvinklet. Merk også at planet \(AFG\) konstruert på denne måten er vinkelrett på begge planene \(\xi\) og \(\pi\) . Derfor kan vi si det annerledes:\(\xi\) og \(\pi\) er vinkelen mellom to kryssende linjer \(c\in \xi\) og \(b\in\pi\) som danner et plan vinkelrett på og \(\xi\ ), og \(\pi\) .
Oppgave 1 #2875
Oppgavenivå: Vanskeligere enn Unified State-eksamenen
Dana firkantet pyramide, som alle kanter er like, og basen er en firkant. Finn \(6\cos \alpha\) , hvor \(\alpha\) er vinkelen mellom de tilstøtende sideflatene.
La \(SABCD\) – denne pyramiden(\(S\) er et toppunkt) hvis kanter er lik \(a\) . Følgelig er alle sideflater like likesidede trekanter. La oss finne vinkelen mellom flatene \(SAD\) og \(SCD\) .

La oss gjøre \(CH\perp SD\) . Fordi \(\triangle SAD=\triangle SCD\), da vil \(AH\) også være høyden på \(\triangle SAD\) . Derfor, per definisjon, er \(\angle AHC=\alpha\) den lineære vinkelen til den dihedrale vinkelen mellom flatene \(SAD\) og \(SCD\) .
Siden grunnflaten er en firkant, så \(AC=a\sqrt2\) . Merk også at \(CH=AH\) er høyden likesidet trekant med siden \(a\) , derfor \(CH=AH=\frac(\sqrt3)2a\) .
Deretter, ved cosinussetningen fra \(\triangle AHC\): \[\cos \alpha=\dfrac(CH^2+AH^2-AC^2)(2CH\cdot AH)=-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\]
Svar: -2
Oppgave 2 #2876
Oppgavenivå: Vanskeligere enn Unified State-eksamenen
Planene \(\pi_1\) og \(\pi_2\) skjærer hverandre i en vinkel hvis cosinus er lik \(0,2\). Planene \(\pi_2\) og \(\pi_3\) skjærer hverandre i rette vinkler, og skjæringslinjen for planene \(\pi_1\) og \(\pi_2\) er parallell med skjæringslinjen til planene \(\pi_2\) og \(\ pi_3\) . Finn sinusen til vinkelen mellom planene \(\pi_1\) og \(\pi_3\) .
La skjæringslinjen for \(\pi_1\) og \(\pi_2\) være en rett linje \(a\), skjæringslinjen til \(\pi_2\) og \(\pi_3\) være en rett linje linje \(b\), og skjæringslinjen \(\pi_3\) og \(\pi_1\) – rett linje \(c\) . Siden \(a\parallell b\) , så \(c\parallell a\parallell b\) (ifølge teoremet fra delen av den teoretiske referansen "Geometri i rommet" \(\høyrepil\) "Introduksjon til stereometri, parallellisme").

La oss merke punktene \(A\i a, B\i b\) slik at \(AB\perp a, AB\perp b\) (dette er mulig siden \(a\parallell b\) ). La oss merke \(C\in c\) slik at \(BC\perp c\) , derfor \(BC\perp b\) . Deretter \(AC\perp c\) og \(AC\perp a\) .
Faktisk, siden \(AB\perp b, BC\perp b\) , så er \(b\) vinkelrett på planet \(ABC\) . Siden \(c\parallell a\parallell b\), så er linjene \(a\) og \(c\) også vinkelrett på planet \(ABC\), og derfor til enhver linje fra dette planet, spesielt , linjen \ (AC\) .
Det følger av det \(\angle BAC=\angle (\pi_1, \pi_2)\), \(\angle ABC=\angle (\pi_2, \pi_3)=90^\circ\), \(\angle BCA=\angle (\pi_3, \pi_1)\). Det viser seg at \(\triangel ABC\) er rektangulær, som betyr \[\sin \angle BCA=\cos \angle BAC=0.2.\]
Svar: 0,2
Oppgave 3 #2877
Oppgavenivå: Vanskeligere enn Unified State-eksamenen
Gitt rette linjer \(a, b, c\) som krysser i ett punkt, og vinkelen mellom to av dem er lik \(60^\circ\) . Finn \(\cos^(-1)\alpha\) , hvor \(\alpha\) er vinkelen mellom planet dannet av linjer \(a\) og \(c\) og planet dannet av linjer \( b\) og \(c\) . Gi svaret i grader.
La linjene krysse i punktet \(O\) . Siden vinkelen mellom to av dem er lik \(60^\sirkel\), kan ikke alle de tre rette linjene ligge i samme plan. La oss markere punktet \(A\) på linjen \(a\) og tegne \(AB\perp b\) og \(AC\perp c\) . Da \(\triangle AOB=\triangle AOC\) som rektangulær langs hypotenusen og spiss vinkel. Derfor, \(OB=OC\) og \(AB=AC\) .
La oss gjøre \(AH\perp (BOC)\) . Så ved teoremet om tre perpendikulære \(HC\perp c\) , \(HB\perp b\) . Siden \(AB=AC\) , da \(\triangle AHB=\triangle AHC\) som rektangulær langs hypotenusen og benet. Derfor, \(HB=HC\) . Dette betyr at \(OH\) er halveringslinjen til vinkelen \(BOC\) (siden punktet \(H\) er like langt fra sidene av vinkelen).

Legg merke til at vi på denne måten også konstruerte den lineære vinkelen til den dihedriske vinkelen dannet av planet dannet av linjene \(a\) og \(c\) og planet dannet av linjene \(b\) og \(c \) . Dette er vinkelen \(ACH\) .
La oss finne denne vinkelen. Siden vi valgte punktet \(A\) vilkårlig, la oss velge det slik at \(OA=2\) . Så i rektangulær \(\triangle AOC\): \[\sin 60^\circ=\dfrac(AC)(OA) \quad\Rightarrow\quad AC=\sqrt3 \quad\Rightarrow\quad OC=\sqrt(OA^2-AC^2)=1.\ ] Siden \(OH\) er en halveringslinje, så \(\angle HOC=30^\circ\) , derfor i en rektangulær \(\triangle HOC\) : \[\mathrm(tg)\,30^\circ=\dfrac(HC)(OC)\quad\Rightarrow\quad HC=\dfrac1(\sqrt3).\] Så fra den rektangulære \(\triangle ACH\) : \[\cos\angle \alpha=\cos\angle ACH=\dfrac(HC)(AC)=\dfrac13 \quad\Rightarrow\quad \cos^(-1)\alpha=3.\]
Svar: 3
Oppgave 4 #2910
Oppgavenivå: Vanskeligere enn Unified State-eksamenen
Planene \(\pi_1\) og \(\pi_2\) skjærer hverandre langs den rette linjen \(l\) som punktene \(M\) og \(N\) ligger på. Segmentene \(MA\) og \(MB\) er vinkelrett på den rette linjen \(l\) og ligger i henholdsvis planene \(\pi_1\) og \(\pi_2\), og \(MN = 15 \) , \(AN = 39\) , \(BN = 17\) , \(AB = 40\) . Finn \(3\cos\alpha\) , hvor \(\alpha\) er vinkelen mellom planene \(\pi_1\) og \(\pi_2\) .

Trekanten \(AMN\) er rettvinklet, \(AN^2 = AM^2 + MN^2\), hvorfra \ Trekanten \(BMN\) er rettvinklet, \(BN^2 = BM^2 + MN^2\), hvorfra \Vi skriver cosinussetningen for trekanten \(AMB\): \ Da \ Siden vinkelen \(\alpha\) mellom planene er en spiss vinkel, og \(\angle AMB\) viste seg å være stump, så er \(\cos\alpha=\dfrac5(12)\) . Da \
Svar: 1,25
Oppgave 5 #2911
Oppgavenivå: Vanskeligere enn Unified State-eksamenen
\(ABCDA_1B_1C_1D_1\) er et parallellepiped, \(ABCD\) er et kvadrat med siden \(a\), punktet \(M\) er bunnen av perpendikulæren droppet fra punktet \(A_1\) til planet \ ((ABCD)\) , i tillegg er \(M\) skjæringspunktet mellom diagonalene til kvadratet \(ABCD\) . Det er kjent at \(A_1M = \dfrac(\sqrt(3))(2)a\). Finn vinkelen mellom planene \((ABCD)\) og \((AA_1B_1B)\) . Gi svaret i grader.
La oss konstruere \(MN\) vinkelrett på \(AB\) som vist i figuren.

Siden \(ABCD\) er et kvadrat med siden \(a\) og \(MN\perp AB\) og \(BC\perp AB\) , så \(MN\parallell BC\) . Siden \(M\) er skjæringspunktet mellom diagonalene til kvadratet, så er \(M\) midten av \(AC\), derfor er \(MN\) midtlinjen og \(MN =\frac12BC= \frac(1)(2)a\).
\(MN\) er projeksjonen av \(A_1N\) på planet \((ABCD)\), og \(MN\) er vinkelrett på \(AB\), deretter, ved teoremet om tre perpendikulære, \ (A_1N\) er vinkelrett på \(AB \) og vinkelen mellom planene \((ABCD)\) og \((AA_1B_1B)\) er \(\vinkel A_1NM\) .
\[\mathrm(tg)\, \angle A_1NM = \dfrac(A_1M)(NM) = \dfrac(\frac(\sqrt(3))(2)a)(\frac(1)(2)a) = \sqrt(3)\qquad\Rightarrow\qquad\angle A_1NM = 60^(\circ)\]
Svar: 60
Oppgave 6 #1854
Oppgavenivå: Vanskeligere enn Unified State-eksamenen
I en firkant \(ABCD\) : \(O\) – skjæringspunktet mellom diagonalene; \(S\) – ligger ikke i kvadratets plan, \(SO \perp ABC\) . Finn vinkelen mellom planene \(ASD\) og \(ABC\) hvis \(SO = 5\) og \(AB = 10\) .

Rettvinklede trekanter \(\triangle SAO\) og \(\triangle SDO\) er like i to sider og vinkelen mellom dem (\(SO \perp ABC\) \(\Høyrepil\) \(\angle SOA = \angle SOD = 90^\circ\); \(AO = DO\) , fordi \(O\) – skjæringspunktet mellom diagonalene til kvadratet, \(SO\) – felles side) \(\Høyrepil\) \(AS = SD\) \(\Høyrepil\) \(\triangle ASD\) – likebenet. Punktet \(K\) er midten av \(AD\), så er \(SK\) høyden i trekanten \(\triangel ASD\), og \(OK\) er høyden i trekanten \( AOD\) \(\ Høyrepil\) plan \(SOK\) er vinkelrett på plan \(ASD\) og \(ABC\) \(\Høyrepil\) \(\vinkel SKO\) – lineær vinkel lik ønsket dihedral vinkel.

I \(\triangle SKO\) : \(OK = \frac(1)(2)\cdot AB = \frac(1)(2)\cdot 10 = 5 = SO\)\(\Høyrepil\) \(\trekant SOK\) – likebenet rettvinklet trekant \(\Høyrepil\) \(\vinkel SKO = 45^\sirkel\) .
Svar: 45
Oppgave 7 #1855
Oppgavenivå: Vanskeligere enn Unified State-eksamenen
I en firkant \(ABCD\) : \(O\) – skjæringspunktet mellom diagonalene; \(S\) – ligger ikke i kvadratets plan, \(SO \perp ABC\) . Finn vinkelen mellom planene \(ASD\) og \(BSC\) hvis \(SO = 5\) og \(AB = 10\) .
Rette trekanter \(\triangle SAO\) , \(\triangle SDO\) , \(\triangle SOB\) og \(\triangle SOC\) er like i to sider og vinkelen mellom dem (\(SO \perp ABC \) \(\Høyrepil\) \(\angle SOA = \angle SOD = \angle SOB = \angle SOC = 90^\circ\); \(AO = OD = OB = OC\), fordi \(O\) – skjæringspunktet mellom diagonalene til kvadratet, \(SO\) – felles side) \(\Høyrepil\) \(AS = DS = BS = CS\) \(\Høyrepil\) \( \triangle ASD\) og \(\triangle BSC\) er likebente. Punktet \(K\) er midten av \(AD\), så er \(SK\) høyden i trekanten \(\triangel ASD\), og \(OK\) er høyden i trekanten \( AOD\) \(\ Høyrepil\) plan \(SOK\) er vinkelrett på planet \(ASD\) . Punkt \(L\) er midten av \(BC\), så er \(SL\) høyden i trekanten \(\triangel BSC\), og \(OL\) er høyden i trekanten \( BOC\) \(\ Høyrepil\) planet \(SOL\) (aka planet \(SOK\)) er vinkelrett på planet \(BSC\) . Dermed får vi at \(\angle KSL\) er en lineær vinkel lik ønsket dihedral vinkel.

\(KL = KO + OL = 2\cdot OL = AB = 10\)\(\Høyrepil\) \(OL = 5\) ; \(SK = SL\) – like høyder likebente trekanter, som kan bli funnet ved hjelp av Pythagoras teorem: \(SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50\). Det kan merkes \(SK^2 + SL^2 = 50 + 50 = 100 = KL^2\)\(\Høyrepil\) for en trekant \(\triangel KSL\) den inverse Pythagoras teorem har \(\Høyrepil\) \(\trekant KSL\) – rettvinklet trekant \(\Høyrepil\) \(\vinkel KSL = 90 ^\ circ\) .
Svar: 90
Å forberede studentene til å ta Unified State-eksamen i matematikk, begynner som regel med å gjenta grunnleggende formler, inkludert de som lar deg bestemme vinkelen mellom flyene. Til tross for at denne delen av geometri er dekket i tilstrekkelig detalj innenfor skolepensum, må mange nyutdannede gjenta grunnleggende materiale. Ved å forstå hvordan de finner vinkelen mellom flyene, vil elever på videregående skole raskt kunne beregne det riktige svaret når de løser et problem og regne med å få anstendige poengsum på resultatene av å bestå den enhetlige statenseksamenen.
Hovednyanser
For å sikre at spørsmålet om hvordan du finner en dihedral vinkel ikke forårsaker vanskeligheter, anbefaler vi å følge en løsningsalgoritme som vil hjelpe deg med å takle Unified State Examination-oppgaver.
Først må du bestemme den rette linjen langs hvilken flyene krysser hverandre.
Deretter må du velge et punkt på denne linjen og tegne to perpendikulære til det.
Neste trinn- å finne trigonometrisk funksjon dihedral vinkel dannet av perpendikulære. Den mest praktiske måten å gjøre dette på er ved hjelp av den resulterende trekanten, som vinkelen er en del av.
Svaret vil være verdien av vinkelen eller dens trigonometriske funksjon.
Å forberede seg til eksamensprøven med Shkolkovo er nøkkelen til din suksess
I timene dagen før bestått Unified State-eksamenen Mange skoleelever står overfor problemet med å finne definisjoner og formler som lar dem beregne vinkelen mellom 2 plan. Skolebok Den er ikke alltid tilgjengelig når du trenger den. Og å finne nødvendige formler og eksempler på riktig bruk, inkludert for å finne vinkelen mellom flyene på Internett, noe som noen ganger krever mye tid.
Den matematiske portalen "Shkolkovo" tilbyr ny tilnærmingå forberede seg til statseksamen. Klasser på nettsiden vår vil hjelpe elevene å identifisere de vanskeligste delene for seg selv og fylle hull i kunnskap.
Vi har forberedt og tydelig presentert alt nødvendig materiale. Grunnleggende definisjoner og formler er presentert i delen "Teoretisk informasjon".
For å bedre forstå materialet, foreslår vi også at du øver på de riktige øvelsene. Stort utvalg av oppgaver varierende grad kompleksitet, for eksempel, presenteres i "Katalog"-delen. Alle oppgaver inneholder en detaljert algoritme for å finne riktig svar. Listen over øvelser på nettsiden blir kontinuerlig supplert og oppdatert.
Mens de øver på å løse problemer som krever å finne vinkelen mellom to plan, har elevene muligheten til å lagre enhver oppgave på nettet som "Favoritter." Takket være dette vil de kunne vende tilbake til ham nødvendig mengde tid og diskutere fremdriften av sin beslutning med skolelærer eller en veileder.
