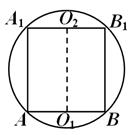
Ќе одговориме усно! Дали е вистина дека може да се опише сфера околу која било триаголна пирамида? Дали е можно да се опише сфера околу која било четириаголна пирамида? Какви својства мора да има пирамидата за да опише сфера околу неа? Пирамида е впишана во сфера, чиј страничен раб е нормален на основата. Како да се најде центарот на сферата? Сфера е опишана во близина на правилна пирамида. Како се наоѓа неговиот центар во однос на елементите на пирамидата?
Слајд 17од презентацијата „Проблеми по геометрија“ 11 одд. Големината на архивата со презентацијата е 1032 KB.Геометрија 11 одделение
резиме на други презентации„Концепт на централна симетрија“ - Мапирање на просторот на себе. Централна симетрија. Фигурата се нарекува симетрична. Централната симетрија е движење. Движење на просторот. Точките М и М1 се нарекуваат симетрични. Имотот. Движења. Се запознавме со движењата на авионот. Задача. Централната симетрија е посебен случај на ротација.
„Проблеми за пресметување на плоштината на триаголник“ - Иван Нивен. Решавање на еден проблем. Мото на лекцијата. Лични цели. Најдете ја областа на фигурата. Математички диктат. Методи за наоѓање плоштина на триаголник. Изберете изјава. Минута за физичко образование. Пресметајте ја плоштината на сликата. Областа на фигурата. Проверка на напредокот. Плоштад.
„Задачи во стереометрија“ - Најдете го квадратот на растојанието помеѓу темињата. Задачи. Дијаметар на оловната топка. Волумен на топката и неговите делови. Најдете го аголот на полиедарот. Најдете го волуменот на пирамидата. Најди ја ординатата на точката А. Кружен сектор. Најдете го волуменот V на цилиндерот. Најдете ја површината на полиедарот. Најдете ја областа на трапезоидот. Обем.
„Пресметајте го волуменот на телото на ротација“ - Сфера. Цилиндар и конус. Конус. Цилиндрите се насекаде околу нас. Том V на конус. Коцка Дефиниција за конус. Видови тела на ротација. Топка. Томови на тела на револуцијата. Слика. Најдете ја јачината на звукот. Цилиндричен сад. Дефиниција за цилиндар. радиуси. Цилиндар. Волумен на конус.
„Волумени и површини на тела на револуција“ - Предлагање и тестирање хипотези. Сумирајте го знаењето. Волумени и површини на тела на ротација. Идентификувајте ја геометриската форма. Формулирање на проблемот. Проблем. Примери од практични активности. Зошто резервоарот за термометар се загрева побрзо? Чајникот во форма на топка има најмала површина. Томови.
„Тела на ротација околу нас“ - Тела на ротација околу нас. Индустриска опрема. Најдете тела на ротација. Шумски конус смрека. Кривата кула во Италија. Во вселената. Куќата на Мелников. Конус. Тркалезни кули. Историја на тркалезната зграда. Космички тела.
Комбинации на полиедри и тркалезни тела
Поими за сфера и топка.
Сферае фигура која се состои од множество од сите точки во просторот, од кои растојанието од секоја до дадена точка O е еднакво на даден позитивен број r. Точката О се нарекува центарсфера, а отсечка што поврзува точка со која било точка на сферата е нејзина радиус. Сите радиуси на сферата имаат должина r. Бројот r се нарекува радиус на сферата.
Сферата го дели множеството од сите точки во просторот што не ѝ припаѓаат на две подмножества: внатрешенИ надворешенповршина во однос на сферата. Внатрешниот регион ги вклучува оние точки во просторот, од кои растојанието од секоја до центарот е помало од радиусот, а надворешниот регион ги вклучува тие точки, од кои растојанието од секоја до центарот е поголемо од радиусот.
Топкае фигура која се состои од збир на сите точки во просторот, од кои растојанието од секоја до дадена точка O не е поголемо од даден позитивен број r. Точката О се нарекува центартопка, а бројот r е негов радиус. Се нарекува сфера со центар O со радиус r површинаили границата на топката. Сите точки на топката што не припаѓаат на нејзината површина се нарекуваат внатрешни точки на топката или точки што лежат во внатрешноста на топката. Така, топката е фигура која се состои од обединување на сите точки на сферата (површината на топката) и множеството на сите внатрешни точки во однос на оваа сфера.
Тангентата рамнина на површината на топката се нарекува тангентна рамнинадо топката. Рамнината е тангента на топката ако и само ако минува низ точка на површината на топката нормална на радиусот нацртан до оваа точка. Забележете исто така дека низ секоја точка на површината на топката поминува една и само една рамнина тангента на топката.
Сфера ограничена на полиедар.
Дефиниција.Сферата се нарекува опишан околу полиедарот, ако сите темиња на полиедарот лежат на сферата.
Теорема 1.Може да се опише сфера околу која било триаголна пирамида.
Множеството точки подеднакво оддалечени од темињата на основата на пирамидата е нормално извлечено од центарот на опишаната кружница во близина на основата (HMT во просторот подеднакво оддалечен од темињата на даден многуаголник постои ако може да се опише круг околу ова многуаголник, и има нормална поставена на рамнината на овој многуаголник низ центарот на опишаната кружница). Центарот на кружниот круг е точката на пресек на нормалните симетрали на основата на пирамидата.
За да го пронајдете центарот на ограничената сфера, нацртајте рамнина низ точката М - средината на страничниот раб АД. Оваа рамнина ќе ја пресече нормалната (наведена порано) во точката S. По конструкција SA=SB=SC, а исто така и од фактот дека триаголникот ASD е рамнокрак (исто така по конструкција) произлегува дека SA=SD. Според тоа, растојанијата од сите темиња на пирамидата до точката S се еднакви, а ова растојание е еднакво на радиусот на опишаната сфера во близина на пирамидата ABCD (SA=SB=SC=SD=R).
Пример 1
. Најдете го радиусот на сфера ограничена на правилен тетраедар. 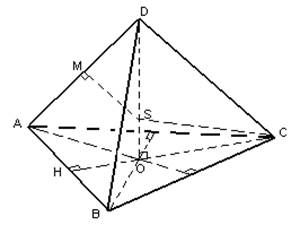
Размислете за триаголник SOC. Ќе биде правоаголен со прав агол O (по конструкција, OD ќе биде висината на пирамидата).
![]() , бидејќи О е точката на пресек на медијаните.
, бидејќи О е точката на пресек на медијаните.
![]() , каде DO е висината на пирамидата.
, каде DO е висината на пирамидата.
Потоа според Питагоровата теорема следува дека ![]() или
или
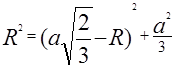
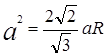
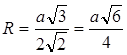
Одговор: Радиусот на сфера ограничена на правилен тетраедар е еднаков на
Теорема 2. Ако може да се опише круг околу основата на пирамидата, тогаш може да се опише сфера околу пирамидата.
Веќе разгледавме посебен случај. Во општиот случај, доказот е сличен.
Теорема 3 . Невозможно е да се опише сфера во близина на навалена призма; во близина на права призма можете да опишете сфера, ако во близина на основата на призмата можете да опишете круг.
1) Прво да го разгледаме случајот кога призмата е наклонета (да земеме за пример триаголна призма). Точката на еднаква оддалеченост од точките A, B и C ќе биде на правата линија OS 1, која е нормална на рамнината на триаголникот ABC, а основата на нормалната е на пресечната точка на бисекторските перпендикулари нацртани на страните на триаголникот ABC .
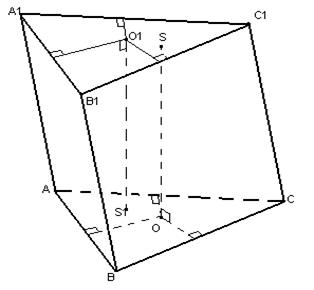
Слично на тоа, точките на еднаква оддалеченост од точките A 1, B 1, C 1 лежат на нормалната на рамнината на триаголникот A 1 B 1 C 1 – O 1 S. Бидејќи призмата е наклонета, правата OS 1 и O 1 S ќе да бидат паралелни, но не и соодветни. И тоа значи дека тие нема да имаат заеднички точки, затоа: не постои точка таква што растојанието од кое до сите темиња на призмата е исто, што е слично на неможноста да се конструира сфера опишана околу наклонета призма.
2) Размислете за права призма, во близина на чија основа може да се опише круг. Точките O и O 1 се центри на ограничени кругови во близина на долната и горната основа, соодветно. Бидејќи призмата е права, правата линија OO 1 ќе биде нормална на рамнините на основата.
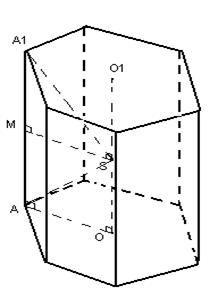
Тогаш рамнината што минува низ средината на страничните ребра ќе биде паралелна со рамнината на основата и ќе се сече OO 1 во точката S - средината на OO 1. Тогаш растојанието од сите темиња на призмата до количката S ќе биде исто (по конструкција), затоа, S е центарот на сферата опишана околу правилната призма.
Значи, ние сме убедени дека е невозможно да се опише сфера во близина на навалена призма, но во близина на права призма е можно ако може да се опише круг во близина на нејзината основа.
Теорема 4. Сфера може да се опише околу скратена пирамида ако и само ако може да се опишат кругови околу нејзините основи и правата линија што ги поврзува центрите на овие кругови е нормална на рамнините на базите..
Првиот услов значи дека перпендикуларите, кои се HMT, на базите што се еднакво оддалечени од темињата на многуаголниците ќе постојат, а вториот - дека тие се совпаѓаат, затоа, ќе има точка што ќе биде еднакво оддалечена од сите темиња на скратена пирамида.
XV ГРАДСКА ОТВОРЕНА КОНФЕРЕНЦИЈА НА СТУДЕНТИ
„ИНТЕЛЕКТУАЛЦИ НА XXI ВЕК“
Дел: МАТЕМАТИКА
Опишаната област на олимпијадите и обединетиот државен испит
Кијаева Ана Анатолевна
Оренбург – 2008 година
1.2 Опишан опсег
1.2.1 Основни својства и дефиниции
1.2.2 Комбинација на пирамида
1.2.3 Комбинација со призма
1.2.4 Комбинација со цилиндар
1.2.5 Комбинација со конус
2 Примери за задачи на Олимпијадата
2.1 Примери за задачи на Олимпијадата со пирамида
2.2 Примери за задачи на Олимпијадата со призма
2.3 Примери за задачи на Олимпијадата со цилиндар
2.4 Примери за задачи на Олимпијадата со конус
3.3 Примери на задачи за унифициран државен испит со цилиндар
3.4 Примери за задачи за унифициран државен испит со конус
Вовед
Оваа работа се изведува како дел од проектот за креирање математичка страница за ученици на веб-страницата на интернатот и ќе биде објавена во делот „Математички методи“.
Целработа - создавање референтна книга посветена на методот на решавање на геометриски проблеми со опишаната сфера на олимпијадите и обединетиот државен испит.
За да ја постигнеме оваа цел, требаше да го решиме следново задачи :
1) запознајте се со концептот на опишаната сфера;
2) проучување на карактеристиките на комбинации на опишаната сфера со пирамида, призма, цилиндар и конус;
3) меѓу геометриските проблеми, изберете ги оние што го содржат условот за присуство на опишана сфера;
4) го анализира, систематизира и класифицира собраниот материјал;
5) направи избор на проблеми за самостојно решавање;
6) да го претстави резултатот од истражувањето во форма на апстракт.
Во текот на истражувањето, дознавме дека проблемите со опишаната област доста често им се нудат на учениците на Единствениот државен испит, така што способноста за решавање проблеми од овој тип игра многу важна улога во успешното полагање на испитите. Исто така, проблемите со опишаната област често се среќаваат на математичките олимпијади на различни нивоа. Релевантни примери се дадени во нашата работа. Оваа тема е релевантни, бидејќи задачите од овој тип обично предизвикуваат тешкотии кај учениците.
Практично значење– Материјалите што ги подготвивме може да се користат за подготовка на ученици за олимпијади, обединет државен испит и последователни студии на универзитет.
1 Сфера и топка
1.1 Сфера и топка: основни поими и дефиниции
Сферае површина која се состои од сите точки во просторот лоцирани на дадено растојание од дадена точка.
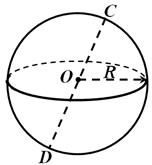
Оваа точка се нарекува центар на сферата(точка ЗАво Сл. 1), и ова растојание радиус на сферата. Секој сегмент што го поврзува центарот и која било точка на сферата се нарекува и радиус на сферата. Се вика отсечка што поврзува две точки на сфера и минува низ нејзиниот центар дијаметар на сфера(линиски сегмент DCво Сл. 1). Забележете дека сфера може да се добие со ротирање на полукруг околу неговиот дијаметар.
Топкасе нарекува тело ограничено со сфера. Центарот, радиусот и дијаметарот на сферата се нарекуваат и центар , радиусИ дијаметар на топката. Очигледно, топка со радиус Рцентриран во ЗАги содржи сите точки во просторот кои се наоѓаат од точката ЗАна растојание што не надминува Р(вклучувајќи точка ЗА), и не содржи други точки. Топканаречена и фигура на ротација на полукруг околу неговиот дијаметар. Сегмент на топка- дел од топката отсечен од него со некој авион. Секој дел од топката покрај рамнина е круг. Центарот на овој круг е основата на нормалната извлечена од центарот на топката на рамнината за сечење. Авионот што минува низ центарот на топката се нарекува дијаметрална рамнина.Пресекот на топката по дијаметралната рамнина се нарекува голем круг, а пресекот на сферата е голем круг. Сектор за топки -геометриско тело кое се добива со ротирање на кружен сектор со агол помал од 90° околу права линија која содржи еден од радиусите што го ограничува кружниот сектор. Сферичниот сектор се состои од сферичен сегмент и конус со заедничка основа.
Површина на сфера:
С = 4π Р 2 ,
Каде Р- радиус на топката, С- областа на сферата.
Волумен на сфера
Каде В– волумен на топката
Волумен на секторот на топката
,В – волумен на сферичниот сегмент.
Сегментална површина
- висина на сегментот, сегментна површинаРадиус на основата на сегментот
Сферична површина на сегмент на топка
- површина на сферичната површина на сферичниот сегмент.Во вселената, за топка и авион, можни се три случаи:
1) Ако растојанието од центарот на топката до рамнината е поголемо од радиусот на топката, тогаш топката и рамнината немаат заеднички точки.
2) Ако растојанието од центарот на топката до рамнината е еднакво на радиусот на топката, тогаш рамнината има само една заедничка точка со топката и сферата што ја ограничува.
3) Ако растојанието од центарот на топката до рамнината е помало од радиусот на топката, тогаш пресекот на топката со рамнината е круг. Центарот на овој круг е проекцијата на центарот на топката на дадена рамнина. Пресекот на рамнината со сферата е обемот на наведениот круг.
1.2 Опишана сфера
1.2.1 Дефиниции и својства
Сферата се нарекува опишан околу полиедарот(а полиедарот е вклучени во сферата), ако сите темиња на полиедарот лежат на сферата.
Од дефиницијата на опишаната сфера произлегуваат два факти:
1) сите темиња на полиедар впишан во сфера се подеднакво оддалечени од одредена точка (од центарот на ограничената сфера);
2) секое лице на многуедар впишан во сфера е многуаголник впишан во одреден круг, токму во кругот што се добива во пресекот на сферата со рамнината на лицето; во овој случај, основата на перпендикуларите спуштени од центарот на ограничената сфера на рамнината на лицата се центри на кругови опкружени околу лицата.
Теорема 1 . Сфера може да се опише околу полиедар ако и само ако некој од следниве услови е исполнет:
а) круг може да се опише околу секое лице на полиедар, а оските на круговите опишани околу лицата на полиедарот се сечат во една точка;
б) рамнините нормални на рабовите на полиедарот и минуваат низ нивните средни точки се сечат во една точка;
в) има една точка еднакво оддалечена од сите темиња на полиедарот.
Доказ.
Потреба.Нека се опише сфера околу полиедарот. Да докажеме дека условот а) е исполнет. Навистина, бидејќи рамнината на даденото лице на полиедарот пресекува сфера долж круг, тогаш темињата на лицето што припаѓаат на сферата и рамнината на лицето припаѓаат на линијата на нивното пресекување - кругот. Бидејќи центарот на сферата е подеднакво оддалечен од сите темиња на даденото лице, тој лежи на нормално на ова лице исцртано низ центарот на кругот опкружен околу лицето.
Адекватност.Нека условот а) е задоволен. Да докажеме дека може да се опише сфера околу полиедар. Всушност, бидејќи заедничката точка на перпендикуларите на лицата исцртани низ центрите на круговите опкружени околу лицата е подеднакво оддалечена од сите темиња на полиедарот, околу полиедарот е опишана сфера со центар во оваа точка.
Условот а) во овој случај е еквивалентен на условите б) и в).
Ако сферата е оградена околу полиедар, тогаш: а) основата на нормалната спуштена од центарот на сферата на кое било лице е центар на кругот опфатен околу ова лице (како основата на висината на пирамидата со еднаква странични рабови - радиусите на сферата повлечени од нејзиниот центар до темињата на даденото лице); б) центарот на сферата оградена околу полиедарот може да се наоѓа внатре во полиедарот, на неговата површина (во центарот на кругот опкружен со лице, особено во средината на некој раб), надвор од полиедарот.
1.2.2 Ограничена сфера и пирамида
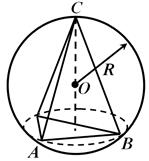
Теорема 2 . Сфера може да се опише околу пирамидата ако и само ако може да се опише круг околу нејзината основа.
Доказ.Нека се опише круг околу основата на пирамидата. Тогаш овој круг и точка надвор од рамнината на овој круг - врвот на пирамидата - дефинираат една сфера, која ќе биде опкружена околу пирамидата. И назад. Ако сферата е оградена околу пирамида, тогаш пресекот на сферата со рамнината на основата на пирамидата е круг опкружен околу основата.
Заклучок 1.Може да се опише сфера околу кој било тетраедар.
Заклучок 2.Околу секоја правилна пирамида може да се опише сфера чиј центар лежи на висината на пирамидата или нејзиното проширување.
Центарот на сферата опишан во близина на пирамидата може да биде:
· со врвот на пирамидата на едната страна од рамнината на нејзината основа - внатре во пирамидата, во рамнината на страничното лице (во центарот на кругот опишан околу ова лице), надвор од пирамидата;
· во рамнината на основата - во центарот на кругот опишан во близина на основата;
· со врвот на пирамидата на спротивните страни од рамнината на нејзината основа.
Теорема 3 . Ако страничните рабови на пирамидата се подеднакво наклонети кон рамнината на нејзината основа, тогаш може да се опише сфера околу пирамидата.
Доказ.Бидејќи страничните рабови се подеднакво наклонети кон рамнината на основата на пирамидата, може да се опише круг во близина на основата на пирамидата, а потоа може да се опише сфера во близина на пирамидата.
Оваа теорема може да се формулира поинаку: ако пирамидата има еднакви странични рабови, тогаш може да се опише сфера околу пирамидата.
Конверзна теорема не е вистина
Теорема 4. Ако топката е опишана во близина на пирамида, тогаш нејзиниот центар е пресечната точка на сите рамнини повлечени низ средните точки на рабовите на пирамидата нормални на овие рабови.
Доказ.Всушност, секоја точка еднакво оддалечена од две темиња на пирамидата во непосредна близина на едниот раб лежи во рамнина нацртана нормално на овој раб на пирамидата низ нејзината средина. Затоа, центарот на опишаната топка, што е подеднакво оддалечен од сите темиња на пирамидата, мора да се наоѓа во секоја од таквите рамнини, т.е. тоа е пресечната точка на сите овие рамнини. Кога прават цртеж, учениците често го поставуваат центарот на опишаната топка по случаен избор, без доволно добро да ја замислат дадената просторна конфигурација, а особено без да водат никакво размислување за положбата на овој центар. Во овој случај, по правило, центарот се става во внатрешноста на пирамидата. Во меѓувреме, центарот на опишаната топка може да лежи внатре, надвор или на површината на пирамидата (во зависност од специфичниот тип на пирамида).
Теорема 5 . Сфера може да се опише околу скратена пирамида ако и само ако некој од следниве услови е исполнет:
а) кругови се опишани во близина на основите на пирамидата, линијата на центрите на која е нормална на нивните рамнини;
б) сите странични рабови на пирамидата се подеднакво наклонети кон рамнината на една од основите;
в) сите странични рабови на пирамидата се еднакви еден на друг;
г) сите странични лица на пирамидата се рамнострани трапезоиди.
Доказ.Да претпоставиме дека круговите може да се опишат во близина на основите на дадена скратена пирамида, а рамнините на овие кругови се нормални на линијата на нивните центри. Тогаш, како што е познато, таквите два круга дефинираат една сфера, која ќе биде опкружена околу оваа пирамида.
Да претпоставиме, напротив, дека сфера е опишана околу дадена скратена пирамида. Тогаш деловите на сферата по рамнините на основите на пирамидата ќе бидат кругови опишани околу основите. Понатаму. Права линија нормална на рамнините на основите на пирамидата и минува низ центарот на сферата ќе помине низ центрите на круговите опишани околу основите.
Состојба а) е еквивалентно на условите б), в), г).
Последица.Може да се опише сфера околу секоја редовна скратена пирамида.
1.2.3 Ограничена сфера и призма
Теорема 6. Сферата може да се опише околу призмата ако и само ако призмата е права и може да се опише круг околу нејзината основа.
Доказ.
Потреба.Ако призмата е впишана во сфера, тогаш секое нејзино лице е впишано во круг - дел од сферата по рамнината на ова лице. Тоа значи дека во близина на основата на призмата може да се опише круг, а сите странични лица на призмата се како паралелограми впишани во круговите - правоаголници и затоа призмата е права.
Адекватност.Нека призмата е права и нека биде опишан круг околу нејзината основа. Тогаш круговите опкружени околу основите на призмата, чии рамнини се нормални на линијата на нивните центри, дефинираат една сфера, која ќе биде оградена околу призмата.
Последици:
а) сфера може да се опише околу која било правилна призма;
б) може да се опише сфера околу која било правоаголна триаголна призма;
в) може да се опише сфера околу кој било правоаголен паралелепипед;
Центарот на сферата опкружена со призмата е подеднакво оддалечен од рамнините на основите на призмата и може да се наоѓа внатре во призмата, на нејзиното странично лице (во центарот на кругот опишан за лицето), надвор од призмата.
1.2.4 Ограничена сфера и цилиндар
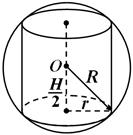
Сферата се нарекува опишано за цилиндерот, ако на него лежат круговите на основите на цилиндерот (сл. 4). Секогаш можете да опишете сфера околу цилиндар.
.1.2.5 Опишана сфера и конус
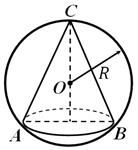
Сферата се нарекува опишан околу конусот, ако на него лежат темето и кругот на основата на конусот (сл. 5). Секогаш е можно да се опише сфера околу конус; неговиот радиус е еднаков на радиусот на кругот опишан околу аксијалниот пресек на конусот. Скратен конус се нарекува впишаниво топка ако нејзините основи се делови од површината на топката.
2 Примери за задачи на Олимпијадата
2.1 Примери за задачи на Олимпијадата со пирамида
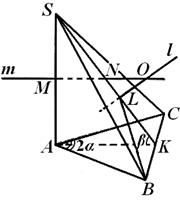
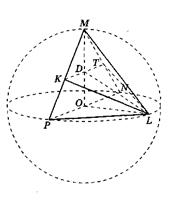
Пример 1. Во триаголна пирамида С ABC раб BC е еднаков на a, AB=AC, раб С И нормално на основата на пирамидата ABC, диедралниот агол на работ С А е еднакво на 2α , а на работ BC е еднаков на β (сл. 6) . Најдете го радиусот на ограничената сфера.
Решение.Размислете за пирамида С ABC,што се дискутира во изјавата за проблемот. Од работ С.А.нормално на рамнината на основата, тогаш
VA С = CAS= 90°, а со тоа и аголот ВИЕе токму линеарниот агол на диедралниот агол на работ С.А.. Така, во основата на пирамидата лежи рамнокрак триаголник со агол од 2 α на врвот, а висината на пирамидата се совпаѓа со работ С А.Од проекциите на страничните ребра С.Б.И С СОна рамнината на основата се еднакви, тогаш самите овие рабови се еднакви. Затоа работ ВО С СО- рамнокрак триаголник, а неговата висина спуштена од темето С, паѓа во средината ДОребра Сонцето.Според теоремата за три нормални АК- висина на триаголникот ВИЕ.Од ова е јасно дека аголот С CA- линеарен агол на диедралниот агол на работ сонце,т.е.
С CA = β .Центарот на ограничената топка лежи на пресекот на линијата л, нормално на рамнината ВО С СОи минувајќи низ центарот на кругот опфатен околу триаголникот ВО С СО,со рамнина што минува низ средината на работ А Снормално на него. Директно ллежи во авион А С ДО:всушност, авион ВО С СОминува низ права линија сонце,нормално на рамнината А С ДОт.е. авиони ВО С СОИ А С ДОнормално; во исто време директно лнормално на рамнината ВО С СОи минува низ линијата на вкрстување на овие рамнини, така што лежи во рамнината А С ДО .
Значи, центарот на топката лежи во авионот А С ДО. Ајде да го однесеме овој авион на посебен цртеж. Центар за топка ЗАтогаш ќе лежи на пресекот на линијата ли директно м, нормално на А Си минува низ нејзината средина. Но, општо земено, може да се појават три можности: директни лИ Тсе сечат внатре или надвор од триаголникот А С ДОили на негова страна, и ќе треба да ги разгледаме сите овие можности (види Сл. 7, 8, 9). Подолу, во текот на пресметките, ќе покажеме дека две од нив всушност не се имплементирани. Ние сме заинтересирани за радиусот Рограничена топка, т.е. растојание од точка ЗА- точки на пресек на перпендикулари ТИ лна страните на аголот ДО С А- до точка С, темињата на овој агол. Прво, да најдеме SL- проекција на потребното растојание на страна С.К.тријаголник КАС. Бидејќи во триаголник АК Б(сл. 6) ја знаеме ногата VK=
Аи агол KAV = α,Тоа АК= А ctg α .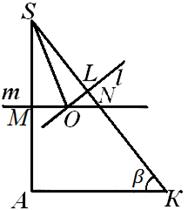
С.К. =
.Бидејќи Л- центар опишан за триаголникот ВО С СОкругови, тогаш Л.С. = Л ВО,а бидејќи од триаголникот VC Лго наоѓаме тоа ( С ДО- SL ) 2 + HF 2 = Б Л 2 , т.е.
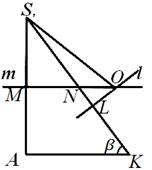
Напоменувајќи дека пресметките на сегментот SLво никој случај не зависеше од локацијата на центарот ЗАопишана топка, да се вратиме на Сл. 7, 8, 9. Да означиме со Нточка на пресек на правата мсо страната С ДО.Јасно е дека директно лИ Тсе вкрстуваат надвортријаголник CA С , Ако СН <SL(сл. 8); ако С N> SL , потоа посочете ЗАлежи во овој триаголник (сл. 7); конечно, ако СН = SL , потоа посочете ЗАлежи на страна С ДОовој триаголник (сл. 9). Дозволете ни да дознаеме која од овие одредби всушност се применува.
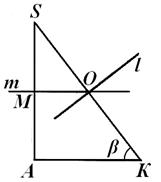
Бидејќи МН CA С , Тоа СН =
С ДО. Споредување на должините на отсечките СНИ SL, лесно можеме да го докажеме тоа за било кој а, αИ(од геометриски размислувања произлегува дека А> 0,0°<
< 90° и 0°< β < 90°). Следовательно, каковы бы ни были размеры А , α И β пирамиди С ABC,центар ЗАограничена топка секогаш лежи надвор од пирамидата. Ова пак значи дека рамната конфигурација што ја извадивме во авионот CA Сможе да ја има само формата прикажана на Слика 8; локациите прикажани на сл. 7 и 9 всушност не можат да се одржат. Гледајќи на Сл. 8, лесно можеме да покажеме дека = β , а со тоа и Л.О. = NL tg β = (SL -С N) tg β. Заменувајќи ги овде изразите добиени погоре за SLИ С Н, добиваме по очигледни пресметки:Л О =
А tg α грев β .Конечно, од правоаголен триаголник ЗА Л.С.ние најдовме
= .Како што можеме да видиме, пресметките во проблемот се покажаа едноставни - главната тешкотија на решението лежи во расудувањето што ја утврдува позицијата на центарот на ограничената топка.
Одговор: Р =
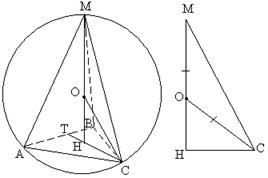
.Пример 2. Правилна триаголна пирамида со рамен агол на врвот е впишана во топка со радиус R. Најдете го волуменот на пирамидата, како и страничната површина на конусот опишана околу наведената пирамида .
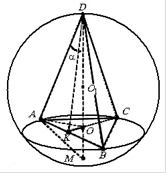
Решение.Нека биде страната на основата на пирамидата а, радиусот на основата на конусот опишан околу оваа пирамида е еднаков на р, Потоа
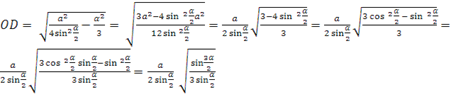 .
.
ДМ– дијаметар на топката. Потоа во делот на топката што минува низ дијаметарот ДМи период А, добиваме правоаголен триаголник АМД. Од метричките односи во правоаголен триаголник имаме
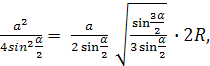 каде
каде Потоа ја наоѓаме областа на основата користејќи ја формулата:
.И од формулата
најдете го волуменот на пирамидата: .Работ АДпо дефиниција, ограничен конус е неговата генератрикс. Потоа ја наоѓаме страничната површина на ограничениот конус користејќи ја формулата Сстрана = р л :
.Одговор:
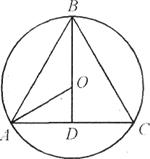
Пример 3. Во основата на пирамидата лежи квадрат со страна a. Висината на пирамидата минува низ средината на еден од рабовите на основата и е еднаква на
. Најдете го радиусот на сферата опкружена околу пирамидата.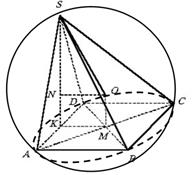
Решение.Типична грешка при решавање на овој проблем е изјавата дека центарот на опишаната сфера е на работ SBC(сл. 11). Во реалноста позицијата на поентата ЗАне е поврзан со работ SBC.
Поради еквидистанцата на точката ЗАод врвовите S, A, B, C, Dследи тоа OABCD- правилна четириаголна пирамида. Затоа, до работ А БЕ ЦЕ ДЕточка ЗАпроектирани до точка М– точка на пресек на дијагонали. Тријаголник А.С.Д.рамнокрак, потоа висината на пирамидата С.К.е средина на триаголникот А.С.Д. ,
. Од правоаголен триаголник С.А.К.ќе најдеме С.А. :Затоа триаголникот С.А.Д.– рамностран и OASD- правилна триаголна пирамида. Потоа посочете ЗАпроектиран до работ С.А.Д.до центарот на триаголникот С.А.Д.. Од тука
Од триаголник СИНнајдете го потребниот радиус ПА,
,Одговор:
.Пример 4. До топка со радиус Р испишана е правилна хексагонална скратена пирамида, во која рамнината на долната основа поминува низ центарот на топката, а страничниот раб прави агол од 60 со рамнината на основата.
. Одреди го волуменот на пирамидата.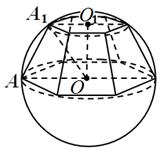
Решение.По услов,
ОАА 1 = 60 (слика 12); Средства, ЗА 1 ОП 1 = 30 и А 1 ЗА 1 = А 1 О = ,О.О. 1 = .Сдолна основа = 6
Конечно добиваме
.Одговор:
2.2 Примери за задачи на Олимпијадата со призма
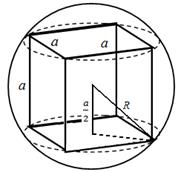
Пример 1. Во топка чиј волумен е еднаков на В , е впишана правоаголна триаголна призма. Основата на призмата е правоаголен триаголник со остар агол
, а неговото најголемо странично лице е квадрат. Најдете го волуменот на призмата.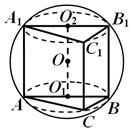
Решение.Прво, ја одредуваме положбата на центарот на топката во однос на призмата. Пресеците на топката по рамнините на основите на призмата се круговите во кои се впишани овие основи (сл. 13), а бидејќи основите на призмата се еднакви, круговите на пресеците се еднакви и подеднакво оддалечени од центарот на топката. Секој од центрите ЗА 1 и ЗА 2 се совпаѓа со средината на соодветната хипотенуза.
Од својствата на пресеците на топката со рамнина се знае дека нормалната извлечена од центарот на топката ЗАрамнината на кругот на попречниот пресек, поминува низ центарот на овој круг. Оттука, ЗА 1 ЗА
рамнина ABC.Директно ЗА 1 ЗАисто така поминува низ О 2 и нормално на рамнината. Така, центарот на топката лежи на лицето во средината на сегментот О 1 О. Сите странични лица на призмата се правоаголници, а лицето - најголемиот од нив (од AB -хипотенуза на триаголник А Сонцето). Ова лице по конвенција е квадрат. Пресекот на топката покрај рамнината на лицето е голем круг на топката, затоа радиусот на кругот е прикажан на сл. 14, еднаков на радиусот на топката Р . Забележете дека висината на призмата АА 1 = а 4 = . Сега останува само да се најде областа на основата:С А Б СО =
ние имаме AC = AB
, Средства,С А Б СО =
.Сега добиваме:
Внаграда.
.По услов,
Р 3 = В ,каде Р 3 =
, оттука,Внаграда.
Одговор: Внаграда.
Пример 2. Најдете го односот на површината и волуменот на сферата, соодветно, на површината и волуменот на впишаната коцка
Решение.Нека биде радиусот на топката Р , работ на коцката е еднаков на А;
Потоа Р 2 -
, каде a= .Да ги означиме волумените и површините на сфера и коцка, соодветно, со В 1 , В 2 , И С 1 , С 2 .
, В 2 = = , С 1 =4, С 2 = 6А 2 =8Р 2 , В 2 = , С 1 С 2 = .Одговор: В 1
В 2 = , С 1 С 2 = .2.3 Примери за задачи на Олимпијадата со цилиндар
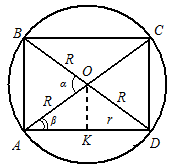
Пример. Најдете го односот на волуменот на сферата со волуменот на десниот кружен цилиндар впишан во оваа сфера, ако се знае дека помалиот агол помеѓу дијагоналите на аксијалниот пресек на цилиндерот е еднаков на
а дијаметарот на основата е поголем од висината на цилиндерот (сл. 18).Решение.Го знаеме волуменот на сферата
, и го наоѓаме волуменот на цилиндерот користејќи ја формулата, но затоаНека А БЕ ЦЕ ДЕ- аксијален пресек на цилиндерот (види слика 18). Бидејќи дијаметарот на основата е поголем од висината на цилиндерот, тогаш
- агол AOB.Од триаголник AVOпроизлегува дека висината на цилиндеротРадиус на основата на цилиндарот
. .Излегува дека
Ајде да ги замениме пронајдените податоци во формулата за волумен на цилиндар:
;Така,
Ајде да најдеме врска
Одговор:
2.4 Примери за задачи на Олимпијадата со конус
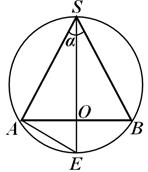
Пример 1. До топка со радиус Р впишан е кружен конус; аголот помеѓу генератриците на конусот во аксијалниот пресек е еднаков на α. Најдете ја висината што го формира радиусот на основата на конусот.
Решение.Пресекот на топката што минува низ оската на конусот е големиот круг на топката во кој
АБ С(сл. 19), каде А ВО- дијаметар на основата на конусот. Да ја продолжиме висината (оската) на конусот ПАдодека не ја пресече големата кружница во точката Еи размислете Е С А:во овој триаголник
С.Е. = 2Р ,
С AE = 90° И А С Е= .А С = 2Р
.Сега од
А ОСние најдовмеА ЗА = р = 2R
Одговори : SO= 2Р
А С = 2Р , А ЗА =.Пример 2. Односот на висината на конусот со радиусот на топката опкружена околу него е еднаков на к . Најдете го односот на волумените на овие тела. Дознајте на што к задачата има смисла.
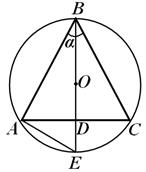
Решение.Да го разгледаме аксијалниот пресек на конусот (слика 20). Нека ч- висина на конусот, Р- радиус на сфера ограничена околу конус. Потоа, по услов,
=к, т.е. ч = kR .Да го изразиме радиусот росновата на конусот низ Р; имајќи ги предвид акордите ACИ БИДИ,добиваме:
ВО Д
Д Е = А Д Д СО(затоа што AD=DC ,- правоаголни, АД – висина падна од темето на прав агол).
(оттука, к < 2).
В w =
; В k ==Така,
Одговор:
Пример 3. Во скратен конус, радиусите на долната и горната основа се еднакви, соодветно р 1 И р 2 , а генератриксот на конусот е наклонет кон рамнината на долната основа под агол α (сл. 21). Најдете го радиусот на сферата во која е впишан дадениот скратен конус.
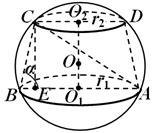
Решение.Во делот на топката што минува низ оската на скратениот конус, се добива голем круг од топката, во која е впишан трапез. ABC Д. Ајде да размислиме
А сонце,кој е впишан и во големиот круг на топката. Аголот во овој триаголник е познат СО Б.А. = α . Врз основа на синусната теорема, AC = 2Р. Така, да се утврди Рдоволно е да се најде AC.Да отфрлиме од поентата СОнормално SEна АБ.Очигледно,AE= р 1 + р 2 ,БИДИ = р 1 - р 2, а CE = ( р 1 - р 2 )
.Затоа, според Питагоровата теорема
= = = од каде Р = .
.
Одговор: Р
 .
.
3 Примери на задачи за унифициран државен испит
3.1 Примери на задачи за обединет државен испит со пирамида
Пример 1. Сегментот П Н , еднаков на 8, е дијаметарот на сферата. Поени М, Л легнете на сферата така што волуменот на пирамидата е P Н М Л најголемиот (сл. 22). Најдете ја плоштината на триаголникот К Л Т, каде K и T се средните точки на рабовите на PM и Н М соодветно.
Решение.Нека ЗАе центарот на сферата и Р- неговиот радиус. Затоа што Р Н = 2Р= 8 и точки МИ Ллегнете на сферата, тогаш ИЛИ = О Л = О Н = ОМ = Р = 4. Пресеци на сфера по рамнини Р LNИ РМ Н- радиус на кругот Р = 4, опишан за триаголници Р LNИ РМ Н , и
РМ Н = Р LN= 90°, како впишани агли врз основа на дијаметарот Р Н .Нека Н- висината на пирамидата, спуштена од врвот М, А ч- висина на триаголникот Р LN , се држи на страна Р Н . Од поентата Млежи на сферата, а рамнината Р LNго содржи центарот на сферата, тогаш Н
Р , и Н = Р , Ако MO Р NL . Исто така, од поентата Ллежи на сферата, тогаш ч Р , и ч = Р , Ако Л ЗА Р Н .Оттука за волуменот на пирамидата Р Н М Лние имаме
, .
Значи пирамидата Р Н М Лима најголем волумен ако триаголниците Р LNИ РМ Нправоаголни, рамнокраки со заедничка хипотенуза Р Н, лежејќи во меѓусебно нормални рамнини. Од триаголници Л ЗА Н , Л ИЛИ, Л ОМ, РОМ, Н ОМсе еднакви на две краци, потоа триаголниците Л М НИ Л Г-динточни со страна
NL =Стр Л = НА
=4Оттука произлегува дека медијаните Л ДОИ Л Товие триаголници се еднакви и
Л ДО =
= 2.Тријаголник ДО Л Трамнокрак и неговата висина LDе средина на правоаголен рамнокрак триаголник Л ОМ.Од тука
LD =
КТ- средна линија на триаголникот РМ На со тоа и КТ = 0,5Р Н =Р . Затоа, областа С ДО Л Т =
КТ LD = 4.Одговор: 4
.
Пример 2. Во правилна триаголна пирамида, страната на основата е 5, а страничните ребра се наклонети кон основата под агол од 60О. Најдете го радиусот на сферата опкружена околу пирамидата.
Решение.Нека ABCMнаведената пирамида (види слика 23) Центарот на опишаната сфера лежи на висината на пирамидата, бидејќи пирамидата е правилна.
Основата на висината на пирамидата е центарот на триаголникот ABC, односно точката на пресек на медијаните. Потоа:
ST =Сега разгледајте го триаголникот МНС.Еве го аголот МСНеднаква на 60°, како агол помеѓу страничниот раб ГОСПОЃИЦАи основата ABC. Катче NMSеднакво на 30
. MO=OSкако радиуси. Значи тоа е триаголник MOSрамнокрак. Како што знаете, во рамнокрак триаголник аглите на основата се еднакви. Оттука, OSM = Задолжително медицинско осигурување = 30, OSN = МСН - МЦО = 60 - 30= 30.Од правоаголен триаголник OSNда ја дефинираме хипотенузата ОСкористејќи ја врската на тригонометриските функции во правоаголен триаголник:
=Одговор: О.Ц. =
.3.2 Примери за КОРИСТЕТЕ задачи со призма
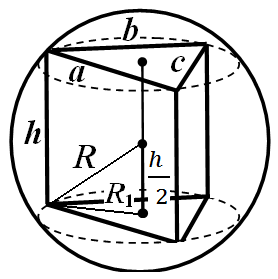
Пример 1. Основата на призмата е триаголник со страни а , б , в . Висина на призмата ч (Слика 25). Најдете го радиусот на ограничената сфера.
Решение.Бидејќи сферата е опкружена околу призмата, призмата е права, а страничниот раб е еднаков на неговата висина. Радиусот на кругот опишан околу основата на призмата се пресметува со формулата
Одговор:
Пример 2. Радиус на топка Р . Правилна n-гонална призма со висина 2 е впишана во сфера. ч (Слика 26). Најдете ја страната на основата на призмата.
Решение.Нека ДО– центарот на ограничената сфера. Ние имаме: К.Б. = Р , добро = ч. Нека ОМ
АБ, ПотоаО.Б. =
(од триаголник ОКБ).
Од триаголник ОМБние најдовме
а = 2М.Б. = 2О.Б.
.Значи, а =
Одговор: а =
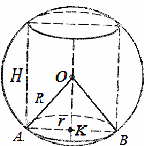
3.3 Примери на задачи за унифициран државен испит со цилиндар
Пример 1. Висината на кружниот цилиндар е 10 поголема од радиусот на основата, а вкупната површина е 144
. Најдете го радиусот на ограничената сфера.Решение.Радиус на ограничена сфера
(Сл. 27).Површина на цилиндерот
, 144,Ајде да го поедноставиме овој израз:
.Добиваме квадратна равенка
Ајде да ги најдеме корените на оваа равенка
, не е погоден бидејќи е негативен. ВисинаАјде да го најдеме радиусот на ограничената сфера:
.Одговор:
.Пример 2. Прав кружен цилиндар е впишан во топка (сл. 28). Колку пати волуменот на сферата е поголем од волуменот на цилиндерот ако се знае дека односот на радиусот на сферата и радиусот на основата на цилиндерот е половина поголем од односот на површината на сфера на страничната површина на цилиндерот.
Решение.Однос на волуменот на сферата со волуменот на впишан цилиндар
.
По услов се знае дека
; –рамностран
Да го најдеме односот на волумените на сфера и впишан цилиндар
Одговор: 16:9.
3.4 Примери за задачи за унифициран државен испит со конус
Пример 1. Дијаметарот на основата на конусот е 6 m, генератриксот е наклонет кон рамнината на основата под агол од 60 ° (слика 29). Најдете ја областа на сферата ограничена околу конусот.
Решение.Нека СО -врвот на конусот ЗА -центарот на неговата основа, ДИА -аксијален пресек на конусот. Бидејќи генератриксот на конусот е наклонет кон рамнината на основата под агол од 60° и COе висината на конусот, потоа правата линија AB -директна проекција САна рамнината на основата на конусот. Оттука,
ТАКСИеднаков на аголот помеѓу генератриксот на конусот и површината на неговата основа. Затоа CAB= 60° и рамнокрак триаголник ABC -точно. Го следи тоаCA = AB = BC= 6м.
Дозволете ни да ја најдеме положбата на центарот на сферата ограничена околу конусот. По дефиниција за таква сфера, обемот на основата на конусот е дел од ограничената сфера и темето на конусот лежи на оваа сфера. Според својството на дијаметарот на сферата што минува низ центарот на кој било дел од неа, правата линија COнормална на рамнината на основата на конусот и затоа центарот ЗА 1 од ограничената сфера лежи на права линија CO.Следи дека центарот ЗА 1 од сфера оградена околу конус е центарот на кругот опфатен околу неговиот аксијален дел.
Во правоаголен триаголник
ABC Р = О 1 В =
Ајде да ја најдеме областа на сферата:
(м2).Одговор: 48
m 2.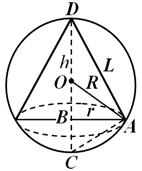
Пример 2. До топка со радиус Р = Впишан конус висок 6 cm ч (Сл. 30). Изразете ја волуменот и страничната површина на конусот во функција на аргументот ч .
Решение.Ние имаме:
Каде р - радиус на основата, Л- формирање на конус.
со оглед на тоа р = VA -висината спуштена од темето на правиот агол до хипотенузата имаме: и . Или р 2 иСега добиваме:
Одговор:
Пример 3. Во топката е впишан конус, чија генератрикс е еднаква на дијаметарот на основата (сл. 31). Најдете го односот на површината на конусот со површината на топката.
Решение.Дозволете ни да го прикажеме аксијалниот дел на конусот, кој ќе помине низ центарот на топката. Бидејќи дијаметарот на основата на конусот е еднаков на генератриксот, во делот добиваме правилен триаголник впишан во круг (сл. 31). Нека радиусот на топката е еднаков на Р : Потоа
АБ =Р
, А Д =Да ја означиме вкупната површина на конусот со С 1, а површината на топката низ С 2. Ние имаме
каде С 1: С 2 = 9:16.
Одговор: С 1: С 2 = 9:16.
Заклучок
Во текот на истражувањето, дознавме дека проблемите со опишаната област доста често им се нудат на учениците на Единствениот државен испит, така што способноста за решавање проблеми од овој тип игра многу важна улога во успешното полагање на испитите. Исто така, проблемите со опишаната област често се среќаваат на математичките олимпијади на различни нивоа. Релевантни примери се дадени во нашата работа. Во оваа фаза, се ограничивме на разгледување на проблеми кои вклучуваат комбинација на ограничена сфера со пирамида, призма, цилиндар и конус. Избрани задачи за самостојна работа. Во процесот на извршување на работата ги користевме следните методи: работа со научна и научна литература, собирање информации на Интернет, анализа, систематизација, класификација и обработка на компјутер. Резултатите моментално се претставени во апстрактна форма. Во иднина се планира дополнување на работата со нови задачи.
Библиографија
1. Абрамович М.И., Стародубцев М.Т. Математика (геометрија и тригонометриски функции). Учебник за подготвителни катедри на универзитетите - М: Виша школа, 1976. - 304 стр.
2. Воитович Ф.С. Комбинации на геометриски тела: (впишани и ограничени сфери): Книга за ученици. – Минск: Народна Асвета, 1992. – 160 стр.
3. Говоров В.М., Дибов П.Т., Мирошин Н.В. И други.Список на натпреварувачки задачи по математика (со методолошки упатства и решенија): учебник. – второ издание – М: Наука, 1986. – 384 стр.
4. Денишчева Л.О., Безрукова Г.К., Бојченко Е.М. и други.Унифициран државен испит, математика, контролни мерни материјали - М: Образование 2005. - 80 стр.
5. Денишчева Л.О., Глазков Ју.А., Красњанскаја К.А. и други.Унифициран државен испит. Математика. Едукативни и обучувачки материјали за подготовка на студенти / FIPI - M: Intellect-Center, 2008. - 240 стр.
6. Дорофеев Г.В., Потапов К.М., Розов Н.К. Прирачник по математика за оние кои влегуваат на универзитетите - М: Наука 1972. - 528 стр.
7. Егерев В.К., Заицев В.В., Кордемски Б.А. и други 2500 задачи по математика со решенија за оние кои влегуваат во универзитетите: - М: ДОО Издавачка куќа „ОНИКС 21 век“: ДОО Издавачка куќа „Свет и образование“, 2002. - 912 стр.
8. Звавич Л.И., Рјазановски А.Р. Геометрија во табели - M: Bustard 2007. - 128 стр.
9. Климин С.В., Стрункина Т.В., Пантелеева Е.И. и други.Унифициран државен испит, тест задачи - М: Образование 2002. - 24 стр.
10. Моденов В.П., Дорофеев Г.В., Новоселов С.И. и други Прирачник за математика - М: Издавачка куќа на Московскиот универзитет, 1972. - 404 стр.
11. Шувалова Е.З., Каплун В.И. Геометрија: учебник за подготвителни одделенија на универзитетите - М: Виша школа, 1980. - 265 стр.
12. http://kvant.mirror1.mccme.ru/pdf/2000/06/kv0600solut.pdf
13. http://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D1%80%D1%82%D0%B0%D0%BB:%D0%9D%D0%B0%D1% 83%D0%BA%D0%B0
14. http://rgp.nm.ru/geometriia/praktika11/zadatcha119.html
Апликација. Задачи за самостојно решение
1. Во пирамидата FABCрабовите ABFИ ABCнормално, Б.Ф. :Ф.А. = 15:11. Тангента на аголот помеѓу права линија п.н.е.и авион ABFеднакво на 5. Точка Мизбрани на работ п.н.е.Значи Б М :М В = 4:11. Точка Тлежи на права линија Ф.А.и подеднакво оддалечени од точките МИ ВО.Центар на сфера оградена околу пирамида FABC , лежи на работ АБ, површината на оваа сфера е 36
. Најдете го волуменот на пирамидата АСМТ. (Одговор: 6)2. Основата на пирамидата FABCDе правоаголник А БЕ ЦЕ ДЕ . Рамнина А.Ф.Ц.нормално на рамнината ABC , тангента на аголот FACеднакви
, тангента на аголот помеѓу правата п.н.е.и авион А.Ф.Ц.еднаква на . Точка Млежи на работ п.н.е. , В.М =п.н.е. . Точка Ллежи на права линија Ф.А.и подеднакво оддалечени од точките МИ В . Волумен на пирамидата Л ВО Д Ме еднакво на 72. Центар на сферата оградена околу пирамидата FABCD , лежи на рамнината на неговата основа. Најдете го радиусот на оваа сфера. (Одговор: 5)3. Во близина на редовната пирамида FABCопишува сфера чиј центар лежи во рамнината на основата ABCпирамиди. Точка Млежи на работ АБЗначи А М :М Б= 1:3. Точка Тлежи на права линија Ф.А.и на еднакво растојание од точката МИ ВО. Волумен на пирамидата ТВСМеднакви
. Најдете го радиусот на сферата опкружена со пирамидата FABC . (Одговор: )4. Линиски сегмент АБ– дијаметар на сферата. Поени СО, Д А БЕ ЦЕ ДЕнајголем. Најдете го косинусот на аголот помеѓу правите ЦМИ АБ,Ако М– средината на реброто БД . (Одговор:
)5. Линиски сегмент Р Н , еднаков на 8, е дијаметарот на сферата. Точка М, Ллежат на сферата така што волуменот на пирамидата Р Н М Лнајголем. Најдете ја плоштината на триаголникот KLT , Каде КИ Т – средината на ребрата РМИ Н Мсоодветно. (Одговор: 4
)6. Дадена е сфера со радиус 6. Рамниот пресек на сферата е круг со дијаметар КТ. Рамнината на пресекот се отстранува од центарот на сферата на растојание од 5. Точка Рсе избира на сферата, а точката Л РК Л Тнајголем. Најдете го аголот помеѓу правата линија Л.М.и авион ПТК , Ако Мсредно ребро РК. (Одговор: 30
)7. Преку центарот ЗА Фсе избира на сферата, а точките А , Б , В , Д – FABCDнајголем. Поени М, Т, Л – средината на ребрата ФБ , ЦДИ АДсоодветно. Плоштина на триаголник MLTеднакво на 64
. Најдете го радиусот на сферата. (Одговор: 2)8. Преку центарот ЗАод оваа сфера е направен пресек. Точка Фсе избира на сферата, а точките А , Б , В , Д – последователно на кругот на попречниот пресек така што волуменот на пирамидата FABCDнајголем. Најдете го синусот на аголот помеѓу правата AMи авион Б.Ф.Д. . (Одговор:
)9. Дадена е сфера со радиус 10. Рамниот пресек на оваа сфера е круг со дијаметар АБ.Рамнината на пресекот се отстранува од центарот на сферата на растојание од 8. Точка Дсе избира на сферата, а точката СО– на обемот на напречниот пресек така што волуменот на пирамидата ABC Днајголем. Најдете ја областа на лицето ACD .(Одговор: 27
)10. Основата на пирамидата е правоаголник. Рамнината е нормална на рамнината ABC, тангента на аголот помеѓу правата Сонцетои авион FACеднакво на 2. Точка Млежи на работ СонцетоИ МВ =
Точка Ллежи на права линија Ф.А.и подеднакво оддалечени од точките МИ СО. Центар на сфера оградена околу пирамида Ф.А. ВО ЦД, лежи во рамнината на основата на пирамидата, радиусот на оваа сфера е 4. Најдете го волуменот на пирамидата Л.А. ГОСПОЃИЦА. (Одговор: 48)11. Во топка, радиус 2
ABCA 1 ВО 1 СО 1 . Директно AC 1 Форми со авион АББ (Одговор: 288)12. Правилна триаголна призма е впишана во сфера ABCA 1 ВО 1 СО 1, чиј волумен е 4,5. Директно VA 1 форми со авион VSS 1 агол45
. Најдете ја површината на сферата. (Одговор: 11)13. Во топка со радиус
е впишана правилна триаголна призма ABCA 1 ВО 1 СО 1 . Директно АБ 1 форми со авион ACC 1 агол 45. Најдете ја волуменот на призмата. (Одговор: 36)14. Пресметајте ги рабовите на правилна триаголна призма, знаејќи го радиусот Рограничена сфера и агол на наклон α радиусот на оваа топка повлечен до темето на призмата, до страничното лице што го содржи ова теме. (Одговор: 2
)15. До топка со радиус Рвпишан е десен кружен конус. Најдете ја страничната површина на конусот ако неговата висина е ч . (Одговор:
16. Конус е впишан во сфера. Областа на аксијалниот пресек на конусот е еднаква на С. Аголот помеѓу неговата висина и генераторот е еднаков на α . Најдете го волуменот на сферата. (Одговор:
)17. Одредете ја страничната површина на конусот, знаејќи ја должината на радиусот Рсферата опкружена околу неа и аголот α, под кој од центарот на топката е видлива генератриксот на конусот. (Одговор:
18. Најдете го односот на вкупната површина на десниот конус впишан во топката со површината на оваа топка, ако аголот на врвот на аксијалниот пресек на конусот е еднаков на α И
. (Одговор:19. Конус е впишан во топка така што неговата висина е поделена со центарот на топката во среден и екстремен однос. Најдете го аголот на врвот на аксијалниот пресек на конусот. Определи колку пати волуменот на сферата е поголем од волуменот на конусот. (Одговор:
; 4 пати )Пример 2.Во правилна триаголна пирамида, страната на основата е 5, а страничните ребра се наклонети кон основата под агол од 60О. Најдете го радиусот на сферата опкружена околу пирамидата.
Решение.Нека ABCMнаведената пирамида (види слика 23) Центарот на опишаната сфера лежи на висината на пирамидата, бидејќи пирамидата е правилна.
Основата на висината на пирамидата е центарот на триаголникот ABC, односно точката на пресек на медијаните. Потоа:
CH=
ST =
![]() CH=
CH=
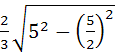 =
=
=
=
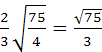 .
.
Сега разгледајте го триаголникот МНС.Еве го аголот МСНеднаква на 60°, како агол помеѓу страничниот раб ГОСПОЃИЦАи основата ABC. Катче NMSеднакви 30. MO=OSкако радиуси. Значи тоа е триаголник MOSрамнокрак. Како што знаете, во рамнокрак триаголник аглите на основата се еднакви. Оттука,
OSM = Задолжително медицинско осигурување = 30, OSN = МСН - МЦО = 60 - 30= 30.
Од правоаголен триаголник OSNда ја дефинираме хипотенузата ОСкористејќи ја врската на тригонометриските функции во правоаголен триаголник:
ОС= = .
Одговор: О.Ц.= .
3.2 Примери за КОРИСТЕТЕ задачи со призма
Пример 1.Основата на призмата е триаголник со страниа, б, в. Висина на призматач(Слика 25). Најдете го радиусот на ограничената сфера.
Решение.Бидејќи сферата е опкружена околу призмата, призмата е права, а страничниот раб е еднаков на неговата висина. Радиусот на кругот опишан околу основата на призмата се пресметува со формулата
Одговор:
![]()

Пример 2.Радиус на топкаР. Правилна n-гонална призма со висина 2 е впишана во топка.ч(Слика 26). Најдете ја страната на основата на призмата.
Решение.Нека ДО– центарот на ограничената сфера. Ние имаме: К.Б.= Р, добро= ч. Нека ОМАБ, Потоа
О.Б.=
(од триаголник ОКБ).
Од триаголник ОМБние најдовме
а= 2М.Б.= 2О.Б..
Значи, а=
![]() .
.
Одговор: а= .
3.3 Примери на задачи за унифициран државен испит со цилиндар
Пример 1.Висината на кружниот цилиндар е 10 поголема од радиусот на основата, а вкупната површина е 144. Најдете го радиусот на ограничената сфера.
Решение.Радиус на ограничена сфера
Површина на цилиндерот
Ајде да го поедноставиме овој израз:
Добиваме квадратна равенка
![]()
Ајде да ги најдеме корените на оваа равенка
Коренот не е погоден бидејќи е негативен. Висина
Ајде да го најдеме радиусот на ограничената сфера:
Одговор: .
Пример 2.Прав кружен цилиндар е впишан во топка (сл. 28). Колку пати волуменот на сферата е поголем од волуменот на цилиндерот ако се знае дека односот на радиусот на сферата и радиусот на основата на цилиндерот е половина поголем од односот на површината на сфера на страничната површина на цилиндерот.

Решение.Однос на волуменот на сферата со волуменот на впишан цилиндар
По услов се знае дека
рамностран
Да го најдеме односот на волумените на сфера и впишан цилиндар
![]() .
.
Одговор: 16:9.
3.4 Примери за задачи за унифициран државен испит со конус
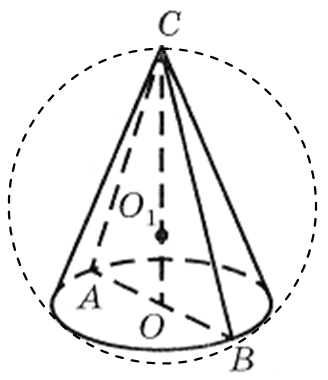
Пример 1.Дијаметарот на основата на конусот е 6 m, генератриксот е наклонет кон рамнината на основата под агол од 60 ° (слика 29). Најдете ја областа на сферата ограничена околу конусот.
Решение.Нека СО -врвот на конусот ЗА -центарот на неговата основа, ДИА -аксијален пресек на конусот. Бидејќи генератриксот на конусот е наклонет кон рамнината на основата под агол од 60° и COе висината на конусот, потоа правата линија AB -директна проекција САна рамнината на основата на конусот. Оттука, ТАКСИеднаков на аголот помеѓу генератриксот на конусот и површината на неговата основа. Затоа CAB= 60° и рамнокрак триаголник ABC -точно. Го следи тоа
CA = AB = BC= 6м.
Дозволете ни да ја најдеме положбата на центарот на сферата ограничена околу конусот. По дефиниција за таква сфера, обемот на основата на конусот е дел од ограничената сфера и темето на конусот лежи на оваа сфера. Според својството на дијаметарот на сферата што минува низ центарот на кој било дел од неа, правата линија COнормална на рамнината на основата на конусот и затоа центарот ЗА 1 од ограничената сфера лежи на права линија CO.Следи дека центарот ЗА 1 сфера ограничена околу конус е центарот на кругот опфатен околу неговиот аксијален дел.
Во правоаголен триаголник
ABCР=
О 1 В=
![]() (м)
(м)
Пример 3.Во топката е впишан конус, чија генератрикс е еднаква на дијаметарот на основата (сл. 31). Најдете го односот на површината на конусот со површината на топката.
Решение.Дозволете ни да го прикажеме аксијалниот дел на конусот, кој ќе помине низ центарот на топката. Бидејќи дијаметарот на основата на конусот е еднаков на генератриксот, во делот добиваме правилен триаголник впишан во круг (сл. 31). Нека биде радиусот на топката Р: Потоа
АБ= Р , АД =
Да ја означиме вкупната површина на конусот со С 1, а површината на топката низ С 2. Ние имаме
каде С 1: С 2 = 9:16.
Одговор:С 1: С 2 = 9:16.
Заклучок
Во текот на истражувањето, дознавме дека проблемите со опишаната област доста често им се нудат на учениците на Единствениот државен испит, така што способноста за решавање проблеми од овој тип игра многу важна улога во успешното полагање на испитите. Исто така, проблемите со опишаната област често се среќаваат на математичките олимпијади на различни нивоа. Релевантни примери се дадени во нашата работа. Во оваа фаза, се ограничивме на разгледување на проблеми кои вклучуваат комбинација на ограничена сфера со пирамида, призма, цилиндар и конус. Избрани задачи за самостојна работа. Во процесот на извршување на работата ги користевме следните методи: работа со научна и научна литература, собирање информации на Интернет, анализа, систематизација, класификација и обработка на компјутер. Резултатите моментално се претставени во апстрактна форма. Во иднина се планира дополнување на работата со нови задачи.
Библиографија
Абрамович М.И., Стародубцев М.Т. Математика (геометрија и тригонометриски функции). Учебник за подготвителни катедри на универзитетите - М: Виша школа, 1976. - 304 стр.
Воитович Ф.С. Комбинации на геометриски тела: (впишани и ограничени сфери): Книга за ученици. – Минск: Народна Асвета, 1992. – 160 стр.
Говоров В.М., Дибов П.Т., Мирошин Н.В. И други.Список на натпреварувачки задачи по математика (со методолошки упатства и решенија): учебник. – второ издание – М: Наука, 1986. – 384 стр.
Денишчева Л.О., Безрукова Г.К., Бојченко Е.М. и други.Унифициран државен испит, математика, контролни мерни материјали - М: Образование 2005. - 80 стр.
Денишчева Л.О., Глазков Ју.А., Красњанскаја К.А. и други.Унифициран државен испит. Математика. Едукативни и обучувачки материјали за подготовка на студенти / FIPI - M: Intellect-Center, 2008. - 240 стр.
Дорофеев Г.В., Потапов К.М., Розов Н.К. Прирачник по математика за оние кои влегуваат на универзитетите - М: Наука 1972. - 528 стр.
Егерев В.К., Заицев В.В., Кордемски Б.А. и други 2500 задачи по математика со решенија за оние кои влегуваат во универзитетите: - М: ДОО Издавачка куќа „ОНИКС 21 век“: ДОО Издавачка куќа „Свет и образование“, 2002. - 912 стр.
Звавич Л.И., Рјазановски А.Р. Геометрија во табели - M: Bustard 2007. - 128 стр.
Климин С.В., Стрункина Т.В., Пантелеева Е.И. и други.Унифициран државен испит, тест задачи - М: Образование 2002. - 24 стр.
Моденов В.П., Дорофеев Г.В., Новоселов С.И. и други Прирачник за математика - М: Издавачка куќа на Московскиот универзитет, 1972. - 404 стр.
Шувалова Е.З., Каплун В.И. Геометрија: учебник за подготвителни одделенија на универзитетите - М: Виша школа, 1980. - 265 стр.
http :// квантна. огледало1. mccme. ru/ pdf/2000/06/ kv0600 растворувач. pdf
http :// ru. википедија. org/ вики/% Д0%9 Ф% Д0% БИДИ% Д1%80% Д1%82% Д0% Б0% Д0% ББ:% Д0%9 Д% Д0% Б0% Д1%83% Д0% Б.А.% Д0% Б0
rgp . nm. ru/ геометрија/ практично11/ задатча119. html
Апликација. Задачи за самостојно решение
Темата „Различни проблеми за полиедар, цилиндар, конус и топка“ е една од најтешките во предметот геометрија од 11-то одделение. Пред да решат геометриски проблеми, тие обично ги проучуваат релевантните делови од теоријата на кои се повикуваат при решавање проблеми. Во учебникот на С. Атанасјан и други на оваа тема (стр. 138) може да се најдат само дефиниции за полиедар опишан околу сфера, полиедар впишан во сфера, сфера впишана во полиедар и сфера опишана околу полиедар. Методолошките препораки за овој учебник (видете ја книгата „Изучување на геометријата во 10-11 одделение“ од С.М. Сахакјан и В.Ф. Бутузов, стр. 159) кажуваат кои комбинации на тела се земаат предвид при решавање на проблемите бр. 629-646 и се привлекува внимание на фактот дека „при решавање на одреден проблем, пред сè, неопходно е да се осигура дека учениците добро ги разбираат релативните позиции на телата наведени во состојбата“. Следното е решение за проблемите бр. 638(а) и бр.640.
Имајќи го предвид сето горенаведено, и фактот дека најтешките проблеми за учениците е комбинацијата на топка со други тела, неопходно е да се систематизираат релевантните теоретски принципи и да се соопштат на студентите.
Дефиниции.
1. Топката се нарекува впишана во полиедар, а полиедар опишан околу топката ако површината на топката ги допира сите лица на полиедарот.
2. Топката се нарекува ограничена околу полиедарот, а полиедарот впишан во топката, ако површината на топката минува низ сите темиња на многуедарот.
3. Се вели дека топката е впишана во цилиндар, скратен конус (конус), а цилиндар, скратен конус (конус) се вели дека е впишан околу топката ако површината на топката ги допира основите (основата) и сите генератриките на цилиндерот, скратен конус (конус).
(Од оваа дефиниција произлегува дека големиот круг на топката може да биде впишан во кој било аксијален дел од овие тела).
4. Се вели дека топката е ограничена околу цилиндар, скратен конус (конус), ако круговите на основите (основниот круг и врвот) припаѓаат на површината на топката.
(Од оваа дефиниција произлегува дека околу секој аксијален дел од овие тела може да се опише кругот на поголем круг на топката).
Општи белешки за положбата на центарот на топката.
1. Центарот на топката впишана во полиедар лежи на точката на пресек на симетралните рамнини на сите диедрални агли на полиедарот. Се наоѓа само внатре во полиедарот.
2. Центарот на топката опкружена со полиедар лежи на пресечната точка на рамнините нормални на сите рабови на полиедарот и минуваат низ нивните средни точки. Може да се наоѓа внатре, на површината или надвор од полиедарот.
Комбинација на сфера и призма.
1. Топка впишана во права призма.
Теорема 1. Сферата може да се впише во права призма ако и само ако може да се впише круг на основата на призмата, а висината на призмата е еднаква на дијаметарот на овој круг.
Заклучок 1.Центарот на сферата впишана во десната призма лежи на средината на висината на призмата што минува низ центарот на кругот впишан во основата.
Заклучок 2.Топката, особено, може да се впише во прави линии: триаголна, правилна, четириаголна (во која збировите на спротивните страни на основата се еднакви една со друга) под услов H = 2r, каде што H е висината на призма, r е радиусот на кругот впишан во основата.
2. Сфера ограничена на призма.
Теорема 2. Сферата може да се опише околу призмата ако и само ако призмата е права и може да се опише круг околу нејзината основа.
Заклучок 1. Центарот на сферата опкружена со права призма лежи на средината на висината на призмата извлечена низ центарот на кругот опфатен околу основата.
Заклучок 2.Топката, особено, може да се опише: во близина на правоаголна триаголна призма, во близина на правилна призма, во близина на правоаголен паралелепипед, во близина на правоаголна четириаголна призма, во која збирот на спротивните агли на основата е еднаков на 180 степени.
Од учебникот на Л.С. Атанасјан може да се предложат задачи бр.
Комбинација на топка со пирамида.
1. Топка опишана во близина на пирамида.
Теорема 3. Топката може да се опише околу пирамидата ако и само ако може да се опише круг околу нејзината основа.
Заклучок 1.Центарот на сферата опкружена со пирамида лежи на точката на пресек на права линија нормална на основата на пирамидата што минува низ центарот на кругот опкружен околу оваа основа и рамнина нормална на кој било страничен раб повлечен низ средината на овој раб.
Заклучок 2.Ако страничните рабови на пирамидата се еднакви еден со друг (или подеднакво наклонети кон рамнината на основата), тогаш околу таквата пирамида може да се опише топка. Центарот на оваа топка во овој случај лежи на точката на пресек на висината на пирамидата (или нејзиното продолжување) со оската на симетрија на страничниот раб што лежи во рамнината страничен раб и висина.
Заклучок 3.Топката, особено, може да се опише: во близина на триаголна пирамида, во близина на правилна пирамида, во близина на четириаголна пирамида во која збирот на спротивните агли е 180 степени.
2. Топка впишана во пирамида.
Теорема 4. Ако страничните лица на пирамидата се подеднакво наклонети кон основата, тогаш може да се впише топка во таква пирамида.
Заклучок 1.Центарот на топката впишана во пирамида чии странични лица се подеднакво наклонети кон основата лежи во точката на пресек на висината на пирамидата со симетралата на линеарниот агол на кој било диедрален агол во основата на пирамидата, страната од кои е висината на страничното лице извлечено од врвот на пирамидата.
Заклучок 2.Можете да вклопите топка во обична пирамида.
Од учебникот на Л.С. Атанасјан може да се предложат проблеми бр.
Комбинација на топка со скратена пирамида.
1. Топка оградена околу правилна скратена пирамида.
Теорема 5. Може да се опише сфера околу секоја редовна скратена пирамида. (Овој услов е доволен, но не е неопходен)
2. Топка впишана во редовна скратена пирамида.
Теорема 6. Топката може да се впише во правилна скратена пирамида ако и само ако апотемата на пирамидата е еднаква на збирот на апотемите на основите.
Има само еден проблем за комбинацијата на топка со скратена пирамида во учебникот на Л.С. Атанасјан (бр. 636).
Комбинација на топка со тркалезни тела.
Теорема 7. Сфера може да се опише околу цилиндар, скратен конус (прав кружен) или конус.
Теорема 8. Топката може да се впише во (прав кружен) цилиндар ако и само ако цилиндерот е рамностран.
Теорема 9. Може да ставите топка во кој било конус (право кружен).
Теорема 10. Топката може да се впише во скратен конус (прав кружен) ако и само ако нејзиниот генератор е еднаков на збирот на радиусите на основите.
Од учебникот на Л.С.Атанасјан, може да се предложат проблеми бр.
За поуспешно проучување на материјалот на оваа тема, неопходно е да се вклучат усни задачи во лекциите:
1. Работ на коцката е еднаков на a. Најдете ги радиусите на топчињата: впишани во коцката и ограничени околу неа. (r = a/2, R = a3).
2. Дали е можно да се опише сфера (топка) околу: а) коцка; б) правоаголен паралелепипед; в) наклонет паралелепипед со правоаголник во основата; г) праволиниски паралелепипед; д) наклонет паралелепипед? (а) да; б) да; в) не; г) не; г) не)
3. Дали е вистина дека може да се опише сфера околу која било триаголна пирамида? (Да)
4. Дали е можно да се опише сфера околу која било четириаголна пирамида? (Не, не во близина на која било четириаголна пирамида)
5. Какви својства мора да има пирамидата за да опише сфера околу неа? (Во неговата основа треба да има многуаголник околу кој може да се опише круг)
6. Пирамида е впишана во сфера, чиј страничен раб е нормален на основата. Како да се најде центарот на сферата? (Центарот на сферата е пресечна точка на две геометриски места на точки во просторот. Првата е нормална поставена на рамнината на основата на пирамидата, низ центарот на кругот опкружен околу неа. Вториот е рамнина нормално на даден страничен раб и повлечен низ неговата средина)
7. Под кои услови можете да опишете сфера околу призма, во чија основа е трапез? (Прво, призмата мора да биде права, а второ, трапезот мора да биде рамнокрак за да може да се опише круг околу него)
8. Кои услови треба да ги исполнува една призма за да може да се опише сфера околу неа? (Призмата мора да биде права, а нејзината основа мора да биде многуаголник околу кој може да се опише круг)
9. Сфера е опишана околу триаголна призма, чиј центар лежи надвор од призмата. Кој триаголник е основата на призмата? (тап триаголник)
10. Дали е можно да се опише сфера околу навалена призма? (Не, не можеш)
11. Под кој услов ќе се наоѓа центарот на сфера опфатена со правоаголна триаголна призма на една од страничните страни на призмата? (Основата е правоаголен триаголник)
12. Основата на пирамидата е рамнокрак трапез Ортогоналната проекција на врвот на пирамидата на рамнината на основата е точка која се наоѓа надвор од трапезот. Дали е можно да се опише сфера околу таков трапез? (Да, можеш. Тоа што ортогоналната проекција на врвот на пирамидата се наоѓа надвор од нејзината основа не е важно. Важно е дека во основата на пирамидата лежи рамнокрак трапез - многуаголник околу кој може да биде кружна опишано)
13. Сфера е опишана во близина на правилна пирамида. Како се наоѓа неговиот центар во однос на елементите на пирамидата? (Центарот на сферата е на нормална поставена на рамнината на основата низ нејзиниот центар)
14. Под која состојба лежи центарот на сферата опишана околу правоаголна триаголна призма: а) внатре во призмата; б) надвор од призмата? (Во основата на призмата: а) остар триаголник; б) тап триаголник)
15. Опишана е сфера околу правоаголен паралелепипед чии рабови се 1 dm, 2 dm и 2 dm. Пресметајте го радиусот на сферата. (1,5 dm)
16. Во каков скратен конус може да се вклопи сферата? (Кај скратен конус, во чиј аксијален дел може да се впише круг. Аксијалниот пресек на конусот е рамнокрак трапез, збирот на неговите основи мора да биде еднаков на збирот на неговите странични страни. Со други зборови, збирот на радиусите на основите на конусот мора да биде еднаков на генераторот)
17. Во скратен конус е впишана сфера. Под кој агол е видлива генератриксот на конусот од центарот на сферата? (90 степени)
18. Какво својство треба да има правата призма за да биде впишана сфера во неа? (Прво, во основата на права призма мора да има многуаголник во кој може да се впише круг, и, второ, висината на призмата мора да биде еднаква на дијаметарот на кругот впишан во основата)
19. Наведи пример за пирамида која не може да одговара на сфера? (На пример, четириаголна пирамида со правоаголник или паралелограм во основата)
20. Во основата на права призма е ромб. Дали е можно да се вклопи сфера во оваа призма? (Не, тоа е невозможно, бидејќи воопшто е невозможно да се опише круг околу ромб)
21. Под кој услов може сфера да се впише во правоаголна триаголна призма? (Ако висината на призмата е двапати од радиусот на кругот впишан во основата)
22. Под кој услов може сфера да се впише во правилна четириаголна скратена пирамида? (Ако пресекот на дадена пирамида е рамнина што минува низ средината на страната на основата нормална на неа, тоа е рамнокрак трапез во кој може да се впише круг)
23. Во триаголна скратена пирамида е впишана сфера. Која точка на пирамидата е центарот на сферата? (Центарот на сферата впишана во оваа пирамида е на пресекот на три бисектрални рамнини на агли формирани од страничните страни на пирамидата со основата)
24. Дали е можно да се опише сфера околу цилиндар (десно кружно)? (Да ти можеш)
25. Дали е можно да се опише сфера околу конус, скратен конус (прав кружен)? (Да, можеш и во двата случаи)
26. Може ли сфера да се впише во кој било цилиндар? Какви својства треба да има цилиндерот за да се вклопи сфера во него? (Не, не секој пат: аксијалниот дел на цилиндерот мора да биде квадрат)
27. Може ли сфера да се впише во кој било конус? Како да се одреди положбата на центарот на сферата впишана во конус? (Да, апсолутно. Центарот на впишаната сфера е на пресекот на висината на конусот и симетралата на аголот на наклонетост на генератриксот до рамнината на основата)
Авторот верува дека од трите лекции за планирање на тема „Различни проблеми на полиедри, цилиндар, конус и топка“, препорачливо е да се посветат две лекции за решавање проблеми за комбинирање на топка со други тела. Не се препорачува докажување на теоремите дадени погоре поради недоволно време на час. Можете да ги поканите студентите кои имаат доволно вештини за тоа да ги докажат така што ќе го наведат (по дискреција на наставникот) текот или планот на доказот.
