Решавање системи на линеарни равенки со помош на Гаусовиот метод. Шема за единечна поделба

При решавање на систем од равенки

Наједноставната верзија на Гаусовиот метод резултира со големи грешки. Причината е појавата на големи коефициенти, чие заокружување резултира со голема апсолутна грешка D ~ 0,5. За возврат, големите коефициенти се добиваат по делењето со мал водечки коефициент .

Заклучок:За да го намалите влијанието на грешките во заокружувањето, треба да изберете водечки елемент кој не се разликува само од 0, туку и доволно голем.

Прва модификација на методот на Гаус– пребарување по жици. Во алгоритмот, водечкиот елемент мора да биде избран од условот.

Недостаток на модификација. Да претпоставиме дека x i е пронајден со грешка од D. Потоа, кога се бара било кој x s, потребно е, според инверзната формула, да се множи . Во овој случај, грешката D исто така ќе се помножи со . Ако вредноста е голема, грешката ќе се зголеми.

Заклучок:неопходно е да се осигура дека водечкиот елемент не е само голем, туку најголемиот модул во неговата линија. Потоа, при нормализирање на водечката линија, сите други коефициенти, според формулата (5), ќе бидат помали од 1 во апсолутна вредност, а грешките ќе бидат намалување.

Втора модификација на методот Гаус– пребарување по колони. Ова барање може да се исполни ако непознатите x i се исклучат по случаен редослед, и се бара водечката линија, испорачува . Ова ќе биде следниот водечки елемент. Откако ќе го одредите водечкиот елемент, заменете ги k-тата и r-тата колони.

Внимание.Со ваква замена се менува нумерирањето на непознатите x i. За да се обезбеди таква замена, потребно е да се внесе низа p 1 ,…p n со реалните броеви на непознатите за време на програмирањето. На почетокот на движењето напред, сите p i = i се вообичаеното нумерирање. Откако ќе го пронајдете водечкиот елемент, заменете ги p k и p r. За време на обратниот удар, пренумерираните x i се пресметуваат со помош на формулата (7). По пресметувањето на сите непознати, мора да ставиме y]:=x[i], и низа y[i]ќе биде конечното решение на проблемот.

Третата модификација на методот Гаус- целосно пребарување. Елементот за испорака е избран како лидер. Во овој случај, k-тата и r-тата колона, p k и p r, како и m-тата и k-тата редови се заменети. Оваа модификација обезбедува максимална точност, но е и најсложена.

Примена на Гаусовиот метод за решавање на различни линеарни алгебарски проблеми

1. Инверзија на матрица.Нека биде неопходно да се пресмета инверзната матрица на квадратната матрица A. Да означиме X = A –1. Како што знаете, AX = I, каде што I е идентитетската матрица, во која 1 се наоѓаат по дијагоналата, а останатите елементи се 0. Со други зборови, i-тата колона од матрицата I е еднаква на

(1 е на i-то место). Нека x (i) е i-та колона од матрицата X. Тогаш, врз основа на правилото за множење на матрицата (редата се множи со колоната), имаме A x (i) = e (i). Ова значи дека за да ја инвертираме матрицата треба да ја решиме nсистеми на линеарни равенки со идентични матрици и различни десни страни:

О = д (1) ; О = д (2) ; …; О = д (n) . (2.1)

Откако ги решивме овие системи, откриваме дека пронајдените решенија x (1), x (2), ..., x (n) се колони од матрицата A –1.

2. Пресметка на детерминанти.Во процесот на претворање на матрицата А во триаголна форма користејќи го Гаусовиот метод, ги извршивме следните дејства со неа:

1) преуредени редови или колони во зависност од модификацијата на методот;

2) поделете ја водечката линија со водечки елемент што не е нула;

3) во редовите на матрицата беше додаден водечки ред помножен со одреден број.

Како што е познато, при такви трансформации детерминантата на матрицата претрпува соодветни промени:

1) го менува знакот;

2) се дели со истиот елемент;

3) не се менува.

По движењето напред, матрицата А ќе се сведе на горната триаголна форма со оние на главната дијагонала. Детерминантата на таквата матрица очигледно е еднаква на 1. Земајќи ги предвид промените што ги претрпе детерминантата на матрицата А при процесот на трансформација, ја имаме следната формула:

det A = (–1) s × a 11 × a 22 ×…× a n n,

каде што j j се водечки елементи, s е бројот на пермутации на редови и/или колони при пребарување на водечки елементи.

ТЕСТ ПРАШАЊА И ЗАДАЧИ

1. Рачноимплементирајте го Гаусовиот метод (со пребарување во редови, колони, низ целата матрица - во зависност од опцијата за задача) за даден систем на равенки

и завршете ги следните задачи

1) Решете го овој систем на равенки

2) Пресметајте ја детерминантата на матрицата на овој систем ( Гаусовиот метод– види стр 2 ).

3) Инвертирајте ја матрицата на овој систем ( Гаусовиот метод– види стр 1 ).

Во иднина, искористете го резултатот од решавањето на овој проблем како тест пример.

2. Креирајте програма за решавање на линеарен систем користејќи го Гаусовиот метод (со пребарување во редови, колони, низ целата матрица - во зависност од верзијата на задачата) и изведете инверзија на матрицата користејќи ја оваа програма.

Продолжуваме да ги разгледуваме системите на линеарни равенки. Оваа лекција е трета на оваа тема. Ако имате нејасна идеја за тоа што е воопшто систем на линеарни равенки, ако се чувствувате како чајник, тогаш препорачувам да започнете со основите на страницата Следно, корисно е да ја проучувате лекцијата.

Гаусовиот метод е лесен!Зошто? Познатиот германски математичар Јохан Карл Фридрих Гаус, за време на неговиот живот, го доби признанието како најголем математичар на сите времиња, гениј, па дури и прекарот „Крал на математиката“. И сè генијално, како што знаете, е едноставно!Патем, пари не добиваат само цицачите, туку и генијалците - портретот на Гаус беше на банкнотата од 10 германски марки (пред воведувањето на еврото), а Гаус сè уште мистериозно им се насмевнува на Германците од обичните поштенски марки.

Гаусовиот метод е едноставен по тоа што ЗНАЕЊЕТО НА УЧЕНИК ОД ПЕТО ОДДЕЛЕНИЕ Е ДОВОЛНО за да го совладате. Мора да знаете како да собирате и множите!Не случајно наставниците често го разгледуваат методот на последователно исклучување на непознати во изборните предмети по математика во училиштата. Тоа е парадокс, но на студентите им е најтежок Гаусовиот метод. Ништо изненадувачки - се работи за методологијата и ќе се обидам да зборувам за алгоритмот на методот во достапна форма.

Прво, да систематизираме малку знаење за системите на линеарни равенки. Систем од линеарни равенки може:

1) Имајте уникатно решение. 2) Имајте бесконечно многу решенија. 3) Немате решенија (бидете незаеднички).

Гаусовиот метод е најмоќната и универзална алатка за изнаоѓање решение било којсистеми на линеарни равенки. Како што се сеќаваме, Крамерово правило и метод на матрицасе несоодветни во случаи кога системот има бесконечно многу решенија или е неконзистентен. И методот на секвенцијална елиминација на непознати Како и да еќе не доведе до одговорот! Во оваа лекција, повторно ќе го разгледаме методот Гаус за случајот бр. 1 (единственото решение за системот), статија е посветена на ситуациите од точките бр. 2-3. Забележувам дека алгоритамот на самиот метод работи исто во сите три случаи.

Да се вратиме на наједноставниот систем од лекцијата Како да се реши систем од линеарни равенки?и да го решите со помош на Гаусовиот метод.

Првиот чекор е да се запише проширена системска матрица: . Мислам дека секој може да види по кој принцип се напишани коефициентите. Вертикалната линија во внатрешноста на матрицата нема никакво математичко значење - таа е едноставно пробив за леснотија на дизајнирање.

Референца : Ви препорачувам да запомните термини линеарна алгебра. Системска матрица е матрица составена само од коефициенти за непознати, во овој пример матрицата на системот: . Проширена системска матрица – ова е истата матрица на системот плус колона со слободни термини, во овој случај: . За краткост, која било од матриците може едноставно да се нарече матрица.

Откако ќе се напише проширената системска матрица, неопходно е да се извршат некои дејства со неа, кои се нарекуваат и елементарни трансформации.

Постојат следните елементарни трансформации:

1) Стринговиматрици Може преуредина некои места. На пример, во матрицата што се разгледува, можете безболно да ги преуредите првиот и вториот ред:

2) Ако има (или се појавиле) пропорционални (како посебен случај - идентични) редови во матрицата, тогаш треба да избришиСите овие редови се од матрицата освен еден. Размислете, на пример, матрицата . Во оваа матрица, последните три реда се пропорционални, па доволно е да оставите само еден од нив: .

3) Ако во матрицата се појави нулта ред за време на трансформациите, тогаш треба да биде избриши. Јас нема да цртам, се разбира, нултата линија е линијата во која сите нули.

4) Редот на матрицата може да биде множи (подели)на кој било број не-нула. Размислете, на пример, матрицата . Овде препорачливо е да се подели првата линија со -3, а втората да се помножи со 2: . Оваа акција е многу корисна бидејќи ги поедноставува понатамошните трансформации на матрицата.

5) Оваа трансформација предизвикува најмногу тешкотии, но всушност нема ништо комплицирано. До ред на матрица можеш додадете уште една низа помножена со број, различно од нула. Да ја погледнеме нашата матрица од практичен пример: . Прво ќе ја опишам трансформацијата во многу детали. Помножете ја првата линија со -2: , И на вториот ред ја додаваме првата линија помножена со –2: . Сега првата линија може да се подели „назад“ со –2: . Како што можете да видите, линијата што е ДОДАДЕНА ЛИ – не се промени. Секогашсе менува линијата КОЈА СЕ ДОДАВА UT.

Во пракса, се разбира, тие не го пишуваат толку детално, туку го пишуваат накратко: Уште еднаш: до втората линија ја додаде првата линија помножена со –2. Линијата обично се множи усно или на нацрт, при што процесот на ментална пресметка оди вака:

„Ја препишувам матрицата и ја препишувам првата линија: »

„Прва колона. На дното треба да добијам нула. Затоа, го помножувам оној од врвот со –2: , а првиот го додавам во вториот ред: 2 + (–2) = 0. Резултатот го пишувам во вториот ред: »

„Сега втората колона. На врвот, множам -1 со -2: . Првиот го додавам во вториот ред: 1 + 2 = 3. Резултатот го пишувам во вториот ред: »

„И третата колона. На врвот множам -5 со -2: . Првиот го додавам во вториот ред: –7 + 10 = 3. Резултатот го пишувам во вториот ред: »

Ве молиме внимателно да го разберете овој пример и да го разберете алгоритмот за секвенцијална пресметка, ако го разбирате ова, тогаш Гаусовиот метод е практично во вашиот џеб. Но, се разбира, ние допрва ќе работиме на оваа трансформација.

Елементарните трансформации не го менуваат решението на системот на равенки

! ВНИМАНИЕ: сметани манипулации не може да се користи, ако ви се понуди задача каде што матриците се дадени „сами“. На пример, со „класична“ операции со матрициВо никој случај не треба да преуредите нешто во матриците! Да се вратиме на нашиот систем. Практично се зема на парчиња.

Дозволете ни да ја запишеме проширената матрица на системот и, користејќи елементарни трансформации, да ја намалиме на зачекорен поглед:

(1) Првиот ред беше додаден на вториот ред, помножен со –2. И повторно: зошто го множиме првиот ред со –2? Со цел да се добие нула на дното, што значи да се ослободиме од една променлива во втората линија.

(2) Поделете ја втората линија со 3.

Целта на елементарните трансформации – намалете ја матрицата во форма на чекор: . Во дизајнот на задачата, тие само ги означуваат „скалите“ со едноставен молив, а исто така ги заокружуваат броевите што се наоѓаат на „чекорите“. Самиот термин „зачекорен поглед“ не е целосно теоретски; во научната и образовната литература често се нарекува трапезоиден погледили триаголен поглед.

Како резултат на елементарни трансформации, добивме еквиваленторигинален систем на равенки:

Сега системот треба да се „одвитка“ во спротивна насока - од дното кон врвот, овој процес се нарекува инверзна на Гаусовиот метод.

Во долната равенка веќе имаме готов резултат: .

Да ја разгледаме првата равенка на системот и да ја замениме веќе познатата вредност на „y“ во неа:

Да ја разгледаме најчестата ситуација, кога Гаусовиот метод бара решавање на систем од три линеарни равенки со три непознати.

Пример 1

Решете го системот на равенки користејќи го методот Гаус:

Ајде да ја напишеме проширената матрица на системот:

Сега веднаш ќе го нацртам резултатот до кој ќе дојдеме за време на решението: И повторувам, нашата цел е да ја доведеме матрицата во чекор напред користејќи елементарни трансформации. Каде да се започне?

Прво, погледнете го горниот лев број: Речиси секогаш треба да биде тука единица. Општо земено, -1 (а понекогаш и други броеви) ќе го направат тоа, но некако традиционално се случувало еден обично да се става таму. Како да се организира единица? Ја гледаме првата колона - имаме завршена единица! Трансформација прва: заменете ја првата и третата линија:

Сега првата линија ќе остане непроменета до крајот на решението. Сега добро.

Единицата во горниот лев агол е организирана. Сега треба да добиете нули на овие места:

Добиваме нули користејќи „тешка“ трансформација. Прво се занимаваме со втората линија (2, –1, 3, 13). Што треба да се направи за да се добие нула на првата позиција? Мора да на вториот ред додадете го првиот ред помножен со –2. Ментално или на нацрт, помножете ја првата линија со –2: (–2, –4, 2, –18). И ние постојано вршиме (повторно ментално или на нацрт) дополнување, на вториот ред ја додаваме првата линија, веќе помножена со –2:

Резултатот го пишуваме во втората линија:

Со третата линија се справуваме на ист начин (3, 2, -5, -1). За да добиете нула на првата позиција, ви треба на третата линија додадете ја првата линија помножена со –3. Ментално или на нацрт, помножете ја првата линија со –3: (–3, –6, 3, –27). И на третиот ред ја додаваме првата линија помножена со –3:

Резултатот го пишуваме во третиот ред:

Во пракса, овие дејства обично се изведуваат усно и се запишуваат во еден чекор:

Нема потреба да броите сè одеднаш и во исто време. Редоследот на пресметките и „запишувањето“ на резултатите конзистентнаи обично е вака: прво го препишуваме првиот ред, и полека се дувнеме - ДОСЛЕДНО и ВНИМАТЕЛНО:
И јас веќе разговарав за менталниот процес на самите пресметки погоре.

Во овој пример, ова е лесно да се направи; ние ја делиме втората линија со –5 (бидејќи сите броеви таму се деливи со 5 без остаток). Во исто време, третата линија ја делиме со –2, бидејќи колку се помали броевите, толку е поедноставно решението:

Во последната фаза на елементарните трансформации, треба да добиете уште една нула овде:

За ова на третата линија ја додаваме втората линија помножена со –2:
Обидете се сами да ја сфатите оваа акција - ментално помножете ја втората линија со –2 и изведете собирање.

Последното извршено дејство е фризурата на резултатот, поделете ја третата линија со 3.

Како резултат на елементарни трансформации, беше добиен еквивалентен систем на линеарни равенки: Кул.

Сега на сцена стапува обратното од Гаусовиот метод. Равенките се „одмотуваат“ од дното кон врвот.

Во третата равенка веќе имаме подготвен резултат:

Да ја погледнеме втората равенка: . Значењето на „зет“ е веќе познато, така што:

И конечно, првата равенка: . „Игрек“ и „зет“ се познати, се работи само за ситници:

Одговори:

Како што веќе беше забележано неколку пати, за секој систем на равенки е можно и неопходно да се провери пронајденото решение, за среќа, тоа е лесно и брзо.

Пример 2

Ова е пример за независно решение, примерок од финалниот дизајн и одговор на крајот од лекцијата.

Треба да се напомене дека вашиот напредокот на одлукатаможеби не се совпаѓа со мојот процес на одлучување, а тоа е карактеристика на Гаусовиот метод. Но, одговорите мора да бидат исти!

Пример 3

Решете систем на линеарни равенки со помош на методот Гаус

Го гледаме горниот лев „чекор“. Таму треба да имаме еден. Проблемот е што воопшто нема единици во првата колона, така што преуредувањето на редовите нема да реши ништо. Во такви случаи, единицата мора да се организира со помош на елементарна трансформација. Ова обично може да се направи на неколку начини. Го направив ова: (1) На првата линија ја додаваме втората линија, помножена со –1. Односно, ментално го помноживме вториот ред со –1 и ги додадовме првиот и вториот ред, додека вториот ред не се промени.

Сега горе лево има „минус еден“, што доста ни одговара. Секој што сака да добие +1 може да изврши дополнително движење: помножете ја првата линија со –1 (променете го неговиот знак).

(2) На вториот ред се додава првиот ред помножен со 5. На третиот ред се додава првиот ред помножен со 3.

(3) Првата линија беше помножена со –1, во принцип, ова е за убавина. Променет е и знакот на третата линија и тој е поместен на второто место, така што на вториот „скалило“ ја имаме потребната единица.

(4) Вториот ред е додаден на третиот ред, помножен со 2.

(5) Третата линија беше поделена со 3.

Лош знак што укажува на грешка во пресметките (поретко, печатна грешка) е „лоша“ крајна линија. Тоа е, ако добиеме нешто како , подолу, и, соодветно, , тогаш со висок степен на веројатност можеме да кажеме дека е направена грешка при елементарни трансформации.

Наплаќаме обратно, при дизајнирањето на примери тие често не го препишуваат самиот систем, туку равенките се „земени директно од дадената матрица“. Обратниот удар, ве потсетувам, работи од дното кон врвот. Да, еве подарок:

Одговори: .

Пример 4

Решете систем на линеарни равенки со помош на методот Гаус

Ова ти е пример сам да го решиш, нешто е покомплицирано. Во ред е ако некој се збуни. Целосно решение и дизајн на примерок на крајот од лекцијата. Вашето решение може да се разликува од моето решение.

Во последниот дел ќе разгледаме некои карактеристики на Гаусовиот алгоритам. Првата карактеристика е дека понекогаш недостасуваат некои променливи во системските равенки, на пример: Како правилно да се напише проширената системска матрица? Веќе зборував за оваа точка на час. Правило на Крамер. Матричен метод. Во проширената матрица на системот, ставаме нули наместо променливите што недостасуваат: Патем, ова е прилично лесен пример, бидејќи првата колона веќе има една нула, а има помалку елементарни трансформации за извршување.

Втората карактеристика е ова. Во сите разгледани примери, ставивме или –1 или +1 на „чекорите“. Дали може да има други бројки таму? Во некои случаи можат. Размислете за системот: .

Овде на горниот лев „чекор“ имаме два. Но, го забележуваме фактот дека сите броеви во првата колона се деливи со 2 без остаток - а другиот е два и шест. И двајцата горе лево ќе ни одговараат! Во првиот чекор, треба да ги извршите следните трансформации: додадете ја првата линија помножена со –1 во втората линија; на третата линија додадете ја првата линија помножена со –3. На овој начин ќе ги добиеме бараните нули во првата колона.

Или друг конвенционален пример: . Тука ни одговараат и трите на вториот „чекор“, бидејќи 12 (местото каде што треба да добиеме нула) се дели со 3 без остаток. Неопходно е да се изврши следнава трансформација: додадете ја втората линија во третата линија, помножена со -4, како резултат на што ќе се добие нулата што ни треба.

Методот на Гаус е универзален, но има една особеност. Можете самоуверено да научите да решавате системи користејќи други методи (метод на Крамер, метод на матрица) буквално прв пат - тие имаат многу строг алгоритам. Но, за да се чувствувате сигурни во Гаусовиот метод, треба да „влезете во забите“ и да решите најмалку 5-10 десет системи. Затоа, на почетокот може да има забуна и грешки во пресметките, и нема ништо необично или трагично во ова.

Дождливо есенско време надвор од прозорецот.... Затоа, за секој што сака покомплексен пример што ќе го реши сам:

Пример 5

Решете систем од 4 линеарни равенки со четири непознати со помош на методот Гаус.

Ваквата задача не е толку ретка во пракса. Мислам дека дури и чајник кој темелно ја проучувал оваа страница ќе го разбере алгоритмот за интуитивно решавање на таков систем. Во основа, сè е исто - има само повеќе акции.

Случаите кога системот нема решенија (неконзистентни) или има бесконечно многу решенија се дискутирани на лекцијата Некомпатибилни системи и системи со заедничко решение. Таму можете да го поправите разгледуваниот алгоритам на Гаусовиот метод.

Ти посакувам успех!

Решенија и одговори:

Пример 2: Решение : Дозволете ни да ја запишеме проширената матрица на системот и, користејќи елементарни трансформации, да ја доведеме во чекор по форма.
Извршени елементарни трансформации: (1) Првиот ред беше додаден на вториот ред, помножен со –2. Првата линија беше додадена на третата линија, помножена со –1. Внимание! Овде може да бидете во искушение да го одземете првиот од третиот ред; топло препорачувам да не го одземате - ризикот од грешка значително се зголемува. Само преклопете го! (2) Знакот на вториот ред е сменет (помножено со –1). Вториот и третиот ред се заменети. Забелешка , дека на „скалите“ се задоволуваме не само со еден, туку и со –1, што е уште позгодно. (3) Вториот ред е додаден на третиот ред, помножен со 5. (4) Знакот на вториот ред е сменет (помножено со –1). Третата линија беше поделена со 14.

Обратно:

Одговори : .

Пример 4: Решение : Дозволете ни да ја запишеме проширената матрица на системот и, користејќи елементарни трансформации, да ја доведеме во чекор по форма:

Извршени конверзии: (1) На првиот ред е додаден втор ред. Така, саканата единица е организирана на горниот лев „чекор“. (2) На вториот ред се додава првиот ред помножен со 7. На третиот ред се додава првиот ред помножен со 6.

Со вториот „чекор“ сè станува полошо , „кандидати“ за него се броевите 17 и 23, а ни треба или еден или –1. Трансформациите (3) и (4) ќе бидат насочени кон добивање на саканата единица (3) Вториот ред беше додаден на третиот ред, помножен со –1. (4) Третиот ред беше додаден на вториот ред, помножен со –3. Потребната ставка на вториот чекор е примена. . (5) Вториот ред е додаден на третиот ред, помножен со 6. (6) Втората линија беше помножена со –1, третата линија беше поделена со -83.

Обратно:

Одговори :

Пример 5: Решение : Дозволете ни да ја запишеме матрицата на системот и, користејќи елементарни трансформации, да ја доведеме во чекор напред:

Извршени конверзии: (1) Првиот и вториот ред се заменети. (2) Првиот ред беше додаден на вториот ред, помножен со –2. Првата линија беше додадена на третата линија, помножена со –2. Првата линија беше додадена на четвртата линија, помножена со –3. (3) Вториот ред е додаден на третиот ред, помножен со 4. Вториот ред е додаден на четвртиот ред, помножен со –1. (4) Знакот на вториот ред е сменет. Четвртата линија беше поделена со 3 и ставена на местото на третата линија. (5) Третиот ред беше додаден на четвртиот ред, помножен со –5.

Обратно:

Одговори :

Гаусовиот методсовршен за решавање системи на линеарни алгебарски равенки (SLAEs). Има голем број на предности во споредба со другите методи:

прво, нема потреба прво да се испита системот на равенки за конзистентност;
второ, Гаусовиот метод може да реши не само SLAE во кои бројот на равенките се совпаѓа со бројот на непознати променливи и главната матрица на системот е неединечна, туку и системи на равенки во кои бројот на равенки не се совпаѓа со бројот на непознати променливи или детерминантата на главната матрица е еднаков на нула;
трето, Гаусовиот метод води до резултати со релативно мал број на пресметковни операции.

Краток преглед на статијата.

Прво, ги даваме потребните дефиниции и воведуваме ознаки.

Следно, ќе го опишеме алгоритмот на методот Гаус за наједноставниот случај, односно за системи на линеарни алгебарски равенки, бројот на равенки во кои се совпаѓа со бројот на непознати променливи и детерминантата на главната матрица на системот е не е еднаква на нула. При решавање на вакви системи на равенки најјасно се гледа суштината на методот Гаус, а тоа е последователно елиминирање на непознатите променливи. Затоа, Гаусовиот метод се нарекува и метод на последователна елиминација на непознати. Ќе прикажеме детални решенија на неколку примери.

Како заклучок, ќе го разгледаме решението со Гаусовиот метод на системи на линеарни алгебарски равенки, чија главна матрица е или правоаголна или еднина. Решението на таквите системи има некои карактеристики, кои ќе ги испитаме детално користејќи примери.

Навигација на страницата.

Основни дефиниции и нотации.

Размислете за систем од p линеарни равенки со n непознати (p може да биде еднаков на n):

Каде што има непознати променливи, се броеви (реални или сложени) и се слободни термини.

Ако , тогаш се нарекува системот на линеарни алгебарски равенки хомогенаинаку - хетерогени.

Се нарекува множеството вредности на непознати променливи за кои сите равенки на системот стануваат идентитети одлука на SLAU.

Ако има барем едно решение за систем од линеарни алгебарски равенки, тогаш тоа се нарекува зглобинаку - незаеднички.

Ако SLAE има единствено решение, тогаш тоа се нарекува одредени. Ако има повеќе од едно решение, тогаш системот се повикува неизвесна.

Велат дека системот е напишан координатна форма, ако ја има формата
.

Овој систем во матрична формаевиденцијата има форма , каде - главната матрица на SLAE, - матрицата на колоната од непознати променливи, - матрицата на слободни членови.

Ако на матрицата А додадеме матрица-колона од слободни членови како (n+1)-та колона, ќе ја добиеме т.н. проширена матрицасистеми на линеарни равенки. Вообичаено, продолжената матрица се означува со буквата Т, а колоната со слободни термини е одделена со вертикална линија од преостанатите колони, т.е.

Се нарекува квадратната матрица А дегенерира, ако нејзината детерминанта е нула. Ако , тогаш се повикува матрицата А недегенериран.

Треба да се забележи следнава точка.

Ако ги извршите следните дејства со систем на линеарни алгебарски равенки

замени две равенки,
помножете ги двете страни на која било равенка со произволен и ненула реален (или сложен) број k,
на двете страни на која било равенка додадете ги соодветните делови од друга равенка, помножени со произволен број k,

тогаш добивате еквивалентен систем кој ги има истите решенија (или, исто како и оригиналниот, нема решенија).

За проширена матрица на систем од линеарни алгебарски равенки, овие дејства ќе значат извршување на елементарни трансформации со редовите:

замена на две линии,
множење на сите елементи од која било редица од матрицата Т со ненула број k,
додавајќи ги на елементите на која било редица од матрицата соодветните елементи од друга редица, помножени со произволен број k.

Сега можеме да продолжиме со описот на методот Гаус.

Решавање системи на линеарни алгебарски равенки, во кои бројот на равенките е еднаков на бројот на непознати, а главната матрица на системот е неединечна, со помош на Гаусовиот метод.

Што би правеле на училиште ако ни се даде задача да најдеме решение за систем од равенки? .

Некои би го направиле тоа.

Забележете дека со додавање на левата страна на првата на левата страна на втората равенка, а десната страна на десната страна, можете да се ослободите од непознатите променливи x 2 и x 3 и веднаш да најдете x 1:

Пронајдената вредност x 1 =1 ја заменуваме во првата и третата равенка на системот:

Ако ги помножиме двете страни на третата равенка на системот со -1 и ги додадеме на соодветните делови од првата равенка, ќе се ослободиме од непознатата променлива x 3 и можеме да најдеме x 2:

Добиената вредност x 2 = 2 ја заменуваме во третата равенка и ја наоѓаме преостанатата непозната променлива x 3:

Други би постапиле поинаку.

Да ја решиме првата равенка на системот во однос на непознатата променлива x 1 и да го замениме добиениот израз во втората и третата равенка на системот за да ја исклучиме оваа променлива од нив:

Сега да ја решиме втората равенка на системот за x 2 и да го замениме добиениот резултат во третата равенка за да ја елиминираме непознатата променлива x 2 од неа:

Од третата равенка на системот е јасно дека x 3 =3. Од втората равенка наоѓаме , и од првата равенка добиваме .

Познати решенија, нели?

Овде најинтересно е што вториот метод на решение е во суштина методот на секвенцијално елиминирање на непознатите, односно Гаусовиот метод. Кога ги изразивме непознатите променливи (прва x 1, во следната фаза x 2) и ги заменивме во преостанатите равенки на системот, со тоа ги исклучивме. Спроведовме елиминација додека не остана само една непозната променлива во последната равенка. Процесот на секвенцијално елиминирање на непознатите се нарекува директен Гаусовиот метод. По завршувањето на движењето напред, имаме можност да ја пресметаме непознатата променлива пронајдена во последната равенка. Со негова помош ја наоѓаме следната непозната променлива од претпоследната равенка итн. Процесот на секвенцијално наоѓање непознати променливи додека се движите од последната равенка до првата се нарекува инверзна на Гаусовиот метод.

Треба да се забележи дека кога ќе изразиме x 1 во однос на x 2 и x 3 во првата равенка, а потоа ќе го замениме добиениот израз во втората и третата равенка, следните дејства доведуваат до истиот резултат:

Навистина, таквата постапка исто така овозможува да се елиминира непознатата променлива x 1 од втората и третата равенка на системот:

Нијанси со елиминација на непознати променливи со помош на Гаусовиот метод се појавуваат кога равенките на системот не содржат некои променливи.

На пример, во SLAU во првата равенка нема непозната променлива x 1 (со други зборови, коефициентот пред неа е нула). Затоа, не можеме да ја решиме првата равенка на системот за x 1 за да ја елиминираме оваа непозната променлива од останатите равенки. Излезот од оваа ситуација е да се заменат равенките на системот. Бидејќи ги разгледуваме системите на линеарни равенки чии детерминанти на главните матрици се различни од нула, секогаш постои равенка во која е присутна променливата што ни треба и можеме да ја преуредиме оваа равенка на позицијата што ни треба. За нашиот пример, доволно е да се заменат првата и втората равенка на системот , тогаш можете да ја решите првата равенка за x 1 и да ја исклучите од преостанатите равенки на системот (иако x 1 повеќе не е присутна во втората равенка).

Се надеваме дека ја разбирате суштината.

Ајде да опишеме Алгоритам на Гаусовиот метод.

Да претпоставиме дека треба да решиме систем од n линеарни алгебарски равенки со n непознати променливи од формата , и нека детерминантата на нејзината главна матрица е различна од нула.

Ќе го претпоставиме тоа, бидејќи секогаш можеме да го постигнеме ова со преуредување на равенките на системот. Да ја елиминираме непознатата променлива x 1 од сите равенки на системот, почнувајќи од втората. За да го направите ова, на втората равенка на системот ја додаваме првата, помножена со , на третата равенка ја додаваме првата, помножена со и така натаму, на n-тата равенка ја додаваме првата, помножена со . Системот на равенки по таквите трансформации ќе добие форма

каде, и .

Ќе дојдевме до истиот резултат ако изразевме x 1 во однос на други непознати променливи во првата равенка на системот и го заменивме добиениот израз со сите други равенки. Така, променливата x 1 е исклучена од сите равенки, почнувајќи од втората.

Следно, продолжуваме на сличен начин, но само со дел од добиениот систем, кој е означен на сликата

За да го направите ова, на третата равенка на системот ја додаваме втората, помножена со , на четвртата равенка ја додаваме втората, помножена со и така натаму, на n-тата равенка ја додаваме втората, помножена со . Системот на равенки по таквите трансформации ќе добие форма

каде, и . Така, променливата x 2 е исклучена од сите равенки, почнувајќи од третата.

Следно, продолжуваме со елиминирање на непознатото x 3, додека слично постапуваме со делот од системот означен на сликата.

Така ја продолжуваме директната прогресија на Гаусовиот метод додека системот не добие форма

Од овој момент започнуваме обратно од Гаусовиот метод: го пресметуваме x n од последната равенка како , користејќи ја добиената вредност на x n наоѓаме x n-1 од претпоследната равенка, и така натаму, наоѓаме x 1 од првата равенка .

Ајде да го погледнеме алгоритмот користејќи пример.

Пример.

Гаусовиот метод.

Решение.

Коефициентот a 11 не е нула, па да продолжиме со директната прогресија на Гаусовиот метод, односно со исклучување на непознатата променлива x 1 од сите равенки на системот освен првата. За да го направите ова, на левата и десната страна на втората, третата и четвртата равенка, додадете ги левата и десната страна од првата равенка, помножени со, соодветно. И:

Непознатата променлива x 1 е елиминирана, ајде да преминеме на елиминирање на x 2 . На левата и десната страна на третата и четвртата равенка на системот ги додаваме левата и десната страна на втората равенка, помножени со соодветно И :

За да ја завршиме напредната прогресија на Гаусовиот метод, треба да ја елиминираме непознатата променлива x 3 од последната равенка на системот. Дозволете ни да ги додадеме на левата и десната страна на четвртата равенка, соодветно, левата и десната страна на третата равенка, помножени со :

Можете да започнете обратно од Гаусовиот метод.

Од последната равенка што ја имаме ,
од третата равенка добиваме,
од вториот,
од првиот.

За да проверите, можете да ги замените добиените вредности на непознатите променливи во оригиналниот систем на равенки. Сите равенки се претвораат во идентитети, што покажува дека решението со методот на Гаус е пронајдено правилно.

Одговор:

Сега да дадеме решение за истиот пример користејќи го Гаусовиот метод во матрична нотација.

Пример.

Најдете го решението на системот равенки Гаусовиот метод.

Решение.

Проширената матрица на системот ја има формата . На врвот на секоја колона се непознатите променливи кои одговараат на елементите на матрицата.

Директниот пристап на Гаусовиот метод овде вклучува намалување на продолжената матрица на системот до трапезоидна форма користејќи елементарни трансформации. Овој процес е сличен на елиминацијата на непознати променливи што го направивме со системот во координатна форма. Сега ќе го видите ова.

Ајде да ја трансформираме матрицата така што сите елементи во првата колона, почнувајќи од втората, ќе станат нула. За да го направите ова, на елементите од втората, третата и четвртата линија ги додаваме соодветните елементи од првата линија помножени со, и соодветно:

Следно, ја трансформираме добиената матрица така што во втората колона сите елементи, почнувајќи од третата, стануваат нула. Ова би одговарало на елиминирање на непознатата променлива x 2 . За да го направите ова, на елементите од третиот и четвртиот ред ги додаваме соодветните елементи од првиот ред од матрицата, помножени со соодветно И :

Останува да се исклучи непознатата променлива x 3 од последната равенка на системот. За да го направите ова, на елементите од последниот ред од добиената матрица ги додаваме соодветните елементи од претпоследниот ред, помножени со :

Треба да се забележи дека оваа матрица одговара на систем од линеарни равенки

што беше добиено порано по движење напред.

Време е да се вратиме назад. Во матричната нотација, инверзната на Гаусовиот метод вклучува трансформација на добиената матрица така што матрицата означена на сликата

стана дијагонална, односно зеде форма

каде има некои бројки.

Овие трансформации се слични на напредните трансформации на Гаусовиот метод, но се изведуваат не од првата линија до последната, туку од последната кон првата.

На елементите од третиот, вториот и првиот ред додадете ги соодветните елементи од последната линија, помножени со , на и натаму соодветно:

Сега додадете ги на елементите од втората и првата линија соодветните елементи од третата линија, помножени со и со, соодветно:

На последниот чекор од обратниот Гаусовиот метод, на елементите од првиот ред ги додаваме соодветните елементи од вториот ред, помножени со:

Добиената матрица одговара на системот на равенки , од каде ги наоѓаме непознатите променливи.

Одговор:

ЗАБЕЛЕШКА.

Кога се користи методот на Гаус за решавање на системи на линеарни алгебарски равенки, треба да се избегнуваат приближни пресметки, бидејќи тоа може да доведе до целосно неточни резултати. Препорачуваме да не заокружувате децимали. Подобро е да се премести од децимални фракции на обични фракции.

Пример.

Решете систем од три равенки користејќи го методот Гаус .

Решение.

Забележете дека во овој пример непознатите променливи имаат различна ознака (не x 1, x 2, x 3, туку x, y, z). Ајде да преминеме на обичните дропки:

Да ја исклучиме непознатата x од втората и третата равенка на системот:

Во добиениот систем, непознатата променлива y е отсутна во втората равенка, но y е присутна во третата равенка, затоа, ајде да ги замениме втората и третата равенка:

Ова ја комплетира директната прогресија на методот Гаус (нема потреба да се исклучи y од третата равенка, бидејќи оваа непозната променлива повеќе не постои).

Ајде да започнеме обратно движење.

Од последната равенка наоѓаме ,
од претпоследниот

од првата равенка што ја имаме

Одговор:

X = 10, y = 5, z = -20.

Решавање системи на линеарни алгебарски равенки во кои бројот на равенките не се совпаѓа со бројот на непознати или главната матрица на системот е еднина, со помош на методот Гаус.

Системите на равенки, чија главна матрица е правоаголна или квадратна еднина, може да немаат решенија, може да имаат едно решение или може да имаат бесконечен број решенија.

Сега ќе разбереме како Гаусовиот метод ни овозможува да ја утврдиме компатибилноста или недоследноста на системот на линеарни равенки, а во случај на неговата компатибилност, да ги одредиме сите решенија (или едно единствено решение).

Во принцип, процесот на елиминација на непознати променливи во случај на такви SLAE останува ист. Сепак, вреди да се навлезе во детали за некои ситуации што може да се појават.

Да преминеме на најважната фаза.

Значи, да претпоставиме дека системот на линеарни алгебарски равенки, по завршувањето на напредната прогресија на методот Гаус, добива форма а ниту една равенка не беше сведена на (во овој случај би заклучиле дека системот е некомпатибилен). Се поставува логично прашање: „Што да се прави следно“?

Да ги запишеме непознатите променливи кои се на прво место во сите равенки на добиениот систем:

Во нашиот пример тоа се x 1, x 4 и x 5. На левите страни од равенките на системот ги оставаме само оние поими што ги содржат напишаните непознати променливи x 1, x 4 и x 5, а останатите членови се пренесуваат на десната страна од равенките со спротивен знак:

Да им дадеме на непознатите променливи кои се наоѓаат на десната страна на равенките произволни вредности, каде - произволни броеви:

После ова, десните страни на сите равенки на нашиот SLAE содржат броеви и можеме да продолжиме на обратна страна од Гаусовиот метод.

Од последната равенка на системот што ја имаме, од претпоследната равенка ја наоѓаме, од првата равенка добиваме

Решението за систем на равенки е збир на вредности на непознати променливи

Давање броеви различни вредности, ќе добиеме различни решенија на системот на равенки. Односно, нашиот систем на равенки има бесконечно многу решенија.

Одговор:

Каде - произволни броеви.

За да го консолидираме материјалот, детално ќе ги анализираме решенијата на уште неколку примери.

Пример.

Решавање на хомоген систем на линеарни алгебарски равенки Гаусовиот метод.

Решение.

Да ја исклучиме непознатата променлива x од втората и третата равенка на системот. За да го направите ова, на левата и десната страна на втората равенка, ги додаваме, соодветно, левата и десната страна од првата равенка, помножени со , и на левата и десната страна од третата равенка, ги додаваме левата и десната страна на првата равенка, помножена со:

Сега да го исклучиме y од третата равенка на добиениот систем на равенки:

Добиениот SLAE е еквивалентен на системот .

На левата страна на системските равенки ги оставаме само поимите што ги содржат непознатите променливи x и y, а поимите со непознатата променлива z ги преместуваме на десната страна:

Гаусовиот метод, наречен и метод на последователна елиминација на непознати, е како што следува. Со помош на елементарни трансформации, системот на линеарни равенки е доведен до таква форма што неговата матрица на коефициенти се покажува како трапезоиден (исто како триаголен или скалест) или блиску до трапезоиден (директен удар на Гаусовиот метод, во натамошниот текст - едноставно директен удар). Пример за таков систем и негово решение е на сликата погоре.

Во таков систем, последната равенка содржи само една променлива и нејзината вредност може недвосмислено да се најде. Вредноста на оваа променлива потоа се заменува со претходната равенка ( инверзна на Гаусовиот метод , потоа само обратно), од која се наоѓа претходната променлива итн.

Во трапезоиден (триаголен) систем, како што гледаме, третата равенка повеќе не содржи променливи yИ x, а втората равенка е променливата x .

Откако матрицата на системот ќе добие трапезоидна форма, веќе не е тешко да се разбере прашањето за компатибилноста на системот, да се одреди бројот на решенија и да се најдат самите решенија.

Предности на методот:

кога се решаваат системи на линеарни равенки со повеќе од три равенки и непознати, методот на Гаус не е толку тежок како Крамеровиот метод, бидејќи решавањето со Гаусовиот метод бара помалку пресметки;
Гаусовиот метод може да решава неопределени системи на линеарни равенки, односно да има општо решение (и ќе ги анализираме во оваа лекција), а користејќи го Крамер методот, можеме само да констатираме дека системот е неопределен;
можете да решавате системи на линеарни равенки во кои бројот на непознати не е еднаков на бројот на равенки (ние исто така ќе ги анализираме во оваа лекција);
Методот се заснова на елементарни (училишни) методи - метод на замена на непознати и метод на собирање равенки, кои ги допревме во соодветната статија.

Со цел сите да ја разберат едноставноста со која се решаваат трапезоидни (триаголни, чекор) системи на линеарни равенки, презентираме решение за таков систем користејќи обратно движење. Брзо решение за овој систем беше прикажано на сликата на почетокот на лекцијата.

Пример 1.Решете систем на линеарни равенки користејќи инверзна:

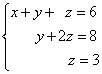
Решение. Во овој трапезоиден систем променливата zможе единствено да се најде од третата равенка. Ја заменуваме неговата вредност во втората равенка и ја добиваме вредноста на променливата y:

Сега ги знаеме вредностите на две променливи - zИ y. Ги заменуваме во првата равенка и ја добиваме вредноста на променливата x:

Од претходните чекори го запишуваме решението на системот на равенки:

За да се добие таков трапезоиден систем на линеарни равенки, кој го решивме многу едноставно, неопходно е да се користи напреден удар поврзан со елементарни трансформации на системот на линеарни равенки. Исто така, не е многу тешко.

Елементарни трансформации на систем од линеарни равенки

Повторувајќи го училишниот метод на алгебарско собирање на равенките на системот, дознавме дека на една од равенките на системот можеме да додадеме уште една равенка на системот, а секоја од равенките може да се помножи со некои броеви. Како резултат на тоа, добиваме систем на линеарни равенки еквивалентни на оваа. Во него, една равенка веќе содржеше само една променлива, заменувајќи ја вредноста со други равенки, доаѓаме до решение. Таквото додавање е еден од видовите на елементарна трансформација на системот. Кога го користиме Гаусовиот метод, можеме да користиме неколку видови трансформации.

Анимацијата погоре покажува како системот на равенки постепено се претвора во трапезоиден. Тоа е, онаа што ја видовте во првата анимација и се уверивте дека е лесно да се најдат вредностите на сите непознати од неа. Како да се изврши таква трансформација и, се разбира, примери ќе се дискутира понатаму.

При решавање системи на линеарни равенки со кој било број равенки и непознати во системот на равенки и во проширената матрица на системот Може:

преуредете ги линиите (ова беше споменато на самиот почеток на овој напис);
ако другите трансформации резултираат со еднакви или пропорционални редови, тие можат да се избришат, освен еден;
отстранете ги редовите „нула“ каде што сите коефициенти се еднакви на нула;
множи или дели која било низа со одреден број;
на која било линија додадете друга линија, помножена со одреден број.

Како резултат на трансформациите, добиваме систем на линеарни равенки еквивалентни на оваа.

Алгоритам и примери за решавање на систем на линеарни равенки со квадратна матрица на системот со помош на методот Гаус

Прво да разгледаме решавање на системи на линеарни равенки во кои бројот на непознати е еднаков на бројот на равенки. Матрицата на таков систем е квадрат, односно бројот на редови во него е еднаков на бројот на колони.

Пример 2.Решете систем на линеарни равенки со помош на методот Гаус

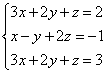
При решавање на системи на линеарни равенки со помош на училишни методи, една од равенките помноживме по член, така што коефициентите на првата променлива во двете равенки беа спротивни броеви. Кога се собираат равенки, оваа променлива се елиминира. Гаусовиот метод функционира слично.

За да се поедностави изгледот на решението ајде да создадеме проширена матрица на системот:

Во оваа матрица, коефициентите на непознатите се наоѓаат лево пред вертикалната линија, а слободните членови се наоѓаат десно после вертикалната линија.

За погодност за делење коефициенти за променливи (да се добие поделба по единство) Ајде да ги замениме првиот и вториот ред од системската матрица. Добиваме систем еквивалентен на овој, бидејќи во систем на линеарни равенки равенките може да се заменуваат:

Користење на новата прва равенка елиминирајте ја променливата xод втората и сите наредни равенки. За да го направите ова, во вториот ред од матрицата го додаваме првиот ред помножен со (во нашиот случај со ), во третиот ред - првиот ред помножен со (во нашиот случај со ).

Ова е можно затоа што

Ако има повеќе од три равенки во нашиот систем, тогаш на сите последователни равенки ќе треба да ја додадеме првата линија, помножена со односот на соодветните коефициенти, земени со знакот минус.

Како резултат на тоа, добиваме матрица еквивалентна на овој систем на нов систем на равенки, во кој сите равенки, почнувајќи од второто не содржат променлива x :

За да се поедностави втората линија на добиениот систем, помножете ја со и повторно добијте ја матрицата на систем од равенки еквивалентни на овој систем:

Сега, задржувајќи ја првата равенка на добиениот систем непроменета, користејќи ја втората равенка ја елиминираме променливата y од сите наредни равенки. За да го направите ова, во третиот ред од системската матрица го додаваме вториот ред, помножен со (во нашиот случај со ).

Ако има повеќе од три равенки во нашиот систем, тогаш ќе треба да додадеме втора линија на сите последователни равенки, помножена со односот на соодветните коефициенти земени со знакот минус.

Како резултат на тоа, повторно ја добиваме матрицата на систем еквивалентен на овој систем на линеарни равенки:

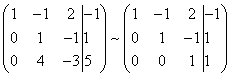
Добивме еквивалентен трапезоиден систем на линеарни равенки:

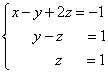
Ако бројот на равенки и променливи е поголем отколку во нашиот пример, тогаш процесот на секвенцијално елиминирање на променливите продолжува додека матрицата на системот не стане трапезоидна, како во нашиот демо пример.

Решението ќе го најдеме „од крајот“ - обратен потег. За ова од последната равенка што ја одредуваме z:
.
Заменувајќи ја оваа вредност во претходната равенка, ќе најдеме y:

Од првата равенка ќе најдеме x:

Одговор: решението на овој систем на равенки е .

: во овој случај истиот одговор ќе биде даден доколку системот има единствено решение. Ако системот има бесконечен број решенија, тогаш ова ќе биде одговорот, а ова е предмет на петтиот дел од оваа лекција.

Решете сами систем од линеарни равенки користејќи го Гаусовиот метод, а потоа погледнете го решението

Тука повторно имаме пример на конзистентен и дефинитивен систем на линеарни равенки, во кој бројот на равенките е еднаков на бројот на непознати. Разликата од нашиот демо пример од алгоритмот е тоа што веќе има четири равенки и четири непознати.

Пример 4.Решете систем на линеарни равенки користејќи го методот Гаус:

Сега треба да ја користите втората равенка за да ја елиминирате променливата од следните равенки. Ајде да ја извршиме подготвителната работа. За да го направите поудобно со односот на коефициентите, треба да добиете еден во втората колона од вториот ред. За да го направите ова, одземете ја третата од втората линија и помножете ја добиената втора линија со -1.

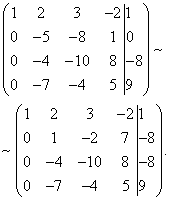
Сега да ја извршиме вистинската елиминација на променливата од третата и четвртата равенка. За да го направите ова, додајте ја втората линија, помножена со , на третата линија, а втората, помножена со, на четвртата линија.

Сега, користејќи ја третата равенка, ја елиминираме променливата од четвртата равенка. За да го направите ова, додадете ја третата линија во четвртата линија, помножена со . Добиваме продолжена трапезоидна матрица.

Добивме систем од равенки на кои дадениот систем е еквивалентен:

Следствено, добиените и дадените системи се компатибилни и дефинитивни. Конечното решение го наоѓаме „од крајот“. Од четвртата равенка можеме директно да ја изразиме вредноста на променливата „x-four“:

Оваа вредност ја заменуваме во третата равенка на системот и добиваме

Конечно, замена на вредноста

Првата равенка дава

каде го наоѓаме „х прво“:

Одговор: овој систем на равенки има единствено решение .

Можете исто така да го проверите решението на системот на калкулатор користејќи го методот на Крамер: во овој случај, истиот одговор ќе биде даден ако системот има уникатно решение.

Решавање на применети проблеми со помош на методот Гаус користејќи пример на проблем на легури

Системите на линеарни равенки се користат за моделирање на реални објекти во физичкиот свет. Ајде да решиме еден од овие проблеми - легурите. Слични проблеми се проблемите на мешавините, цената или учеството на поединечните стоки во група стоки и слично.

Пример 5.Три парчиња легура имаат вкупна маса од 150 кг. Првата легура содржи 60% бакар, втората - 30%, третата - 10%. Притоа, во втората и третата легура земени заедно има 28,4 kg помалку бакар отколку во првата легура, а во третата легура има 6,2 kg помалку бакар отколку во втората. Најдете ја масата на секое парче од легурата.

Решение. Ние составуваме систем на линеарни равенки:

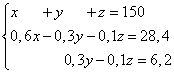
Втората и третата равенка ги помножуваме со 10, добиваме еквивалентен систем на линеарни равенки:

Ние создаваме проширена матрица на системот:

Внимание, право напред. Со додавање (во нашиот случај, одземање) еден ред помножен со број (го применуваме двапати), се случуваат следните трансформации со продолжената матрица на системот:

Директниот потег заврши. Добивме проширена трапезоидна матрица.

Го применуваме обратното движење. Решението го наоѓаме од крајот. Го гледаме тоа.

Од втората равенка наоѓаме

Од третата равенка -

За едноставноста на методот на Гаус сведочи фактот дека на германскиот математичар Карл Фридрих Гаус му биле потребни само 15 минути за да го измисли. Покрај методот именуван по него, изреката „Не треба да го мешаме она што ни изгледа неверојатно и неприродно со апсолутно невозможното“ е позната од делата на Гаус - еден вид кратка инструкција за правење откритија.

Во многу применети проблеми можеби нема трето ограничување, односно трета равенка, тогаш треба да решите систем од две равенки со три непознати користејќи го Гаусовиот метод, или, обратно, има помалку непознати од равенките. Сега ќе започнеме да решаваме такви системи на равенки.

Користејќи го Гаусовиот метод, можете да одредите дали некој систем е компатибилен или некомпатибилен nлинеарни равенки со nпроменливи.

Гаусовиот метод и системи на линеарни равенки со бесконечен број решенија

Следниот пример е конзистентен, но неодреден систем на линеарни равенки, односно има бесконечен број решенија.

По извршувањето на трансформациите во проширената матрица на системот (преуредување редови, множење и делење редови со одреден број, додавање уште еден на еден ред), може да се појават редови од формата.

Ако во сите равенки кои имаат форма

Слободните членови се еднакви на нула, тоа значи дека системот е неопределен, односно има бесконечен број решенија, а равенките од овој тип се „излишни“ и ги исклучуваме од системот.

Пример 6.

Решение. Ајде да создадеме проширена матрица на системот. Потоа, користејќи ја првата равенка, ја елиминираме променливата од следните равенки. За да го направите ова, во втората, третата и четвртата линија додадете ја првата, помножена со:

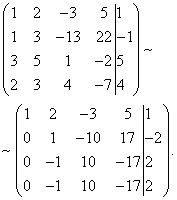
Сега да ја додадеме втората линија на третата и четвртата.

Како резултат на тоа, пристигнуваме до системот

Последните две равенки се претворија во равенки на формата. Овие равенки се задоволени за која било вредност на непознатите и може да се отфрлат.

За да ја задоволиме втората равенка, можеме да избереме произволни вредности за и, тогаш вредноста за ќе се определи уникатно: . Од првата равенка вредноста за исто така се наоѓа единствено: .

И дадениот и последниот систем се конзистентни, но неизвесни, и формулите

за произволно и да ни ги даде сите решенија на даден систем.

Гаусовиот метод и системи на линеарни равенки без решенија

Следниот пример е неконзистентен систем на линеарни равенки, односно оној кој нема решенија. Одговорот на ваквите проблеми е формулиран вака: системот нема решенија.

Како што веќе беше споменато во врска со првиот пример, по извршувањето на трансформациите, редовите на формата може да се појават во проширената матрица на системот

што одговара на равенка на формата

Ако меѓу нив има барем една равенка со слободен член не нула (т.е. ), тогаш овој систем на равенки е неконзистентен, односно нема решенија и неговото решение е целосно.

Пример 7.Решете го системот на линеарни равенки користејќи го методот Гаус:

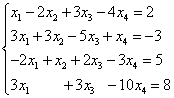
Решение. Составуваме проширена матрица на системот. Користејќи ја првата равенка, ја исклучуваме променливата од следните равенки. За да го направите ова, додадете ја првата линија помножена со на втората линија, првата линија помножена со третата линија и првата линија помножена со четвртата линија.

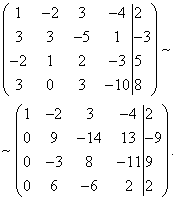
Сега треба да ја користите втората равенка за да ја елиминирате променливата од следните равенки. За да добиеме целоброен однос на коефициенти, ги заменуваме вториот и третиот ред од продолжената матрица на системот.

За да ги исклучите третата и четвртата равенка, додајте ја втората помножена со , на третата линија, а втората помножена со , на четвртата линија.

Сега, користејќи ја третата равенка, ја елиминираме променливата од четвртата равенка. За да го направите ова, додадете ја третата линија во четвртата линија, помножена со .

Затоа, дадениот систем е еквивалентен на следново:

Резултирачкиот систем е неконзистентен, бидејќи неговата последна равенка не може да се задоволи со никакви вредности на непознатите. Затоа, овој систем нема решенија.

2. Модификации на методот Гаус

Гаусовиот метод со избор на главниот елемент. Главното ограничување на Гаусовиот метод е претпоставката дека сите елементи на кои се врши поделба на секој чекор напред не се еднакви на нула. Овие елементи се нарекуваат главни елементи и се наоѓаат на главната дијагонала на матрицата А.

Ако на некој чекор од движењето напред главниот елемент = 0, тогаш понатамошното решение на системот е невозможно. Ако главниот елемент има мала вредност, блиску до нула, тогаш е можно силно зголемување на грешката поради нагло зголемување на апсолутната вредност на коефициентите добиени како резултат на поделбата. Во такви ситуации, Гаусовиот метод станува нестабилен.

Гаусовиот метод со изборот на главниот елемент ни овозможува да ја исклучиме појавата на такви случаи.

Идејата на овој метод е како што следува. На некој k-ти чекор од движењето напред, не е следната нумерирана променлива x k која е исклучена од равенките, туку променливата чиј коефициент е најголем во апсолутна вредност. Ова осигурува дека нема поделба со нула и дека методот останува стабилен.

Ако во k-тиот чекор ¹ е избран како главен елемент, тогаш во матрицата A¢ редовите со броевите k и p и колоните со броевите k и q мора да се заменат.

Преуредувањето на редовите не влијае на решението, бидејќи одговара на менување на равенките во системот, но преуредувањето на колоните значи менување на нумерирањето на променливите. Затоа, информациите за сите преуредени колони мора да се зачуваат, така што по завршувањето на обратното движење, оригиналното нумерирање на променливите може да се врати.

Постојат две поедноставни модификации на методот Гаус:

Со избор на главниот елемент по колона;

Со избор на главниот елемент по линија.

Во првиот случај, најголемиот елемент во апсолутна вредност на k-тиот ред (меѓу елементите, i = ) е избран како главен елемент. Во вториот - најголемиот елемент во апсолутна вредност на k-тата колона (меѓу елементите , i = ). Првиот пристап е најраспространет, бидејќи нумерирањето на променливите не се менува овде.

Треба да се забележи дека овие модификации се однесуваат само на движењето напред на Гаусовиот метод. Обратно движење се врши без промени, но по добивањето решение, можеби ќе биде потребно да се врати првобитното нумерирање на променливите.

LU распаѓање. Во современиот компјутерски софтвер, методот Гаус се имплементира со користење на разложување на LU, што се подразбира како што ја претставува коефициентната матрица A како производ A = LU од две матрици L и U, каде што L е долната триаголна матрица, U е горната триаголна матрица.

Ако се добие проширувањето на LU, тогаш решението на оригиналниот систем на равенки (2) се сведува на секвенцијалното решение на следните два системи на равенки со триаголни коефициентни матрици

линеарна алгебарска равенка нумеричка

каде што Y = е вектор на помошни променливи.

Овој пристап ви овозможува постојано да решавате системи на линеарни равенки со различни десни страни Б. Во овој случај, најтрудоинтензивниот дел (LU распаѓање на матрицата А) се изведува само еднаш. Оваа постапка одговара на напредното движење на Гаусовиот метод и има проценка на сложеноста од O(n 3). Понатамошното решавање на системите на равенките (6) и (7) може да се изврши повеќекратно (за различни Б), а решението на секој од нив одговара на инверзната на Гаусовиот метод и има проценка на пресметковната сложеност од O(n 2 ).

За да го добиете распаѓањето на LU, можете да го користите следниов алгоритам.

1. За оригиналниот систем (1), изведете ја напредната прогресија на Гаусовиот метод и добијте систем од триаголни равенки (5).

2. Определи ги елементите на матрицата U според правилото

u ij = C ij (i = ; j = )

3. Пресметај ги елементите на матрицата L според правилата

Формулите за пресметка за решавање на системот (6) ја имаат следната форма:

y 1 = b 1 / l 11 ;

Формули за пресметка за систем за решавање (7)

(i = n - 1, n - 2, ..., 1).

Во исто време, всушност наоѓањето на инверзната матрица е прилично трудоинтензивен процес и неговото програмирање тешко може да се нарече елементарна задача. Затоа, во пракса почесто се користат нумерички методи за решавање системи на линеарни равенки. Нумеричките методи за решавање системи на линеарни равенки го вклучуваат следново: Гаусовиот метод, Крамер метод, итеративни методи. Во Гаусовиот метод, на пример, работат на ...

35437 x4=0.58554 5 x1=1.3179137 x2=-1.59467 x3=0.35371 x4=0.58462 6 x1=1.3181515 x2=-1.59506 x3=0.35455 различни нуларативни методи. интеграција 5.1 Методи на нумеричка диференцијација 5.1. 1 Метод на опис Да претпоставиме дека во соседството на точката xi функцијата F (x) е диференцијабилна доволен број пати. ...

Во Турбо Паскал 7.0 за решавање системи на линеарни алгебарски равенки со помош на методот на едноставна итерација. 1.2. 1.3 Преглед на постоечки нумерички методи за решавање на проблемот Гаусовиот метод Кај Гаусовиот метод матрицата SLAE користејќи еквивалентни...

Броеви). Следно, користејќи формули (2), xn-1, xn-2,..., x1 се сукцесивно пронајдени за i=n-1, n-2,...,1, соодветно. Така, решението на равенките од типот (1) се опишува со методот наречен метод на поместување, кој се сведува на пресметки со користење на три едноставни формули: наоѓање на т.н. ,2,…,n (директно бришење), а потоа непознато xi со...