Меѓу функционалните серии, најважно место заземаат сериите за напојување.
Моќната серија е серија
чии поими се функции на моќност распоредени во зголемување на ненегативни цели броеви x, А в 0 , в 1 , в 2 , в n - константни вредности. Броеви в 1 , в 2 , в n - коефициенти на сериски членови, в 0 - бесплатен член. Условите на серијата моќност се дефинирани на целата нумеричка линија.
Ајде да се запознаеме со концептот области на конвергенција на сериите на моќност.Ова е збир на променливи вредности x, за што се конвергира серијата. Моќните серии имаат прилично едноставен регион на конвергенција. За реални вредности на променливи xрегионот на конвергенција се состои или од една точка, или е одреден интервал (интервал на конвергенција), или се совпаѓа со целата оска Вол .
При замена на вредностите во сериите на моќност x= 0 ќе резултира со бројна серија
в 0 +0+0+...+0+... ,
кој конвергира.
Затоа, кога x= 0 која било серија на моќност конвергира и затоа, неговата област на конвергенцијане може да биде празното множество. Структурата на регионот на конвергенција на сите серии на моќност е иста. Може да се утврди со помош на следнава теорема.
Теорема 1 (Абелова теорема). Ако серијата на моќност конвергира на некоја вредност x = x 0, различно од нула, тогаш се конвергира и, згора на тоа, апсолутно, за сите вредности на | x| < |x 0 | . Забележете: и почетната вредност „X е нула“ и секоја вредност на „X“ што се споредува со почетната вредност се земаат модуло - без да се земе предвид знакот.
Последица. Ако сериите на моќност се разминуваатпо некоја вредност x = x 1, тогаш се разминува за сите вредности на | x| > |x 1 | .
Како што веќе дознавме порано, секоја серија на моќност конвергира по вредноста x= 0. Постојат серии на моќност кои се спојуваат само кога x= 0 и се разминуваат за други вредности X. Исклучувајќи го овој случај од разгледување, претпоставуваме дека серијата на моќност конвергира во одредена вредност x = x 0, различно од нула. Потоа, според Абеловата теорема, таа конвергира во сите точки на интервалот ]-| x 0 |, |x 0 |[ (интервал чии леви и десни граници се x вредностите на кои се конвергира серијата моќност, земени со знак минус и знак плус, соодветно), симетрично за потеклото.
Ако серијата на моќност се разминува при одредена вредност x = x 1, тогаш, врз основа на последицата на Абеловата теорема, таа се разминува во сите точки надвор од сегментот [-| x 1 |, |x 1 |] . Следи дека за која било серија на моќност постои интервал симетричен во однос на потеклото, наречен интервал на конвергенција, во секоја точка од која серијата конвергира, на границите може да се спојува, или може да се разминува, и не мора во исто време, а надвор од сегментот серијата се разминува. Број Рсе нарекува радиус на конвергенција на серијата на моќност.
Во посебни случаи интервал на конвергенција на сериите на моќностможе да се дегенерира до точка (тогаш серијата конвергира само кога x= 0 и се смета дека Р= 0) или да ја претстави целата бројна права (тогаш серијата конвергира во сите точки на бројната права и се претпоставува дека ).
Така, одредувањето на регионот на конвергенција на енергетската серија се состои во одредување на неговата радиус на конвергенција Ри проучување на конвергенцијата на серијата на границите на интервалот на конвергенција (на ).
Теорема 2. Ако сите коефициенти на серијата на моќност, почнувајќи од одредена, се различни од нула, тогаш неговиот радиус на конвергенција е еднаков на границата на односот на апсолутните вредности на коефициентите на заедничките членови на сериите што го следат, т.е.
Пример 1. Најдете го регионот на конвергенција на серијата на моќност
Решение. Еве
Користејќи ја формулата (28), го наоѓаме радиусот на конвергенција на оваа серија:
Да ја проучуваме конвергенцијата на сериите на краевите на интервалот на конвергенција. Примерот 13 покажува дека оваа серија конвергира во x= 1 и се разминува во x= -1. Следствено, регионот на конвергенција е полуинтервалот.
Пример 2. Најдете го регионот на конвергенција на серијата на моќност
Решение. Коефициентите на серијата се позитивни, и
Да ја најдеме границата на овој сооднос, т.е. радиус на конвергенција на сериите на моќност:
Дозволете ни да ја проучуваме конвергенцијата на сериите на краевите на интервалот. Замена на вредности x= -1/5 и x= 1/5 во овој ред дава:
Првата од овие серии се спојува (види Пример 5). Но, тогаш, врз основа на теоремата во делот „Апсолутна конвергенција“, втората серија исто така конвергира, а регионот на нејзината конвергенција е сегментот
Пример 3. Најдете го регионот на конвергенција на серијата на моќност
Решение. Еве
Користејќи ја формулата (28) го наоѓаме радиусот на конвергенција на серијата:
Дозволете ни да ја проучиме конвергенцијата на сериите за вредностите на . Заменувајќи ги во оваа серија, соодветно добиваме
Двете серии се разминуваат затоа што неопходниот услов за конвергенција не е задоволен (нивните заеднички термини не се склони кон нула на ). Значи, на двата краја на интервалот на конвергенција, оваа серија се разминува, а регионот на нејзината конвергенција е интервалот.
Пример 5. Најдете го регионот на конвергенција на серијата на моќност
Решение. Ја наоѓаме релацијата каде , и 
:
Според формулата (28), радиусот на конвергенција на оваа серија
,
односно серијата конвергира само кога x= 0 и се разминува за други вредности X.
Примерите покажуваат дека на краевите на интервалот на конвергенција сериите се однесуваат поинаку. Во примерот 1, на едниот крај од интервалот на конвергенција, серијата конвергира, а на другиот, таа се разминува; во примерот 2, таа конвергира на двата краја; во примерот 3, таа се разминува на двата краја.
Формулата за радиусот на конвергенција на сериите на моќност се добива под претпоставка дека сите коефициенти на сериските членови, почнувајќи од одредена точка, се различни од нула. Затоа, употребата на формулата (28) е дозволена само во овие случаи. Ако овој услов е прекршен, тогаш радиусот на конвергенција на серијата на моќност треба да се бара со користење на тестот на d'Alembert, или, со замена на променливата, трансформирање на серијата во форма во која е задоволена наведениот услов.
Пример 6. Најдете го интервалот на конвергенција на серијата на моќност
Решение. Оваа серија не содржи термини со непарни степени X. Затоа, ја трансформираме серијата, поставувајќи . Потоа ја добиваме серијата
да го најдеме радиусот на конвергенција на кој можеме да ја примениме формулата (28). Бидејќи , a , тогаш радиусот на конвергенција на оваа серија
Од еднаквоста што ја добиваме, оваа серија конвергира на интервалот.
Збир на серии на моќност. Диференцијација и интеграција на сериите на моќностДозволете за серијата моќ
радиус на конвергенција Р> 0, т.е. оваа серија конвергира во интервалот.
Потоа секоја вредност Xод интервалот на конвергенција одговара на одредена сума од серијата. Според тоа, збирот на сериите на моќност е во функција на Xна интервалот на конвергенција. Означувајќи го со ѓ(x), можеме да ја напишеме еднаквоста
разбирајќи го во смисла дека збирот на сериите во секоја точка Xод интервалот на конвергенција е еднаков на вредноста на функцијата ѓ(x) во оваа точка. Во истата смисла, ќе кажеме дека серијата на моќност (29) конвергира во функцијата ѓ(x) на интервалот на конвергенција.
Надвор од интервалот на конвергенција, еднаквоста (30) нема смисла.
Пример 7. Најдете го збирот на сериите на моќност
Решение. Ова е геометриска серија за која а= 1, а q= x. Според тоа, нејзиниот збир е функција 
. Серијата конвергира ако , и е нејзиниот интервал на конвергенција. Затоа еднаквост
важи само за вредности, иако функцијата 
дефинирани за сите вредности X, освен X= 1.
Може да се докаже дека збирот на серијата моќ ѓ(x) е континуирано и диференцијабилно на кој било интервал во интервалот на конвергенција, особено во која било точка од интервалот на конвергенција на серијата.
Дозволете ни да ги претставиме теоремите за диференцијација по термин и интеграција на сериите на моќност.
Теорема 1. Серијата на моќност (30) во интервалот на нејзината конвергенција може да се диференцира член по член неограничен број пати, а добиените серии на моќност имаат ист радиус на конвергенција како и оригиналната серија, а нивните збирови се соодветно еднакви на .
Теорема 2. Серијата на моќност (30) може да се интегрира член по член неограничен број пати во опсег од 0 до X, ако , и добиената серија на моќност има ист радиус на конвергенција како и оригиналната серија, а нивните збирови се соодветно еднакви
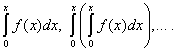
Нека е дадена функцијата ѓ(x), која треба да се прошири во серија на моќност, т.е. претставуваат во форма (30):
Задачата е да се одредат коефициентите 
ред (30). За да го направите ова, разликувајќи ја еднаквоста (30) по поим, постојано наоѓаме:
……………………………………………….. (31)
Претпоставувајќи во еднаквости (30) и (31) X= 0, наоѓаме
Заменувајќи ги пронајдените изрази во еднаквост (30), добиваме
(32)
Дозволете ни да го најдеме проширувањето на серијата Maclaurin на некои елементарни функции.
Пример 8. Проширете ја функцијата во серија Maclaurin
Решение. Дериватите на оваа функција се совпаѓаат со самата функција:
Затоа, кога X= 0 имаме
Заменувајќи ги овие вредности во формулата (32), го добиваме саканото проширување:
(33)
Оваа серија конвергира на целата бројна права (нејзиниот радиус на конвергенција).
Во теоријата на функционални серии, централното место го зазема делот посветен на проширување на функцијата во серија.
Така се поставува задачата: за дадена функција треба да најдеме таква моќна серија
кој се спојувал на одреден интервал и неговиот збир бил еднаков на 
,
тие.
=
..
Оваа задача се нарекува проблемот на проширување на функцијата во енергетска серија.
Неопходен услов за разградливост на функција во енергетска серијае неговата диференцијабилност бесконечен број пати - ова произлегува од својствата на конвергентните серии на моќност. Овој услов е задоволен, по правило, за елементарните функции во нивниот домен на дефиниција.
Значи, да претпоставиме дека функцијата 
има деривати од кој било ред. Дали е можно да се прошири во серии за напојување?Ако е така, како можеме да ја најдеме оваа серија? Вториот дел од проблемот е полесен за решавање, па да почнеме со него.
Да претпоставиме дека функцијата 
може да се претстави како збир на серии на моќност кои се конвергираат во интервалот што ја содржи точката X 0 :
=
..
(*)
Каде А 0 , А 1 , А 2 ,...,А П ,... – непознати (сеуште) коефициенти.
Да ја ставиме во еднаквост (*) вредноста x = x 0 , тогаш добиваме
.
Дозволете ни да ја разликуваме серијата на моќност (*) по член по член
=
..
и верувајќи овде x = x 0 , добиваме
.
Со следната диференцијација ја добиваме серијата
=
..
верувајќи x = x 0 ,
добиваме 
, каде 
.
По П-повеќекратна диференцијација добиваме
Претпоставувајќи во последната еднаквост x = x 0 ,
добиваме 
, каде
Значи, коефициентите се пронајдени
,
,
,
…,
,….,
заменувајќи го во серијата (*), добиваме
Добиената серија се нарекува веднаш до Тејлорза функција
.
Така, го утврдивме тоа ако функцијата може да се прошири во серија на моќност во моќности (x - x 0 ), тогаш оваа експанзија е единствена и добиената серија е нужно серија на Тејлор.
Забележете дека серијата Тејлор може да се добие за која било функција која има изводи од кој било ред во точката x = x 0 . Но, тоа не значи дека може да се стави знак за еднаквост помеѓу функцијата и добиената серија, т.е. дека збирот на серијата е еднаков на оригиналната функција. Прво, таквата еднаквост може да има смисла само во регионот на конвергенција, а Тејлоровата серија добиена за функцијата може да се разминува, и второ, ако серијата Тејлор се конвергира, тогаш нејзиниот збир може да не се совпаѓа со оригиналната функција.
3.2. Доволни услови за разградливост на функција во Тејлоровата серијаДозволете ни да формулираме изјава со чија помош ќе се реши задачата.
Доколку функцијата
во некое соседство на точката x 0 има деривати до (n+
1) од ред инклузивно, тогаш во оваа населба имамеформулаТејлор
КадеР n (X)- преостанатиот член од формулата на Тејлор - ја има формата (Лагранжова форма)
Каде точкаξ лежи помеѓу x и x 0 .
Забележете дека постои разлика помеѓу Тејлоровата серија и Тејлоровата формула: Тејлоровата формула е конечен збир, т.е. П -фиксен број.
Потсетиме дека збирот на серијата С(x) може да се дефинира како граница на функционална низа од парцијални суми С П (x) во одреден интервал X:
.
Според ова, да се прошири функцијата во серија на Тејлор значи да се најде серија таква што за која било XX
Да ја напишеме формулата на Тејлор во форма каде
забележи, тоа 
ја дефинира грешката што ја добиваме, заменете ја функцијата ѓ(x)
полином С n (x).
Ако 
, Тоа 
, оние. функцијата е проширена во серија на Тејлор. обратно, ако 
, Тоа 
.
Така докажавме критериум за разградливост на функција во Тејлоровата серија.
Со цел за функцијатаѓ(x) се проширува во серија на Тејлор, потребно е и доволно на овој интервал
, КадеР n (x) е преостанатиот термин од серијата Тејлор.
Користејќи го формулираниот критериум, може да се добие доволноуслови за разградливост на функција во Тејлоровата серија.
Доколку вонекое соседство на точката x 0 апсолутните вредности на сите деривати на функцијата се ограничени на истиот број М≥ 0, т.е.
, Тo во ова соседство функцијата се проширува во серија на Тејлор.
Од горенаведеното следува алгоритампроширување на функцијатаѓ(x) во серијата Тејлорво близина на точка X 0 :
1. Наоѓање деривати на функции ѓ(x):
f(x), f’(x), f”(x), f’”(x), f (n) (x),…
2. Пресметајте ја вредноста на функцијата и вредностите на нејзините деривати во точката X 0
f(x 0 ), f'(x 0 ), f“ (x 0 ), ѓ“ (x 0 ), ѓ (n) (х 0 ),…
3. Ние формално ја пишуваме Тејлоровата серија и го наоѓаме регионот на конвергенција на добиената серија на моќност.
4. Проверуваме исполнување на доволни услови, т.е. утврдуваме за кои Xод регионот на конвергенција, преостанат рок Р n (x)
има тенденција на нула како 
или
.
Проширувањето на функциите во серија на Тејлор со користење на овој алгоритам се нарекува проширување на функцијата во серија на Тејлор по дефиницијаили директно распаѓање.
Како да вметнете математички формули на веб-локација?
Ако некогаш треба да додадете една или две математички формули на веб-страница, тогаш најлесниот начин да го направите тоа е како што е опишано во статијата: математичките формули лесно се вметнуваат на страницата во форма на слики кои автоматски се генерираат од Wolfram Alpha . Покрај едноставноста, овој универзален метод ќе помогне да се подобри видливоста на страницата во пребарувачите. Работи долго време (и, мислам, ќе работи засекогаш), но веќе е морално застарен.
Ако редовно користите математички формули на вашиот сајт, тогаш ви препорачувам да користите MathJax - специјална библиотека JavaScript која прикажува математичка нотација во веб-прелистувачите користејќи ознака MathML, LaTeX или ASCIIMathML.
Постојат два начина да започнете со користење на MathJax: (1) со користење на едноставен код, можете брзо да поврзете MathJax скрипта на вашата веб-локација, која автоматски ќе се вчита од оддалечен сервер во вистинско време (список на сервери); (2) преземете ја скриптата MathJax од оддалечен сервер на вашиот сервер и поврзете ја на сите страници на вашата страница. Вториот метод - покомплексен и одзема многу време - ќе го забрза вчитувањето на страниците на вашата страница, и ако матичниот сервер MathJax поради некоја причина привремено стане недостапен, тоа нема да влијае на вашата веб-страница на кој било начин. И покрај овие предности, го избрав првиот метод бидејќи е поедноставен, побрз и не бара технички вештини. Следете го мојот пример и за само 5 минути ќе можете да ги користите сите карактеристики на MathJax на вашата страница.
Можете да ја поврзете скриптата за библиотека MathJax од оддалечен сервер користејќи две опции за код земени од главната веб-локација на MathJax или на страницата со документација:
Една од овие опции за код треба да се копира и залепи во кодот на вашата веб-страница, по можност помеѓу ознаките и или веднаш по ознаката. Според првата опција, MathJax се вчитува побрзо и помалку ја успорува страницата. Но, втората опција автоматски ги следи и вчитува најновите верзии на MathJax. Ако го вметнете првиот код, тој ќе треба периодично да се ажурира. Ако го вметнете вториот код, страниците ќе се вчитуваат побавно, но нема да треба постојано да ги следите ажурирањата на MathJax.
Најлесен начин за поврзување на MathJax е во Blogger или WordPress: во контролната табла на страницата, додајте графичка контрола дизајнирана за вметнување JavaScript код од трета страна, копирајте ја првата или втората верзија на кодот за преземање претставен погоре во него и поставете го додатокот поблиску до почетокот на шаблонот (патем, ова воопшто не е потребно, бидејќи скриптата MathJax се вчитува асинхроно). Тоа е се. Сега научете ја синтаксата за обележување на MathML, LaTeX и ASCIIMathML и подготвени сте да вметнете математички формули во веб-страниците на вашата страница.
Секој фрактал е конструиран според одредено правило, кое постојано се применува неограничен број пати. Секое такво време се нарекува итерација.
Итеративниот алгоритам за конструирање на сунѓер Менгер е прилично едноставен: оригиналната коцка со страна 1 е поделена со рамнини паралелни на нејзините лица на 27 еднакви коцки. Од него се отстрануваат една централна коцка и 6 коцки во непосредна близина на неа по лицата. Резултатот е сет кој се состои од преостанатите 20 помали коцки. Правејќи го истото со секоја од овие коцки, добиваме сет составен од 400 помали коцки. Продолжувајќи го овој процес бескрајно, добиваме сунѓер Менгер.
Ако функцијата f(x) има изводи од сите редови на одреден интервал што ја содржи точката a, тогаш на неа може да се примени Тејлоровата формула:
,
Каде r n– таканаречениот остаток член или остаток од серијата, може да се процени со помош на Лагранжовата формула:
, каде што бројот x е помеѓу x и a.
f(x)=
во точка x 0 = Број на елементи на редот 3 4 5 6 7
Користете го проширувањето на елементарните функции e x , cos(x), sin(x), ln(1+x), (1+x) m
Правила за внесување функции:
Ако за некоја вредност X r n→0 во n→∞, тогаш во границата Тејлоровата формула станува конвергентна за оваа вредност Тејлор серија:
,
Така, функцијата f(x) може да се прошири во Тејлоровата серија во точката x што се разгледува ако:
1) има деривати од сите нарачки;
2) конструираната серија конвергира во оваа точка.
Кога a = 0 добиваме серија наречена Maclaurin серија:
,
Проширување на наједноставните (елементарни) функции во серијата Maclaurin:
Експоненцијални функции
, R=∞
Тригонометриски функции 
, R=∞ 
, R=∞
, (-π/2< x < π/2), R=π/2
Функцијата actgx не се шири во моќи на x, бидејќи ctg0=∞
Хиперболични функции
Логаритамски функции
, -1