Tund teemal: "Funktsioonide ekstreempunktide leidmine. Näited"
Lisamaterjalid
Kallid kasutajad, ärge unustage jätta oma kommentaare, ülevaateid, soove! Kõik materjalid on viirusetõrjeprogrammiga kontrollitud.
Käsiraamatud ja simulaatorid veebipoes Integral 10. klassile alates 1C
Geomeetria ülesannete lahendamine. Interaktiivsed ehitusülesanded 7.-10. klassile
Tarkvarakeskkond "1C: Mathematical Constructor 6.1"
Mida me uurime:
1. Sissejuhatus.
2. Miinimum- ja maksimumpunktid.
4. Kuidas arvutada äärmusi?
5. Näited.
Function Extrema sissejuhatus
Poisid, vaatame teatud funktsiooni graafikut:
Pange tähele, et meie funktsiooni y=f (x) käitumine on suures osas määratud kahe punktiga x1 ja x2. Vaatame lähemalt funktsiooni graafikut nendes punktides ja nende ümber. Kuni punktini x2 funktsioon suureneb, punktis x2 toimub kääne ja kohe pärast seda punkti väheneb funktsioon punktiks x1. Punktis x1 funktsioon paindub uuesti ja pärast seda suureneb uuesti. Praegu nimetame punkte x1 ja x2 käändepunktideks. Joonistame nendesse punktidesse puutujad:
Meie punktide puutujad on paralleelsed x-teljega, mis tähendab, et puutuja kalle on null. See tähendab, et meie funktsiooni tuletis nendes punktides on võrdne nulliga.
Vaatame selle funktsiooni graafikut:
Punktides x2 ja x1 on võimatu tõmmata puutujasirge. See tähendab, et nendes punktides tuletist ei eksisteeri. Vaatame nüüd uuesti oma punkte kahel graafikul. Punkt x2 on punkt, kus funktsioon saavutab oma suurima väärtuse mõnes piirkonnas (punkti x2 lähedal). Punkt x1 on punkt, kus funktsioon saavutab oma väikseima väärtuse mingis piirkonnas (punkti x1 lähedal).
Miinimum- ja maksimumpunktid
Definitsioon: Punkti x= x0 nimetatakse funktsiooni y=f(x) miinimumpunktiks, kui on olemas punkti x0 naabrus, milles kehtib võrratus: f(x) ≥ f(x0).
Definitsioon: Punkti x=x0 nimetatakse funktsiooni y=f(x) maksimumpunktiks, kui on olemas punkti x0 naabrus, milles kehtib võrratus: f(x) ≤ f(x0).
Poisid, mis on naabruskond?
Definitsioon: Punkti naabrus on punktide kogum, mis sisaldab meie punkti ja selle lähedal asuvaid punkte.
Naabruskonna saame ise määrata. Näiteks punkti x=2 korral saame naabruskonna määratleda punktide 1 ja 3 kujul.
Tuleme tagasi oma graafikute juurde, vaatame punkti x2, see on suurem kui kõik teised punktid teatud naabruskonnast, siis definitsiooni järgi on see maksimumpunkt. Vaatame nüüd punkti x1, see on väiksem kui kõik teised punktid teatud naabruskonnast, siis definitsiooni järgi on see miinimumpunkt.
Poisid, tutvustame tähistust:
Y min – miinimumpunkt,
y max – maksimumpunkt.
Tähtis! Poisid, ärge ajage maksimum- ja miinimumpunkte segamini funktsiooni väikseima ja suurima väärtusega. Minimaalseid ja maksimaalseid väärtusi otsitakse kogu antud funktsiooni definitsioonipiirkonnas ning miinimum- ja maksimumpunkte teatud naabruses.
Funktsiooni äärmus
Miinimum- ja maksimumpunktide jaoks on ühine termin - äärmuspunktid.
Ekstreemum (lat. extremum – äärmuslik) – funktsiooni maksimaalne või minimaalne väärtus antud hulgal. Ekstreemumi saavutamise punkti nimetatakse ekstreemumipunktiks.
Vastavalt sellele, kui saavutatakse miinimum, nimetatakse äärmuspunkti miinimumpunktiks ja maksimumpunkti saavutamisel nimetatakse seda maksimumpunktiks.
Kuidas otsida funktsiooni äärmusi?
Läheme tagasi oma graafikute juurde. Meie punktides tuletis kas kaob (esimesel graafikul) või ei eksisteeri (teisel graafikul).
Siis saame teha olulise väite: Kui funktsioonil y= f(x) on ekstreemum punktis x=x0, siis selles punktis on funktsiooni tuletis kas null või seda pole olemas.
Nimetatakse punkte, kus tuletis on võrdne nulliga paigal.
Nimetatakse punkte, kus funktsiooni tuletist ei eksisteeri kriitiline.
Kuidas arvutada äärmusi?
Poisid, lähme tagasi funktsiooni esimese graafiku juurde:
Seda graafikut analüüsides ütlesime: kuni punktini x2 funktsioon suureneb, punktis x2 toimub kääne ja pärast seda punkti funktsioon väheneb punktini x1. Punktis x1 funktsioon paindub uuesti ja pärast seda funktsioon uuesti suureneb.
Sellise arutluse põhjal võime järeldada, et äärmuspunktides olev funktsioon muudab monotoonsuse olemust ja seetõttu muudab tuletisfunktsioon märki. Tuletame meelde: kui funktsioon väheneb, on tuletis väiksem või võrdne nulliga ja kui funktsioon suureneb, siis on tuletis suurem või võrdne nulliga.
Võtame saadud teadmised kokku järgmise väitega:
Teoreem: Ekstreemumi piisav tingimus: olgu funktsioon y=f(x) pidev mingil intervallil X ja sellel on intervalli sees statsionaarne või kriitiline punkt x= x0. Seejärel:
Probleemide lahendamiseks pidage meeles järgmisi reegleid: Kui tuletiste märgid on määratletud, siis:
Algoritm pideva funktsiooni y= f(x) uurimiseks monotoonsuse ja ekstreemsuse korral:
- Leia y' tuletis.
- Leida statsionaarsed punktid (tuletis on null) ja kriitilised punktid (tuletist ei eksisteeri).
- Märgi arvjoonele statsionaarsed ja kriitilised punktid ning määra saadud intervallidel tuletise märgid.
- Ülaltoodud väidete põhjal tehke järeldus ekstreemumipunktide olemuse kohta.
Näited äärmuslike punktide leidmiseks
1) Leidke funktsiooni äärmuspunktid ja määrake nende olemus: y= 7+ 12*x - x 3
Lahendus: meie funktsioon on pidev, siis kasutame oma algoritmi:
a) y"= 12–3x2,
b) y"= 0, x = ±2, 
Punkt x= -2 on funktsiooni miinimumpunkt, punkt x= 2 on funktsiooni maksimumpunkt.
Vastus: x= -2 on funktsiooni miinimumpunkt, x= 2 on funktsiooni maksimumpunkt.
2) Leidke funktsiooni äärmuspunktid ja määrake nende olemus.
Lahendus: meie funktsioon on pidev. Kasutame oma algoritmi: A)
b) punktis x= 2 tuletist ei eksisteeri, sest Nulliga jagada ei saa 
Funktsiooni määratluspiirkond: , selles punktis ekstreemumit pole, sest punkti naabruskond ei ole määratletud. Leiame väärtuse, mille korral tuletis on võrdne nulliga: 
c) Märkige arvujoonele statsionaarsed punktid ja määrake tuletise märgid: 
d) vaadake meie joonist, mis näitab äärmuste määramise reegleid. Punkt x= 3 on funktsiooni miinimumpunkt.
Vastus: x= 3 on funktsiooni miinimumpunkt.
3) Leidke funktsiooni y= x - 2cos(x) äärmuspunktid ja määrake nende olemus, kui -π ≤ x ≤ π.
Lahendus: meie funktsioon on pidev, kasutame meie algoritmi:
a) y"= 1 + 2sin(x),
b) leidke väärtused, milles tuletis on võrdne nulliga: 1 + 2sin(x)= 0, sin(x)= -1/2,
sest -π ≤ x ≤ π, siis: x= -π/6, -5π/6,
c) märkige arvjoonele statsionaarsed punktid ja määrake tuletise märgid: 
d) vaadake meie joonist, mis näitab äärmuste määramise reegleid.
Punkt x= -5π/6 on funktsiooni maksimumpunkt.
Punkt x= -π/6 on funktsiooni miinimumpunkt.
Vastus: x= -5π/6 on funktsiooni maksimumpunkt, x= -π/6 on funktsiooni miinimumpunkt.
4) Leidke funktsiooni äärmuspunktid ja määrake nende olemus:
Lahendus: Meie funktsioonil on katkestus ainult ühes punktis x= 0. Kasutame algoritmi: A)
b) leidke väärtused, milles tuletis on võrdne nulliga: y"= 0 x= ±2, c) märkige arvjoonele statsionaarsed punktid ja määrake tuletise märgid:
d) vaadake meie joonist, mis näitab äärmuste määramise reegleid.
Punkt x= -2 on funktsiooni miinimumpunkt.
Punkt x= 2 on funktsiooni miinimumpunkt.
Punktis x= 0 funktsiooni ei eksisteeri.
Vastus: x= ±2 - funktsiooni miinimumpunktid.
Iseseisvalt lahendatavad probleemid
a) Leidke funktsiooni äärmuspunktid ja määrake nende olemus: y= 5x 3 - 15x - 5.b) Leidke funktsiooni äärmuspunktid ja määrake nende olemus:
c) Leidke funktsiooni äärmuspunktid ja määrake nende olemus: y= 2sin(x) - x π ≤ x ≤ 3π korral. d) Leidke funktsiooni äärmuspunktid ja määrake nende olemus:
Funktsioonid, pole üldse vaja teada esimese ja teise tuletise olemasolust ja mõista nende füüsilist tähendust. Kõigepealt peate mõistma järgmist:
- funktsiooni äärmused maksimeerivad või, vastupidi, minimeerivad funktsiooni väärtuse suvaliselt väikeses naabruskonnas;
- äärmuspunktis ei tohiks olla funktsiooni katkestust.
Ja nüüd sama asi, ainult lihtsas keeles. Vaadake pastapliiatsi otsa. Kui pliiats asetseb vertikaalselt, kirjutusotsaga ülespoole, siis on palli keskpunkt äärmus – kõrgeim punkt. Sel juhul räägime maksimumist. Kui nüüd pliiats kirjutusotsaga allapoole keerata, siis palli keskel on juba minimaalne funktsioon. Siin toodud joonist kasutades võite ette kujutada kirjatarvete pliiatsi loetletud manipuleerimisi. Seega on funktsiooni äärmused alati kriitilised punktid: selle maksimum või miinimum. Graafiku külgnev osa võib olla nii terav või sile, kui soovitakse, kuid see peab olema mõlemal pool, ainult sel juhul on punkt ekstreemum. Kui graafik on ainult ühel küljel, ei ole see punkt ekstreemum, isegi kui ühel küljel on äärmuslikud tingimused täidetud. Nüüd uurime funktsiooni äärmusi teaduslikust vaatenurgast. Selleks, et punkti saaks pidada ekstreemumiks, on vajalik ja piisav, et:
- esimene tuletis oli null või seda punktis ei eksisteerinud;
- esimene tuletis muutis sel hetkel oma märki.
Tingimust tõlgendatakse kõrgemat järku tuletiste seisukohast veidi erinevalt: punktis diferentseeruva funktsiooni jaoks piisab, kui on paaritu järku tuletis, mis ei võrdu nulliga, samas kui kõik madalamat järku tuletised peavad olemas olema. ja olema võrdne nulliga. See on õpikute teoreemide võimalikult lihtne tõlgendus, kuid kõige tavalisematel inimestel tasub seda punkti selgitada näitega. Aluseks on tavaline parabool. Teeme kohe broneeringu: nullpunktis on sellel miinimum. Natuke matemaatikat:
- esimene tuletis (X 2) | = 2X, nullpunkti jaoks 2X = 0;
- teine tuletis (2X) | = 2, nullpunkti puhul 2 = 2.
Sel lihtsal viisil on illustreeritud tingimused, mis määravad funktsiooni äärmuse nii esimest kui ka kõrgemat järku tuletistele. Sellele võib lisada, et teine tuletis on täpselt sama paaritu järgu tuletis, mis ei võrdu nulliga, millest oli juttu just eespool. Kui tegemist on kahe muutuja funktsiooni äärmustega, peavad tingimused olema täidetud mõlema argumendi jaoks. Üldistamise korral kasutatakse osatuletisi. See tähendab, et ekstreemumi olemasoluks punktis on vajalik, et mõlemad esimest järku tuletised oleksid võrdsed nulliga või vähemalt ühte neist ei eksisteeri. Tagamaks, et ekstreemumi olemasolu on piisav, uuritakse avaldist, mis on funktsiooni teist järku tuletiste korrutise ja segatud teist järku tuletise ruudu vahe. Kui see avaldis on suurem kui null, siis on ekstreemum, aga kui see on võrdne nulliga, jääb küsimus lahtiseks ja tuleb teha lisauuringuid.
Vaatleme pideva funktsiooni graafikut y=f(x) näidatud joonisel.
Funktsiooni väärtus punktis x 1 on suurem kui funktsiooni väärtused kõigis naaberpunktides nii vasakul kui ka paremal x 1 . Sel juhul ütleme, et funktsioonil on punkt x 1 maksimum. Punktis x Funktsioonil 3 on ilmselgelt ka maksimum. Kui me mõtleme asjale x 2, siis on funktsiooni väärtus selles väiksem kui kõik naaberväärtused. Sel juhul ütleme, et funktsioonil on punkt x 2 miinimum. Sama ka punkti kohta x 4 .
Funktsioon y=f(x) punktis x 0 on maksimaalselt, kui funktsiooni väärtus selles punktis on suurem kui selle väärtused mõne punkti sisaldava intervalli kõigis punktides x 0, st. kui on selline punkti naabruskond x 0, mis sobib kõigile x≠x 0 , kuuludes sellesse naabruskonda, kehtib ebavõrdsus f(x)<f(x 0 ) .
Funktsioon y=f(x) Sellel on miinimum punktis x 0 , kui on selline punkti naabruskond x 0 , see on kõigile x≠x 0, mis kuulub sellesse naabruskonda, kehtib ebavõrdsus f(x)>f(x 0.
Punkte, kus funktsioon saavutab maksimumi ja miinimumi, nimetatakse äärmuspunktideks ja funktsiooni väärtusi nendes punktides nimetatakse funktsiooni ekstreemumideks.
Pöörame tähelepanu asjaolule, et lõigul defineeritud funktsioon võib saavutada maksimumi ja miinimumi ainult vaadeldava lõigu punktides.
Pange tähele, et kui funktsioonil on mingis punktis maksimum, ei tähenda see, et sellel hetkel on funktsioonil suurim väärtus kogu määratluspiirkonnas. Eespool käsitletud joonisel funktsioon punktis x 1 on maksimum, kuigi on punkte, kus funktsiooni väärtused on suuremad kui punktis x 1 . Eriti, f(x 1) < f(x 4) st. funktsiooni miinimum on suurem kui maksimum. Maksimumi definitsioonist järeldub vaid, et see on funktsiooni suurim väärtus maksimumpunktile piisavalt lähedal asuvates punktides.
Teoreem 1. (Vajalik tingimus ekstreemumi olemasoluks.) Kui diferentseeritav funktsioon y=f(x) on punktis x=x 0 ekstreemum, siis muutub selle tuletis selles punktis nulliks.
Tõestus. Olgu kindluse mõttes punktis x Funktsioonil 0 on maksimum. Seejärel piisavalt väikeste sammude korral Δ x meil on f(x 0 + Δ x)
Nende ebavõrdsuste üleminek piirini Δ x→ 0 ja võttes arvesse, et tuletis f "(x 0) on olemas ja seetõttu ei sõltu vasakpoolne piirang sellest, kuidas Δ x→ 0, saame: juures Δ x → 0 – 0 f"(x 0) ≥ 0 a juures Δ x → 0 + 0 f"(x 0) ≤ 0. Alates f"(x 0) defineerib arvu, siis on need kaks võrratust ühilduvad ainult siis, kui f"(x 0) = 0.
Tõestatud teoreem väidab, et maksimum- ja miinimumpunktid võivad olla ainult nende argumendi väärtuste hulgas, mille korral tuletis muutub nulliks.
Vaatlesime juhtumit, kui funktsioonil on tuletis teatud segmendi kõigis punktides. Milline on olukord juhtudel, kui tuletist ei eksisteeri? Vaatame näiteid.
Näited.
- y=|x|.
Funktsioonil ei ole punktis tuletist x=0 (sellel hetkel ei ole funktsiooni graafikul defineeritud puutujat), kuid sellel hetkel on funktsioonil miinimum, kuna y(0)=0 ja kõigi jaoks x≠ 0y > 0.
- Lase x< x
0 . Siis c< x
0 ja f "(c)> 0.
Sellepärast f "(c)(x-x 0)<
0 ja seetõttu
f(x) - f(x 0 )< 0, st. f(x)< f(x 0 ).
- Lase x > x 0 . Siis c>x 0 ja f "(c)< 0. Tähendab f "(c)(x-x 0)< 0. Sellepärast f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .
- Leia funktsiooni domeen f(x).
- Leia funktsiooni esimene tuletis f "(x).
- Määrake selle jaoks kriitilised punktid:
- leida võrrandi tegelikud juured f "(x)=0;
- leida kõik väärtused x mille puhul tuletis f "(x) ei eksisteeri.
- Määrake kriitilisest punktist vasakul ja paremal asuva tuletise märk. Kuna tuletise märk jääb kahe kriitilise punkti vahel konstantseks, siis piisab tuletise märgi määramisest kriitilisest punktist ühes punktis vasakul ja ühes punktis paremal.
- Arvutage funktsiooni väärtus äärmuspunktides.
- Leia kõik funktsiooni kriitilised punktid vahemikus ( a, b) ja arvutage funktsiooni väärtused nendes punktides.
- Arvutage funktsiooni väärtused segmendi otstes, kui x = a, x = b.
- Valige kõigi saadud väärtuste hulgast suurim ja väikseim.
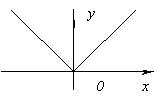
Funktsioonil ei ole tuletist at x=0, kuna see läheb lõpmatusse punktis x=0. Kuid sel hetkel on funktsioonil maksimum.
Funktsioonil ei ole tuletist at x=0, alates 
juures x→0. Sel hetkel ei ole funktsioonil ei maksimumi ega miinimumi. Tõesti, f(x)=0 ja at x<0f(x)<0, а при x>0f(x)>0.
Seega on antud näidete ja sõnastatud teoreemi põhjal selge, et funktsioonil saab ekstreemum olla ainult kahel juhul: 1) punktides, kus tuletis on olemas ja võrdub nulliga; 2) kohas, kus tuletist ei eksisteeri.
Kui aga ühel hetkel x 0 me teame seda f "(x 0 ) =0, siis ei saa sellest järeldada, et punktis x 0 funktsioonil on äärmus.
Näiteks. 
.
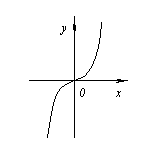
Aga periood x=0 ei ole äärmuspunkt, kuna sellest punktist vasakul asuvad funktsiooni väärtused telje all Ox ja ülal paremal.
Argumendi väärtusi funktsiooni domeenist, mille juures funktsiooni tuletis kaob või ei eksisteeri, nimetatakse kriitilised punktid.
Kõigest eelnevast järeldub, et funktsiooni äärmuspunktid kuuluvad kriitiliste punktide hulka, kuid mitte iga kriitiline punkt ei ole äärmuspunkt. Seetõttu peate funktsiooni ekstreemumi leidmiseks leidma kõik funktsiooni kriitilised punktid ja seejärel uurima iga punkti eraldi maksimumi ja miinimumi jaoks. Seda täidab järgmine teoreem.
Teoreem 2. (Piisav tingimus ekstreemumi olemasoluks.) Olgu funktsioon pidev mingil kriitilist punkti sisaldaval intervallil x 0 ja on diferentseeritav selle intervalli kõigis punktides (välja arvatud võib-olla punkt ise x 0). Kui selle punkti kaudu vasakult paremale liikudes muudab tuletis märgi plussist miinusesse, siis punktis x = x Funktsioonil 0 on maksimum. Kui läbimisel x 0 vasakult paremale, tuletis muudab märgi miinusest plussiks, siis on funktsioonil selles punktis miinimum.
Seega, kui
Tõestus. Oletame esmalt, et läbisõidul x 0 tuletis muudab märgi plussist miinusesse, st. kõigi ees x, punkti lähedal x 0 f "(x)> 0 eest x< x 0 , f "(x)< 0 eest x> x 0 . Rakendame erinevusele Lagrange'i teoreemi f(x) - f(x 0 ) = f "(c)(x-x 0), kus c jääb vahele x Ja x 0 .
Seega kõigi väärtuste puhul x piisavalt lähedal x 0 f(x)< f(x 0 ) . Ja see tähendab, et hetkel x Funktsioonil 0 on maksimum.
Samamoodi on tõestatud ka miinimumteoreemi teine osa.
Illustreerime selle teoreemi tähendust joonisel. Lase f "(x 1 ) =0 ja mis tahes x, piisavalt lähedal x 1, on ebavõrdsused täidetud
f "(x)< 0 kl x< x 1 , f "(x)> 0 kl x> x 1 .
Seejärel punktist vasakule x 1 funktsioon suureneb ja väheneb paremal, seega millal x = x 1 funktsioon läheb suurenevalt kahanemisele, see tähendab, et sellel on maksimum.
Samamoodi võime kaaluda punkte x 2 ja x 3 .
Kõik ülaltoodud on skemaatiliselt kujutatud pildil:
Ekstreemumi funktsiooni y=f(x) uurimise reegel
Näited. Uurige miinimum- ja maksimumfunktsioone.
Segmendi FUNKTSIOONIDE MAKSIMAALSED JA VÄIKSEIMAD VÄÄRTUSED
Suurima funktsiooni väärtus intervallil on suurim kõigist selle väärtustest sellel intervallil ja kõige väiksem– kõigist selle väärtustest väikseim.
Mõelge funktsioonile y=f(x) pidev lõigul [ a, b]. Teatavasti saavutab selline funktsioon oma maksimum- ja miinimumväärtused kas lõigu piiril või selle sees. Kui funktsiooni suurim või väikseim väärtus saavutatakse segmendi sisemises punktis, siis on see väärtus funktsiooni maksimum või miinimum, see tähendab, et see saavutatakse kriitilistes punktides.
Seega saame järgmise reegel funktsiooni suurima ja väikseima väärtuse leidmiseks segmendis[ a, b] :
Funktsiooni äärmus
2. definitsioon
Punkti $x_0$ nimetatakse funktsiooni $f(x)$ maksimumpunktiks, kui selle punkti naabrus on selline, et kogu selle naabruskonna $x$ korral on ebavõrdsus $f(x)\le f(x_0) $ hoiab.
3. definitsioon
Punkti $x_0$ nimetatakse funktsiooni $f(x)$ maksimumpunktiks, kui selle punkti naabrus on selline, et kogu selle naabruskonna $x$ korral on ebavõrdsus $f(x)\ge f(x_0) $ hoiab.
Funktsiooni ekstreemumi mõiste on tihedalt seotud funktsiooni kriitilise punkti mõistega. Tutvustame selle määratlust.
4. definitsioon
$x_0$ nimetatakse funktsiooni $f(x)$ kriitiliseks punktiks, kui:
1) $x_0$ - määratluspiirkonna sisepunkt;
2) $f"\left(x_0\right)=0$ või seda pole olemas.
Ekstreemumi mõiste jaoks saame sõnastada teoreeme selle olemasolu piisavate ja vajalike tingimuste kohta.
2. teoreem
Ekstreemumi jaoks piisav seisund
Olgu punkt $x_0$ funktsiooni $y=f(x)$ jaoks kriitiline ja asub intervallis $(a,b)$. Olgu igal intervallil $\left(a,x_0\right)\ ja\ (x_0,b)$ tuletis $f"(x)$ olemas ja säilitab konstantse märgi. Seejärel:
1) Kui intervallil $(a,x_0)$ on tuletis $f"\left(x\right)>0$ ja intervallil $(x_0,b)$ on tuletiseks $f"\left( x\paremale)
2) Kui intervallil $(a,x_0)$ on tuletis $f"\left(x\right)0$, siis punkt $x_0$ on selle funktsiooni miinimumpunkt.
3) Kui nii intervallil $(a,x_0)$ kui ka intervallil $(x_0,b)$ on tuletis $f"\left(x\right) >0$ või tuletis $f"\left(x \paremal)
Seda teoreemi illustreerib joonis 1.
Joonis 1. Ekstreemide olemasolu piisav tingimus
Näited äärmustest (joonis 2).
Joonis 2. Näited äärmuslikest punktidest
Ekstreemumi funktsiooni uurimise reegel
2) Leia tuletis $f"(x)$;
7) Tehke teoreemi 2 abil järeldused maksimumide ja miinimumide olemasolu kohta igal intervallil.
Funktsioonide suurendamine ja vähendamine
Tutvustame esmalt kasvavate ja kahanevate funktsioonide definitsioone.
Definitsioon 5
Funktsioon $y=f(x)$, mis on defineeritud intervallil $X$, kasvab, kui mis tahes punktis $x_1,x_2\in X$ kohas $x_1
Definitsioon 6
Funktsioon $y=f(x)$, mis on defineeritud intervallis $X$, on kahanev, kui mis tahes punktis $x_1,x_2\in X$ väärtuses $x_1f(x_2)$.
Suurendamise ja kahanemise funktsiooni uurimine
Tuletise abil saate uurida suurenevaid ja kahanevaid funktsioone.
Funktsiooni suurendamise ja kahanemise intervallide uurimiseks peate tegema järgmist.
1) Leia funktsiooni $f(x)$ definitsioonipiirkond;
2) Leia tuletis $f"(x)$;
3) Leia punktid, kus kehtib võrdus $f"\left(x\right)=0$;
4) Leia punktid, kus $f"(x)$ ei eksisteeri;
5) Märgi koordinaatjoonele kõik leitud punktid ja selle funktsiooni määratluspiirkond;
6) Määrake tuletise $f"(x)$ märk igal saadud intervallil;
7) Tee järeldus: intervallidel, kus $f"\left(x\right)0$ funktsioon suureneb.
Näiteid äärmuspunktide suurenemise, vähendamise ja esinemise funktsioonide uurimise probleemidest
Näide 1
Uurige suurendamise ja vähendamise funktsiooni ning maksimum- ja miinimumpunktide olemasolu: $f(x)=(2x)^3-15x^2+36x+1$
Kuna esimesed 6 punkti on samad, siis teostame need kõigepealt.
1) Määratluspiirkond – kõik reaalarvud;
2) $f"\left(x\right)=6x^2-30x+36$;
3) $f"\left(x\right)=0$;
\ \ \
4) $f"(x)$ eksisteerib definitsioonipiirkonna kõigis punktides;
5) Koordinaatjoon:
Joonis 3.
6) Määrake tuletise $f"(x)$ märk igal intervallil:
\ \}