Komplekse afledte opgaver. Komplekse derivater

Og sætningen om derivatet af en kompleks funktion, hvis formulering er som følger:

Lad 1) funktionen $u=\varphi (x)$ på et tidspunkt have $x_0$ den afledte $u_(x)"=\varphi"(x_0)$, 2) funktionen $y=f(u)$ har ved det tilsvarende i punktet $u_0=\varphi (x_0)$ den afledte $y_(u)"=f"(u)$. Så vil den komplekse funktion $y=f\left(\varphi (x) \right)$ i det nævnte punkt også have en afledt lig med produktet af afledte af funktionerne $f(u)$ og $\varphi ( x)$:

$$ \left(f(\varphi (x))\right)"=f_(u)"\left(\varphi (x_0) \right)\cdot \varphi"(x_0) $$

eller i kortere notation: $y_(x)"=y_(u)"\cdot u_(x)"$.

I eksemplerne i dette afsnit har alle funktioner formen $y=f(x)$ (dvs. vi betragter kun funktioner af én variabel $x$). Derfor er den afledte $y"$ i alle eksempler taget med hensyn til variablen $x$. For at understrege, at den afledte tages med hensyn til variablen $x$, skrives $y"_x$ ofte i stedet for $y "$.

Eksempel nr. 1, nr. 2 og nr. 3 skitserer den detaljerede proces til at finde den afledede af komplekse funktioner. Eksempel nr. 4 er beregnet til en mere fuldstændig forståelse af den afledte tabel, og det giver mening at sætte dig ind i den.

Det er tilrådeligt, efter at have studeret materialet i eksempel nr. 1-3, at gå videre til selvstændig løsning af eksempel nr. 5, nr. 6 og nr. 7. Eksempel #5, #6 og #7 indeholder en kort løsning, så læseren kan kontrollere rigtigheden af sit resultat.

Eksempel nr. 1

Find den afledede af funktionen $y=e^(\cos x)$.

Vi skal finde den afledede af en kompleks funktion $y"$. Siden $y=e^(\cos x)$, så $y"=\left(e^(\cos x)\right)"$. Til find den afledede $ \left(e^(\cos x)\right)"$ vi bruger formel nr. 6 fra tabellen over afledte. For at bruge formel nr. 6 skal vi tage højde for, at i vores tilfælde $u=\cos x$. Den yderligere løsning består i blot at erstatte udtrykket $\cos x$ i stedet for $u$ i formel nr. 6:

$$ y"=\venstre(e^(\cos x) \right)"=e^(\cos x)\cdot (\cos x)" \tag (1.1)$$

Nu skal vi finde værdien af udtrykket $(\cos x)"$. Vi vender igen til tabellen med afledte værdier og vælger formel nr. 10 fra den. Ved at erstatte $u=x$ med formel nr. 10, har vi : $(\cos x)"=-\ sin x\cdot x"$ Lad os nu fortsætte ligheden (1.1) og supplere det med resultatet:

$$ y"=\venstre(e^(\cos x) \right)"=e^(\cos x)\cdot (\cos x)"= e^(\cos x)\cdot (-\sin x \cdot x") \tag (1.2) $$

Siden $x"=1$ fortsætter vi ligestilling (1.2):

$$ y"=\venstre(e^(\cos x) \right)"=e^(\cos x)\cdot (\cos x)"= e^(\cos x)\cdot (-\sin x \cdot x")=e^(\cos x)\cdot (-\sin x\cdot 1)=-\sin x\cdot e^(\cos x) \tag (1.3) $$

Så fra lighed (1.3) har vi: $y"=-\sin x\cdot e^(\cos x)$. Naturligvis springes forklaringer og mellemliggende ligheder over, idet fundet af den afledede nedskrives på én linje, som i ligheden (1.3) Så den afledede af den komplekse funktion er fundet, er der kun tilbage at skrive svaret ned.

Svar: $y"=-\sin x\cdot e^(\cos x)$.

Eksempel nr. 2

Find den afledede af funktionen $y=9\cdot \arctg^(12)(4\cdot \ln x)$.

Vi skal beregne den afledte $y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"$. Til at begynde med bemærker vi, at konstanten (dvs. tallet 9) kan tages ud af det afledte tegn:

$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)" \tag (2.1) $$

Lad os nu gå til udtrykket $\left(\arctg^(12)(4\cdot \ln x) \right)"$. For at gøre det nemmere at vælge den ønskede formel fra tabellen over afledte vil jeg præsentere udtrykket det pågældende spørgsmål i denne form: $\left( \left(\arctg(4\cdot \ln x) \right)^(12)\right)"$. Nu er det klart, at det er nødvendigt at bruge formel nr. 2, dvs. $\left(u^\alpha \right)"=\alpha\cdot u^(\alpha-1)\cdot u"$. Lad os erstatte $u=\arctg(4\cdot \ln x)$ og $\alpha=12$ i denne formel:

Ved at supplere lighed (2.1) med det opnåede resultat har vi:

$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)"= 108\cdot\left(\arctg(4\cdot \ln x) \right)^(11)\cdot (\arctg(4\cdot \ln x))" \tag (2.2) $$

I denne situation begår der ofte en fejl, når løseren ved første trin vælger formlen $(\arctg \; u)"=\frac(1)(1+u^2)\cdot u"$ i stedet for formlen $\left(u^\ alpha \right)"=\alpha\cdot u^(\alpha-1)\cdot u"$. Pointen er, at den afledede af den eksterne funktion skal komme først. For at forstå, hvilken funktion der vil være ekstern til udtrykket $\arctg^(12)(4\cdot 5^x)$, forestil dig, at du beregner værdien af udtrykket $\arctg^(12)(4\cdot 5^ x)$ til en vis værdi $x$. Først vil du beregne værdien af $5^x$, derefter gange resultatet med 4, hvilket får $4\cdot 5^x$. Nu tager vi arctangensen fra dette resultat og opnår $\arctg(4\cdot 5^x)$. Så hæver vi det resulterende tal til tolvte potens og får $\arctg^(12)(4\cdot 5^x)$. Den sidste handling, dvs. at hæve til magten 12 vil være en ekstern funktion. Og det er ud fra dette, vi skal begynde at finde den afledte, hvilket blev gjort i lighed (2.2).

Nu skal vi finde $(\arctg(4\cdot \ln x))"$. Vi bruger formel nr. 19 i derivattabellen og erstatter $u=4\cdot \ln x$ i den:

$$ (\arctg(4\cdot \ln x))"=\frac(1)(1+(4\cdot \ln x)^2)\cdot (4\cdot \ln x)" $$

Lad os forenkle det resulterende udtryk lidt, idet vi tager $(4\cdot \ln x)^2=4^2\cdot (\ln x)^2=16\cdot \ln^2 x$ i betragtning.

$$ (\arctg(4\cdot \ln x))"=\frac(1)(1+(4\cdot \ln x)^2)\cdot (4\cdot \ln x)"=\frac( 1)(1+16\cdot \ln^2 x)\cdot (4\cdot \ln x)" $$

Ligestilling (2.2) bliver nu:

Det er tilbage at finde $(4\cdot \ln x)"$. Lad os tage konstanten (dvs. 4) ud af det afledte tegn: $(4\cdot \ln x)"=4\cdot (\ln x)" $. For For at finde $(\ln x)"$ bruger vi formel nr. 8, der erstatter $u=x$: $(\ln x)"=\frac(1)(x)\cdot x "$. Siden $x"=1$, derefter $(\ln x)"=\frac(1)(x)\cdot x"=\frac(1)(x)\cdot 1=\frac(1)(x) $. Ved at erstatte det opnåede resultat med formel (2.3), opnår vi:

$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)"=\\ =108\cdot\left(\arctg(4\cdot \ln x) \right)^(11)\cdot (\arctg(4\cdot \ln x))"=108\cdot \left(\arctg(4\cdot \ln x) \right)^(11)\cdot \frac(1)(1+16\cdot \ln^2 x)\cdot (4\cdot \ln x)" =\\ =108\cdot \left(\arctg(4\cdot \ln x) \right)^(11)\cdot \frac(1)(1+16\cdot \ln^2 x)\cdot 4\ cdot \frac(1)(x)=432\cdot \frac(\arctg^(11)(4\cdot \ln x))(x\cdot (1+16\cdot \ln^2 x)).

Lad mig minde dig om, at den afledede af en kompleks funktion oftest findes i én linje, som skrevet i den sidste lighed. Ved udarbejdelse af standardberegninger eller kontrolarbejde er det derfor slet ikke nødvendigt at beskrive løsningen så detaljeret.

Svar: $y"=432\cdot \frac(\arctg^(11)(4\cdot \ln x))(x\cdot (1+16\cdot \ln^2 x))$.

Eksempel nr. 3

Find $y"$ af funktionen $y=\sqrt(\sin^3(5\cdot9^x))$.

Lad os først transformere funktionen $y$ lidt, der udtrykker radikalen (roden) som en potens: $y=\sqrt(\sin^3(5\cdot9^x))=\left(\sin(5\cdot 9) ^x) \right)^(\frac(3)(7))$. Lad os nu begynde at finde den afledte. Siden $y=\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))$, så:

$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)" \tag (3.1) $$

Lad os bruge formel nr. 2 fra tabellen over afledte, og erstatte $u=\sin(5\cdot 9^x)$ og $\alpha=\frac(3)(7)$ i den:

$$ \left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)"= \frac(3)(7)\cdot \left( \sin(5\cdot 9^x)\right)^(\frac(3)(7)-1) (\sin(5\cdot 9^x))"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))" $$

Lad os fortsætte ligheden (3.1) ved at bruge det opnåede resultat:

$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))" \tag (3.2) $$

Nu skal vi finde $(\sin(5\cdot 9^x))"$. Til dette bruger vi formel nr. 9 fra tabellen over afledte, og erstatter $u=5\cdot 9^x$ i den:

$$ (\sin(5\cdot 9^x))"=\cos(5\cdot 9^x)\cdot(5\cdot 9^x)" $$

Efter at have suppleret lighed (3.2) med det opnåede resultat, har vi:

Det er tilbage at finde $(5\cdot 9^x)"$. Lad os først tage konstanten (tallet $5$) uden for det afledte tegnet, dvs. $(5\cdot 9^x)"=5\cdot (9) ^x) "$. For at finde den afledte $(9^x)"$ skal du anvende formel nr. 5 i tabellen over afledte værdier, idet du erstatter $a=9$ og $u=x$: $(9^x) )"=9^x\cdot \ ln9\cdot x"$. Siden $x"=1$, derefter $(9^x)"=9^x\cdot \ln9\cdot x"=9^x\cdot \ln9$. Nu kan vi fortsætte ligestilling (3.3):

$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)"=\frac(3)(7)\cdot \venstre(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))"=\\ =\frac(3) (7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) \cos(5\cdot 9^x)\cdot(5\cdot 9 ^x)"= \frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) \cos(5\cdot 9 ^x)\cdot 5\cdot 9^x\cdot \ln9=\\ =\frac(15\cdot \ln 9)(7)\cdot \left(\sin(5\cdot 9^x)\right) ^(-\frac(4)(7))\cdot \cos(5\cdot 9^x)\cdot 9^x. $$

Vi kan igen vende tilbage fra magter til radikaler (dvs. rødder) ved at skrive $\left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7))$ i formen $\ frac(1)(\left(\sin(5\cdot 9^x)\right)^(\frac(4)(7)))=\frac(1)(\sqrt(\sin^4(5\ cdot 9^x)))$. Derefter vil den afledede blive skrevet i denne form:

$$ y"=\frac(15\cdot \ln 9)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7))\cdot \cos(5\cdot 9^x)\cdot 9^x= \frac(15\cdot \ln 9)(7)\cdot \frac(\cos (5\cdot 9^x)\cdot 9^x) (\sqrt(\sin^4(5\cdot 9^x))).

Svar: $y"=\frac(15\cdot \ln 9)(7)\cdot \frac(\cos (5\cdot 9^x)\cdot 9^x)(\sqrt(\sin^4(5\ cdot 9^x)))$.

Eksempel nr. 4

Vis, at formlerne nr. 3 og nr. 4 i tabellen over derivater er et specialtilfælde af formel nr. 2 i denne tabel.

Formel nr. 2 i derivattabellen indeholder den afledede af funktionen $u^\alpha$. Ved at erstatte $\alpha=-1$ i formel nr. 2 får vi:

$$(u^(-1))"=-1\cdot u^(-1-1)\cdot u"=-u^(-2)\cdot u"\tag (4.1)$$

Da $u^(-1)=\frac(1)(u)$ og $u^(-2)=\frac(1)(u^2)$, så kan lighed (4.1) omskrives som følger: $ \left(\frac(1)(u) \right)"=-\frac(1)(u^2)\cdot u"$. Dette er formel nr. 3 i derivattabellen.

Lad os igen vende tilbage til formel nr. 2 i tabellen over derivater. Lad os erstatte $\alpha=\frac(1)(2)$ i det:

$$\left(u^(\frac(1)(2))\right)"=\frac(1)(2)\cdot u^(\frac(1)(2)-1)\cdot u" =\frac(1)(2)u^(-\frac(1)(2))\cdot u"\tag (4.2) $$

Siden $u^(\frac(1)(2))=\sqrt(u)$ og $u^(-\frac(1)(2))=\frac(1)(u^(\frac( 1) )(2)))=\frac(1)(\sqrt(u))$, så kan lighed (4.2) omskrives som følger:

$$ (\sqrt(u))"=\frac(1)(2)\cdot \frac(1)(\sqrt(u))\cdot u"=\frac(1)(2\sqrt(u) )\cdot u" $$

Den resulterende lighed $(\sqrt(u))"=\frac(1)(2\sqrt(u))\cdot u"$ er formel nr. 4 i tabellen over afledte. Som du kan se, er formlerne nr. 3 og nr. 4 i derivattabellen hentet fra formel nr. 2 ved at erstatte den tilsvarende $\alpha$-værdi.

Hvis du følger definitionen, så er den afledede af en funktion i et punkt grænsen for forholdet mellem tilvæksten af funktionen Δ y til argumenttilvæksten Δ x:

Alt ser ud til at være klart. Men prøv at bruge denne formel til at beregne f.eks. den afledede af funktionen f(x) = x 2 + (2x+ 3) · e x synd x. Hvis du gør alt pr. definition, falder du simpelthen i søvn efter et par siders beregninger. Derfor er der enklere og mere effektive måder.

Til at begynde med bemærker vi, at vi fra hele rækken af funktioner kan skelne de såkaldte elementære funktioner. Det er relativt simple udtryk, hvis afledninger længe er blevet beregnet og indført i tabellen. Sådanne funktioner er ret nemme at huske - sammen med deres derivater.

Afledte af elementære funktioner

Elementære funktioner er alle dem, der er anført nedenfor. Afledte af disse funktioner skal kendes udenad. Desuden er det slet ikke svært at huske dem - det er derfor, de er elementære.

Så afledte af elementære funktioner:

Navn	Fungere	Afledte
Konstant	f(x) = C, C ∈ R	0 (ja, nul!)
Magt med rationel eksponent	f(x) = x n	n · x n − 1
Bihule	f(x) = synd x	cos x
Cosinus	f(x) = cos x	−synd x(minus sinus)
Tangent	f(x) = tg x	1/cos 2 x
Cotangens	f(x) = ctg x	− 1/synd 2 x
Naturlig logaritme	f(x) = log x	1/x
Vilkårlig logaritme	f(x) = log -en x	1/(x ln -en)
Eksponentiel funktion	f(x) = e x	e x(intet ændrede sig)

Hvis en elementær funktion ganges med en vilkårlig konstant, beregnes den afledede af den nye funktion også let:

(C · f)’ = C · f ’.

Generelt kan konstanter tages ud af fortegn for den afledte. For eksempel:

(2x 3)' = 2 · ( x 3)' = 2 3 x 2 = 6x 2 .

Det er klart, at elementære funktioner kan lægges til hinanden, ganges, divideres - og meget mere. Sådan vil nye funktioner fremstå, ikke længere særligt elementære, men også differentierede efter bestemte regler. Disse regler diskuteres nedenfor.

Afledt af sum og forskel

Lad funktionerne være givet f(x) Og g(x), hvis afledte er kendt af os. For eksempel kan du tage de elementære funktioner diskuteret ovenfor. Så kan du finde den afledede af summen og forskellen af disse funktioner:

(f + g)’ = f ’ + g ’
(f − g)’ = f ’ − g ’

Så den afledte af summen (forskel) af to funktioner er lig summen (forskel) af de afledte. Der kan være flere vilkår. For eksempel, ( f + g + h)’ = f ’ + g ’ + h ’.

Strengt taget er der ikke noget begreb om "subtraktion" i algebra. Der er et begreb om "negativt element". Derfor forskellen f − g kan omskrives som en sum f+ (−1) g, og så er der kun én formel tilbage - den afledede af summen.

f(x) = x 2 + sin x; g(x) = x 4 + 2x 2 − 3.

Fungere f(x) er summen af to elementære funktioner, derfor:

f ’(x) = (x 2 + synd x)’ = (x 2)’ + (synd x)’ = 2x+ cos x;

Vi ræsonnerer på samme måde for funktionen g(x). Kun der er allerede tre udtryk (fra et algebra synspunkt):

g ’(x) = (x 4 + 2x 2 − 3)’ = (x 4 + 2x 2 + (−3))’ = (x 4)’ + (2x 2)’ + (−3)’ = 4x 3 + 4x + 0 = 4x · ( x 2 + 1).

Svar:
f ’(x) = 2x+ cos x;
g ’(x) = 4x · ( x 2 + 1).

Afledt af produktet

Matematik er en logisk videnskab, så mange mennesker tror, at hvis den afledede af en sum er lig med summen af afledte, så er den afledte af produktet strejke">lig med produktet af derivater. Men pyt dig! Den afledte af et produkt beregnes ved hjælp af en helt anden formel. Nemlig:

(f · g) ’ = f ’ · g + f · g ’

Formlen er enkel, men den bliver ofte glemt. Og ikke kun skolebørn, men også studerende. Resultatet er forkert løste problemer.

Opgave. Find afledede funktioner: f(x) = x 3 cos x; g(x) = (x 2 + 7x− 7) · e x .

Fungere f(x) er produktet af to elementære funktioner, så alt er enkelt:

f ’(x) = (x 3 cos x)’ = (x 3)’ cos x + x 3 (cos x)’ = 3x 2 cos x + x 3 (-synd x) = x 2 (3cos x − x synd x)

Fungere g(x) den første multiplikator er lidt mere kompliceret, men den generelle ordning ændres ikke. Det er klart, den første faktor af funktionen g(x) er et polynomium, og dets afledte er den afledede af summen. Vi har:

g ’(x) = ((x 2 + 7x− 7) · e x)’ = (x 2 + 7x− 7)’ · e x + (x 2 + 7x− 7) · ( e x)’ = (2x+ 7) · e x + (x 2 + 7x− 7) · e x = e x· (2 x + 7 + x 2 + 7x −7) = (x 2 + 9x) · e x = x(x+ 9) · e x .

Svar:
f ’(x) = x 2 (3cos x − x synd x);
g ’(x) = x(x+ 9) · e x .

Bemærk venligst, at i det sidste trin faktoriseres den afledte. Formelt set skal dette ikke gøres, men de fleste afledte beregnes ikke alene, men for at undersøge funktionen. Det betyder, at yderligere vil den afledede blive lig med nul, dens fortegn vil blive bestemt, og så videre. I et sådant tilfælde er det bedre at få et udtryk faktoriseret.

Hvis der er to funktioner f(x) Og g(x), og g(x) ≠ 0 på det sæt, vi er interesseret i, kan vi definere en ny funktion h(x) = f(x)/g(x). For en sådan funktion kan du også finde den afledede:

Ikke svag, vel? Hvor kom minuset fra? Hvorfor g 2? Og sådan her! Dette er en af de mest komplekse formler - du kan ikke finde ud af det uden en flaske. Derfor er det bedre at studere det med specifikke eksempler.

Opgave. Find afledede funktioner:

Tælleren og nævneren for hver brøk indeholder elementære funktioner, så alt, hvad vi behøver, er formlen for den afledede af kvotienten:

Ifølge traditionen, lad os faktorisere tælleren - dette vil i høj grad forenkle svaret:

En kompleks funktion er ikke nødvendigvis en halv kilometer lang formel. For eksempel er det nok at tage funktionen f(x) = synd x og erstatte variablen x, siger, på x 2 + ln x. Det vil nok gå f(x) = synd ( x 2 + ln x) - dette er en kompleks funktion. Det har også en derivat, men det vil ikke være muligt at finde det ved at bruge reglerne diskuteret ovenfor.

Hvad skal jeg gøre? I sådanne tilfælde hjælper det at erstatte en variabel og formel for den afledede af en kompleks funktion:

f ’(x) = f ’(t) · t', hvis x erstattes af t(x).

Som regel er situationen med at forstå denne formel endnu mere trist end med kvotientens afledte. Derfor er det også bedre at forklare det ved hjælp af specifikke eksempler med en detaljeret beskrivelse af hvert trin.

Opgave. Find afledede funktioner: f(x) = e 2x + 3 ; g(x) = synd ( x 2 + ln x)

Bemærk, at hvis i funktionen f(x) i stedet for udtryk 2 x+ 3 vil være let x, så får vi en elementær funktion f(x) = e x. Derfor laver vi en erstatning: lad 2 x + 3 = t, f(x) = f(t) = e t. Vi leder efter den afledede af en kompleks funktion ved hjælp af formlen:

f ’(x) = f ’(t) · t ’ = (e t)’ · t ’ = e t · t ’

Og nu - opmærksomhed! Vi udfører den omvendte udskiftning: t = 2x+ 3. Vi får:

f ’(x) = e t · t ’ = e 2x+ 3 (2 x + 3)’ = e 2x+ 3 2 = 2 e 2x + 3

Lad os nu se på funktionen g(x). Det er klart, at det skal udskiftes x 2 + ln x = t. Vi har:

g ’(x) = g ’(t) · t’ = (synd t)’ · t’ = cos t · t ’

Omvendt udskiftning: t = x 2 + ln x. Derefter:

g ’(x) = cos ( x 2 + ln x) · ( x 2 + ln x)' = cos ( x 2 + ln x) · (2 x + 1/x).

Det er alt! Som det fremgår af det sidste udtryk, er hele problemet reduceret til at beregne den afledte sum.

Svar:
f ’(x) = 2 · e 2x + 3 ;
g ’(x) = (2x + 1/x) fordi ( x 2 + ln x).

Meget ofte i mine lektioner, i stedet for udtrykket "afledt", bruger jeg ordet "prime". For eksempel er summens streg lig med summen af streger. Er det klarere? Det var da godt.

Beregning af den afledte kommer således ned til at slippe af med de samme slag i henhold til reglerne diskuteret ovenfor. Som et sidste eksempel, lad os vende tilbage til den afledte potens med en rationel eksponent:

(x n)’ = n · x n − 1

De færreste kender det i rollen n kan godt være et brøktal. Roden er f.eks x 0,5. Hvad hvis der er noget fancy under roden? Igen bliver resultatet en kompleks funktion - de giver gerne sådanne konstruktioner i prøver og eksamener.

Opgave. Find den afledede af funktionen:

Lad os først omskrive roden som en potens med en rationel eksponent:

f(x) = (x 2 + 8x − 7) 0,5 .

Nu laver vi en erstatning: lad x 2 + 8x − 7 = t. Vi finder den afledede ved hjælp af formlen:

f ’(x) = f ’(t) · t ’ = (t 0,5)' · t’ = 0,5 · t−0,5 · t ’.

Lad os gøre den omvendte udskiftning: t = x 2 + 8x− 7. Vi har:

f ’(x) = 0,5 · ( x 2 + 8x− 7) −0,5 · ( x 2 + 8x− 7)' = 0,5 · (2 x+ 8) ( x 2 + 8x − 7) −0,5 .

Til sidst tilbage til rødderne:

Siden du kom her, har du sikkert allerede set denne formel i lærebogen

og lav et ansigt som dette:

Ven, bare rolig! Faktisk er alt simpelthen skandaløst. Du vil helt sikkert forstå alt. Bare en anmodning - læs artiklen langsomt, prøv at forstå hvert trin. Jeg skrev så enkelt og tydeligt som muligt, men du skal stadig forstå ideen. Og sørg for at løse opgaverne fra artiklen.

Hvad er en kompleks funktion?

Forestil dig, at du flytter til en anden lejlighed og derfor pakker tingene ned i store kasser. Antag, at du skal samle nogle småting, for eksempel skoleskrivemateriale. Hvis du bare smider dem i en kæmpe kasse, vil de bl.a. For at undgå dette putter du dem først fx i en pose, som du så putter i en stor kasse, hvorefter du forsegler den. Denne "mest komplekse" proces er præsenteret i diagrammet nedenfor:

Det ser ud til, hvad har matematik med det at gøre? Ja, på trods af at en kompleks funktion er dannet på NØJAGTIG SAMME måde! Kun vi "pakker" ikke notesbøger og kuglepenne, men $x$, mens "pakkerne" og "æskerne" er forskellige.

Lad os for eksempel tage x og "pakke" det ind i en funktion:

Som et resultat får vi selvfølgelig $\cos⁡x$. Dette er vores "pose med ting". Lad os nu lægge det i en "kasse" - pak det for eksempel i en kubisk funktion.

Hvad vil der ske i sidste ende? Ja, det er rigtigt, der vil være en "pose ting i en kasse", det vil sige "cosinus af X i terninger."

Det resulterende design er en kompleks funktion. Det adskiller sig fra det simple FLERE "påvirkninger" (pakker) anvendes på et X i træk og det viser sig som om "funktion fra funktion" - "emballage i emballage".

Der er meget få typer af disse "pakker" i skoleforløbet, kun fire:

Lad os nu "pakke" X først i en eksponentiel funktion med grundtallet 7 og derefter i en trigonometrisk funktion. Vi får:

$x → 7^x → tg⁡(7^x)$

Lad os nu "pakke" x to gange i trigonometriske funktioner, først i og derefter i:

$x → sin⁡x → cotg⁡ (sin⁡x)$

Simpelt, ikke?

Skriv nu selv funktionerne, hvor x:
- først "pakkes" den ind i en cosinus og derefter i en eksponentiel funktion med grundtallet $3$;
- først til femte potens og derefter til tangenten;
- først til logaritmen til grundtallet $4$ , derefter til magten $-2$.

Find svarene på denne opgave i slutningen af artiklen.

Kan vi "pakke" X ikke to, men tre gange? Intet problem! Og fire, og fem og femogtyve gange. Her er for eksempel en funktion, hvor x er "pakket" $4$ gange:

$y=5^(\log_2⁡(\sin⁡(x^4))))$

Men sådanne formler findes ikke i skolens praksis (elever er heldigere - deres kan være mere komplicerede☺).

"Udpakning" af en kompleks funktion

Se på den forrige funktion igen. Kan du finde ud af "pakke"-sekvensen? Hvad X blev proppet i først, hvad så, og så videre til det sidste. Det vil sige, hvilken funktion er indlejret inden for hvilken? Tag et stykke papir og skriv ned, hvad du synes. Du kan gøre dette med en kæde med pile som vi skrev ovenfor eller på anden måde.

Nu er det rigtige svar: først blev x "pakket" i $4$'te potens, derefter blev resultatet pakket ind i sinus, det blev igen placeret i logaritmen til grundtallet $2$ , og til sidst blev hele denne konstruktion skubbet ind i power-femterne.

Det vil sige, at du skal afvikle sekvensen I OVERSÆTTET RÆKKE. Og her er et tip til, hvordan du gør det nemmere: se straks på X'et - du skal danse ud fra det. Lad os se på et par eksempler.

For eksempel, her er følgende funktion: $y=tg⁡(\log_2⁡x)$. Vi ser på X - hvad sker der først med det? Taget fra ham. Og så? Tangensen af resultatet tages. Rækkefølgen vil være den samme:

$x → \log_2⁡x → tg⁡(\log_2⁡x)$

Et andet eksempel: $y=\cos⁡((x^3))$. Lad os analysere - først lagde vi X i terninger og tog derefter cosinus af resultatet. Dette betyder, at sekvensen vil være: $x → x^3 → \cos⁡((x^3))$. Vær opmærksom, funktionen ser ud til at ligne den allerførste (hvor den har billeder). Men det er en helt anden funktion: her i terningen er x (det vil sige $\cos⁡((x·x·x)))$, og der i terningen er cosinus $x$ ( det vil sige $\cos⁡ x·\cos⁡x·\cos⁡x$). Denne forskel opstår fra forskellige "paknings"-sekvenser.

Det sidste eksempel (med vigtig information): $y=\sin⁡((2x+5))$. Det er tydeligt, at vi her først lavede aritmetiske operationer med x, derefter tog vi sinus af resultatet: $x → 2x+5 → \sin⁡((2x+5))$. Og det er en vigtig pointe: på trods af at regneoperationer ikke er funktioner i sig selv, fungerer de også her som en måde at "pakke". Lad os dykke lidt dybere ned i denne subtilitet.

Som jeg sagde ovenfor, er x i simple funktioner "pakket" én gang, og i komplekse funktioner - to eller flere. Desuden er enhver kombination af simple funktioner (det vil sige deres sum, forskel, multiplikation eller division) også en simpel funktion. For eksempel er $x^7$ en simpel funktion, og det samme er $ctg x$. Det betyder, at alle deres kombinationer er simple funktioner:

$x^7+ ctg x$ - enkel,
$x^7· barneseng x$ – enkel,
$\frac(x^7)(ctg x)$ – simpelt osv.

Men hvis en funktion mere anvendes på en sådan kombination, bliver det en kompleks funktion, da der vil være to "pakker". Se diagram:

Okay, gå videre nu. Skriv rækkefølgen af "indpakning"-funktioner:
$y=cos(⁡(sin⁡x))$
$y=5^(x^7)$
$y=arctg⁡(11^x)$
$y=log_2⁡(1+x)$
Svarene er igen i slutningen af artiklen.

Interne og eksterne funktioner

Hvorfor skal vi forstå funktionsnesting? Hvad giver det os? Faktum er, at uden en sådan analyse vil vi ikke være i stand til pålideligt at finde derivater af funktionerne diskuteret ovenfor.

Og for at komme videre har vi brug for yderligere to begreber: interne og eksterne funktioner. Dette er en meget enkel ting, desuden har vi faktisk allerede analyseret dem ovenfor: Hvis vi husker vores analogi helt i begyndelsen, så er den interne funktion en "pakke", og den eksterne funktion er en "kasse". De der. det, X først er "indpakket" i, er en intern funktion, og det, som den indre funktion er "indpakket" i, er allerede eksternt. Nå, det er klart hvorfor - hun er udenfor, det betyder ekstern.

I dette eksempel: $y=tg⁡(log_2⁡x)$, er funktionen $\log_2⁡x$ intern, og
- eksternt.

Og i denne: $y=\cos⁡((x^3+2x+1))$, er $x^3+2x+1$ intern, og
- eksternt.

Gennemfør den sidste praksis med at analysere komplekse funktioner, og lad os endelig gå videre til det, vi alle blev startet for - vi vil finde afledte af komplekse funktioner:

Udfyld de tomme felter i tabellen:

Afledt af en kompleks funktion

Bravo til os, vi nåede endelig til "chefen" for dette emne - faktisk afledet af en kompleks funktion, og specifikt til den meget forfærdelige formel fra begyndelsen af artiklen.☺

$(f(g(x)))"=f"(g(x))\cdot g"(x)$

Denne formel lyder således:

Den afledte af en kompleks funktion er lig med produktet af den afledte af den eksterne funktion med hensyn til en konstant intern funktion og den afledte af den indre funktion.

Og se straks på parsingdiagrammet "ord for ord" for at forstå, hvad der er hvad:

Jeg håber, at udtrykkene "afledt" og "produkt" ikke volder nogen vanskeligheder. "Kompleks funktion" - vi har allerede ordnet det. Fangsten er i "afledet af en ekstern funktion med hensyn til en konstant intern funktion." Hvad er det?

Svar: dette er den sædvanlige afledning af en ekstern funktion, hvor kun den eksterne funktion ændres, og den indre forbliver den samme. Stadig ikke klart? Okay, lad os bruge et eksempel.

Lad os have en funktion $y=\sin⁡(x^3)$. Det er klart, at den interne funktion her er $x^3$, og den eksterne
. Lad os nu finde den afledede af det ydre med hensyn til det konstante indre.

Hvis g(x) Og f(u) – differentiable funktioner af deres argumenter, henholdsvis på punkter x Og u= g(x), så er den komplekse funktion også differentierbar på punktet x og findes ved formlen

En typisk fejl ved løsning af afledte problemer er mekanisk overførsel af reglerne for differentiering af simple funktioner til komplekse funktioner. Lad os lære at undgå denne fejl.

Eksempel 2. Find den afledede af en funktion

Forkert løsning: beregn den naturlige logaritme for hvert led i parentes og se efter summen af de afledte:

Korrekt løsning: igen bestemmer vi, hvor "æblet" er, og hvor "hakket kød" er. Her er den naturlige logaritme af udtrykket i parentes et "æble", det vil sige en funktion over det mellemliggende argument u, og udtrykket i parentes er "hakket kød", altså et mellemargument u ved uafhængig variabel x.

Derefter (ved hjælp af formel 14 fra derivattabellen)

I mange virkelige problemer kan udtrykket med en logaritme være noget mere kompliceret, hvorfor der er en lektie

Eksempel 3. Find den afledede af en funktion

Forkert løsning:

Korrekt løsning. Endnu en gang bestemmer vi, hvor "æblet" er, og hvor "farsen" er. Her er cosinus for udtrykket i parentes (formel 7 i tabellen over afledte) et "æble", det er fremstillet i tilstand 1, som kun påvirker det, og udtrykket i parentes (afledet af graden er nummer 3 i tabellen over derivater) er "hakket kød", det er tilberedt under tilstand 2, som kun påvirker det. Og som altid forbinder vi to derivater med produkttegnet. Resultat:

Afledet af en kompleks logaritmisk funktion er en hyppig opgave i test, så vi anbefaler stærkt, at du deltager i lektionen "Afledt af en logaritmisk funktion."

De første eksempler var på komplekse funktioner, hvor mellemargumentet på den uafhængige variabel var en simpel funktion. Men i praktiske opgaver er det ofte nødvendigt at finde den afledede af en kompleks funktion, hvor mellemargumentet enten selv er en kompleks funktion eller indeholder en sådan funktion. Hvad skal man gøre i sådanne tilfælde? Find afledte funktioner af sådanne funktioner ved hjælp af tabeller og differentieringsregler. Når den afledede af mellemargumentet er fundet, erstattes den blot på det rigtige sted i formlen. Nedenfor er to eksempler på, hvordan dette gøres.

Derudover er det nyttigt at vide følgende. Hvis en kompleks funktion kan repræsenteres som en kæde af tre funktioner

så skal dens derivat findes som produktet af derivaterne af hver af disse funktioner:

Mange af dine hjemmeopgaver kræver muligvis, at du åbner dine guider i nye vinduer. Handlinger med kræfter og rødder Og Operationer med brøker .

Eksempel 4. Find den afledede af en funktion

Vi anvender reglen om differentiering af en kompleks funktion uden at glemme, at der i det resulterende produkt af afledte er et mellemliggende argument med hensyn til den uafhængige variabel xændres ikke:

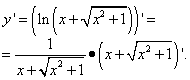
Vi forbereder den anden faktor af produktet og anvender reglen for at differentiere summen:

Det andet led er roden, så

Således fandt vi ud af, at mellemargumentet, som er en sum, indeholder en kompleks funktion som et af begreberne: at hæve til en potens er en kompleks funktion, og hvad der hæves til en potens er et mellemargument med hensyn til den uafhængige variabel x.

Derfor anvender vi igen reglen for at differentiere en kompleks funktion:

Vi omdanner graden af den første faktor til en rod, og når du differentierer den anden faktor, glem ikke, at den afledede af konstanten er lig nul:

Nu kan vi finde den afledede af det mellemliggende argument, der er nødvendig for at beregne den afledede af en kompleks funktion, der kræves i problemformuleringen y:

Eksempel 5. Find den afledede af en funktion

Først bruger vi reglen til at differentiere summen:

Vi fik summen af afledte af to komplekse funktioner. Lad os finde den første:

Her er det en kompleks funktion at hæve sinus til en potens, og selve sinus er et mellemargument for den uafhængige variabel x. Derfor vil vi bruge reglen om differentiering af en kompleks funktion undervejs tage faktoren ud af parentes :

Nu finder vi det andet led af funktionens afledte y:

Her er det en kompleks funktion at hæve cosinus til en potens f, og selve cosinus er et mellemargument i den uafhængige variabel x. Lad os igen bruge reglen til at differentiere en kompleks funktion:

Resultatet er den nødvendige afledte:

Tabel over afledte funktioner af nogle komplekse funktioner

For komplekse funktioner, baseret på reglen om differentiering af en kompleks funktion, antager formlen for den afledede af en simpel funktion en anden form.

1. Afledt af en kompleks potensfunktion, hvor u x
2. Afledt af udtrykkets rod
3. Afledt af en eksponentiel funktion
4. Særligt tilfælde af eksponentiel funktion
5. Afledt af en logaritmisk funktion med en vilkårlig positiv base EN
6. Afledt af en kompleks logaritmisk funktion, hvor u– argumentets differentierbare funktion x
7. Afledt af sinus
8. Afledt af cosinus
9. Afledt af tangent
10. Afledt af cotangens
11. Afledt af arcsine
12. Afledt af arccosine
13. Afledt af arctangens
14. Afledt af lysbue cotangens