المؤسسة التعليمية "الدولة البيلاروسية
الأكاديمية الزراعية"
قسم الرياضيات العليا
القواعد الارشادية
دراسة موضوع "المتغيرات العشوائية" لطلبة كلية المحاسبة للتعليم بالمراسلة (NISPO)
غوركي، 2013
المتغيرات العشوائية
المتغيرات العشوائية المنفصلة والمستمرة
أحد المفاهيم الرئيسية في نظرية الاحتمالات هو المفهوم متغير عشوائي . متغير عشوائي هي الكمية التي، نتيجة للاختبار، تأخذ قيمة واحدة فقط من قيمها المحتملة العديدة، ولا يُعرف مقدمًا أي منها.
هناك متغيرات عشوائية منفصلة ومستمرة . المتغير العشوائي المنفصل (DRV) هو متغير عشوائي يمكن أن يأخذ عددا منتهيا من القيم المنعزلة عن بعضها البعض، أي إذا كان من الممكن إعادة حساب القيم المحتملة لهذه الكمية. المتغير العشوائي المستمر (CNV) هو متغير عشوائي، جميع قيمه الممكنة تملأ فترة معينة من خط الأعداد بالكامل.
يتم الإشارة إلى المتغيرات العشوائية بأحرف كبيرة من الأبجدية اللاتينية X، Y، Z، وما إلى ذلك. تتم الإشارة إلى القيم المحتملة للمتغيرات العشوائية بالأحرف الصغيرة المقابلة.
سِجِلّ 
يعني "احتمال وجود متغير عشوائي Xسوف تأخذ قيمة 5، تساوي 0.28."
مثال 1 . يتم رمي النرد مرة واحدة. في هذه الحالة، قد تظهر الأرقام من 1 إلى 6، مما يدل على عدد النقاط. دعونا نشير إلى المتغير العشوائي X=(عدد النقاط المتراكمة). وهذا المتغير العشوائي نتيجة للاختبار يمكن أن يأخذ قيمة واحدة فقط من ست قيم: 1، 2، 3، 4، 5 أو 6. ولذلك فإن المتغير العشوائي Xهناك DSV.
مثال 2 . عندما يتم رمي حجر، فإنه يقطع مسافة معينة. دعونا نشير إلى المتغير العشوائي X=(مسافة طيران الحجر). يمكن لهذا المتغير العشوائي أن يأخذ أي قيمة، ولكن واحدة فقط، من فترة زمنية معينة. وبالتالي المتغير العشوائي Xهناك NSV.
قانون التوزيع للمتغير العشوائي المنفصل
يتميز المتغير العشوائي المنفصل بالقيم التي يمكن أن يأخذها والاحتمالات التي يتم بها أخذ هذه القيم. يسمى المراسلات بين القيم المحتملة للمتغير العشوائي المنفصل والاحتمالات المقابلة لها قانون توزيع المتغير العشوائي المنفصل .
إذا كانت جميع القيم الممكنة معروفة 
متغير عشوائي Xوالاحتمالات 
ظهور هذه القيم، فإنه يعتقد أن قانون توزيع DSV Xمعروفة ويمكن كتابتها على شكل جدول:
|
|
|
|
|
|
|||
|
|
|
|
|
|
يمكن تصوير قانون توزيع DSV بيانياً إذا تم تصوير النقاط في نظام إحداثيات مستطيل 
,
,
…,
وربطها بقطع مستقيمة. ويسمى الشكل الناتج مضلع التوزيع.
مثال 3 . الحبوب المخصصة للتنظيف تحتوي على 10% من الحشائش. تم اختيار 4 حبات عشوائياً. دعونا نشير إلى المتغير العشوائي X=(عدد الحشائش من بين الأربعة المختارة). بناء قانون التوزيع DSV Xومضلع التوزيع.
حل . وفقا لشروط المثال. ثم:
لنكتب قانون التوزيع لـ DSV X في شكل جدول ونبني مضلع التوزيع:
|
|
توقع وجود متغير عشوائي منفصل
يتم وصف أهم خصائص المتغير العشوائي المنفصل من خلال خصائصه. واحدة من هذه الخصائص هي القيمة المتوقعة متغير عشوائي.
فليكن معروفًا قانون توزيع DSV X:
|
|
|
|
|
|
|||
|
|
|
|
|
|
التوقع الرياضي
دي إس في Xهو مجموع منتجات كل قيمة من هذه الكمية والاحتمال المقابل: 
.
إن التوقع الرياضي للمتغير العشوائي يساوي تقريباً الوسط الحسابي لجميع قيمه. لذلك، في المسائل العملية، غالبًا ما يتم اعتبار القيمة المتوسطة لهذا المتغير العشوائي بمثابة التوقع الرياضي.
مثال 8 . يسجل مطلق النار 4 و8 و9 و10 نقاط باحتمالات 0.1 و0.45 و0.3 و0.15. أوجد التوقع الرياضي لعدد النقاط برصاصة واحدة.
حل . دعونا نشير إلى المتغير العشوائي X=(عدد النقاط المسجلة). ثم . وبالتالي، فإن متوسط عدد النقاط المتوقعة من طلقة واحدة هو 8.2، ومع 10 طلقات - 82.
الخصائص الرئيسية التوقعات الرياضية هي:
.
.
، أين 
,
.
.
، أين Xو يهي متغيرات عشوائية مستقلة.
اختلاف 
مُسَمًّى انحراف
متغير عشوائي Xمن توقعاتها الرياضية. وهذا الاختلاف هو متغير عشوائي وتوقعه الرياضي صفر، أي. 
.
تباين المتغير العشوائي المنفصل
لتوصيف متغير عشوائي، بالإضافة إلى التوقع الرياضي، نستخدم أيضًا تشتت مما يتيح تقدير تشتت (انتشار) قيم المتغير العشوائي حول توقعه الرياضي. عند مقارنة متغيرين عشوائيين متجانسين لهما توقعات رياضية متساوية، فإن القيمة "الأفضل" تعتبر هي القيمة الأقل انتشارا، أي. أقل تشتت.
التباين متغير عشوائي Xيسمى التوقع الرياضي لمربع انحراف المتغير العشوائي عن توقعه الرياضي : .
في المسائل العملية، يتم استخدام صيغة مكافئة لحساب التباين.
الخصائص الرئيسية للتشتت هي:
.
Xيُعطى بواسطة قانون التوزيع الاحتمالي: فإن انحرافه المعياري يساوي ... 0.80
حل:
يتم تعريف الانحراف المعياري للمتغير العشوائي X على أنه 
حيث يمكن حساب تباين متغير عشوائي منفصل باستخدام الصيغة ثم و 
حل:
أ(الكرة المسحوبة عشوائيًا تكون سوداء) نطبق صيغة الاحتمال الإجمالي: هنا هو احتمال نقل كرة بيضاء من الجرة الأولى إلى الجرة الثانية؛ - احتمال نقل كرة سوداء من الجرة الأولى إلى الجرة الثانية؛ - الاحتمال المشروط بأن تكون الكرة المسحوبة سوداء إذا تم نقل كرة بيضاء من الجرة الأولى إلى الثانية؛ - الاحتمال المشروط أن تكون الكرة المسحوبة سوداء إذا تم نقل كرة سوداء من الجرة الأولى إلى الثانية.
يتم إعطاء المتغير العشوائي المنفصل X بموجب قانون التوزيع الاحتمالي: ثم الاحتمال 
متساوي...
حل:
يمكن حساب تباين المتغير العشوائي المنفصل باستخدام الصيغة. ثم
أو . وبحل المعادلة الأخيرة، نحصل على جذرين و
الموضوع: تحديد الاحتمالية
في مجموعة مكونة من 12 جزءًا، هناك 5 أجزاء معيبة. تم اختيار ثلاثة أجزاء عشوائيا. فيكون احتمال عدم وجود أجزاء مناسبة بين الأجزاء المختارة يساوي...
حل:
لحساب الحدث أ (لا يوجد أجزاء مناسبة بين الأجزاء المختارة)، نستخدم الصيغة حيث ن م- عدد النتائج الأولية المؤاتية لحدوث الحدث أ. في حالتنا، فإن العدد الإجمالي للنتائج الأولية المحتملة يساوي عدد الطرق التي يمكن من خلالها استخلاص ثلاث تفاصيل من الـ 12 المتاحة، أي.
والعدد الإجمالي للنتائج الإيجابية يساوي عدد الطرق التي يمكن من خلالها استخراج ثلاثة أجزاء معيبة من خمسة، أي. 
يصدر البنك 44% من إجمالي القروض للكيانات القانونية و56% للأفراد. احتمال عدم قيام الكيان القانوني بسداد القرض في الوقت المحدد هو 0.2؛ وبالنسبة للفرد هذا الاحتمال هو 0.1. إذن فإن احتمال سداد القرض التالي في الوقت المحدد هو ...
| 0,856 |
حل:
لحساب احتمال وقوع حدث ما أ(سيتم سداد القرض الصادر في الوقت المحدد) قم بتطبيق صيغة الاحتمال الإجمالي: . هنا احتمال أن يكون القرض قد تم إصداره لكيان قانوني؛ - احتمال إصدار القرض لفرد؛ - الاحتمال المشروط بأن يتم سداد القرض في الوقت المحدد إذا تم إصداره لكيان قانوني؛ – الاحتمال المشروط بأن يتم سداد القرض في الوقت المحدد إذا تم إصداره لفرد. ثم 
الموضوع: قوانين التوزيع الاحتمالي للمتغيرات العشوائية المنفصلة
للمتغير العشوائي المنفصل X 
| 0,655 |
الموضوع: تحديد الاحتمالية
يتم دحرجة النرد مرتين. إذن فإن احتمال أن مجموع النقاط المدرفلة لا يقل عن تسعة هو ...
حل:
لحساب الحدث (مجموع النقاط التي تم الحصول عليها سيكون تسعة على الأقل)، نستخدم الصيغة حيث العدد الإجمالي للنتائج الأولية المحتملة للاختبار، و م- عدد النتائج الأولية المؤاتية لحدوث الحدث أ. في حالتنا فمن الممكن 
نتائج الاختبار الابتدائي، منها نتائج إيجابية من الشكل، و، و، و، و، و، أي. لذلك، 
الموضوع: قوانين التوزيع الاحتمالي للمتغيرات العشوائية المنفصلة
دالة التوزيع الاحتمالي لها الشكل: 
ثم يمكن أن تكون قيمة المعلمة مساوية لـ ...
| 0,7 | |||
| 0,85 | |||
| 0,6 |
حل:
أ-بريوري 
. ولذلك و. ويتم استيفاء هذه الشروط، على سبيل المثال، بالقيمة
الموضوع: الخصائص العددية للمتغيرات العشوائية
يتم تحديد المتغير العشوائي المستمر بواسطة دالة التوزيع الاحتمالي: 
ثم تباينه...
حل:
يتم توزيع هذا المتغير العشوائي بشكل موحد في الفترة. ثم يمكن حساب التباين باستخدام الصيغة 
. إنه 
الموضوع: الاحتمال الكلي. صيغ بايز
الجرة الأولى تحتوي على 6 كرات سوداء و4 كرات بيضاء. الجرة الثانية تحتوي على 2 كرات بيضاء و 8 كرات سوداء. تم أخذ كرة واحدة من جرة عشوائية، والتي تبين أنها بيضاء اللون. إذن احتمال سحب هذه الكرة من الجرة الأولى هو...
حل:
أ(الكرة المسحوبة عشوائيا تكون بيضاء) حسب معادلة الاحتمال الكلي: . هنا هو احتمال سحب الكرة من الجرة الأولى؛ هو احتمال سحب الكرة من الجرة الثانية؛ - الاحتمال المشروط أن تكون الكرة المسحوبة بيضاء إذا تم سحبها من الجرة الأولى؛ هو الاحتمال المشروط أن تكون الكرة المسحوبة بيضاء إذا سحبت من الجرة الثانية.
ثم 
.
الآن دعونا نحسب الاحتمال الشرطي لسحب هذه الكرة من الجرة الأولى باستخدام صيغة بايز: 
الموضوع: الخصائص العددية للمتغيرات العشوائية
المتغير العشوائي المنفصل Xيتم إعطاؤه بواسطة قانون التوزيع الاحتمالي: 
ثم تباينه...
| 7,56 | |||
| 3,2 | |||
| 3,36 | |||
| 6,0 |
حل:
يمكن حساب تباين المتغير العشوائي المنفصل باستخدام الصيغة
الموضوع: قوانين التوزيع الاحتمالي للمتغيرات العشوائية المنفصلة
حل:
أ-بريوري . ثم
أ) عند ،،
مضرب ، ،
قطة ، ،
د) في ، ،
د) عند ، .
لذلك،
الموضوع: تحديد الاحتمالية
ألقيت نقطة عشوائيا داخل دائرة نصف قطرها 4. إذن احتمال أن تكون النقطة خارج المربع الموجود في الدائرة هو...
الموضوع: تحديد الاحتمالية
في مجموعة مكونة من 12 جزءًا، هناك 5 أجزاء معيبة. تم اختيار ثلاثة أجزاء عشوائيا. إذن فإن احتمال عدم وجود أجزاء معيبة بين الأجزاء المختارة يساوي ...
حل:
لحساب الحدث (لا توجد أجزاء معيبة بين الأجزاء المحددة)، نستخدم الصيغة أين نهو العدد الإجمالي لنتائج الاختبار الابتدائي المحتملة، و م- عدد النتائج الأولية المؤاتية لحدوث الحدث. في حالتنا، فإن العدد الإجمالي للنتائج الأولية المحتملة يساوي عدد الطرق التي يمكن من خلالها استخلاص ثلاثة تفاصيل من الـ 12 المتاحة، أي. والعدد الإجمالي للنتائج الإيجابية يساوي عدد الطرق التي يمكن من خلالها استخراج ثلاثة أجزاء غير معيبة من سبعة، أي. لذلك، 
الموضوع: الاحتمال الكلي. صيغ بايز
| 0,57 | |||
| 0,43 | |||
| 0,55 | |||
| 0,53 |
حل:
لحساب احتمال وقوع حدث ما أ
ثم 
الموضوع: قوانين التوزيع الاحتمالي للمتغيرات العشوائية المنفصلة
يتم تحديد المتغير العشوائي المنفصل بواسطة قانون التوزيع الاحتمالي:
ثم الاحتمال 
متساوي...
حل:
دعونا نستخدم الصيغة 
. ثم 
الموضوع: الاحتمال الكلي. صيغ بايز
| 0,875 | |||
| 0,125 | |||
| 0,105 | |||
| 0,375 |
حل:
دعونا أولا نحسب احتمالية الحدث أ 
.
.
الموضوع: الخصائص العددية للمتغيرات العشوائية
ثم توقعها الرياضي هو ...
حل:
دعونا نستخدم الصيغة . ثم .
الموضوع: تحديد الاحتمالية
حل:
الموضوع: الخصائص العددية للمتغيرات العشوائية
يتم تحديد المتغير العشوائي المستمر بواسطة كثافة التوزيع الاحتمالي 
. ثم التوقع الرياضي أوالانحراف المعياري لهذا المتغير العشوائي يساوي ...
 |
|||
 |
|||
 |
|||
 |
حل:
كثافة التوزيع الاحتمالي للمتغير العشوائي الموزع بشكل طبيعي لها الشكل 
، أين ، . لهذا .
الموضوع: قوانين التوزيع الاحتمالي للمتغيرات العشوائية المنفصلة
يتم تحديد المتغير العشوائي المنفصل بواسطة قانون التوزيع الاحتمالي:
ثم القيم أو بقد تكون متساوية...
 |
|||
 |
|||
 |
|||
 |
حل:
بما أن مجموع احتمالات القيم الممكنة يساوي 1، إذن. الجواب يحقق هذا الشرط: .
الموضوع: تحديد الاحتمالية
يتم وضع دائرة أصغر نصف قطرها 5 في دائرة نصف قطرها 8. ومن ثم فإن احتمال سقوط نقطة عشوائية في الدائرة الأكبر في الدائرة الأصغر هو ...
حل:
لحساب احتمالية الحدث المرغوب، نستخدم الصيغة، حيث مساحة الدائرة الصغرى، ومساحة الدائرة الأكبر. لذلك، .
الموضوع: الاحتمال الكلي. صيغ بايز
الجرة الأولى تحتوي على 3 كرات سوداء و 7 كرات بيضاء. الجرة الثانية تحتوي على 4 كرات بيضاء و5 كرات سوداء. تم نقل كرة واحدة من الجرة الأولى إلى الجرة الثانية. إذن فإن احتمال أن تكون الكرة المسحوبة عشوائيًا من الجرة الثانية بيضاء اللون هو...
| 0,47 | |||
| 0,55 | |||
| 0,35 | |||
| 0,50 |
حل:
لحساب احتمال وقوع حدث ما أ(الكرة المسحوبة عشوائيًا تكون بيضاء) طبق معادلة الاحتمال الإجمالي: . هنا هو احتمال أن تكون الكرة البيضاء قد انتقلت من الجرة الأولى إلى الجرة الثانية؛ - احتمال نقل كرة سوداء من الجرة الأولى إلى الجرة الثانية؛ - الاحتمال المشروط بأن تكون الكرة المسحوبة بيضاء إذا تم نقل كرة بيضاء من الجرة الأولى إلى الجرة الثانية؛ - الاحتمال المشروط أن تكون الكرة المسحوبة بيضاء إذا نقلت كرة سوداء من الجرة الأولى إلى الجرة الثانية.
ثم 
الموضوع: قوانين التوزيع الاحتمالي للمتغيرات العشوائية المنفصلة
للمتغير العشوائي المنفصل:
دالة التوزيع الاحتمالي لها الشكل:
ثم يمكن أن تكون قيمة المعلمة مساوية لـ ...
| 0,7 | |||
| 0,85 | |||
| 0,6 |
المهمة رقم 10 أبلغ عن خطأ
الموضوع: الاحتمال الكلي. صيغ بايز
يصدر البنك 70٪ من جميع القروض للكيانات القانونية و 30٪ للأفراد. احتمال عدم قيام الكيان القانوني بسداد القرض في الوقت المحدد هو 0.15؛ وبالنسبة للفرد هذا الاحتمال هو 0.05. وصلت رسالة تفيد بعدم سداد القرض. إذن فإن احتمال عدم قيام الكيان القانوني بسداد هذا القرض هو ...
| 0,875 | |||
| 0,125 | |||
| 0,105 | |||
| 0,375 |
حل:
دعونا أولا نحسب احتمالية الحدث أ(لن يتم سداد القرض الصادر في الوقت المحدد) حسب معادلة الاحتمال الإجمالي: . هنا احتمال أن يكون القرض قد تم إصداره لكيان قانوني؛ - احتمال إصدار القرض لفرد؛ - الاحتمال المشروط بعدم سداد القرض في الوقت المحدد إذا تم إصداره لكيان قانوني؛ – الاحتمال المشروط بعدم سداد القرض في الوقت المحدد إذا تم إصداره لفرد. ثم .
الآن دعونا نحسب الاحتمال المشروط بأن هذا القرض لم يتم سداده من قبل كيان قانوني، باستخدام صيغة بايز: .
المهمة رقم 11 أبلغ عن خطأ
الموضوع: تحديد الاحتمالية
في مجموعة مكونة من 12 جزءًا، هناك 5 أجزاء معيبة. تم اختيار ثلاثة أجزاء عشوائيا. فيكون احتمال عدم وجود أجزاء مناسبة بين الأجزاء المختارة يساوي...
حل:
لحساب الحدث (لا توجد أجزاء مناسبة بين الأجزاء المحددة)، نستخدم الصيغة أين نهو العدد الإجمالي لنتائج الاختبار الابتدائي المحتملة، و م- عدد النتائج الأولية المؤاتية لحدوث الحدث. في حالتنا، فإن العدد الإجمالي للنتائج الأولية المحتملة يساوي عدد الطرق التي يمكن من خلالها استخلاص ثلاثة تفاصيل من الـ 12 المتاحة، أي. والعدد الإجمالي للنتائج الإيجابية يساوي عدد الطرق التي يمكن من خلالها استخراج ثلاثة أجزاء معيبة من خمسة، أي. لذلك،
المهمة رقم 12 أبلغ عن خطأ
الموضوع: الخصائص العددية للمتغيرات العشوائية
يتم تحديد المتغير العشوائي المستمر بواسطة كثافة التوزيع الاحتمالي: 
ثم تباينه...
حل:
يمكن حساب تباين المتغير العشوائي المستمر باستخدام الصيغة
ثم 
الموضوع: قوانين التوزيع الاحتمالي للمتغيرات العشوائية المنفصلة
يتم تحديد المتغير العشوائي المنفصل بواسطة قانون التوزيع الاحتمالي:
ثم دالة التوزيع الاحتمالي لها الشكل ...
| |
|||
 |
|||
 |
|||
 |
حل:
أ-بريوري . ثم
أ) عند ،،
مضرب ، ،
قطة ، ،
د) في ، ،
د) عند ، .
لذلك، 
الموضوع: الاحتمال الكلي. صيغ بايز
هناك ثلاث جرار تحتوي على 5 كرات بيضاء و5 كرات سوداء، وسبع جرار تحتوي على 6 كرات بيضاء و4 كرات سوداء. يتم سحب كرة واحدة من جرة عشوائية. إذن احتمال أن تكون هذه الكرة بيضاء هو...
| 0,57 | |||
| 0,43 | |||
| 0,55 | |||
| 0,53 |
حل:
لحساب احتمال وقوع حدث ما أ(الكرة المسحوبة عشوائيًا تكون بيضاء) طبق معادلة الاحتمال الإجمالي: . هذا هو احتمال سحب كرة من السلسلة الأولى من الجرار؛ - احتمال سحب الكرة من السلسلة الثانية من الجرار؛ - الاحتمال المشروط بأن تكون الكرة المسحوبة بيضاء إذا تم سحبها من السلسلة الأولى من الجرار؛ - الاحتمال المشروط أن تكون الكرة المسحوبة بيضاء إذا كانت مسحوبة من السلسلة الثانية من الجرار.
ثم .
الموضوع: قوانين التوزيع الاحتمالي للمتغيرات العشوائية المنفصلة
يتم تحديد المتغير العشوائي المنفصل بواسطة قانون التوزيع الاحتمالي:
ثم الاحتمال متساوي...
الموضوع: تحديد الاحتمالية
يتم دحرجة النرد مرتين. إذن احتمال أن يكون مجموع النقاط المرسومة عشرة هو...
التعريف 2.3. يسمى المتغير العشوائي، الذي يشار إليه بـ X، منفصلاً إذا كان يأخذ مجموعة محدودة أو قابلة للعد من القيم، أي. مجموعة - مجموعة محدودة أو معدودة.
دعونا نفكر في أمثلة للمتغيرات العشوائية المنفصلة.
1.
يتم رمي عملتين معدنيتين مرة واحدة. عدد الشعارات في هذه التجربة هو متغير عشوائي X. قيمها المحتملة هي 0،1،2، أي. 
– مجموعة منتهية .
2. يتم تسجيل عدد مكالمات الإسعاف خلال فترة زمنية معينة. قيمة عشوائية X- عدد المكالمات. قيمها المحتملة هي 0، 1، 2، 3، ...، أي. =(0,1,2,3,...) هي مجموعة قابلة للعد.
3. هناك 25 طالبا في المجموعة. في يوم معين، يتم تسجيل عدد الطلاب الذين حضروا إلى الفصل - وهو متغير عشوائي X. قيمها المحتملة: 0، 1، 2، 3، ...،25 أي. =(0، 1، 2، 3، ...، 25).
على الرغم من أن جميع الأشخاص الـ 25 في المثال 3 لا يمكنهم تفويت الفصول الدراسية، إلا أن المتغير العشوائي Xيمكن أن تأخذ هذه القيمة. وهذا يعني أن قيم المتغير العشوائي لها احتمالات مختلفة.
دعونا نفكر في نموذج رياضي لمتغير عشوائي منفصل.
لنقم بإجراء تجربة عشوائية تتوافق مع مساحة محدودة أو معدودة من الأحداث الأولية. دعونا نفكر في تعيين هذا الفضاء على مجموعة الأعداد الحقيقية، أي دعونا نخصص لكل حدث أولي رقمًا حقيقيًا معينًا. مجموعة الأرقام يمكن أن تكون محدودة أو قابلة للعد، أي. 
أو
نظام المجموعات الفرعية، الذي يتضمن أي مجموعة فرعية، بما في ذلك مجموعة من نقطة واحدة، يشكل جبرًا لمجموعة رقمية (- محدودة أو قابلة للعد).
لأن أي حدث أولي يرتبط باحتمالات معينة باي(في حالة كل شيء محدود)، ومن ثم يمكن ربط كل قيمة لمتغير عشوائي باحتمال معين باي، مثل ذلك .
يترك Xهو عدد حقيقي تعسفي. دعونا نشير ص × (خ)احتمال المتغير العشوائي Xأخذت قيمة تساوي X، أي. ف س (س)=ف(س=س). ثم الوظيفة ص × (خ)يمكن أن تأخذ قيمًا موجبة فقط لتلك القيم X، والتي تنتمي إلى مجموعة محدودة أو معدودة 
ولجميع القيم الأخرى احتمالية هذه القيمة ف × (س) = 0.
لذلك، قمنا بتعريف مجموعة القيم -الجبر كنظام لأي مجموعات فرعية ولكل حدث ( س = س) مقارنة الاحتمال لأي، أي. بنيت مساحة الاحتمال.
على سبيل المثال، فضاء الأحداث الأولية لتجربة تتكون من رمي قطعة نقود متناظرة مرتين يتكون من أربعة أحداث أولية: ، حيث
عندما ألقيت العملة مرتين، ظهر ذيلان؛ وعندما ألقيت العملة مرتين، سقط شعاران؛
في أول رمية للعملة، ظهرت علامة التجزئة، وفي الثانية ظهر شعار النبالة؛
في أول رمية للعملة، ظهر شعار النبالة، وفي الثانية ظهرت علامة التجزئة.
دع المتغير العشوائي X- عدد المتسربين من الشبكة. يتم تعريفه على مجموعة قيمه 
. جميع المجموعات الفرعية الممكنة، بما في ذلك المجموعات ذات النقطة الواحدة، تشكل جبرًا، أي. =(Ø، (1)، (2)، (0،1)، (0،2)، (1،2)، (0،1،2)).
احتمال وقوع حدث ( س = س ط}, і = 1,2,3، نحدده على أنه احتمال وقوع حدث هو النموذج الأولي له:
وهكذا، في الأحداث الأولية ( X = الحادي عشر) تعيين وظيفة عددية آر إكس، لذا 
.
التعريف 2.4. قانون توزيع المتغير العشوائي المنفصل هو مجموعة من أزواج الأرقام (x i, п i)، حيث x i هي القيم المحتملة للمتغير العشوائي، و п i هي الاحتمالات التي يأخذ بها هذه القيم، و .
إن أبسط شكل لتحديد قانون توزيع المتغير العشوائي المنفصل هو جدول يسرد القيم المحتملة للمتغير العشوائي والاحتمالات المقابلة:
| … | … | ||||
| … | … |
يسمى هذا الجدول بسلسلة التوزيع. ولإضفاء مظهر أكثر وضوحًا على سلسلة التوزيع، تم تصويرها بيانيًا: على المحور أوهالنقاط × طورسم خطوط عمودية على الطول منها باي. يتم توصيل النقاط الناتجة ويتم الحصول على مضلع، وهو أحد أشكال قانون التوزيع (الشكل 2.1).
وبالتالي، لتحديد متغير عشوائي منفصل، تحتاج إلى تحديد قيمه والاحتمالات المقابلة.
مثال 2.2.يتم تشغيل فتحة النقود بالجهاز في كل مرة يتم فيها إدخال عملة معدنية مع احتمالية ذلك ر. بمجرد تشغيله، لا تنزل العملات المعدنية. يترك X- عدد العملات المعدنية التي يجب إدخالها قبل تشغيل فتحة النقود بالجهاز. بناء سلسلة توزيع لمتغير عشوائي متقطع X.
حل.القيم المحتملة للمتغير العشوائي X: س 1 = 1، س 2 = 2،...، س ك = ك، ...لنجد احتمالات هذه القيم: ص 1– احتمال أن يعمل متلقي الأموال في المرة الأولى التي يتم فيها خفضه، و ص 1 = ص؛ ص 2 –احتمال إجراء محاولتين. للقيام بذلك، من الضروري أن: 1) لا يعمل جهاز استقبال الأموال في المحاولة الأولى؛ 2) في المحاولة الثانية نجح الأمر. احتمال هذا الحدث هو (1 – ص) ص. على نفس المنوال 
وما إلى ذلك وهلم جرا، 
. نطاق التوزيع Xسوف تأخذ النموذج
| 1 | 2 | 3 | … | ل | … | |
| ر | qp | س 2 ص | ف ص -1 ص |
لاحظ أن الاحتمالات ص كشكل تقدمًا هندسيًا مع المقام: 1 – ع = ف, س<1, ولذلك يسمى هذا التوزيع الاحتمالي هندسي.
دعونا نفترض كذلك أنه تم بناء نموذج رياضي 
التجربة الموصوفة بواسطة متغير عشوائي منفصل X، والنظر في حساب احتمالات وقوع الأحداث التعسفية.
دع حدثًا عشوائيًا يحتوي على مجموعة محدودة أو قابلة للعد من القيم × ط: أ= {× 1، × 2،...، × ط، ...) .حدث أيمكن تمثيله على أنه اتحاد لأحداث غير متوافقة بالشكل: . ثم باستخدام بديهية كولموجوروف 3 , نحن نحصل
حيث أننا حددنا أن احتمالات وقوع الأحداث تساوي احتمالات وقوع الأحداث التي هي نماذجها الأولية. وهذا يعني أن احتمال أي حدث 
، ، يمكن حسابها باستخدام الصيغة، حيث يمكن تمثيل هذا الحدث في شكل اتحاد للأحداث، حيث .
ثم وظيفة التوزيع F(س) = Р(–<Х<х) تم العثور عليه بواسطة الصيغة. ويترتب على ذلك أن دالة التوزيع لمتغير عشوائي منفصل Xمتقطعة وتزداد في القفزات، أي أنها دالة خطوة (الشكل 2.2):
إذا كانت المجموعة محدودة، فإن عدد الحدود في الصيغة يكون محدودًا، ولكن إذا كانت قابلة للعد، فإن عدد الحدود يكون قابلاً للعد.
مثال 2.3.يتكون الجهاز الفني من عنصرين يعملان بشكل مستقل عن بعضهما البعض. احتمال فشل العنصر الأول خلال الزمن T هو 0.2، واحتمال فشل العنصر الثاني هو 0.1. قيمة عشوائية X– عدد العناصر الفاشلة خلال الزمن T. ابحث عن دالة التوزيع للمتغير العشوائي وارسم الرسم البياني الخاص بها.
حل.يتم تحديد فضاء الأحداث الأولية لتجربة تتكون من دراسة ثبات عنصرين من عناصر جهاز تقني من خلال أربعة أحداث أولية , , : - كلا العنصرين عاملين؛ - العنصر الأول يعمل، والثاني معيب؛ - العنصر الأول معيب، والثاني يعمل؛ - كلا العنصرين معيبان. يمكن التعبير عن كل حدث من الأحداث الأولية من خلال الأحداث الأولية للمساحات 
و 
حيث - العنصر الأول جاهز للعمل؛ - فشل العنصر الأول؛ - العنصر الثاني عملي؛ - العنصر الثاني فشل. ثم، وبما أن عناصر الجهاز الفني تعمل بشكل مستقل عن بعضها البعض، إذن
8. ما هو احتمال أن تنتمي قيم المتغير العشوائي المنفصل إلى الفترة؟
منفصلة يسمى متغيرًا عشوائيًا يمكن أن يأخذ قيمًا منفصلة ومعزولة باحتمالات معينة.
مثال 1.عدد مرات ظهور شعار النبالة في ثلاث رميات للعملة المعدنية. القيم المحتملة: 0، 1، 2، 3، احتمالاتها متساوية على التوالي:
ف(0) = ; ص(1) = ; ص(2) = ; ص(3) = .
مثال 2.عدد العناصر الفاشلة في جهاز مكون من خمسة عناصر. القيم المحتملة: 0، 1، 2، 3، 4، 5؛ تعتمد احتمالاتها على موثوقية كل عنصر.
المتغير العشوائي المنفصل Xيمكن الحصول عليها من خلال سلسلة التوزيع أو دالة التوزيع (قانون التوزيع المتكامل).
بالقرب من التوزيع هي مجموعة كل القيم الممكنة Xأناوالاحتمالات المقابلة لها رط = ص(س = سأنا), يمكن تحديده كجدول:
| × ط | س ن |
|||
| باي | ص ن |
وفي نفس الوقت الاحتمالات رأناتلبية الشرط
رأنا= 1 لأن 
أين هو عدد القيم الممكنة نقد تكون محدودة أو لا نهائية.
تمثيل رسومي لسلسلة التوزيع يسمى مضلع التوزيع . ولبنائه القيم الممكنة للمتغير العشوائي ( Xأنا) يتم رسمها على طول المحور السيني، والاحتمالات رأنا- على طول المحور الإحداثي؛ نقاط أأنابالإحداثيات ( Xأنا، صأنا) متصلة بواسطة خطوط متقطعة.
وظيفة التوزيع متغير عشوائي Xتسمى وظيفة F(X), الذي قيمته عند هذه النقطة Xيساوي احتمال المتغير العشوائي Xسيكون أقل من هذه القيمة X، إنه
و(س) = ف(س< х).
وظيفة F(X) ل المتغير العشوائي المنفصلتحسب بواسطة الصيغة
F(×) = رأنا , (1.10.1)
حيث يتم الجمع على جميع القيم أنا، لأي منهم Xأنا< х.
مثال 3.من مجموعة تحتوي على 100 منتج، منها 10 منتجات معيبة، يتم اختيار خمسة منتجات بشكل عشوائي للتحقق من جودتها. بناء سلسلة من التوزيعات لرقم عشوائي Xالمنتجات المعيبة الواردة في العينة.
حل. نظرًا لأن عدد المنتجات المعيبة في العينة يمكن أن يكون أي عدد صحيح يتراوح من 0 إلى 5، فإن القيم المحتملة Xأنامتغير عشوائي Xمتساوون:
× 1 = 0، × 2 = 1، × 3 = 2، × 4 = 3، × 5 = 4، × 6 = 5.
احتمالا ر(س = ك) التي تحتويها العينة بالضبط ك(ك = 0، 1، 2، 3، 4، 5) المنتجات المعيبة، يساوي
ف (س = ك) = .
نتيجة للحسابات باستخدام هذه الصيغة بدقة 0.001 نحصل على:
ر 1 = ص(س = 0) @ 0,583;ر 2 = ص(س = 1) @ 0,340;ر 3 = ص(س = 2) @ 0,070;
ر 4 = ص(س = 3) @ 0,007;ر 5 = ص(X= 4) @ 0;ر 6 = ص(س = 5) @ 0.
استخدام المساواة للتحقق رك=1، نتأكد من إجراء الحسابات والتقريب بشكل صحيح (انظر الجدول).
| × ط | ||||||
| باي |
مثال 4.نظرا لسلسلة التوزيع لمتغير عشوائي X :
| × ط | |||||
| باي |
أوجد دالة التوزيع الاحتمالي F(X) لهذا المتغير العشوائي وقم بإنشائه.
حل. لو X 10 جنيهات إسترلينية إذن F(X)= ص(X<X) = 0;
إذا 10<X 20 جنيهًا إسترلينيًا إذن F(X)= ص(X<X) = 0,2 ;
إذا 20<X 30 جنيهًا إسترلينيًا إذن F(X)= ص(X<X) = 0,2 + 0,3 = 0,5 ;
إذا 30<X 40 جنيهًا إسترلينيًا إذن F(X)= ص(X<X) = 0,2 + 0,3 + 0,35 = 0,85 ;
إذا 40<X 50 جنيهًا إسترلينيًا إذن F(X)= ص(X<X) = 0,2 + 0,3 + 0,35 + 0,1=0,95 ;
لو X> 50 إذن F(X)= ص(X<X) = 0,2 + 0,3 + 0,35 + 0,1 + 0,05 = 1.
في تطبيقات نظرية الاحتمالات، تعتبر الخصائص الكمية للتجربة ذات أهمية أساسية. الكمية التي يمكن تحديدها كمياً والتي يمكن أن تأخذ، نتيجة للتجربة، قيماً مختلفة حسب الحالة تسمى متغير عشوائي.
أمثلة على المتغيرات العشوائية:
1. عدد المرات التي يظهر فيها عدد زوجي من النقاط في عشر رميات نرد.
2. عدد الضربات على الهدف من قبل مطلق النار الذي يطلق سلسلة من الطلقات.
3. عدد شظايا القذيفة المنفجرة.
في كل من الأمثلة المقدمة، يمكن للمتغير العشوائي أن يأخذ فقط قيمًا معزولة، أي القيم التي يمكن ترقيمها باستخدام سلسلة طبيعية من الأرقام.
يسمى هذا المتغير العشوائي الذي تكون قيمه المحتملة أرقامًا فردية معزولة، والتي يأخذها هذا المتغير باحتمالات معينة، منفصلة.
يمكن أن يكون عدد القيم الممكنة للمتغير العشوائي المنفصل محدودًا أو لا نهائيًا (قابل للعد).
قانون التوزيعالمتغير العشوائي المنفصل عبارة عن قائمة بقيمه المحتملة والاحتمالات المقابلة لها. يمكن تحديد قانون توزيع المتغير العشوائي المنفصل على شكل جدول (سلسلة التوزيع الاحتمالي)، تحليلياً وبيانياً (مضلع التوزيع الاحتمالي).
عند إجراء التجربة، يصبح من الضروري تقييم القيمة قيد الدراسة "في المتوسط". يتم لعب دور القيمة المتوسطة للمتغير العشوائي بواسطة خاصية عددية تسمى توقع رياضي,الذي تحدده الصيغة
أين س 1 ، س 2 ,.. , س ن- قيم متغيرة عشوائية X، أ ص 1 ,ص 2 , ... , ص ن- احتمالات هذه القيم (لاحظ ذلك ص 1 + ص 2 +…+ ص ن = 1).
مثال. يتم إطلاق النار على الهدف (الشكل 11).
الضربة في I تعطي ثلاث نقاط، في II – نقطتان، في III – نقطة واحدة. عدد النقاط التي تم تسجيلها في طلقة واحدة من قبل أحد الرماة له قانون توزيع بالشكل
لمقارنة مهارة الرماة، يكفي مقارنة متوسط قيم النقاط المسجلة، أي. التوقعات الرياضية م(X) و م(ي):
م(X) = 1 0,4 + 2 0,2 + 3 0,4 = 2,0,
م(ي) = 1 0,2 + 2 0,5 + 3 0,3 = 2,1.
يعطي مطلق النار الثاني في المتوسط عددا أعلى قليلا من النقاط، أي. سيعطي نتائج أفضل عند إطلاقه بشكل متكرر.
ولنلاحظ خصائص التوقع الرياضي:
1. التوقع الرياضي لقيمة ثابتة يساوي الثابت نفسه:
م(ج) =ج.
2. التوقع الرياضي لمجموع المتغيرات العشوائية يساوي مجموع التوقعات الرياضية للمصطلحات:
م =(X 1 + X 2 +…+ X ن)= م(X 1)+ م(X 2)+…+ م(X ن).
3. التوقع الرياضي لمنتج المتغيرات العشوائية المستقلة يساوي منتج التوقعات الرياضية للعوامل
م(X 1 X 2 … X ن) = م(X 1)م(X 2)… م(X ن).
4. النفي الرياضي للتوزيع ذي الحدين يساوي حاصل ضرب عدد المحاولات واحتمال وقوع حدث في تجربة واحدة (المهمة 4.6).
م(X) = العلاقات العامة.
لتقييم مدى انحراف المتغير العشوائي "في المتوسط" عن توقعاته الرياضية، أي. من أجل توصيف انتشار قيم المتغير العشوائي في نظرية الاحتمالات، يتم استخدام مفهوم التشتت.
التباينمتغير عشوائي Xيسمى التوقع الرياضي للانحراف التربيعي:
د(X) = م[(X - م(X)) 2 ].
التشتت هو خاصية عددية لتشتت متغير عشوائي. يتضح من التعريف أنه كلما كان تشتت المتغير العشوائي أصغر، كلما اقتربت قيمه المحتملة حول التوقع الرياضي، أي كلما كانت قيم المتغير العشوائي تتميز بتوقعها الرياضي بشكل أفضل .
ويترتب على التعريف أنه يمكن حساب التباين باستخدام الصيغة
.
من الملائم حساب التباين باستخدام صيغة أخرى:
د(X) = م(X 2) - (م(X)) 2 .
يتميز التشتت بالخصائص التالية:
1. تباين الثابت هو صفر:
د(ج) = 0.
2. يمكن إخراج العامل الثابت من إشارة التشتت بتربيعها:
د(تجربة العملاء) = ج 2 د(X).
3. إن تباين مجموع المتغيرات العشوائية المستقلة يساوي مجموع تباين المصطلحات:
د(X 1 + X 2 + X 3 +…+ X ن)= د(X 1)+ د(X 2)+…+ د(X ن)
4. إن تباين التوزيع ذي الحدين يساوي حاصل ضرب عدد المحاولات واحتمال وقوع أو عدم وقوع حدث في تجربة واحدة:
د(X) = نبق.
في نظرية الاحتمالات، غالبًا ما يتم استخدام خاصية عددية تساوي الجذر التربيعي لتباين متغير عشوائي. تسمى هذه الخاصية العددية متوسط انحراف المربع ويشار إليها بالرمز
.
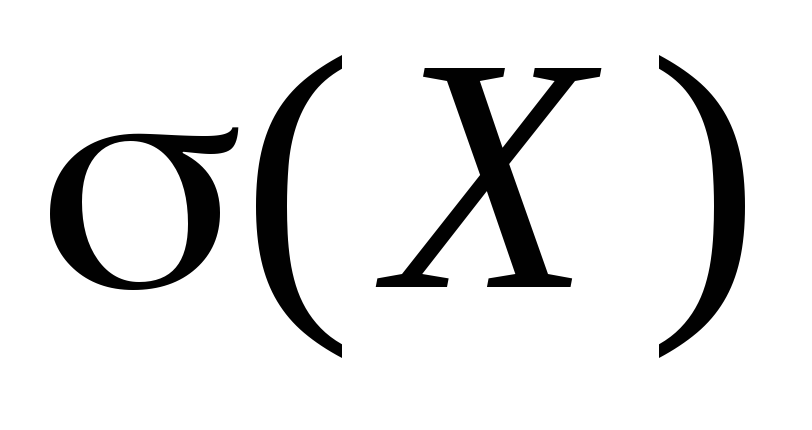وهو يصف الحجم التقريبي لانحراف المتغير العشوائي عن قيمته المتوسطة وله نفس البعد للمتغير العشوائي.
4.1. يطلق مطلق النار ثلاث طلقات على الهدف. احتمال إصابة الهدف بكل طلقة هو 0.3.
إنشاء سلسلة توزيع لعدد الزيارات.
حل. عدد الزيارات هو متغير عشوائي منفصل X. كل قيمة س ن متغير عشوائي Xيتوافق مع احتمال معين ص ن .
يمكن تحديد قانون توزيع المتغير العشوائي المنفصل في هذه الحالة بالقرب من التوزيع.
في هذه المشكلة Xيأخذ القيم 0، 1، 2، 3. حسب صيغة برنولي
,
لنجد احتمالات القيم المحتملة للمتغير العشوائي:
ر 3 (0) = (0,7) 3 = 0,343,
ر 3 (1)
=
0,3(0,7) 2
= 0,441,
ر 3 (2)
=
(0,3) 2 0,7
= 0,189,
ر 3 (3) = (0,3) 3 = 0,027.
من خلال ترتيب قيم المتغير العشوائي Xوبترتيب متزايد نحصل على سلسلة التوزيع:
|
X ن | ||||
لاحظ أن المبلغ
يعني احتمال المتغير العشوائي Xسيأخذ قيمة واحدة على الأقل من بين القيم المحتملة، وبالتالي فإن هذا الحدث موثوق
.
4.2 هناك أربع كرات في الجرة ذات أرقام من 1 إلى 4. يتم إخراج كرتين. قيمة عشوائية X- مجموع أرقام الكرة. بناء سلسلة توزيع لمتغير عشوائي X.
حل.قيم متغيرة عشوائية Xهي 3، 4، 5، 6، 7. دعونا نجد الاحتمالات المقابلة. قيمة المتغير العشوائي 3 Xيمكن قبوله في الحالة الوحيدة عندما يكون لإحدى الكرات المختارة الرقم 1 والأخرى 2. عدد نتائج الاختبار المحتملة يساوي عدد مجموعات من أربعة (عدد أزواج الكرات المحتملة) من اثنين.
باستخدام صيغة الاحتمال الكلاسيكية نحصل عليها
على نفس المنوال،
ر(X= 4) =ر(X= 6) =ر(X= 7) = 1/6.
يمكن أن يظهر مجموع 5 في حالتين: 1 + 4 و 2 + 3، لذلك
.
Xلديه النموذج:
ابحث عن دالة التوزيع F(س) متغير عشوائي Xورسمها. احسب ل Xتوقعاتها الرياضية والتباين.
حل. يمكن تحديد قانون توزيع المتغير العشوائي بواسطة دالة التوزيع
F(س) = ف(X س).
وظيفة التوزيع F(س) هي دالة غير متناقصة ومستمرة من اليسار محددة على خط الأعداد بأكمله، بينما
F (- )= 0,F (+ )= 1.
بالنسبة للمتغير العشوائي المنفصل، يتم التعبير عن هذه الوظيفة بالصيغة
.
ولذلك في هذه الحالة
الرسم البياني لوظيفة التوزيع F(س) هو خط متدرج (الشكل 12)
|
F(س) | ||||||
القيمة المتوقعةم(X) هو المتوسط الحسابي المرجح للقيم X 1 ، اكس 2 ،……X نمتغير عشوائي Xمع المقاييس ρ 1, ρ 2, …… , ρ ن ويسمى القيمة المتوسطة للمتغير العشوائي X. وفقا للصيغة
م(X)= س 1 ρ 1 + س 2 ρ 2 +……+ س ن ρ ن
م(X) = 3·0.14+5·0.2+7·0.49+11·0.17 = 6.72.
تشتتيميز درجة تشتت قيم المتغير العشوائي من قيمته المتوسطة ويشار إليه د(X):
د(X)= م[(جلالة الملك(X)) 2 ]= م(X 2) –[م(X)] 2 .
بالنسبة للمتغير العشوائي المنفصل، فإن التباين له الشكل
أو يمكن حسابها باستخدام الصيغة
باستبدال البيانات العددية للمشكلة في الصيغة، نحصل على:
م(X 2) = 3 2 ∙ 0,14+5 2 ∙ 0,2+7 2 ∙ 0,49+11 2 ∙ 0,17 = 50,84
د(X) = 50,84-6,72 2 = 5,6816.
4.4. يتم رمي حجري نرد مرتين في نفس الوقت. اكتب قانون ذي الحدين لتوزيع المتغير العشوائي المنفصل X- عدد مرات ظهور العدد الإجمالي الزوجي للنقاط على حجري النرد.
حل. دعونا نقدم حدثا عشوائيا
أ= (حجري نرد برمية واحدة يؤديان إلى إجمالي عدد زوجي من النقاط).
باستخدام التعريف الكلاسيكي للاحتمال نجد
ر(أ)=
,
أين ن - تم العثور على عدد نتائج الاختبار المحتملة وفقًا للقاعدة
عمليه الضرب:
ن = 6∙6 =36,
م - عدد الأشخاص الذين يؤيدون الحدث أالنتائج - متساوية
م= 3∙6=18.
وبالتالي فإن احتمال النجاح في تجربة واحدة هو
ρ = ص(أ)= 1/2.
تم حل المشكلة باستخدام نظام اختبار برنولي. أحد التحديات هنا هو رمي حجري نرد مرة واحدة. عدد هذه الاختبارات ن = 2. متغير عشوائي Xيأخذ القيم 0، 1، 2 مع الاحتمالات
ر 2 (0)
=
,ر 2 (1)
=
∙
,ر 2 (2)
=
التوزيع ذو الحدين المطلوب لمتغير عشوائي Xيمكن تمثيلها كسلسلة توزيع:
|
X ن | |||
|
ρ ن |
4.5 . في مجموعة من ستة أجزاء هناك أربعة أجزاء قياسية. تم اختيار ثلاثة أجزاء عشوائيا. إنشاء توزيع احتمالي لمتغير عشوائي متقطع X– عدد الأجزاء القياسية بين تلك المختارة وإيجاد توقعها الرياضي.
حل.قيم متغيرة عشوائية Xهي الأرقام 0،1،2،3. انه واضح ر(X=0)=0، نظرًا لوجود جزأين غير قياسيين فقط.
ر(X=1) =
=1/5,
ر(س= 2) =
= 3/5,
ر(X=3) =
= 1/5.
قانون التوزيع للمتغير العشوائي Xلنعرضها على شكل سلسلة توزيع:
|
X ن | ||||
|
ρ ن |
القيمة المتوقعة
م(X)=1 ∙ 1/5+2 ∙ 3/5+3 ∙ 1/5=2.
4.6 . اثبات أن التوقع الرياضي لمتغير عشوائي متقطع X- عدد مرات حدوث الحدث أالخامس نتجارب مستقلة، في كل منها يكون احتمال وقوع حدث مساويًا لـ ρ - يساوي حاصل ضرب عدد المحاولات في احتمال وقوع حدث في تجربة واحدة، أي إثبات أن التوقع الرياضي للتوزيع ذي الحدين
م(X) =ن . ρ ,
والتشتت
د(X) =n.p. .
حل.قيمة عشوائية Xيمكن أن تأخذ القيم 0، 1، 2...، ن. احتمالا ر(X= k) تم العثور عليه باستخدام صيغة برنولي:
ر(X=ك)= ر ن(ك)= 
ρ
ل
(1-ρ
) ن-ل
سلسلة توزيع متغير عشوائي Xلديه النموذج:
|
X ن | |||||
|
ρ ن |
س ن |
|
|
|
ρq ن- 1
ρq ن- 2
ρ
نأين س= 1- ρ .
بالنسبة للتوقع الرياضي لدينا التعبير:
م(X)=
ρq ن -
1
+2
ρ
2
س ن -
2
+…+.ن
ρ
ن
في حالة اختبار واحد، أي مع ن = 1 للمتغير العشوائي X 1- عدد مرات حدوث الحدث أ- سلسلة التوزيع لها الشكل :
|
X ن | ||
|
ρ ن |
م(X 1)= 0∙س + 1 ∙ ص = ص
د(X 1) = ص – ص 2 = ص(1- ص) = pq.
لو Xك – عدد مرات حدوث الحدث أفي أي اختبار، ثم ر(X ل)= ρ و
س = س 1 +X 2 +….+X ن .
من هنا نحصل
م(X)= م(X 1 )+م(X 2)+ … +م(X ن)= ن,
د(X)=د(X 1)+د(X 2)+ ... +د(X ن)=npq.
4.7. يقوم قسم مراقبة الجودة بفحص المنتجات للتأكد من مطابقتها للمعايير. احتمال أن يكون المنتج قياسيًا هو 0.9. تحتوي كل دفعة على 5 منتجات. أوجد التوقع الرياضي لمتغير عشوائي متقطع X- عدد الدفعات التي ستحتوي كل منها على 4 منتجات قياسية - إذا كانت 50 دفعة خاضعة للفحص.
حل. احتمال وجود 4 منتجات قياسية في كل دفعة تم اختيارها عشوائيًا هو احتمال ثابت؛ دعونا نشير إلى ذلك بواسطة ρ ثم التوقع الرياضي للمتغير العشوائي Xيساوي م(X)= 50∙ρ.
دعونا نجد الاحتمال ρ حسب صيغة برنولي:
ρ=P 5 (4)=
= 0,94∙0,1=0,32.
م(X)= 50∙0,32=16.
4.8 . يتم رمي ثلاثة النرد. أوجد التوقع الرياضي لمجموع النقاط المسقطة.
حل.يمكنك العثور على توزيع متغير عشوائي X- مجموع النقاط المسقطة ومن ثم توقعها الرياضي. ومع ذلك، فإن هذا المسار مرهق للغاية. من الأسهل استخدام تقنية أخرى تمثل متغيرًا عشوائيًا X، والتي يجب حساب التوقع الرياضي لها، في شكل مجموع عدة متغيرات عشوائية أبسط، والتي يكون حساب التوقع الرياضي لها أسهل. إذا كان المتغير العشوائي X أناهو عدد النقاط المتداولة أنا– العظام ( أنا= 1، 2، 3)، ثم مجموع النقاط Xسيتم التعبير عنها في النموذج
س = س 1 + X 2 + X 3 .
ولحساب التوقع الرياضي للمتغير العشوائي الأصلي، كل ما تبقى هو استخدام خاصية التوقع الرياضي
م(X 1 + X 2 + X 3 )= م(X 1 )+ م(X 2)+ م(X 3 ).
من الواضح أن
ر(X أنا = ك)= 1/6، ل= 1, 2, 3, 4, 5, 6, أنا= 1, 2, 3.
وبالتالي فإن التوقع الرياضي للمتغير العشوائي X أنايشبه
م(X أنا) = 1/6∙1 + 1/6∙2 +1/6∙3 + 1/6∙4 + 1/6∙5 + 1/6∙6 = 7/2,
م(X) = 3∙7/2 = 10,5.
4.9. حدد التوقع الرياضي لعدد الأجهزة التي فشلت أثناء الاختبار إذا:
أ) احتمال الفشل لجميع الأجهزة هو نفسه ر، وعدد الأجهزة قيد الاختبار يساوي ن;
ب) احتمال الفشل ل أنا – الجهاز يساوي ص أنا , أنا= 1, 2, … , ن.
حل.دع المتغير العشوائي Xهو عدد الأجهزة الفاشلة، إذن
س = س 1 + X 2 +…+X ن ,
X أنا
=
انه واضح
ر(X أنا = 1)= ر أنا , ر(X أنا = 0)= 1– ر أنا ,أنا= 1, 2, … ,ن.
م(X أنا)= 1∙ر أنا + 0∙(1-ر أنا)= ف أنا ,
م(X)= م(X 1)+م(X 2)+…+م(X ن)= ف 1 +ص 2 + … + ص ن .
في الحالة "أ"، يكون احتمال فشل الجهاز هو نفسه
ر أنا =p,أنا= 1, 2, … ,ن.
م(X)= n.p..
ويمكن الحصول على هذه الإجابة فوراً إذا لاحظنا أن المتغير العشوائي Xلديه توزيع ذو الحدين مع المعلمات ( ن, ص).
4.10. يتم رمي حجري النرد مرتين في وقت واحد. اكتب قانون ذي الحدين لتوزيع المتغير العشوائي المنفصل X -عدد لفات عدد زوجي من النقاط على حجري نرد.
حل. يترك
أ=(رمي رقم زوجي في حجر النرد الأول)،
ب =(رمي رقم زوجي على النرد الثاني).
يتم التعبير عن الحصول على رقم زوجي على كلا النرد في رمية واحدة بواسطة المنتج أ.ب.ثم
ر
(أ.ب)
= ر(أ)∙ر(في)
=
.
نتيجة الرمية الثانية لنردين لا تعتمد على الأولى، لذلك تنطبق صيغة برنولي متى
ن = 2,ع = 1/4, س = 1- ع = 3/4.
قيمة عشوائية Xيمكن أن تأخذ القيم 0، 1، 2 , يمكن العثور على احتمالها باستخدام صيغة برنولي:
ر(س= 0)= ص 2 (0) = س 2 = 9/16,
ر(س= 1)= ص 2
(1)= ج 
,ر∙س
=
6/16,
ر(س= 2)= ص 2
(2)= ج 
,
ر 2
=
1/16.
سلسلة توزيع متغير عشوائي العاشر:
4.11. يتكون الجهاز من عدد كبير من العناصر التي تعمل بشكل مستقل مع نفس احتمالية فشل كل عنصر مع مرور الوقت ر. ابحث عن متوسط عدد حالات الرفض بمرور الوقت رالعناصر، إذا كان احتمال فشل عنصر واحد على الأقل خلال هذا الوقت هو 0.98.
حل. عدد الأشخاص الذين رفضوا مع مرور الوقت رالعناصر - متغير عشوائي Xوالتي يتم توزيعها حسب قانون بواسون، حيث أن عدد العناصر كبير، فإن العناصر تعمل بشكل مستقل واحتمال فشل كل عنصر صغير. متوسط عدد مرات حدوث حدث ما نالاختبارات تساوي
م(X) = n.p..
منذ احتمال الفشل لعناصر من نيتم التعبير عنها بواسطة الصيغة
ر ن
(ل)
,
حيث = n.p.، ثم احتمال عدم فشل أي عنصر خلال الوقت ر وصلنا إلى ك = 0:
ر ن (0)= ه - .
ولذلك فإن احتمال وقوع الحدث المعاكس يقع في الزمن ر فشل عنصر واحد على الأقل – يساوي 1 - ه - . ووفقا لشروط المشكلة، فإن هذا الاحتمال هو 0.98. من مكافئ.
1 - ه - = 0,98,
ه - = 1 – 0,98 = 0,02,
من هنا = -ln 0,02 4.
لذلك، في الوقت المناسب رتشغيل الجهاز، في المتوسط، سوف تفشل 4 عناصر.
4.12 . يتم رمي النرد حتى يظهر الرقم "اثنين". أوجد متوسط عدد الرميات.
حل. دعونا نقدم متغير عشوائي X– عدد الاختبارات التي يجب إجراؤها حتى حدوث الحدث الذي يهمنا. احتمال ذلك X= 1 يساوي احتمال ظهور الرقم "اثنين" خلال رمية واحدة للنرد، أي.
ر(س= 1) = 1/6.
حدث X= 2 يعني أنه في الاختبار الأول لم يظهر الرقم "2"، ولكنه ظهر في الاختبار الثاني. احتمالية وقوع الحدث X= 2 تم العثور عليه من خلال قاعدة ضرب احتمالات الأحداث المستقلة:
ر(س= 2) = (5/6)∙(1/6)
على نفس المنوال،
ر(س= 3) = (5/6) 2 ∙1/6, ر(س= 4) = (5/6) 2 ∙1/6
إلخ. نحصل على سلسلة من التوزيعات الاحتمالية:
|
(5/6) ل ∙1/6 |
متوسط عدد الرميات (التجارب) هو التوقع الرياضي
م(X) = 1∙1/6 + 2∙5/6∙1/6 + 3∙(5/6) 2 ∙1/6 + … + ل (5/6) ل -1 ∙1/6 + … =
1/6∙(1+2∙5/6 +3∙(5/6) 2 + … + ل (5/6) ل -1 + …)
لنجد مجموع المتسلسلة:
لز
ل -1
= (
ز ل)
ز
.
لذلك،
م(X) = (1/6) (1/ (1 – 5/6) 2 = 6.
وبالتالي، عليك أن تقوم برمي النرد بمعدل 6 رميات حتى يظهر الرقم "اثنين".
4.13. يتم إجراء اختبارات مستقلة بنفس احتمالية وقوع الحدث أفي كل اختبار. العثور على احتمال وقوع حدث أإذا كان التباين في عدد تكرارات حدث ما في ثلاث تجارب مستقلة هو 0.63 .
حل.عدد تكرارات الحدث في ثلاث تجارب هو متغير عشوائي X، موزعة وفقا لقانون ذات الحدين. إن تباين عدد تكرارات حدث ما في التجارب المستقلة (مع نفس احتمال وقوع الحدث في كل تجربة) يساوي حاصل ضرب عدد التجارب في احتمالات وقوع الحدث وعدم وقوعه (مشكلة 4.6)
د(X) = npq.
بالشرط ن = 3, د(X) = 0.63، حتى تتمكن من ذلك رتجد من المعادلة
0,63 = 3∙ر(1-ر),
الذي له حلان ر 1 = 0.7 و ر 2 = 0,3.